2. 浙江大学 信息与电子工程学院, 浙江 杭州 310027;
3. 浙江工业大学 计算机科学与技术学院, 浙江 杭州 310023;
4. Electrical Computer Engineering, University of California, Santa Barbara, Santa Barbara 93106, USA
2. College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou 310027, China;
3. College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China;
4. Electrical Computer Engineering, University of California, Santa Barbara, Santa Barbara 93106, USA
近年来, 越来越多的处理核心被集成到单一芯片中, 以满足不断增长的计算需求.片上网络(network-on-chip, NoC)是解决多核互连问题的有效手段之一[1-3].随着核心数量的不断增长, 芯片面积不断增大, 器件数量不断上升, 片上网络的缺陷率随之上升, 进而降低了整个系统的良率[4-5].在过去, 良率是评估芯片是否可以正常工作的唯一指标, 冗余技术是提升良率的通用手段[6-10].
片上网络的良率分析与一般ASIC芯片不同.片上网络本身是一个具有冗余特性的系统, 在分析片上网络良率时, 当出现因生产缺陷导致的不可工作核心(称为错误核心)时, 且有足够数量的冗余核心前提下, 可以用这些冗余核心替换错误核心, 从而保证系统处于物理连通状态:这种物理连通的片上网络实例被认为是可工作的[8-10].
错误核心的替换过程会导致其他问题, 可能使得片上网络无法工作.替换过程使得网络拓扑变得不规则, 导致了额外的通信开销.若通信开销过大, 则计算性能会受到影响;若计算性能下降较严重, 则无法满足需求, 这样的片上网络认为是不可工作的.另一方面, 替换过程对网络拓扑的改变, 甚至可能使得某些网络节点之间无法通信, 即节点在物理上是连通的, 但在逻辑上是不连通:这样的片上网络是不可工作的.片上网络良率分析仅能覆盖“物理不连通”的情形, 但无法分析“物理连通, 但逻辑不连通”的情形.
笔者根据这一发现, 提出“可工作性”这一概念, 并进一步提出可工作性评估框架.可工作性定义为“在运行时可正常工作的片上网络芯片的概率”.可工作性的定义强调片上网络设计的逻辑连通性.本文提出框架整合了三个影响可工作性的模块, 从顶层的应用层(即映射算法)、架构层(即路由策略), 到底层的物理层(即良率分析).良率分析可以从片上网络的冗余器件估计.映射算法和路由策略可以分别从应用程序和架构设计中提取.除该三个模块之外, 框架还包含一个基于蒙特卡洛的分析流程.该框架能够评估片上网络设计的可工作性, 与良率相比, 可工作性更接近片上网络的实际工作情况, 因此更准确;基于评估结果, 设计者能够进一步优化片上网络的设计, 达到最佳的可工作性.
本文的主要贡献有以下3点:1) 发现在良率之外, 还有其他细节需要考虑, 如任务映射的结果和路由策略引入的通信约束, 能够准确确认片上网络系统是否能正常工作.2) 基于这一发现, 提出可工作性的概念.这一概念包含了影响片上网络正常工作的全部因素.3) 提出可工作性评估框架, 并展示了如何使用该框架分析片上网络的可工作性, 从而有针对性地优化片上网络设计.
1 相关研究工作分别总结物理层、架构层、应用层及一些跨层次的主要研究工作.在物理层, 研究工作主要采用蒙特卡洛方法, 评估物理层的良率, 进而估计片上网络的成本[8-10].由于蒙特卡洛方法的评估速度较慢, Lan等[11]简介了一种基于Gibbs采样技术的加速方法.随着3D芯片研究的流行, Kologeski等[12]研究针对3D片上网络分析良率问题.此外, Kahng等[13]建立片上网络的功耗和面积模型.该模型广泛用于片上网络系统性能仿真器中, 但仅能够用于估计功耗和面积.
在架构层, 研究工作主要评估片上网络的通信性能, 并寻找更优的路由策略, 以便实现更优的网络通信性能.在评估片上网络性能方面, 主要有以下2种手段:1) 采用分析模型, 用数学求解的方法计算网络性能;2) 采用网络仿真器, 通过仿真网络中的通信包, 估计网络性能.在分析模型方面, Cheng等[14]通过拆解片上网络的路由路径, 并应用排队理论, 实现了一个准确的分析模型.在仿真器方面, 于绩洋等[15]针对光电混合片上网络, 设计了一套系统的仿真方法.片上网络的性能很大程度上依赖于架构层的路由策略实现, 许多架构层的研究工作尝试寻找更优的路由策略, 如:Chiu[16]提出称为奇偶路由的具有适应性的路由策略, 与传统的XY路由相比, 奇偶路由需要更少的路由限制, 同时能够提供一定的适应性;Mejia等[17-18]提出的segment路由和region路由是全局路由策略的论文, 全局路由策略需要从全局搜索整个网络, 能够很好地避开不可靠的硬件资源;全励等[19]针对特定应用的实时性要求, 设计一种具有高实时性的路由策略.
在应用层, 研究工作主要针对应用的任务划分, 如Hu等[20]提出任务的分支定界映射算法, 该算法能够得到理论上最优的性能/功耗映射结果.此外, Khoroush等[21]研究将片上网络作为一种专用芯片, 根据应用需要定制整个片上网络.
以上总结了片上网络中针对单一层次的主要研究工作.有些研究者开始探索片上网络中跨层次的问题, 如:Cong等[22-23]同时考虑了架构层的路由特性和应用层的任务特性, 根据应用任务特性, 有针对性地添加虚通道, 并进一步提出消除信道依赖环(channel dependency cycle)方法, 解决了路由死锁问题.
从以上相关工作的调研与分析情况来看, 许多工作仅考虑了影响可工作性的一方面或两方面因素, 没有研究多方面因素的工作.本文的研究首次整合了三方面因素, 从而为三者折衷提供了可能性.
2 片上网络的可工作性评估框架可工作性评估框架如图 1所示.框架包含3个模块和1个分析流程.框架的输入包括:物理层、应用层、架构层和网络设计细节.

|
图 1 可工作性评估框架 Fig. 1 Workability evaluation framework |
良率模块(yield component)检查片上网络实例的物理连通性.良率模块需要物理层的良率信息, 从而模拟片上网络实例中, 由生产过程中的缺陷导致的错误情况.若一实例未能通过良率模块, 则该实例被直接标记为“失效的”(failed), 并且不需要后续分析.仅通过良率模块的实例会被送至后续模块.
映射模块(mapping component)负责将软件和硬件整合到同一个环境中.映射模块需要应用层的通信任务图(communication task graph, CTG)[20].映射算法将通信任务图中的所有任务, 映射到片上网络的各个节点上, 同时保证满足各种约束(通常是功耗约束).映射后的片上网络实例包含了硬件资源可用性和软件通信需求两方面信息.某些映射算法在执行映射之前, 需要预先分配路由路径, 如分支定界映射算法[20], 在图 1中以虚线箭头表达这一情况.
路由模块(routing component)检查片上网络实例的逻辑连通性.路由模块首先从架构层提取出路由约束, 然后根据这些约束, 重现片上网络实例的运行时状态.若某一实例的所有通信需求都能满足, 则该实例通过路由模块, 即该实例为可工作的, 标记为“通过的”(passed);否则, 标记为“失效的”(failed).
分析流程使用蒙特卡洛方法评估可工作性, 即首先随机生成大量的片上网络实例, 并将生成的这些实例依次交给3个模块.分析流程需要片上网络设计作为输入, 以便确定如何产生片上网络实例.同时, 分析流程从其他模块的输出中, 收集“通过的”和“失效的”(passed/failed)结果, 并计算可工作性.
2.1 良率模块Shamshiri等[8]将片上网络的良率定义为“有足够数量无缺陷节点的网络的概率”.其中, “足够数量”的具体数值由应用程序需求决定;“无缺陷节点”指节点和节点间的互连都需要“无缺陷”.该定义考虑了片上网络的冗余特性, 因此与基于负二项分布[4]的典型IC良率(如ASIC)的定义有一定区别.该定义关注于片上网络的物理连通性, 一个物理连通的片上网络实例是可工作性分析的基础.
使用二维mesh拓扑的同构片上网络, 如图 2所示.一个片上网络由两类器件组成:节点(node)和互连(link).一个节点(node)包含了一个处理核心(core)和一个路由器(router).一个互连(link)包含多条连线(wire).各器件有各自的良率, 即Ynod、Ycor、Yrou、Ylin和Ywir.各器件的无缺陷概率等于良率.各器件良率之间的关系如下所示:

|
图 2 片上网络的良率模型 Fig. 2 Modeling NoC's yield |
| $ {Y_{{\rm{nod}}}} = {Y_{{\rm{cor}}}}{Y_{{\rm{rou}}}}, $ | (1) |
| $ {Y_{{\rm{lin}}}} = \prod\limits_{i = 1}^N {{Y_{{\rm{wir}}}}} . $ | (2) |
式中:N为一条互连中包含连线的数量.由于多条连线共同组成一个互连, Ywir应相乘N次.这会显著地降低Ylin, 因为N一般是一个较大的值(本文中假设N=64).为了保证较高的Ylin, 往往需要添加冗余连线.当添加冗余连线之后, 式(2) 被改写如下:
| $ \begin{array}{l} {Y_{{\rm{lin}}}} = Y_{{\rm{wir}}}^{N + E} + C_{N + E}^1Y_{{\rm{wir}}}^{N + E-1}\left( {1-{Y_{{\rm{wir}}}}} \right) + ... + \\ \;\;\;\;\;\;\;C_{N + E}^EY_{{\rm{wir}}}^N{\left( {1-{Y_{{\rm{wir}}}}} \right)^E}. \end{array} $ | (3) |
式中:E为冗余连线的数量, C为组合数.式(3) 的基本思想如下:列出所有至少N条连线是无缺陷的情形(这些情形对应无缺陷的互连), 并分别计算概率, 最后全部相加.
各器件只有两种可能的状态, 即有缺陷和无缺陷, 因此可以用伯努利(Bernoulli)分布描述器件的状态.对于任意一个器件, 器件状态可用随机变量Xi表示, 即Xi~B(1, Ydev).其中B表示二项分布(伯努利分布的一般形式), Ydev可以是Ynod或Ylin(取决于器件类型, 并应用式(1)~(3)).Xi的概率质量函数f(Xi)的定义为
| $ f\left( {{X_{_i}}} \right) = \left\{ \begin{array}{l} {Y_{{\rm{dev}}}}, \;\;\;\;\;\;{X_i} = 1;\\ 1-{Y_{{\rm{dev}}}}, \;\;\;{X_i} = 0. \end{array} \right. $ | (4) |
对于整个片上网络中的所有p个器件, 可以使用多维随机变量X=[X1, X2, …, Xp]T描述p个器件的状态.f(X)=f(X1)·f(X2)…f(Xp)为X的联合概率质量函数.定义一个指示函数如下:
| $ C\left( \boldsymbol{X} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;\;\boldsymbol{X}对应物理连通网络;\\ 0, \;\;\;\;\;\boldsymbol{X}对应物理不连通网络. \end{array} \right. $ | (5) |
该函数用于描述多维随机变量X是否对应物理连通网络.式中:C(X)为良率模块的输出, 即物理连通性.若C(X)=1, 则X对应的片上网络实例是连通的, 应交给后续模块分析.若C(X)=0, 则X对应的片上网络实例是不连通的, 即不可用的, 不需要进行后续分析, 良率模块直接输出“失效的”(failed)实例.
2.2 映射模块映射模块将通信任务图(CTG)[20]中的各个任务, 映射到唯一的节点中.一般来说, 映射算法通常还需要满足其他约束条件[20], 如功耗约束.映射算法能够帮助避免有缺陷的硬件资源.一个良好的映射算法会将通信较重的任务映射到连通性较良好的区域, 而非连通性不好的区域, 因此能够提升通信的可靠性.
某些映射算法, 如分支定界算法[20], 需要在映射过程中预先知道路由路径.这导致了映射模块和路由模块之间的循环依赖, 如图 1的虚线箭头所示.具体而言, 映射算法需要通过路由路径, 计算源节点和目标节点之间的距离, 从而判断映射结果的优劣.
本文重点关注映射算法的输入输出数据结构.映射算法的输入输出数据可用下式描述:
| $ \boldsymbol{S} = M\left( {\boldsymbol{X}, {\rm{CTG}}} \right). $ | (6) |
式中:M指映射算法;X为片上网络实例;CTG指通信任务图;S为映射模块的输出结果, 是一个方阵, 一般为稀疏矩阵.S将用于路由模块的逻辑连通性检查.
不同的映射算法M会有不同的结果, 本文使用3种不同的映射算法, 分别是:顺序映射、贪婪映射和分支定界映射[20].顺序映射是最简单的映射算法, 它将CTG中的任务依次顺序地映射到无缺陷节点中.贪婪映射试图保证通信较重的任务映射在一起:它首先将CTG中的任务按通信量由大到小排序, 再将排序后的任务依次映射到无缺陷节点中.分支定界映射[20]采用分支定界算法实现任务映射, 该算法较复杂, 不作详细介绍, 一般来说, 采用分支定界映射算法可以获得最优的映射结果.
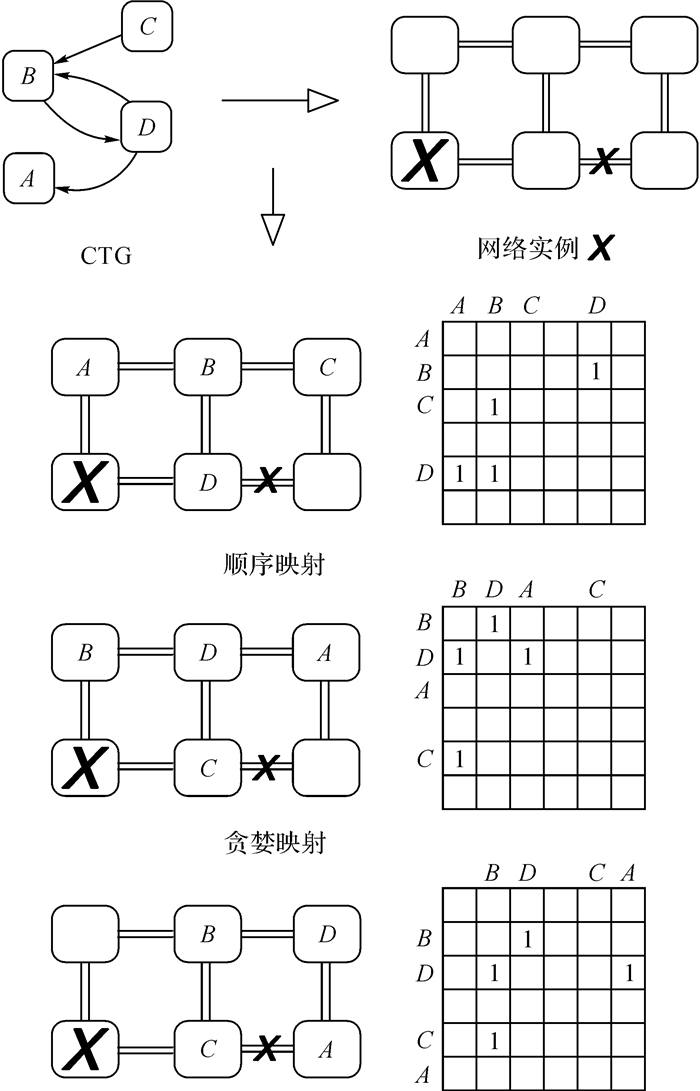
图 3以一个具体的CTG(图 3左上)和网络实例X(图 3右上)为例, 展示映射模块的输入输出数据以及不同映射算法的结果.
|
图 3 映射模块的例子 Fig. 3 Example of mapping component |
如图 3所示, 顺序映射将4个任务依次映射到无缺陷节点中, 右侧是稀疏矩阵S的结果;在贪婪映射中, 任务B和任务D的通信较重, 因此优先被映射, 之后映射余下的两个任务, 右侧是稀疏矩阵S;分支定界映射的结果明显比其他两者好, 因为该结果中的所有通信都能不经过其他节点直接到达(在顺序映射中, D到A需要经过B;在贪婪映射中, C到B需要经过D).
映射模块不会将片上网络实例进行标记(既不会标记为“失效的”(failed), 也不会标记为“通过的”(passed)), 即所有映射模块处理的片上网络实例都会送至路由模块进行后续分析.
2.3 路由模块路由模块负责检查片上网络实例是否逻辑连通.具体来说, 路由模块首先从架构设计中提取路由策略, 然后检查映射后的每一组通信节点对是否能够正常通信.由于路由中可能会遇到死锁或活锁问题, 路由策略中往往会加入一些限制, 以确保不会出现死锁或活锁现象.这些路由限制有时可能会阻断正常通信.此外, 路由模块为映射模块提供路由路径信息, 而路由路径信息在某些映射算法中是必要的, 如分支定界算法[20].
在评估框架中, 路由模块将S转化为最终的“通过的”(passed)或“失效的”(failed)结果.该结果对应网络实例是否可工作, 可以用下式表达:
| $ W\left( \boldsymbol{X} \right) = C\left( \boldsymbol{X} \right) \cdot R\left( {M\left( {\boldsymbol{X}, {\rm{CTG}}} \right)} \right). $ | (7) |
式中:W表示对应片上网络实例的可工作性, R为路由策略.由于良率模块会输出“失效的”(failed)结果, R与C相乘的结果是最终的可工作性.
与映射算法M类似, 不同的路由策略R会有不同的结果.使用3种不同的路由策略, 分别是:XY路由、odd-even路由[16]和segment路由[17-18].后两个路由策略较复杂, 这里不作具体介绍.XY路由较简单, 路由路径总是从源节点开始, 先往X方向前进, 直到X坐标与目标节点相同, 再转到Y方向前进;若源节点和目标节点的X坐标相同, 则直接往Y方向前进.
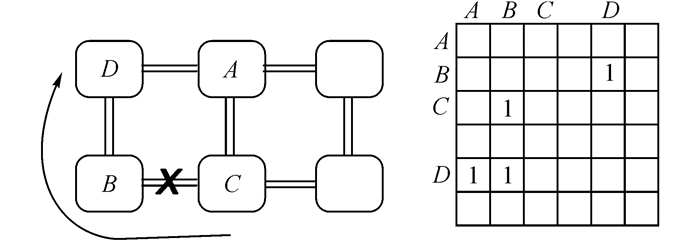
图 4以图 3中的顺序映射结果为例, 解释路由策略对可工作性结果的影响.图 4中, 从节点D到节点A的通信, 在XY路由策略和odd-even路由策略下, 都会经过左下角的有缺陷节点, 因此通信受阻, 不能正常工作, 如图 4的箭头所示;在segment路由策略下, 节点D到节点A的通信会经过节点B, 因此能够正常通信.
|
图 4 路由模块的例子 Fig. 4 Example of routing component |
如果能够穷举全部网络实例, 即穷举全部可能的多维随机变量X取值, 则片上网络的可工作性可以由下式计算:
| $ W = \sum\limits_{\boldsymbol{X} = {{\left[{0, 0, ..., 0} \right]}^{\rm{T}}}}^{\boldsymbol{X} = {{\left[{1, 1, ..., 1} \right]}^{\rm{T}}}} {C\left( \boldsymbol{X} \right) \cdot R\left( {M\left( {\boldsymbol{X}, {\rm{CTG}}} \right)} \right).} $ | (8) |
式中:W为片上网络的可工作性, 从X=[0, 0, …, 0]T到X=[1, 1, …, 1]T的求和表示所有可能的X取值都需要计算.
按式(8) 穷举全部网络实例是不现实的, 在通常情况下, 可以采用蒙特卡洛方法[24]计算式(8).蒙特卡洛方法的原理如下:随机产生足够数量N′的样本, 计算这些样本的平均W(X)值, 将该值作为实际可工作性W的一个估计WMC, 如下所示:
| $ {W^{{\rm{MC}}}} = \frac{1}{{N'}}\sum\limits_{n = 1}^{N'} {C\left( {{\boldsymbol{X}^{\left( n \right)}}} \right) \cdot R\left( {M\left( {{\boldsymbol{X}^{\left( n \right)}}, {\rm{CTG}}} \right)} \right).} $ | (9) |
式中:X(n)为f(X)的第n个样本.
WMC的方差σ2等于WMC(1-WMC)/N′[24], 正比于1/N′.根据数理统计理论[25]可知, 若需要95%的置信区间, 即[WMC-1.96σ, WMC+1.96σ]和5%的置信度α=5%, 则样本容量N′必须满足下式:
| $ N' \ge \frac{{{{1.96}^2}}}{{{\alpha ^2}}}\frac{{1-\sigma }}{\sigma }. $ | (10) |
式(10) 用作蒙特卡洛方法的停止条件.
算法1 可工作性评估算法
1) 使用式(1)~(3) 计算Ynod和Ylin
2) 初始化可工作性W:=0
3) 初始化蒙特卡洛样本容量N′:=0
4) repeat
5) 随机生成片上网络实例X(i).
6) 执行物理连通性检查, 即计算C(X(i)).
7) N′:=N′+1
8) if C(X(i))=1
9) 应用映射算法和路由策略,
即计算R(M(X(i), CTG))
10) if R(M(X(i), CTG))=1
11) W:=W+1.
12) end if
13) end if
14) 当前可工作性的估计WMC:= W/N′
15) until满足停止条件, 即N′满足式(10)
根据式(9)、(10), 给出分析流程的完整算法, 如算法1所示.在算法1中, 步骤5) 生成片上网络实例;步骤6) 对应良率模块, 负责计算C(X(i));步骤9) 对应映射模块和路由模块, 负责计算R(M(X(i), CTG)).每一轮迭代, 在步骤14), 可工作性结果都会更新为W/N′.该结果将用于检查停止条件是否满足, 如步骤15) 所示.
3 实验数据及分析所有的实验都采用mesh拓扑, 但需要注意, 本文的评估框架不依赖于特定的拓扑, 评估框架可以应用到任意拓扑.
3.1 实验配置使用的物理层参数如表 1所示, 这些参数将用于生成片上网络实例.假设需要9个可工作节点数量, 每个可工作互连中至少有64条无缺陷连线, Ynod和Ywir都为0.995.
| 表 1 实验中使用的物理层参数 Table 1 Physical parameters used in experiments |
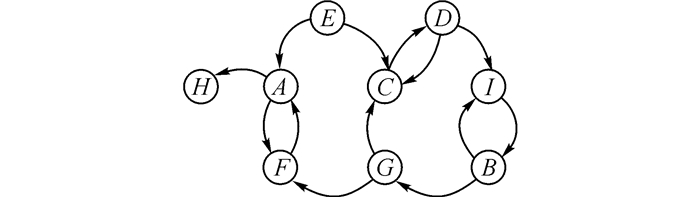
如图 5所示为一个多媒体应用中的通信任务子图.全部实验都以图 5所示的通信任务图为例进行分析.图 5中, 带字母的各个节点表示一个任务, 节点之间的箭头表示任务之间的通信需求, 例如任务E有数据发送给任务C, 而任务C与任务D之间有双向的数据通信需求.
|
图 5 通信任务图例子 Fig. 5 Example of CTG |
在实验过程中, 可以调整以下两个参数:1) mesh, 该参数对应冗余节点的数量;2) 互连中冗余连线的数量.在实验过程中, 使用了3×3、3×4、4×4和4×5, 总共4种不同的mesh, 分别对应0、3、7和11个冗余节点;使用0、+1和+2, 总共3种不同的冗余连线数量.
对于映射算法和路由策略, 采用3种映射算法, 分别是:顺序映射、贪婪映射和分支定界映射[20];采用3种路由策略, 分别是XY路由、odd-even路由[16]和segment路由[17-18].
3.2 良率实验与分析良率是可工作性的上界, 因为若一个片上网络在物理上是损坏的, 则它不可能正常工作.分析式(9) 可以从另一个角度解释该结论.由于R(M(X(i), CTG))≤1(R(M(X(i), CTG))只有0或1两种可能结果值), 则
| $ {W^{{\rm{MC}}}} \le \frac{1}{{N'}}\sum\limits_{n = 1}^{N'} {C\left( {{\boldsymbol{X}^{\left( n \right)}}} \right) = {Y^{{\rm{MC}}}}} . $ | (11) |
式中:YMC为良率的估计.
结合式(11) 和算法1, 整理出更简洁的良率评估算法, 如算法2所示.
算法2 良率评估算法
1) 利用式(1)~(3) 计算Ynod和Ylin
2) 初始化可良率Y:=0
3) 初始化蒙特卡洛样本容量N′:=0
4) repeat
5) 随机生成片上网络实例X(i)
6) 执行物理连通性检查, 即计算C(X(i))
7) N′:=N′+1
8) if C(X(i))=1
9) Y:=Y+1
10) end if
11) 当前良率的估计YMC:= Y/N′
12) until满足停止条件, 即N′满足式(10)
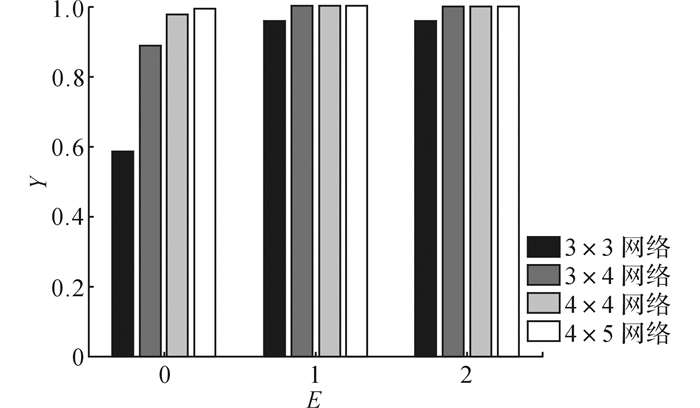
良率的实验结果如图 6所示.当冗余连线数量较少时, 添加冗余节点(即增大网络大小)是比较低效的手段;与之相比, 添加冗余连线更高效.当冗余连线为0时, 从3×3到4×5, 节点数量翻倍, 但良率仅提升了约40%.对于3×3网络, 从0冗余连线到1冗余连线, 仅添加1条冗余连线, 提升了约37%的良率.不断添加冗余连线会饱和在某一良率, 如3×3网络下, 无论添加多少冗余连线, 良率都会饱和在96%上.
|
图 6 片上网络的良率 Fig. 6 Yield of NoC |
这一现象的原因在于冗余连线和冗余节点是从不同的角度提升良率的.添加冗余连线, 会直接提升互连的良率, 是一种直接的良率提升方式.添加冗余节点, 不能直接提升节点的良率, 但是能够找到规则的拓扑提供更大的可能性, 是一种间接的良率提升方式.
3.3 可工作性实验与分析以4×4 mesh拓扑为例, 展示各因素对可工作性的影响以及如何利用可工作性选择设计方案.本文的框架不局限于该特例, 本文的框架可以用于任意大小的网络和任意网络拓扑.选用4×4 mesh下的良率结果为参考, 对比可工作性与良率的区别.
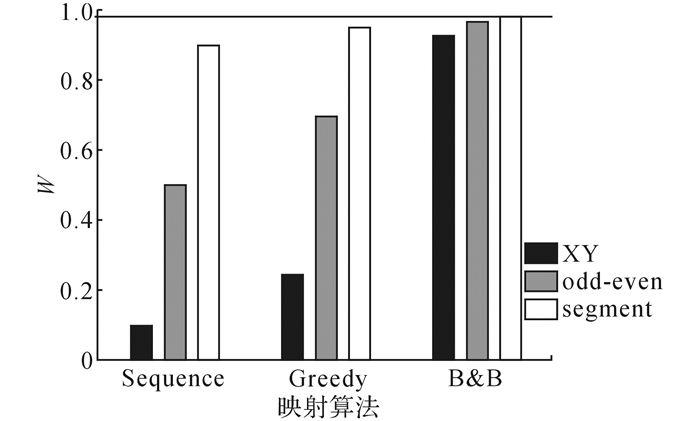
1) 不同因素对可工作性的影响.首先, 将冗余连线数量设为0, 观察不同映射算法和路由策略对可工作性的影响, 实验结果如图 7所示.图中, 顶部的水平线表示可工作性的上限, 即良率.由图 7可见, 映射和路由都能够在一定程度上提升可工作性.在顺序映射(图中记为Sequence)和贪婪映射(图中记为Greedy)下, 与XY路由(图中记为XY)相比, 具有适应性的odd-even路由(图中记为odd-even)能够提升约40%的可工作性.这表示路由的适应性能够提升可工作性, 因为具有适应性的路由策略能够有更多机会找到无缺陷的备选路由路径, 尽管提升之后的可工作性较低.
|
图 7 片上网络的可工作性 Fig. 7 Workability of NoC |
如图 7所示, 与XY路由相比, segment路由(图中记为segment)能够显著提升可工作性(>70%).这是由于segment路由需要学习整个网络硬件资源的可用性, 具有全局性.这能够帮助segment路由定位有缺陷器件, 并在运行时避免它们.
如图 7所示, 对于映射算法, 分支定界映射(图中记为B & B)是提升可工作性手段中最具竞争力的手段.它在全部路由条件下, 都能够达到最高的可工作性.这有以下两方面因素:1) 分支定界映射中使用的分支定界算法本身是一个全局最优解搜索算法, 能够保证返回最佳映射方案;2) 分支定界映射算法在映射过程中, 需要预先知道路由路径, 这保证了映射算法和路由策略的匹配程度, 能够为特定路由策略定制一个匹配的映射结果.
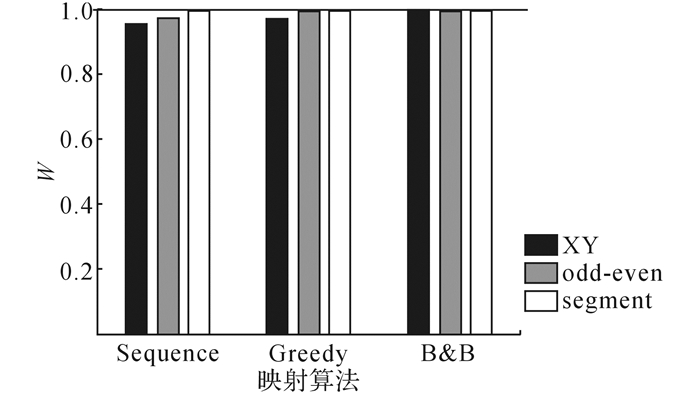
2) 利用可工作性选择设计方案.为了达到某一特定的可工作性, 有时会有多种可选的设计方案.如图 8、9所示, 假设可工作性目标为90%, 如顶部虚线水平线所示.

|
图 8 在硬件资源受限情况下的设计方案选择 Fig. 8 Design options when hardware resource is limited |
|
图 9 在硬件资源充足情况下的设计方案选择 Fig. 9 Design options when hardware resource is sufficient |
在某些情形下, 硬件资源比较有限, 且添加过多的冗余硬件资源是不可接受的.这些情形可以对应冗余连线为0的网络设计, 如图 8所示.在这种情形下, 要想达到90%的可工作性, 仅有的选项是使用分支定界映射算法或segment路由策略.这两种方案在前文的分析中被证实为是提升可工作性的最有效手段.
如果硬件资源的优先级较低, 可以添加冗余连线, 那么为了达到90%的目标可工作性, 有更多的选择, 甚至可以使用最简单的映射算法和路由策略.如图 9所示, 当冗余连线为1时, 全部方案都能够达到90%的目标可工作性.这是由于添加了冗余连线之后, 评估框架更容易找到规则的拓扑, 以满足通信任务图的需求.在这种情况下, 为了简单设计复杂度, 一般可以直接采用最简单的映射算法和路由策略, 即顺序映射和XY路由.
4 结语本文提出新的“可工作性”概念, 该概念关注片上网络芯片在运行时是否可以正常工作.本文进一步提出可工作性评估框架.该框架包含良率、映射、路由3个模块以及1个分析流程.整合了这些模块的可工作性评估框架, 为设计者在早期设计阶段提供了一个强大的工具, 使得设计者有更多的折衷空间, 在达到某一特定可工作性需求时, 会有更多的选项.
| [1] | MARCULESCU R, OGRAS U Y, PEH L S, et al. Outstanding research problems in NoC design: system, microarchitecture, and circuit perspectives[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2009, 28(1): 3–21. DOI:10.1109/TCAD.2008.2010691 |
| [2] | BELL S, EDWARDS B, AMANN J, et al. TILE64 processor: a 64-core SoC with mesh interconnect [C]//IEEE International Solid-State Circuits Conference-Digest of Technical Papers. San Francisco: IEEE, 2008: 88-89. |
| [3] | VANGAL S, HOWARD J, RUHL G, et al. An 80-Tile 1.28TFLOPS network-on-chip in 65nm CMOS[C]//IEEE International Solid-State Circuits Conference-Digest of Technical Papers. San Francisco: IEEE, 2007: 98-99. |
| [4] | KOREN I, KOREN Z. Defect tolerance in VLSI circuits: techniques and yield analysis[J]. Proceedings of the IEEE, 1998, 86(9): 1819–1838. DOI:10.1109/5.705525 |
| [5] | KAHLE J A, DAY M N, HOFSTEE H P, et al. Introduction to the cell multiprocessor[J]. IBM Journal of Research and Development, 2005, 49(4.5): 589–604. DOI:10.1147/rd.494.0589 |
| [6] | PALESI M, KUMAR S, CATANIA V. Leveraging partially faulty links usage for enhancing yield and performance in Networks-on-Chip[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2010, 29(3): 426–440. DOI:10.1109/TCAD.2010.2041851 |
| [7] | RODRIGO S, HERNANDEZ C, FLICH J, et al. Yield-oriented evaluation methodology of network-on-chip routing implementations [C]//International Symposium on System-on-Chip. Tampere: IEEE, 2009: 100-105. |
| [8] | SHAMSHIRI S, CHENG K T. Modeling yield, cost, and quality of a spare-enhanced multicore chip[J]. IEEE Transactions on Computer, 2011, 60(9): 1246–1259. DOI:10.1109/TC.2011.32 |
| [9] | SHAMSHIRI S, CHENG K T. Yield and cost analysis of a reliable NoC [C]//IEEE VLSI Test Symposium. Washington: IEEE, 2009: 173-178. |
| [10] | SHAMSHIRI S, CHENG K T. Modeling yield, cost, and quality of an NoC with uniformly and non-uniformly distributed redundancy [C]//VLSI Test Symposium. Santa Cruz: IEEE, 2010: 194-199. |
| [11] | LAN Fan, PAN Yun, CHENG K T. An efficient network-on-chip yield estimation approach based on Gibbs sampling[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2016, 35(3): 447–457. DOI:10.1109/TCAD.2015.2474401 |
| [12] | KOLOGESKI A, CONCATTO C, MATOS D, et al. Combining fault tolerance and serialization effort to improve yield in 3D networks-on-chip [C]//International Conference on Electronics, Circuits, and Systems. Dubayy: IEEE, 2013: 125-128. |
| [13] | KAHNG A B, LI B, PEH L S, et al. Orion 2.0: a fast and accurate NoC power and area model for early-stage design space exploration [C]//Design, Automation Test in Europe Conference Exhibition. France: IEEE, 2009: 423-428. |
| [14] | CHENG Ai-lian, PAN Yun, YAN Xiao-lang, et al. A general communication performance evaluation model based on routing path decomposition[J]. Journal of Zhejiang University-Science C: Computers and Electronics, 2011, 12(7): 561–573. |
| [15] |
于绩洋, 刘鹏, 华幸成, 等. 片上光电互连的多核系统仿真方法[J].
浙江大学学报:工学版, 2015, 49(11): 2214–2222.
YU Ji-yang, LIU Peng, HUA Xing-cheng, et al. Simulation approach of nybrid optical-electrical on-chip interconnects for multicore systems[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(11): 2214–2222. |
| [16] | CHIU G M. The odd-even turn model for adaptive routing[J]. IEEE Transactions on Parallel and Distributed Systems, 2000, 11(7): 729–738. DOI:10.1109/71.877831 |
| [17] | MEJIA A, FLICH J, DUATO J, et al. Segment-based routing: an efficient fault-tolerant routing algorithm for meshes and tori [C]//Parallel and Distributed Processing Symposium. Rhodes Island: IEEE, 2006: 10-15. |
| [18] | FLICH J, MEJIA A, LOPEZ P, et al. Region-based routing: an efficient routing mechanism to tackle unreliable hardware in network on chips [C]//International Symposium on Networks-on-Chip. Princeton: IEEE, 2007: 183-194. |
| [19] |
全励, 程爱莲, 潘赟, 等. 基于旁路通道的片上网络差别型服务实现方法[J].
浙江大学学报:工学版, 2013, 47(6): 957–968.
QUAN Li, CHENG Ai-lian, PAN Yun, et al. Bypassed channels based differentiated service implementation method for network-on-chip[J]. Journal of Zhejiang University: Engineering Science, 2013, 47(6): 957–968. |
| [20] | HU J, MARCULESCU R. Energy-and performance-aware mapping for regular NoC architectures[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 24(4): 551–562. DOI:10.1109/TCAD.2005.844106 |
| [21] | KHOROUSH S, RESHADI M. A fault tolerant approach for application-specific network-on-chip [C]//NORCHIP. Lithuania: IEEE, 2013: 1-6. |
| [22] | CONG J, LIU C, REINMAN G. Aces: application-specific cycle elimination and splitting for deadlock-free routing on irregular network-on-chip [C]//Design Automation Conference (DAC). Anaheim: IEEE, 2010: 443-448. |
| [23] | PALESI M, HOLSMARK R, KUMAR S, et al. Application specific routing algorithms for networks on chip[J]. IEEE Transactions on Parallel and Distributed Systems, 2009, 20(3): 316–330. DOI:10.1109/TPDS.2008.106 |
| [24] | ROBERT C, GEORGE C. Monte Carlo statistical methods[M]. 2nd ed. New York: Springer, 2004: 325-330. |
| [25] | SHAO J. Mathematical statistics[M]. 2nd ed. New York: Springer, 2003: 524-530. |



