随着技术的快速发展和成熟,虚拟现实(VR)不仅受到学术领域的关注[1],也正逐步市场化并走向普通消费应用,尤其是近期的Oculus Rift、HTC Vive以及索尼的PSVR等头戴虚拟现实设备都已量产并销售.随着头盔等移动设备的快速普及,人机自然交互技术[2]也越来越成熟,甚至包括眼动追踪技术[4-5]等.与此同时,头戴显示设备的设计也越来越接近人体的舒适度[6-8].尽管VR设备有较为宽广的应用范围,比如仿真、影视等领域,其目前主要还是用于娱乐场合.因为VR设备可增加游戏的真实度和更强沉浸感的互动体验.
有关在虚拟现实环境中创建三维模型已经有不少研究[9-13],但其更多基于参数化建模,限制较为多.Google公司开发的基于Htc Vive平台的绘图工具TiltBrush[14]从发布到现在一直都受到较高的评价,堪称VR体验的杀手级应用,其主要特点为用户可使用手中的手柄绘出各种物体并组合成五彩的虚拟世界.这验证了在VR环境中建模工作的可行性,而且可以降低建模难度,并将枯燥的建模工作变成有趣的娱乐活动.但TiltBrush所生成的组件模型只能在VR虚拟空间中交互和观看,不具有实际的几何体积,即不能将所建模型进一步加工成型或三维打印.
文献[13]给出了一种基于卷积曲面的VR环境下的建模方法,可直接将所生成模型进行三维打印或机器人三维模型雕刻[15].其中所使用的卷积曲面尽管可保证所生成曲面的二维流形表面,但巨大的卷积势能值计算必须借助GPU的并行加速才能达到交互速度,并且该系统采用基于骨架的隐式曲面,更适合生成模型的躯干模型,不适合生成细节丰富的流形表面.
针对该问题,本文给出一种基于曲面变形的VR环境下三维模型雕刻方法.尽管目前已有一些数字雕刻软件[16-17]可在粗糙模型[18]基础上迭代生成三维细节,但二维的显示空间一定程度上限制了用户对模型的深度感知和创造力.本文系统在VR沉浸环境下通过对初始基本模型的迭代影响区域查询、加权变形、局部拓扑重构等过程逐步雕刻生成目标形状,该过程使用基于CGAL库中的半边结构网格表示,执行过程采用空间加速结构实现单线程CPU端实时交互.
1 系统工作流程本文系统以HTC Vive头盔为实验硬件平台(如图 1所示),通过头盔眼镜用户和所建三维模型处于同一三维空间,采用其配套手柄进行输入.其中,左手手柄用于整体变换网格位置及旋转(如图 2所示),右手手柄表示输入画刷当前位置和形状(图中线框模型).

|
图 1 用户交互环境 Fig. 1 User interaction environment |

|
图 2 双手交互手柄输入 Fig. 2 Bimanual interactive handle input |
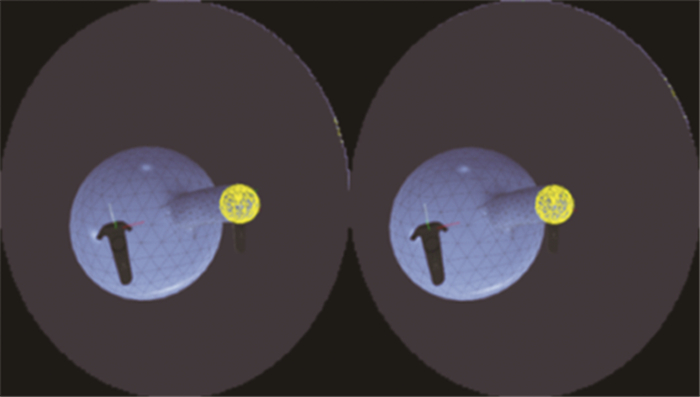
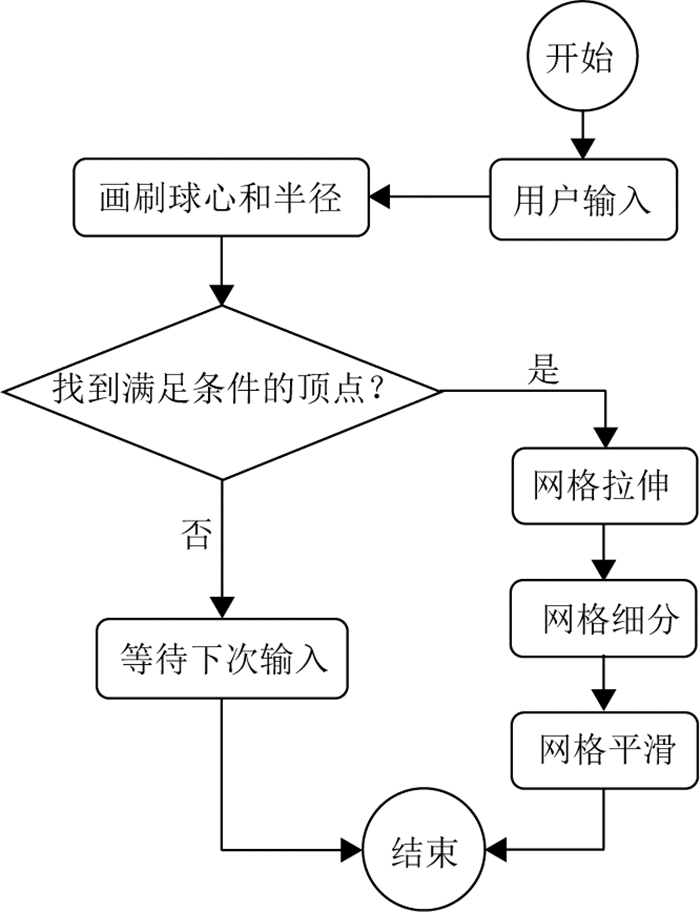
如图 3所示,根据系统的初始球形网格(642个顶点+1 280个面片),用户可使用画刷修改初始网格的表面,从而生成模型分枝及细节.对于用户的每一次输入,系统处理流程图 4所示,经过多次的迭代输入,完整模型的雕刻过程序列如图 5所示.
|
图 3 基于画刷的网格表面形变雕刻 Fig. 3 Brush-based mesh surface deformation sculpture |
|
图 4 单次用户输入的系统响应过程 Fig. 4 System response process to single user input |

|
图 5 动物模型雕刻序列 Fig. 5 Carving sequence of animal model |
对现有模型的雕刻过程,即是查询笔刷对模型M的影响区域并将其迭代变形.用户使用画刷输入的一个球形区域S,令其球心位置C(x0, y0, z0)及半径R,为寻找M表面在球S之内的顶点集合V,需要遍历M上的所有顶点vi并计算vi与点C距离d.若d < R,则vi在S内;若否,则在S外.
为加速实时查询满足要求的顶点集合V,本文采用等空间划分算法,首先将Vive活动空间等分为若干子空间Uk,同时确保所有网格顶点落在该子空间集合U内,因此只需在中心点与C距离满足条件的Uk中查询vi.
2.1 等空间划分与网格顶点载入假设用户活动空间范围为(x, y, z)∈[-A, A; -A, A; -A, A],空间网格间隔为a,划分的空间网格数为
| $ m = 2A/a. $ | (1) |
分别沿3个坐标轴等距划分,产生m3个子空间网格
| $ {S_{i,j,k}} = \left( {x,y,z} \right), $ |
其中,
| $ \left. \begin{array}{l} x \in \left[ { - A + ia, - A + \left( {i + 1} \right)a} \right],\\ y \in \left[ { - A + ja, - A + \left( {j + 1} \right)a} \right],\\ z \in \left[ { - A + ka, - A + \left( {k + 1} \right)a} \right],\\ i,j,k = 0,1,2, \cdots ,m - 1. \end{array} \right\} $ | (2) |
设Si, j, k中包含的网格顶点为PtInGrid (i, j, k),对网格M的任一顶点p(xp, yp, zp),根据其坐标值确定其所属子空间Si, j, k的下标ip, jp, kp并将p插入对应PtInGrid (ip, jp, kp)中,其中,
| $ \left. \begin{array}{l} {i_p} = \left[ {{x_p} + A} \right]/a,\\ {j_p} = \left[ {{y_p} + A} \right]/a,\\ {k_p} = \left[ {{z_p} + A} \right]/a. \end{array} \right\} $ | (3) |
交互操作过程中,根据用户输入的球心C和半径R查找满足应该遍历的子空间Si, j, k:
| $ \left. \begin{array}{l} {i_{\min }} \le i \le {i_{\max }},\\ {j_{\min }} \le j \le {j_{\max }},\\ {k_{\min }} \le k \le {k_{\max }}. \end{array} \right\} $ | (4) |
其中i限定为
| $ \left. \begin{array}{l} {i_{\min }} = \left\lfloor {\left[ {{x_0} - R + A} \right]/a} \right\rfloor ,\\ {i_{\max }} = \left\lfloor {\left[ {{x_0} + R + A} \right]/a} \right\rfloor + 1. \end{array} \right\} $ | (5) |
将满足以下条件的点p插入到PtList(i, j, k):
| $ p \in {\rm{PtInGrid}}\left( {i,j,k} \right)\& \left| {p - C} \right| \le R, $ |
则离画刷距离小于R的所有点集为
| $ {\rm{PtList}} = \bigcup\nolimits_{i,j,k} {{\rm{PtList}}\left( {i,j,k} \right)} . $ | (6) |
为逼近用户输入笔刷形状,网格面片过大时对于笔刷的逼近较差,需要根据笔刷的大小将网格细分以更好地逼近笔刷.
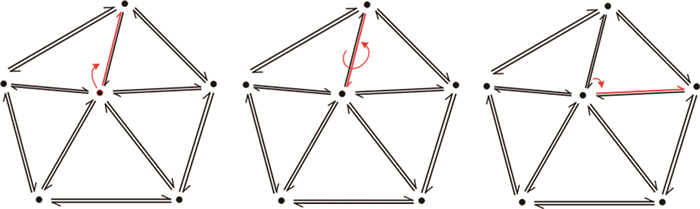
3.1 基于半边结构的局部网格细分策略如图 6,半边结构相邻顶点之间分为2个半边,2个半边的方向相反,分别属于该边的左、右2个平面.访问一个顶点的一阶邻域的过程如图 7所示.

|
图 6 网格拓扑的半边结构表示 Fig. 6 Half-edge structure of mesh topology |
|
图 7 基于半边结构的一环邻域 Fig. 7 One-ring neighborhood based on half-edge structure |
设某条边的2个半边分别为H1和H2,当网格细分阈值(即允许的最大边长)为Lm时,针对H1细分:首先,记H1的起始点Pfrom、终点Pto以及H1所属三角形的第三个顶点Ptri;其次删除该边,同时在该边的中点插入新的点Vnew,此时,H1、H2及其所属的2个面都将被删除,形成新的四条半边;然后,依次连接Pfrom、Pnew、Ptri及Pnew、Pto、Ptri,形成新的2个面取代原H1所属的三角形.最后,在对H1进行操作的同时,对H2也进行相同的操作.这样,原来的2个较大面就被分成了4个较小面,如图 8所示.

|
图 8 基于最长边的网格细分 Fig. 8 Mesh subdivision based on longest edge |
为逼近画刷形状,根据网格顶点p与画刷球心点C的距离来确定其每一帧的移动速度v,若p与C的距离为d,其移动速度v为
| $ v = \left( {R - d} \right)\gamma . $ | (7) |
其中γ为速度调节因子,可由用户调节.
迭代细分过程如下:
1) 对∀p∈PtList,遍历p的所有相关边L,将所有满足L>Lmax & L∉eList的边L插入eList中,则eList就是此次修改过程中所有需要细分的边.
2) 将eList按照边长从大到小排序,若eList为空,则结束本次修改,否则取出最长边Lmax,进行一次细分并得到Pnew,若|Pnew-C| < R遍历Pnew的所有边Lnew,将满足Lnew>Lm的边插入eList中.
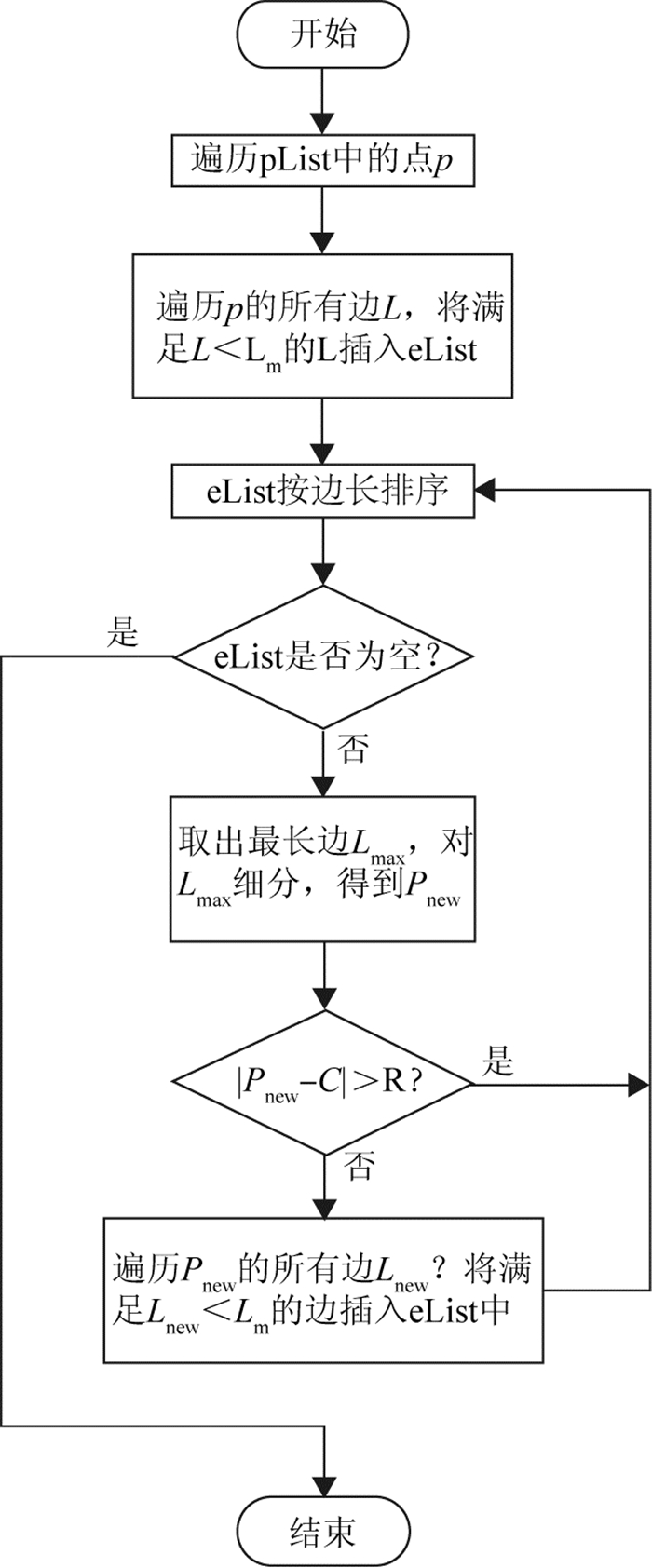
重复2)直至eList为空.具体流程如图 9所示.
|
图 9 笔刷引导的网格局部细分流程图 Fig. 9 Flow chart of brush-guided local mesh subdivision |
为保证细分后网格的质量及后续网格形变的鲁棒性,需要对细分网格进行优化处理,本文采用基于顶点邻域平面拟合来优化新插入顶点位置.
4.1 切平面拟合对于点v的所有一阶邻域点Pi(xi, yi, zi), i=0, 1, …, n-1, 求一平面F:
| $ z = {a_0}x + {a_1}y + {a_2}. $ | (8) |
使得该n个点到该平面距离之和S最小:
| $ S = \sum\nolimits_{n = 0}^{n - 1} {{{\left( {{a_0}x + {a_1}y + {a_2} - z} \right)}^2}} , $ | (9) |
| $ \frac{{\partial S}}{{\partial {a_k}}} = 0,\;\;\;k = 0,1,2. $ | (10) |
即
| $ \left. \begin{array}{l} \sum {2\left( {{a_0}{x_i} + {a_1}{y_i} + {a_2} - {z_i}} \right){x_i} = 0} ,\\ \sum {2\left( {{a_0}{x_i} + {a_1}{y_i} + {a_2} - {z_i}} \right){y_i} = 0} ,\\ \sum {2\left( {{a_0}{x_i} + {a_1}{y_i} + {a_2} - {z_i}} \right) = 0} . \end{array} \right\} $ | (11) |
可求得平面方程参数:
| $ \left( {\begin{array}{*{20}{c}} {{a_0}}\\ {{a_1}}\\ {{a_2}} \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} {\sum {x_i^2} }&{\sum {{x_i}{y_i}} }&{\sum {{x_i}} }\\ {\sum {{x_i}{y_i}} }&{\sum {y_i^2} }&{\sum {{y_i}} }\\ {\sum {{x_i}} }&{\sum {{y_i}} }&n \end{array}} \right)^{ - 1}}\left( {\begin{array}{*{20}{c}} {\sum {{x_i}{z_i}} }\\ {\sum {{y_i}{z_i}} }\\ {\sum {{z_i}} } \end{array}} \right). $ | (12) |
网格M上顶点p(xp, yp, zp)在拟合平面F上的投影为q(xq, yq, zq)应满足
| $ {z_q} = {a_0}{x_q} + {a_1}{y_q} + {a_2}. $ | (13) |
投影向量pq=(xq-xp, yq-yp, zq-zp),平面F的法向量n=(a0, a1, -1), 则pq应与n平行,因此
| $ \frac{{{x_q} - {x_p}}}{{{a_0}}} = \frac{{{y_q} - {y_p}}}{{{a_1}}} = \frac{{{z_q} - {z_p}}}{{ - 1}} = k. $ | (14) |
由式(13)、(14)解得
| $ k = - \frac{{{a_0}{x_p} + {a_1}{y_p} - {z_p} + {a_2}}}{{a_0^2 + a_1^2 + 1}}. $ | (15) |
因此,点Q的坐标为(xp+ka0, yp+ka1, zp-1),对上述拟合该平面的n个点:pi(xi, yi, zi), i=0, 1, 2, …, n-1,分别计算其投影点pi′(xi′, yi′, zi′), 并求其均值点:
| $ \bar p\left( {\bar x,\bar y,\bar z} \right) = \frac{1}{n}\sum\nolimits_{i = 0}^{n - 1} {\left( {{{x'}_i},{{y'}_i},{{z'}_i}} \right)} . $ | (16) |
对当前待平滑的点u(xu, yu, zu),计算其投影点u′(xu′, yu′, zu′),可得投影向量
| $ \mathit{\boldsymbol{uu'}} = \left( {{{x'}_u} - {x_u},{{y'}_u} - {y_u},{{z'}_u} - {z_u}} \right). $ | (17) |
则新点
| $ \begin{array}{l} u'' = \bar p + \mathit{\boldsymbol{uu'}} = \\ \left( {{{x'}_u} + \bar x - {x_u},{{y'}_u} + \bar y - {y_u},{{z'}_u} + \bar z - {z_u}} \right). \end{array} $ | (18) |
将M移动M″的位置,即完成该点的平滑.
5 实验结果与分析为验证算法的有效性,实验过程在配置4.0 GHZ Intel i7-6700K CPU、8 G内存、NVIDIA GTX 1070显卡的电脑上进行.
交互式建模系统对交互的实时性要求极高,为尽可能提高本文系统效率,空间等网格划分的加速效果如表 1所示,其中Ntotal表示模型顶点总数,Ns表示查询到的顶点数,t表示查询时间.从图中可看出,模型越大、笔刷越小,则加速比越大,因此本文的加速策略非常适合雕刻模型细节.
| 表 1 空间划分对雕刻过程的加速效果 Table 1 Spatial partition-based carving acceleration |
图 10中分别给出采用局部细分前后的对比效果,可见细分过程对笔刷的逼近效果有明显改进.由于本文系统在VR环境下建模,将用户与模型置于同一三维空间,大大降低了建模的难度,非专业建模人员也能快速生成复杂模型,如图 11所示.

|
图 10 网格顶点细分优化效果 Fig. 10 Mesh improvement by vertex subdivision |

|
图 11 非专业用户在本文HMD VR系统中创建模型 Fig. 11 Models created by non-professional users using our modeling system in HMD VR environment |
| [1] |
PICK S, WEYERS B, HENTSCHEL B, et al. Design and evaluation of data annotation workflows for CAVE-like virtual environments[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(4): 1452-1461. DOI:10.1109/TVCG.2016.2518086 |
| [2] |
冯志全, 梁丽伟, 徐涛, 等. 虚拟装配交互界面中的隐式交互算法研究[J]. 计算机辅助设计与图形学学报, 2017, 29(10): 1952-1962. FENG Zhi-quan, LIANG Li-wei, XU Tao, et al. Research on implicit interaction in virtual assembly interactive interface[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(10): 1952-1962. DOI:10.3969/j.issn.1003-9775.2017.10.022 |
| [3] |
刘慧, 冯志全, 梁丽伟, 等. 虚拟界面自然交互模型和算法[J]. 浙江大学学报:工学版, 2016, 50(6): 1168-1175. LIU Hui, FENG Zhi-quan, LIANG Li-wei, et al. Natural interaction model and algorithm based on virtual interface[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(6): 1168-1175. |
| [4] |
周小龙, 汤帆扬, 管秋, 等. 基于3D人眼模型的视线跟踪技术综述[J]. 计算机辅助设计与图形学学报, 2017, 29(9): 1579-1589. ZHOU Xiao-long, TANG Fan-yang, GUAN Qiu, et al. A survey of 3D eye model based gaze tracking[J]. Journal of Computer-Aided Design and Computer Graphics, 2017, 29(9): 1579-1589. |
| [5] |
程时伟, 陆煜华, 蔡红刚. 移动设备眼动跟踪技术[J]. 浙江大学学报:工学版, 2016, 50(6): 1160-1167. CHENG Shi-wei, LU Yu-hua, CAI Hong-gang. Mobile device based eye tracking technology[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(6): 1160-1167. |
| [6] |
KOULIERIS G A, BUI B, BANKS M S, et al. Accommodation and comfort in head-mounted displays[J]. ACM Transactions on Graphics, 2017, 36(4): 87:1-87:11. |
| [7] |
KONRAD R, PADMANABAN N, MOLNER K, et al. Accommodation-invariant computational near-eye displays[J]. ACM Transactions on Graphics, 2017, 36(4): 88:1-88:12. |
| [8] |
肖翱, 徐枫, 雍俊海, 等. 针对虚拟现实眼镜的近/远视反卷积矫正算法[J]. 计算机辅助设计与图形学学报, 2017, 29(7): 1169-1176. XIAO Ao, XU Feng, YONG Jun-hai, et al. A fast deconvolution algorithm for correcting myopia/hyperopia in head mounted display[J]. Journal of Computer-Aided Design and Computer Graphics, 2017, 29(7): 1169-1176. |
| [9] |
WESCHE G, SEIDEL H P. Freedrawer: a free-form sketching system on the responsive workbench[C]//Proceedings of the ACM Symposium on Virtual Reality Software and Technology. Alberta: ACM, 2001: 167-174. http://citeseerx.ist.psu.edu/showciting?cid=3610359
|
| [10] |
KEEFE D F, FDLIZ D A, MOSCOVICH T, et al. Cavepainting: a fully immersive 3D artistic medium and interactive experience[C]//Proceedings of the Symposium on Interactive 3D Graphics. North Carolina: ACM, 2001: 85-93. https://experts.umn.edu/en/publications/cavepainting-a-fully-immersive-3d-artistic-medium-and-interactive
|
| [11] |
KEEFE D F, ZELEZNIK R C, LAIDLAW D H. Drawing on air:input techniques for controlled 3D line illustration[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(5): 1067-1081. DOI:10.1109/TVCG.2007.1060 |
| [12] |
JACKSON B, KEEFE D F. Lift-off:using reference imagery and freehand sketching to create 3D models in VR[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(4): 1442-1451. DOI:10.1109/TVCG.2016.2518099 |
| [13] |
ZHU X, SONG L, YOU L, et al. Brush2Model: convolution surface-based brushes for 3D modelling in HMD-based virtual environments[J/OL]. Computer Animation and Virtual Worlds, 2017, e1764. https://doi.org/10.1002/cav.1764. https://www.researchgate.net/publication/316247283_Brush2Model_Convolution_surface-based_brushes_for_3D_modelling_in_head-mounted_display-based_virtual_environments_Brush2Model
|
| [14] |
Google's Tilt Brush. [EB/OL]. [2017-03-19]. www.tiltbrush.com.
|
| [15] |
何雪军, 王进, 陆国栋, 等. 基于三角网切片及碰撞检测的工业机器人三维头像雕刻[J]. 浙江大学学报:工学版, 2017, 51(6): 1104-1110. HE Xue-jun, WANG Jin, LU Guo-dong, et al. 3D head portrait sculpture by industrial robot based on triangular mesh slicing and collision detection[J]. Journal of Zhejiang University:Engineering Science, 2017, 51(6): 1104-1110. |
| [16] |
PIXOLOGIC: Zbrush[EB/OL]. [2017-05-04]. http://pixologic.com/.
|
| [17] |
AUTODESK: Mudbox 2017[EB/OL]. [2017-06-15]. http://www.autodesk.com/products/mudbox/overview.
|
| [18] |
JI Z, LIU L, WANG Y. B-Mesh:a modeling system for base meshes of 3D articulated shapes[J]. Computer Graphics Forum, 2010, 29(7): 2169-2177. DOI:10.1111/cgf.2010.29.issue-7 |



