2. 中铁隧道装备制造有限公司, 河南 郑州 450016
2. China Railway Tunnelling Equipment Co. Ltd, Zhengzhou 450016, China
硬岩掘进装备(tunnel boring machine, TBM)是铁路、公路等基础设施建设的急需装备, 也是我国装备制造业急需突破解决的问题之一[1].TBM在发达国家已有百余年的发展历史[2], 目前在设计与制造技术方面基本形成垄断.我国从20世纪60年代中期开始隧道掘进机研究, 历经50多年发展, 目前在土压平衡掘进机和泥水加压盾构技术方面已达国际先进水平[3-6].但关于硬岩掘进机的研究则刚刚起步.所见文献多数是介绍机器各部分的组成与功用[7-9], 或是从施工技术角度说明机器的性能和使用参数[10-12], 关于硬岩掘进机支撑-推进-换步机构设计与分析方法的文献鲜见报导[13-14].牛文文[15]针对该机构的结构与工况特点, 初步开展了机构的运动特性分析, 但未给出令人信服的结论.Huang等[16]采用螺旋理论系统研究了机构的力学性能, 指出机构是一种含有冗余自由度和内闭环支链的并联机构的结论, 但对其拓扑特性未做深入的分析.
目前, 国内外学者对并联机构的结构学、运动学及静力学等方面的研究已较为深入[17-21].但对于支撑-推进-换步机构这种特殊形式的并联机构, 其拓扑结构对TBM的运动特性和动力特性的影响仍有待深入研究.
本文在介绍机构拓扑结构和工作原理的基础上, 研究机构的拓扑结构与作业性能间的内在规律, 建立机构的在线调向运动方程, 以期为该类机构的创新设计与精准调向作业提供理论依据.
1 支撑-推进-换步机构简介 1.1 机构的组成支撑-推进-换步机构CAD模型和机构简图如图 1所示, 主要包括:刀盘2, 顶护盾3, 主梁4, 左、右2组扭矩油缸5, 鞍架6, 左、右撑靴7, 后支腿8, 十字销轴9, 左、右水平支撑油缸10, 左、右2组推进油缸11, 底护盾12及侧护盾13等.

|
图 1 支撑-推进-换步机构示意图 Fig. 1 Diagram of gripping-thrusting-regrippingmechanism |
主梁与鞍架通过导轨组成移动副, 扭矩油缸两端分别与鞍架和水平支撑油缸缸筒通过球铰连接, 左右水平支撑油缸分别与左、右撑靴通过球铰连接, 左、右两组推进油缸两端分别通过U副与主梁和撑靴连接.鞍架通过特殊的十字销轴(水平轴9-1和竖直轴9-2间由圆柱副和球副连接, 可产生相对转动和移动)与水平支撑油缸连接.支撑-推进-换步机构的拓扑结构如图 2所示.图 2中的(a)~(d)分别表示主梁-鞍架支链(P)、扭矩油缸支链(SPS)、十字销轴支链(SC)、左、右水平支撑油缸支链(P).可见, 机构是由2条对称的推进油缸(UCU)支链和1条复杂的混合支链构成的空间并联机构.
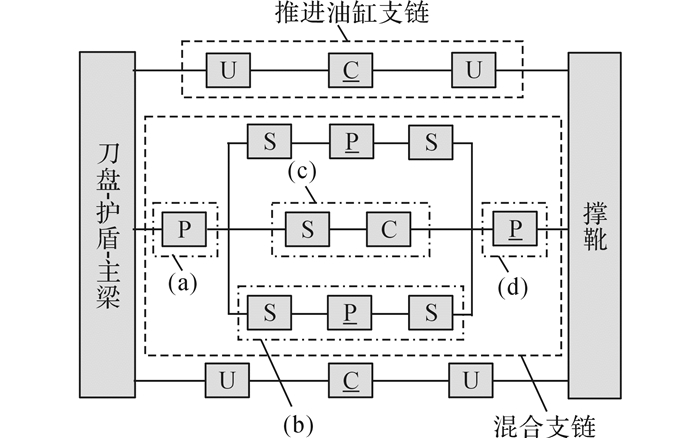
|
图 2 支撑-推进-换步机构拓扑结构 Fig. 2 Topological configuration of gripping-thrusting-regripping mechanism |
机构由推进油缸、扭矩油缸及水平支撑油缸驱动.左、右2组推进油缸和水平支撑油缸均为同一油路控制;而左、右2组扭矩油缸则分别独立驱动, 但每一组均为同一油路控制.各组油缸均采用压力流量控制方式.TBM通过这3组油缸驱动实现周期性循环作业.1个运动周期包括以下3个阶段.
1) 支撑岩壁:左右水平支撑油缸伸长, 驱动两侧撑靴缓慢撑紧岩壁.通过撑靴与岩壁间产生的摩擦力为TBM提供掘进力.撑靴撑紧岩壁后收起后支腿.
2) 推进作业:分为直线推进和在线调向2种工况.受地质环境影响, TBM常会出现偏离预定轨迹的现象, 因此多数处于在线调向工况下作业以便进行轨迹纠偏.调向工况下推进油缸用于驱动刀盘推进, 水平支撑油缸和扭矩油缸分别用于控制TBM的左右和俯仰调向.
3) 换步复位:待后支腿伸长撑紧地面与底护盾共同支撑TBM主机自重后, 各组驱动油缸以主梁为机架, 快速收缩复位至一个运动周期的初始状态.
当TBM进行俯仰调向时, 需要控制左、右2组扭矩油缸同步幅伸缩运动, 因此这2组油缸虽然分别独立驱动, 但应视为1个主动件.仅当TBM发生侧滚并纠偏[8]时, 视为2个主动件.
2 机构的拓扑特性分析 2.1 机构的自由度机构在推进作业中以撑靴为机架, 在换步复位工况中以主梁为机架, 因此可根据G-K公式分别计算其自由度[22]:
| $ M = d\left( {n-g-1} \right) + \sum\limits_{i = 1}^g {{f_i} + \nu-\zeta .} $ | (1) |
式中:M为机构的自由度;d为机构的阶数, d=6-λ,λ为机构的公共约束数, 由于2条对称的UCU支链和混联支链对主梁均无约束作用, λ=0;n为机架的构件数目;g为运动副的数目;fi为第i个运动副的自由度;v为多环并联机构在去除公共约束的因素后的冗余约束的数目;ζ为机构中存在的局部自由度.
2.1.1 推进作业工况(1) 主梁(刀盘架)的自由度.
在作业工况下, 撑靴为机架, 推进油缸、扭矩油缸及水平支撑油缸为驱动件, 主梁具有绕3个坐标轴的转动和沿z轴移动的4个可控自由度.由式(1) 计算主梁的自由度为6, 大于可控自由度4.说明主梁还存在沿x轴和y轴的2个不可控自由度, 如图 3所示, 即就机构本身而言,其运动是不确定的.但必须指出的是, 为保证刀盘中心始终沿预定轨迹, TBM在作业中要求护盾与岩壁必须处于撑紧状态(直径与理论隧道直径相等), 因此需要约束主梁的这2个自由度, 使机构具有确定的运动.
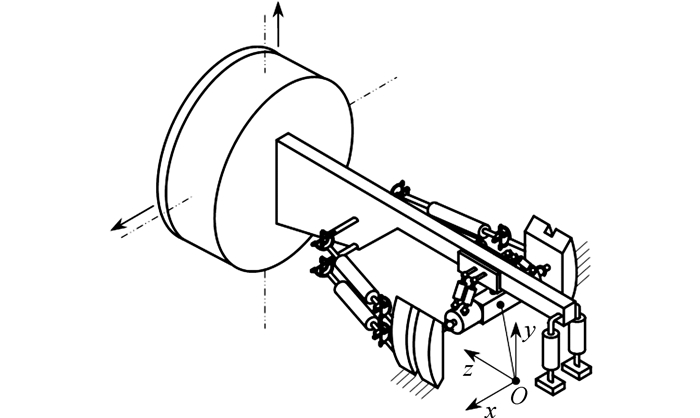
|
图 3 主梁(刀盘架)不可控自由度示意图 Fig. 3 Schematic diagram of main beam (cutter frame) uncontrollable DOF |
(2) 鞍架的自由度.
在调向作业下, 鞍架在扭矩油缸的驱动下, 具有沿y轴和绕z轴的2个可控自由度.由式(1) 计算得鞍架的自由度为4, 大于可控自由度2.说明鞍架存在绕x轴和y轴的2个不可控自由度, 如图 4所示.但当围岩通过护盾约束主梁的2个不可控自由度的同时, 鞍架的这2个不可控自由度也随之被约束.
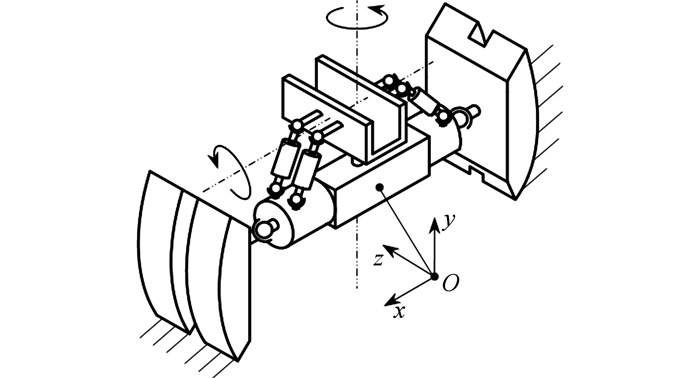
|
图 4 鞍架不可控自由度示意图 Fig. 4 Schematic diagram of saddle uncontrollable DOF |
该工况主梁为机架, 推进油缸、扭矩油缸及水平支撑油缸为主动件.撑靴在3组油缸的驱动下, 具有沿三坐标轴和绕z轴的4个可控自由度.由式(1) 计算得其自由度为6,这说明撑靴存在绕x轴与y轴的2个微幅转动, 如图 5所示.显然, 为保证撑靴复位至初始姿态, 应限制这2个自由度;而另一方面, 为使撑靴在作业工况下能与不规则岩壁紧密接触, 又应释放这2个自由度.

|
图 5 撑靴不可控自由度示意图 Fig. 5 Schematic diagram of gripper shoe uncontrollable DOF |
为满足这种需求, 可采用施加力约束的方式.如在撑靴球铰链周围均布小油缸, 在撑靴与推进油缸的U副处设置板簧[8], 分别约束这2个自由度.但在作业工况, 当对撑靴的驱动力大于预定值时会释放这2个自由度.
2.2 拓扑特性与设计准则 2.2.1 等效拓扑结构由1.1节可知, 机构中复杂的混合支链用于TBM调向作业.为深入分析机构的拓扑特性, 首先建立该支链的等效拓扑模型.
TBM需通过伸缩水平支撑油缸和扭矩油缸实现调向作业.当扭矩油缸带动鞍架沿y轴移动时, 通过鞍架拉动主梁产生绕x轴的微幅摆动, 这一运动过程相当于沿y轴的移动和绕x轴的转动;同理, 水平支撑油缸带动鞍架沿x轴移动时, 通过鞍架也带动主梁产生绕y轴的微幅摆动, 这一运动过程相当于沿x轴的移动和绕y轴的转动.鞍架同时存在沿y轴的转动和移动, 可等效为存在圆柱副.因此混合支链可等效为R-C支链,如图 6所示.
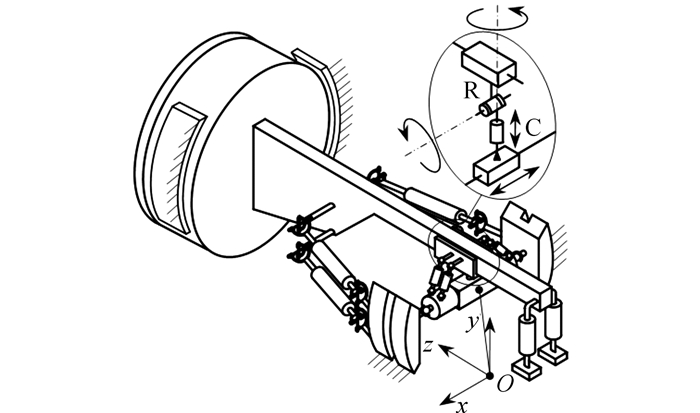
|
图 6 调向作业时混合支链的等效拓扑结构 Fig. 6 Equivalent topological structure of mixed branched chain in steering |
TBM在作业中面临复杂的地质环境, 承受强冲击载荷.当由于地质条件变化或护盾支撑油缸与接触构件弹性等因素, 对主梁度起不到理想的刚性约束时, 主梁会发生沿2个不可控自由度的微幅摆动.因此, 当TBM承受来自于掌子面的冲击载荷时, 混合支链可等效为如图 7所示的拓扑结构.

|
图 7 强冲击载荷下混合支链的等效拓扑结构 Fig. 7 Equivalent topological structure of mixed branched chain under strong impact loading |
由混合支链的等效拓扑结构可知, 机构在调向作业和强冲击载荷下会表现出不同的结构特征,在掘进作业中呈现以下特点.
1) 实现力的增益和精准调向控制.
机构在调向作业中不仅要克服掘进作业负荷, 也需要克服巨大的调向作业负荷.采用这种欠约束的结构形式, 可在鞍架与掌子面间形成以护盾为瞬时支点的力放大机构, 以满足调向作业负荷需求, 其原理如图 8所示.需要指出的是, 也是通过这个杠杆机构, 将鞍架的调向位移缩比至刀盘的微小位移, 从而实现精准调向.图中, F1和F2分别为作用于鞍架的水平和俯仰调向力, FL0和FD0分别为作用于刀盘左侧和底部的调向作业负荷, P为掘进作业负荷, l1为边刀[8]距护盾中心的距离, l2为护盾中心距鞍架中心的距离.
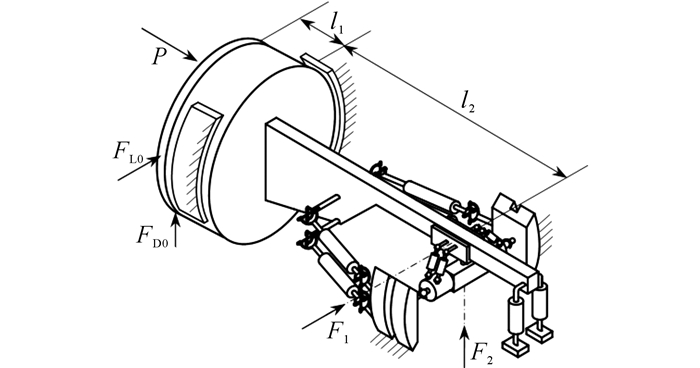
|
图 8 TBM在线调向力增益示意图 Fig. 8 Schematic diagram of TBM force gain in onlinesteering |
2) 自适应冲击载荷和避免重力负荷.
由图 7的等效拓扑结构可知, 当主梁在强冲击载荷下引发振动时, 由于围岩或接触构件具有弹性等原因, 可将主梁的横向振动转化为沿其2个不可控自由度的微幅摆动, 从而避免恰约束机构由于强冲击载荷导致零部件破损的现象.另一方面, 围岩对主梁提供约束的同时, 也支撑了TBM主机的大部分自重.因此, 这种拓扑结构也可避免恰约束机构须承担零部件重力的不足, 或由于围岩地质差异(或空洞)等引发的附加力负荷, 可有效提高动力传递效率.
必须指出的是, 由于TBM在作业中必须借助围岩提供的约束实现确定的运动, 围岩的物理性能必定会对TBM的作业性能产生很大的影响.这也是开敞式TBM存在定向性和稳定性差、以及易于出现偏离掘进轨迹现象的主要原因之一.
2.2.3 拓扑结构设计准则为满足强冲击载荷与复杂地质环境作业的工况特点, 机构的拓扑结构设计须满足以下准则:1) 可放大调向驱动力和微动控制作业姿态;2) 能够转换或吸收强冲击载荷所引发的振动能量;3) 可避免复杂地质环境变化引起的重力负荷.
3 机构的运动特性分析 3.1 机构的运动方程TBM通常采用正切法或侧移法进行在线调向作业.正切法要求作业中刀盘中心线与隧道中心线始终相切.下面以正切法为例建立机构的水平调向运动方程.
设在任一个运动周期内, TBM采用正切法进行水平调向作业.由初始位置1运动至任意位置2时, 机构的运动轨迹如图 9所示.图中, R为预估调向作业的掘进轨迹半径, θ为轨迹对应圆心角, β为水平转角, l0为鞍架中心沿z轴到刀盘中点的距离, s为掘进距离, Δx为水平支撑油缸沿x轴的移动量.
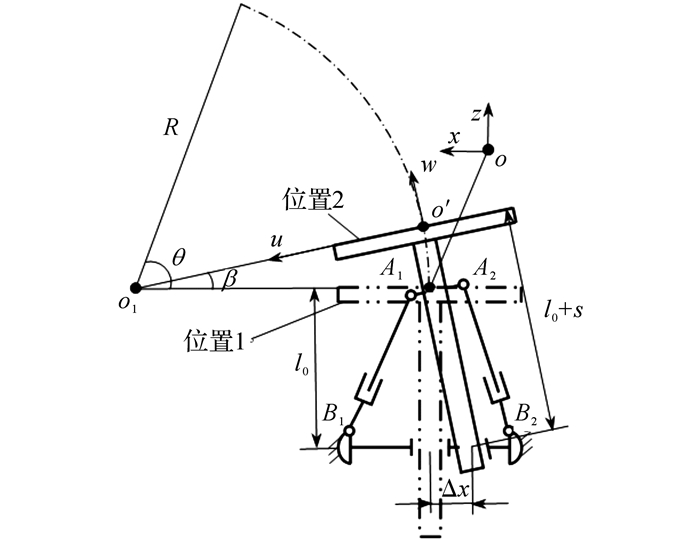
|
图 9 TBM水平调向示意图 Fig. 9 Schematic diagram of TBM horizontal steering |
以刀盘中点为点O, x轴与水平支撑油缸轴线平行, z轴与掘进轨迹重合, y轴满足右手定制, 建立参考系O-x-y-z;过刀盘中点O′, w轴与掘进轨迹重合, u轴与水平支撑油缸轴线平行, v轴满足右手定则, 建立连体系O′-u-v-w.当TBM处于初始状态时, 两坐标系重合.刀盘中点O′在参考系O-x-y-z下的坐标为[(l0+s)sin β-Δx 0 (l0+s)cos β-l0]T.
在参考系O-x-y-z下, 刀盘中点O′位矢r可通过运动链O-Bi-Ai-O′表示为
| $ \boldsymbol{r} = {l_{{A_i}{B_i}}}{\boldsymbol{S}_{{A_i}{B_i}}} + {\boldsymbol{b}_i}-{\boldsymbol{R}_y}{\boldsymbol{a}_i}, i = 1, 2. $ | (2) |
式中:Ry为基本旋转矩阵;ai为点Ai在连体系O′-u-v-w下的位矢;bi为点Bi在参考系O-x-y-z下的位矢;SAiBi为推进油缸单位位矢;lAiBi为推进油缸杆长.
可得, 推进油缸杆长lAiBi与水平支撑油缸移动量Δx间的映射关系:
| $ {l_{{A_i}{B_i}}} = \left\| {\boldsymbol{r} + {\boldsymbol{R}_y}{\boldsymbol{a}_i}-{\boldsymbol{b}_i}} \right\|, {\rm{ }}i = 1, 2. $ | (3) |
TBM的预估掘进轨迹可以是圆形、椭圆形等轨迹, 下面以圆形轨迹为例进行分析.为确保刀盘中点O′始终在预估掘进轨迹上, 且在任一瞬时TBM的掘进方向均与预估掘进轨迹相切, 需要分别建立圆形轨迹约束方程和斜率约束方程, 即
| $ \begin{array}{l} {\left[{\left( {{l_0} + s} \right){\rm{sin}}\;\beta-\Delta x-{R^2}} \right]^2} + \\ \;\;\;\;\;\;{\left[{({l_0} + s)cos\beta-{l_0}} \right]^2} = {R^2}, \end{array} $ | (4) |
| $ \frac{{({l_0} + s){\rm{cos}}\;\beta-{l_0}}}{{({l_0} + s){\rm{sin}}\;\beta-\Delta x-R}}\cdot\frac{{({l_0} + s){\rm{cos}}\beta }}{{({l_0} + s){\rm{sin}}\beta }} = - 1. $ | (5) |
联立式(4)、(5), 并化简得
| $ \Delta {x^2} + 2\Delta xR-2{l_0}s-{s^2} = 0. $ | (6) |
在实际作业时, 为降低刀具损伤, 规定在掘进距离s内, 边刀移动量应不超过Δa, 即
| $ R\left( {1-{\rm{cos}}\;\frac{s}{R}} \right) \le \Delta a. $ | (7) |
化简为
| $ s \le R\cdot{\rm{arccos}}\;\left( {{\rm{}}1-\Delta \frac{a}{R}} \right) \le {s_0}. $ | (8) |
式中:s0为一个掘进行程.随边刀磨损增大, 限制量Δa也相应减小.
综上所述, 联立式(3)、(6)、(8) 可得TBM在一个运动周期内, 推进油缸杆长lAiBi、水平支撑油缸移动量Δx及轨迹半径R间的映射关系.
TBM的液压系统均采用压力与流量控制方式.设TBM在预估掘进轨迹上运动至任意位置时, 推进油缸总流量ΔVAiBi、水平支撑油缸总流量ΔVr分别为
| $ \Delta {V_{{A_i}{B_i}}} = {\rm{\pi }}({l_{{A_i}{B_i}}}-{l_{{A_0}{B_0}}})r_{\rm{t}}^2, \;\;\;\;i = 1, 2. $ | (9) |
| $ \Delta {V_{\rm{r}}} = {\rm{\pi }}\Delta xr_{\rm{r}}^2. $ | (10) |
式中:lA0B0为推进油缸初始杆长, rt为推进油缸半径, rr为水平支撑油缸半径.
当TBM各驱动油缸总流量确定后, 可为各驱动油缸的流量控制提供数据支撑.
3.2 纠偏轨迹规划开敞式TBM的定向性与稳定性差, 又因受围岩软硬不均等影响, 即使在直线推进作业时, 也会出现偏离预定轨迹的现象.因此, 需要根据TBM的实时偏差数据(位置和方向), 快速规划出最短纠偏轨迹, 进而实现快速纠偏.
以水平纠偏为例, 设在直线推进作业时, TBM在某时刻偏离预定轨迹(位置1), 此时根据偏差数据, 快速规划出最短纠偏轨迹, 使TBM在该纠偏轨迹上通过连续水平调向, 实现轨迹纠偏, 如图 10所示.图中, R1和θ1、R2和θ2分别为纠偏轨迹圆弧BC、CD所对应的半径和圆心角, e为水平偏差, φ为TBM(位置1) 掘进方向与预定轨迹的夹角.由几何关系可知:
| $ {\theta _1} = {\theta _2} + \varphi, $ | (11) |
| $ {R_1}({\rm{cos}}\;{\theta _2}-{\rm{cos}}\;\varphi ) + e = {R_2}(1-{\rm{cos}}\;{\theta _2}). $ | (12) |
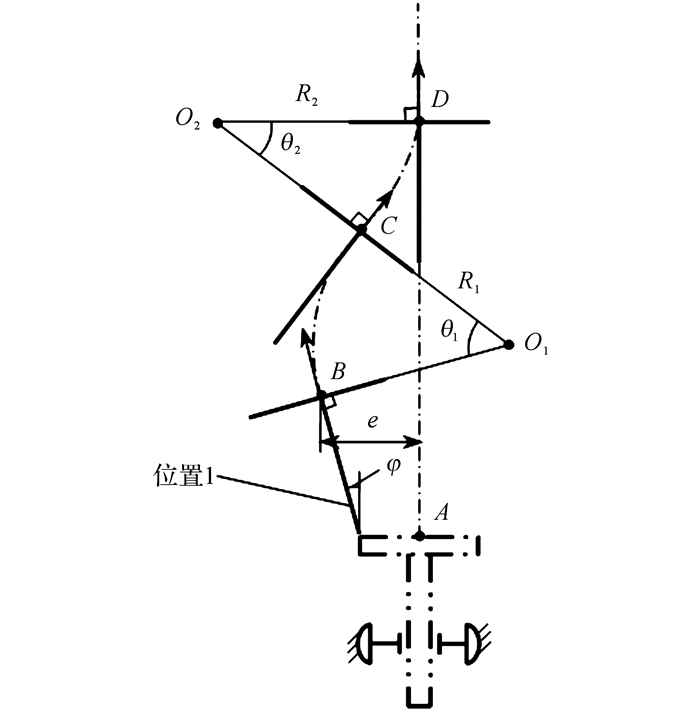
|
图 10 TBM水平纠偏示意图 Fig. 10 Schematic diagram of TBM horizontal correction |
且纠偏轨迹半径需满足:
| $ {R_i} \ge {R_{{\rm{min}}}}, {\rm{ }}i = 1, 2. $ | (13) |
式中:Rmin为TBM最小水平转弯半径.
最短水平纠偏轨迹为
| $ {l_{{\rm{min}}}} = {R_1}{\theta _1} + {R_2}{\theta _2}. $ | (14) |
联立式(11)~(14) 可得最短水平纠偏轨迹的作业参数.
4 算例以某开敞式TBM(刀盘直径为8 m)支撑-推进-换步机构样机为例, 对TBM的在线调向及纠偏轨迹规划进行仿真分析.样机的主要结构和工作参数如表 1所示.
| 表 1 样机主要结构和工作参数 Table 1 Main structure and working parameters of prototype |
1) 在线调向
根据3.1小节得到的机构水平调向运动方程, 在Matlab环境下, 仿真TBM在全域内左右推进油缸总流量、水平支撑油缸总流量与轨迹半径间变化关系, 如图 11所示.图中, V为TBM驱动油缸的流量, s为TBM掘进距离.
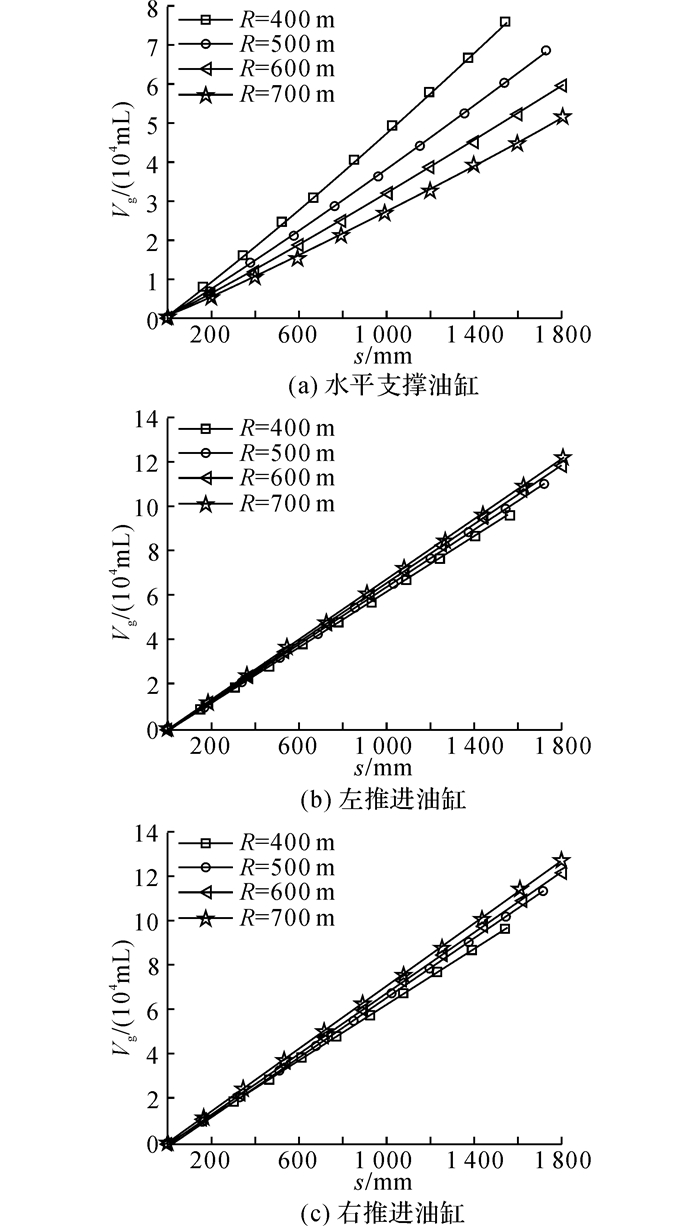
|
图 11 TBM各驱动油缸流量随轨迹半径的变化 Fig. 11 Variation of TBM cylinders' flow with trajectory radius |
当TBM进行在线调向作业时, 可利用图 11中的TBM各驱动油缸流量数据, 为各驱动油缸的流量控制提供数据支撑, 从而为TBM的精准在线调向的实现提供理论依据.
2) 纠偏轨迹规划
根据第3.2节得到的TBM水平纠偏轨迹规划算法, 以TBM水平偏差为30 mm,偏差角为0.1°~0.5°为例, 在Matlab环境下, 仿真TBM在不同偏差下的纠偏轨迹, 如图 12所示.由图可知, 3条纠偏轨迹均为光滑曲线, 且纠偏轨迹末端均与预估掘进轨迹相切.则该算法可行且能根据不同偏差数据快速规划出所需的纠偏轨迹.图中, e为水平偏差, s1为纠偏里程.

|
图 12 TBM水平纠偏轨迹示意图 Fig. 12 Schematic diagram of TBM horizontal correction track |
在此基础上, 根据3.1节的机构运动方程, 可得TBM在纠偏作业时左右推进油缸、水平支撑油缸的总流量, 进而通过控制各驱动油缸的流量变化, 实现TBM的在线纠偏作业.
5 结论(1) 本文分析了开敞式TBM支撑-推进-换步机构在强冲击载荷工况下应具有的拓扑特性, 建立了在线调向工况下的运动方程.
(2) 在推进作业时, 机构应为欠约束机构, 以自适应载荷冲击和地质环境变化引起的重力载荷;在调向或纠偏时, 机构应为恰约束机构, 能实现精准调向和放大调向扭矩的功能.
(3) 建立了开敞式TBM支撑-推进-换步机构的推进油缸、调向油缸及作业参数间的运动方程,为TBM在线精准调向或轨迹纠偏控制提供了有效的计算方法.
| [1] |
陆燕荪. 中国制造任重道远装备中国责无旁贷-中国装备制造业现状与发展战略[J].
机械工程学报, 2007, 43(1): 2–6.
LU Yan-sun. Current situation and development strategy of Chinese equipment manufacturing industry[J]. Chinese Journal of Mechanical Engineering, 2007, 43(1): 2–6. |
| [2] |
张镜剑. 隧道掘进机在我国应用的进展[J].
岩石力学与工程学报, 2007, 26(2): 226–238.
ZHANG Jing-jian. Advances in tunnel boring machine application in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 226–238. |
| [3] | YANG H Y, SHI H, GONG G F. Electro-hydraulic proportional control of thrust system for shield tunneling machine[J]. Automation in Construction, 2009, 18(7): 950–956. DOI:10.1016/j.autcon.2009.04.005 |
| [4] | YANG H Y, SHI H, GONG G F. Motion control of thrust system for shield tunneling machine[J]. Journal of Central South University of Technology, 2010, 17(3): 537–543. DOI:10.1007/s11771-010-0519-z |
| [5] | SHI H, YANG H Y, GONG G F, et al. Determination of the cutterhead torque for EPB shield tunneling machine[J]. Automation in Construction, 2011, 20(8): 1087–1095. DOI:10.1016/j.autcon.2011.04.010 |
| [6] | ZHAO Y, WANG H, YU H D, et al. A stiffness matching based evaluation approach for compliance of mechanical systems in shield tunneling machines[J]. Science China Technological Sciences, 2012, 55(10): 2926–2935. DOI:10.1007/s11431-012-4968-5 |
| [7] | DAVID T C, SEATTLE, WASH. Earth boring machine and method: 3861748[P]. 1975-01-21. |
| [8] | 杜彦良, 杜立杰著. 全断面隧道掘进机系统原理与集成设计[M]. 武汉: 华中科技大学出版社, 2011. |
| [9] | BERNHARD M, et al. Hard rock tunnel boring machines[M]. Beilin: Ernst and Sohn, 2008. |
| [10] |
王梦恕. 开敞式TBM在铁路长隧道特硬岩、软岩地层的施工技术[J].
土木工程学报, 2005, 38(5): 54–58.
WANG Meng-shu. Construction technique open TBM for long railway tunnels in very hard or soft rock strata[J]. China Civil Engineering Journal, 2005, 38(5): 54–58. |
| [11] | The Robbins Company. Service manual MB 332-335 & 336 preliminary issue[M]. Solon: the Robbins Company, 2009. |
| [12] |
周建军, 杨振兴. 深埋长隧道TBM施工关键问题探讨[J].
岩土力学, 2014, 35(Suppl.2): 299–305.
ZHOU Jian-jun, YANG Zheng-xing. Discussion on key issues of TBM construction for long and deep tunnels[J]. Rock and Soil Mechanics, 2014, 35(Suppl.2): 299–305. |
| [13] | WANG K, YANG Y H, SHEN Z G, et al. Research on the experimental test system of TBM gripping-thrusting-regripping mechanism[C] // 2016 MESA International Conference of IEEE. Auckland: IEEE, 2016:1-5. |
| [14] | GAO X X, YANG Y H. Finite element modeling of gripping-thrusting-regripping mechanism of TBM based on SAMCEF[C] // 8th International Conference on Intelligent Robotics and Applications. Portsmouth: ICIRA, 2015: 481-488. |
| [15] |
牛文文. TBM支撑推进机构掘进性能分析[D]. 天津: 天津大学, 2014.
NIU Wen-wen. Analysis on excavating performance of gripper and thrust mechanism of TBM[D]. Tianjin: Tianjin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10056-1016192100.htm |
| [16] | HUANG T, WANG X L, LIU H T, et al. Force analysis of a TBM gripping-thrusting-regripping mechanism[J]. Mechanism and Machine Theory, 2016, 98: 101–113. DOI:10.1016/j.mechmachtheory.2015.12.003 |
| [17] |
余发国, 高峰, 史巧硕. 基于GF集的锻造操作机构型方法[J].
机械工程学报, 2008, 44(11): 152–159.
YU Fa-guo, GAO Feng, SHI Qiao-shuo. Type synthesis for forging manipulators based on GF set[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11): 152–159. |
| [18] | GE H, GAO F. Type design for heavy-payload forging manipulators[J]. Chinese Journal of Mechanical Engineering, 2012, 25(2): 197–205. DOI:10.3901/CJME.2012.02.197 |
| [19] | TASI L W, JOSHI S. Kinematic analysis of 3-DOF position mechanisms for use in hybrid kinematic machines[J]. Journal of Mechanical Design, 2002, 124(2): 245–253. DOI:10.1115/1.1468860 |
| [20] | YAN C Y, GAO F, ZHANG Y. Kinematic modeling of a serial-parallel forging manipulator with application to heavy-duty manipulations[J]. Mechanics Based Design of Structures and Machines, 2010, 38(1): 105–129. DOI:10.1080/15397730903455344 |
| [21] | HUANG T, LIU H T, CHETWYND D G. Generalized jacobian analysis of lower mobility manipulators[J]. Mechanism and Machine Theory, 2011, 46(6): 831–844. DOI:10.1016/j.mechmachtheory.2011.01.009 |
| [22] | 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006: 116-127. |



