在电动力学的静电学中，带电细圆环是一个很重要的物理模型，关于其电势问题，因物理图像清晰、求解方法多样，文献[1-3]等曾有讨论.基于此本文提出带电细圆环和介质球系统的电势分布的求解方法，即在球坐标系中，利用叠加原理和拉普拉斯方程，得到带电细圆环和均匀介质球系统电势分布的解析式；用Matlab软件绘制等势线；最后通过带电细圆环和均匀介质球系统的电势解析式推出了介质球球心、远区、系统轴线上以及带电细圆环和导体球系统的电势分布.

用本文的方法易求解一类具有轴对称的静电场或静磁场系统的电势或磁矢势，如带电圆环和均匀介质球壳系统的电势、圆电流和磁介质球或磁介质球壳系统的磁矢势、带电圆环和无限长介质圆柱系统的电势、圆电流和无限长磁介质圆柱系统的磁矢势.用该方法求解此类物理问题具有物理图像清晰、易被学生接受等优点，同时有利于提高学生利用特殊函数求解相关物理问题的能力.

1 带电细圆环和介质球系统的电势分布

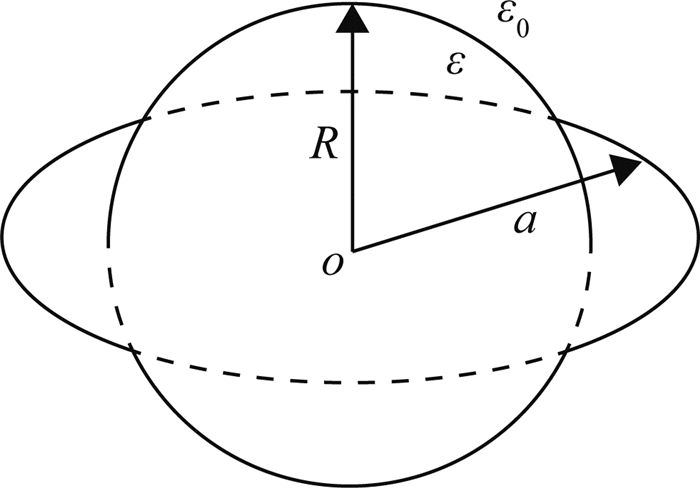
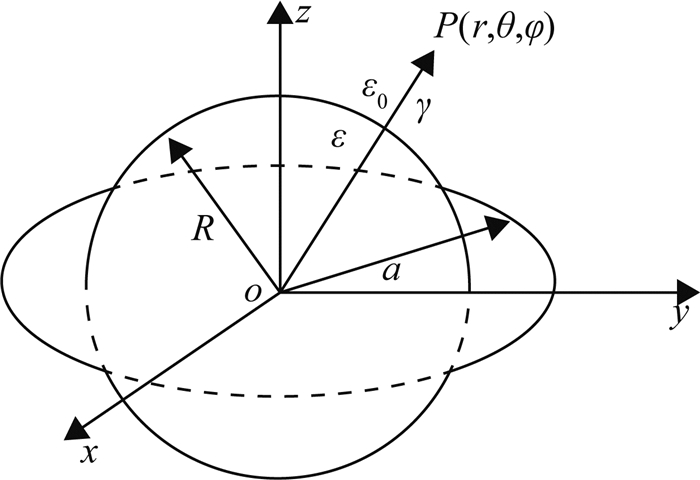
如图 1所示，真空中有一半径为a，带电量为q的细圆环，环内有一半径为R，介电常量为ε的介质球，球心和圆环中心重合于点o.由文献[1]知，在图 2所示的球坐标系中，带电细圆环在以a为半径的球面内的电介质及球面外的真空中产生的电势分别为

$ \begin{array}{l} {u_{q1}}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r < a, \end{array} $

(1)

$ \begin{array}{l} {u_{q2}}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( {\cos \theta } \right)} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;r > a. \end{array} $

(2)

如图 3所示，带电细圆环和介质球系统的电势在介质球内外(除带电圆环所在的位置外)均满足拉普拉斯方程

$ {\nabla ^2}{u_1} = 0,r < R, $

(3)

$ {\nabla ^2}{u_2} = 0. $

(4)

介质球处于带电细圆环的电场中，故介质球内外的电势应由两部分组成：细圆环产生的电势u_q(r, θ), 和介质球受到带电细圆环的电场作用而出现的极化电荷所产生的电势u′(r, θ).由电势叠加原理知，系统的电势为

$ {u_1}\left( {r,\theta } \right) = {u_{{q_1}}}\left( {r,\theta } \right) + {{u'}_1}\left( {r,\theta } \right),r < R, $

(5)

$ {u_2}\left( {r,\theta } \right) = {u_{{q_2}}}\left( {r,\theta } \right) + {{u'}_2}\left( {r,\theta } \right),r > R. $

(6)

考虑到本问题的对称性，极化电荷所产生的电势u′(r, θ)与方位角φ无关，应满足球坐标系中的拉普拉斯方程，由u′₁|_r=0=有限值，u′₂|_r→∞=0知，在介质球内外，极化电荷所产生的电势分别为

$ {{u'}_1}\left( {r,\theta } \right) = \sum\limits_{n = 0}^\infty {{A_n}{r^n}{P_n}\left( {\cos \theta } \right)} , $

(7)

$ {{u'}_2}\left( {r,\theta } \right) = \sum\limits_{n = 0}^\infty {\frac{{{B_n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \theta } \right)} . $

(8)

将式(1)、(2)、(7)、(8)代入式(5)和(6)，得到在介质球内、介质球表面和以a为半径的球面之间、以a为半径的球面外3个区域内的电势分别为

$ \begin{array}{l} {u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 0}^\infty {{A_n}{r^n}{P_n}\left( {\cos \theta } \right)} ,r < R, \end{array} $

(9)

$ \begin{array}{l} {u_2}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 0}^\infty {\frac{{{B_n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \theta } \right)} ,R < r < a, \end{array} $

(10)

$ \begin{array}{l} {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 0}^\infty {\frac{{{B_n}}}{{{r^{n + 1}}}}{P_n}\left( {\cos \theta } \right)} ,r > a. \end{array} $

(11)

由本问题的已知条件可以断定，空间电势u(r, θ)应当与oxy面对称，即u(r, θ)=u(r, π-θ)，又P_n[cos(π-θ)]=(-1)ⁿP_n(cos θ)，则要求式(9)~(11)中的n只能取偶数.即n=2l, l=0, 1, 2, …，将式(9)~(11)中的n用2l表示，得到

$ \begin{array}{l} {u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^\infty {{A_{2l}}{r^{2l}}{P_{2l}}\left( {\cos \theta } \right)} , \end{array} $

(12)

$ \begin{array}{l} {u_2}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^\infty {\frac{{{B_{2l}}}}{{{r^{2l + 1}}}}{P_{2l}}\left( {\cos \theta } \right)} , \end{array} $

(13)

$ \begin{array}{l} {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 0}^\infty {\frac{{{B_{2l}}}}{{{r^{2l + 1}}}}{P_{2l}}\left( {\cos \theta } \right)} . \end{array} $

(14)

将介质球表面r=R处满足的边界条件u₁|_r=R=u₂|_r=R，$\varepsilon \frac{{\partial {u_1}}}{{\partial r}}{|_{r = R}} = {\varepsilon _0}\frac{{\partial {u_2}}}{{\partial r}}{|_{r = R}}$代入式(12)和(13)，得

$ \begin{array}{l} \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{R}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \sum\limits_{l = 0}^\infty {{A_{2l}}{R^{2l}}{P_{2l}}\left( {\cos \theta } \right)} = \\ \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{R}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \sum\limits_{l = 0}^\infty {\frac{{{B_{2l}}}}{{{R^{2l + 1}}}}{P_{2l}}\left( {\cos \theta } \right)} , \end{array} $

(15)

$ \varepsilon \sum\limits_{l = 0}^\infty {2l{A_{2l}}{R^{2l - 1}}{P_{2l}}\left( {\cos \theta } \right)} = - {\varepsilon _0}\sum\limits_{l = 0}^\infty {\left( {2l + 1} \right)\frac{{{B_{2l}}}}{{{R^{2l + 2}}}}{P_{2l}}\left( {\cos \theta } \right)} . $

(16)

式(15)和(16)的两边乘以P_2l(cos θ)sin θ(l=0, 1, 2, …)，对θ从0→π积分，再根据勒让德多项式的正交性能，可推得以下结论：

$ \begin{array}{l} \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}{P_{2l}}\left( 0 \right){\left( {\frac{R}{a}} \right)^{2l}} + {A_{2l}}{R^{2l}} = \\ \;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}{P_{2l}}\left( 0 \right){\left( {\frac{R}{a}} \right)^{2l}} + \frac{{{B_{2l}}}}{{{R^{2l + 2}}}}, \end{array} $

(17)

$ 2\varepsilon {A_{2l}}l{R^{2l - 1}} = - {\varepsilon _0}\left( {2l + 1} \right)\frac{{{B_{2l}}}}{{{R^{2l + 2}}}}. $

(18)

解式(17)和(18)，得

$ {A_{2l}} = - \frac{q}{{4{\rm{ \mathsf{ π} }}}}\frac{{\left( {2l + 1} \right){\varepsilon _0}\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2{\varepsilon ^2}{\varepsilon _0}l + \varepsilon \varepsilon _0^2\left( {2l + 1} \right)}}\frac{{{P_{2l}}\left( 0 \right)}}{{{a^{2l + 1}}}}, $

(19)

$ {B_{2l}} = \frac{q}{{4{\rm{ \mathsf{ π} }}}}\frac{{2l\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2\varepsilon {\varepsilon _0}l + \varepsilon _0^2\left( {2l + 1} \right)}}\frac{{{R^{4l + 1}}}}{{{a^{2l + 1}}}}{P_{2l}}\left( 0 \right). $

(20)

将式(19)、(20)代入式(12)~(14)，得系统在3个区域内的电势分别为：

$ \begin{array}{l} {u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{\left( {2l + 1} \right){\varepsilon _0}\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2{\varepsilon ^2}{\varepsilon _0}l + \varepsilon \varepsilon _0^2\left( {2l + 1} \right)}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{P_{2l}}\left( 0 \right)}}{{{a^{2l}}}}{r^{2l}}{P_{2l}}\left( {\cos \theta } \right),r < R, \end{array} $

(21)

$ \begin{array}{l} {u_2}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{2l\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2\varepsilon {\varepsilon _0}l + \varepsilon _0^2\left( {2l + 1} \right)}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}{P_{2l}}\left( 0 \right)\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( {\cos \theta } \right),R < r < a, \end{array} $

(22)

$ \begin{array}{l} {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( {\cos \theta } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{2l\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2\varepsilon {\varepsilon _0}l + \varepsilon _0^2\left( {2l + 1} \right)}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}{P_{2l}}\left( 0 \right)\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( {\cos \theta } \right),r > a. \end{array} $

(23)

由式(21)~(23)，用Matlab软件在oxz面内作带电圆环和介质球系统的等势线，如图 4所示.

2 讨论 2.1 介质球球心的电势

在式(21)中，取l=0的对应项，得介质球球心处的电势为

$ {u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}. $

(24)

2.2 远离圆环各点的电势

在式(23)中，当r≫a时，取l=0的对应项，求得远离圆环处的电势为

$ {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}. $

(25)

式(25)表明，远离圆环处的电势与位于介质球球心处电量为q的点电荷的电势相同.

2.3 带电圆环轴线上的电势分布

圆环轴线上的点对应的角θ=0或π，将P_2n(cosθ)=1代入式(21)~(23)，得圆环轴线上各点的电势分别为

$ \begin{array}{l} {u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}\varepsilon a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{\left( {2l + 1} \right){\varepsilon _0}\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2{\varepsilon ^2}{\varepsilon _0}l + \varepsilon \varepsilon _0^2\left( {2l + 1} \right)}}\frac{{{P_{2l}}\left( 0 \right)}}{{{a^{2l}}}}{r^{2l}}} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;r < R, \end{array} $

(26)

$ \begin{array}{l} {u_2}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{r}{a}} \right)}^{2l}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{2l\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2\varepsilon {\varepsilon _0}l + \varepsilon _0^2\left( {2l + 1} \right)}}\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{{{P_{2l}}\left( 0 \right)}}{{{r^{2l + 1}}}},} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;R < r < a, \end{array} $

(27)

$ \begin{array}{l} {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{P_{2l}}\left( 0 \right){{\left( {\frac{a}{r}} \right)}^{2l + 1}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}a}}\sum\limits_{l = 0}^\infty {\frac{{2l\left( {{\varepsilon _0} - \varepsilon } \right)}}{{2\varepsilon {\varepsilon _0}l + \varepsilon _0^2\left( {2l + 1} \right)}}} \frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{{{P_{2l}}\left( 0 \right)}}{{{r^{2l + 1}}}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;r > a. \end{array} $

(28)

2.4 带电细圆环和导体球系统的电势分布

当ε/ε₀→∞，介质球相当于导体球，此时，由式(21)~(23)，可得带电细圆环和导体球构成的系统的电势分布为

$ \begin{array}{*{20}{c}} {{u_1}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}} + \frac{{{\varepsilon _0}}}{\varepsilon }\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{4l + 1}}{{2l}}{{\left( {\frac{r}{a}} \right)}^{2l}}} \times }\\ {{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}},r < R,} \end{array} $

(29)

式(29)表明导体球内为等电势区域.

$ \begin{array}{l} {u_2}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} = \\ \;\;\;\;\;\;\;\frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} + \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\;\;\frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} - \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} = \\ \;\;\;\;\;\;\;\frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} + \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{r}{a}} \right)}^{2l}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} ,\\ \;\;\;\;\;\;\;R < r < a. \end{array} $

(30)

由文献[4]知，式(30)中最后一项正是半径为$\frac{{{R^2}}}{a}$、电量为$ - \frac{{qR}}{a}$和原带电圆环同心的“像细圆环”产生的电势，由式(30)知, 在R < r < a区域, 带电细圆环和导体球系统的电势是由位于球心位置的电量为$\frac{{qR}}{a}$的像电荷、原带电圆环和半径为$\frac{{{R^2}}}{a}$、电量为$ - \frac{{qR}}{a}$和原圆环同心的“像细圆环”共同激发的.这与文献[4-5]利用电像法和场的叠加原理得到的结果一致.

$ \begin{array}{l} {u_3}\left( {r,\theta } \right) = \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} = \\ \;\;\;\;\;\frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} + \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{a}{r}} \right)}^{2l + 1}}} \times \\ \;\;\;\;\;{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right) - \frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} - \\ \;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} = \\ \;\;\;\;\;\frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}r}}\frac{{qR}}{a} + \frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 0}^\infty {{{\left( {\frac{a}{r}} \right)}^{2l + 1}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} - \\ \;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}a}}\sum\limits_{l = 1}^\infty {\frac{{{R^{4l + 1}}}}{{{a^{2l}}}}\frac{1}{{{r^{2l + 1}}}}{P_{2l}}\left( 0 \right){P_{2l}}\left( {\cos \theta } \right)} ,r > a. \end{array} $

(31)

同理，由式(31)知，在r>a区域，带电细圆环和导体球系统的电势同样是由球心位置电量为$\frac{{qR}}{a}$的像电荷、原带电圆环和半径为$\frac{{{R^2}}}{a}$、电量为$ - \frac{{qR}}{a}$并和原圆环同心的“像细圆环”共同激发的.

采用本文的思路和求解方法，还可以得到带电细圆环和电介质球壳构成的系统的电势分布，不再赘述.