对于大规模正定线性方程组的求解问题,迭代法是目前的主要方法. 2001年,BAI等[1]提出了一类HSS迭代法,该方法因具有形式简单、易程序化等优点,成为当前的研究热点,得到了许多新的推广.基于HSS迭代法,BAI等[2]给出了PSS算法, CAO等[3]对PSS算法做了改进,给出了广义PSS(GPSS)算法,LI等[4]给出了修正的GPSS算法;HUANG等[5]将系数矩阵分解成正定和半正定两部分,在这两部分之间进行迭代;2007年,LI等[6]提出了一类LHSS(Lopsided HSS)迭代算法,在系数矩阵的埃尔米特和非埃尔米特之间做非对称迭代,此算法格式简单,在参数较为松弛的约束条件下即可达到收敛;后来,POUR等[7]在LHSS法基础上提出了一类新的HSS方法,围绕系数矩阵的埃尔米特部分做二步非对称迭代.
本文对LHSS迭代法做进一步研究,将方程组的系数矩阵分解成2个正定部分,然后在这2个正定部分间做非对称迭代,给出了一类广义LHSS迭代法.数值结果表明,只要恰当地将系数矩阵分解为2个正定部分,广义LHSS迭代法在处理某些问题时能取得比HSS迭代法更好的效果.
1 背景知识在多学科领域常出现Ax=b形式的大规模线性方程组,其中A∈Cn×n为非埃尔米特正定矩阵.为了求解该方程,BAI等[1]在矩阵的HS分解(埃尔米特和反埃尔米特分解)基础上提出了HSS迭代算法, 该算法基于以下分解:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{H}} + \mathit{\boldsymbol{S}}, $ | (1) |
其中,
然后给出一个初始向量x(0)∈Cn,通过以下2步计算x(k+1),直到迭代序列{x(k)}收敛:
| $ \left\{ \begin{array}{l} \left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{H}}} \right){\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} = \left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right){\mathit{\boldsymbol{x}}^{\left( k \right)}} + \mathit{\boldsymbol{b}},\\ \left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{S}}} \right){\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = \left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}} \right){\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} + \mathit{\boldsymbol{b}}, \end{array} \right. $ | (2) |
其中α为大于0的常数.对于HSS迭代法,BAI等[1]证明了其迭代矩阵的谱半径小于1,即HSS算法收敛.
2007年,LI等[6]提出了一类LHSS迭代法,该迭代法在系数矩阵A的埃尔米特部分H和反埃尔米特部分S之间做非对称二步迭代. LHSS迭代法的迭代过程如下:
给定初始向量x(0)∈Cn,通过以下2步计算x(k+1),直到序列{x(k)}满足停止条件:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} = - \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{x}}^{\left( k \right)}} + \mathit{\boldsymbol{b}},\\ \left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{S}}} \right){\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = \left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}} \right){\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} + \mathit{\boldsymbol{b}}, \end{array} \right. $ | (3) |
其中α为大于0的常数.
2 广义LHSS迭代法本文对LHSS迭代法做进一步研究,给出了广义LHSS(GLHSS)迭代算法以及相应迭代法的格式.
首先,任意非埃尔米特正定矩阵A有以下分裂形式[3]:
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{G}} + \mathit{\boldsymbol{K}} + \mathit{\boldsymbol{S}}, $ | (4) |
其中,S表示反埃尔米特矩阵,G和K表示埃尔米特正定矩阵.
其次,任意非埃尔米特正定矩阵A又可分裂为以下形式:
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{P}}_2}. $ | (5) |
其中,P1和P2为正定矩阵.
P1和P2的2种可供选择的格式如下:
| $ {\mathit{\boldsymbol{P}}_1} = \mathit{\boldsymbol{D}} + 2{\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}},{\mathit{\boldsymbol{P}}_2} = \mathit{\boldsymbol{K}} + \mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}^ * - {\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}} + \mathit{\boldsymbol{S}}; $ |
| $ {\mathit{\boldsymbol{P}}_1} = \mathit{\boldsymbol{D}} + 2\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}^ * ,{\mathit{\boldsymbol{P}}_2} = \mathit{\boldsymbol{K}} + {\mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}} - \mathit{\boldsymbol{L}}_\mathit{\boldsymbol{G}}^ * + \mathit{\boldsymbol{S}}. $ |
其中, D为矩阵G的对角部分,LG为矩阵G的严格下三角部分,LG*为LG的共轭转置.
最后,在系数矩阵A的分裂矩阵P1和P2之间做非对称的二步迭代,得到GLHSS迭代法.
算法1 GLHSS迭代算法.
给定初始向量x(0)∈Cn,通过以下2步计算x(k+1),直到迭代序列{x(k)}满足停止条件:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} = - {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{x}}^{\left( k \right)}} + \mathit{\boldsymbol{b}},\\ \left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right){\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = \left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right){\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} + \mathit{\boldsymbol{b}}, \end{array} \right. $ | (6) |
其中α为大于0的常数.
3 收敛性证明为得到GLHSS迭代法的收敛性质,需要以下引理:
引理1[8] 设A∈Cn×n,A=Mi-Ni(i=1, 2)为矩阵A的2种分裂格式,x(0)∈Cn为一个给定的初始向量,由矩阵A的2种分裂格式得到的二步迭代格式为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} = {\mathit{\boldsymbol{N}}_1}{\mathit{\boldsymbol{x}}^{\left( k \right)}} + \mathit{\boldsymbol{b}},\\ {\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{N}}_2}{\mathit{\boldsymbol{x}}^{\left( {k + \frac{1}{2}} \right)}} + \mathit{\boldsymbol{b}}. \end{array} \right. $ | (7) |
由上述二步迭代生成的迭代序列{x(k)}为
| $ {\mathit{\boldsymbol{x}}^{\left( {k + 1} \right)}} = \mathit{\boldsymbol{M}}_2^{ - 1}{\mathit{\boldsymbol{N}}_2}\mathit{\boldsymbol{M}}_1^{ - 1}{\mathit{\boldsymbol{N}}_1}{\mathit{\boldsymbol{x}}^{\left( k \right)}} + \mathit{\boldsymbol{M}}_2^{ - 1}\left( {\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{N}}_2}\mathit{\boldsymbol{M}}_1^{ - 1}} \right)\mathit{\boldsymbol{b}}. $ | (8) |
若该二步迭代法的迭代矩阵M2-1N2M1-1N1的谱半径ρ满足:
| $ \rho \left( {\mathit{\boldsymbol{M}}_2^{ - 1}{\mathit{\boldsymbol{N}}_2}\mathit{\boldsymbol{M}}_1^{ - 1}{\mathit{\boldsymbol{N}}_1}} \right) < 1, $ | (9) |
则对于任意初向量x(0)∈Cn,矩阵序列{x(k)}收敛于线性方程Ax=b的唯一解x*∈Cn.
引理2 对∀α>0, 若矩阵P为复数域上的正定矩阵,则‖P(αI+P)-1‖2 < 1,其中‖ ‖2表示矩阵的二范数.
证明 因P为正定矩阵,P*也为正定矩阵,α为一个大于0的常数,则对任意非零向量y有
| $ \left\langle {\left( {{\alpha ^2}\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{P}}^ * }} \right)\mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle > 0, $ | (10) |
其中〈, 〉表示向量内积,式(10)两端同时加上〈P*Py, y〉有
| $ \left\langle {\left( {{\alpha ^2}\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{P}}^ * } + {\mathit{\boldsymbol{P}}^ * }\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle > \left\langle {{\mathit{\boldsymbol{P}}^ * }\mathit{\boldsymbol{Py}},\mathit{\boldsymbol{y}}} \right\rangle , $ | (11) |
整理后即得
| $ \left\langle {\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}},\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}}} \right\rangle > \left\langle {\mathit{\boldsymbol{Py}},\mathit{\boldsymbol{Py}}} \right\rangle . $ | (12) |
令x=(αI+P)y,由于矩阵αI+P非奇异,所以对于任意非零向量x,都可找到一个非零向量y与之对应,经变换,式(12)可化为
| $ \left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}} \right\rangle > \left\langle {\mathit{\boldsymbol{P}}{{\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)}^{ - 1}}\mathit{\boldsymbol{x}},\mathit{\boldsymbol{P}}{{\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)}^{ - 1}}\mathit{\boldsymbol{x}}} \right\rangle , $ | (13) |
于是可得
| $ \frac{{{{\left\| {\mathit{\boldsymbol{P}}{{\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)}^{ - 1}}\mathit{\boldsymbol{x}}} \right\|}_2}}}{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_2}}} < 1. $ | (14) |
由向量x的任意性可得
| $ {\left\| {\mathit{\boldsymbol{P}}{{\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right)}^{ - 1}}} \right\|_2} < 1. $ | (15) |
证毕!
引理3 若P为复数域上的正定矩阵,记H=(P+P*)为埃尔米特正定矩阵,若
| $ {\left\| {\left( {\alpha \mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}} \right\|_2} < 1. $ |
证明 ∀y≠0∈Cn,若
| $ \left\langle {\alpha \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle < \left\langle {\mathit{\boldsymbol{Hy}},\mathit{\boldsymbol{y}}} \right\rangle . $ |
代入H=(P+P*),得到
| $ \left\langle {\alpha \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle < \left\langle {\left( {\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{P}}^ * }} \right)\mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle . $ | (16) |
式(16)两边做进一步整理,得
| $ \left\langle {\left( {{\alpha ^2}\mathit{\boldsymbol{I}} - \alpha \mathit{\boldsymbol{P}} - \alpha {\mathit{\boldsymbol{P}}^ * } + {\mathit{\boldsymbol{P}}^ * }\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}}} \right\rangle < \left\langle {{\mathit{\boldsymbol{P}}^ * }\mathit{\boldsymbol{Py}},\mathit{\boldsymbol{y}}} \right\rangle . $ | (17) |
于是有
| $ \left\langle {\left( {\alpha I - \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}},\left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{y}}} \right\rangle < \left\langle {\mathit{\boldsymbol{Py}},\mathit{\boldsymbol{Py}}} \right\rangle . $ | (18) |
令x=Py,由于y为任意非零向量且矩阵P为非奇异矩阵,因此,x可选取为任意非零向量,经变换,式(18)可化为
| $ \left\langle {\left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{x}},\left( {\alpha I - \mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{x}}} \right\rangle < \left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}} \right\rangle , $ | (19) |
变形后得到
| $ \frac{{{{\left\| {\left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{x}}} \right\|}_2}}}{{{{\left\| \mathit{\boldsymbol{x}} \right\|}_2}}} < 1. $ | (20) |
由于x的选取是任意的,因此,对于任意大于0的常数α有
| $ {\left\| {\left( {\alpha \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{P}}} \right){\mathit{\boldsymbol{P}}^{ - 1}}} \right\|_2} < 1. $ | (21) |
证毕!
定理1 假设P1和P2为复数域上的正定矩阵,记H=(P1+P1*)为一个由P1决定的埃尔米特正定矩阵,若
证明 由引理1,GLHSS迭代法对应的迭代矩阵为
| $ \mathit{\boldsymbol{M}}\left( \alpha \right) = {\left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right)^{ - 1}}\left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right)\mathit{\boldsymbol{P}}_1^{ - 1}\left( { - {\mathit{\boldsymbol{P}}_2}} \right). $ | (22) |
式(22)相似于:
| $ \mathit{\boldsymbol{M'}}\left( \alpha \right) = \left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right)\mathit{\boldsymbol{P}}_1^{ - 1}\left( { - {\mathit{\boldsymbol{P}}_2}} \right){\left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right)^{ - 1}}. $ | (23) |
对M′(α)谱半径ρ(M′(α)),有:
| $ \begin{array}{l} \rho \left( {\left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right)\mathit{\boldsymbol{P}}_1^{ - 1}} \right)\left( { - {\mathit{\boldsymbol{P}}_2}} \right){\left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right)^{ - 1}} \le \\ \;\;\;\;\;\;\;\;{\left\| {\left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right)\mathit{\boldsymbol{P}}_1^{ - 1}\left( { - {\mathit{\boldsymbol{P}}_2}} \right){{\left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right)}^{ - 2}}} \right\|_2} \le \\ \;\;\;\;\;\;\;\;{\left\| {\left( {\alpha \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_1}} \right)\mathit{\boldsymbol{P}}_1^{ - 1}} \right\|_2}{\left\| {\left( { - {\mathit{\boldsymbol{P}}_2}} \right){{\left( {\alpha \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_2}} \right)}^{ - 1}}} \right\|_2}. \end{array} $ | (24) |
由引理2可得‖(-P2)(αI+P2)-1‖2<1;由引理3可得‖(αI-P1)P1-1‖2<1.
综上, 即可得到M′(α)的谱半径ρ(M′(α))<1;再由矩阵的相似性质,即可得到ρ(M(α))<1.
证毕!
4 数值实验数值实验中用Matlab编程求解以下大型稀疏矩阵的线性方程组:
| $ \begin{array}{l} \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}},\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{B}} + {\mathit{\boldsymbol{B}}^{\rm{T}}} \otimes \mathit{\boldsymbol{I}}, \end{array} $ |
其中,
| 表 1 n=8时HSS和GLHSS法的迭代次数和迭代时间比较 Table 1 Comparison of IT and CPU between HSS and GLHSS when n=8 |
| 表 2 n=16时HSS和GLHSS法的迭代次数和迭代时间比较 Table 2 Comparison of IT and CPU between HSS and GLHSS when n=16 |

|
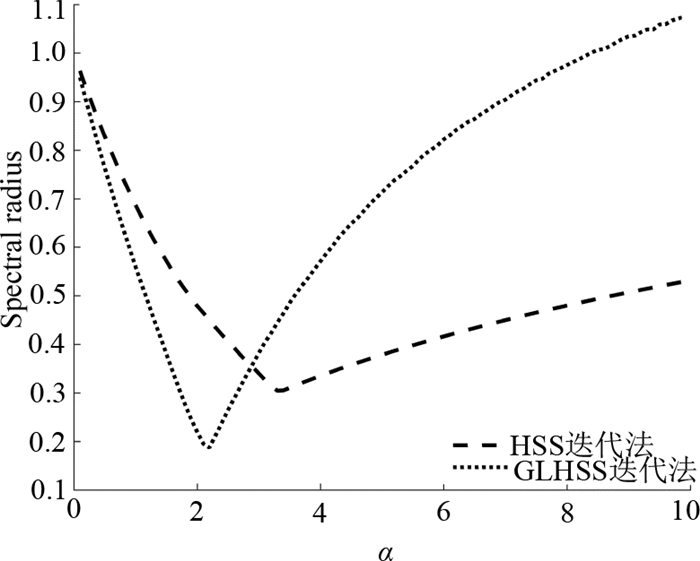
图 1 n=8时HSS与GLHSS法谱半径比较 Fig. 1 Comparison of spectral radius between HSS and GLHSS when n=8 |
|
图 2 n=16时HSS与GLHSS法谱半径比较 Fig. 2 Comparison of spectral radius between HSS and GLHSS when n=16 |
|
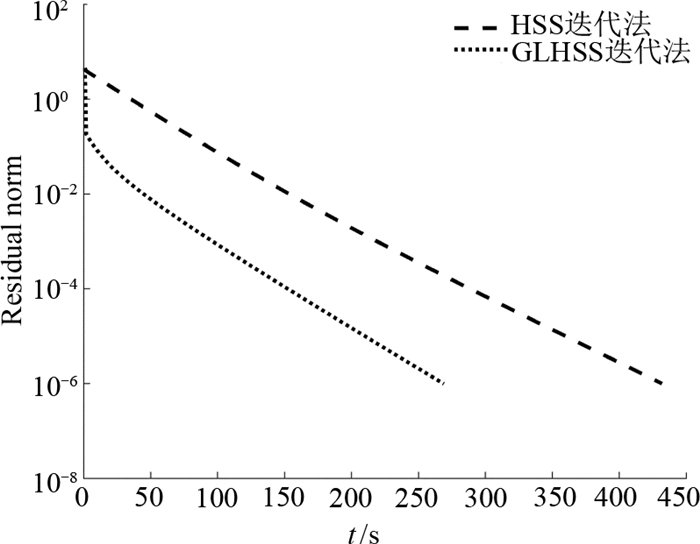
图 3 n=8时HSS与GLHSS法残量下降速度比较 Fig. 3 Comparison of residual decline between HSS and GLHSS when n=8 |
|
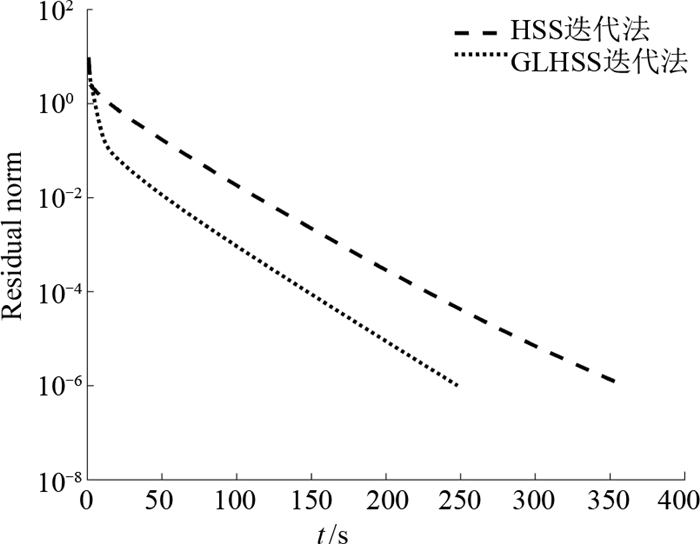
图 4 n=16时HSS与GLHSS法残量下降速度比较 Fig. 4 Comparison of residual decline between HSS and GLHSS when n=16 |
从图 1~图 4、表 1和表 2中可以看出,对于本文中的算例,GLHSS法到达截断误差所需的迭代步数及迭代时间均优于HSS,GLHSS迭代矩阵的最小谱半径优于HSS,且残量下降速度亦优于HSS.
当α大到一定程度后,GLHSS迭代法的收敛性弱于HSS,这是由于α的取值受限于埃尔米特正定矩阵H=(P1+P1*)的最小特征值.
5 总结提出了一种广义的LHSS(GLHSS)迭代法用于求解大规模正定线性方程组,数值结果表明,该方法在求解某些问题时较经典的HSS迭代法效果更好.将来的研究可以围绕如何选取更佳的正定矩阵来开展.
| [1] | BAI Z Z, GOLUB C H, NG M K. Hermitian and skew-Hermitian splitting methods for non-Hermiti-an positive definite linear systems[J]. SIAM Journal on Matrix Analysis and Applications, 2003, 24(3): 603–626. DOI:10.1137/S0895479801395458 |
| [2] | BAI Z Z, GOLUB G H, LU L Z. Block-triangula-r and skew-Hermitian splitting methods for positive definite linear systems[J]. SIAM Journal on Scientific Computing, 2005, 26(3): 844–863. DOI:10.1137/S1064827503428114 |
| [3] | CAO Y, TAN W W, JIANG M Q. A generalization of the positive-definite and skew-Hermitian splitting iteration[J]. Numerical algebra, Control and Optimization, 2012, 2(4): 811–821. DOI:10.3934/naco |
| [4] | LI W W, WANG X. A modified GPSS method for non-Hermitian positive definite linear system[J]. Applied Mathematics and Computation, 2014, 234(C): 253–259. |
| [5] | HUANG N, MA C F. Positive definite and semi-definite splitting methods for non-Hermitian positive definite linear systems[J]. Journal of Computational Mathematics, 2016, 34(3): 300–316. DOI:10.4208/jcm |
| [6] | LI L, HUANG T Z, LIU X P. Modified Hermitian and skew-Hermitian splitting methods for non-Hermitian positive-definite linear systems[J]. Numerical Linear Algebra and with Applications, 2007, 14(3): 217–235. DOI:10.1002/(ISSN)1099-1506 |
| [7] | POUR H N, GOUGHERY H S. New Hermitian and skew-Hermitian splitting methods for non-Hermitian positive-definite linear systems[J]. Numerical Algorithms, 2015, 69(1): 207–225. DOI:10.1007/s11075-014-9890-4 |
| [8] |
李文伟.一类线性方程组和矩阵方程的数值求解方法的研究[D].南昌: 南昌大学, 2014.
LI W W.The Study of Numerical Methods for A Kind of Linear Equations and Matrix Equations[D]. Nanchang: Nanchang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10403-1014055451.htm |



