近几十年来, 数学工作者十分关注偏微分方程尤其是非线性椭圆方程解的存在性、唯一性、正则性等问题.本文在加权Sobolev空间框架下,研究一类带有退化强制项的非线性椭圆方程
| $ \left\{ \begin{array}{l} - {\rm{div}}\left( {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}}} \right) + g\left( {x,u} \right) = f,x \in \Omega ,\\ u = 0,\;\;\;\;\;x \in \partial \Omega , \end{array} \right. $ | (1) |
其中Ω是RN(N≥2)中的有界区域,γ > 0, f∈L1(Ω),W01, p(Ω, ω)为加权的Sobolev空间,ω ={ωi(x)}0≤i≤N为权函数,p为满足1 < p < ∞的实数.此外,假设:
H1 a (x, ξ)={ai(x, ξ)}1≤i≤N:Ω×RN→RN是一个Carathéodory向量值函数,对任意的x∈Ω,每一个ξ∈RN有以下不等式成立:
| $ \left| {{a_i}\left( {x,\xi } \right)} \right| \le \beta \omega _i^{\frac{1}{p}}\left( x \right)\left[ {k\left( x \right) + \sum\limits_{j = 1}^N {\omega _i^{\frac{1}{{p'}}}\left( x \right){{\left| {{\xi _j}} \right|}^{p - 1}}} } \right], $ | (2) |
| $ \mathit{\boldsymbol{a}}\left( {x,\xi } \right) \cdot \xi \ge \alpha \sum\limits_{i = 1}^N {{\omega _i}\left( x \right){{\left| {{\xi _i}} \right|}^p}} , $ | (3) |
| $ \left[ {\mathit{\boldsymbol{a}}\left( {x,\xi } \right) - \mathit{\boldsymbol{a}}\left( {x,\eta } \right)} \right] \cdot \left( {\xi - \eta } \right) > 0,\xi \ne \eta \in {R^N}, $ | (4) |
其中,k(x)是Lp′(Ω)中一个正函数,
H2 g(x, s)是一个Carathéodory函数,对几乎所有的x∈Ω,每一个ξ∈RN,且对任意的k∈R+,有
| $ g\left( {x,s} \right) \cdot s \ge 0, $ | (5) |
| $ \sup \left| {g\left( {x,s} \right)} \right| = {h_k}\left( x \right) \in {L^1}\left( \Omega \right). $ | (6) |
H3 ω ={ωi(x)}0≤i≤N是一个在Ω上几乎处处严格正的可测权函数向量, 满足
| $ {\omega _i} \in L_{{\rm{loc}}}^1\left( \Omega \right),\;\;\;\;\omega _i^{ - \frac{1}{{p - 1}}} \in L_{{\rm{loc}}}^1\left( \Omega \right). $ |
下文将从两方面来陈述所研究问题的特点.首先,与其他文献最主要的区别是,本研究的椭圆问题(1)在加权的Sobolev空间,权函数的引入,使得嵌入关系发生了很大的变化,这给问题的解决带来了一定的困难.另外,很多文献关注了与式(1)类似的问题[1-7],文献[1]考虑了在空间不加权的框架下,当p=2,0≤γ < 1,f∈Lm(Ω)且g(x, u)=0时f可积性的变化对u正则性的影响. BOCCARDO等[8]同样在空间不加权的情形下,研究了当g(x, u)=u, f∈Lm(Ω)时问题(1)解的存在性与非存在性. CROCE等[6]证明了在空间不加权的情形下,当g(x, u)=|u|q-1u时,存在解u∈Lq(Ω),并讨论了指标q对解u正则性的影响.
其次, 问题(1)的假设条件(2)意味着当u很大时,
首先,介绍常指数情形下加权Sobolev空间的相关知识[9].
(1) Lp(Ω, γ)空间
| $ {L^p}\left( {\Omega ,\mathit{\boldsymbol{\gamma }}} \right) = \left\{ {u = u\left( x \right):u{\mathit{\boldsymbol{\gamma }}^{\frac{1}{p}}} \in {L^p}\left( \Omega \right)} \right\}, $ |
其中γ为权函数, 赋予以下Luxemburg范数:
| $ {\left\| u \right\|_{p,\mathit{\boldsymbol{\gamma }}}} = {\left( {\int_\Omega {{{\left| {u\left( x \right)} \right|}^p}\mathit{\boldsymbol{\gamma }}\left( x \right){\rm{d}}x} } \right)^{\frac{1}{p}}}. $ |
(2) W01, p(Ω, ω)空间
记X=:W01, p(Ω, ω)空间为所有实值函数u∈Lp(Ω, ω0)所构成的空间,对所有的i=1, 2, …, N,其弱导数满足
| $ \frac{{\partial u}}{{\partial {x_i}}} \in {L^p}\left( {\Omega ,{\omega _i}} \right). $ |
赋予范数
| $ \begin{array}{l} {\left\| u \right\|_{1,p,\mathit{\boldsymbol{\omega }}}} = \left( {\int_\Omega {{{\left| {u\left( x \right)} \right|}^p}{\omega _0}\left( x \right){\rm{d}}x} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\sum\limits_{i = 1}^N {\int_\Omega {{{\left| {\frac{{\partial u\left( x \right)}}{{\partial {x_i}}}} \right|}^p}{\omega _i}\left( x \right){\rm{d}}x} } } \right)^{\frac{1}{p}}}. \end{array} $ |
定义在X上的范数为
| $ {\left\| u \right\|_X}: = {\left( {\sum\limits_{i = 1}^N {\int_\Omega {{{\left| {\frac{{\partial u\left( x \right)}}{{\partial {x_i}}}} \right|}^p}{\omega _i}\left( x \right){\rm{d}}x} } } \right)^{\frac{1}{p}}}, $ |
等价于‖·‖1, p, ω.(X, ‖·‖1, p, ω)是一个自反的Banach空间, 其对偶空间为W0-1, p′(Ω, ω*), 其中
(3) 加权的Hardy型不等式
一般情形下,存在权函数ω (x)和实数q(1 < q < ∞),满足σ1-q′∈L1(Ω),
| $ {\left( {\int_\Omega {{{\left| {u\left( x \right)} \right|}^q}\sigma {\rm{d}}x} } \right)^{\frac{1}{q}}} \le C{\left( {\sum\limits_{i = 1}^N {\int_\Omega {{{\left| {\frac{{\partial u\left( x \right)}}{{\partial {x_i}}}} \right|}^p}{\omega _i}\left( x \right){\rm{d}}x} } } \right)^{\frac{1}{p}}}. $ |
进而,X紧嵌入Lq(Ω, σ)中.有关加权的Hardy不等式例子可参见文献[10-11].
其次, 介绍截断函数的相关知识.一般情形下, 对于在R中的s, k, 其中k≥0, 高度为k的Truncation函数[12-13]定义为
| $ {T_k}\left( s \right) = \max \left( { - k,\min \left( {k,s} \right)} \right) = \left\{ \begin{array}{l} s,\left| s \right| < k,\\ k,s \ge k,\\ - k,s \le - k. \end{array} \right. $ |
鉴于其重要性,给出其简图,见图 1.
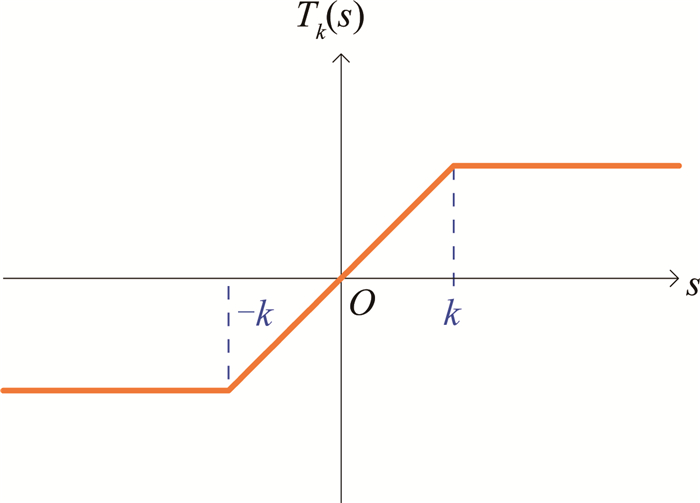
|
图 1 Tk(s) Fig. 1 Tk(s) |
Marcinkiewicz空间的定义由BÉNLIAN等[14]提出.
定义1 若一个可测函数f:Ω→R相应的分布函数ϕf(k)≤meas{x∈Ω:|f(x)| > k}, k > 0, 满足
| $ {\phi _f}\left( k \right) \le C{k^{ - q}},C\;为常数, $ |
则称f属于Marcinkiewicz空间Μq(Ω).
下面给出问题(1)重整化解的定义, 此定义在带有扩散项的微分方程理论中是非常经典的.
定义2 若满足
(1) Tk(u)∈W01, p(Ω, ω), k > 0;
(2) g(x, u)∈L1(Ω),同时
| $ \mathop {\lim }\limits_{j \to \infty } \int_{\Omega \cap \left\{ {j \le \left| u \right| \le j + 1} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}}\nabla u{\rm{d}}x} = 0; $ | (7) |
(3) 对每一个具有紧支集的函数S∈W1, ∞(R),对任何ζ∈W01, p(Ω, ω)∩L∞(Ω)均有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}} \cdot \nabla \left( {S\left( u \right)\zeta } \right){\rm{d}}x} + \\ \;\;\;\;\int_\Omega {g\left( {x,u} \right)S\left( u \right)\zeta {\rm{d}}x} = \int_\Omega {fS\left( u \right)\zeta {\rm{d}}x} , \end{array} $ | (8) |
则称可测函数u∈W01, p(Ω, ω)是问题(1)的重整化解.
2 重整化解的存在性定理1 假设H1~H3成立,f∈L1(Ω),则问题(1)至少存在1个重整化解u.
证明 分5步完成.
第1步 逼近问题及先验估计.
先建立问题(1)的逼近问题.对n∈ N, 设un满足
| $ \left\{ \begin{array}{l} - {\rm{div}}\left( {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}} \right) + {g_n}\left( {x,{u_n}} \right) = {f_n},\;\;\;x \in \Omega ,\\ {u_n} = 0,\;\;\;\;\;\;x \in \partial \Omega , \end{array} \right. $ | (9) |
其中fn是L∞(Ω)中的函数序列且在L1(Ω)中强收敛于f并且‖fn‖L1(Ω)≤‖f‖L1(Ω),gn(x, s)=Tng(x, s), 且满足式(5)和(6).由文献[15]的pseudo-monotone算子理论可知, 逼近问题(9)至少存在1个弱解且对任意v∈W01, p(Ω, ω)∩L∞(Ω), 有
| $ \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}} \cdot \nabla v{\rm{d}}x + \int_\Omega {{g_n}\left( {x,{u_n}} \right)v{\rm{d}}x} = \int_\Omega {{f_n}v{\rm{d}}x} . $ | (10) |
接下来, 对解序列un做一些先验估计, 选取式(9)中Tk(un)(k > 0)作为检验函数, 则有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right.}^\gamma }}}} \cdot \nabla {T_k}\left( {{u_n}} \right){\rm{d}}x + \\ \;\;\;\;\;\int_\Omega {{g_n}\left( {x,{u_n}} \right){T_k}\left( {{u_n}} \right){\rm{d}}x} = \int_\Omega {{f_n}{T_k}\left( {{u_n}} \right){\rm{d}}x} . \end{array} $ | (11) |
由于Tk(s)与s同号,结合式(5),式(11)左端第2项为非负项,去掉非负项可得
| $ \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right.}^\gamma }}}} \cdot \nabla {T_k}\left( {{u_n}} \right){\rm{d}}x \le k\int_\Omega {\left| {{f_n}} \right|{\rm{d}}x} . $ |
考虑式(3),并选取n > k,有
| $ \frac{\alpha }{{{{\left( {1 + k} \right)}^\gamma }}}\sum\limits_{i = 1}^N {\int_\Omega {{\omega _i}\left( x \right){{\left| {\frac{{\partial {T_k}\left( {{u_n}} \right)}}{{\partial {x_i}}}} \right|}^p}{\rm{d}}x} } \le k\int_\Omega {\left| {{f_n}} \right|{\rm{d}}x} . $ | (12) |
因此,对所有的k > 0,有
| $ \sum\limits_{i = 1}^N {\int_\Omega {{\omega _i}\left( x \right){{\left| {\frac{{\partial {T_k}\left( {{u_n}} \right)}}{{\partial {x_i}}}} \right|}^p}{\rm{d}}x} } \le \frac{{k{{\left( {1 + k} \right)}^\gamma }{{\left\| f \right\|}_{{L^1}\left( \Omega \right)}}}}{{{c_0}}}. $ | (13) |
如果k≥1, 有
| $ \sum\limits_{i = 1}^N {\int_\Omega {{\omega _i}\left( x \right){{\left| {\frac{{\partial {T_k}\left( {{u_n}} \right)}}{{\partial {x_i}}}} \right|}^p}{\rm{d}}x} } \le \frac{{{2^\gamma }{k^{\gamma + 1}}{{\left\| f \right\|}_{{L^1}\left( \Omega \right)}}}}{{{c_0}}}. $ | (14) |
由加权Hardy不等式,同时结合式(14)以及σ1-q′∈L1(Ω),当k≥1,p > γ+1时,有
| $ \begin{array}{l} \left| {\left\{ {\left| {{u_n}} \right| > k} \right\}} \right| = \int_{\left\{ {\left| {{u_n}} \right| > k} \right\}} {\frac{{\left| {{T_k}\left( {{u_n}} \right)} \right|{\sigma ^{\frac{1}{q}}}}}{{k{\sigma ^{\frac{1}{q}}}}}{\rm{d}}x} \le \\ \;\;\;\;\frac{1}{k}{\left( {\int_\Omega {{{\left| {{T_k}\left( {{u_n}} \right)} \right|}^q}\sigma {\rm{d}}x} } \right)^{\frac{1}{q}}}{\left( {\int_\Omega {{\sigma ^{ - \frac{{q'}}{q}}}{\rm{d}}x} } \right)^{\frac{1}{q}}} \le \\ \;\;\;\;\frac{1}{k}{\left( {\sum\limits_{i = 1}^N {\int_\Omega {{\omega _i}\left( x \right)\left| {\frac{{\partial {T_k}\left( {{u_n}} \right)}}{{\partial {x_i}}}} \right|{\rm{d}}x} } } \right)^{\frac{1}{p}}}{\left( {\int_\Omega {{\sigma ^{ - \frac{{q'}}{q}}}{\rm{d}}x} } \right)^{\frac{1}{{q'}}}} \le \\ \;\;\;\;C{k^{\frac{{\gamma + 1 - p}}{p}}}{\left\| {{\sigma ^{1 - q'}}} \right\|_{{L^1}\left( \Omega \right)}}, \end{array} $ |
其中C为常数,当0 < k < 1时,显然
| $ {\rm{meas}}\left\{ {\left| {{u_n}} \right| > k} \right\} \le \left| \Omega \right|, $ |
得到
| $ \mathop {\lim }\limits_{k \to + \infty } {\rm{meas}}\left\{ {\left| {{u_n}} \right| > k} \right\} = 0,关于\;n\;一致. $ | (15) |
第2步 un在Ω上几乎处处收敛.
先证un依测度收敛.注意到对任意的k, ε > 0, 有
| $ \begin{array}{l} \left\{ {\left| {{u_n} - {u_m}} \right| > t} \right\} \subset \left\{ {\left| {{u_n}} \right| > k} \right\} \cup \left\{ {\left| {{u_m}} \right| > k} \right\} \cup \\ \;\;\;\;\;\left\{ {{T_k}\left( {{u_n}} \right) - {T_k}\left( {{u_m}} \right)\left| { > t} \right.} \right\}, \end{array} $ |
即
| $ \begin{array}{l} {\rm{meas}}\left\{ {\left| {{u_n} - {u_m}} \right| > t} \right\} \le {\rm{meas}}\left\{ {\left| {{u_n}} \right| > k} \right\} + \\ \;\;\;\;\;\;{\rm{meas}}\left\{ {\left| {{u_m}} \right| > k} \right\} + {\rm{meas}}\left\{ {{T_k}\left( {{u_n}} \right) - {T_k}\left( {{u_m}} \right)\left| { > t} \right.} \right\}. \end{array} $ | (16) |
由式(13)可知,Tk(un)在W01, p(Ω, ω)中有界,那么存在νk∈W01, p(Ω, ω),使得对任意的k > 0, 有Tk(un)→νk于W01, p(Ω, ω)中弱收敛,Tk(un)→νk于Lq(Ω, σ)中强收敛,且在Ω上几乎处处收敛.
由此可知,Tk(un)是在Ω中依测度收敛的柯西列.那么,对任意的ε > 0,存在k(ε) > 0,当m,n充分大时,并结合式(16)可得,un是一个依测度收敛的Cauchy序列,因此,un依测度收敛[16].根据Riesz定理,un存在一个子列(仍记其本身)以及一个可测函数u,使得
| $ {u_n} \to u\;在\;\Omega \;上几乎处处收敛. $ | (17) |
联合式(13)和(17),对任意的k > 0,有
| $ {T_k}\left( {{u_n}} \right) \to {T_k}\left( u \right)\; 于\;W_0^{1,p}\left( {\Omega ,\mathit{\boldsymbol{\omega }}} \right)\;中弱收敛, $ | (18) |
| $ {T_k}\left( {{u_n}} \right) \to {T_k}\left( u \right)在\;\Omega \;上几乎处处收敛. $ | (19) |
因此,对任意的k > 0, 有Tk(u)∈W01, p(Ω, ω).
第3步 gn(x, un)在L1(Ω)中强收敛.
证明
| $ {g_n}\left( {x,{u_n}} \right) \to g\left( {x,u} \right)\;于\;{L^1}\left( \Omega \right)\;中强收敛. $ | (20) |
直观起见,给出θl1(s)的简图如图 2所示.在式(9)中选取θl1(un)=Tl+1(un)-Tl(un) (l > 0)作为检验函数,则有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}} \cdot \nabla \left( {{T_{l + 1}}\left( {{u_n}} \right) - {T_{l + 1}}\left( {{u_n}} \right)} \right){\rm{d}}x + \\ \;\;\;\;\;\;\int_\Omega {{g_n}\left( {x,{u_n}} \right)\left( {{T_{l + 1}}\left( {{u_n}} \right) - {T_{l + 1}}\left( {{u_n}} \right)} \right){\rm{d}}x} = \\ \;\;\;\;\;\;\int_\Omega {{f_n}\left( {{T_{l + 1}}\left( {{u_n}} \right) - {T_l}\left( {{u_n}} \right)} \right){\rm{d}}x} . \end{array} $ |
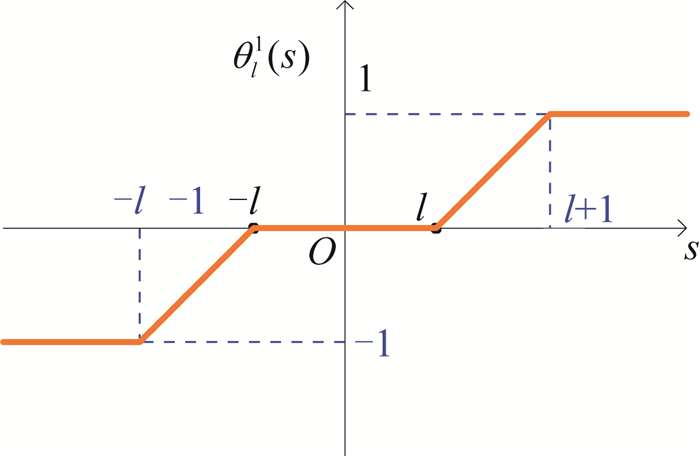
|
图 2 θl1(s) Fig. 2 θl1(s) |
整理后可得
| $ \begin{array}{l} \int_{\left\{ {l \le \left| {{u_n}} \right| \le l + 1} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\nabla {u_n}{\rm{d}}x} + \\ \;\;\;\;\;\int_{\left\{ {\left| {{u_n}} \right| \ge l} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} \le \int_{\left\{ {\left| {{u_n}} \right| \ge l} \right\}} {\left| {{f_n}} \right|{\rm{d}}x} . \end{array} $ |
由式(3)可知,上式左端第1项为非负项,去掉非负项,有
| $ \int_{\left\{ {\left| {{u_n}} \right| \ge l} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} \le \int_{\left\{ {\left| {{u_n}} \right| \ge l} \right\}} {\left| {{f_n}} \right|{\rm{d}}x} . $ |
注意到式(15)以及fn在L1(Ω)中强紧,有
| $ \mathop {\lim }\limits_{k \to + \infty } \mathop {\sup }\limits_{n \in N} \int_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}} {\left| {{f_n}} \right|{\rm{d}}x = 0} . $ |
设ε > 0,存在l(ε)≥1,使得
| $ \int_{\left\{ {\left| {{u_n}} \right| \ge l\left( \varepsilon \right)} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} \le \frac{\varepsilon }{2}. $ | (21) |
对于Ω中的任何可测子集E,有
| $ \begin{array}{l} \int_E {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} \le \int_{E \cap \left\{ {\left| {{u_n}} \right| \ge l\left( \varepsilon \right)} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} + \\ \;\;\;\;\int_{E \cap \left\{ {\left| {{u_n}} \right| > l\left( \varepsilon \right)} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} \le \int_E {\left| {{h_{l\left( \varepsilon \right)}}\left( x \right)} \right|{\rm{d}}x} + \\ \;\;\;\;\int_{E \cap \left\{ {\left| {{u_n}} \right| > l\left( \varepsilon \right)} \right\}} {\left| {{g_n}\left( {x,{u_n}} \right)} \right|{\rm{d}}x} . \end{array} $ |
注意到式(6),存在η(ε) > 0,满足meas(E) < η(ε),使得
| $ \int_E {\left| {{h_{l\left( \varepsilon \right)}}\left( x \right)} \right|{\rm{d}}x} \le \frac{\varepsilon }{2}. $ | (22) |
综上,结合式(21)和(22),易得对所有的E,若满足meas(E) < η(ε),则有∫E|gn(x, un)|dx≤ε.同时由式(17)可知,gn(x, un)→g(x, u)在Ω上几乎处处收敛.根据Vitali定理,有
gn(x, un)→g(x, u)于L1(Ω)中强收敛.
第4步 Tk(un)在W01, p(Ω, ω)中强收敛于Tk(u).
下面证明对每一个k > 0, Tk(un)在W01, p(Ω, ω)中强收敛于Tk(u).设h > k,选取T2k(un-Th(un)+ Tk(un)-Tk(u))作为式(9)的1个检验函数,有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}} \cdot \nabla {T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + {T_k}\left( {{u_n}} \right) - } \right.\\ \;\;\;\;\;\;\left. {{T_k}\left( u \right)} \right){\rm{d}}x + \int_\Omega {{g_n}\left( {x,{u_n}} \right){T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + } \right.} \\ \;\;\;\;\;\;\left. {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right){\rm{d}}x = \int_\Omega {{f_n}{T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + } \right.} \\ \;\;\;\;\;\;\left. {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right){\rm{d}}x. \end{array} $ | (23) |
方便起见,将式(23)记为
| $ {I_1} + {I_2} = {I_3}, $ |
同时定义εn, h为
| $ \mathop {\lim }\limits_{h \to + \infty } \mathop {\lim }\limits_{n \to + \infty } {\varepsilon _{n,h}} = 0, $ |
类似地,εn表示
关于I2,I3,结合式(17)和(20),以及fn在L1(Ω)中强紧,有
| $ \begin{array}{l} \int_\Omega {{g_n}\left( {x,{u_n}} \right){T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + {T_k}\left( {{u_n}} \right) - } \right.} \\ \;\;\;\;\;\;\;\left. {{T_k}\left( u \right)} \right){\rm{d}}x = {\varepsilon _{n,h}}, \end{array} $ | (24) |
| $ \int_\Omega {{f_n}{T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + {T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right){\rm{d}}x} = {\varepsilon _{n,h}}. $ | (25) |
关于I1,令M=4k+h,易知当|un| > M时,
| $ \nabla {T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + {T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right) = 0, $ |
I1可化为
| $ \begin{array}{l} {I_1} = \int_{\left\{ {\left| {{u_n}} \right| < k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}} \cdot \nabla {T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + } \right.} \\ \;\;\;\;\;\;\left. {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right){\rm{d}}x + \int_{\left\{ {\left| {{u_n}} \right| < k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}} \cdot } \\ \;\;\;\;\;\;\nabla {T_{2k}}\left( {{u_n} - {T_h}\left( {{u_n}} \right) + {T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right){\rm{d}}x. \end{array} $ |
考虑到在集合{|un| < k}上,un-Th(un)=0,集合{|un|≥k}上,∇Tk(un)=0,并注意到a(x, ξ)·ξ≥0,有
| $ \begin{array}{l} {I_1} \ge \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right)\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} + \\ \;\;\;\;\;\;\int_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\nabla \left( {{u_n} - {T_h}\left( {{u_n}} \right)} \right){\rm{d}}x} - \\ \;\;\;\;\;\;\int_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\nabla {T_h}\left( u \right){\rm{d}}x} . \end{array} $ |
去掉上式右端第2个非负项,有
| $ \begin{array}{l} {I_1} \ge \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right)\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} - \\ \;\;\;\;\;\;\int_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\nabla {T_k}\left( u \right){\rm{d}}x} . \end{array} $ |
并对右端第1项进行整理,可得
| $ \begin{array}{l} {I_1} \ge \\ \int_\Omega {\frac{{\left[ {\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right) - \mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( u \right)} \right)} \right]\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} + \\ \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( u \right)} \right)\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} - \\ \int_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}} {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\nabla {T_k}\left( u \right){\rm{d}}x} = \\ {I_{11}} + {I_{12}} + {I_{13}}. \end{array} $ |
关于I12,由式(2)可知,
| $ {I_{12}} = {\varepsilon _n}. $ | (26) |
关于I13,可整理为
| $ {I_{13}} = - \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_M}\left( {{u_n}} \right)} \right)\nabla {T_k}\left( u \right){{\rm{ \mathsf{ χ} }}_{\left\{ {\left| {{u_n}} \right| \ge k} \right\}}}}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} . $ |
令n > M,当n→∞时,
| $ {I_{13}} = {\varepsilon _n}. $ |
因而,结合I12,I13的估计式,I1可整理为
| $ \begin{array}{l} {I_1} \ge \\ \int_\Omega {\frac{{\left[ {\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right) - \mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( u \right)} \right)} \right]\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}{\rm{d}}x} . \end{array} $ |
综上,注意到式(24)和(25),对n > M > h > k,有
| $ \begin{array}{l} {\varepsilon _{n,h}} = {I_1} \ge \\ \int_\Omega {\frac{{\left[ {\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right) - \mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( u \right)} \right)} \right]\nabla \left( {{T_k}\left( {{u_n}} \right) - {T_k}\left( u \right)} \right)}}{{{{\left( {1 + k} \right)}^\gamma }}}{\rm{d}}x} . \end{array} $ |
考虑到式(4),则有
| $ \begin{array}{l} \mathop {\lim }\limits_{n \to \infty } \int_\Omega {\left[ {\mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( {{u_n}} \right)} \right) - \mathit{\boldsymbol{a}}\left( {x,\nabla {T_k}\left( u \right)} \right)} \right]\nabla \left( {{T_k}\left( {{u_n}} \right) - } \right.} \\ \;\;\;\;\;\;\left. {{T_k}\left( u \right)} \right){\rm{d}}x = 0. \end{array} $ |
于是可得,当n→∞时,有
| $ {T_k}\left( {{u_n}} \right) \to {T_k}\left( u \right)\;于\;{\left( {{L^p}\left( {\Omega ,\mathit{\boldsymbol{\omega }}} \right)} \right)^N}\;中强收敛. $ | (27) |
第5步 u为重整化解.
选取unζ作为式(9)的一个检验函数,其中ζ∈D(Ω),且S∈W1, ∞(Ω)具有紧支集,有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{\left( {1 + {T_n}\left( {{u_n}} \right)} \right)}^{\gamma }}\zeta } \cdot \nabla S\left( {{u_n}} \right){\rm{d}}x + \\ \;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}S\left( {{u_n}} \right)} \cdot \nabla \zeta {\rm{d}}x + \\ \;\;\;\;\;\int_\Omega {{g_n}\left( {x,{u_n}} \right)S\left( {{u_n}} \right)\zeta {\rm{d}}x} = \int_\Omega {{f_n}S\left( {{u_n}} \right)\zeta {\rm{d}}x} . \end{array} $ | (28) |
由于fn在L1(Ω)中是强紧的,且S(un)ζ在L∞(Ω)中有界,结合式(17)和(20),当n→∞时,可得
| $ \begin{array}{*{20}{c}} {\int_\Omega {{g_n}\left( {x,{u_n}} \right)S\left( {{u_n}} \right)\zeta {\rm{d}}x} \to \int_\Omega {g\left( {x,u} \right)S\left( u \right)\zeta {\rm{d}}x} ,}\\ {\int_\Omega {{f_n}S\left( {{u_n}} \right)\zeta {\rm{d}}x} \to \int_\Omega {fS\left( u \right)\zeta {\rm{d}}x} } \end{array} $ |
因为函数S,S′具有紧支集,那么存在L > 0,使得suppS⊂[-L, L],suppS′⊂[-L, L].当n充分大时,结合式(9)和(17),有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^{\gamma }}\zeta } \cdot \nabla S\left( {{u_n}} \right){\rm{d}}x = \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_L}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_L}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\zeta } \cdot \nabla S\left( {{u_n}} \right){\rm{d}}x \to \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_L}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_L}\left( u \right)} \right|} \right)}^\gamma }}}\zeta } \cdot \nabla S\left( u \right){\rm{d}}x = \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + u} \right)}^\gamma }}}\zeta } \cdot \nabla S\left( u \right){\rm{d}}x. \end{array} $ |
注意到式(2)和(27),当n充分大时,有
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}} S\left( {{u_n}} \right) \cdot \nabla \zeta {\rm{d}}x = \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_L}\left( {{u_n}} \right)} \right)}}{{{{\left( {1 + \left| {{T_L}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}S\left( {{u_n}} \right)} \cdot \nabla \zeta {\rm{d}}x \to \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {T_L}\left( u \right)} \right)}}{{{{\left( {1 + \left| {{T_L}\left( u \right)} \right|} \right)}^\gamma }}}S\left( u \right)} \cdot \nabla \zeta {\rm{d}}x = \\ \;\;\;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + u} \right)}^\gamma }}}S\left( u \right)} \cdot \nabla \zeta {\rm{d}}x. \end{array} $ |
综上,对式(28)在n→∞时取极限,可得
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}}\zeta } \cdot \nabla S\left( u \right){\rm{d}}x + \\ \;\;\;\;\;\int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}}S\left( u \right)} \cdot \nabla \zeta {\rm{d}}x + \\ \;\;\;\;\;\int_\Omega {g\left( {x,u} \right)S\left( u \right)\zeta {\rm{d}}x} = \int_\Omega {fS\left( u \right)\zeta {\rm{d}}x} , \end{array} $ |
此式等价于式(8).
现证明重整化解存在的条件,即当j→∞时,
| $ \begin{array}{l} \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla {u_n}} \right)}}{{{{\left( {1 + \left| {{T_n}\left( {{u_n}} \right)} \right|} \right)}^\gamma }}}\zeta } \cdot \left| {\nabla \left( {{T_{j + 1}}\left( {{u_n}} \right) - } \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {{T_j}\left( {{u_n}} \right)} \right)} \right|{\rm{d}}x \to \int_\Omega {\frac{{\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right)}}{{{{\left( {1 + \left| u \right|} \right)}^\gamma }}}\zeta } \cdot \\ \;\;\;\;\;\;\left| {\nabla \left( {{T_{j + 1}}\left( {{u_n}} \right) - {T_j}\left( u \right)} \right)} \right|{\rm{d}}x, \end{array} $ |
令j→∞,即可得到
| $ \int_{\left\{ {j < \left| u \right| < j + 1} \right\}} {\mathit{\boldsymbol{a}}\left( {x,\nabla u} \right) \cdot \nabla u{\rm{d}}x} \to 0. $ |
| [1] | BOCCARDO L, DALL'AGLIO A, ORSINA L. Existence and regularity results for some elliptic equations with degenerate coercivity[J]. Atti del Semimario Matematico e Fisico dell' Universitã di Modena, 1998, 46: 51–82. |
| [2] | DAIL L, GAO W J, LI Z Q. Existence of solutions for degenerate elliptic problems in weighted Sobolev space[J]. Journal of Function Spaces, 2015, 2015(71): 1–9. |
| [3] | GIACHETTI D, PORZIO M M. Existence results for some nonuniformly elliptic equations with irregular data[J]. Journal of Mathematical Analysis and Applications, 2001, 257(1): 100–130. DOI:10.1006/jmaa.2000.7324 |
| [4] | GIACHETTI D, PORZIO M M. Elliptic equations with degenerate coercivity:Gradient regularity[J]. Acta Mathematica Sinica, 2003, 19(2): 349–370. DOI:10.1007/s10114-002-0235-1 |
| [5] | PORRETTA A. Uniqueness and homogenization for a class of non coercive operators in divergence form[J]. Atti del Semimario Matematico e Fisico dell' Universitã di Modena, 1998, 46: 915–936. |
| [6] | CROCE G. The regularizing effects of some lower order terms in an elliptic equation with degenerate coercivity[J]. Rendiconti di Matematica, 2007, 27: 299–314. |
| [7] | LEONE C, PORRETTA A. Entropy solutions for nonlinear elliptic equations in L1(Ω)[J]. Nonlinear Analysis Theory Methods and Applications, 1998, 32(3): 325–334. DOI:10.1016/S0362-546X(96)00323-9 |
| [8] | BOCCARDO L, CROCE G, ORSINA L. Nonlinear degenerate elliptic problems with W01, 1(Ω) solutions[J]. Manuscripta Mathematica, 2012, 137(3/4): 419–439. |
| [9] | GOL'DSHTEIN V, UKHLOV A. Weighted Sobolev spaces and embedding theorems[J]. Transactions of the American Mathematical Society, 2009, 361(7): 3829–3850. DOI:10.1090/S0002-9947-09-04615-7 |
| [10] | DRÁBEK P, KUFNER A, MUSTONEN V. Pseudo-monotonicity and degenerated or singular elliptic operators[J]. Bulletin of the Australian Mathematical Society, 1998, 58(2): 213–221. DOI:10.1017/S0004972700032184 |
| [11] | AZORERO J P G, ALONSO I P. Hardy inequalities and some critical elliptic and parabolic problems[J]. Journal of Differential Equations, 1998, 144(2): 441–476. DOI:10.1006/jdeq.1997.3375 |
| [12] | BLANCHARD D. Truncations and monotonicity methods for parabolic equations[J]. Nonlinear Analysis:Theory, Methods and Applications, 1993, 21(10): 725–743. DOI:10.1016/0362-546X(93)90120-H |
| [13] | BLANCHARD D, MURAT F, REDWANE H. Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems[J]. Journal of Differential Equations, 2001, 177(2): 331–374. DOI:10.1006/jdeq.2000.4013 |
| [14] | BENILAN P, BREZIS H, CRANDALL M G. A semilinear equation in L1(RN)[J]. Annali della Scuola Normale Superiore di Pisa, Classe di Scienze(Serie Ⅳ), 1975, 2(4): 523–555. |
| [15] | LIONS J L. Quelques Méthodes de Résolution des Problemes aux Limites Nonlinéaires[M]. Paris: Dunod, 1969. |
| [16] | SCHAFT A V D. Nonlinear systems analysis:M. Vidyasagar[J]. Automatica, 1994, 30(10): 1631–1632. DOI:10.1016/0005-1098(94)90103-1 |


