0 引言

设P为由v个元素组成的有限集(其中的元素称为点)，B为由P的k元子集组成的集合(其元素称为区)，2-(v, k, 1)设计D=(P, B)是由P和B构成的二元系，满足P中任意2元子集恰好包含在唯一的区内. k满足2≤k＜v，记v=|P|，b=|B|，则r表示经过一个点的不同区的个数，有

$ \ \ \ \ \ \ \ \ \ \ bk=vr, \\ bk(k-1)=v(v-1), $

且Fisher不等式b≥v^[1]成立.

假设π是点集P的一个置换，若将D的区仍变为D的区，则称π是设计D的一个自同构.记Aut(D)为D的全体自同构组成的群.设G≤Aut(D)，若G作用在D的区集(点集)上是传递的，则称G是区传递(点传递)的.若G作用在D的区集(点集)上是本原的，则称G是区本原(点本原)的.称点区对(α, B)(α∈B)为设计D的旗.若G在D的旗集合上传递，则称G是旗传递的.已知结果：若G是区传递的，则G也是点传递的^[2]; 若G是旗传递的，则G是点本原的.

在研究具有良好传递性的2-(v, k, 1)设计时，一个很重要的问题就是区传递2-(v, k, 1)设计的分类.

目前，旗传递2-(v, k, 1)设计的分类问题已基本解决.对于可解的区传递2-(v, k, 1)设计，已成功实现对3≤k≤9的分类^[3-8]，针对自同构群为非可解群的情形，LI^[9]对2-(v, 4, 1)设计进行了分类，HAN等^[10]对2-(v, 5, 1)设计进行了成功分类.经国内外学者的不断努力，区传递2-(v, k, 1)设计的分类问题取得了丰富成果^[3-19].

本文讨论非可解的区传递2-(v, 6, 1)设计，得到：

定理  设D为2-(v, 6, 1)设计，其自同构群G≤Aut(D)是区传递、点本原但非旗传递的.若v为奇数，则G的基柱Soc(G)不是有限域GF(q)上的典型单群PSp_n(q).

1 预备知识

本文中的典型单群是指辛群PSp_n(q).记V为定义在有限域GF(q)上的n维向量空间，这里q=p^f，p为素数.因为PSp₂(q)=PSL₂(q)，该单群放在PSL_n(q)中处理，故约定n≥4.本文采用文献[20]的术语和符号.

引理1^[17]  设D是2-(v, k, 1)设计，且G≤Aut(D)为区传递的.若k|v，则G是旗传递的.

引理2^[10]  设G是点集P上的传递置换群，T≤G≤Aut(T)，记Γ为G的次轨道，则Γ为T的某些等长的次轨道的并.

引理3^[10]  设D，G满足定理的条件，基柱Soc(G)=T，则|T|≤$ \left\lceil {\frac{v}{\lambda }} \right\rceil $|T_α|²|GG：T|，这里α∈P，λ为G的最长次轨道的长度，$ \left\lceil {\frac{v}{\lambda }} \right\rceil $表示数$ {\frac{v}{\lambda }}$的Ceiling函数.

引理4^[14]  设D为区传递的2-(v, k, 1)设计，D的自同构群G是几乎单群，且G的基柱T为李型单群，若T∩G_α为T的抛物子群，则G是旗传递的.

2 定理的证明

设D, G满足定理条件，以下用反证法证明定理.设G的基柱Soc(G)为典型单群PSp_n(q).方-李参数的定义^[16]如下：

$ k_v=(k, v), \ k_r=(k, r)=(k, v-1), \\ b_v=(b, v), \ b_r=(b, r)=(b, v-1). $

文献[16]证明了以下不等式：

$ k = {k_v}{k_r}{\rm{, }}\;b = {b_v}{b_r}{\rm{, }}\;v = {k_v}{b_v}{\rm{, }}\;r = {k_r}{b_r}. $

接下来证明设计D的一些性质，该性质在下文的证明中将起到至关重要的作用.

命题1  设D, G满足定理条件，且T_α=T∩G_α(α∈P)，则以下性质成立：

性质1  v=1+30b_r或v=1+10b_r；

性质2  当v=1+30b_r时，$ \frac{v}{x}$＜31|G：T|；当v=1+10b_r时，$ \frac{v}{x}$＜11|G：T| (这里x为T的任一非平凡次轨道长度)；

性质3  当v=1+30b_r时，$ \frac{y}{x}$＜29|G：T|；当v=1+10b_r时，$ \frac{y}{x}$＜9|G：T|(这里x，y为T的任意2个非平凡次轨道长度)；

性质4  当v=1+30b_r时，$ \frac{{\left| T \right|}}{{{{\left| {{T_\alpha }} \right|}^2}}}$＜16|G：T|；当v=1+10b_r时，$ \frac{{\left| T \right|}}{{{{\left| {{T_\alpha }} \right|}^2}}}$＜6|G：T|；

性质5  若(v-1, q)=1，则T_α具有非平凡轨道Γ，其长度y满足y||T_α|_P′.

性质1的证明  由于kb=vr，且r=$ \frac{{v - 1}}{{k - 1}}$，故有

$ k\left( {k - 1} \right)b = v\left( {v - 1} \right), $

再利用方-李参数，可得

$ {k_r}\left( {k - 1} \right){b_r} = v - 1, $

所以有

$ v = 1 + {k_r}\left( {k - 1} \right){b_r}. $

因为G是非旗传递的，根据Camina-Gagen定理^[17]可得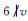，故k_v=1或2或3.又因为(k_r, k_v)=1且k=k_rk_v，所以k_r分别为6或3或2.

当k_v=1时，v=1+30b_r，v为奇数；当k_v=2时，v为偶数，与定理条件不符；当k_v=3时，代入可得v=1+10b_r，v为奇数.

综上，v=1+30b_r或v=1+10b_r.

性质2的证明  假设Γ₁是T的任意一个非平凡次轨道，Γ是G的包含Γ₁的次轨道，x与λ分别表示Γ₁和Γ的长度，由引理2可知λ≤x|GG：T|，又由文献[9]引理2.1可得b_r|λ，所以b_r≤λ≤x|G：T|.

当v=1+30b_r时，若b_r＞1，有

$ \frac{v}{{x\left| {G\;:\;T} \right|}} \le \frac{v}{\lambda } \le \frac{v}{{{b_r}}} < 31. $

若b_r=1，因为Γ₁是T的非平凡次轨道，所以有b_r＜λ≤x|G：T|，从而有

$ \frac{v}{{x\left| {G\;:\;T} \right|}} \le \frac{v}{\lambda } \le \frac{v}{{{b_r}}} < 31. $

其余类似证明.

性质3的证明  设Δ₁和Δ₂是T的任意2个非平凡次轨道，Γ₁和Γ₂为G的2个非平凡次轨道，且Δ₁⊆Γ₁(α∈P)，令x，y，λ₁和λ₂分别表示Δ₁，Δ₂，Γ₁和Γ₂的长度，则由引理2可知

$ {\lambda _1} = {t_1}x, \;{\lambda _2} = {t_2}y, \; $

这里t₁，t₂是|G：T|的因子.

当v=1+30b_r时, $ \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{{t_1}x}}{{{t_2}y}}$≤29，从而$ \frac{x}{y}$≤29|G：T|.其余类似证明.

性质4的证明  设B={1, 2, …, 6}为D的一个区，则子群G^B的结构、群G的秩和次轨道的以下2种情形不成立：

$ \begin{array}{l} {G^B}{\rm{的结构}}\;\;\;G{\rm{的秩}}\;\;\;{\rm{次轨道}}\\ \left\langle 1 \right\rangle \;\;\;\;\;\;\;\;\;\;\;\;31\;\;\;\;\;\;\;\;\;1, \overbrace {{b_r}, \cdots , {b_r} }^{30}, \end{array} $

或

$ \begin{array}{l} {G^B}{\rm{的结构}}\;\;\;G{\rm{的秩}}\;\;\;{\rm{次轨道}}\\ \left\langle 1 \right\rangle \;\;\;\;\;\;\;\;\;\;\;\;11\;\;\;\;\;\;\;\;\;1, \overbrace {{b_r}, \cdots , {b_r}}^{10}. \end{array} $

否则，由文献[4]的结果可得G的阶为奇数(因G^B的阶为奇数)，故G的最长次轨道的长度λ≥2b_r.由引理2可知性质4成立.

性质5的证明  由文献[10]的结果可知性质5成立.

因为G为点本原，而且v=1+30b_r或v=1+10b_r为奇数，故G为奇数次本原群.由奇数次本原群分类定理^[21]得G的基柱H=G_α(α∈P)为下列情形之一：

(1) 若q为偶数，则H∩T是T的抛物子群.

若q为奇数，则下列(2)~(4)之一成立：

(2) H=N_G(T(q₀))，这里q=q₀^c且c为奇素数.

(3) H为V的非奇异子空间的稳定化子.

(4) T∩H为V的直和分解V=⊕V_i的稳定化子，其中V_i相互等距，且dim(V_i)是一常数.

接下来，将情形(1)~(4)一一排除.

命题1  情形(1)不成立.

证明  若H∩T为T的抛物子群，则G_α∩T也是T的抛物子群，由引理4知G是旗传递的，与已知条件矛盾.

命题2  情形(2)不成立.

证明  设H=N_G(T(Q₀))，这里q=q₀^c且c为奇素数，易见此时f≥c≥3.又因T(q₀)为T(q)的极大子群^[20]，从而T_α=T∩G_α=T(q₀).因为|T|= |PSp_n(q)|=$ \frac{1}{{\left( {2, q - 1} \right)}}{q^{\frac{{{n^2}}}{4}}}$(q²-1)(q⁴-1)…(qⁿ-1)，|T_α|=|PSp_n(q₀)|= $ \frac{1}{{\left( {2, q_0 - 1} \right)}}q_0^{\frac{{{n^2}}}{4}}$(q₀²-1)×(q₀⁴-1)…(q₀ⁿ-1)，那么

$ \frac{{\left| {T\left( q \right)} \right|}}{{|T({q_0}){|^2}}} > 2q_0^{\frac{{\left( {c - 2} \right)n\left( {n + 1} \right)}}{2}} > 32f \ge 16\left| {G\;:\;T} \right|, $

与性质4矛盾.

命题3  情形(3)不成立.

证明  设H为V的任意非奇异子空间的稳定化子，T=PSp_n(q).

由文献[18]知，PSp_n(q)(n≥4)的非奇异子空间的稳定化子为Sp_m(q)⊥Sp_n-m(q)型，其中，m为偶数，且2≤m＜$ \frac{n}{2}$.

当m≥4时，设W和$ {\tilde W}$的一组基分别为

$ \begin{array}{l} \;\;\;\;\left\{ {{e_1}, \;{f_1};\; \cdots \;;{e_{\frac{{m - 2}}{2}}}, \;{f_{\frac{{m - 2}}{2}}};\;{e_{\frac{m}{2}}}, {\rm{ }}{f_{\frac{m}{2}}}} \right\}, \\ \left\{ {{e_1}, \;{f_1};\; \cdots \;;{e_{\frac{{m - 2}}{2}}}, \;{f_{\frac{{m - 2}}{2}}};\;{e_{\frac{{m + 2}}{2}}}, {\rm{ }}{f_{\frac{{m + 2}}{2}}}} \right\}, \end{array} $

其稳定化子分别为T_α和T_β，故

$ {T_{\alpha \beta }} = \left\{ {A|A \in S{p_n}\left( q \right), {\rm{且}}\mathit{A}{\rm{具有形式}}\left( {\begin{array}{*{20}{c}} {{A_1}}&{}&{}&{}\\ {}&{{A_2}}&{}&{}\\ {}&{}&{{A_3}}&{}\\ {}&{}&{}&{{A_4}} \end{array}} \right)} \right\}, $

这里A₁∈Sp_m-2(q), A₂, A₃∈Sp₂(q), A₄∈Sp_n-m-2(q), 从而v和x(x为β所在T_α的轨道长度)分别为

$ \begin{array}{l} \;\;\;v = \frac{{{q^{\frac{{nm - {m^2}}}{2}}}\prod\limits_{i = \frac{{m + 2}}{2}}^{\frac{n}{2}} {({q^{2i}} - 1)} }}{{\prod\limits_{i = 1}^\frac{n - m}{2} {({q^{2i}} - 1)} }}{\rm{, }}\\ x = \frac{{{q^{n - 4}}({q^m} - 1)({q^{n - m}} - 1)}}{{{{({q^2} - 1)}^2}}}, \end{array} $

故

$ \frac{v}{x} > {q^{\frac{{nm - 4n + 14}}{2}}}. $

(1)

当m≥4时，由式(1)得$ \frac{v}{x}$＞q⁷＞31|G：T|，与性质2矛盾.当m=2时，v和x分别为

$ v = \frac{{{q^{n - 2}}({q^n} - 1)}}{{({q^2} - 1)}}, \;x = \frac{{{q^{n - 4}}({q^{n - 2}} - 1)}}{{({q^2} - 1)}}, $

故$ \frac{v}{x}$＞q⁴＞31|G：T|，与性质2矛盾.

命题4  情形(4)不成立.

证明  由文献[18]知，PSp_n(q)的正交分解V=⊕_i=1^tV_i的稳定化子为Sp_n(q)ιS_t型，其中，n=mt, t≥2，且m为偶数.

当m=2k≥4时，设V_i的一组基为{e_i1, f_i1; …; e_ik, f_ik}(i=1, 2, …, t)，取

$ \begin{array}{l} {{V'}_1} = \{ {e_{11}}, \;{\rm{ }}{f_{11}};{\rm{ }} \cdots;\;{e_{1(k - 1)}}\;, \;{\rm{ }}{f_{1(k - 1)}}\;;\;{e_{2k}}, {\rm{ }}{f_{2k}}\} , \\ {{V'}_2} = \{ {e_{21}}, \;{f_{21}};{\rm{ }} \cdots ;\;{e_{2(k - 1)}}\;, \;{\rm{ }}{f_{2(k - 1)}}\;;\;{e_{1k}}, {\rm{ }}{f_{1k}}\} {\rm{, }}\\ {{V'}_i} = {V_i}{\rm{, }}\;i = 3, {\rm{ }}4, \; \cdots , \;t, \end{array} $

则V=⊕_i=1^tV′_i，记T_β为正交分解V=⊕_i=1^tV′_i的稳定化子，则T_αβ中的元素具有形式

$ \left( {\begin{array}{*{20}{c}} A&{}&{}&{}&{}\\ {}&{{A_1}}&{}&{}&{}\\ {}&{}&B&{}&{}\\ {}&{}&{}&{{B_1}}&{}\\ {}&{}&{}&{}&C \end{array}} \right){\rm{或}}\left( {\begin{array}{*{20}{c}} {}&{}&A&{}&{}\\ {}&{}&{}&{{A_1}}&{}\\ B&{}&{}&{}&{}\\ {}&{{B_1}}&{}&{}&{}\\ {}&{}&{}&{}&C \end{array}} \right), $

其中, A, B∈Sp_m-2(q)，A₁, B₁∈Sp₂(q)^*，C∈Sp_n-m(q)，且C为与正交分解⊕_i=3^tV_i相对应的稳定化子.通过计算T的非平凡次轨道的长度x和v，由性质2得矛盾.

当m=2时，考虑$ \frac{{\left| T \right|}}{{{{\left| {{T_\alpha }} \right|}^2}}}$，利用性质4得矛盾.

由命题1~命题4，定理证毕.