0 引言

Gorenstein同调代数自20世纪60年代以来就受到众多学者的关注，对一些经典的同调代数很多学者给出了对应的Gorenstein同调代数结果. 2014年，EMMANOUIL等^[1]研究了具有有限Gorenstein投射维数的模类的性质, 通过具有有限Gorenstein投射维数的模类以及Gorenstein投射模类形成的稳定范畴构造了2对伴随函子, 并给出了Gorenstein同调代数维数的有限判定条件.为深入研究Gorenstein内射模, 2008年，MAO等^[2]引入了Gorenstein FP-内射模, 得到了很好的性质. 2010年，GILLESPIE^[3]将Gorenstein FP-内射模命名为Ding-内射模.本文主要从稳定范畴的角度建立Ding-内射模的维数的有限判定条件.

1 预备知识

本节主要回顾Ding-内射模的定义, 并给出具有有限Ding-内射维数的模类的基本性质.

定义1^[4]  如果对任意有限表示的R-模N都有Ext_R¹(N, M)=0, 则称R-模M是FP-内射的.记FI表示所有FP-内射R-模组成的模类.

定义2^[2]  设R为任意环, 如果存在一个Hom_R(FI, -)正合的内射R-模的正合列：

$ \cdots \to {E_1} \to {E_0} \to {E^0} \to {E^1} \to \cdots , $

使得M=ker(E⁰→E¹)，则称R-模M是Ding-内射的.

记Did_R(M)和id_R(M)分别为模M的Ding-内射维数和内射维数，利用标准方法可以定义模的Ding-内射维数.

引理1^[2]  设M是Ding-内射R-模, F是任意具有有限FP-内射维数的R-模, 则对任意的i≥0, 有Ext_Rⁱ(N, M)=0.

命题1^[5]  R-模M是Ding-内射的当且仅当存在一个R-模短正合列0→Q′→E→Q→0，使得E是内射模、Q′是Ding-内射模.

命题2  设M为任意R-模, n为非负整数，则下列条件等价：

(1) Did_R(M)≤n；

(2) 存在R-模的短正合列0→M→Q→L→0, 使得Q是Ding-内射的并且id_R(L)≤n-1;

(3) 存在R-模的短正合列0→Q′→B→M→0, 使得Q′是Ding-内射的并且id_R(B)≤n.

证明  由文献[6]可得(1)⇔(2).

(2)⇒(3)  假设存在(2)中的短正合列, 因Q是Ding-内射的, 则由命题1可得短正合列

$ 0 \to Q' \to E \to Q \to 0, $

使得E是内射模、Q′是Ding-内射模.考虑下列拉回交换图：

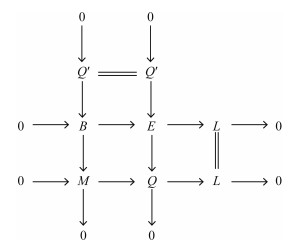
由于id_R(L)≤n-1, 于是id_R(B)≤n.因此存在R-模的短正合列0→Q′→B→M→0, 使得Q′是Ding-内射的并且id_R(B)≤n.

(3)⇒(2)  假设存在(3)中的短正合列, 因为id_R(B)≤n, 则存在短正合列

$ 0 \to B \to E \to L \to 0, $

使得E是内射模且id_R(L)≤n-1.考虑下列推出交换图：

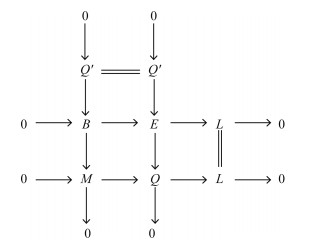
由文献[5]定理2.8可得, Q是Ding-内射的, 因此存在R-模的短正合列0→M→Q→L→0, 使得Q是Ding-内射的并且id_R(B)≤n-1.

推论1  设R-模M有有限Ding-内射维数.则

(1) M是Ding-内射的当且仅当对任意具有有限内射维数的模L都有Ext_R¹(L, M)=0;

(2) M有有限内射维数当且仅当对任意的Ding-内射模Q′都有Ext_R¹(M, Q)=0.

证明  (1) 如果M是Ding-内射的, 由引理1可得，对任意的有有限内射维数的模L都有Ext_R¹(L, M)=0.其次, 考虑短正合列：

$ 0 \to M \to Q \to L \to 0, $

其中Q是Ding-内射的并且id_R(L)≤n-1.因为Ext_R¹(L, M)=0, 所以上述短正合列是可裂的.再由文献[5]中的推论2.9可得，M是Ding-内射的.

(2) 如果M有有限内射维数, 则对任意的Ding-内射模Q′都有Ext_R¹(M, Q′)=0.其次, 考虑短正合列：

$ 0 \to Q' \to B \to M \to 0, $

其中，Q′是Ding-内射的并且id_R(B)≤n.因为Ext_R¹(M, Q′)=0, 所以上述短正合列是可裂的.于是有M是B的直和项, M有有限内射维数.

引理2  设M是任意的有有限Ding-内射维数的R-模.

(ⅰ) 设0→M→Q→L→0和0→M→Q→L→0是2个短正合列, 其中L, L有有限的内射维数, Q, Q是Ding-内射模.则有同构$ \mathit{Q}\oplus \mathit{\bar{L}}\simeq \mathit{\bar{Q}}\oplus \mathit{L}$.

(ⅱ) 设0→Q′→B→M→0和0→Q′→B→M→0是2个短正合列，其中B，B有有限内射维数，Q′，Q′是Ding-内射模.则有同构B⊕Q′$ \simeq $B⊕Q′.

证明  (ⅰ) 假设存在(ⅰ)中的2个短正合列，考虑下列推出交换图：

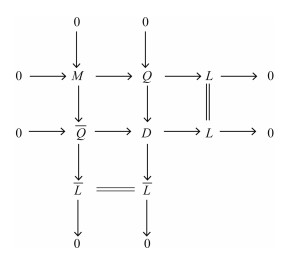
由Ext_R¹(L, Q)=Ext_R¹(L, Q)=0, 得Q⊕L $ \simeq $D$ \simeq $Q⊕L.

(ⅱ) 由(ⅰ)对偶可证：

2 关于有有限内射维数的模类的稳定性

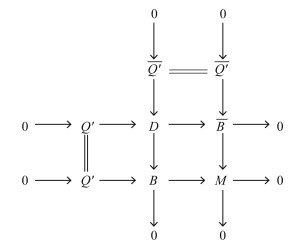
设M, N是2个R-模.则所有可以通过具有有限内射维数的模分解的M到N的态射组成的集合是阿贝尔群Hom_R(M, N)的子群.记对应的商群为FI-Hom_R(M, N)，并且对任意的f∈Hom_R(M, N)，设[f]=[f]$ _{\mathscr{FI}}$.接下来考虑所有的R-Mod，态射集为$ \mathscr{FI}$-Hom_R(M, N)的范畴$ \mathscr{FI}$-R-Mod.

引理3  设M, N为2个有有限Ding-内射维数的R-模，f：M→N为任意态射.考虑下列2个R-模的短正合列：

$ 0 \to M\xrightarrow{\alpha }Q\xrightarrow{\beta }L \to 0 $

和

$ 0 \to N\xrightarrow{{\alpha '}}Q'\xrightarrow{{\beta '}}L' \to 0, $

其中，L, L′有有限内射维数，Q, Q′是Ding-内射的，则

(ⅰ) 存在态射g：Q→Q′, 使得gα=α′f;

(ⅱ) 如果g, g′：Q→Q′是2个态射，使得gα=α′f，g′α=α′f, 则[g]=[g′]∈$ \mathscr{FI}$-Hom_R(Q, Q′);

(ⅲ) 如果[f]=[0]∈$ \mathscr{FI}$-Hom_R(M, N), 对任意的态射g：Q→Q′使得gα=α′f, 则[g]=[0]∈$ \mathscr{FI}$-Hom_R(Q, Q′).

证明  (ⅰ) 因为Ext_R¹(L, Q′)=0, 所以存在态射g：Q→Q′, 使得gα=α′f.

(ⅱ) 设g, g′：Q→Q′是2个态射，使得gα=α′f，g′α=α′f：

则

$ \left( {g - g'} \right)\alpha = g\alpha - g'\alpha = \alpha 'f - \alpha 'f = 0, $

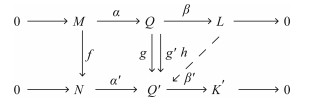
因此存在态射h：L→Q′，使得g-g′=hβ.因为L有有限内射维数, 所以[g]=[g′]∈$ \mathscr{FI}$-Hom_R(Q, Q′).

(ⅲ) 设f由通过有有限内射维数的R-模I分解, 即

$ M\xrightarrow{\gamma }I\xrightarrow{\delta }N, $

则对I有下列短正合列：

$ 0 \to I\xrightarrow{i}E \to I' \to 0, $

使得E是内射的、I′有有限内射维数.由(ⅰ)知, 存在γ′：Q→E和δ′：E→Q′，使得下列图可交换.

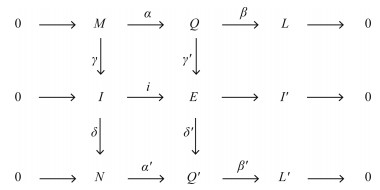
即有α′δ=δ′i且iγ=γ′α.因此(δ′γ′)α=(δ′i)γ=α′(δγ)=α′f.于是, 对任意的态射g：Q→Q′使得gα=α′f, 由(ⅱ)可得，[g]=[δ′γ′]=[0]∈$ \mathscr{FI}$-Hom_R(Q, Q′).

设范畴$ \mathscr{FI}$-DI(R)和$ \mathscr{FI}$-FDI(R)是$ \mathscr{FI}$-R-Mod的全子范畴, 他们的对象分别为Ding-内射模以及有有限Ding-内射维数的模.于是, $ \mathscr{FI}$-DI(R)是$ \mathscr{FI}$-FDI(R)的全子范畴.由引理2(ⅰ)和引理3可得, 存在一个良定的加法函子：

$ \mu : = \mathscr{F}\mathscr{J} - {\rm{FDI}}\left( R \right) \to \mathscr{F}\mathscr{J} - {\rm{DI}}\left( R \right), $

且有

定理1  加法函子μ：$ \mathscr{FI}$-FDI(R)→ $ \mathscr{FI}$-DI(R)是嵌入函子$ \mathscr{FI}$-DI(R)$ \mapsto \mathscr{FI}$-FDI(R)的左伴随.

证明  设M有有限Ding-内射维数, T为Ding-内射模.则有短正合列：

$ 0 \to M\xrightarrow{\alpha }Q\xrightarrow{\beta }L \to 0, $

使得Q是Ding-内射的并且id_R(L)＜∞.由伴随同构的定义, 只需证明

$ {\left[ \alpha \right]^ * }:\mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {Q,T} \right) \to \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,T} \right) $

是双射的并且在M, T处具有自然性.由引理3易得[α]^*在M, T处具有自然性.

下面说明[α]^*是双射的.事实上, 由Ext_R¹(L, T)=0可得

$ {\left[ \alpha \right]^ * }:{\rm{Ho}}{{\rm{m}}_R}\left( {Q,T} \right) \to {\rm{Ho}}{{\rm{m}}_R}\left( {M,T} \right) $

是满的, 因此[α]^*是满的.其次, 设g：Q→T是任意的一个态射，使得

$ \left[ {g\alpha } \right] = \left[ g \right]\left[ \alpha \right] = {\left[ \alpha \right]^ * }\left[ g \right] = \left[ 0 \right] \in \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,T} \right). $

考虑下列交换图：

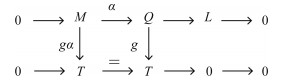
由引理3(ⅲ), 有[g]=0∈$ \mathscr{FI}$-Hom_R(Q, T).

推论2  设M有有限Ding-内射维数, 则下列条件等价：

(ⅰ) M有有限的内射维数;

(ⅱ) 对任意Ding-内射模T有

$ \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,T} \right) = 0; $

(ⅲ) 存在一个短正合列

$ 0 \to M\xrightarrow{\alpha }Q\xrightarrow{\beta }L \to 0, $

其中，Q是Ding-内射的并且id_R(L)＜∞, 使得

$ \left[ \alpha \right] = \left[ 0 \right] \in \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,Q} \right). $

证明  (ⅰ)⇒(ⅱ)和(ⅱ)⇒(ⅲ)显然.

(ⅲ)⇒(ⅰ)  由定理1可知

$ {\left[ \alpha \right]^ * }:\mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {Q,Q} \right) \to \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,Q} \right) $

是双射的.因此, 如果

$ {\left[ \alpha \right]^ * }\left[ {1Q} \right] = \left[ {1Q} \right]\left[ \alpha \right] = \left[ \alpha \right] = \left[ 0 \right] \in \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {M,Q} \right), $

则

$ \left[ {1Q} \right] = \left[ 0 \right] \in \mathscr{F}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {Q,Q} \right), $

由此可得Q是某个有有限内射维数的模的直和项, 即Q有有限内射维数.再由Q是Ding-内射的，可得Q是内射的，于是M有有限内射维数.

证毕！

3 关于Ding-内射模类的稳定性

设M, N是2个R-模，则所有可以通过Ding-内射模分解的M到N的态射形成的集合是阿贝尔群Hom_R(M, N)的子群.记对应的商群为$ \mathscr{DI}$-Hom_R(M, N), 并且对任意的f∈Hom_R(M, N), 设[f]=[f]$ _{\mathscr{DI}}$.接下来考虑的对象为所有的R-Mod, 态射集为$ \mathscr{DI}$-Hom_R(M, N)的范畴$ \mathscr{DI}$-R-Mod，

引理4  设M, N为2个有有限Ding-内射维数的R-模, f：M→N为任意态射.考虑下列2个R-模的短正合列：

$ 0 \to Q'\xrightarrow{\alpha }B\xrightarrow{\beta }M \to 0 $

和

$ 0 \to \bar Q'\xrightarrow{\alpha }\bar B\xrightarrow{{\beta '}}N \to 0, $

其中，B，B有有限内射维数，Q′，Q′是Ding-内射的，则

(ⅰ) 存在态射g：B→B, 使得fβ=β′g;

(ⅱ) 如果g, g′：B→B是2个态射，使得fβ=β′g和fβ=β′g′, 则[g]=[g′]∈$ \mathscr{DI}$-Hom_R(B, B);

(ⅲ) 如果[f]=[0]∈$ \mathscr{DI}$-Hom_R(M, N), 任意态射g：B→B使得fβ=β′g, 则[g]=[0]∈$ \mathscr{DI}$-Hom_R(B, B).

证明  (ⅰ) 因为Ext_R¹(B, Q′)=0, 所以存在态射g：B→B, 使得ga=a′f.

(ⅱ) 设g, g′：B→B是2个态射，使得fβ=β′g和fβ=β′g′：

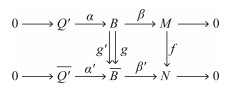
则β′(g-g′)=β′g-β′g′=fβ-fβ=0, 因此存在态射h：B→Q′使得g-g′=a′h.因为Q′是Ding-内射的, 所以[g]=[g′]∈$ \mathscr{DI}$-Hom_R(B, B).

(ⅲ) 设f通过Ding-内射R-模E分解, 即

$ M\xrightarrow{\gamma }E\xrightarrow{\delta }N, $

则对E，有下列短正合列

$ 0 \to E' \to I\xrightarrow{\theta }E \to 0, $

使得I是内射的、E′是Ding-内射的.因此由(ⅰ), 存在γ′：B→I和δ′：I→B，使得下列图可交换:

即有θγ′=γβ且β′δ′=δθ.因此β′(δ′γ′)=δ(θγ′)=(δ)γβ=fβ.于是, 对任意态射g：B→B使得fβ=β′g，由(ⅱ)可得

$ \left[ g \right] = \left[ {\delta '\gamma '} \right] = \left[ 0 \right] \in \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,\bar B} \right). $

设范畴$ \mathscr{DI}$-FI(R)和$ \mathscr{DI}$-FDI(R)是$ \mathscr{FI}$-R-Mod的全子范畴, 他们的对象分别为有有限内射维数的模以及有有限Ding-内射维数的模.于是, $ \mathscr{DI}$-FI(R)是$ \mathscr{DI}$-FDI(R)的全子范畴.由引理2(ⅱ)和引理4可得，存在一个良定的加法函子

$ \nu :\mathscr{D}\mathscr{J} - {\rm{FDI}}\left( R \right) \to \mathscr{D}\mathscr{J} - {\rm{FI}}\left( R \right), $

且有

定理2  加法函子ν：$ \mathscr{DI}$-FDI(R)→$ \mathscr{DI}$-FI(R)是嵌入函子$ \mathscr{DI}$-FI(R)$ \mapsto \mathscr{DI}$-FDI(R)的右伴随.

证明  设M有有限Ding-内射维数, A有有限内射维数.则有短正合列

$ 0 \to Q'\xrightarrow{\alpha }B\xrightarrow{\beta }M \to 0, $

使得Q′是Ding-内射的并且id_R(B)＜∞.根据伴随同构定义, 只需证明

$ {\left[ \beta \right]_ * }:\mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {A,B} \right) \to \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {A,M} \right) $

是双射的并且在M, A处具有自然性.由引理4易得[β]_*在M, A处具有自然性.

下面说明[β]_*是双射的.事实上, 由Ext_R¹(A, Q)=0, 可得

$ {\left[ \beta \right]_ * }:{\rm{Ho}}{{\rm{m}}_R}\left( {A,B} \right) \to {\rm{Ho}}{{\rm{m}}_R}\left( {A,M} \right) $

是满的, 因此[β]_*是满的.其次, 设g：A→B为一任意态射，使得

$ \left[ {\beta g} \right] = \left[ \beta \right]\left[ g \right] = {\left[ \beta \right]_ * }\left[ g \right] = \left[ 0 \right] \in \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {A,M} \right). $

考虑下列交换图：

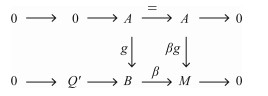
由引理4(ⅲ)，[g]=0∈$ \mathscr{DI}$-Hom_R(A, B).

证毕！

推论3  设M有有限Ding-内射维数, 则下列条件等价：

(ⅰ) M是Ding-内射的;

(ⅱ) 对任意有有限内射维数的模T都有$ \mathscr{DI}$-Hom_R(T, M)=0;

(ⅲ) 存在一个短正合列

$ 0 \to Q'\xrightarrow{\alpha }B\xrightarrow{\beta }M \to 0, $

其中Q′是Ding-内射的并且id_R(B)＜∞, 使得

$ \left[ \beta \right] = \left[ 0 \right] \in \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,M} \right). $

证明  (ⅰ)⇒(ⅱ)和(ⅱ)⇒(ⅲ)显然.

(ⅲ)⇒(ⅰ)  由定理2, 特别地

$ {\left[ \beta \right]_ * }:\mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,B} \right) \to \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,M} \right) $

是双射的.因此, 如果

$ {\left[ \beta \right]_ * }\left[ {{1_B}} \right] = \left[ \beta \right]\left[ {{1_B}} \right] = \left[ \beta \right] = 0 \in \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,M} \right), $

则

$ \left[ {{1_B}} \right] = \left[ 0 \right] \in \mathscr{D}\mathscr{J} - {\rm{Ho}}{{\rm{m}}_R}\left( {B,B} \right), $

因此可得B是某个Ding-内射模的直和项, 即B是Ding-内射的, 于是M是Ding-内射的.