布尔导数和e导数能反映布尔函数值随变量变化的关系,二者被广泛应用于图像处理[1]、逻辑电路的故障检测[2-5]和布尔函数密码学性质的研究[6-9].
目前,学者对布尔e导数求解方法的研究主要有3种:基于K图和降维K图的图形法[10]、基于最小项的表格法[11]和基于改进D图的算法[12].利用K图和降维K图求解布尔e导数,具有计算方法简单、物理意义清晰的特点,但随着输入变量数n的增大,其图形规模将以2n的速度迅速增加,因此此方法对输入变量超过30的大逻辑函数不适用;同样,通过列布尔1值最小项表求解布尔e导数,其最小项数量与输入变量数n成2n关系,亦不适合处理大函数;而基于改进D图求解布尔e导数的方法,其图形规模不仅与输入变量数n成an(1<a≤2)关系,而且还与阶数有关,同样不适合处理大函数.
布尔e偏导数[13]的求解较布尔e导数更难.文献[11]提出了一种基于最小项表求解布尔e偏导数的方法,即根据待求导变量累次列布尔1值最小项求解布尔e偏导数,其与基于最小项的布尔e导数求解方法一样,亦不适合求解大函数的布尔e偏导数.
本文给出了一种便于计算机编程实现的逻辑函数高阶布尔e导数和e偏导数的求解算法.利用乘积项集合之间的不相交操作[14],实现逻辑函数的逻辑“与”操作,并结合布尔e导数和e偏导数的定义,给出了求解算法.采用二级逻辑综合工具espresso,对算法的最终输出结果进行简化,进而得到更加紧凑的求导结果.
1 定义一个n变量布尔函数f(x1~xn)总可以写成式(1)所示的乘积项之和(sum of product, SOP):
| $ f = \sum\limits_{i = 0}^{k - 1} {{p_i}} , $ | (1) |
式(1)中pi为布尔函数f的第i个乘积项,k为乘积项的个数,符号“∑”表示乘积项之间是逻辑“或”关系,并记f的乘积项集合为Cf.若乘积项pi∈Cf,则pi可写成:
| $ {p_i} = {{\dot x}_0}{{\dot x}_1} \cdots {{\dot x}_j} \cdots {{\dot x}_{n - 1}}, $ | (2) |
式(2)中,n为变量的个数,
本文约定:DC(x1, x2, …, xk)表示k个变量x1~xk的取值全为“-”,且DC(X)=DC(X),X表示k变量矢量;EN(x1, x2, …, xk)表示k个变量x1~xk中至少有1个变量取值不为“-”.
例如,乘积项p=x1x2x3=-1-,按上述约定可将变量x1, x3全取“-”,写成DC(x1, x3);变量x1, x2, x3不全取“-”写成EN(x1, x2, x3).
定义1 设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj(1≤j≤n)的一阶布尔e导数为
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{e}}f\left( {{x_1} \sim {x_n}} \right)}}{{{\rm{e}}{x_j}}} \buildrel \Delta \over = f\left( {{x_1} \cdots {x_j} \cdots {x_n}} \right) \cdot f\left( {{x_1} \cdots \overline {{x_j}} \cdots {x_n}} \right) = }\\ {\sum\limits_{i = 0}^{k - 1} {{p_{i\left| {{x_j}} \right.}}} \cdot \sum\limits_{i = 0}^{k - 1} {{p_{i\left| {\overline {{x_j}} } \right.}}} ,} \end{array} $ | (3) |
式(3)中
定义2 设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj1~xjk(2≤k≤n)的k阶布尔e导数可表示为
| $ \begin{array}{l} \frac{{{{\rm{e}}^k}f\left( {{x_1} \sim {x_n}} \right)}}{{{\rm{e}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)}} \buildrel \Delta \over = \\ f\left( {{x_1} \cdots {x_{{j_1}}} \sim {x_{{j_k}}} \cdots {x_n}} \right) \cdot f\left( {{x_1} \cdots {{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}} \cdots {x_n}} \right) = \\ \sum\limits_{i = 0}^{m - 1} {{p_{i\left| {{x_{{j_1}}} \sim {x_{{j_k}}}} \right.}}} \cdot \sum\limits_{i = 0}^{m - 1} {{p_{i\left| {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right.}}} , \end{array} $ | (4) |
式(4)中,
推论1 设n变量布尔函数f对应的乘积项集合Cf由(s+t)个不相交乘积项构成,即pi·pj=∅ (i≠j),其中, s个乘积项中的待求导变量均不出现,而另外t个乘积项中的每个乘积项至少有1个待求导变量出现,则k(1≤k≤n)阶布尔e导数可表示为
| $ \begin{array}{l} \frac{{{{\rm{e}}^k}f}}{{{\rm{e}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)}} = \\ \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} + \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} \cdot \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right)} \right.}}} , \end{array} $ | (5) |
式(5)中,
证明 将构成逻辑函数f的(s+t)个不相交乘积项拆分成g和h两部分,且f=g+h.其中,g中包含s个不相交乘积项,且任一乘积项中的待求导变量均未出现;h中包含t个不相交乘积项,显然属于h的任一乘积项中的待求导变量至少出现1个.因此,g和h可以表示为
| $ g = \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} ,h = \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} , $ |
由条件pi·pj=∅(i≠j)可知g·h=∅,故
| $ \begin{array}{l} \frac{{{{\rm{e}}^k}f}}{{{\rm{e}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)}} = \frac{{{{\rm{e}}^k}\left( {g + h} \right)}}{{{\rm{e}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)}} = \\ \left\{ {g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right\} \cdot \left\{ {g\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) + h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right)} \right\} = \\ g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot g\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) + \\ g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) = \\ g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) + g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) = \\ g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot \left( {1 + h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right)} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) = \\ g\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) + h\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right) \cdot h\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right) = \\ \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} + \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} \cdot \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{{\bar x}_{{j_1}}} \sim {{\bar x}_{{j_k}}}} \right)} \right.}}} . \end{array} $ |
证毕!
例1
解 由推论1可得
| $ \begin{array}{l} \frac{{{{\rm{e}}^2}f}}{{{{\rm{e}}^2}\left( {{x_1},{x_2}} \right)}} = \sum\limits_{i = 0}^{1 - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_1},{x_2}} \right)} \right.}}} + \sum\limits_{i = 0}^{2 - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_1},{x_2}} \right)} \right.}}} \cdot \sum\limits_{i = 0}^{2 - 1} {{p_{i\left| {{\rm{EN}}\left( {{{\bar x}_1},{{\bar x}_2}} \right)} \right.}}} = \\ \left\{ {{{\bar x}_3}{x_4}} \right\} + \left\{ {{x_1}{x_2}{x_3} + {{\bar x}_1}{x_3}} \right\} \cdot \left\{ {{{\bar x}_1}{{\bar x}_2}{x_3} + {x_1}{x_3}} \right\} = \\ {{\bar x}_3}{x_4} + {x_1}{x_2}{x_3} + {{\bar x}_1}{{\bar x}_2}{x_3}, \end{array} $ |
由定义2及计算可得
| $ \begin{array}{l} \frac{{{{\rm{e}}^2}f}}{{{\rm{e}}\left( {{x_1},{x_2}} \right)}} = \sum\limits_{i = 0}^{3 - 1} {{p_{i\left| {{x_1},{x_2}} \right.}}} \cdot \sum\limits_{i = 0}^{3 - 1} {{p_{i\left| {{{\bar x}_1},{{\bar x}_2}} \right.}}} = \\ \;\;\;\;\;\;\;\left\{ {{x_1}{x_2}{x_3} + {{\bar x}_1}{x_3} + {{\bar x}_3}{x_4}} \right\} \cdot \left\{ {{{\bar x}_1}{{\bar x}_2}{x_3} + {x_1}{x_3} + {{\bar x}_3}{x_4}} \right\} = \\ \;\;\;\;\;\;\;{x_1}{x_2}{x_3} + {{\bar x}_1}{{\bar x}_2}{x_3} + {{\bar x}_3}{x_4}. \end{array} $ |
以上2种方法的计算结果是一致的.用推论1来实现布尔e导数,其求导过程中逻辑表达式之间的逻辑“与”操作更加简单.
定义3 设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj(1≤j≤n)的一阶布尔e偏导数为一阶布尔e导数.
定义4 设f(x1~xn)为n变量的布尔函数,则f(x1~xn)对于变量xj1~xjk(2≤k≤n)的k阶布尔e偏导数可表示为
| $ \begin{array}{l} \frac{{{{\rm{e}}^k}f\left( {{x_1} \sim {x_n}} \right)}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_k}}}}} \buildrel \Delta \over = \\ \;\;\;\;\;\;\;\;\;\frac{{\rm{e}}}{{{\rm{e}}{x_{{j_k}}}}}\left( {\frac{{\rm{e}}}{{{\rm{e}}{x_{{j_{k - 1}}}}}} \cdots \left( {\frac{{\rm{e}}}{{{\rm{e}}{x_{{j_2}}}}}\left( {\frac{{{\rm{e}}f\left( {{x_1} \sim {x_n}} \right)}}{{{\rm{e}}{x_{{j_1}}}}}} \right)} \right) \cdots } \right). \end{array} $ | (6) |
推论2 设n变量布尔函数f对应乘积项集合Cf由pi·pj=∅(i≠j)个不相交乘积项构成,即pi·pj=∅(i≠j),其中s个乘积项中的待求偏导变量均不出现,而另外t个乘积项中每项至少有1个待求偏导变量,则k(1≤k≤n)阶布尔e偏导数可表示为
| $ \frac{{{{\rm{e}}^k}f}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_k}}}}} = \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} + \frac{{{{\rm{e}}^k}h}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_k}}}}}, $ | (7) |
式(7)中,h为布尔函数f的子函数,
| $ h = \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_{{j_1}}} \sim {x_{{j_k}}}} \right)} \right.}}} . $ |
证明 用数学归纳法:
(1) 当阶数k=1时,由定义3知,利用推论1可证明式(7)成立,即
| $ \begin{array}{l} \frac{{{\rm{e}}f}}{{{\rm{e}}{x_j}}} = \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_j}} \right)} \right.}}} + \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{x_j}} \right)} \right.}}} \cdot \sum\limits_{i = 0}^{t - 1} {{p_{i\left| {{\rm{EN}}\left( {{{\bar x}_j}} \right)} \right.}}} = \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_j}} \right)} \right.}}} + \frac{{{\rm{e}}h}}{{{\rm{e}}{x_j}}}. \end{array} $ |
(2) 假设当阶数k=q(1<q<n)时,式(7)成立,即
| $ \frac{{{{\rm{e}}^q}f}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_q}}}}} = \sum\limits_{i = 0}^{s - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_q}}}} \right)} \right.}}} + \frac{{{{\rm{e}}^q}h}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_q}}}}}, $ |
(3) 令
| $ \begin{array}{l} \frac{{{{\rm{e}}^{q + 1}}f}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_{q + 1}}}}}} = \frac{{\rm{e}}}{{{\rm{e}}{x_{{j_{q + 1}}}}}}\left\{ {\frac{{{{\rm{e}}^q}f}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_q}}}}}} \right\} = \\ \;\;\;\;\;\;\frac{{{\rm{e}}F}}{{{\rm{e}}{x_{{j_{q + 1}}}}}} = \frac{{{\rm{e}}\left( {G + H} \right)}}{{{\rm{e}}{x_{{j_{q + 1}}}}}} = \\ \;\;\;\;\;\;\left\{ {G\left( {{x_{{j_{q + 1}}}}} \right) + H\left( {{x_{{j_{q + 1}}}}} \right)} \right\} \cdot \left\{ {G\left( {{{\bar x}_{{j_{q + 1}}}}} \right) + H\left( {{{\bar x}_{{j_{q + 1}}}}} \right)} \right\} = \\ \;\;\;\;\;\;G\left( {{x_{{j_{q + 1}}}}} \right) + H\left( {{x_{{j_{q + 1}}}}} \right) \cdot H\left( {{{\bar x}_{{j_{q + 1}}}}} \right) = \\ \;\;\;\;\;\;G\left( {{x_{{j_{q + 1}}}}} \right) + \frac{{{\rm{e}}H}}{{{\rm{e}}{x_{{j_{q + 1}}}}}} = \\ \;\;\;\;\;\;\sum\limits_{i = 0}^{u - 1} {{p_{i\left| {{\rm{DC}}\left( {{x_{{j_1}}} \sim {x_{{j_{q + 1}}}}} \right)} \right.}}} + \frac{{{{\rm{e}}^{q + 1}}h'}}{{{\rm{e}}{x_{{j_1}}} \sim {\rm{e}}{x_{{j_{q + 1}}}}}}. \end{array} $ |
其中,h′是f的子函数,且
由步骤(1)~(3)可知,对任意阶数k(1≤k≤n),推论2成立.
证毕!
2 算法实现由布尔e导数和e偏导数的定义可知,逻辑函数的布尔e导数和e偏导数的求解过程中都涉及求解函数之间的“与”运算.因此,求解逻辑函数的逻辑“与”直接影响布尔e导数的求解速度和规模.下文将讨论逻辑函数之间“与”运算的求解方法以及大函数高阶布尔e导数和e偏导数算法.考虑现有的布尔e导数和e偏导数的求解方法只适用于输入变量较少的逻辑函数的低阶求导,且对求导结果未进行逻辑简化,本文将借用已有的二级逻辑综合工具espresso,对布尔e导数及e偏导数的计算结果进行逻辑简化.
2.1 逻辑函数之间逻辑“与”运算的实现定义5 若Cf和Cg分别为逻辑函数f和g所对应的乘积项集合,则Cf与Cg之间的不相交运算用CfⓧCg表示,且CfⓧCg=Cf-Cf∩Cg,符号“ⓧ”为2个逻辑函数之间的不相交运算符.
从定义5可以看出,CfⓧCg的实质是在Cf中除去与Cg相交的部分,因此,CfⓧCg的结果属于Cf且不与Cg相交的部分;由此可得:Cf与Cg相交部分等于在Cf中除去与Cg不相交的部分,即逻辑函数f和g“与”的结果可表示为
| $ {C_f} \cap {C_g} = {C_f} \otimes \left( {{C_f} \otimes {C_g}} \right). $ | (8) |
算法伪代码如下:
图 1中,Cf和Cg分别包含w和v个乘积项,Cdis=piΘqj表示乘积项pi与qj之间进行不相交锐积运算,运算结果寄存在Cdis中.显然,结合图 1算法和式(8)可实现逻辑函数f和g之间的逻辑“与”运算.

|
图 1 CfⓧCg算法伪代码 Fig. 1 Pseudocode for the algorithm of CfⓧCg |
由推论1可知,k(1≤k≤n)阶布尔e导数的求解结果由两部分组成:(1)待求导变量均不出现的乘积项集合部分,即
本文中,k阶布尔e导数运算用程序E_Derivative(Cf, L)来实现,其中Cf是布尔函数f转化为不相交乘积项SOP形式的乘积项集合,L是一个链表,用来寄存待求导变量,其伪代码如下:
图 2中,Cen和Cr_en为2个乘积项集合缓存,CT是运算结果;子函数Apart(Cf, L)的功能是根据链表L中寄存的待求导变量出现的情况将Cf中的乘积项拆分成两部分,其中集合Cdc中寄存待求导变量均不出现的乘积项,剩余部分寄存在集合Cen中;子函数Reverse(Cen, L)的功能是将Cen中在全部乘积项中出现的待求导变量取反;Cand=Cenⓧ(CenⓧCr_en)实现了Cen∩Cr_en功能,即实现2个逻辑函数之间的逻辑“与”运算;最后,借用espresso工具对CT进行逻辑简化,得到更加紧凑的逻辑表达形式.

|
图 2 k阶布尔e导数算法伪代码 Fig. 2 Pseudocode for the algorithm of k-order Boolean e-derivative |
由推论2可知,k(1≤k≤n)阶布尔e偏导数的求解结果由两部分组成:(1)待求偏导变量均不出现的乘积项集合部分,即
本文k阶布尔e偏导数运算可用程序E_PartialDerivative(Cf, L)来实现,其中Apart(Cf, L)的含义同图 2,其伪代码如下:
图 3中的Cen是乘积项集合缓存,CT是运算结果;Cpar=e_Derivative(Cen, Lxi)表示对链表Lxi中的唯一待求偏导变量xi求一阶布尔e导数,即一阶布尔e偏导数;最后,借用espresso对CT实现逻辑简化.
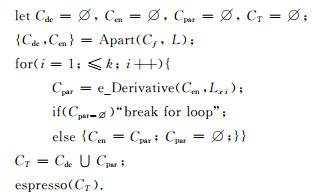
|
图 3 k阶布尔e偏导数算法伪代码 Fig. 3 Pseudocode for the algorithm of k-order Boolean e-partial derivative |
例2 设f(x1~x5)=x1x2x3+x1x2x4+x1x5,求
解 首先,将函数f对应的乘积项集合Cf拆分成Cdc和Cen两部分,拆分结果为Cdc={x1x5},Cen={x1x2x3, x1x2x4}.
其次,将Cen中每个乘积项中的变量x2取反,其结果为Cr_en= {x1x2x3, x1x2x4}.
之后求Cen∩Cr_en,即
| $ \begin{array}{l} {C_{{\rm{en}}}} \cap {C_{r\_{\rm{en}}}} = {C_{{\rm{en}}}} \otimes \left( {{C_{{\rm{en}}}} \otimes {C_{r\_{\rm{en}}}}} \right) = \\ \left\{ {{x_1}{x_2}{x_3},{x_1}{{\bar x}_2}{x_4}} \right\} \cap \left( {\left\{ {{x_1}{x_2}{x_3},{x_1}{{\bar x}_2}{x_4}} \right\} \cap } \right.\\ \left. {\left\{ {{x_1}{{\bar x}_2}{x_3},{x_1}{x_2}{x_4}} \right\}} \right) = \\ \left\{ {{x_1}{x_2}{x_3},{x_1}{{\bar x}_2}{x_4}} \right\} \cap \left\{ {{x_1}{x_2}{x_3}{x_4},{x_1}{{\bar x}_2}{x_3}{x_4}} \right\} = \\ \left\{ {{x_1}{x_2}{x_3}{x_4},{x_1}{{\bar x}_2}{x_3}{x_4}} \right\}. \end{array} $ |
然后,令
最终CT=Cdc∪∅={x1x5},即为求解结果.
而按照定义4直接可求得
本文给出的逻辑函数高阶布尔e导数和e偏导数的求解算法已经在Windows10/CPU 2.40 GHz/ RAM 8.00 GB/VS2010环境下使用C语言编程实现,并利用MCNC标准测试电路进行了实验验证.
表 1给出的是k阶布尔e导数和e偏导数的实验数据.表 1中的电路f取自MCNC标准测试电路;i/o/p分别表示电路f对应的输入变量、输出变量和乘积项的数量;阶数k表示对电路f的任意k个变量求解布尔e导数和e偏导数,1≤k≤n,n为变量数;Cd表示布尔e导数计算结果经espresso逻辑简化后的乘积项数量;Cp表示布尔e偏导数计算结果经espresso逻辑简化后的乘积项数量;td表示布尔e导数的求解时间,单位ms;tp表示布尔e偏导数的求解时间,单位ms;“<1”表示求解时间小于1 ms.
| 表 1 布尔e导数和e偏导数的实验数据 Table 1 Experimental data of Boolean e-derivative and e-partial derivative |
表 1给出了11组MCNC测试电路的实验数据,这些电路的变量数为7~199,其输出和乘积项数均具有一定的规模;每个电路均测试了3组不同阶数k的情况.从表 1中可以明显看出,算法处理时间较短,大部分都<1 ms,无超过1 s的.
如果用|Cd|和|Cp|分别表示Cd和Cp中所包含的乘积项数量,从表 1可以看出,一般情况下|Cd|≥|CP|,其原因除了与espresso逻辑优化有关外,还与它们的定义有关.对于逻辑函数f的k阶布尔e导数而言,是2个逻辑函数之间的“与”运算;但对于k阶布尔e偏导数,则是2k个逻辑函数之间的“与”运算;一般情况下,2k个逻辑函数之间的公共部分更少,即多次“与”运算后对应的乘积项数量更少,导致|Cd|≥|Cp|.
函数间不相交运算的速度与每个函数包含的乘积项数量有关,待处理的逻辑函数的输入变量数对其不敏感.有些函数适合拆分,拆分后实际参与不相交运算的乘积项数量不多,因此速度快.例如电路i7、xparc.本文中逻辑函数的布尔e导数用不相交运算来求解,显然不相交运算的调用次数将直接影响算法的速度.对于逻辑函数f的k阶布尔e导数而言,由式(8)知,需要2次不相交运算,但k阶布尔e偏导数却需要2k次不相交运算,因此有tp≥td.
4 结论实现大函数的布尔e导数和e偏导数的求解主要由以下两部分构成:(1)用逻辑函数之间的不相交运算替代.待处理的逻辑函数的输入变量数对不相交运算的速度不敏感,故在处理大逻辑函数时效率较高;(2)在求导过程中,将函数拆分成两部分,即不包含待求导变量的乘积项集合Cdc和包含待求导变量的乘积项集合Cen.Cdc求布尔e导数的结果是其本身,因此,实际上只有Cen参与了求导过程中的不相交运算,显然Cen中包含的乘积项数量不会大于原函数,从而达到减少参与不相交运算的乘积项数量的目的,提高了算法速度.实验表明,本文提出的方法可以快速计算输入变量数在199内的大函数的高阶布尔e导数和e偏导数.为了简化求导后的逻辑函数的表达式,算法最后借用二级逻辑综合工具espresso,实现了函数的逻辑简化.
| [1] | AGAIAN S S, PANETTA K A, NERCESSIAN S C, et al. Boolean derivatives with application to edge detection for imaging systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B:Cybernetics, 2010, 40(2): 371–382. DOI:10.1109/TSMCB.2009.2024771 |
| [2] | LI W W, WANG Z, HUANG J L. The e-derivative of Boolean functions and its application in the fault detection and cryptographic system[J]. Kybernetes, 2011, 40(6): 905–911. |
| [3] | LI H T, WANG Y Z. Boolean derivative calculation with application to fault detection of combinational circuits via the semi-tensor product method[J]. Automatica, 2012, 48(4): 688–693. DOI:10.1016/j.automatica.2012.01.021 |
| [4] | LEE S C, AULA F T. Fault detection in word-level NanoICs using vector Boolean derivative[C]//Proceedings of SPIE-Nanosensors, Biosensors, and Info-Tech Sensors and Systems. San Diego: Society of Photo-Optical Instrumentation Engineers (SPIE), 2013, 86910E. Doi: 10.1117/12.2009527. |
| [5] | LIU Z B, WANG Y Z, LI H T. New approach to derivative calculation of multi-valued logical functions with application to fault detection of digital circuits[J]. IET Control Theory Applications, 2014, 8(8): 554–560. DOI:10.1049/iet-cta.2013.0104 |
| [6] | ZHANG Z J. The correlation between the internal construction and the property of Bent functions in cryptographic system[C]//2nd IEEE International Conference on Computer Science and Information Technology. Beijing: IEEE Conference Publications, 2009: 329-332. |
| [7] | LI W W. Correlation-immunity study of balanced H-Boolean functions[J]. Tongxin Xuebao/Journal on Communications, 2013, 34(8): 82–87. |
| [8] | HUANG J L, WANG Z, ZHANG J. Effects of e-derivative on algebraic immunity, correlation immunity and algebraic degree of H Boolean functions[J]. Applied Mechanics and Materials, 2013, 411/412/413/414: 45–48. |
| [9] | DUAN M, YANG M H, SUN X R, et al. Distinguishing properties and applications of higher order derivatives of Boolean functions[J]. Information Sciences, 2014, 271: 224–235. DOI:10.1016/j.ins.2014.02.108 |
| [10] |
厉晓华, 郑强, 杭国强. 基于K图的布尔E-导数计算的图形方法[J].
浙江大学学报(理学版), 2013, 40(3): 260–262.
LI X H, ZHENG Q, HANG G Q. Graphic method calculating Boolean E-derivative based on K-map[J]. Journal of Zhejiang University(Science Edition), 2013, 40(3): 260–262. |
| [11] |
马汝星, 陈偕雄. 基于最小项表计算e导数的方法[J].
浙江大学学报(理学版), 2013, 40(5): 531–534.
MA R X, CHEN X X. Method of computing e-derivative based on minterm table[J]. Journal of Zhejiang University(Science Edition), 2013, 40(5): 531–534. |
| [12] |
马汝星. 基于分解表计算逻辑函数e导数的新方法[J].
科技通报, 2014, 30(1): 141–144.
MA R X. A new method of calculating e-derivative of Boolean function based on the decomposition table[J]. Bulletin of Science and Technology, 2014, 30(1): 141–144. |
| [13] | WANG F. Research on properties of e-partial derivative[J]. Journal of Theoretical and Applied Information Technology, 2013, 47(1): 201–205. |
| [14] |
王玉花, 王伦耀, 夏银水. 基于不相交项并行列表技术的FPRM实现[J].
电子与信息学报, 2014, 36(9): 2258–2264.
WANG Y H, WANG L Y, XIA Y S. FPRM conversion using parallel tabular technique with disjointed products[J]. Journal of Electronics & Information Technology, 2014, 36(9): 2258–2264. |



