耗散结构和差分变异混合的鸡群算法

引用本文 [复制中英文]

韩萌. 耗散结构和差分变异混合的鸡群算法[J]. 浙江大学学报(理学版), 2018, 45(3): 272-283. DOI: 10.3785/j.issn.1008-9497.2018.03.002.

HAN Meng. Hybrid chicken swarm algorithm with dissipative structure and differential mutation[J]. Journal of Zhejiang University(Science Edition), 2018, 45(3): 272-283. DOI: 10.3785/j.issn.1008-9497.2018.03.002.

[复制英文]

基金项目

国家自然科学基金资助项目（61373174）

作者简介

韩萌(1993-), ORCID:http://orcid.org/0000-0002-4176-9014, 女, 硕士, 主要从事智能优化算法、最优化理论及其应用研究, E-mail:meng_10110826@163.com

文章历史

收稿日期：2017-08-24

Contents Abstract Full text Figures/Tables PDF

耗散结构和差分变异混合的鸡群算法

韩萌

西安电子科技大学数学与统计学院, 陕西西安 710126

收稿日期：2017-08-24

基金项目：国家自然科学基金资助项目（61373174）

作者简介：韩萌(1993-), ORCID:http://orcid.org/0000-0002-4176-9014, 女, 硕士, 主要从事智能优化算法、最优化理论及其应用研究, E-mail:meng_10110826@163.com

摘要: 针对标准鸡群算法在求解高维优化问题时过早收敛于局部最优和收敛速度慢等问题，提出了一种耗散结构和差分变异混合的鸡群算法.该算法通过将耗散结构引入至雄鸡位置的更新公式，扩大了鸡群的搜索空间，增强了算法的全局搜索能力；同时，通过对随机选择的个体进行差分变异操作，增强了算法的收敛性能.对选取的18个标准函数进行仿真实验，结果表明，算法的收敛精度、收敛速度和稳定性均明显优于其他几种算法.

关键词: 鸡群算法耗散结构差分变异高维优化问题

Hybrid chicken swarm algorithm with dissipative structure and differential mutation

HAN Meng

School of Mathematics and Statistics, Xidian University, Xi'an 710126, China

Abstract: To overcome the drawbacks that the chicken swarm algorithm is liable to fall into the local optimum and is slow when solving the high-dimension problems, this paper proposes a hybrid chicken swarm algorithm with dissipative structure and differential mutation. A dissipative structure is adapted in cock position to enlarge the search space of the whole flock, so as to enhance the global searching ability. Meanwhile, differential mutation is applied in some randomly selected individuals to improve the convergence of the chicken swarm algorithm. Numerical experiments conducted on the 18 classical test functions that the proposed algorithm is superior to other algorithms.

Key words: chicken swarm algorithm dissipative structure differential mutation high-dimensional optimization problem

0 引言

高维优化是指对维数超过100的函数的优化，科学技术和工程实际中有许多高维优化问题^[1]，由于其维数较大，传统优化方法面临诸多局限.为此，国内外出现了大量群智能优化算法^[2](swarm intelligence algorithm，SIA)以解决这类问题.谭皓等^[3]将基本粒子群算法和蚁群算法相结合，提出了一种混合的粒子群算法，用以解决高维复杂函数的优化问题，并取得了良好的效果；刘昌芬等^[4]将广义的逆向学习方法应用于差分进化算法，提出了一种广义逆向学习方法的自适应差分算法，该算法在处理高维优化问题时可有效提高差分进化算法的寻优精度；盛孟龙等^[5]将自适应和交叉变换的方法引入到蝙蝠算法中，在解决高维复杂问题时取得了比较好的结果；龙文等^[6]提出了一种基于混沌和精英反向学习的混合灰狼优化算法来解决高维优化问题.

鸡群算法(chicken swarm optimization，CSO)是由MENG等^[7]于2014年提出的一种群智能优化算法.该算法具有原理简单、易于实现、全局搜索能力较强等优点，被广泛应用于多种工程优化问题：如非线性约束优化计算^[8]、非线性系统的参数估计^[9-10]和多分类器系数优化^[11]等.但在求解高维复杂优化问题时，鸡群算法和其他群智能优化算法一样，存在早熟收敛和收敛精度低等缺点，因此，一些学者提出了改进方法.QU等^[12]提出了一种精英反向学习的鸡群优化算法，采用自适应t分布代替雄鸡群体中的高斯分布，并将精英反向学习引入雌鸡群体中；孔飞等^[13]和WU等^[14]通过在小鸡位置更新公式中加入向自身所在子群的雄鸡学习部分，提出了一种改进的鸡群算法，此算法在求解高维优化问题时更容易搜索到全局最优解；李振壁等^[15]将模拟退火的思想引入鸡群算法.以上改进策略有效提高了算法的收敛速度和寻优精度，但在求解高维问题上仍存在早熟及寻优效果差等问题.

为了克服鸡群算法的上述缺陷，本文提出了一种将耗散结构和差分变异混合的鸡群算法(hybrid chicken swarm algorithm with dissipative structure and differential mutation，DMCSO).通过对多个典型的标准测试函数的寻优仿真表明，DMCSO算法具有较强的跳出局部最优解的能力，且可明显改善算法的收敛速度和寻优精度.

1 基本鸡群算法

鸡群算法是模拟鸡群等级制度和鸡群搜索食物行为的一种随机优化算法.在描述该算法之前先做4个假设：

假设1 整个鸡群有若干子群，子群数目由雄鸡个数确定，即每个雄鸡对应一个子群，每个子群中还包括一些雌鸡和小鸡.

假设2 根据适应度值的大小将整个鸡群分为雄鸡、雌鸡和小鸡3种类别.雄鸡由适应度值较好的若干个体组成，适应度值较差的若干个体作为小鸡，其他个体作为雌鸡.每只雄鸡作为各自子群的领头鸡，雌鸡随机选择要跟随的雄鸡，雌鸡和小鸡的母子关系也是随机建立的.

假设3 鸡群中的等级制度、支配关系和母子关系进化G代后进行更新.

假设4 每个子群中的雄鸡可以带领该子群的其他个体搜索食物，并且这些雄鸡可以阻止其他个体偷取自己已经发现的食物；小鸡追随自己所选择的妈妈雌鸡寻找食物；在食物竞争过程中，具有支配地位的个体更具有优势.

N_R、N_H、N_C和N_M分别指雄鸡、雌鸡、小鸡和妈妈雌鸡的个数，N_M是从N_H个雌鸡中随机选择的妈妈雌鸡个数. N为整个鸡群个体数，D为鸡群寻找食物的空间维数. x_{i, j}^t表示第i个个体在第t次迭代时的位置，i∈[1, 2, …, N]，j∈[1, 2, …, D].

1.1 雄鸡位置更新

与适应度值差的雄鸡相比，适应度值好的雄鸡在食物竞争中更具优势，而且能够在更广泛的空间中寻找食物.雄鸡位置更新公式如下：

$ \begin{array}{l} x_{i, j}^t = x_{i, j}^t \times \left( {1 + {\rm{rand}}\;n\left( {0, {\sigma ^2}} \right)} \right), \\ {\sigma ^2} = \left\{ \begin{array}{l} 1, \;\;{f_i} \le {f_k}, \\ \exp \left( {\frac{{\left( {{f_k}- {f_i}} \right)}}{{|{f_i} + \varepsilon |}}} \right), \;\;\;{f_i} > {f_k}, \end{array} \right.\\ k = \left[{1, {N_R}} \right], \;\;k \ne i, \end{array} $

(1)

式中rand n(0, σ²)表示满足均值为0、标准差为σ²的高斯分布的随机数，为防止式中分母为0，ε为一个很小的常数，k为雄鸡中除去第i个个体外的任意一个个体.

1.2 雌鸡位置更新

雌鸡不仅跟随其所在子群的雄鸡寻找食物，而且可以随机偷取其他鸡发现的食物.在食物竞争期间，适应度值高的雌鸡比适应度值低的雌鸡更具优势.雌鸡更新公式如下：

$ \begin{array}{l} x_{i, j}^t = x_{i, j}^t + {s_1} \times {\rm{rand}} \times \left( {x_{r1, j}^t-x_{i, j}^t} \right) + \\ \;\;\;\;\;\;\;{s_2} \times {\rm{rand}} \times \left( {x_{r2, j}^t-x_{i, j}^t} \right), \end{array} $

(2)

其中，s₁=exp((f_i-f_r1)/(|f_i|+ε))，s₂=exp(f_r2-f_i)，式中rand为[0, 1]之间均匀分布的随机数，r₁为第i个雌鸡所在子群中的雄鸡个体，r₂是从鸡群的雄鸡和雌鸡中随机选择的任意个体，且r₁≠r₂.

1.3 小鸡位置更新

小鸡跟随自己的雌鸡寻找食物，小鸡的位置更新公式如下：

$ x_{i, j}^t = x_{i, j}^t + FL \times \left( {x_{m, j}^t-x_{i, j}^t} \right), $

(3)

其中，m为第i只小鸡跟随的雌鸡，FL为跟随系数，取值范围为[0, 2].

2 耗散结构和差分变异混合的鸡群算法(DMCSO) 2.1 耗散结构

由鸡群算法的原理可知，雄鸡作为鸡群中每个子群的领头鸡，带领鸡群搜索食物；雌鸡参考所在子群的雄鸡位置进行更新；小鸡参考跟随雌鸡的位置进行更新；由此可见，雌鸡和小鸡都依靠雄鸡的信息搜寻食物，雄鸡影响整个鸡群的搜索方向和搜索速度.因此，当雄鸡陷入局部最优时，整个鸡群的寻优能力会受到影响.

耗散结构是指处在远离平衡态的开放系统，通过不断地与外界进行能量或物质交换，使原来的无序状态变成时间、空间或功能有序的状态^[16]. XIE等^[17]提出了一种耗散粒子群算法，首次实现了将耗散结构引入到粒子群算法中，在一定条件下通过将种群中个体的位置和速度重新扩散，为种群有效地补充有差异的新个体，增加种群多样性，从而提高算法的优化性能.本文将耗散结构引入鸡群算法的雄鸡更新公式中，扩大雄鸡个体的搜索空间，增强算法的全局搜索能力，从而有效降低整个鸡群落入局部最优的风险.具体实现如下：

$ \begin{array}{l} \;\;\;\;{\rm{if}}\left( {{\rm{rand}} < {c_v}} \right)\\ {x_i} = {\rm{random}}\left( {{l_d}, {u_d}} \right)\\ \;\;\;\;\;\;\;\;\;\;{\rm{end}} \end{array} $

(4)

式中c_v为扩散因子，取值范围为[0, 1]，x_i表示当前个体的位置，random(l_d, u_d)表示随机生成的个体(l_d和u_d分别表示群体空间的上界和下界)，本文取c_v=0.1^[18-19].

2.2 差分变异

随着迭代次数的不断增加，鸡群算法在进化后期个体差异程度越来越小，种群多样性逐渐下降，尤其在处理高维时，算法容易过早收敛陷入局部最优，难以获得最优解.本文将差分变异操作^[20-21]引入至鸡群算法中，以增加种群多样性.具体实现如下：

$ \begin{array}{l} {\rm{if}}\;{\rm{Mod}}\left( {t, G} \right)0\& \left| {{f_{{\rm{best}}}}\left( t \right)-{f_{{\rm{best}}}}\left( {t-G + 1} \right)} \right| \le \delta \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{for}}\;k = 1:H\\ \;\;\;\;\;x_{k, j}^t = x_{a, j}^t + F\left( {x_{b, j}^t-x_{c, j}^t} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{end}}\;{\rm{for}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{end}}\;{\rm{if}} \end{array} $

(5)

其中，G为种群更新代数；f_best(t)表示第t代的最优适应度值；H为随机选取种群规模10%~20%的个体数；本文取H=int(N*0.2)，int表示取整函数；其中a、b、c是从[1, N]中随机选取的3个个体，且a≠b≠c≠k，F为缩放比例因子，ε为早熟检验阀值，本文取δ=1.0×10^-10.

如果连续进化G代数，群体中的最优适应度值无明显变化，则进行个体差分变异.本文从鸡群中随机选择3个不同的个体x_a、x_b和x_c，通过对差分矢量(x_b-x_c)进行缩放并与x_a合并后对鸡群中随机选择的20%的个体进行差分变异操作. F的作用是对差分矢量(x_b-x_c)进行缩放，以确定当前个体搜索最优解的范围，从而生成新的变异个体.当F采用较大值时，算法可以在较大范围内进行搜索，但其收敛速度较慢；当F采用较小值时，虽然搜索较快，但易收敛到非最优解.为此，提出一种随机的缩放因子：

$ F = \left( {\frac{{{F_{\max }}-{F_{\min }}}}{M} \times \left( {M-t} \right) + {F_{\min }}} \right) \times {\rm{rand}}, $

(6)

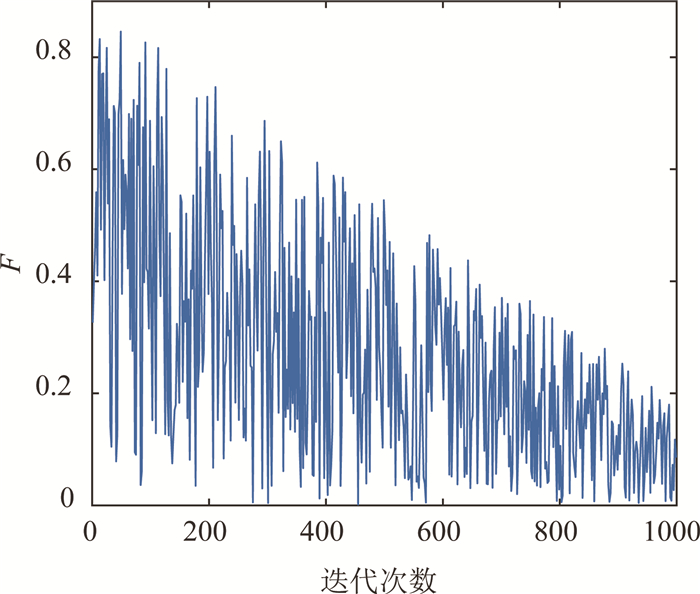
其中，M表示最大迭代次数，t为当前迭代次数，rand为[0, 1]之间均匀分布的随机数，由文献[22]可知，一般情况下，F的取值范围为[0.2, 0.9].图 1为缩放因子F随迭代次数的变化曲线.

图 1 随机缩放因子 Fig. 1 Random scale factor

从图 1中可以看出，rand的加入可以使个体在进化过程中有机会取得较小或较大的缩放因子，使得本算法可以更加灵活地调节局部和全局搜索能力.

2.3 算法的具体步骤

步骤1 初始化参数.鸡群规模为N，鸡群搜索空间的维数为D，种群更新代数G=10^[13]，雄鸡个体所占比例为20%，雌鸡个体(包括妈妈雌鸡)所占的比例为60%，小鸡个体所占比例为20%，妈妈雌鸡所占的比例为10%(占雌鸡个数)，最大迭代次数为M，早熟检验阀值δ.

步骤2 初始化种群，置t=1，设置适应度函数，计算鸡群中每个个体的适应度值，并初始化算法的个体和全局最优位置.

步骤3 若满足mod(t, G)=1，根据个体的适应度值对鸡群中所有个体进行排序，按照假设2对鸡群进行等级划分，根据雄鸡个数确定子群数目，并随机建立雌鸡和小鸡的母子关系.

步骤4 鸡群中各雄鸡按照式(1)和(4)更新位置，根据式(2)更新雌鸡位置，按式(3)更新小鸡位置.

步骤5 更新鸡群当前的个体最优位置和全局最优位置.

步骤6 早熟检验跳出局部最优.在种群中随机选择一部分个体利用式(5)和(6)进行变异操作，并更新个体最优.

步骤7 计算各个体的适应度值，重新进行适应度值排序，按照步骤3重新建立鸡群等级制度，重新对鸡群进行搜索分组.

步骤8 置t=t+1，若未达到最大迭代次数则转步骤3；否则继续.

步骤9 输出最优解.

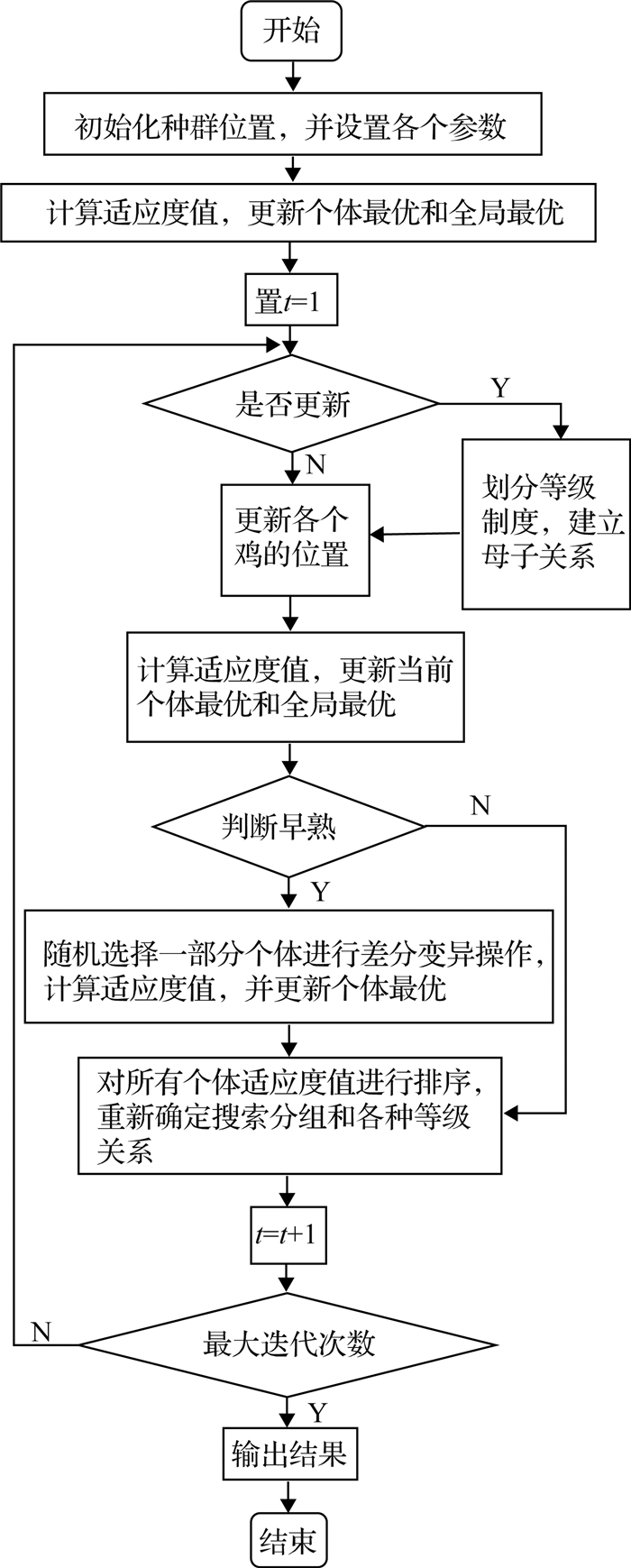
为进一步理解DMCSO算法的工作原理，图 2给出了其具体操作流程.

图 2 DMCSO算法流程图 Fig. 2 Flow chart of DMCSO algorithm

3 仿真实验与分析 3.1 参数设置

为验证DMCSO算法的性能，选取18个标准的测试函数与基本鸡群算法^[7](CSO)、粒子群算法^[23](particle swarm optimization，PSO)、蝙蝠算法^[24](bat algorithm，BA)和差分进化算法^[25](differential evolution algorithm，DE)进行仿真对比分析. 表 1给出了这些测试函数的名称、表达式、空间搜索范围和理论最优值.遵循公平原则，设定各算法初始种群为100，空间维数为100, 200(测试表 1前5个标准函数)，函数最大迭代次数为1 000，为避免单独运行给算法评价带来的误差，各算法均独立运行30次，其他参数说明详见表 2.

表 1 标准测试函数 Table 1 Benchmark test functions

名称	表达式	搜索范围	最优解
f₁: Sphere	$ {f_1} = \sum\limits_{i = 1}^D {x_i^2} $	[-100, 100]]^D	0
f₂: Rastrigin	$ {f_2} = \sum\limits_{i = 1}^D {\left[{x_i^2-10\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right) + 10} \right]} $	[-5.12, 5.12]^D	0
f_3: Ackley	$ \begin{array}{l} {f_3} = 20 + {\rm{e}}-20\exp \left( {-0.2\sqrt {\frac{1}{D}\sum\limits_i^D {x_i^2} } } \right)-\\ \;\;\;\;\;\;\;\;\exp \left( {\frac{1}{D}\sum\limits_{i = 1}^D {\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} } \right) \end{array}$	[-32, 32]^D	0
f₄: Griewank	$ {f_4} = 1 + \frac{1}{{4000}}\sum\limits_{i = 1}^D {x_i^2}-\prod\limits_{i = 1}^D {\cos \left( {{x_i}/\sqrt {\rm{i}} } \right)} $	[-600, 600]^D	0
f₅: Rosenbrock	$ {f_5} = \sum\limits_{i = 1}^{D- 1} {\left[{100{{\left( {{x_{i + 1}}-x_i^2} \right)}^2} + {{\left( {{x_i}-1} \right)}^2}} \right]} $	[-30, 30]^D	0
f₆: Schwefel	$ {f_6} = 418.9829D-\sum\limits_{i = 1}^D {{x_i}\sin \left( {\sqrt {\|{x_i}\|} } \right)} $	[-100, 100]^D	0
f₇: Schwefel1.2	$ {f_7} = \sum\limits_{i = 1}^D {{{\left( {\sum\limits_{j = 1}^i {{x_j}} } \right)}^2}} $	[-100, 100]^D	0
f₈: Schwefel2.22	$ {f_8} = \sum\limits_{i = 1}^D {\|{x_i}\|} + \prod\limits_{i = 1}^D {\|{x_i}\|} $	[-10, 10]^D	0
f₉: Discus	$ {f_9} = {10^6}x_1^2 + \sum\limits_{i = 2}^D {x_i^2} $	[-100, 100]^D	0
f₁₀: BentCigar	$ {f_{10}} = x_1^2 + {10^6} \times \sum\limits_{i = 2}^D {x_i^2} $	[-100, 100]^D	0
f₁₁: High Conditioned Elliptic	$ {f_{11}} = \sum\limits_{i = 1}^D {{{\left( {{{10}^6}} \right)}^{\frac{{i-1}}{{D-1}}}}x_i^2} $	[-100, 100]^D	0
f₁₂: Alpine	$ {f_{12}} = \sum\limits_{i = 1}^D {\|{x_i}\sin \left( {{x_i}} \right) + 0.1{x_i}\|} $	[-10, 10]^D	0
f₁₃: Zakharov	$ {f_{13}} = \sum\limits_{i = 1}^D {x_i^2} + {\left( {\sum\limits_{i = 1}^D {0.5i{x_i}} } \right)^2} + {\left( {\sum\limits_{i = 1}^D {0.5i{x_i}} } \right)^4}$	[-5, 10]^D	0
f₁₄: Sum of different powers	$ {f_{14}} = \sum\limits_{i = 1}^D {\|{x_i}{\|^{i + 1}}} $	[-1, 1]^D	0
f₁₅: Dixonprice	$ {f_{15}} = {\left( {{x_1}-1} \right)^2} + \sum\limits_{i = 2}^D {i\left( {2x_i^2-x_{i-1}^2} \right)} $	[-10, 10]^D	0
f₁₆: Weierstrass	$ \begin{array}{l} {f_{16}} = \sum\limits_{i = 1}^D {\left( {\sum\limits_{k = 0}^{{k_{\max }}} {\left[{{a^k}\cos \left( {2{\rm{ \mathsf{ π} }}{b^k}\left( {{x_i} + 0.5} \right)} \right)} \right]} } \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;D\sum\limits_{k = 0}^{{k_{\max }}} {\left[{{a^k}\cos \left( {2{\rm{ \mathsf{ π} }}{b^k} \times 0.5} \right)} \right]} \end{array}$ a=0.5;b=3;k_max=20;	[-0.9, 0.9]^D	0
f₁₇: Levy	$ {f_{17}} = \sum\limits_{i = 1}^{D- 1} {\left[{{{\left( {{y_i}-1} \right)}^2}\left( {1 + 10{{\sin }^2}\left( {{\rm{ \mathsf{ π} }}{y_i} + 1} \right)} \right)} \right]} + $ (y_D-1)²(1+10sin²(2πy_D))+sin²(πy₁) y_i=1+(x_i-1)/4, i=1, 2, …, D	[-10, 10]^D	0
f₁₈: Powell	$ {f_{18}} = \sum\limits_{i = 1}^{d/4} {[{{\left( {{x_{4i-3}} + 10{x_{4i-2}}} \right)}^2} + 5{{\left( {{x_{4i-1}} - {x_{4i}}} \right)}^2}} + $ (x_4i-2-2x_4i-1)⁴+10(x_4i-3+x_4i)⁴]	[-10, 10]^D	0

表 1 标准测试函数 Table 1 Benchmark test functions

表 2 5种算法的相关参数 Table 2 The related parameter values for five algorithms

实验环境：所有实验均在Intel(R) Xeon(R) CPU E5620 @ 2.40GHz、8.00GB内存、2.40GHz主频的计算机上进行，软件运行环境为Matlab 2016a.

3.2 算法的性能分析

为充分评价DMCSO算法的优化性能，考虑以下几个评价准则：1)算法寻优精度：在有限的函数评价次数条件下，算法搜索到的最优适应度值. 2)算法的收敛速度：算法在达到相同评价次数时，若适应度值较好，则算法收敛速度快. 3)稳定性：即算法独立运行多次以后，各个算法所得到适应度值的方差.

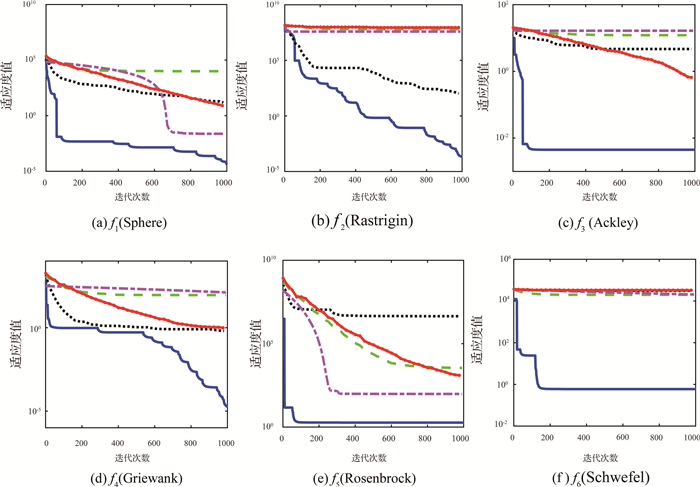
3.2.1 混合策略的有效性

为验证2种不同策略混合后用于鸡群算法的有效性和可行性，选取表 1前5个具有代表性的测试函数进行仿真实验，其中，f₁和f₅是单峰函数，用来测试算法的寻优精度；f₂、f₃、f₄为多峰函数，用来验证算法逃离局部极值的能力.将DMCSO算法与CSO、耗散机制的DCSO算法(CSO算法中引入耗散结构)及差分变异的MCSO算法(CSO算法中引入差分变异)进行比较.求取4种算法各自在100维的情况下独立运行30次的平均值和标准差.相关实验数据如表 3所示.

表 3 鸡群算法在不同策略下的优化结果 Table 3 Optimization results of CSO on different strategy

函数f₁(Sphere)是一种比较简单的单峰二次函数，较容易搜索到最优值.从表 3的数据中可以看出，对于函数f₁，DMCSO、MCSO和DCSO算法的寻优精度均较CSO算法有所提高，且DMCSO算法寻优效果最好，较CSO算法提高了5个数量级，较DCSO算法提高了2个数量级，较MCSO算法提高了4个数量级. DMCSO算法稳定性更好.

复杂多峰函数f₂(Rastrigin)、f₃(Ackley)、f₄(Griewank)有多个局部极值点，较难搜索到全局极小值.从表 3中可以看出，对于函数f₂，MCSO算法的寻优精度略高于DMCSO算法，但DMCSO算法取得的优化结果显著优于CSO和DCSO算法. DMCSO算法搜索到了函数f₃最好的优化结果. CSO和MCSO算法对函数f₄的寻优结果相当，DMCSO算法取得的优化结果和标准差最好.

函数f₅(Rosenbrock)是典型的单峰难优化函数，该函数全局极值点处在一个抛物线形的狭长峡谷底端，使得算法在搜索全局最优解时非常困难.从表 3的数据中可以看出，DMCSO算法无论是平均值还是方差在函数f₅上取得的结果都明显优于其他算法.

以上分析说明：相较于MCSO和DCSO算法，DMCSO算法不仅大幅度提高了算法的搜索精度，而且有效减小了算法陷入局部最优的可能.该实验结果充分表明了将2种策略混合后用于鸡群算法是有效和可行的.

3.2.2 算法寻优精度和稳定性比较

为验证DMCSO算法的收敛精度和稳定性，统计PSO、BA、DE、CSO和DMCSO 5种算法对表 1中18种测试函数分别独立运行30次的最优适应度值、最差适应度值、平均适应度值和标准差，表 4给出了函数f₁~f₁₈在100维时的实验数据，表 5给出了函数f₁~f₅在200维时的实验数据.

表 4 函数f₁~f₁₈的测试结果(D=100) Table 4 Test statistical results of functions f₁~f₁₈(D=100)

函数	维数	指标	PSO	BA	DE	CSO	DMCSO
f₁	100	最好值	2.700 0×10^-2	1.487 9×10^-2	2.116 1	5.280 6×10^-5	5.226 7×10^-14
		最差值	3.000 0×10⁴	2.894 3×10^-2	9.859 9	4.540 9×10²	1.098 4×10^-2
		平均值	8.000 3×10³	1.950 5×10^-2	4.294 4	42.592	5.862 9×10^-4
		标准差	8.468 7×10³	2.700 0×10^-3	1.600 6	1.055 1×10²	2.093 3×10^-3
f₂	100	最好值	4.351 5×10²	1.807 5×10²	8.265 5×10²	1.019 4×10^-10	2.261 2×10^-13
		最差值	7.189 7×10²	8.331 0×10²	9.050 9×10²	4.262 7×10^-4	8.858 8×10^-6
		平均值	5.899 9×10²	4.048 3×10²	8.686 7×10²	3.029 7×10^-5	6.662 9×10^-7
		标准差	64.131	1.581 8×10²	20.715	8.835 4×10^-5	2.008 4×10^-6
f₃	100	最好值	2.717 5	14.583	0.268 90	1.300 0×10^-3	1.319 5×10^-7
		最差值	15.962	18.525	0.947 43	10.147	9.296 3×10^-2
		平均值	10.142	16.625	0.663 93	5.043 1	9.540 7×10^-3
		标准差	3.995 0	1.019 7	0.171 39	3.629 9	2.247 9×10^-2
f₄	100	最好值	3.650 0×10^-2	1.132 8×10²	0.768 09	2.357 9×10^-7	1.043 6×10^-13
		最差值	1.809 6×10²	6.405 0×10²	1.069 1	10.080	1.527 0×10^-4
		平均值	54.385	3.432 8×10²	0.935 23	0.859 60	1.516 2×10^-5
		标准差	65.324	1.497 2×10²	9.416 0×10^-2	2.046 2	3.802 8×10^-5
f₅	100	最好值	3.088 9×10²	94.176	7.535 1×10²	2.559 1×10⁶	2.167 1×10^-5
		最差值	9.093 5×10⁴	5.138 6×10²	1.587 7×10³	2.437 5×10⁷	15.966
		平均值	2.309 6×10⁴	1.422 9×10²	1.042 9×10³	8.507 9×10⁶	1.191 2
		标准差	3.828 7×10⁴	82.984	1.962 5×10²	5.272 2×10⁶	3.264 8
f₆	100	最好值	1.271 5×10⁴	1.796 3×10⁴	3.132 3×10⁴	2.532 6×10⁴	1.400 0×10^-3
		最差值	1.951 7×10⁴	2.651 0×10⁴	4.189 3×10⁴	3.263 8×10⁴	4.419 1
		平均值	1.584 8×10⁴	2.081 8×10⁴	3.352 8×10⁴	3.030 3×10⁴	0.545 91
		标准差	1.880 7×10³	1.855 0×10³	2.332 3×10³	1.655 1×10⁴	1.194 15
f₇	100	最好值	1.256 4×10⁴	4.254 4×10²	1.004 6×10⁵	2.216 7×10⁴	2.522 8×10^-3
		最差值	8.615 4×10⁵	3.776 0×10⁴	1.799 8×10⁵	6.903 7×10⁴	3.377 2×10²
		平均值	1.325 0×10⁵	1.182 6×10⁴	1.427 4×10⁵	3.595 6×10⁴	49.334
		标准差	1.405 4×10⁵	1.188 5×10⁴	2.305 6×10⁴	1.066 8×10⁴	88.535
f₈	100	最好值	30.471	6.383 0	0.970 20	1.896 0×10^-32	1.493 2×10^-29
		最差值	1.608 1×10²	8.416 9×10¹⁸	2.309 0	3.736 9×10^-15	1.377 2×10^-25
		平均值	1.007 0×10²	2.897 8×10¹⁷	1.502 9	8.267 6×10^-16	1.126 9×10^-26
		标准差	31.745	1.535 8×10¹⁸	0.333 81	1.081 1×10^-15	2.701 9×10^-26
f₉	100	最好值	1.000 0×10⁴	1.857 0×10⁴	2.458 8	9.089 0×10^-7	5.082 1×10^-16
		最差值	8.000 0×10⁴	2.610 3×10⁵	8.645 9	1.695 2×10²	7.804 7×10^-4
		平均值	4.190 1×10⁴	1.445 9×10⁵	4.708 5	11.143	1.168 2×10^-4
		标准差	1.911 9×10⁴	7.882 4×10⁴	1.288 3	32.691	2.037 2×10^-4
f₁₀	100	最好值	2.050 2×10⁴	1.201 2×10⁶	1.545 6×10⁶	6.603 1×10³	2.245 4×10^-7
		最差值	2.000 0×10¹⁰	9.961 1×10⁶	8.336 2×10⁶	3.250 1×10⁸	3.276 2×10⁵
		平均值	6.667 1×10⁹	2.799 4×10⁶	3.889 5×10⁶	5.898 8×10⁷	2.271 4×10⁴
		标准差	7.580 9×10⁹	2.947 7×10⁶	1.559 2×10⁶	9.367 0×10⁷	6.838 3×10⁴
f₁₁	100	最好值	9.454 1×10⁷	4.034 9×10⁵	3.773 0×10³	5.325 7×10^-15	1.234 9×10^-11
		最差值	1.252 6×10⁹	2.486 0×10⁷	1.204 9×10⁵	3.043 0×10⁴	1.072 6×10^-2
		平均值	5.077 8×10⁸	3.344 8×10⁶	6.482 7×10³	2.296 2×10³	3.823 9×10^-4
		标准差	3.330 3×10⁸	4.753 0×10⁶	2.350 3×10³	6.231 0×10³	1.954 8×10^-3
f₁₂	100	最好值	4.763 4	3.758 2	0.192 80	4.657 2×10^-19	9.547 1×10^-30
		最差值	54.425	26.861	0.717 40	0.816 10	9.215 1×10^-2
		平均值	27.818	13.877	0.300 14	0.134 90	9.237 9×10^-3
		标准差	11.208	5.118 7	0.110 61	0.168 70	1.949 3×10^-2
f₁₃	100	最好值	1.392 9×10³	0.104 69	6.323 1×10²	91.715	2.445 6×10^-6
		最差值	2.646 7×10³	3.370 1	9.651 2×10²	2.313 7×10²	3.174 5×10²
		平均值	1.986 8×10³	0.856 80	8.140 68×10²	1.539 1×10²	1.211 8×10²
		标准差	2.851 7×10²	0.704 40	93.663	43.179	1.147 0×10²
f₁₄	100	最好值	5.395 6×10^-17	1.059 9×10^-8	2.933 8×10^-21	4.700 2×10^-48	2.047 0×10^-52
		最差值	4.370 3×10^-11	5.011 9×10^-7	3.674 1×10^-13	2.366 0×10^-9	3.616 6×10^-16
		平均值	1.687 6×10^-12	8.900 2×10^-8	1.763 9×10^-14	9.492 9×10^-11	1.524 5×10^-17
		标准差	7.941 3×10^-12	8.986 7×10^-8	6.919 4×10^-14	4.321 5×10^-10	6.768 2×10^-17
f₁₅	100	最好值	53.699	1.592 5	25.055	1.127 6×10⁴	0.234 33
		最差值	1.616 8×10⁶	10.577	96.847	6.242 9×10⁵	0.950 06
		平均值	4.713 2×10⁵	3.604 4	55.707	1.980 3×10⁵	0.394 95
		标准差	4.286 4×10⁵	1.969 5	16.924	1.563 4×10⁵	0.193 41
f₁₆	100	最好值	26.957	48.332	79.889	0	0
		最差值	61.230	65.704	83.563	1.272 7×10^-9	8.095 9×10^-9
		平均值	48.647	56.308	81.689	4.956 9×10^-11	2.807 5×10^-10
		标准差	9.702 9	4.005 5	0.947 40	2.317 4×10^-10	1.476 2×10^-9
f₁₇	100	最好值	11.706	19.761	0.107 50	11.764	3.558 3×10^-7
		最差值	2.062 2×10²	84.129	2.048 0	73.187	1.461 1×10^-2
		平均值	1.083 9×10²	42.279	0.766 90	33.783	1.184 2×10^-3
		标准差	47.122	17.075	0.532 71	16.405	2.998 0×10^-3
f₁₈	100	最好值	1.002 2×10⁴	1.353 9	35.923	1.121 8×10³	4.527 4×10^-5
		最差值	9.481 6×10⁴	2.306 8	1.350 0×10²	2.000 7×10⁴	7.694 7×10^-2
		平均值	4.290 9×10⁴	1.782 5	74.292	6.884 8×10³	1.151 7×10^-2
		标准差	2.167 6×10⁴	0.222 16	26.594	4.389 7×10³	1.962 0×10^-2

表 4 函数f₁~f₁₈的测试结果(D=100) Table 4 Test statistical results of functions f₁~f₁₈(D=100)

表 5 函数f₁~f₅测试结果(D=200) Table 5 Test statistical results of functions f₁~f₅(D=200)

函数	维数	指标	PSO	BA	DE	CSO	DMCSO
f₁	200	最好值	1.124 0×10⁴	8.680 0×10^-2	4.448 2×10²	21.083	1.346 1×10^-5
		最差值	9.283 0×10⁴	54.761	1.383 7×10³	2.349 3×10⁴	3.742 4
		平均值	4.183 6×10⁴	2.838 2	8.740 0×10²	3.485 5×10³	0.557 20
		标准差	1.709 4×10⁴	10.338	2.205 6×10²	4.723 4×10³	0.881 10
f₂	200	最好值	1.173 5×10³	3.524 9×10²	1.724 6×10³	1.800 0×10^-2	5.204 3×10^-4
		最差值	1.539 0×10³	9.513 0×10²	1.910 3×10³	0.818 10	1.370 1
		平均值	1.359 5×10³	5.828 7×10²	1.843 7×10³	0.272 10	0.199 7
		标准差	99.284	1.859 4×10²	40.873	0.265 51	0.346 30
f₃	200	最好值	13.675	13.675	3.959 6	8.779 6	1.264 1×10^-3
		最差值	19.067	19.067	5.091 0	12.034	0.388 69
		平均值	17.688	17.688	4.560 6	10.368	5.100 9×10^-2
		标准差	1.108 99	1.108 9	2.517 6	0.697 1	7.910 3×10^-2
f₄	200	最好值	27.878	50.927	6.306 9	0.817 50	1.145 7×10^-3
		最差值	8.227 5×10²	1.491 2×10³	17.497	237.81	0.458 76
		平均值	3.896 2×10²	7.430 0×10²	9.884 3	49.030	7.180 8×10^-2
		标准差	2.076 9×10²	3.364 1×10²	2.517 6	57.729	0.117 19
f₅	200	最好值	4.133 3×10⁵	2.021 6×10²	8.861 3×10⁴	1.909 2×10⁷	4.965 6×10^-3
		最差值	2.417 8×10⁸	5.282 7×10²	5.018 5×10⁵	5.233 1×10⁷	59.135
		平均值	8.746 3×10⁷	2.800 8×10²	1.922 7×10⁵	3.232 1×10⁷	6.9383
		标准差	7.478 5×10⁷	98.833	7.956 4×10⁴	9.389 2×10⁶	13.347

表 5 函数f₁~f₅测试结果(D=200) Table 5 Test statistical results of functions f₁~f₅(D=200)

1) 从表 4的数据中可以看出，相较PSO、BA、DE和CSO 4种算法，无论是单峰函数f₁还是多峰复杂函数f₂、f₃、f₄，DMCSO算法均取得了较好的寻优效果.对于难测函数f₅、f₆和f₇，PSO、BA、DE和CSO 4种算法搜索到的优化结果均较差，但DMCSO算法搜索到了较好的优化结果，表现了较强的寻优能力.对于函数f₈，DMCSO、CSO算法取得了较PSO、BA和DE 3种算法更好的寻优结果，虽然CSO算法搜索到了最好的最优适应度值，但DMCSO算法的平均适应度、标准差和最差适应度均优于CSO算法.对于f₉、f₁₀、f₁₁ 3个单峰函数，除DMCSO算法外，其他算法取得的优化结果和理论最优解偏差圴较大，寻优精度较低.对函数f₁₂，DE、DMCSO和CSO算法分别取得了较好的结果，但DMCSO算法的寻优能力更强.对于函数f₁₃，BA算法的结果较好，DMCSO算法的优化结果和CSO算法的很接近，但DMCSO算法略优于CSO算法. PSO、BA、DE、CSO和DMCSO 5种算法对函数f₁₄均有良好的寻优能力，且DMCSO算法搜索到了最好的优化结果.对函数f₁₅，DMCSO算法的寻优能力最强，BA和DE算法次之，PSO和CSO算法的优化结果较差. DMCSO和CSO算法对f₁₆函数的搜索精度均较高，取得的优化结果高出PSO、BA、DE算法各10个数量级.对f₁₇、f₁₈函数，DMCSO算法的寻优精度均高于其他算法，其最优值、平均值、标准差和最差值均较好.

从表 5的测试数据中可以看出，在200维的情况下，DMCSO算法对函数f₁~f₅均取得了最好的最优值、平均值、标准差，而PSO、BA和DE 3种算法寻优较困难，均未获得全局最优值.

上述分析表明，相较其他算法，DMCSO算法具有较强的寻优能力，有效提高了解的质量和算法的收敛精度.从表 4和表 5的数据中可以看出，DMCSO算法的寻优能力受维数的影响较小，而其余算法的进化能力随着维数的增加都有不同程度下降.

2) 从表 4和表 5的数据中可以看出，DMCSO算法较PSO、BA、DE和CSO 4种算法的标准差小，说明DMCSO算法稳定性更好.

3.2.3 算法收敛速度比较

对表 1中的18个测试函数进行仿真模拟，图 3(a)~(r)为CSO、PSO、BA、DE和DMCSO 5种算法求解各函数100维最优适应度值随迭代次数变化的收敛曲线，曲线横坐标表示进化代数，纵坐标表示适应度值.

图 3 函数f₁~f₁₈的收敛曲线 Fig. 3 Convergence curves comparison of functions f₁~f₁₈

从图 3中可以看出，对大多数函数来说，PSO、BA和DE 3种算法，迭代一段时间后，寻优结果基本不再发生变化，陷入了局部最优无法跳出，取得的优化结果不太理想. CSO算法在部分函数上表现出较好的寻优能力，收敛速度也相对较高，但略逊DMCSO算法.除函数f₁₃外(对函数f₁₃，在迭代次数小于50时，DMCSO算法的收敛速度更快、收敛精度也更高，但在迭代后期，BA算法的表现更加显著)，DMCSO算法对其他函数均有较强的寻优能力，均以较快的收敛速度搜索到了精度较高的适应度值.因此，DMCSO算法相较于PSO、BA、DE和CSO 4种算法，收敛速度更快、搜索精度更高.

4 结论

针对鸡群算法在求解高维复杂优化问题中的一些弊端，本文将耗散结构、带有随机缩放因子的差分变异2种策略混合后用于鸡群算法，有效解决了鸡群算法在求解高维复杂问题时难度大、精度低、收敛速度慢的问题.通过与其他群智能算法对18个测试函数进行仿真对比，结果表明：DMCSO算法不仅较明显改善了算法的稳定性，而且其收敛速度和寻优精度得到了有效提高，充分证明了DMCSO算法的有效性和可行性.当然，此算法也有其局限性：算法对该扩散因子的设置比较敏感，参数未能实现自适应，仍然需要根据先验知识确定等.

参考文献

[1]	RAHNAMAYAN S, WANG G G. Solving large scale optimization problems by opposition based differential evolution (ODE)[J]. WSEAS Transactions on Computers, 2008, 7(10): 1792–1804.
[2]	BEHESHTI Z, SHAMSUDDIN S M H. A review of population based metaheuristic algorithms[J]. Int J Adv Soft Comput Appl, 2013, 5(1): 1–35.
[3]	谭皓, 沈春林, 李锦. 混合粒子群算法在高维复杂函数寻优中的应用[J]. 系统工程与电子技术, 2005, 27(8): 1471–1574. TAN H, SHEN C L, LI J. Hybrid particle swarm optimization algorithm for high-dimension complex functions[J]. Systems Engineering and Electronics, 2005, 27(8): 1471–1574.
[4]	刘昌芬, 韩红桂, 乔俊飞, 等. 广义逆向学习方法的自适应差分算法[J]. 智能系统学报, 2015, 10(1): 131–137. LIU C F, HAN H G, QIAO J F. Self-adaptive DE algorithm via generalized opposition based learning[J]. CAAI Transactions on Intelligent System, 2015, 10(1): 131–137.
[5]	盛孟龙, 贺兴时, 王慧敏. 一种改进的自适应变异蝙蝠算法[J]. 计算机技术与发展, 2014(10): 131–134. SHENG M L, HE X S, WANG H M. An improved algorithm for adaptive mutation bat[J]. Computer Technology and Development, 2014(10): 131–134.
[6]	龙文, 蔡绍洪, 焦建军, 等. 求解高维优化问题的混合灰狼优化算法[J]. 控制与决策, 2016, 31(11): 1991–1997. LONG W, CAI S H, JIAO J J, et al. Hybrid grey wolf optimization algorithm for high-dimensional opt-imization[J]. Control and Decision, 2016, 31(11): 1991–1997.
[7]	MENG X, LIU Y, GAO X, et al. A new bio-inspired algorithm: chicken swarm optimization[C]//International Conference in Swarm Intelligence. Heidelberg: Springer International Publishing, 2014: 86-94.
[8]	CHEN Y L, HE P L, ZHANG Y H. Combining penalty function with modified chicken swarm optimization for constrained optimization[J]. Advances in Intelligent Systems Research, 2015, 126: 1899–1907.
[9]	CHEN S, YANG R, YANG R, et al. A parameter estimation method for nonlinear systems based on improved boundary chicken swarm optimization[J]. Discrete Dynamics in Nature and Society, 2016, 2016(15): 1–11.
[10]	CHEN S L, YAN R H. Parameter estimation for chaotic systems based on improved boundary chicken swarm optimization[C]//International Symposium on Optoelectronic Technology and Application 2016. Beijing: International Society for Optics and Photonics, 2016: 101571K-101571K-6. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=2577548
[11]	洪杨, 于凤芹. 改进的鸡群算法并用于多分类器系数优化[J]. 计算机工程与应用, 2017, 53(9): 158–161. HOMG Y, YU F Q. Improved chicken swarm optimization and its application in coefficients optimization of multi-classifier[J]. Computer Engineering and Applications, 2017, 53(9): 158–161. DOI:10.3778/j.issn.1002-8331.1511-0121
[12]	QU C W, ZHAO S A, FU Y M, et al. Chicken swarm optimization based on elite opposition-Based learning[J]. Mathematical Problems in Engineering, 2017, 2017(11): 1–20.
[13]	孔飞, 吴定会. 一种改进的鸡群算法[J]. 江南大学学报(自然科学版), 2015, 14(6): 681–688. KONG F, WU D H. An improved chicken swarm optimization algorithm[J]. Journal of Jiangnan University(Natural Science Edition), 2015, 14(6): 681–688.
[14]	WU D, XU S, KONG F. Convergence analysis and improvement of chicken swarm optimization[J]. IEEE Access, 2016(4): 9400–9412.
[15]	李振璧, 王康, 姜媛媛. 基于模拟退火的改进鸡群优化算法[J]. 微电子学与计算机, 2017, 34(2): 30–33. LI Z B, WANG K, JIANG Y Y. The study of improved chicken swarm optimization algorithm based on simulated annealing[J]. Microelectronics and Computer, 2017, 34(2): 30–33.
[16]	于惠, 王洪国, 庄波, 等. 一种基于耗散理论的遗传算法及其应用[J]. 计算机工程与应用, 2008, 44(21): 113–115. YU H, WANG H G, ZHUANG B, et al. Genetic algorithm based on dissipative theory and it's application[J]. Computer Engineering and Applications, 2008, 44(21): 113–115. DOI:10.3778/j.issn.1002-8331.2008.21.031
[17]	XIE X F, ZHANG W J, YANG Z L. Dissipative particle swarm optimization[C]//Evolutionary Computation, 2002. CEC'02. Proceedings of the 2002 Congress on. Piscataway: IEEE Computer Society, 2002: 1456-1461. http://doi.ieeecomputersociety.org/10.1109/CEC.2002.1004457
[18]	任小波, 杨忠秀. 耗散粒子群算法的性能分析[J]. 计算机仿真, 2010, 27(2): 204–207. REN X B, YANG Z X. Performance analysis on dissipative particle swarm optimization[J]. Computer Simulation, 2010, 27(2): 204–207.
[19]	任小波, 杨忠秀. 一种动态扩散粒子群算法[J]. 计算机应用, 2010, 30(1): 159–161. REN X B, YANG Z X. Dynamic diffusion particle swarm optimization[J]. Journal of Computer Applications, 2010, 30(1): 159–161.
[20]	刘三阳, 张晓伟. 混合差分变异策略[J]. 智能系统学报, 2008, 3(6): 487–491. LIU S Y, ZHANG X W. A hybrid strategy for differential variation[J]. CAAI Transactions on Intelligent System, 2008, 3(6): 487–491.
[21]	高卫峰, 刘三阳, 姜飞, 等. 混合人工蜂群算法[J]. 系统工程与电子技术, 2011, 33(5): 1167–1170. GAO W F, LIU S Y, JIANG F, et al. Hybrid artificial bee colony algorithm[J]. Systems Engineering and Electronics, 2011, 33(5): 1167–1170.
[22]	袁俊刚, 孙治国, 曲广吉. 差异演化算法的数值模拟研究[J]. 系统仿真学报, 2007, 19(20): 4646–4648. YUNA J G, SUN Z G, QU G J. Simulation study of differential evolution[J]. Journal of System Simulation, 2007, 19(2): 4646–4648.
[23]	CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. Evolutionary Computation IEEE Transactions on, 2002, 6(1): 58–73. DOI:10.1109/4235.985692
[24]	YANG X S. A new metaheuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Heidelberg: Springer, 2010: 65-74.
[25]	STORN R, PRICE K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341–359. DOI:10.1023/A:1008202821328