基于动态分级和邻域反向学习的改进粒子群算法

引用本文 [复制中英文]

任燕芝. 基于动态分级和邻域反向学习的改进粒子群算法[J]. 浙江大学学报(理学版), 2018, 45(3): 261-271. DOI: 10.3785/j.issn.1008-9497.2018.03.001.

REN Yanzhi. An improved particle swarm algorithm based on dynamic segmentation and neighborhood reverse learning[J]. Journal of Zhejiang University(Science Edition), 2018, 45(3): 261-271. DOI: 10.3785/j.issn.1008-9497.2018.03.001.

[复制英文]

基金项目

国家自然科学基金资助项目（61373174）

作者简介

任燕芝(1992-), ORCID:http://orcid.org/0000-0003-1109-8050, 女, 硕士, 主要从事智能优化算法、最优化理论及其应用研究, E-mail:yzren@stu.xidian.edu.cn

文章历史

收稿日期：2017-08-24

Contents Abstract Full text Figures/Tables PDF

基于动态分级和邻域反向学习的改进粒子群算法

任燕芝

西安电子科技大学数学与统计学院, 陕西西安 710126

收稿日期：2017-08-24

基金项目：国家自然科学基金资助项目（61373174）

作者简介：任燕芝(1992-), ORCID:http://orcid.org/0000-0003-1109-8050, 女, 硕士, 主要从事智能优化算法、最优化理论及其应用研究, E-mail:yzren@stu.xidian.edu.cn

摘要: 针对粒子群算法容易陷入局部最优解的问题，提出了一种基于动态分级和邻域反向学习的改进粒子群算法.该算法通过构建动态分级机制，将种群中的粒子动态地划分成3个等级，对不同等级内的粒子采取不同的扰动行为，使得粒子在增强种群多样性的同时保持向全局最优方向进化；采用粒子智能更新方式，提高了粒子的搜索能力；引入动态邻域反向学习点建立全局搜索策略，促使种群快速寻优.最后，利用多种典型测试函数对该算法进行仿真实验，结果表明，与其他几种优化算法相比，本算法具有较好的收敛性和稳定性.

关键词: 粒子群算法动态分级机制邻域反向学习全局搜索策略

An improved particle swarm algorithm based on dynamic segmentation and neighborhood reverse learning

REN Yanzhi

School of Mathematics and Statistics, Xidian University, Xi'an 710126, China

Abstract: In order to solve the problem that the particle swarm optimization algorithm is likely to fall into local optimum, an improved particle swarm algorithm based on dynamic segmentation and neighborhood reverse learning (DSNRPSO) is proposed. By setting up a dynamic segmentation mechanism, the algorithm divides the particles in the population into three grades, then employs different perturbation strategies for the particles in different grades, so that the particles maintain the evolution to the global optimal direction while the diversity of the population is enhanced. Furthermore, it adopts the method of particle intelligent updating to promote the search ability of particles, and introduces the dynamic neighborhood reverse point enabling a global search to improve the particle searching speed. The preliminary results show that the proposed algorithm has better convergence and stability than several other kinds of optimization algorithms.

Key words: particle swarm algorithm dynamic segmentation mechanism neighborhood reverse learning global search strategy

智能优化算法是建立在生物智能或物理现象基础之上，通过模拟某些自然现象或过程来求解复杂优化问题的一种方法^[1].常见的智能算法有：粒子群算法(particle swarm optimization, PSO)^[2]、人工蜂群算法(artificial bee colony, ABC)^[3]、人群搜索算法(seeker optimization algorithm, SOA)^[4]、蝙蝠算法(bat algorithm, BA)^[5]、布谷鸟算法(cuckoo search, CS)^[6]等, 这些算法为解决传统优化算法难以处理的问题提供了切实可行的方案.

粒子群算法(PSO)是由美国的KENNEDY等^[2]基于鸟群飞行觅食的行为提出的一种有效的全局寻优算法.与其他智能算法相比，PSO算法操作简单，具有记忆全局极值和个体极值的功能，能根据当前的搜索情况动态地调整搜索策略，在较少的迭代次数内找到最优解. PSO算法已被广泛应用于函数优化、数据挖掘、神经网络训练等领域.但PSO算法存在易早熟收敛、易陷入局部最优等缺点，为此，专家学者们提出了许多改进措施.文献[7]提出由种群多样性引导的粒子群算法(ARPSO)，该算法在迭代过程中，通过种群多样性的大小判断粒子处于吸引还是排斥阶段.当种群多样性下降到最小阈值时，采用种群增加机制，此为吸引阶段；当种群多样性增加到最大阈值时，采用精英选择机制，此为排斥阶段.但粒子的种群多样性往往处于二者之间，因此改进算法的效果不太明显，而且该算法需要在每一次迭代中计算种群的多样性，增加了算法的复杂度. 2013年，WANG等^[8]提出了基于邻域搜索的粒子群算法(DNSPSO), 以一定的概率从父代种群和子代种群中随机选择粒子作为试验个体，采用贪婪策略更新粒子，然后通过邻居搜索策略使粒子之间实现信息交互，此算法对复杂问题的优化有较好的寻优效果.

目前，大多数改进PSO算法所提出的改进策略是作用在整个种群上的，由自然环境对生物的选择可知，同一环境下，不同生物对环境的适应度不同，进化速度和方式也不同；不同环境下，同一生物的进化方向也有不同.为此，本文提出一种基于动态分级和邻域反向学习的改进粒子群算法.在算法中，根据函数评价次数和每次迭代时粒子的适应度值将种群中的粒子动态地划分成3个等级，并分别对不同等级内的粒子执行不同的扰动策略，使得粒子在增强种群多样性的同时保持向全局最优方向进化，在此基础上，采取新的粒子位置更新方式，提高粒子的寻优能力.另外，为了加快算法的收敛速度，平衡种群的局部开采和全局探测能力，引入了动态邻域反向点来构建全局搜索策略.仿真结果表明，该算法在求解不同类型测试函数时均取得了较好的实验效果.

1 PSO算法

在粒子群算法中，每个粒子代表寻优空间中一个潜在的解，对应一个由适应度函数决定的适应度值，粒子根据本身找到的最优解和整个种群当前找到的最优解进行更新迭代，直到找到全局最优解为止.

假设在D维的可行解空间，初始化N个粒子x=(x₁, x₂, …, x_N), 其中第i个粒子表示为x_i=(x_i1, x_i2, …, x_iD), 代表第i个粒子在搜索空间的位置，第i个粒子的速度定义为v_i=(v_i1, v_i2, …, v_iD).在每次迭代中计算各粒子的适应度值，确定t时刻第i个粒子迄今为止搜索到的最优位置，即个体极值pbest_i=(pbest_i1, pbest_i2, …，pbest_iD)，以及整个种群迄今为止搜索到的最优位置，即全局极值gbest=(gbest₁, gbest₂, …, gbest_D).

$ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = {v_{ij}}\left( t \right) + {c_1}{r_1}\left( {{\rm{pbes}}{{\rm{t}}_{ij}}\left( t \right)-{x_{ij}}\left( t \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{c_2}{r_2}\left( {{\rm{gbes}}{{\rm{t}}_j}\left( t \right)-{x_{ij}}\left( t \right)} \right), \end{array} $

(1)

$ {x_i}\left( {t + 1} \right) = {x_i}\left( t \right) + {v_i}\left( {t + 1} \right), $

(2)

其中，c₁和c₂(非负常数)为学习因子, 控制粒子向个体极值和全局极值学习能力的大小；r₁, r₂为[0, 1]内的随机数；t为迭代次数.在迭代过程中，根据式(1)和式(2)更新粒子的速度和位置.

1998年，EBERHART等对式(1)进行了改进，形成了目前通用的粒子群算法速度更新公式：

$ \begin{array}{l} {v_{ij}}\left( {t + 1} \right) = w{v_{ij}}\left( t \right) + {c_1}{r_1}\left( {{\rm{pbes}}{{\rm{t}}_{ij}}\left( t \right)-{x_{ij}}\left( t \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{c_2}{r_2}\left( {{\rm{gbes}}{{\rm{t}}_j}\left( t \right)-{x_{ij}}\left( t \right)} \right), \end{array} $

(3)

其中，w为惯性权重, 控制前一速度对当前速度的影响, 使其保持运动惯性，有能力搜索新的区域.

2 基于动态分级和邻域反向学习的改进PSO算法(DSNRPSO) 2.1 动态分级扰动策略

在标准PSO算法中，种群中的粒子在每一次迭代时单纯地按照式(2)和式(3)更新，使得种群在收敛时，降低了多样性，导致算法陷入局部最优无法跳出，最优解不被更新的可能性变大，增加了无效搜索次数.另外，在求解多峰或具有极强跳跃性特点的函数时，当前最优个体的前进方向不一定就是全局最优方向，因此，当种群的多样性降低、算法中的最优个体领导能力下降时，有必要对种群中的最优个体进行扰动.本文基于函数评价次数和粒子的适应度值动态地将种群中的粒子划分为3个等级，对不同等级中的粒子执行不同的扰动策略.这种动态分级扰动策略在增加种群多样性的同时，一定程度上也促使了粒子向全局最优进化.

2.1.1 动态分级机制

本文只考虑无约束最小化优化问题，将其目标函数作为算法的适应度函数，在每一次迭代中，根据适应度函数值重新排列粒子，使得当粒子x_i的下标从1到N时, 适应度值变大，粒子变差，在此基础上根据函数评价次数的变化情况动态地将粒子分为最优、次优、最差3个等级.在迭代初期，种群中的大部分粒子距离全局最优点较远，因此使最优等级中的粒子占主导地位，有利于加快算法的收敛速度；在迭代中期，粒子接近全局最优点或者局部最优点，需要粒子细致地搜索解空间，以提高算法的收敛精度；在迭代后期，算法可能陷入局部最优，此时，可通过增加随机游走粒子，尽量使算法跳出局部极值的约束.具体的分级方法如下：

$ {x_i} \in \left\{ {\begin{array}{*{20}{l}} {最优, }&{i = 1, 2, \cdots, m, }\\ {次优, }&{i = m, m + 1, \cdots, n, }\\ {最差, }&{i = n, n + 1, \cdots, N, } \end{array}} \right. $

(4)

其中,

$ m = \left\lfloor {\frac{N}{4} + N \times {{\left( {0.5-\frac{t}{T}} \right)}^3}} \right\rfloor, $

(5)

$ n = \left\lfloor {\frac{{3N}}{4} + N \times {{\left( {0.5-\frac{t}{T}} \right)}^3}} \right\rfloor, $

(6)

其中，N为种群规模；t为当前函数评价次数；T为最大函数评价次数.种群中粒子等级的划分及每个等级内的粒子数随评价次数变化的趋势图如图 1所示.

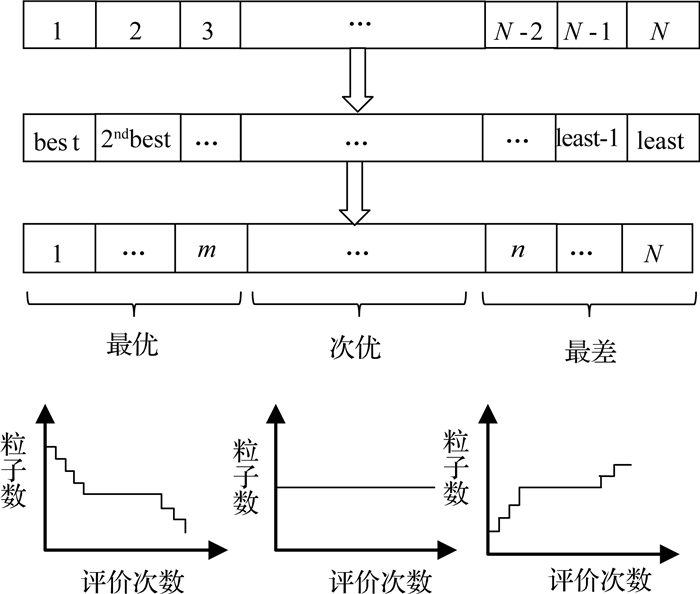
图 1 粒子分级示意图 Fig. 1 Illustration of the particle classification

2.1.2 扰动机制

最优等级中的粒子x_i(i=1, 2, …, m)影响种群的进化方向，引导种群向最优解方向进化，故保留当前的最优粒子.其粒子位置的扰动公式为

$ {x_i}\left( t \right) = {x_i}\left( t \right). $

(7)

次优等级中的粒子x_i(i=m, m+1, …, n)与全局极值gbest=(gbest₁, gbest₂, …, gbest_D)进行2点交叉操作，促进粒子的信息交流.具体操作为：随机设置交叉点g, h∈[1, N]且g＜h，交叉二者之间的维数，形成新粒子x_i=(x_i1, …, x_i(k-1), gbest_g…, gbest_h, x_i(h+1), …, x_iD).其粒子位置的扰动公式为

$ {x_i}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {{x_i}\left( t \right), }&{{\rm{if}}\;\;\;{r_3} < {p_{\rm{r}}}, }\\ {{{\bar x}_i}\left( t \right), }&{{\rm{otherwise}}, } \end{array}} \right. $

(8)

其中，p_r为选择概率；r₃为[0, 1]上满足均匀分布的随机数.

最差等级中的粒子x_i(i=n, n+1, …, N)对种群寻优的贡献不大，故将其作为游荡者，以增加种群多样性，避免种群中粒子陷入局部最优.其粒子位置的扰动公式为

$ {x_{ij}}\left( t \right) = \left\{ {{x_{ij}}\left( t \right) + \frac{{x_{ij}^{\rm{u}}-x_{ij}^1}}{N}, }~~~{{\rm{if}}\;\;\;{m_{\rm{c}}} > 0.5, }\\ {{{\dot x}_{ij}}\left( t \right), }~~~{{\rm{otherwise}}, } \right. $

(9)

其中，

$ {{\dot x}_{ij}}\left( t \right) = \left( {1-2\frac{{{x_{ij}}\left( t \right)-\min \;{p_j}}}{{{x_{ij}}\left( t \right)-\max \;{p_j}}}} \right)\left( {\max \;{p_j} - \min \;{p_j}} \right), $

(10)

$ \max {p_j} = \max \left\{ {{\rm{pbes}}{{\rm{t}}_{ij}}\left( t \right)|i = 1, 2, \cdots, N} \right\}, $

(11)

$ \min {p_j} = \min \left\{ {{\rm{pbes}}{{\rm{t}}_{ij}}\left( t \right)|i = 1, 2, \cdots, N} \right\}, $

(12)

m_c=1-t/T，称为游走转换因子，控制粒子的游走方式；x_ij^u和x_ij^l分别为x_ij的上界和下界.

2.2 改进粒子位置的更新方式

在PSO寻优过程中，粒子收敛速度过快是导致算法陷入局部最优的原因之一，因此，为了控制粒子的更新速度，构建了粒子位置的更新公式：

$ {x_i}\left( {t + 1} \right) = {x_i}\left( t \right) + \left( {1-\frac{t}{T}} \right){v_i}\left( {t + 1} \right). $

(13)

按此更新方式，粒子在迭代初期，以较快的速度向全局极值方向进化，提高了算法的搜索速度；在迭代后期，粒子以较慢的速度进化，提高了种群的寻优能力，避免粒子更新过快，跳过最优解.

2.3 动态邻域反向学习全局搜索策略

对种群中每个粒子来说，其邻域中的粒子很可能优于该粒子，并且算法总是以一定的概率对解空间进行搜索，故对粒子进行邻域搜索可以增强算法的寻优能力.本文采用文献[10]中的环形拓扑结构，设种群中第i个粒子为x_i, i=1, 2, …, N，其中N为种群规模. N个粒子按照其下标形成环状的拓扑结构.对每个粒子x_i, 定义邻域的半径为k(0≤ $ k \le \frac{{N-1}}{2}$，且为整数，本文设置k=2), 则粒子x_i的邻域由x_i-k, …, x_i, …, x_i+k组成，如图 2所示.另外，由于粒子的邻域是根据粒子的下标号选取的，实际上这些粒子位置可能并不相邻，导致算法很难收敛，所以使粒子同时进行反向学习是必要的.同时，由文献[13]知，动态反向点比一般的反向点更接近全局最优.受此启发，结合二者的优点对种群中的粒子定义了动态邻域反向点.

图 2 环状拓扑结构和当k=2时粒子x_i的邻域 Fig. 2 The circle topology and 2-neighborhood

定义假设种群中第i个粒子为x_i, i=1, 2, …, N，其中N为种群规模. x_m和x_n为x_i邻域中的2个粒子，满足m≠n≠i，则在第t次迭代过程中，x_i的动态邻域反向点为

$ {\tilde x_i} = \alpha \left( {{x_m} + {x_n}} \right)-{x_i}, $

(14)

置$\alpha = \frac{{{\rm{fitness}}\left( {{\rm{pbes}}{{\rm{t}}_i}} \right)}}{{{\rm{fitness}}\left( {{x_i}} \right)}} $，显然0≤α≤1.

通过定义动态邻域反向点，可以较好地平衡算法的全局和局部搜索能力.例如，从x_i邻域中随机选取2个粒子x_m和x_n，此时x_i的动态邻域反向点$ {{\tilde x}_i}$的位置有2种情况：当x_m和x_n位于x_i两侧时，$ {{\tilde x}_i}$在x_i的邻域范围内，对粒子x_i的邻域进行小范围搜索，可增强算法的探索能力；当x_m和x_n位于x_i同侧时，$ {{\tilde x}_i}$跳出了x_i的当前邻域范围，需对粒子x_i的邻域进行大范围搜索，从而增强了算法的开发能力，如图 3所示.另外，粒子的邻域反向学习能力通过粒子x_i与个体极值pbest_i的适应度值的比值来自适应调整，当α→1时，粒子x_i的适应度值接近个体极值的适应度值，此时粒子较优，采用较大的α值以提高邻域反向学习能力，增强局部搜索能力；当α→0时，粒子x_i的适应度值远大于个体极值的适应度值，粒子较差，此时$ {{\tilde x}_i}$为与x_i运动方向相反的粒子，通过采用较小的α值的方法，减弱邻域反向学习能力，增强全局搜索能力.

图 3 动态邻域反向点的例子 Fig. 3 An example for dynamic neighborhood reverse point

为了进一步提高算法的全局搜索能力，引导种群向全局最优点方向进化，加快算法的收敛速度，结合上述定义的动态邻域反向点和全局极值点构建全局搜索策略：

$ g{x_i} = \left( {1-{r_4}} \right) \cdot {\rm{gbest}} + {r_4} \cdot {{\tilde x}_i}, $

(15)

$ g{v_i} = {v_i}, $

(16)

其中，x_i为种群中的第i个粒子，gbest为全局极值，$ {{\tilde x}_i}$为x_i的动态邻域反向点，r₄为服从N(0.5, 0.5)正态分布的随机数.

2.4 DSNRPSO算法步骤：

步骤1 随机初始化种群，设置学习因子c₁和c₂、惯性权重w、最大函数评价次数T、种群规模N、维数D、邻域半径k、函数评价次数t=0；

步骤2 计算粒子的适应度值，初始化全局极值gbest和个体极值pbest；

步骤3 根据粒子的适应度值对粒子排序，按式(4)~(6)将种群中的粒子进行动态分级，对不同等级粒子按式(7)~(9)对其扰动；

步骤4 如果rand＜p_ns，按式(15)和(16)形成新粒子gx_i(i=1, 2, …, N)，若新粒子gx_i优于x_i，更新粒子为gx_i，否则保留粒子x_i；

步骤5 更新个体极值pbest和全局极值gbest；

步骤6 若达到最大函数评价次数，则停止迭代，输出全局极值，否则，t=t+1，转步骤3.

综上所述，基于动态分级和邻域反向学习的改进粒子群算法的流程图如图 4所示.

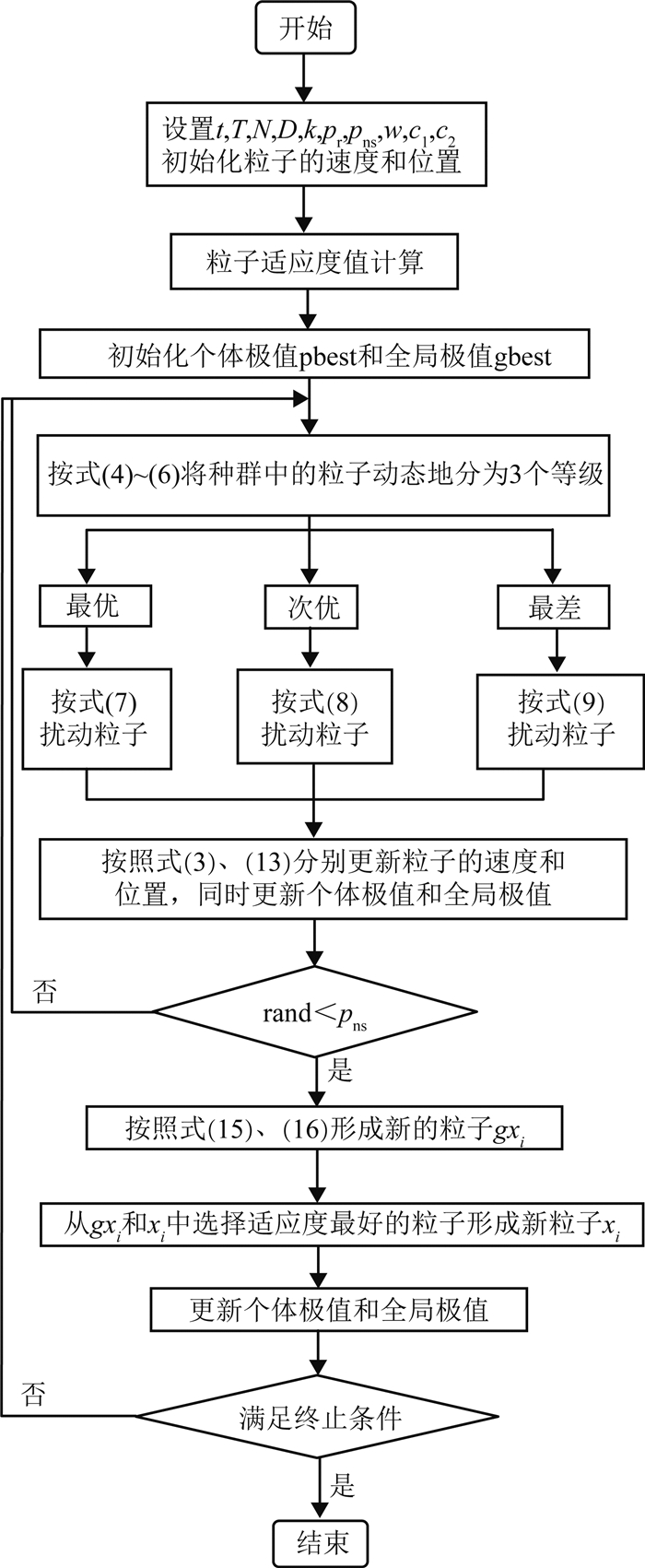
图 4 DSNRPSO算法流程图 Fig. 4 Flowchart of DSNRPSO

3 数值试验及结果分析 3.1 测试函数及评价标准

为了验证本算法的有效性和可行性，采用4种类型的标准测试函数^[14-15]对算法进行仿真：单峰及简单的多峰函数(f₁~f₄)、非旋转的多峰函数(f₅~f₇)、旋转的多峰函数(f₈~f₁₀)和高维的漂移函数(f₁₁~f₁₅)，具体如表 1所示.通过统计适应度误差的均值和方差评价算法的优化性能，其中适应度误差值为(f(x)~f(x^*))(x和x^*分别为算法所获的最优值和理论最优值).

表 1 标准测试函数 Table 1 Benchmark function

测试函数	表达式	维数	解空间	f(x^*)
f₁ Sphere	$ {f_1}\left( x \right) = \sum\limits_{i = 1}^n {x_i^2} $	30	[-100, 100]	0
f₂ Rosenbrock	${f_2}\left( x \right)=\sum\limits_{i = 1}^n {\left[{100{{\left( {{x_{i + 1}}-x_i^2} \right)}^2} + {{\left( {{x_i}-1} \right)}^2}} \right]} $	30	[-2.048，2.048]	0
f₃ Schwefel 2. 22	$ {f_3}\left( x \right) = \sum\limits_{i = 1}^n {\|{x_i}\|} + \prod\limits_{i = 1}^n {\|{x_i}\|} $	30	[-10, 10]	0
f₄ Schwefel 2. 21	f₄=max\|x_i\|, 0＜i≤N	30	[-100, 100]	0
f₅ Rastrigin	$ {f_5}\left( x \right) = \sum\limits_{i = 1}^n {\left[{x_i^2-10\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right) + 10} \right]} $	30	[-5.12, 5.12]	0
f₆ Ackley	$ \begin{array}{l} {f_6}\left( x \right) =-20\exp \left( {-0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } } \right)\\ \;-\exp \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\cos \left( {2{\rm{ \mathsf{ π} }}{x_i}} \right)} } \right) + 20 + {\rm{e}} \end{array}$	30	[-32, 32]	0
f₇ Griewank	$ {f_7}\left( x \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^n {x_i^2}-\prod\limits_{i = 1}^n {\cos \left( {\frac{{{x_i}}}{{\sqrt {\rm{i}} }}} \right) + 1} $	30	[-600, 600]	0
f₈ Rotated Ackley	$ \begin{array}{l} {f_8}\left( x \right) =-20\exp \left( {-0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {z_i^2} } } \right)-\\ \;\;\exp \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\cos \left( {2{\rm{ \mathsf{ π} }}{z_i}} \right)} } \right) + 20 + {\rm{e}} \end{array}$ z=x×M(M为D×D的正交矩阵)	30	[-32, 32]	0
f₉ Rotated Griewanks	$ {f_9}\left( x \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^n {z_i^2}-\prod\limits_{i = 1}^n {\cos \left( {\frac{{{z_i}}}{{\sqrt {\rm{i}} }}} \right) + 1} $ z=x×M(M为D×D的正交矩阵)	30	[-600, 600]	0
f₁₀ Rotated Rastrigin	$ {f_{10}}\left( x \right) = \sum\limits_{i = 1}^n {\left[{z_i^2-10\cos \left( {2{\rm{ \mathsf{ π} }}{z_i}} \right) + 10} \right]} $ z=x×M(M为D×D的正交矩阵)	30	[-5.12，5.12]	0
f₁₁ Shifted Sphere	$ {f_{11}}\left( x \right) = \sum\limits_{i = 1}^n {z_i^2} + f\_{\rm{bias}}$ z=x-o, f_bias=-450	100	[-100, 100]	-450
f₁₂ Shifted Schwefel	${f_{12}} = \mathop {\max }\limits_i \left\{ {\|{z_i}\|, 0 < i \le N} \right\} + f\_{\rm{bias}} $ z=x-o, f_bias=-450	100	[-100, 100]	-450
f₁₃ Shifted Ackley	$ \begin{array}{l} {f_{13}}\left( x \right) =-20\exp \left( {-0.2\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {z_i^2} } } \right)-\\ \exp \left( {\frac{1}{n}\sum\limits_{i = 1}^n {\cos \left( {2{\rm{ \mathsf{ π} }}{z_i}} \right)} } \right) + 20 + {\rm{e}} + f\_{\rm{bias}} \end{array}$ z=x-o, f_bias=-140	100	[-32, 32]	-140
f₁₄ Shifted Rosenbrock	$ \begin{array}{l} {f_{14}}\left( x \right) = \sum\limits_{i = 1}^n {\left[{100{{\left( {{x_{i + 1}}-x_i^2} \right)}^2} + {{\left( {{x_i}-1} \right)}^2}} \right]} + \\ \;\;\;\;f\_{\rm{bias}}, \;\;z = x -o, f\_{\rm{bias}} = 390 \end{array}$	100	[-100, 100]	390
f₁₅ Shifted Griewanks	$ \begin{array}{l} {f_{15}}\left( x \right) = \frac{1}{{4000}}\sum\limits_{i = 1}^n {z_i^2}-\prod\limits_{i = 1}^n {\cos \left( {\frac{{{z_i}}}{{\sqrt {\rm{i}} }}} \right) + 1} + \\ \;\;f\_{\rm{bias, }}\;\;z = x-o, f\_{\rm{bias}} =-180 \end{array}$	100	[-600, 600]	-180

表 1 标准测试函数 Table 1 Benchmark function

3.2 仿真实验与仿真环境

实验分为4部分：实验1：参数敏感性分析.算法中参数p_r和p_ns分别控制较优等级中粒子的交叉概率和种群中粒子信息交互的能力，本文分别取p_r=0.1, 0.3, 0.5和p_ns=0.4, 0.6, 0.8, 1.0对标准测试函数进行测试，p_r和p_ns参数有12种组合.为了简化数据，选取仿真结果相对较优的参数和其对应的实验结果，具体见表 2.实验2：本文主要提出了3个策略：分级扰动机制、粒子智能更新行为和邻域反向学习的全局搜索策略.为了探讨各策略对算法的影响，验证各策略的有效性，将标准的PSO、基于分级扰动机制的PSO(SPSO)、基于分级扰动机制和邻域反向学习的PSO(SNRPSO)和包含所有机制的PSO(DSNRPSO)对简单的单峰和多峰标准测试函数进行仿真实验.实验3：将本文提出的算法DSNRPSO与标准的PSO^[2]、基于自然选择的PSO(NPSO)^[1]、基于邻域搜索增加种群多样性的PSO(DNSPSO)^[8]、人群搜索算法(SOA)^[4]、布谷鸟算法(CS)^[6]的实验结果进行对比.实验4：为了分析本文算法对高维测试函数的收敛性和稳定性，将测试函数的维度D设为300，测试函数为f₁，f₂和f₆，给出几种算法在这3个函数上的统计结果并进行比较，评价指标为最优值、最差值、均值和方差.

表 2 不同p_r和p_ns组合对应的DSNRPSO算法在测试函数上的适应度误差的均值 Table 2 Mean error values achieved by DSNRPSO with different p_r and p_ns

函数	维数	p_r=0.1 p_ns=0.8	p_r=0.1 p_ns=1.0	p_r=0.3 p_ns=0.6	p_r=0.3 p_ns=0.8	p_r=0.5 p_ns=0.6	p_r=0.5 p_ns=0.8
f₁	30	0. 00	0. 00	0. 00	0. 00	0. 00	0. 00
f₂	30	2. 45×10^-15	8. 49×10^-16	3. 41×10^-14	2. 54×10^-14	7. 52×10^-14	2. 93×10^-15
f₃	30	4. 04×10^-260	3. 21×10^-259	8. 17×10^-259	1. 13×10^-264	1. 33×10^-263	5. 33×10^-266
f₄	30	2. 38×10^-215	1. 12×10^-189	6. 20×10^-204	6. 61×10^-216	3. 91×10^-196	2. 32×10^-214
f₅	30	0. 00	0. 00	0. 00	0. 00	0. 00	0. 00
f₆	30	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16
f₇	30	0. 00	0. 00	0. 00	0. 00	0. 00	0. 00
f₈	30	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16	8. 88×10^-16
f₉	30	0. 00	0. 00	0. 00	0. 00	0. 00	0. 00
f₁₀	30	0. 00	0. 00	0. 00	0. 00	0. 00	0. 00
f₁₁	100	5. 35×10^-9	8. 19×10^-9	3. 45×10^-8	3. 18×10^-8	1. 20×10^-7	7. 58×10^-8
f₁₂	100	57. 5	66. 9	59. 3	59. 6	58. 6	58. 1
f₁₃	100	15. 8	15. 9	17. 7	12. 0	16. 5	16. 0
f₁₄	100	1. 41×10²	1. 07×10²	1. 35×10²	1. 03×10²	1. 01×10²	98. 8
f₁₅	100	3. 67×10^-3	3. 63×10^-2	6. 96×10^-2	5. 00×10^-2	8. 33×10^-2	4. 24×10^-3

表 2 不同p_r和p_ns组合对应的DSNRPSO算法在测试函数上的适应度误差的均值 Table 2 Mean error values achieved by DSNRPSO with different p_r and p_ns

仿真实验环境：处理器：Pentium(R) Dual-Core CPU E5800 @3.20 GHz；RAM: 2 GB；系统类型：Win8.1 64位操作系统；语言：Matlab；版本：R2014a.

3.3 实验参数设定

为了保证比较的公平性，本文在选取相同通用参数的基础上，各进化算法参数采用参考文献中的建议设置，停止准则为函数评价次数达到最大函数评价次数，其中，30维测试函数的最大函数评价次数T=300 000，100维和300维测试函数的最大函数评价次数T=500 000，种群规模N=40，权重因子w=0.729 84，学习因子c₁=c₂=1.469 18.除相同的参数外，各优化算法的其他参数设置如下：DNSPSO^[8]中邻域半径k=2，参数p_r=0.9，p_ns=0.6；SOA^[4]中最大隶属度值u_max=0.950 0, 最小隶属度值u_min=0.011 1，权重最大值w_max=0.9，权重最小值w_min=0.1；CS^[6]中被宿主发现的概率p_a=0.25.在每个实验中，6种算法分别进行30次独立实验测试.实验统计结果见表 2~表 5，收敛趋势图如图 5所示.其中，黑体数值表示对比算法在相应函数上的寻优效果最好.

表 3 不同策略作用在PSO上时标准测试函数仿真的适应度误差均值 Table 3 The mean value of fitness values simulated by different strategies in PSO on test functions

表 4 6种算法在标准测试函数上的适应度误差均值和方差 Table 4 Comparison results of mean function error values and standard deviations

函数	维数	误差	PSO	NPSO	SOA	CS	DNSPSO	DSNRPSO
f₁	30	均值方差	6. 89×10^-153 3. 55×10^-152	2. 80×10^-155 0. 00	1. 80×10^-4 4. 24×10^-5	1. 10×10^-12 8. 14×10^-13	0. 00 0. 00	0. 00 0. 00
f₂	30	均值方差	31. 6 1. 84	6. 44 3. 42	27. 6 1. 44	18. 5 0. 749	20. 7 10. 5	2. 45×10^-15 3. 64×10^-15
f₃	30	均值方差	1. 73×10^-63 6. 45×10^-63	0. 103 0. 241	6. 76×10^-2 1. 16×10^-2	1. 53×10^-3 1. 10×10^-3	8. 38×10^-147 2. 24×10^-146	4. 04×10^-260 0. 00
f₄	30	均值方差	1. 81×10^-11 4. 39×10^-11	7. 40×10^-12 9. 50×10^-12	1. 31×10^-2 2. 93×10^-3	9. 44×10^-1 5. 66×10^-1	6. 36×10^-116 2. 75×10^-115	2. 38×10^-215 0. 00
f₅	30	均值方差	39. 9 8. 91	28. 0 4. 28	37. 4 12. 0	1. 17×10² 19. 1	0. 00 0. 00	0. 00 0. 00
f₆	30	均值方差	1. 16 0. 346	1. 08 0. 237	1. 66×10^-2 1. 84×10^-3	1. 71×10^-2 4. 82×10^-2	8. 88×10^-16 0. 00	8. 88×10^-16 0. 00
f₇	30	均值方差	1. 61×10^-2 5. 44×10^-3	1. 94×10^-2 6. 03×10^-3	9. 37×10^-3 1. 00×10^-2	1. 51×10^-3 3. 98×10^-3	0. 00 0. 00	0. 00 0. 00
f₈	30	均值方差	3. 55 2. 31	9. 06 1. 04	20. 9 9. 89×10^-2	20. 9 5. 12×10^-2	8. 88×10^-16 0. 00	8. 88×10^-16 0. 00
f₉	30	均值方差	1. 97×10^-2 1. 56×10^-2	7. 40×10^-4 2. 22×10^-3	2. 70×10^-2 1. 53×10^-2	6. 68×10^-3 8. 59×10^-3	0. 00 0. 00	0. 00 0. 00
f₁₀	30	均值方差	73. 6 59. 7	63. 3 10. 4	51. 9 29. 5	1. 29×10² 14. 3	0. 00 0. 00	0. 00 0. 00
f₁₁	100	均值方差	3. 70×10⁴ 2. 06×10⁴	1. 70×10⁴ 5. 66×10³	1. 11×10³ 9. 82×10	3. 95×10^-4 1. 23×10^-4	4. 24×10^-11 3. 26×10^-11	5. 35×10^-9 6. 08×10^-8
f₁₂	100	均值方差	69. 2 3. 38	60. 9 3. 75	17. 1 1. 35	62. 0 4. 22	28. 2 1. 84	32. 8 30. 2
f₁₃	100	均值方差	84. 0 1. 03	18. 9 1. 88	1. 55 0. 518	1. 64 9. 04	28. 2 3. 74	15. 8 1. 28
f₁₄	100	均值方差	1. 97×10⁹ 2. 55	2. 17×10⁹ 1. 64	2. 37×10² 92. 6	5. 41×10² 1. 47×10²	2. 19×10² 9. 92	1. 41×10² 14. 4
f₁₅	100	均值方差	7. 90×10² 1. 42	2. 35×10² 6. 34	1. 56×10^-2 6. 94×10^-3	8. 70×10^-3 1. 03	2. 93×10^-6 6. 61×10^-6	3. 67×10^-3 7. 76×10^-3

表 4 6种算法在标准测试函数上的适应度误差均值和方差 Table 4 Comparison results of mean function error values and standard deviations

表 5 6种算法在D=300上的标准测试函数统计结果 Table 5 Comparison results of statistical by six algorithms on D=300 standard test function

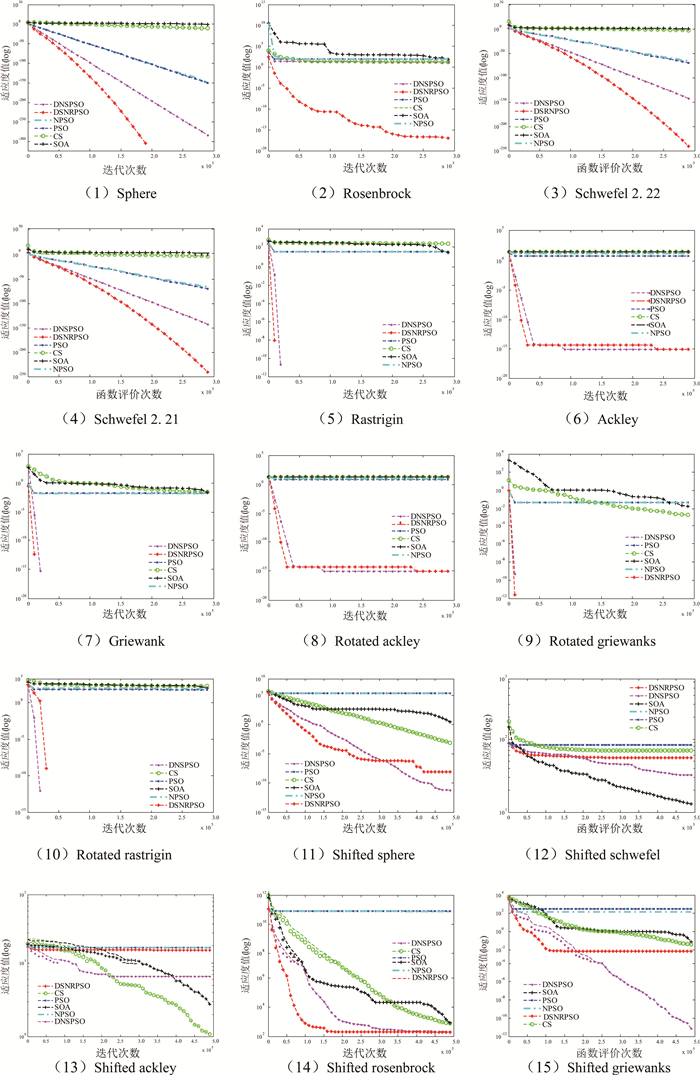
图 5 6种算法在标准测试函数上的收敛曲线 Fig. 5 The convergence curves of six methods on benchmark function

3.4 实验结果分析

实验1 保持种群多样性和提高算法收敛精度是改进PSO算法的关键，通过对比表 2中参数相同p_r、不同p_ns和不同p_r、相同p_ns2种情况下的实验统计结果发现：参数p_r对算法的影响较小，说明采用动态分级机制能够增加种群多样性，参数p_ns对算法的影响较大，故通过定义邻域反向点构建全局搜索策略可以较好地平衡种群的局部开采和全局探测能力，提高算法的收敛精度，并且当取p_r=0.1和p_ns=0.8时，DSNRPSO算法在测试函数上取得了较好的综合寻优效果.

实验2 种群的多样性影响算法的精度，全局搜索策略影响算法的收敛速度，二者相互制约.从表 3可以看出，SPSO算法对测试函数f₂和f₄~f₇的收敛精度优于PSO算法，而对函数f₁和f₃的收敛精度劣于PSO算法，说明采用分级机制可以有效增强种群多样性，但降低了算法的收敛速度；SNRPSO算法的仿真结果除函数f₂外均优于SPSO算法，说明采用邻域反向学习策略极大地提高了算法的收敛精度和速度，但降低了种群的多样性；为了平衡2种策略对算法的影响，在SNRPSO算法的基础上，采用粒子智能更新方式的DSNRPSO算法，仿真结果最优，说明采用粒子智能更新方式调节粒子的更新速度有效地平衡了算法的寻优精度和收敛速度.

实验3 由表 4和图 5可知，6种算法在对不同类型的测试函数进行寻优时，其收敛速度和精度存在以下差异：对函数f₁和f₃，SOA和CS算法陷入局部最优，PSO、NPSO、DNSPSO和DSNRPSO算法收敛性能较好，DSNRPSO算法收敛速度最快；函数f₂为连续凹函数，最优点位于平滑、狭长的抛物线山谷，很难求出全局最优点，只有DSNRPSO算法可以得到较好的寻优效果，其他5种算法均陷入局部最优.说明采用动态分级扰动策略可增加种群多样性，显著改善算法的性能；函数f₄~f₇，f₈~f₁₀，有较多的局部极小值点，CS、SOA、PSO和NPSO算法均陷入了局部最优，DNSPSO和DSNRPSO算法寻找到了全局最优点，二者的收敛曲线比较平滑，收敛速度快，DSNRPSO算法解的方差优于DNSPSO算法，说明DSNRPSO算法的稳定性更好；对函数f₁₁，PSO、NPSO算法收敛能力较差，SOA、CS、DNRPSO和DSNRPSO算法的收敛曲线均平滑下移，DNRPSO和DSNRPSO算法出现了小的跳跃，说明后2种算法的寻优能力更强；对函数f₁₂和f₁₃，改进的PSO算法均陷入了局部最优；对函数f₁₄，SOA和CS算法的收敛速度较慢，DNRPSO和DSNRPSO算法的收敛速度较快，但当函数评价次数达到200 000次时，收敛曲线平稳，有可能陷入局部最优；函数f₁₅为复杂的非线性多模态函数，峰形高低起伏不定，并且具有跳跃性，所以很难找到全局最优解，6种算法中，DNRPSO算法的寻优效果最好，DSNRPSO算法次之.另外，从表 4中可以看出，在漂移测试函数上，DSNRPSO、DNRPSO和SOA算法解的方差较大，相较其他算法，这3种算法有可能寻找到较好的全局最优解.

实验4 从表 5中可以看出，在测试函数f₁和f₆上，DNSPSO和DSNRPSO算法的收敛精度明显优于PSO、NPSO、SOA和CS，在函数f₆上，DSNRPSO算法具有较好的稳定性；对于测试函数f₂，虽然DSNRPSO算法的方差较大，但其最优解和均值明显优于其他算法.表明DSNRPSO算法在求解高维优化问题时同样具有良好的性能.

综上所述，DSNRPSO算法通过引入动态分级扰动机制和全局搜索策略，较好地克服了PSO算法的早熟问题，提高了算法的寻优能力和求解精度.

4 结论

提出了一种基于动态分级和邻域反向学习的改进粒子群算法，该算法将种群动态地划分成3个等级，针对每个等级中的粒子特点对其执行不同的扰动操作，使粒子在增强种群多样性的同时又保持向全局最优点方向进化，克服了标准PSO算法容易收敛于局部最优造成算法早熟的缺陷.在此基础上，引入了结合全局极值和动态邻域反向点构建的全局搜索策略，加快了算法的收敛速度.仿真实验表明，基于动态分级和邻域反向学习的改进粒子群算法，计算精度高、稳定性强.

参考文献

[1]	王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2001: 1-2. WANG L. Intelligent Optimization Algorithm and Its Application[M]. Beijing: Tsinghua University Press, 2001: 1-2.
[2]	KENNEDYJ, EBERHART R C. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995: 1942-1948. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=488968
[3]	KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization:Artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459–47. DOI:10.1007/s10898-007-9149-x
[4]	余胜威, 曹中清. 基于人群搜索算法的PID控制器参数优化[J]. 计算机仿真, 2014, 31(9): 347–350. YU S W, CAO Z Q. Optimization parameters of PID controller parameters based on seeker optimization algorithm[J]. Computer Simulation, 2014, 31(9): 347–350.
[5]	YANG X, GANDOMI A H. Bat algorithm:A nove approach for global engineering optimization[J]. Engineering Computations, 2012, 29(5): 464–4. DOI:10.1108/02644401211235834
[6]	YANG X S, DEB S. Cuckoo search via levy flights[C]//Proceedings of the World Congress on Nature and Biologically Inspired Computing. Coimbatore: Nature & Biologically Inspired Computing, 2010. DOI: 10.1109/NABIC.2009.5393690. http://www.oalib.com/paper/3945721
[7]	RIGET J, VESTERSTRØM J S. A diversity-guided particle swarm optimizer-the ARPSO[J/OL]. ResearchGate. Https://www.researchgate.net/publication/228582468_a_diversity-guide_particle_swarm_optimizer-the_arpso, [2002-01].
[8]	WANG H, SUN H, LI C, et al. Diversity enhanced particle swarm optimization with neighborhood search[J]. Information Sciences, 2013, 223(2): 119–135.
[9]	KENNEDY J. Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance[C]//Evolutionary Computation, 1999. CEC 99. Proceedings of the 1999 Congress on. Piscataway: IEEE Xplore, 1999: 1931-1938. http://www.researchgate.net/publication/3810337_Small_worlds_and_mega-minds_effects_of_neighborhood_topology_onparticle_swarm_performance
[10]	DAS S, ABRAHAM A, CHAKRABORTY U K, et al. Differential evolution using a neighborhood-based mutation operator[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(3): 526–553. DOI:10.1109/TEVC.2008.2009457
[11]	TIZHOOSH H R. Opposition-based learning: A new scheme for machine intelligence[C]//Computational Intelligence for Modelling, Control and Automation, 2005 and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, International Conference on. Washington: IEEE Computer Society, 2005(1): 695-701. http://dl.acm.org/citation.cfm?id=1135200
[12]	魏文红, 王甲海, 陶铭, 等. 基于泛化反向学习的多目标约束差分进化算法[J]. 计算机研究与发展, 2016, 53(6): 1410–1421. WEI W H, WANG J H, TAO M, et al. Multi-objective constrained differential evolution using generalized opposition based learning[J]. Journal of Computer Research and Development, 2016, 53(6): 1410–1421. DOI:10.7544/issn1000-1239.2016.20150806
[13]	WANG H, WU Z, RAHNAMAYAN S, et al. Enhancing particle swarm optimization using generalized opposition based learning[J]. Information Sciences, 2011, 181(20): 4699–4714. DOI:10.1016/j.ins.2011.03.016
[14]	ZHAO S Z, SUGANTHAN P N, DAS S. Self-adaptive differential evolution with modified multi-trajectory search for CEC'2010 large scale optimization[C]//Swarm, Evolutionary, and Memetic Computing. Heidelberg: Springer, 2010: 1-10. http://rd.springer.com/chapter/10.1007/978-3-642-17563-3_1
[15]	LIAO T, STUTZLE T. Benchmark results for a simple hybrid algorithm on the CEC 2013 benchmark set for real-parameter optimization[J]. Evolutionary Computation, 2013, 2013: 1938–1944.
[16]	DANG C T, WU Z, WANG H. A new approach of diversity enhanced particle swarm optimization with neighborhood search and adaptive mutation[C]//Neural Information Processing. Heidelberg: Springer International Publishing, 2014: 143-150. http://www.researchgate.net/publication/301952211_A_New_Approach_of_Diversity_Enhanced_Particle_Swarm_Optimization_with_Neighborhood_Search_and_Adaptive_Mutation
[17]	GAO W F, HUANG L L, LIU S Y, et al. Artificial bee colony algorithm with multiple search strategies[J]. Applied Mathematics & Computation, 2015, 271(C): 269–287.
[18]	GAO W F, LIU S Y, HUANG L L. Particle swarm optimization with chaotic opposition-based population initialization and stochastic search technique[J]. Communications in Nonlinear Science & Numerical Simulation, 2012, 17(11): 4316–4327.