2. 河南工业职业技术学院 汽车工程学院, 河南 南阳 473000;
3. 重庆大学 数学与统计学院, 重庆 401331
2. Department of Automobile Engineering, Henan Polytechnic Institute, Nanyang 473000, Henan Province, China;
3. College of Mathematics and Statistics, Chongqing University, Chongqing 401331, China
1963年, 美国气象学家LORENZ[1]提出了大气热对流过程的动力学模型, 即著名的Lorenz系统,并且发现了著名的蝴蝶效应.随后,众多学者对Lorenz系统的各种动力学行为展开了深入研究, 揭示了Lorenz系统复杂动力学行为的演化过程及混沌的产生机制[2-14],并将Lorenz系统应用于自然科学的各个领域.
著名学者STENFLO在研究大气的热对流运动时,给出了大气热对流运动的四维混沌模型[15-16]:
| $ \left\{ \begin{array}{l} \frac{{{\text{d}}x}}{{{\text{d}}t}} = \alpha \left( {y - x} \right) + \gamma w,\\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = cx - xz - y,\\ \frac{{{\text{d}}z}}{{{\text{d}}t}} = xy - \beta z,\\ \frac{{{\text{d}}w}}{{{\text{d}}t}} = - x - \alpha w, \end{array} \right. $ | (1) |
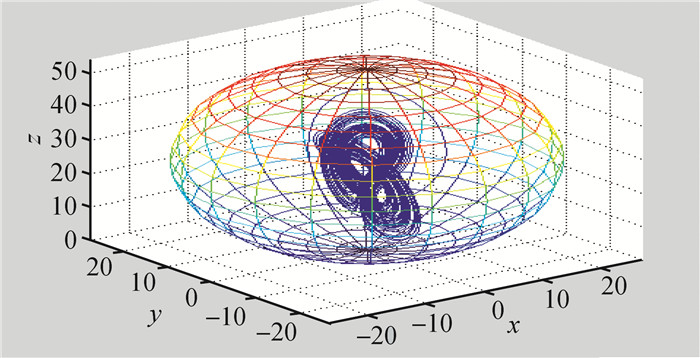
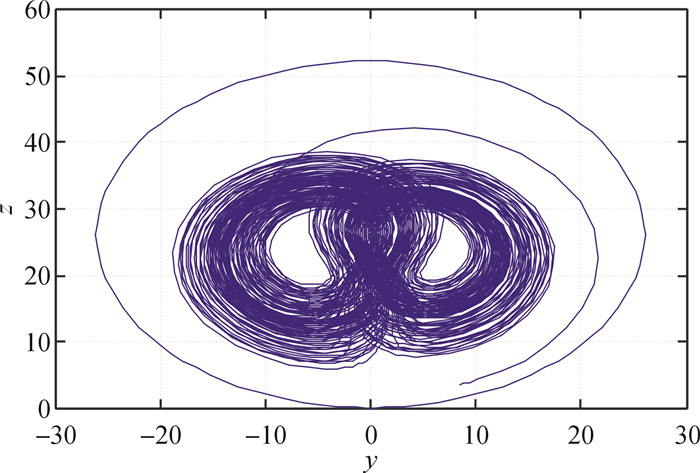
其中α, β, γ, c为系统(1)的正参数,变量w用于描述气流的旋转, 参数γ(>0)是与w相对应的旋转数(rotation number), α(>0)表示普朗特数(Prandtl number), c(>0)表示瑞利数(Rayleigh number),β(>0)为几何参数(geometric parameter).当c=26, β=0.7, γ=1.5, α=1时,系统(1)的混沌吸引子如图 1所示,在平面yoz上的吸引子如图 2所示.

|
图 1 系统(1)在3D空间中轨线的吸引子 Fig. 1 Chaotic attractor of system in 3D space |

|
图 2 系统(1)在yoz平面上轨线的吸引子 Fig. 2 Chaotic attractor of system in yoz plane |
系统(1)的一些动力学行为:模型的推导、混沌行为产生的机理等,文献[12]已有研究.下文主要研究系统(1)的最终界和全局吸引性.
引理1 定义集合
| $ \begin{array}{*{20}{c}} {{\Gamma _1} = \left\{ {\left( {{x_1},{y_1},{z_1},{w_1}} \right)\left| {\frac{{x_1^2}}{{{a^2}}} + \frac{{y_1^2}}{{{b^2}}} + \frac{{{{\left( {{z_1} - c} \right)}^2}}}{{{c^2}}} + } \right.} \right.}\\ {\left. {\frac{{w_1^2}}{{{d^2}}} = 1,a > 0,b > 0,c > 0,d > 0} \right\},} \end{array} $ |
令
| $ \begin{array}{*{20}{c}} {G\left( {{x_1},{y_1},{z_1},{w_1}} \right) = x_1^2 + y_1^2 + z_1^2 + w_1^2,}\\ {H\left( {{x_1},{y_1},{z_1},{w_1}} \right) = x_1^2 + y_1^2 + {{\left( {{z_1} - 2c} \right)}^2} + w_1^2,} \end{array} $ |
则有
| $ \begin{array}{l} \mathop {\max G}\limits_{\left( {{x_1},{y_1},{z_1},{w_1}} \right) \in {\Gamma _1}} = \mathop {\max H}\limits_{\left( {{x_1},{y_1},{z_1},{w_1}} \right) \in {\Gamma _1}} = \\ \left\{ \begin{array}{l} \frac{{{a^4}}}{{{a^2} - {c^2}}},a \ge b,a \ge d,a \ge \sqrt 2 c,\\ \frac{{{b^4}}}{{{b^2} - {c^2}}},b > a,b \ge d,b \ge \sqrt 2 c,\\ \frac{{{d^4}}}{{{d^2} - {c^2}}},d > a,d > b,d \ge \sqrt 2 c,\\ 4{c^2},a < \sqrt 2 c,b < \sqrt 2 c,d < \sqrt 2 c. \end{array} \right. \end{array} $ |
证明 由多元函数求条件极值的拉格朗日乘数法即可证得.
引理2 对任意的λ>0, m>0, α>0, β>0, γ>0, c>0, 令
| $ \begin{array}{l} \Gamma = \left\{ {\left( {x,y,z,w} \right)\left| {\frac{{\lambda {x^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }}}} + } \right.} \right.\\ \;\;\;\;\;\;\frac{{m{y^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \frac{{m\beta {{\left( {z - \frac{{\lambda \alpha + mc}}{{2m}}} \right)}^2}}}{{\frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \\ \;\;\;\;\;\;\left. {\frac{{\lambda \alpha \gamma {w^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} = 1} \right\}, \end{array} $ |
| $ \begin{array}{l} V\left( {x,y,z,w} \right) = \lambda {x^2} + m{y^2} + m{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \gamma {w^2},\;\;\;\;\;\forall \lambda > 0,m > 0, \end{array} $ |
则有
| $ \mathop {\max V}\limits_{\left( {x,y,z,w} \right) \in \Gamma } = \left\{ \begin{array}{l} \frac{{{\beta ^2}{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha \left( {\beta - \alpha } \right)}},\;\;\;\;\alpha \le 1,\beta \ge 2\alpha ,\\ \frac{{{\beta ^2}{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\left( {\beta - 1} \right)}},\;\;\;\;\alpha > 1,\beta \ge 2,\\ \frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{m},\;\;\;\;\;\beta < 2\alpha ,\beta < 2. \end{array} \right. $ |
证明 令
| $ \sqrt \lambda x = {x_1},\sqrt m y = {y_1},\sqrt m z = {z_1},\sqrt {\lambda \gamma } w = {w_1}, $ |
| $ \frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }} = a_1^2,\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}} = b_1^2,\frac{{\lambda \alpha + mc}}{{2\sqrt m }} = {c_1}, $ |
| $ \frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }} = d_1^2, $ |
则有
| $ \begin{array}{l} V\left( {x,y,z,w} \right) = \lambda {x^2} + m{y^2} + \\ \;\;\;\;\;\;\;\;\;m{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)^2} + \lambda \gamma {w^2} = \\ \;\;\;\;\;\;\;\;\;x_1^2 + y_1^2 + {\left( {{z_1} - 2{c_1}} \right)^2} + w_1^2, \end{array} $ |
| $ \begin{array}{l} \Gamma = \left\{ {\left( {x,y,z,w} \right)\left| {\frac{{\lambda {x^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }}}} + \frac{{m{y^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + } \right.} \right.\\ \;\;\;\;\;\;\left. {\frac{{m\beta {{\left( {z - \frac{{\lambda \alpha + mc}}{{2m}}} \right)}^2}}}{{\frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \frac{{{w^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4\lambda m\alpha \gamma }}}} = 1} \right\} = \\ \;\;\;\;\;\;\left\{ {\left( {{x_1},{y_1},{z_1},{w_1}} \right)\left| {\frac{{x_1^2}}{{{a^2}}} + \frac{{y_1^2}}{{{b^2}}} + \frac{{{{\left( {{z_1} - c} \right)}^2}}}{{{c^2}}} + } \right.} \right.\\ \;\;\;\;\;\;\left. {\frac{{w_1^2}}{{{d^2}}} = 1,a \ne 0,b \ne 0,c \ne 0,d \ne 0} \right\}. \end{array} $ |
由引理1即可得到结论.
引理3 定义
| $ \sum { = \left\{ {\left( {{y_1},{z_1}} \right)\left| {\frac{{y_1^2}}{{{b^2}}} + \frac{{{{\left( {{z_1} - c} \right)}^2}}}{{{c^2}}} = 1,b \ne 0,c \ne 0} \right.} \right\}} , $ |
令
| $ \begin{array}{*{20}{c}} {G\left( {{y_1},{z_1}} \right) = y_1^2 + z_1^2,\;\;\;H\left( {{y_1},{z_1}} \right) = y_1^2 + }\\ {{{\left( {{z_1} - 2c} \right)}^2},\;\;\;\;\left( {{y_1},{z_1}} \right) \in \Sigma ,} \end{array} $ |
则有
| $ \mathop {\max G}\limits_{\left( {{y_1},{z_1}} \right) \in \Sigma } = \mathop {\max H}\limits_{\left( {{y_1},{z_1}} \right) \in \Sigma } = \left\{ \begin{array}{l} \frac{{{b^4}}}{{{b^2} - {c^2}}},\;\;\;\;b \ge \sqrt 2 c,\\ 4{c^2},\;\;\;\;\;b < \sqrt 2 c. \end{array} \right. $ |
证明 由多元函数求条件极值的拉格朗日乘数法便可证得.
定理1 对任意的λ>0, m>0, α>0, β>0, γ>0, c>0,
| $ \begin{array}{l} {\Omega _{\lambda ,m}} = \left\{ {\left( {x,y,z,w} \right)\left| {\lambda {x^2} + m{y^2} + m{{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)}^2} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\lambda \gamma {w^2} \le {R^2},\forall \lambda > 0,\forall m > 0} \right\} \end{array} $ | (2) |
为系统(1)正半轨线的一个最终界和正向不变集.其中,
| $ {R^2} = \left\{ \begin{array}{l} \frac{{{\beta ^2}{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha \left( {\beta - \alpha } \right)}},\;\;\;\alpha \le 1,\beta \ge 2\alpha ,\\ \frac{{{\beta ^2}{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\left( {\beta - 1} \right)}},\;\;\;\alpha > 1,\beta \ge 2,\\ \frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{m},\;\;\;\;\beta < 2\alpha ,\beta < 2. \end{array} \right. $ |
证明 定义广义李雅普诺夫函数
| $ \begin{array}{l} V\left( {x,y,z,w} \right) = \lambda {x^2} + m{y^2} + \\ \;\;\;\;\;m{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)^2} + \lambda \gamma {w^2},\;\;\forall \lambda > 0,m > 0, \end{array} $ |
对上述函数求导有
| $ \begin{array}{l} \frac{{{\text{d}}V\left( {x,y,z,w} \right)}}{{{\text{d}}t}}\left| {_{\left( 1 \right)}} \right. = 2\lambda x\frac{{{\text{d}}x}}{{{\text{d}}t}} + 2my\frac{{{\text{d}}y}}{{{\text{d}}t}} + \\ \;\;\;\;\;\;2m\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)\frac{{{\text{d}}z}}{{{\text{d}}t}} + 2\lambda \gamma w\frac{{{\text{d}}w}}{{{\text{d}}t}} = \\ \;\;\;\;\;\;2\lambda x\left( {\alpha y - \alpha x + \gamma w} \right) + 2my\left( {cx - xz - y} \right) + \\ \;\;\;\;\;\;2m\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)\left( {xy - \beta z} \right) + \\ \;\;\;\;\;\;2\lambda w\left( { - x - \alpha w} \right) = - 2\lambda \alpha {x^2} - 2m{y^2} - \\ \;\;\;\;\;\;2m\beta {z^2} + 2\beta \left( {\lambda \alpha + mc} \right)z - 2\lambda \gamma \alpha {w^2}, \end{array} $ |
令
| $ \begin{array}{l} {\Gamma _0} = \left\{ {\left( {x,y,z,w} \right)\left| {\frac{{\lambda {x^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }}}} + \frac{{m{y^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + } \right.} \right.\\ \left. {\;\;\;\;\;\;\;\frac{{m{{\left( {z - \frac{{\lambda \alpha + mc}}{{2m}}} \right)}^2}}}{{\frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \frac{{{w^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4\lambda m\alpha \gamma }}}} = 1} \right\}, \end{array} $ |
在Γ0外面有
下面计算该最大值
| $ \left\{ \begin{array}{l} \max \left\{ {\lambda {x^2} + m{y^2} + m{{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\lambda \gamma {w^2},\left( {x,y,z,w} \right) \in {\Gamma _0}} \right\},\\ {\Gamma _0} = \left\{ {\left( {x,y,z,w} \right)\left| {\frac{{\lambda {x^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m\alpha }}}} + } \right.} \right.\\ \;\;\;\;\;\;\;\frac{{m{y^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \frac{{m{{\left( {z - \frac{{\lambda \alpha + mc}}{{2m}}} \right)}^2}}}{{\frac{{{{\left( {\lambda \alpha + mc} \right)}^2}}}{{4m}}}} + \\ \;\;\;\;\;\;\;\left. {\frac{{{w^2}}}{{\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{4\lambda m\alpha \gamma }}}} = 1} \right\}. \end{array} \right. $ |
由引理2便可得到结论.
容易证明式(2)为系统(1)正半轨线的一个最终界和正向不变集.
注1 (ⅰ) 令λ=1, m=1, 则
| $ {\Omega _{1,1}} = \left\{ {\left( {x,y,z,w} \right)\left| {{x^2} + {y^2} + {{\left( {z - \alpha - c} \right)}^2} + \gamma {w^2} \le {l^2}} \right.} \right\} $ |
是系统(1)正半轨线的一个最终界和不变集,其中,
| $ {l^2} = \left\{ \begin{array}{l} \frac{{{\beta ^2}{{\left( {\alpha + c} \right)}^2}}}{{4\alpha \left( {\beta - \alpha } \right)}},\;\;\;\;\alpha \le 1,\beta \ge 2\alpha ,\\ \frac{{{\beta ^2}{{\left( {\alpha + c} \right)}^2}}}{{4\left( {\beta - 1} \right)}},\;\;\;\;\alpha > 1,\beta \ge 2,\\ {\left( {\alpha + c} \right)^2},\;\;\;\;\beta < 2,\beta < 2\alpha . \end{array} \right. $ |
当c=26, β=0.7, γ=1.5, α=1时,则有
| $ {\Omega _{1,1}} = \left\{ {\left( {x,y,z,w} \right)\left| {{x^2} + {y^2} + {{\left( {z - 27} \right)}^2} + \frac{3}{2}{w^2} \le {{27}^2}} \right.} \right\}. $ |
Ω1, 1在xoyz空间中的投影如图 3所示.
|
图 3 系统(1)xoyz空间中的最终界估计图示 Fig. 3 Bounds of system (1) in xoyz space |
(ⅱ) 基于集合交集的思想,对∀λ>0, ∀m>0, 则
定理2 令(x(t), y(t), z(t), w(t))为系统(1)的任意一个解.则对任意的α>0, β>0, γ>0, c>0,
| $ \Phi = \left\{ {\left( {y,z} \right)\left| {{y^2} + {{\left( {z - c} \right)}^2} \le {l^2}} \right.} \right\} $ | (3) |
为系统(1)的y(t), z(t)的一个最终界.其中,
| $ {l^2} = \left\{ \begin{array}{l} \frac{{{\beta ^2}{c^2}}}{{4\left( {\beta - 1} \right)}},\;\;\;\beta \ge 2,\\ {c^2},\;\;\;\beta < 2. \end{array} \right. $ |
证明 定义广义李雅普诺夫函数
| $ {V_1}\left( {y,z} \right) = {y^2} + {\left( {z - c} \right)^2}, $ |
则有
| $ \left\{ {\frac{{{\text{d}}{V_1}\left( {y,z} \right)}}{{{\text{d}}t}}\left| {_{\left( 1 \right)}} \right. = - 2{y^2} - 2\beta {z^2} + 2\beta cz} \right\}, $ |
令
| $ {\Gamma _2} = \left\{ {\left( {y,z} \right)\left| {\frac{{{y^2}}}{{\frac{{\beta {c^2}}}{4}}} + \frac{{{{\left( {z - \frac{c}{2}} \right)}^2}}}{{\frac{{{c^2}}}{4}}} = 1,\;\;\;\beta \ne 0,c \ne 0} \right.} \right\}, $ |
在Γ2外有
下面计算该最大值
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{\left( {y,z} \right) \in {\Gamma _2}} {V_1}\left( {y,z} \right) = \max \left\{ {{y^2} + {{\left( {z - c} \right)}^2},\left( {y,z} \right) \in {\Gamma _2}} \right\},\\ {\text{s}}{\text{.t}}{\text{.}}\;\;\;\;{\Gamma _2} = \left\{ {\left( {y,z} \right)\left| {\frac{{{y^2}}}{{\frac{{\beta {c^2}}}{4}}} + \frac{{{{\left( {z - \frac{c}{2}} \right)}^2}}}{{\frac{{{c^2}}}{4}}} = 1,\;\;\;\beta \ne 0,c \ne 0} \right.} \right\}, \end{array} \right. $ |
令y=y1, z=z1,
注2 当c=26, β=0.7, γ=1.5, α=1时,有
| $ \mathit{\Phi} =\left\{ \left( y,z \right)|{{y}^{2}}+{{\left( z-26 \right)}^{2}}\le {{26}^{2}} \right\}. $ |
由Φ可以得到系统(1)正半轨线在yoz平面上的最终界估计,见图 4.
|
图 4 系统(1)yoz平面上的最终界估计图示 Fig. 4 Bounds estimate of system (1) in yoz plane |
由从吸引集外的轨线进入吸引集的速率估计,有
定理3 令X(t)=(x(t), y(t), z(t), w(t))为系统(1)的任意一个解.则对任意α>0, β>0, γ>0, c>0,
| $ \begin{array}{l} \Omega = \left\{ {\left( {x,y,z,w} \right)\left| {\lambda {x^2} + m{y^2} + } \right.} \right.\\ \;\;\;\;\;\;m{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)^2} + \lambda \gamma {w^2} \le L,\\ \;\;\;\;\;\;\left. {\forall \lambda > 0,\forall m > 0} \right\} \end{array} $ | (4) |
为系统(1)的一个全局指数吸引集.其中,
| $ L = \frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{{m\theta }},\;\;\;\theta = \min\left\{ {\alpha ,\beta ,1} \right\}. $ |
证明 定义广义李雅普诺夫函数
| $ \begin{array}{*{20}{c}} {V\left( {x,y,z,w} \right) = \lambda {x^2} + m{y^2} + m{{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)}^2} + }\\ {\lambda \gamma {w^2},\;\;\;\;\forall \lambda > 0, m > 0,} \end{array} $ |
当V(X(t))>L, V(X(t0))>L时, 有
| $ \begin{array}{l} \left\{ {\frac{{{\text{d}}V}}{{{\text{d}}t}}\left| {_{\left( 1 \right)}} \right. = 2\lambda x\frac{{{\text{d}}x}}{{{\text{d}}t}} + 2my\frac{{{\text{d}}y}}{{{\text{d}}t}} + } \right.\\ \;\;\;2m\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)\frac{{{\text{d}}z}}{{{\text{d}}t}} + 2\lambda \gamma w\frac{{{\text{d}}w}}{{{\text{d}}t}} = \\ \;\;\;2\lambda x\left( {\alpha y - \alpha x + \gamma w} \right) + 2my\left( {cx - xz - y} \right) + \\ \;\;\;2m\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)\left( {xy - \beta z} \right) + 2\lambda \gamma w\left( { - x - \alpha w} \right) = \\ \;\;\; - 2\lambda \alpha {x^2} - 2m{y^2} - 2m\beta {z^2} + 2\beta \left( {\lambda \alpha + mc} \right)z - \\ \;\;\;2\lambda \alpha \gamma {w^2} = - \lambda \alpha {x^2} - m{y^2} - m\beta {z^2} + \\ \;\;\;2\beta \left( {\lambda \alpha + mc} \right)z - \gamma \lambda \alpha {w^2} - \lambda \alpha {x^2} - m{y^2} - m\beta {z^2} - \\ \;\;\;\lambda \alpha \gamma {w^2} \le - \lambda \alpha {x^2} - m{y^2} - m\beta {\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)^2} - \\ \;\;\; - \lambda \gamma \alpha {w^2} + \frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{m} \le - \theta V\left( {x,y,z,w} \right) + \\ \;\;\;\left. {\frac{{\beta {{\left( {\lambda \alpha + mc} \right)}^2}}}{m} = - \theta \left( {V\left( {x,y,z,w} \right) - L} \right) < 0} \right\}, \end{array} $ |
当V(X(t))>L, V(X(t0))>L时, 有
| $ \begin{array}{*{20}{c}} {V\left( {X\left( t \right)} \right) \le V\left( {X\left( {{t_0}} \right)} \right){{\text{e}}^{ - \theta \left( {t - {t_0}} \right)}} + \int_{{t_0}}^t {\theta L{{\text{e}}^{ - \theta \left( {t - \tau } \right)}}{\text{d}}\tau } = }\\ {V\left( {X\left( {{t_0}} \right)} \right){{\text{e}}^{ - \theta \left( {t - {t_0}} \right)}} + L\left( {1 - {{\text{e}}^{ - \theta \left( {t - {t_0}} \right)}}} \right),} \end{array} $ |
从而有
| $ \left[ {V\left( {X\left( t \right)} \right) - L} \right] \le \left[ {V\left( {{X_0}} \right) - L} \right]{{\text{e}}^{ - \theta \left( {t - {t_0}} \right)}}. $ |
令t→+∞, 对上述不等式两边取上极限,有
| $ \overline {\mathop {\lim }\limits_{t \to + \infty } } V\left( {X\left( t \right)} \right) \le L. $ |
从而有
| $ \begin{array}{l} \Omega = \left\{ {\left( {x,y,z,w} \right)\left| {\lambda {x^2} + m{y^2} + m{{\left( {z - \frac{{\lambda \alpha + mc}}{m}} \right)}^2} + } \right.} \right.\\ \;\;\;\;\;\;\;\left. {\lambda \gamma {w^2} \le L,\forall \lambda > 0,\forall m > 0} \right\} \end{array} $ |
为系统(1)的一个全局指数吸引集.
证毕!
注3 取λ=1, m=1, 则
| $ \Omega = \left\{ {\left( {x,y,z,w} \right)\left| {{x^2} + {y^2} + {{\left( {z - \alpha - c} \right)}^2} + \gamma {w^2} \le \delta } \right.} \right\} $ |
为系统(1)的一个全局指数吸引集,其中,
| $ \delta = \frac{{\beta {{\left( {\alpha + c} \right)}^2}}}{\theta },\;\;\;\theta = \min\left\{ {\alpha ,\beta ,1} \right\}. $ |
研究了一类大气混沌模型的全局吸引性和最终界.本研究方法亦适用于其他混沌系统;研究结果对于该混沌系统的混沌控制及其应用有一定的参考价值.
| [1] | LORENZ E N. Deterministic non periodic flow[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
| [2] | DOEDEL E J, KRAUSKOPF B, OSINGA H M. Global organization of phase space in the transition to chaos in the Lorenz system[J]. Nonlinearity, 2015, 28(11): 113–139. DOI:10.1088/0951-7715/28/11/R113 |
| [3] | MESSIAS M. Dynamics at infinity and the existence of singularly degenerate heteroclinic cycles in the Lorenz system[J]. Journal of Physics A(Mathematical and Theoretical), 2009, 42(11): 115101. |
| [4] | LEONID A B. Short and long-term forecast for chaotic and random systems (50 years after Lorenz's paper)[J]. Nonlinearity, 2014, 27: 51–60. DOI:10.1088/0951-7715/27/9/R51 |
| [5] | SPARROW C. The Lorenz Equations:Bifurcations, Chaos, and Strange Attractors[M]. Netherlands: Springer Science & Business Media, 2012: 20-30. |
| [6] | STEWART I. The Lorenz attractor exists[J]. Nature, 2000, 406: 948–949. DOI:10.1038/35023206 |
| [7] | TUCKER W. The Lorenz attractor exists[J]. Comptes Rendus de l'Académie des Sciences-Series Ⅰ-Mathematics, 1999, 328(12): 1197–1202. DOI:10.1016/S0764-4442(99)80439-X |
| [8] | POGROMSKY A Y, SANTOBONI G, NIJMEIJER H. An ultimate bound on the trajectories of the Lorenz systems and its applications[J]. Nonlinearity, 2003, 16: 1597–1605. DOI:10.1088/0951-7715/16/5/303 |
| [9] | LLIBRE J, ZHANG X. Invariant algebraic surfaces of the Lorenz system[J]. Journal of Mathematical Physics, 2002, 43: 1622–1645. DOI:10.1063/1.1435078 |
| [10] | KRISHCHENKO A P, STARKOV K E. Localization of compact invariant sets of the Lorenz system[J]. Physics Letters A, 2006, 353: 383–388. DOI:10.1016/j.physleta.2005.12.104 |
| [11] | ZHANG F C, ZHANG G Y. Further results on ultimate bound on the trajectories of the Lorenz system[J]. Qualitative Theory of Dynamical Systems, 2016, 15(1): 221–235. DOI:10.1007/s12346-015-0137-0 |
| [12] | ZHANG F C, LIAO X F, ZHANG G Y, et al. Dynamical analysis of the generalized Lorenz systems[J]. Journal of Dynamical and Control Systems, 2017, 23(2): 349–362. DOI:10.1007/s10883-016-9325-8 |
| [13] | ZHANG F C, LIAO X F, ZHANG G Y. Qualitative behavior of the Lorenz-Like chaotic system describing the flow between two concentric rotating spheres[J]. Complexity, 2016, 21(S2): 67–72. DOI:10.1002/cplx.v21.S2 |
| [14] | ZHANG F C, MU C L, ZHOU S M, et al. New results of the ultimate bound on the trajectories of the family of the Lorenz systems[J]. Discrete and Continuous Dynamical Systems:Ser B, 2015, 20(4): 1261–1276. DOI:10.3934/dcdsb |
| [15] | LORENZ S. Generalized Lorenz equations for acoustic-gravity waves in the atmosphere[J]. Physica Scripta, 1996, 53(1): 83–84. DOI:10.1088/0031-8949/53/1/015 |
| [16] |
韩修静, 江波, 毕勤胜. 快慢Lorenz-Stenflo系统分析[J].
物理学报, 2009, 58(7): 4408–4414.
HAN X J, JIANG B, BI Q S. Analysis of the fast-slow Lorenz-Stenflo system[J]. Acta Physica Sinica, 2009, 58(7): 4408–4414. DOI:10.7498/aps.58.4408 |


