有理Bézier曲线在曲线设计中具有非常重要的作用,且在实践中应用广泛.由于有理曲线在进行求导等运算时计算量较大,通常用多项式曲线代替有理曲线.为此不少学者研究并提出了用多项式曲线逼近有理曲线的方法.在一些特定情况下,希望在多项式曲线与有理曲线具有较好拟合效果的基础上尽可能多地通过有理曲线上的某些固定点,因此如何对有理Bézier曲线插值,使得插值曲线与有理曲线有较好的拟合效果,成为重要的课题.
之前学者们已经提出了多种逼近有理曲线的插值方法.例如1987年DEBOOR等[1]提出了高精度的几何Hermite插值方法,在保持固定点处二阶几何连续的情况下,构造了一条三次插值曲线,并且提出了插值曲线存在的条件.2003年YANG[2]在空间Hermite插值的基础上提出了一种用五次Bézier曲线或有理曲线逼近螺旋曲线的方法,并且逼近曲线在端点处满足二阶几何连续.2006年FLOATER[3]提出了一种多项式插值曲线逼近有理曲线的新方法,通过在点的位置和切线方向插值,构造一条新的多项式插值曲线,实现了对任意次有理Bézier曲线的插值.2008年HUANG等[4]提出了用多项式曲线逼近有理曲线的2种简单方法,一种是将有理曲线升阶,用产生的控制顶点所定义的Bézier曲线来逼近有理曲线,第2种是取有理曲线上若干个等分点,以等分点作为控制顶点定义Bézier曲线用于逼近有理曲线.
在此基础上,本文提出了一种新的简单的插值方法.首先运用结式方法将有理曲线的参数形式转化为隐式方程,再将含参数曲线在固定点处插值.通过求解相应的方程组得到待定参数的值,进而获得一条多项式插值曲线来表示有理曲线.
1 预备知识 1.1 有理Bézier曲线的定义与性质 1.1.1 有理Bézier曲线定义[5]n次有理Bézier曲线:
| $ \mathit{\boldsymbol{R}}\left( t \right) = \frac{{\sum\limits_{i = 0}^n {{\omega _i}{\mathit{\boldsymbol{R}}_i}B_i^n\left( t \right)} }}{{\sum\limits_{i = 0}^n {{\omega _i}B_i^n\left( t \right)} }},\;\;\;0 \le t \le 1. $ | (1) |
其中,
设ω0和ωn均不为零,则有理曲线在端点处的函数值及导数值为:
| $ \mathit{\boldsymbol{R}}\left( 0 \right) = {\mathit{\boldsymbol{R}}_0},\mathit{\boldsymbol{R}}\left( 1 \right) = {\mathit{\boldsymbol{R}}_n}, $ |
| $ \mathit{\boldsymbol{R'}}\left( 0 \right) = n\frac{{{\omega _1}}}{{{\omega _0}}}\left( {{\mathit{\boldsymbol{R}}_1} - {\mathit{\boldsymbol{R}}_0}} \right),\mathit{\boldsymbol{R'}}\left( 1 \right) = n\frac{{{\omega _{n - 1}}}}{{{\omega _n}}}\left( {{\mathit{\boldsymbol{R}}_n} - {\mathit{\boldsymbol{R}}_{n - 1}}} \right). $ |
| $ \mathit{\boldsymbol{R}}\left( t \right) = \frac{{\sum\limits_{i = 0}^n {{\omega _i}{\mathit{\boldsymbol{R}}_i}B_i^n\left( t \right)} }}{{\sum\limits_{i = 0}^n {{\omega _i}B_i^n\left( t \right)} }} = \frac{{\sum\limits_{i = 0}^{n + 1} {\omega _i^ * \mathit{\boldsymbol{R}}_i^ * B_i^{n + 1}\left( t \right)} }}{{\sum\limits_{i = 0}^{n + 1} {\omega _i^ * B_i^{n + 1}\left( t \right)} }}. $ |
其中,
| $ \omega _i^ * = \frac{i}{{n + 1}}{\omega _{r - 1}} + \left( {1 - \frac{i}{{n + 1}}} \right){\omega _i}, $ |
| $ \mathit{\boldsymbol{R}}_i^ * = \left( {\frac{i}{{n + 1}}{\omega _{i - 1}}{\mathit{\boldsymbol{R}}_{i - 1}} + \left( {1 - \frac{i}{{n + 1}}} \right){\omega _i}{\mathit{\boldsymbol{R}}_i}} \right)/\omega _i^ * . $ |
对于给定的2条曲线P(t), R(s), t0≤t≤t1, s0≤s≤s1,设2条曲线在端点处重合,即P(t0)=R(s0), P(t1)=R(s1),则2条曲线的Hausdorff距离[6]定义为
| $ \begin{array}{l} {d_H}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\max \left( {{d_1}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right),{d_2}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right)} \right), \end{array} $ |
其中,
| $ {d_1}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right) = \mathop {\max }\limits_{t \in \left[ {{t_0},{t_1}} \right]} \mathop {\min }\limits_{s \in \left[ {{s_0},{s_1}} \right]} \left| {\mathit{\boldsymbol{P}}\left( t \right) - \mathit{\boldsymbol{R}}\left( s \right)} \right|, $ |
| $ {d_2}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right) = \mathop {\max }\limits_{s \in \left[ {{s_0},{s_1}} \right]} \mathop {\min }\limits_{t \in \left[ {{t_0},{t_1}} \right]} \left| {\mathit{\boldsymbol{P}}\left( t \right) - \mathit{\boldsymbol{R}}\left( s \right)} \right|. $ |
本文在估计误差时采用的是离散的Hausdorff距离,分别取2条曲线上的N个点组成2个点的集合A, B,则2条曲线之间离散的Hausdorff距离[6]为
| $ \begin{array}{l} {d_H}\left( {\mathit{\boldsymbol{P}}\left( t \right),\mathit{\boldsymbol{R}}\left( s \right)} \right) = \max \left( {\mathop {\max }\limits_{t \in A} \mathop {\min }\limits_{s \in B} \left| {\mathit{\boldsymbol{P}}\left( t \right) - \mathit{\boldsymbol{R}}\left( s \right)} \right|,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathop {\max }\limits_{s \in B} \mathop {\min }\limits_{t \in A} \left| {\mathit{\boldsymbol{P}}\left( t \right) - \mathit{\boldsymbol{R}}\left( s \right)} \right|} \right). \end{array} $ |
设f(x), g(x)是2个次数分别为m, n的单变量多项式:
| $ f\left( x \right) = {a_m}{x^m} + \cdots + {a_1}x + {a_0}, $ |
| $ g\left( x \right) = {b_n}{x^n} + \cdots + {b_1}x + {b_0}, $ |
其中, am≠0, bn≠0,则m+n阶行列式:
| $ \mathit{\boldsymbol{R}}\left( {f,g} \right) = \left| \begin{array}{l} {a_0}\;\;\;{a_1}\;\;\; \cdots \;\;\;{a_m}\;\;\;\\ \;\;\;\;\;\;{a_0}\;\;\;{a_1}\;\;\; \cdots \;\;\;\;{a_m}\\ \;\;\;\;\;\;\;\; \ddots \;\;\; \ddots \;\;\;\;\;\;\;\;\;\; \ddots \\ \;\;\;\;\;\;\;\;\;\;{a_0}\;\;\;\;{a_1}\;\;\; \cdots \;\;\;\;{a_m}\\ {b_0}\;\;\;{b_1}\;\;\; \cdots \;\;\;{b_n}\;\;\;\\ \;\;\;\;\;\;{b_0}\;\;\;{b_1}\;\;\; \cdots \;\;\;\;{b_n}\\ \;\;\;\;\;\;\;\; \ddots \;\;\; \ddots \;\;\;\;\;\;\;\;\;\; \ddots \\ \;\;\;\;\;\;\;\;\;\;{b_0}\;\;\;\;{b_1}\;\;\; \cdots \;\;\;\;{b_n} \end{array} \right| $ |
称为多项式f(x)、g(x)的结式,记作R(f, g, x).
本文采用结式方法将有理Bézier曲线的参数方程转化为隐式方程.有关有理曲线的参数化方法详见文献[7-9].
2 构造多项式曲线的方法 2.1 构造参数多项式插值曲线定理1[4] 将n次有理Bézier曲线R(t)不断升阶,得到新的控制顶点Ri*, i=0, 1, …, n+1和新的权因子ωi*, i=0, 1, …, n+1,则以控制顶点Ri*, i=0, 1, …, n+1定义的Bézier曲线P(t)一致逼近于原有理Bézier曲线.
定理2[4] 在有理Bézier曲线上取等分点
由定理1和定理2,设有理Bézier曲线升阶一次后的控制顶点为Ri*, i=0, 1, …, n+1,同时取曲线上的等分点Ri, i=0, 1, …, n+1,将2组控制顶点线性组合后产生一组新的含参数的控制顶点Pi, i=0, 1, …, n+1,从而生成一个含参数的Bézier曲线P(t)=(x(t), y(t)).
含参数多项式曲线表示有理曲线时,保持2条曲线在端点处满足G1连续,因此组合后控制顶点在两端点处不变,并且满足端点处的切线方向相同, 故线性组合后的控制顶点为:
| $ {{\mathit{\boldsymbol{\bar P}}}_0} = \mathit{\boldsymbol{R}}_0^ * , $ |
| $ {{\mathit{\boldsymbol{\bar P}}}_1} = {\lambda _1}\mathit{\boldsymbol{R}}_1^ * + \left( {1 - {\lambda _1}} \right)\mathit{\boldsymbol{R}}_0^ * , $ |
| $ {{\mathit{\boldsymbol{\bar P}}}_i} = {\lambda _i}\mathit{\boldsymbol{R}}_i^ * + \left( {1 - {\lambda _i}} \right){{\mathit{\boldsymbol{\bar R}}}_i},\;\;\;\;i = 2,3, \cdots ,n - 1, $ |
| $ {{\mathit{\boldsymbol{\bar P}}}_n} = {\lambda _n}\mathit{\boldsymbol{R}}_n^ * + \left( {1 - {\lambda _n}} \right)\mathit{\boldsymbol{\bar R}}_{n + 1}^ * , $ |
| $ {{\mathit{\boldsymbol{\bar P}}}_{n + 1}} = \mathit{\boldsymbol{R}}_{n + 1}^ * . $ |
此时含参数的多项式曲线为P(t)=(x(t), y(t)).如何选取合适的参数λi,使P(t)与R(t)的Hausdorff距离最小,成为确定插值曲线的关键.
2.2 离散插值求解参数对曲线上的固定点插值时,曲线的参数化形式极为不便,因此需要将曲线转化为隐式方程.首先运用结式方法,将有理曲线R(t)转化为隐式,设其隐式的表达式为F(x(t), y(t), t)=0;然后取参数多项式曲线P(t)上固定的等分点,由于两曲线在端点处G1连续,只需插值除端点以外的n个等分点,设为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar P}}\left( {\frac{i}{{n + 1}}} \right) = \left( {\bar x\left( {\frac{i}{{n + 1}}} \right),\bar y\left( {\frac{i}{{n + 1}}} \right)} \right),}\\ {i = 1,2, \cdots ,n.} \end{array} $ |
代入有理曲线R(t)的隐式方程,得到方程组:
| $ \left\{ \begin{array}{l} F\left( {\bar x\left( {\frac{1}{{n + 1}}} \right),\bar y\left( {\frac{1}{{n + 1}}} \right),\frac{1}{{n + 1}}} \right) = 0,\\ F\left( {\bar x\left( {\frac{2}{{n + 1}}} \right),\bar y\left( {\frac{2}{{n + 1}}} \right),\frac{2}{{n + 1}}} \right) = 0,\\ \cdots \\ F\left( {\bar x\left( {\frac{n}{{n + 1}}} \right),\bar y\left( {\frac{n}{{n + 1}}} \right),\frac{n}{{n + 1}}} \right) = 0. \end{array} \right. $ | (2) |
插值确定参数λi的过程,即为该方程组的求解过程.
对于方程组(2),有理曲线次数越高就越复杂,计算量也大大增加;并且该方程组解的情况复杂多样,甚至存在无解的情况,因此该方法具有一定的局限性.本文只考虑有解的情况.
用Mathematica进行方程组求解,但是在求解参数方程组的过程中需要选择合适的参数值确定插值曲线,使得插值效果最优.为此,需要考虑文献[4]的2种方法得到的多项式曲线与有理曲线图像的特点.在这里限定参数均为正实数,即λi>0,此限定条件可简化求解参数的过程,除去效果不明显的插值曲线.设有k组满足条件的参数值,将满足条件的k组参数值分别代入含参数的插值曲线,设得到的多项式插值曲线为Pi(t), i=1, 2, …, k.在这里将离散的Hausdorff距离作为误差函数, 插值曲线分别代入误差函数,计算插值曲线Pi(t), i=1, 2, …, k与有理Bézier曲线R(t)之间的离散Hausdorff距离.
根据误差大小确定最优参数,通过比较dHi(R(t), Pi(s)), i=1, 2, …, k的大小,选择当dHi(R(t), Pi(s))最小时所对应的一组参数值λi, i=1, 2, …, n,从而得到新的多项式插值曲线P(t).
由于该方法选择的参数值所对应的Hausdorff距离最小,并且此时Hausdorff距离即为插值曲线和原有理曲线之间的误差,理论上此时得到的插值曲线能更好地表示原有理曲线,该求解过程在限定条件λi>0(i=1, 2, …, n)下,计算简便.
2.3 算法实现步骤Step1 利用结式方法将n次有理Bézier曲线R(t)的参数形式转化为隐式:F(x, y)=0.
Step2 将n次有理Bézier曲线R(t)的控制顶点升阶一次得到控制顶点Ri*, i=0, 1, …, n+1,同时,取有理Bézier曲线的n+2等分点(包括两端点)
Step3 利用参数λi对2组控制顶点进行线性组合,形成1组含参数的控制顶点,从而确定该控制顶点所定义的含参数Bézier曲线P(t)=(x(t), y(t)).
Step4 取P(t)上n等分点
| $ F\left( {\bar x\left( {\frac{i}{{n + 1}}} \right),\bar y\left( {\frac{i}{{n + 1}}} \right),\frac{i}{{n + 1}}} \right) = 0,i = 1,2, \cdots ,n. $ |
Step5 利用限定条件求解方程组,初步确定参数值,并将所确定的参数值分别代入参数曲线P(t),计算曲线P(t)与原有理曲线R(t)的Hausdorff距离.
Step6 Hausdorff距离最小时所对应的一组参数λi, i=1, 2, …, n,即为最优参数值,确定此时的插值曲线, 并对2条曲线进行误差分析.
3 数值实例用实例进一步验证多项式曲线插值有理Bézier曲线方法的可行性.分别取曲线上2 000个点作为集合A和B,采用离散的Haussdorff距离进行误差计算.最后,对多项式插值曲线和有理曲线进行误差分析.
例1 设四次对称有理Bézier曲线的控制顶点和权值为(0, 0), (1, 5), (4, 9), (7, 5), (8, 0)和2, 3, 2, 3, 2,则该有理Bézier曲线的表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{R}}\left( t \right) = \left( {\frac{{2t\left( {t\left( {8{t^2} - 3 - 6t} \right) - 3} \right)}}{{2\left( {t - 1} \right)t\left( {1 + 2\left( {t - 1} \right)t} \right) - 1}},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{6\left( {t - 1} \right)t\left( {5 + \left( {t - 1} \right)t} \right)}}{{2\left( {t - 1} \right)t\left( {1 + 2\left( {t - 1} \right)t} \right) - 1}}} \right). \end{array} $ |
首先将该有理曲线转化为隐式:
| $ \begin{array}{l} f\left( {x,y} \right) = - 1888427520x + 893052864{x^2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;164249856{x^3} + 10265616{x^4} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;377685504y + 333891072xy - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;41736384{x^2}y - 74803392{y^2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;63290882x{y^2} + 7911360{x^2}{y^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;10238976{y^3} - 154880{y^4}, \end{array} $ |
有理曲线升阶一次后的控制顶点为:
| $ \mathit{\boldsymbol{R}}_0^ * = \left( {0,0} \right),\mathit{\boldsymbol{R}}_1^ * = \left( {\frac{6}{7},\frac{{30}}{7}} \right),\mathit{\boldsymbol{R}}_2^ * = \left( {\frac{5}{2},7} \right), $ |
| $ \mathit{\boldsymbol{R}}_3^ * = \left( {\frac{{11}}{2},7} \right),\mathit{\boldsymbol{R}}_4^ * = \left( {\frac{{50}}{7},\frac{{30}}{7}} \right),\mathit{\boldsymbol{R}}_5^ * = \left( {8,0} \right). $ |
同时取有理曲线上的五等分点为:
| $ {{\mathit{\boldsymbol{\bar R}}}_0} = \left( {0,0} \right),{{\mathit{\boldsymbol{\bar R}}}_1} = \left( {\frac{{944}}{{761}},\frac{{2904}}{{761}}} \right),{{\mathit{\boldsymbol{\bar R}}}_2} = \left( {\frac{{2324}}{{781}},\frac{{4284}}{{781}}} \right), $ |
| $ {{\mathit{\boldsymbol{\bar R}}}_3} = \left( {\frac{{3924}}{{781}},\frac{{4284}}{{781}}} \right),{{\mathit{\boldsymbol{\bar R}}}_4} = \left( {\frac{{5144}}{{761}},\frac{{2904}}{{761}}} \right),{{\mathit{\boldsymbol{\bar R}}}_5} = \left( {8,0} \right). $ |
其次,2组控制顶点线性组合后得到的新控制顶点为:
| $ {{\mathit{\boldsymbol{\bar P}}}_0} = \mathit{\boldsymbol{R}}_0^ * = \left( {0,0} \right), $ |
| $ {{\mathit{\boldsymbol{\bar P}}}_1} = {\lambda _1}\mathit{\boldsymbol{R}}_1^ * + \left( {1 - {\lambda _1}} \right)\mathit{\boldsymbol{R}}_0^ * = \left( {\frac{{6{\lambda _1}}}{7},\frac{{30{\lambda _1}}}{7}} \right), $ |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar P}}}_2} = {\lambda _2}\mathit{\boldsymbol{R}}_2^ * + \left( {1 - {\lambda _2}} \right){{\bar R}_2} = \\ \;\;\;\;\;\;\;\left( {\frac{{2324}}{{781}} - \frac{{743}}{{1562}}{\lambda _2},\frac{{4284}}{{781}} + \frac{{1183}}{{781}}{\lambda _2}} \right), \end{array} $ |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar P}}}_3} = {\lambda _2}\mathit{\boldsymbol{R}}_3^ * + \left( {1 - {\lambda _2}} \right){{\mathit{\boldsymbol{\bar R}}}_3} = \\ \;\;\;\;\;\;\;\left( {\frac{{3924}}{{781}} + \frac{{743}}{{1562}}{\lambda _2},\frac{{4284}}{{781}} + \frac{{1183}}{{781}}{\lambda _2}} \right), \end{array} $ |
| $ {{{\mathit{\boldsymbol{\bar P}}}_4} = {\lambda _1}\mathit{\boldsymbol{R}}_4^ * + \left( {1 - {\lambda _1}} \right)\mathit{\boldsymbol{R}}_5^ * = \left( {8 - \frac{{6{\lambda _1}}}{7},\frac{{30{\lambda _1}}}{7}} \right),} $ |
| $ {{{\mathit{\boldsymbol{\bar P}}}_5} = \mathit{\boldsymbol{R}}_5^ * = \left( {8,0} \right).} $ |
因此,定义一条含参数多项式曲线:
| $ \begin{array}{l} \mathit{\boldsymbol{\bar P}}\left( t \right) = \left( {\bar x\left( t \right),\bar y\left( t \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\left( {8{t^3} + \left( {5\left( {t - 1} \right)t\left( {10136{t^2} - 23536t - } \right.} \right.} \right.\\ \;\;\;\;\;\;\;\;\;21336{t^3} + \left( {2t - 1} \right)\left( {4686\left( {{\lambda _1} + {\lambda _1}\left( {t - 1} \right)t} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left. {\left. {5201{\lambda _2}\left( {t - 1} \right)t} \right)} \right)} \right)/5467,\\ \;\;\;\;\;\;\;\;\;\left( {10\left( {t - 1} \right)t\left( {49\left( {t - 1} \right)t\left( {612 + 169{\lambda _2}} \right) - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left. {\left. {11715\left( {1 + 3\left( {t - 1} \right)t} \right){\lambda _1}} \right)} \right)/5467} \right). \end{array} $ |
取曲线上五等分点,由于原有理曲线为四次对称曲线,故只需考虑
当
| $ \begin{array}{l} \mathit{\boldsymbol{\bar P}}\left( {\frac{1}{5}} \right) = \left( {{x_1},{y_1}} \right) = \\ \;\;\;\;\;\;\;\left( {\frac{{8\left( {280801 + 105435{\lambda _1} - 22290{\lambda _2}} \right)}}{{2440625}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{8\left( {152295{\lambda _1} + 196\left( {612 + 169{\lambda _2}} \right)} \right)}}{{683375}}} \right); \end{array} $ |
当
| $ \begin{array}{l} \mathit{\boldsymbol{\bar P}}\left( {\frac{2}{5}} \right) = \left( {{x_2},{y_2}} \right) = \\ \;\;\;\;\;\;\;\left( {\frac{{4\left( {12310648 + 667755{\lambda _1} - 234045{\lambda _2}} \right)}}{{17084375}},} \right.\\ \;\;\;\;\;\;\;\left. {\frac{{36\left( {8568 + 3905{\lambda _1} + 2366{\lambda _2}} \right)}}{{97625}}} \right). \end{array} $ |
在五等分点处插值,确定一个方程组:
| $ \left\{ \begin{array}{l} f\left( {{x_1},{y_1}} \right) = \\ \;\;\;\;f\left( {\frac{{8\left( {280801 + 105435{\lambda _1} - 22290{\lambda _2}} \right)}}{{2440625}},} \right.\\ \;\;\;\;\left. {\frac{{8\left( {152295{\lambda _1} + 196\left( {612 + 169{\lambda _2}} \right)} \right)}}{{683375}}} \right) = 0,\\ f\left( {{x_2},{y_2}} \right) = \\ \;\;\;f\left( {\frac{{4\left( {12310648 + 667755{\lambda _1} - 234045{\lambda _2}} \right)}}{{17084375}},} \right.\\ \;\;\;\left. {\frac{{36\left( {8568 + 3905{\lambda _1} + 2366{\lambda _2}} \right)}}{{97625}}} \right) = 0. \end{array} \right. $ |
根据上述方法,通过限制条件解该方程组,可得到参数λ1和λ2的值:
| $ \left\{ \begin{array}{l} {\lambda _1} = 1.35699,\\ {\lambda _2} = 0.4695855, \end{array} \right.\left\{ \begin{array}{l} {\lambda _1} = 1.64636,\\ {\lambda _2} = 0.02172, \end{array} \right.\left\{ \begin{array}{l} {\lambda _1} = 8.01864,\\ {\lambda _2} = 12.3429, \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\lambda _1} = 10.6791,\\ {\lambda _2} = 14.5963, \end{array} \right.\left\{ \begin{array}{l} {\lambda _1} = 11.97964,\\ {\lambda _2} = 7.43366, \end{array} \right.\left\{ \begin{array}{l} {\lambda _1} = 12.1184,\\ {\lambda _2} = 11.41184, \end{array} \right. $ |
将参数值代入曲线P(t),得到多项式曲线Pi(t)=(x(t), y(t))(i=1, 2, …, 6),分别计算它们与原有理曲线R(t)之间离散的Hausdorff距离:
| $ d_H^1\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_1}\left( t \right)} \right) = 0.0105742, $ |
| $ d_H^2\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_2}\left( t \right)} \right) = 0.0926771, $ |
| $ d_H^3\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_3}\left( t \right)} \right) = 20.152628, $ |
| $ d_H^4\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_4}\left( t \right)} \right) = 25.849055, $ |
| $ d_H^5\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_5}\left( t \right)} \right) = 21.643537, $ |
| $ d_H^6\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_6}\left( t \right)} \right) = 24.878414. $ |
显然,取第1组参数值时,插值曲线与原有理曲线的误差最小为0.010 574 2.图 1和2分别给出了插值曲线和原有理曲线以及曲率的对比.
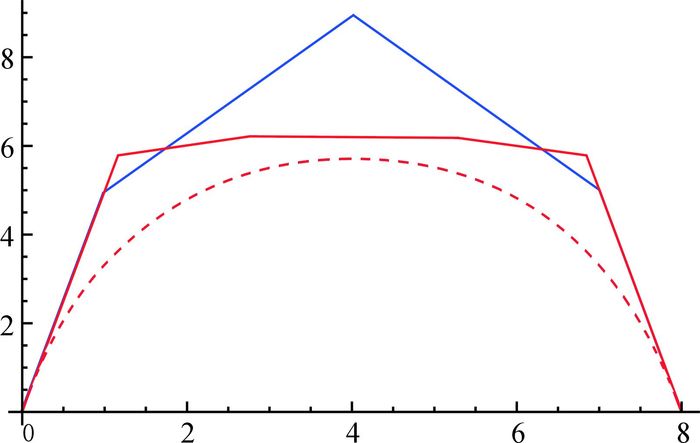
|
图 1 有理曲线与插值曲线 Fig. 1 The rational curve and the interpolation curve 实线为有理曲线,虚线为插值曲线. Solid line: rational curve, dashed: interpolation curve. |
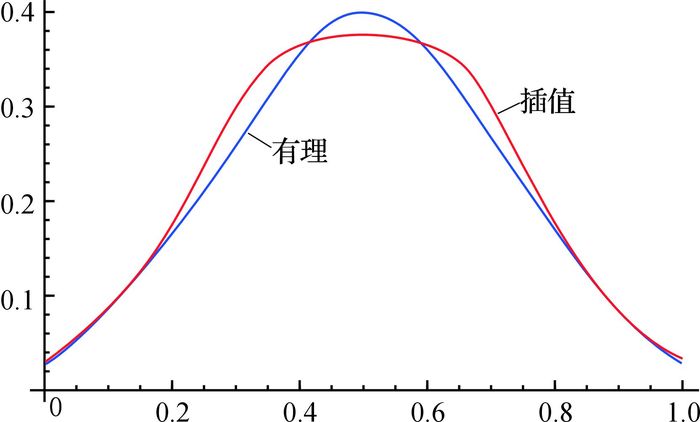
|
图 2 有理曲线与插值曲线曲率 Fig. 2 Curvature between rational curve and interpolation curve |
例2 设一条三次有理Bézier曲线的控制顶点和权因子分别为(0, 0), (2, 4), (4, 6), (9, 0)和1, 3, 2, 1,将该曲线升阶,按照本文插值有理曲线的方法确定含参数多项式曲线为:
| $ \begin{array}{l} \mathit{\boldsymbol{\bar P}}\left( t \right) = \left( {\bar x\left( t \right),\bar y\left( t \right)} \right) = \left( {9{t^2}\left( {2 - {t^2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{6}{{35}}\left( {t - 1} \right)t\left( {7\left( {1 - t} \right)\left( {6\left( {t - 1} \right){\lambda _1} + t{\lambda _2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {100{t^2}{\lambda _3}} \right),\frac{{72}}{{595}}\left( {t - 1} \right)t\left( { - 119{{\left( {t - 1} \right)}^2}{\lambda _1} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left. {2t\left( {7\left( {t - 1} \right)\left( {15 + 2{\lambda _2}} \right) - 85{\lambda _3}} \right)} \right)} \right). \end{array} $ |
根据限定条件,在四等分点处插值求解参数的值为
| $ \left\{ \begin{array}{l} {\lambda _1} = 1.10988,\\ {\lambda _2} = 1.77774,\\ {\lambda _3} = 1.02589. \end{array} \right. $ |
此时,插值曲线P(t)与原有理曲线的误差为0.010 970 1,插值曲线与原有理曲线的图像及曲率变化如图 3和图 4所示.

|
图 3 有理曲线与插值曲线 Fig. 3 The rational curve and the interpolation curve 实线为有理曲线,虚线插值曲线. Solid line: rational curve, dashed: interpolation curve. |
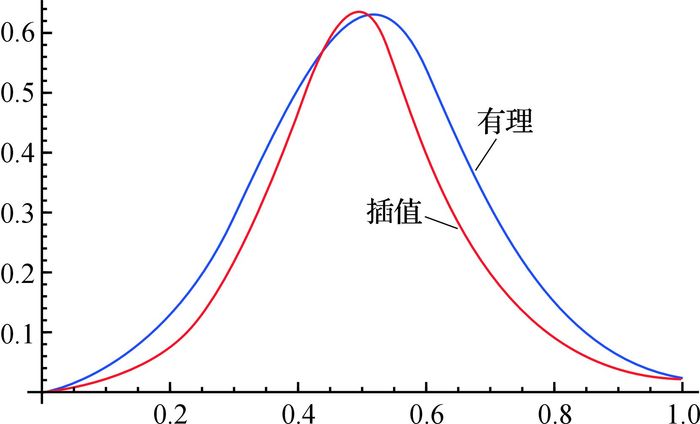
|
图 4 有理曲线与插值曲线曲率 Fig. 4 Curvature between rational curve and interpolation curve |
例3 三次有理Bézier曲线的控制顶点和权因子分别为(0, 0), (2, 5), (4, 0), (6, 5)和2, 3, 2, 1.采用本文的参数多项式曲线插值有理曲线的方法确定含参数多项式曲线为
| $ \begin{array}{l} \mathit{\boldsymbol{\bar P}}\left( t \right) = \left( {\bar x\left( t \right),\bar y\left( t \right)} \right) = \left( {2{t^2}\left( {8 - t\left( {4 + t} \right)} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\frac{{72}}{{11}}{\left( {t - 1} \right)^3}t{\lambda _1} + \frac{4}{{35}}\left( {t - 1} \right){t^2}\left( {7\left( {t - 1} \right){\lambda _2} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {60t{\lambda _3}} \right),\frac{{180}}{{11}}{\left( {1 - t} \right)^3}t{\lambda _1} + \frac{1}{{21}}{t^2}\left( {35\left( {10 + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\left. {\left. {\left. {t\left( {t - 8} \right)} \right) + 4\left( {t - 1} \right)\left( {7{\lambda _2}\left( {t - 1} \right) + 90t{\lambda _3}} \right)} \right)} \right). \end{array} $ |
同理,通过四等分点处插值并根据限定条件确定参数值为
| $ \left\{ \begin{array}{l} {\lambda _1} = 1.19665,\\ {\lambda _2} = 0.335328,\\ {\lambda _3} = 1.09055. \end{array} \right.\;\;\;\;\left\{ \begin{array}{l} {\lambda _1} = 11.403,\\ {\lambda _2} = 45.2022,\\ {\lambda _3} = 3.07046. \end{array} \right. $ |
求出其对应的离散Hausdorff距离分别为:
| $ d_H^1\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_1}\left( t \right)} \right) = 0.00794314, $ |
| $ d_H^2\left( {\mathit{\boldsymbol{R}}\left( t \right),{{\mathit{\boldsymbol{\bar P}}}_2}\left( t \right)} \right) = 17.6052. $ |
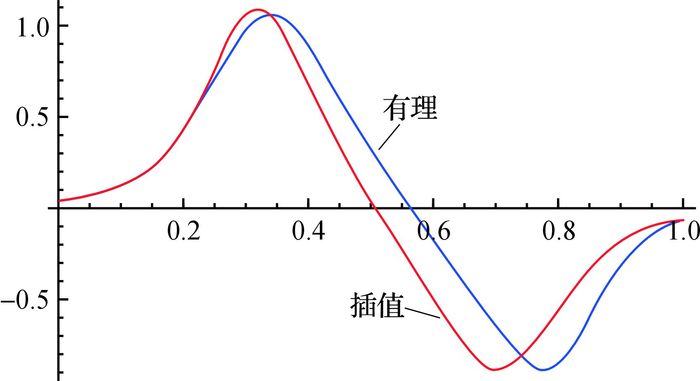
因此,插值曲线P(t)与原有理曲线的误差为0.007 943 14.如图 5和6所示.
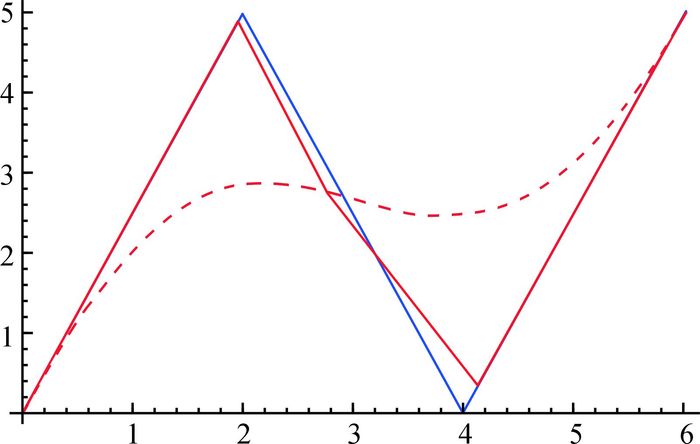
|
图 5 有理曲线与插值曲线 Fig. 5 The rational curve and the interpolation curve |
|
图 6 有理曲线与插值曲线曲率 Fig. 6 Curvature between rational curve and interpolation curve |
由上述3个例子及误差对比可知(见表 1),本文方法插值有理曲线有较好的效果,并且在升阶次数相同时,较文献[11]的方法更优.
| 表 1 上述例子的误差与已有方法的比较 Table 1 The error analysis of case 1 to 3 |
本文只是提供了一种插值思路,其精度与文献[10]相同.
4 结语研究了利用含参数的多项式曲线插值有理Bézier曲线的方法, 该方法不仅具有较好的效果, 而且在应用中可根据实际需要使得插值曲线通过有理曲线上的某些固定点.实例分析证实了该方法的有效性, 具有实际意义.但该方法也存在一定的局限性, 比如在求解非线性方程组时可能含有无解的情况, 并且当有理曲线次数较高或升阶次数较多时, 计算量较大等.另外, 只考虑了平面曲线的插值, 实际上该插值方法还可推广至空间有理曲线.
| [1] | DEBOOR C, HÖLLIG K, SABIN M. High accuracy geometric Hermite interpolation[J]. Computer Aided Geometric Design, 1987, 4(4): 169–178. |
| [2] | YANG X N. High accuracy approximation of helices by quintic curves[J]. Computer Aided Geometric Design, 2003, 20: 303–317. DOI:10.1016/S0167-8396(03)00074-8 |
| [3] | FLOATER M S. High order approximation of rational curves by polynomial curves[J]. Computer Aided Geometric Design, 2006, 23(8): 621–628. DOI:10.1016/j.cagd.2006.06.003 |
| [4] | HUANG Y D, SU H M, LIN H W. A simple method for approximating rational Bézier curve using Bézier curves[J]. Computer Aided Geometric Design, 2008, 25(8): 697–699. DOI:10.1016/j.cagd.2008.03.001 |
| [5] | FARIN G. Curves and Surfaces for Computer Aided Geometric Design, A Practical Guide 5th ed[M]. San Diego: Academic Press, 2002. |
| [6] | CHEN J, WANG G J. A new type of the generalized Bézier curves[J]. Applied Mathematics:A Journal of Chinese Universities (Ser B), 2011(1): 47–56. |
| [7] |
陈发来. 曲面隐式化新发展[J].
中国科学技术大学学报, 2014, 44(5): 345–361.
CHEN F L. Recent advances on surface implicitization[J]. Journal of University of Science and Technology of China, 2014, 44(5): 345–361. |
| [8] |
陈发来. 有理曲线的近似隐式化表示[J].
计算机学报, 1998, 21(9): 855–819.
CHEN F L. The implicitization of ration curves[J]. Chinese Journal of Computers, 1998, 21(9): 855–819. |
| [9] |
李彩云, 朱春钢, 王仁宏. 参数曲线的分段近似隐式化[J].
高校应用数学学报:A辑, 2010, 25(2): 202–210.
LI C Y, ZHU C G, WANG R H. Piecewise approximate implicitization of parametric curves[J]. Applied Mathematics:A Journal of Chinese Universities, 2010, 25(2): 202–210. |
| [10] | FLOATER M S. High order approximation of rational curves by polynomial curves[J]. Computer Aided Geometric Design, 2006, 23(8): 621–628. DOI:10.1016/j.cagd.2006.06.003 |
| [11] |
杨连喜, 徐晨东. 一种用多项式曲线逼近有理曲线的新方法[J].
浙江大学学报:理学版, 2015, 42(1): 21–27.
YANG L X, XU C D. New method of parametric polynomial curves approximation rational curves[J]. Journal of Zhejiang University:Science Edition, 2015, 42(1): 21–27. |



