在压缩感知理论中,广义正交匹配追踪(gOMP)算法属于贪婪算法[1-2],用于解决l0范数的最小化问题.在信道编码中,循环码是线性分组码的一个子类,属于多项式编码,主要用于数据存储和传输等通信领域[3].
本文借助无噪声条件下的压缩感知理论[4-5],采用校验矩阵H作为测量矩阵,伴随式S作为测量信号y,建立了循环码差错图案E重构的压缩感知模型.通过gOMP算法,正确重构了差错图案E,然后对差错图案E与收码R进行模2加运算,计算码字C的估值.
通过gOMP算法,对(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码进行仿真实验,通过误码率和码字C估值的成功率,分析gOMP算法的译码效果.实验结果表明,采用gOMP算法能够实现对(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码的译码.
1 差错图案E的压缩感知模型压缩感知观测模型分为无噪声干扰和有噪声干扰2种[4-5].本文借助无噪声干扰的压缩感知模型实现差错图案E的重构,假设x是稀疏信号,A为测量矩阵,y为测量信号,则y可以表示为[4-5]:
| $ y = \mathit{\boldsymbol{A}} \cdot x, $ | (1) |
假设已知测量矩阵A和测量信号y,如式(2) 所示[4-5]通过求解‖x‖0范数的最小值求得稀疏信号x.
| $ \mathop {\min }\limits_x {\left\| x \right\|_0}\;{\rm{s}}.\;{\rm{t}}.\;\;\mathit{\boldsymbol{A}} \cdot x = y. $ | (2) |
式(2) 为无噪声干扰的压缩感知模型,可以通过贪婪算法求解‖x‖0的最小值,例如广义正交匹配追踪gOMP算法[1-2].
1.1 差错图案E差错图案E等于发码C减去收码R,在二元域内,差错图案E等于发码C与收码R的模2加之和[3]:
| $ \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{C}} \oplus \mathit{\boldsymbol{R}}, $ | (3) |
在随机差错条件下,通常将差错图案E看作一维稀疏信号,由于发码C与校验矩阵H正交,其內积为0,式(3) 右乘以校验矩阵H的转置矩阵HT,由于收码R和HT的內积定义为伴随式S,所以伴随式S与差错图案E的关系为[3]
| $ {\mathbf{S}^{\rm{T}}} = \mathit{\boldsymbol{H}} \cdot {\mathit{\boldsymbol{E}}^{\rm{T}}}. $ | (4) |
由于式(4) 为欠定方程,若每次译码都求解式(4),运算量大.在最大似然译码算法中,通过查找标准阵列译码表得到伴随式S与差错图案E的对应关系.
1.2 求解差错图案E的线性规划模型根据最佳概率译码的准则,选取概率最大的差错图案E作为其估值,通过BSC二进制对称信道可以验证,重量最轻的差错图案E出现的概率最大[3],所以选取重量最轻的差错图案E作为其估值,将式(4) 作为求解差错图案E的约束方程,将求解重量最轻的差错图案E作为目标函数,得到求解差错图案E的线性规划模型[6-7]:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{E}} f = w\left( \mathit{\boldsymbol{E}} \right)\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\;H \cdot {\mathit{\boldsymbol{E}}^{\rm{T}}} = {\mathbf{S}^{\rm{T}}}. $ | (5) |
在二元域内,差错图案E的元素为0或1,差错图案E的重量最轻等效为差错图案E的l0范数‖E‖0最小,式(5) 的目标函数可以用求解‖E‖0范数最小值代替:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{E}} {\left\| \mathit{\boldsymbol{E}} \right\|_0}\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\;\mathit{\boldsymbol{H}} \cdot {\mathit{\boldsymbol{E}}^{\rm{T}}} = {\mathbf{S}^{\rm{T}}}, $ | (6) |
比较式(6) 与式(2) 发现,若将差错图案E作为一维稀疏信号,伴随式S作为测量信号,校验矩阵H作为测量矩阵,可将式(6) 定义为重构差错图案E的压缩感知模型.
与文献[8-10]提供的方法相比,采用压缩感知理论和gOMP算法重构差错图案E不需要查找标准阵列译码表,运算量小,计算过程简单.
2 测量矩阵若把校验矩阵H作为测量矩阵,伴随式S作为测量信号,实现差错图案E的重构.校验矩阵H的稀疏度Spark(H)与差错图案E的l0范数‖E‖0之间的关系为[11]
| $ {\left\| \mathit{\boldsymbol{E}} \right\|_0} < {\rm{spark}}\left( \mathit{\boldsymbol{H}} \right)/2, $ | (7) |
| $ \mathit{\boldsymbol{H}}{\rm{ = }}\left[{{\mathit{\boldsymbol{I}}_{n-k}}\left| \mathit{\boldsymbol{P}} \right.} \right], $ | (8) |
其中,子矩阵P的列向量的最小重量为dmin-1,dmin为码字C的最小距离.
定理1 校验矩阵H的稀疏度Spark为非零码字的最小重量,即循环码码字的最小距离dmin.
证明 在循环码中,校验矩阵H的稀疏度Spark表示校验矩阵H中线性相关的最小列数,码字C与校验矩阵H正交,所以码字C与校验矩阵H的乘积为0,即[15]
| $ \begin{array}{l} \mathit{\boldsymbol{C}} \cdot {\mathit{\boldsymbol{H}}^{\rm{T}}} = \left[{{c_{n-1}}, \cdots, {c_1}, {c_0}} \right]{\left[{{h_{n-1}}, \cdots, {h_1}, {h_0}} \right]^{\rm{T}}} = \\ \;\;\;\;\;{c_{n - 1}} \cdot {h_{n - 1}} + \cdots + {c_1} \cdot {h_1} + {c_0} \cdot {h_0} = 0. \end{array} $ | (9) |
线性分组码非零码字的最小重量为码字的最小距离dmin,码字C的码元cn-1, …, c1, c0至少有dmin个非零元素,式(9) 至少有dmin个非零项,所以校验矩阵H至少有dmin个列线性相关,dmin为校验矩阵H的稀疏度Spark.
定理2 差错图案E重构的必要条件是差错图案E的l0范数小于或等于纠错能力t.
证明 线性分组码的纠错能力t为
| $ t = {\rm{INT}}\left[{\frac{{{d_{\min }}-1}}{2}} \right], $ | (10) |
由于校验矩阵H的稀疏度Spark(H)与循环码码字的最小距离dmin相等,差错图案E的l0范数与校验矩阵H的稀疏度Spark(H)的关系如式(7) 所示,所以有
| $ {\left\| \mathit{\boldsymbol{E}} \right\|_0} \le t. $ | (11) |
能使式(11) 成立的差错图案E就是式(6) 最稀疏的解.
采用循环码的校验矩阵H作为测量矩阵,借助Matlab函数生成校验矩阵H,首先借助函数pol=cyclpoly(n, k)求出生成多项式g(x),然后借助函数H, G]=cyclgen(n, pol)生成校验矩阵H,(7,1)、(7,3) 和(7,4) 循环码的校验矩阵H如下:
| $ {\mathit{\boldsymbol{H}}_{71}} = \left[{\begin{array}{*{20}{l}} {1000001}\\ {0100001}\\ {0010001}\\ {0001001}\\ {0000101}\\ {0000011} \end{array}} \right], {\mathit{\boldsymbol{H}}_{73}} = \left[{\begin{array}{*{20}{l}} {1000110}\\ {0100011}\\ {0010111}\\ {0001101} \end{array}} \right], {\mathit{\boldsymbol{H}}_{74}} = \left[{\begin{array}{*{20}{l}} {1001110}\\ {0100111}\\ {0011101} \end{array}} \right]. $ | (12) |
当循环码的校验矩阵H作为测量矩阵时,可以求出(7,1) 循环码的校验矩阵H的稀疏度Spark为7,由式(7),计算其差错图案E的l0范数最大值为3,根据定理1,其码字的最小距离dmin=7,根据式(10),(7,1) 循环码的纠错能力t为3,所以式(11) 成立.同理可求得:(7,3) 循环码的校验矩阵H的稀疏度Spark为4,其差错图案E的l0范数最大值为1,(7,3) 循环码的纠错能力t为1,所以式(11) 成立;(7,4) 循环码的校验矩阵H的稀疏度Spark为3,其差错图案E的l0范数最大值为1,(7,4) 循环码的纠错能力t为1,所以式(11) 成立.
3 广义正交匹配追踪(gOMP)算法将广义正交匹配追踪(gOMP)算法[1-2]应用于差错图案E的重构,根据差错图案E的压缩感知模型,分析gOMP算法在重构差错图案E时的计算过程和译码效率.
3.1 gOMP算法重构差错图案E的计算过程 3.1.1 输入数据校验矩阵H作为测量矩阵,伴随式S作为测量信号y,差错图案E的稀疏度为K,最大原子选择个数为s.
3.1.2 计算过程1) 参数初始化:求测量矩阵的行数和列数,测量信号y作为初始化残差r0,索引集合Λ0为空集,按照索引集合Λ0选出的矩阵A0为空集,迭代次数l=1.
2) 计算残差rl=〈rl-1, aj〉, 1≤j≤N,并按降序排列,按从大到小的顺序选取s个残差,记录s个残差对应的矩阵A的列数j组成列序号集合J0.
3) 更新索引集合Λl=Λl-1∪J0和索引集合Λl选出的矩阵Al=Al-1∪aj(j∈J0).
4) 计算y=Al·θl的最小二乘解,计算稀疏信号的估值:
| $ {\hat \theta _1} = \arg \mathop {\min }\limits_{{\theta _l}} \left\| {y - {\mathit{\boldsymbol{A}}_l}{\theta _l}} \right\| = {\left( {{\mathit{\boldsymbol{A}}_l}{\;^{\rm{T}}}{\mathit{\boldsymbol{A}}_l}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}_l}^{\rm{T}}y. $ |
5) 更新残差
6) 判断残差rl的值是否小于预设的条件,若小于则跳出循环,或判断迭代次数l+1后是否大于稀疏度K,若大于则结束循环.
3.1.3 输出稀疏信号的估值gOMP算法通过增加原子选择的个数s,提高对稀疏信号的重构效率,在文献[1-2]中,对gOMP、OMP、ROMP、CoSaMP、StOMP算法的重构效率进行了比较,显示gOMP算法对稀疏信号重构具有优越性.
3.2 差错图案E重构以(15,7) 循环码为例,采用gOMP算法重构差错图案E.(15,7) 循环码的校验矩阵H如式(13) 所示.根据收码R和校验矩阵H,计算伴随式S=R·HT,把伴随式S作为测量信号,校验矩阵H作为测量矩阵,通过gOMP算法,重构(15,7) 循环码的差错图案E,如表 1所示.差错图案E也可以通过求解欠定线性方程组S=E·HT得到,求解(15,7) 循环码的差错图案E的线性方程组如式(13) 所示,若(15,7) 循环码的纠错位数取1,将重量为0或1的差错图案E代入线性方程组式(13),求出伴随式S,列出标准阵列译码表,与表 1比较,可以验证gOMP算法重构的差错图案E是正确的.同理,也可以采用gOMP算法正确重构(7,1)、(7,3)、(7,4) 和(31,21) 循环码的差错图案E.
| $ \begin{array}{l} {H_{157}} = \left[{\begin{array}{*{20}{l}} 1&0&0&0&0&0&0&0&1&1&0&1&0&0&0\\ 0&1&0&0&0&0&0&0&0&1&1&0&1&0&0\\ 0&0&1&0&0&0&0&0&0&0&1&1&0&1&0\\ 0&0&0&1&0&0&0&0&0&0&0&1&1&0&1\\ 0&0&0&0&1&0&0&0&1&1&0&1&1&1&0\\ 0&0&0&0&0&1&0&0&0&1&1&0&1&1&1\\ 0&0&0&0&0&0&1&0&1&1&1&0&0&1&1\\ 0&0&0&0&0&0&0&1&1&0&1&0&0&0&1 \end{array}} \right].\\ \;\;\;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{l}} {{s_7} = {e_{14}} + {e_6} + {e_5} + {e_3}, }\\ {{s_6} = {e_{13}} + {e_5} + {e_4} + {e_2}, }\\ {{s_5} = {e_{12}} + {e_4} + {e_3} + {e_1}, }\\ {{s_4} = {e_{11}} + {e_3} + {e_2} + {e_0}, }\\ {{s_3} = {e_{10}} + {e_6} + {e_5} + {e_3} + {e_2} + {e_1}, }\\ {{s_2} = {e_9} + {e_5} + {e_4} + {e_2} + {e_1} + {e_0}, }\\ {{s_1} = {e_8} + {e_6} + {e_5} + {e_4} + {e_1} + {e_0}, }\\ {{s_0} = {e_7} + {e_6} + {e_4} + {e_0}.} \end{array}} \right. \end{array} $ | (13) |
| 表 1 gOMP算法重构(15,7) 循环码的差错图案E的结果 Table 1 gOMP algorithm reconstructing the(15, 7) cyclic code error pattern E results |
采用gOMP算法,实现(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码的纠错,分别采用各自的校验矩阵H作为测量矩阵,分析gOMP算法对循环码的纠错能力以及gOMP算法中原子选择的个数s对循环码纠错位数的影响.
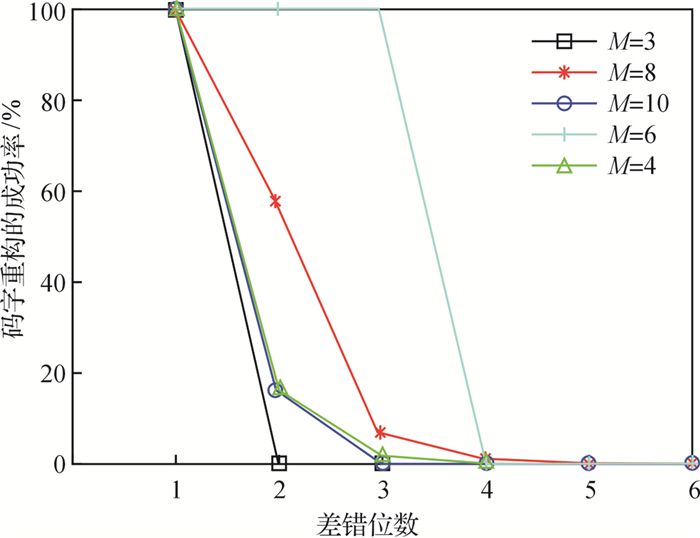
4.1 gOMP算法的循环码纠错能力以(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码为例,测试gOMP算法对循环码的纠错能力,把差错位数从0逐渐增加,能被100%重构的收码的最大差错位数为其纠错能力t,因为测量信号长度M=n-k是伴随式S的长度,采用校验矩阵H作为测量矩阵,伴随式S作为测量信号,差错位数为差错图案E中1的个数.实验结果如图 1所示,可以看出goMP算法对差错位数为3的(7,1) 循环码的纠错能力为100%,对差错位数为1的(7,3)、(7,4)、(15,7) 和(31,21) 循环码的纠错能力为100%.同时可看出gOMP算法对(7,3)、(15,7) 和(31,21) 循环码中差错位数为2和3的收码也有一定的纠错能力.对差错位数为2的(15, 7) 循环码的纠错能力为60%.(7,3) 和(31,21) 循环码的纠错能力近似相同.
|
图 1 测量信号长度M对循环码纠错能力的影响 Fig. 1 Comparison of the error correcting capability of the cyclic code by different measuring signal length M |
在每次迭代时,gOMP算法计算传感矩阵A各列与残差的内积,并按照降序排列,依次选择s个最大的残差来更新索引集合,提高了gOMP算法的重构效率.以(7,1) 循环码为例,选择s=2,3,4,测试gOMP算法对(7,1) 循环码的纠错能力,如图 2所示,可以看出s=2时,能纠正3位错误,s=3时,能纠正2位错误,s=4时,能纠正1位错误,所以原子个数s=2为最佳选择,能够实现(7,1) 循环码的纠错能力为3.同理,可以验证:(7,4) 循环码在s=3时,对差错位数为1的收码重构的成功率为100%.(7,3) 循环码在s=1,2,3,4时,对差错位数为1的收码重构的成功率为100%,当s=4时,对差错位数为2的收码的纠错能力为30%.(15,7) 循环码在s=1,2,3,4时,对差错位数为1的收码重构的成功率为100%,当s=3时,对差错位数为2的收码的纠错能力为80%.(31,21) 循环码在s=1,2,3,4时,对差错位数为1的收码重构的成功率为100%,当s=1时,对差错位数为2的收码的纠错能力为35%.

|
图 2 原子选择个数s对(7,1) 循环码纠错能力的影响(M=6,N=7) Fig. 2 Comparison of the error correction capability of the (7, 1) cyclic codes by different selecting atoms number s(M=6, N=7) |
按照如图 3所示的线性分组码的译码步骤设计仿真实验[3],首先产生N个信息元组m,信息元组m与生成矩阵G相乘生成码字C,对码字C进行2PSK调制,已调信号通过高斯白噪声信道AWGN,信噪比SNR取值范围为0~12 dB,在每个信噪比SNR点,选取N=50 000个m信息分组.在接收端,对接收信号进行2PSK解调,得到收码R,借助校验矩阵H计算伴随式S.将伴随式S作为测量信号,校验矩阵H作为测量矩阵,通过广义正交匹配追踪gOMP算法,重构差错图案E,重构的差错图案E与收码R进行模2加运算,计算码字C的估值.

|
图 3 线性分组码的编译码过程 Fig. 3 Encoding and decoding process of the linear block codes |
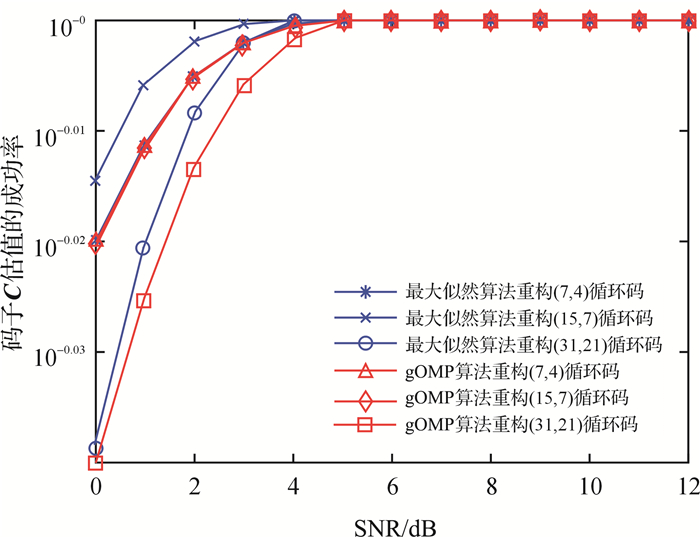
借助Matlab软件编写程序,实现gOMP算法和最大似然译码算法对循环码译码的仿真实验,本文以(7,4)、(15,7) 和(31,21) 循环码为例,从译码的误码率和码字C重构的成功率两方面比较gOMP算法和最大似然译码算法的译码效果[16],译码的误码率如图 4所示,码字C重构的成功率如图 5所示.

|
图 4 循环码译码的误码率比较 Fig. 4 Comparison of the bit error rate(BER) of decoding the cyclic code |
|
图 5 循环码译码的码字C估值成功率比较 Fig. 5 Comparison of the code word C estimating success rate of the decoding of the cyclic code |
从图 4中可以看出,在同一个译码算法中,(15,7) 循环码译码的误码率最低.当信噪比SNR相同时,最大似然算法译(15,7) 循环码的误码率最低,当信噪比SNR为5.2 dB时,其误码率低于10-5.gOMP算法译(31,21) 循环码的误码率最高,当信噪比SNR为7.6 dB时,其误码率低于10-5.采用最大似然算法和gOMP算法译(7,4) 循环码的误码率近似相同,当信噪比SNR为6.6 dB时,其误码率低于10-5.gOMP算法译(15,7) 与(7, 4) 循环码的误码率近似,当信噪比SNR为6.6 dB时,其误码率低于10-5.从图 5中可以看出,最大似然算法译(15,7) 循环码的码字C重构的成功率最高,在信噪比SNR为5.8 dB时,码字C重构的成功率趋于100%.采用最大似然算法和gOMP算法译(7,4) 循环码的码字C重构成功率近似,当信噪比SNR为7.2 dB时,码字C重构的成功率趋于100%.gOMP算法译(15,7) 与(7,4) 循环码码字C重构成功率近似,当信噪比SNR为7.2 dB时,码字C重构的成功率趋于100%.当信噪比相同时,gOMP算法译(31,21) 循环码的码字C重构成功率低于最大似然算法;当信噪比SNR为6.6 dB时,最大似然算法重构(31,21) 循环码的成功率趋于100%;当信噪比SNR为8 dB时,gOMP算法重构(31,21) 循环码的成功率趋于100%.gOMP算法和最大似然算法重构(7,4)、(15,7) 和(31,21) 循环码的差错率和成功率如表 2所示.
| 表 2 循环码重构的差错率和成功率 Table 2 The bit error rate and the success rate of the decoding of the cyclic code |
通过分析仿真实验结果得到:采用gOMP算法能够实现(7,4)、(15,7) 和(31,21) 循环码的译码.与最大似然译码算法相比,在循环码译码的成功率趋于100%的条件下,gOMP算法译码时的信噪比SNR比最大似然算法大1.4 dB.但gOMP算法是根据伴随式S和校验矩阵H重构差错图案E的,从而计算出码字C的估值,不需要查找标准阵列译码表,即可实现对(7,4)、(15,7) 和(31,21) 循环码的译码.
6 结语借助无噪声干扰压缩感知的观测模型,提出了求解差错图案E的线性规划模型和压缩感知模型.采用gOMP算法实现(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码的译码,提出了校验矩阵H作为测量矩阵的构成形式和2个定理.采用伴随式S作为测量信号,通过gOMP算法重构差错图案E,对E与收码R进行模2加运算,计算发码C的估值.借助(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码,分析了gOMP算法对循环码的纠错能力及gOMP算法中原子选取个数s与纠错位数的关系.通过译码的误码率和码字C重构的成功率,比较分析了gOMP算法和最大似然译码算法对(7,4)、(15,7) 和(31,21) 循环码的译码效果.实验结果表明:采用gOMP算法能够实现对(7,1)、(7,3)、(7,4)、(15,7) 和(31,21) 循环码的译码.
| [1] | JIAN W, SEOKBEOP K, BYONGHYO S. Generalized orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6202–6216. DOI:10.1109/TSP.2012.2218810 |
| [2] | WANG J, KWON S, LI P, et al. Recovery of sparse signals via generalized orthogonal matching pursuit:A new analysis[J]. IEEE Transactions on Signal Processing, 2016, 64(4): 1076–1089. DOI:10.1109/TSP.2015.2498132 |
| [3] |
曹雪虹, 张宗橙.
信息论与编码[M]. 2. 北京: 清华大学出版社, 2009.
CAO X H, ZHANG Z C. Information Theory and Coding[M]. 2. Beijing: Tsinghua University Press, 2009. |
| [4] | CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. DOI:10.1109/TIT.2005.862083 |
| [5] | DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [6] | DASKALAKIS C, DIMAKIS A G, KARP R M, et al. Probabilistic analysis of linear programming decoding[J]. IEEE Transactions on Information Theory, 2008, 54(8): 3565–3578. DOI:10.1109/TIT.2008.926452 |
| [7] | DIMAKIS A G, VONTOBEL P O. LP decoding meets LP decoding:A connection between channel coding and compressed sensing[C]//Forty-Seventh Annual Allerton Conference.Illinois:IEEI, 2009:8-15. |
| [8] |
李耀辉, 赵海豹, 马春芽. 循环码译码的Dixon结式方法[J].
应用数学学报, 2011, 34(4): 602–617.
LI Y H, ZHAO H B, MA C Y. Decoding cyclic codes by using Dixon resultant method[J]. Acta Mathematicae Applicatae Sinica, 2011, 34(4): 602–617. |
| [9] | AUGOT D, BARDET M, FAUGÈRE J C. On the decoding of binary cyclic codes with the Newton identities[J]. Journal of Symbolic Computation, 2009, 44(12): 1608–1625. DOI:10.1016/j.jsc.2008.02.006 |
| [10] | LOUSTAUNAU P, YORK E V. On the decoding of cyclic codes using Gr bner bases[J]. Applicable Algebra in Engineering Communication & Computing, 1997, 8(6): 469–483. |
| [11] | ELAD M. Sparse and Redundant Representations:From Theory to Applications in Signal and Image Processing[M]. New York: Springer Publishing Company, 2010: 26-30. |
| [12] | LIN L, LIU F, JIAO L. Compressed sensing by collaborative reconstruction on over complete dictionary[J]. Signal Processing, 2014, 103: 92–102. DOI:10.1016/j.sigpro.2013.11.039 |
| [13] |
董小亮, 杨良龙, 赵生妹, 等. 用信道编码构造压缩感知测量矩阵[J].
信号处理, 2013, 29(7): 809–815.
DONG X L, YANG L L, ZHAO S M, et al. Channel coding for compressed sensing measurement matrix[J]. Journal of Signal Processing, 2013, 29(7): 809–815. |
| [14] |
芦存博, 肖嵩, 权磊. 基于二进制序列族的压缩感知测量矩阵构造[J].
电子与信息学报, 2016, 38(7): 1682–1688.
LU C B, XIAO S, QUAN L. Construction of compressed sensing measurement matrix based on binary sequence family[J]. Introduction of Journal of Electronics & Information Technology, 2016, 38(7): 1682–1688. |
| [15] |
张景雄, 阳柯, 郭建中. 压缩感知的信息论解译[J].
武汉大学学报:信息科学版, 2014, 39(11): 1261–1268.
ZHANG J X, YANG K, GUO J Z. Information-theoretic interpretations of compressive sampling[J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1261–1268. |
| [16] |
张轶, 达新宇, 褚振勇. 低密度奇偶校验码的压缩感知重构[J].
吉林大学学报:工学版, 2015, 45(3): 985–990.
ZHANG Y, DA X Y, CHU Z Y. Compressed sensing reconstruction of LDPC code[J]. Journal of Jilin University:Engineering and Technology Edition, 2015, 45(3): 985–990. |


