2. College of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China
2. 兰州财经大学 信息工程学院, 甘肃 兰州 730020
The graph coloring has a widely applications in many subject. We only consider simple, finite and undirected graph in this paper.
Let G be a graph with maximum degree Δ(G), k be a positive integer. Suppose f is an edge coloring (i.e., f is an assignment of k colors 1, 2, …, k to the edges of G). For each element z∈E(G), the color of z under f is denoted by f(z). For every vertex x, the set of colors of edges incident with x is denoted by Sf(x) (or simply S(x) if no confusion arise), and is called the color set of x under edge coloring f. If f is proper (i.e., any two adjacent edges receive the different colors) and S(u)≠S(v) for each edge uv∈E(G), then f is called a k-adjacent vertex distinguishing proper edge coloring of G(or a k-AVDPEC). The minimum number of colors required in an AVDPEC of G is called the adjacent vertex distinguishing proper edge chromatic number of G, denoted by χ′a(G), i.e.,
| $ {{{{\chi }'}}_{a}}\left( G \right)=\text{min}\{k|G~\text{has}\ \text{a}\ k-\text{AVDPEC}\}. $ |
Suppose g is a total coloring (i.e., g is an assignment of k colors 1, 2, …, k to the vertices and edges of G). For each element z∈V(G)∪E(G), the color of z under g is denoted by g(z). For every vertex x∈V(G), the set of colors of edges incident with x together with the color assigned to x is denoted by Cg(x) (or simply C(x) if no confusion arise), and is called the color set of x under total coloring g. If g is proper (i.e., any two adjacent or incident elements receive the different colors) and C(u)≠C(v) for each edge uv∈E(G), then g is called a k-adjacent vertex distinguishing total coloring of G(or a k-AVDTC). The minimum number of colors required in an AVDTC of G is called the adjacent vertex distinguishing total chromatic number of G, denoted by χ″a(G), i.e.,
| $ {{{{\chi }''}}_{a}}\left( G \right)=\text{min}\{k|G~\text{has}\ \text{a}\ ~k-\text{AVDTC}\}. $ |
The adjacent vertex distinguishing proper edge coloring of graphs is investigated in several papers[1-6]. The adjacent vertex distinguishing total coloring of graphs is proposed in [7] and studied in several papers[7-16]. Especially, the adjacent vertex distinguishing total chromatic number of PmKn is obtained in [11] and the adjacent vertex distinguishing total chromatic numbers of the Cartesian products of Pm with Pn and Cn, and the Cartesian product of Cm with Cn are given in [13]. We use the usual notation as can be found in any book on graph theory[17].
1 PreliminariesLemma 1[6-7] Let G be a simple connected graph with order at least 3. If there are two adjacent vertices of maximum degree in G, then χ′a(G)≥Δ(G)+1 and χ″a(G)≥Δ(G)+2.
Lemma 2[18] χ″=(Cm□Cn)=5(m, n≥3).
From lemma 2, we can obtain the following lemma 3 immediately since an r-regular graph G has (equitable) total chromatic number r+1 if and only if G has adjacent vertex distinguishing proper edge chromatic number r+1.
Lemma 3 χ′a(Cm□Cn)=5(m, n≥3).
Lemma 4[13] (ⅰ)
(ⅱ) χ″a(Cm□Cn)=6, m, n≥3.
Suppose G is a graph. If a bijection σ from V(G) to V(G) preserves the adjacency relation, i.e., σ(u) is adjacent to σ(v) if and only if u is adjacent to v for any two distinct vertices u and v of G, then σ is called an automorphism of graph G.
If G has an automorphism σ, such that for any vertex v∈V(G), v and σ(v) are adjacent (and then v≠σ(v)), then we say that graph G is of property (P).
The Cartesian product of two graphs G and H, denoted by G□H, is a graph with vertex set V(G)×V(H) and edge set {(u, v)(u′, v′)|uu′∈E(G), v=v′or u=u′, vv′∈E(H)}.
Let Qt denote t-cube, i.e.,
| $ {{Q}_{t}}=\underbrace{{{K}_{2}}\square {{K}_{2}}\square \cdots \square {{K}_{2}}}_{t}. $ |
For two types of adjacent vertex distinguishing colorings of the Cartesian product of a graph with another graph which is of property (P), we will give some important results in section 2 and section 3.
2 The relation between AVDPEC andCartesian product of two graphsTheorem 1 Suppose G is a graph without isolated edge and G has property (P), t is a positive integer.
(ⅰ) χ′a(G□K2)≤χ′a(G)+1;
(ⅱ) χ′a(G□Qt)≤χ′a(G)+t, i.e.,
χ′a(G□
(ⅲ) If χ′a(G)=Δ(G)+1, then χ′a(G□K2)=Δ(G)+2;
(ⅳ) If χ′a(G)=Δ(G)+1, then χ′a(G□Qt)=Δ(G)+t+1;
(ⅴ) χ′a(Qt)=t+1, t≥3.
Proof (ⅰ) Since G has property (P), we may suppose that σ is an automorphism of G such that σ(v) is adjacent to v for each vertex v of G. Set V(G)={u1, u2, …, un}, G(1) and G(2) are two disjoint graphs which are isomorphic to G, and V(G(i))={u1(i), u2(i), …, un(i)}, i=1, 2. uj(i) and uk(i) are adjacent in G(i) if and only if uj and uk are adjacent in G, i=1, 2. We construct a graph (which is isomorphic to) G□K2 from G(1)∪G(2) by adding n new edges uj(1)uj(2), j=1, 2, …, n. Setting s=χ′a(G), f is an AVDPEC of G using s colors 1, 2, …, s. Now, we use colors 1, 2, …, s, s+1 to properly color edges of graph G□K2, where the edges of G(1) are colored in the same way as G, i.e., for any edge ujuk∈E(G), we assign color f(ujuk) to edge uj(1)uk(1) of G(1), each edge uj(2)uk(2) of G(2) is colored with the color of edge σ(uj)σ(uk) under f, j, k=1, 2, …, n; We assign color s+1 to all edges uj(1)uj(2), j=1, 2, …, n. The resulting (s+1)-proper edge coloring of G□K2 is denoted by
Obviously, for each j∈{1, 2, …, n}, we have
Theorem 1 (ⅰ) follows.
(ⅱ) Since for any positive integer l, G□Ql is of property (P) when G is of property (P), we can obtain (ⅱ) by applying (ⅰ) repeatedly.
(ⅲ) By theorem 1(ⅰ), χ′a(G□K2)≤Δ(G)+2. On the other hand, G□K2 has adjacent vertices of maximum degree and Δ(G□K2)=Δ(G)+1, so χ′a(G□K2)≥Δ(G)+2 by lemma 1. Therefore, χ′a(G□K2)=Δ(G)+2.
(ⅳ) We can obtain (ⅳ) by using (ⅲ) repeatedly.
(ⅴ) Note that χ′a(Q3)=4=Δ(Q3)+1 (see fig. 1) and Qt=Q3
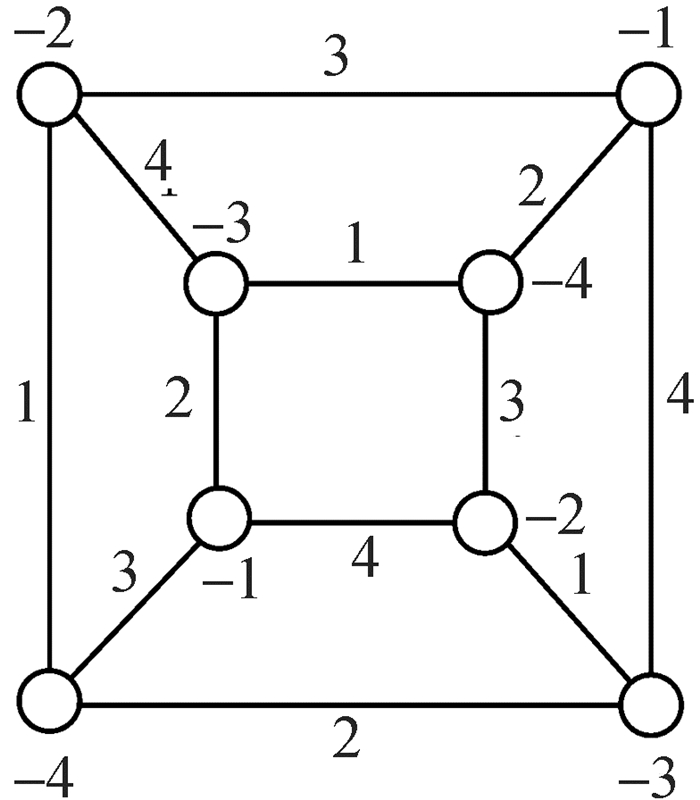
|
Fig. 1 AVDPEC of Q3 |
Lemma 5 For any graph G, G□K2 has property (P).
Proof We use the notations in the proof procedure of theorem 1 (ⅰ). We easily obtain an automorphism σ of G□K2: uj(1)uj(2), uj(2)uj(1), j=1, 2, …, n. Since σ(uj(i)) and uj(i) are adjacent in G□K2, i=1, 2, j=1, 2, …, n, G□K2 has property (P).
From theorem 1 and lemma 5, we may obtain the following corollary 1.
Corollary 1 For any graph G with no isolated edge and integer t(≥1), we have
(ⅰ) χ′a(G□
(ⅱ) If χ′a(G□K2)=Δ(G□K2)+1, then χ′a(G□Qt)=χ′a(G□K2)+t-1.
Note that for any graph G and integer number r(≥3), G□Cr has property (P), so we have the following corollary 2 by theorem 1.
Corollary 2 (ⅰ) χ′a(G□Cr□Qt)≤χ′a(G□Cr)+t;
(ⅱ) If χ′a(G□Cr)=Δ(G□Cr)+1, then χ′a(G□Cr□Qt)=χ′a(G□Cr)+t.
Theorem 2 Suppose that graph G has property (P) and has no isolated edge, r(≥4) is an even integer.
(ⅰ) χ′a(G□Cr)≤χ′a(G)+2;
(ⅱ) If χ′a(G)=Δ(G)+1, then χ′a(G□Cr)=Δ(G)+3.
Proof (ⅰ) Set Cr=v1v2…vrv1, V(G)={u1, u2…, un}. Let G(i) be a graph (which is isomorphic to G) induced by {(u, vi)|u∈V(G)}. If we denote (uj, vi) by uj(i), then V(G(i))={u1(i), u2(i), …, un(i)}, i=1, 2, …, r. Setting s=χ′a(G), f is an AVDPEC of G using s colors, 1, 2, …, s.
We will give an edge coloring of G□Cr using s+2 colors as follows:
We assign the color f(ujuk) to the edge uj(i)uk(i) when i is even; Each edge uj(i)uk(i) of G(i) is colored by the color of edge σ(uj)σ(uk) under f when i is odd; We assign color s+1 to all edges uj(i)uj(i+1) when i is odd; We assign color s+2 to all edges uj(i)uj(i+1) when i is even. Note uj(r+1)=uj(1). So, when i is odd, for any two adjacent vertices uj(i) and uk(i) in G(i), their color sets are S(uj)∪{s+1, s+2} and S(uk)∪{s+1, s+2}, respectively. Obviously, they are different; When i is even, for any two adjacent vertices uj(i) and uk(i) in G(i), their color sets are S(σ(uj))∪{s+1, s+2} and S(σ(uk))∪{s+1, s+2}, respectively. Obviously, they are different. The color sets of uj(i) and uj(i+1) are either S(uj)∪{s+1, s+2} and S(σ(uj))∪{s+1, s+2} or S(σ(uj))∪{s+1, s+2} and S(uj)∪{s+1, s+2}, respectively. Thus uj(i) and uj(i+1) are distinguished (since uj and σ(uj) are distinguished under f).
(ⅱ) By theorem 2(ⅰ), χ′a(G□Cr)≤χ′a(G)+2=Δ(G)+3. Since Δ(G□Cr)=Δ(G)+2 and G□Cr has adjacent vertices of maximum degree, χ′a(G□Cr)≥Δ(G)+3 by lemma 1. Thus χ′a(G□Cr)=Δ(G)+3.
From theorem 2, we will obtain the following corollary 3 immediately.
Corollary 3 Suppose that G is of property (P) and has no isolated edge, r1, r2, …, rs are even integers at least 4.
(ⅰ) χ′a(G□Cr1□Cr2□…□Crs)≤χ′a(G)+2s;
(ⅱ) If χ′a(G)=Δ(G)+1, then χ′a(G□Cr1□Cr2□…□Crs)=Δ(G)+2s+1.
Note that for any integers m, n≥3, we have χ′a(Cm□Cn)=5=Δ(Cm□Cn)+1. By lemma 3, we may obtain the following corollary 4 from theorem 2.
Corollary 4 If m, n, r1, r2, …, rs be integers at least 3, and each of r1, r2, …, rs is even, then χ′a(Cm□Cn□Cr1□Cr2□…□Crs)=2s+5, especially χ′a(Cm□Cn□Cr1)=7.
Theorem 3 If G has three AVDPEC's using χ′a(G) colors, such that for each vertex v∈V(G), the color sets of v are different under the three colorings, then χ′a(G□Cr)≤χ′a(G)+3.
Proof Similar to the proof of theorem 2(ⅰ), we can complete the proof of theorem 3.
3 The relation between AVDTC andCartesian product of two graphsTheorem 4 Suppose G is of property (P), and t is a positive integer.
(ⅰ) χ″a(G□K2)≤χ″a(G)+1;
(ⅱ) χ″a(G□
(ⅲ) If χ″a(G)=Δ(G)+2, then χ″a(G□K2)=Δ(G)+3;
(ⅳ) If χ″a(G)=Δ(G)+2, then χ″a(G□Qt)=Δ(G)+t+2.
(ⅴ) χ″a(Qt)=t+2.
Proof (ⅰ) We use the notations in the proof of theorem 4 (ⅰ). Set s=χ″a(G), g is an AVDTC of G using s colors 1, 2, …, s. Now, we use colors 1, 2, …, s, s+1 to properly color vertices and edges of graph G□K2, so that the vertices and edges of G(1) are colored in the same way as G, i.e., for any vertex uj∈V(G) and edge ujuk∈E(G), we assign color g(uj) to vertex uj(1) of G(1) and g(ujuk) to edge uj(1)uk(1) of G(1); Each vertex uj(2) of G (2) is colored with the color of vertex σ(uj) under g, each edge uj(2)uk(2) of G(2) is colored with the color of edge σ(uj)σ(uk) under g, j, k=1, 2, …, n; We assign color s+1 to all edges uj(1)uj(2), j=1, 2, …, n. The resulting (s+1)-proper total coloring of G□K2 is denoted by
Obviously, for each j∈{1, 2, …, n}, we have
The theorem 4(ⅰ) follows.
(ⅱ) Since for any positive integer l, G□Ql is of property (P) when G is of property (P), we can obtain theorem 4(ⅱ) by applying theorem 4(ⅰ) repeatedly.
(ⅲ) By theorem 4(ⅰ), χ″a(G□K2)≤Δ(G)+2. On the other hand, G□K2 has adjacent vertices of maximum degree and Δ(G□K2)=Δ(G)+1, so χ″a(G□K2)≥Δ(G)+2 by lemma 1. Therefore, χ″a(G□K2)=Δ(G)+2.
(ⅳ) We can obtain theorem 4(ⅳ) by using theorem 4(ⅲ) repeatedly.
(ⅴ) Note that χ″a(K2)=χ″a(Q1)=3=Δ(Q1)+2, and Qt=Qt-1□K2=Qt-2□Q2, we have χ″a(Qt)=t+2 by theorem 4(ⅳ).
From theorem 4 and that G□K2 is of property (P), we obtain the following corollary 5.
Corollary 5 Suppose t(≥2) is an integer.
(ⅰ) χ″a(G□Qt)≤χ″a(G□K2)+t-1.
(ⅱ) If χ″a(G□K2)=Δ(G□K2)+2, then χ″a(G□Qt)=χ″a(G□K2)+t-1.
From theorem 4 and that G□Cr is of property (P), we obtain the following corollary 6.
Corollary 6 (ⅰ) χ″a(G□Cr□Qt)≤χ″a(G□Cr)+t;
(ⅱ) If χ″a(G□Cr)=Δ(G□Cr)+2, then χ″a(G□Cr□Qt)=χ″a(G□Cr)+t.
Theorem 5 Suppose that G is of property (P), r(≥4) is even.
(ⅰ) χ″a(G□Cr)≤χ″a(G)+2;
(ⅱ) If χ″a(G)=Δ(G)+2, then χ″a(G□Cr)=Δ(G)+4.
Proof Similar to the proof of theorem 2, we can complete the proof of theorem 5. The process is easy, so we omitted it.
By generalizing theorem 5, we have
Corollary 7 Suppose G is of property (P) and r1, r2, …, rs(≥4) are even.
(ⅰ) χ″a(G□Cr1□Cr2□…□Crs)≤χ″a(G)+2s;
(ⅱ) If χ″a(G)=Δ(G)+2, then χ″a(G□Cr1□Cr2□…□Crs)=Δ(G)+2s+2.
From lemma 4, theorem 4(ⅳ) and corollary 7(ⅱ), we may deduce the following corollary 8.
Corollary 8 If m≥3, n≥3, t≥1, r1, r2, …, rs(≥4) are even, then
(ⅰ) χ″a(P2□Cn□Qt)=t+5;
(ⅱ) χ″a(P2□Cn□Cr1□Cr2□…□Crs)=2s+5;
(ⅲ) χ″a(Pm□Cn□Qt)=t+6;
(ⅳ) χ″a(Pm□Cn□Cr1□Cr2□…□Crs)=2s+6;
(ⅴ) χ″a(Cm□Cn□Qt)=t+6;
(vi) χ″a(Cm□Cn□Cr1□Cr2□…□Crs)=2s+6.
Theorem 6 If G has three AVDTC's using χ″a(G) colors, such that for each vertex v∈V(G), the color sets of v under the three colorings are different, and the colors of v under the three colorings are different, then χ″a(G□Cr)≤χ″a(G)+3.
Proof Similar to the proof of theorem 5(ⅰ) or theorem 2(ⅰ), we can complete the proof of theorem 6.
| [1] | BALISTER P N, GYÖRI E, LEHEL J, et al. Adjacent vertex distinguishing edge-colorings[J]. SIAM J Discrete Math, 2007, 21(1): 237–250. DOI:10.1137/S0895480102414107 |
| [2] | BARIL J L, KHEDDOUCI H, TOGNI O. Adjacent vertex distinguishing edge colorings of meshes[J]. Australasian Journal of Combinatorics, 2006, 35: 89–102. |
| [3] | GREENHILL C, RUCIИSKI A. Neighbour distinguishing edge colorings of random regular graphs[J]. The Electronic Journal of Combinatorics, 2006, 13(#R77): 1–12. |
| [4] | HATAMI H. Δ+300 is a bound on the adjacent vertex distinguishing edge chromatic number[J]. Journal of Combinatorial Theory:Series B, 2005, 95: 246–256. DOI:10.1016/j.jctb.2005.04.002 |
| [5] | EDWARDS K, HOR AЙÁK M, WO AŹG NIAK M. On the neighbour distinguishing index of a graph[J]. Graphs and Combinatorics, 2006, 22: 341–350. DOI:10.1007/s00373-006-0671-2 |
| [6] | ZHANG Z F, LIU L Z, WANG J F. Adjacent strong edge coloring of graphs[J]. Appl Math Lett, 2002, 15: 623–626. DOI:10.1016/S0893-9659(02)80015-5 |
| [7] | ZANG Z F, CHEN X E, LI J W, et al. On adjacent vertex distinguishing total coloring of graphs[J]. Science in China (Ser A):Mathematics, 2005, 48(3): 289–299. DOI:10.1360/03YS0207 |
| [8] | CHEN X E. Adjacent-vertex-distinguishing total chromatic numbers on K2n+1-E(P3)[J]. International Journal of Pure and Applied Mathematics, 2004, 13(1): 21–29. |
| [9] | CHEN X E. On the adjacent vertex distinguishing total coloring numbers of graphs with Δ=3[J]. Discrete Mathematics, 2008, 308: 4003–4007. DOI:10.1016/j.disc.2007.07.091 |
| [10] | CHEN X E, ZHANG Z F. AVDTC numbers of generalized Halin graphs with maximum degree at least 6[J]. Acta Mathematicae Applicatae Sinica:English Series, 2008, 24(1): 55–58. DOI:10.1007/s10255-005-5222-8 |
| [11] | CHEN X E, ZHANG Z F. Adjacent-vertex-distinguishing total chromatic numbers of Pm×Kn[J]. J Mathematical Research and Exposition, 2006, 26(3): 489–494. |
| [12] | CHEN X E, ZHANG Z F, SUN Y R. Adjacent-vertex-distinguishing total chromatic numbers on monocycle graphs and the square of cycles[J]. International Journal of Pure and Applied Mathematics, 2005, 18(4): 481–491. |
| [13] | CHEN X E, ZHANG Z F, SUN Y R. A note on adjacent-vertex-distinguishing total chromatic numbers for Pm×Pn, Pm×Cn and Cm×Cn[J]. J Mathematical Research and Exposition, 2008, 28(4): 789–798. |
| [14] | HULGAN J. Concise proofs for adjacent vertex distinguishing total colorings[J]. Discrete Mathematics, 2009, 309: 2548–2550. DOI:10.1016/j.disc.2008.06.002 |
| [15] | SUN Y L, SUN L. The (adjacent) vertex-distinguishing total coloring of the Mycielski graphs and the Cartesian product graphs[C]//7-th China-Japan Conference, Discrete Geometry, Combinatorics and Graph Theory. Heidelberg: Springer-Verlag, 2007: 200-205. |
| [16] | WANG H Y. On the adjacent vertex distinguishing total chromatic numbers of graphs with Δ=3[J]. J Comb Optim, 2007, 14: 87–109. DOI:10.1007/s10878-006-9038-0 |
| [17] | BONDY J A, MURTY U S R. Graph Theory with Applications[M]. New York: Elsevier Science Publishing Co. Inc., 1976. |
| [18] | TONG C L, LIN X H, YANG Y S, et al. Equitable total coloring of CmCn[J]. Discrete Applied Mathematics, 2009, 157: 596–601. DOI:10.1016/j.dam.2008.08.030 |


