2. 天津市南开区咸阳路小学, 天津 300110;
3. 吉林省教育学院 信息中心, 吉林 长春 130022
2. Xianyang Road Primary School, Nankai District, Tianjin 300110, China;
3. Information Center, Jilin Provincial Institute of Education, Changchun 130022, China
模糊系统是基于知识或规则的系统, 其核心为由若干条IF…THEN模糊规则所构成的知识库, 不仅能同时处理数据信息和语言信息, 而且可通过仿效人脑实现模糊推理并完善功能.但随着高维系统输入变量的增加,其规则总数通常呈指数增长, 极易出现规则爆炸现象, 甚至导致计算时间延长或计算机记忆溢出.1991年, RAJU等[1]首次提出针对高维模糊系统的递阶衔接系统,以降低规则总数, 但却带来系统内部结构复杂、辨识参数增多等缺陷.1998年, WANG[2]率先提出串联叠加分层方法, 但该方法对被逼近函数和分层后叠加模糊系统要求过高(可微).LIU等[3]指出,文献[2]中叠加系统附加了错误条件, 并对T-S模糊系统重新给出分层后输入输出表达式, 进而证明了系统分层前后输入输出表示的等价性, 从而降低了系统内部的模糊规则数.2004年, 文献[4]通过引入二叉树分层方法对T-S模糊系统实施重新分层, 并对该系统分层前后的等效性进行分析, 但未涉及模糊规则数降低问题.此后, 关于模糊系统的不同分层所产生的等效性和逼近性有了较多研究结果[5-7].
2012年, 文献[5]利用调控参数将Mamdani模糊系统和T-S模糊系统合并建立了混合模糊系统.文献[6]针对将中间变量直接作为模糊单元输出提出一种后件直联型分层方法, 该方法不仅减少了规则数和辨识参数, 而且可避免对中间变量的模糊推理,其缺点是逼近函数条件过高(要求可微).文献[7]基于后件直联型分层方法讨论了混合模糊系统的一类可积函数的逼近性.文献[8]研究了T-S模糊系统的前件模糊集最大交互数问题.这些结果不仅能有效应用于大规模系统的建模, 而且也降低了系统内部的规则总数, 以避免规则爆炸现象.
本文首先给出高维混合模糊系统对连续函数的逼近算法, 并分析规则数变化及其缩减情况; 其次, 通过实例给出三维混合模糊系统分层后对连续函数逼近的实现过程, 并利用t-假设检验方法验证分层混合模糊系统逼近的优越性.
1 分层混合模糊系统在多输入单输出模糊系统中, 单独模糊系统的逼近能力和规则数减少往往是有限的, 尤其当输入变量增加时导致规则总数猛增, 容易出现规则爆炸现象.因此, 将Mamdani和T-S模糊系统合并成一个整体以研究其逼近性.为此, 首先给出等距模糊剖分概念:
定义1 设输入论域X1=X2=…=Xn=[-1, 1].任意给定m∈N, 对每个xi轴上的闭区间[-1, 1]实施等距剖分:-1=ai(-m)<ai(-m+1)<…<0<…<ai(m-1)<aim=1, 分点aij=
依据文献[5], 若设y1, y2, …, yL-1是混合模糊系统分层后的中间变量, 调节参数η∈[0, 1], pi是第xi个坐标轴上的指标变量, i=0, 1, 2, …, n, {Bpi}是第xi轴上前件(输入)模糊集, m是给定剖分数,则分层混合模糊系统可逐层表示为
| $ \begin{array}{l} {{\bar y}_1} = \frac{{\sum\limits_{{p_1}, \cdots ,{p_{{n_1}}} = - m}^m {\left( {\prod\limits_{i = 1}^{{n_1}} {{B_{{p_i}}}\left( {{x_i}} \right)} } \right)} }}{{\sum\limits_{{p_1}, \cdots ,{p_{{n_1}}} = - m}^m {\left( {\prod\limits_{i = 1}^{{n_1}} {{B_{{p_i}}}\left( {{x_i}} \right)} } \right)} }}\left[ {\eta \left( {d_0^1 + \sum\limits_{i = 1}^{{n_1}} {d_i^1{x_i}} } \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {1 - \eta } \right){{\bar y}_{{p_1}{p_2} \cdots {p_{{n_1}}}}}} \right], \end{array} $ |
| $ \begin{array}{*{20}{l}} {{{\bar y}_j} = \frac{{\sum\limits_{{p_{{l_j} + 1}}, \cdots ,{p_{{l_j} + {n_j}}};{q_{j - 1}} = - m}^m {\left( {\prod\limits_{i = {l_j} + 1}^{{l_j} + {n_j}} {{B_{{p_i}}}\left( {{x_i}} \right){C_{{q_{j - 1}}}}\left( {{y_{j - 1}}} \right)} } \right)} }}{{\sum\limits_{{p_{{l_j} + 1}}, \cdots ,{p_{{l_j} + {n_j}}};{q_{j - 1}} = - m}^m {\left( {\prod\limits_{i = {l_j} + 1}^{{l_j} + {n_j}} {{B_{{p_i}}}\left( {{x_i}} \right){C_{{q_{j - 1}}}}\left( {{y_{j - 1}}} \right)} } \right)} }} \times }\\ {\left[ {\eta \left( {d_0^j + c_{{q_{j - 1}}}^j{{\bar y}_{j - 1}} + \sum\limits_{i = {l_j} + 1}^{{l_j} + {n_j}} {d_i^j{x_i}} } \right) + \left( {1 - \eta } \right){{\bar y}_{{p_{{l_j} + 1}} \cdots {p_{{l_j} + {n_j}}}}}} \right],} \end{array} $ | (1) |
其中j=2, 3, …, L; d0j, cqj-1j和diL均为分层后系统后件部分的调节参数, ȳplj+1,…,plj+nj为对应后件(输出)模糊集的中心, Cqj-1既是第j-1层后件模糊集, 又是第j层的前件模糊集.此外, n1是第1层输入变量个数, lj是第j层输入变量的下角标, nj是第j层输入变量的个数.
注1 显然, η=0时分层混合模糊系统退化为Mamdani模糊系统; η=1时退化为T-S模糊系统.因此, 不仅可随意调控参数η使其成为一些数学模型的特例, 还可将其有效应用于模糊控制器设计和系统建模.然而, 实际中被逼近函数通常是未知的,只知道一些通过仪器或实验得到的数据对.所以, 如何构造一个满足给定精度的模糊系统非常重要.通常设计模糊系统的方法有查表法、梯度下降法、最小二乘法和聚类法等多种.关键是分层后混合模糊系统是否还具有逼近性能,以及如何实现混合模糊系统对连续函数类的逼近.文献[5, 7]虽然已从理论上证明了该问题, 但并没有给出具体的逼近算法.
定理1[5] 设紧集论域K=[-1, 1]n, 若形如式(1) 的分层混合模糊系统被分为L层子系统, 其中间变量为y1, y2, …, yL.则∀ε>0及f∈C(K)存在剖分数m0∈N, 使m≥m0时, ‖yL-f‖<ε.
下面, 基于定义1和定理1给出高维混合模糊系统分层后对连续函数的逼近算法.
第1步 设连续函数f∈C(K), ∀x=(x1, x2, …, xn)∈K, 若对充分小的h>0, 令
| $ \begin{array}{l} {H_i}\left( f \right) = \mathop {\sup }\limits_{{x_1},{x_2}, \cdots ,{x_n},{x_i} + h \in \left[ { - 1,1} \right]} \left| {f\left( {{x_1}, \cdots ,{x_{i - 1}},{x_i} + h,} \right.} \right.\\ \left. {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;{x_{i + 1}}, \cdots ,{x_n}} \right) - f\left( {{x_1},{x_2}, \cdots ,{x_n}} \right)/h} \right|,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{D_H}\left( f \right) = \mathop {\max }\limits_{1 \le i \le n} {H_i}\left( f \right), \end{array} $ |
由此分别计算或估算Hi(S)和DH(f)的值.
第2步 按照文献[5]所给方法计算剖分数
第3步 在每个闭区间Xi=[-1, 1]上实施等距模糊剖分, 并定义前件模糊集Bi, j(x)(i=1, 2, …, n; j=0, ±1, ±2, …, ±m0)和后件模糊集Bi, j(y1), Bi, j(y2), …, 通常选取三角形或梯形模糊数即可.
第4步 对控制参数η∈[0, 1], 按文献[5]的迭代公式确定系统的若干调节参数d0j, cqj-1j和diL等.
第5步 通过Matlab编程实现高维混合模糊系统的输出, 并画仿真图形.
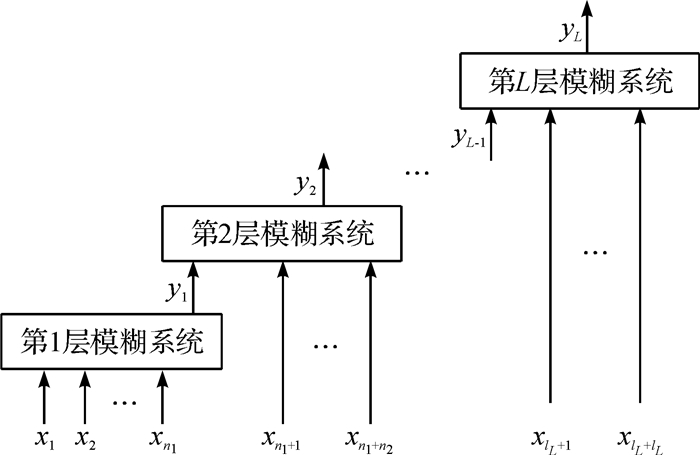
2 模糊规则缩减一般对高维模糊系统来说, 若不对输入变量进行分层, 则系统内部所有可能的规则总数将按维数n呈(2m+1)n指数形式迅猛增长(m是剖分数), 甚至会导致规则爆炸现象的发生.在此情况下, 通过对高维模糊系统的输入变量实施叠加分层输入以缩减规则数则十分必要,如图 1所示.
|
图 1 高维混合模糊系统分层后的输入变量 Fig. 1 Input variables of the layered high-dimensional fuzzy system |
从图 1的叠加分层易看出, 第1层可随机输入n1个变量x1, x2, …, xn1,得到输出y1, 再将输出y1作为第2层输入, 并输出y2.类似地,将第j层输入nj+1个变量xLj+1, xLj+2, …, xLj+nj, 中间变量yj-1是第j-1层的输出, 且满足
事实上, 文献[6-7]所给分层方法是将中间变量y2, y3, …, yL-1直接作用于模糊单元的输出, 中间变量不作为输入, 这也是与本文的主要区别.
命题1[5] 设m是论域X=[-1, 1]上的剖分数, 输入变量为(x1, x2, …, xn).若混合模糊系统(1) 被分成中间变量为y1, y2, …, yL-1的L-层子系统, 即第1层有n1个变量, 第j层有nj+1个输入变量, 且满足nj+1=n1, j=2, 3, …, L.则该混合模糊系统的规则总数为
从命题1不难看出,规则数由(2m+1)n缩减为
| 表 1 高维混合模糊系统输入变量的分层和不分层规则数变化情况 Table 1 Rule number changes of the layered or not layered rules of high-dimensional hybrid fuzzy system |
从表 1可明显看出分层方法不唯一.实际上, 首层输入n1值增大, 层数L变小, 但规则数会变大, 易引发规则爆炸; 相反, n1值减小, 层数L变多, 虽然规则数变小, 但因层数L增多会使系统内部结构变复杂.因此, 如何选择最优的数对(n1, L)至关重要!例如, 若取维数n=5, 剖分数m=16, 则不分层的规则总数为(2×16+1)5=39 135 393;而分层的规则总数为4(2×16+1)2=4 356.因此, 对于5维混合模糊系统,分层比不分层规则数约缩减8 984倍.
3 逼近性检验下面将通过一个模拟实例来说明高维混合模糊系统分层后逼近性的实现, 并借助统计学中的假设检验考证该系统的逼近性能.简单起见,仅在3维欧氏空间给出实例.
例1 针对上述分层混合模糊系统(1), 令n=3, n1=2, n2=1(3变量分2层), 最大交互数c0=2, 调控参数η=
| $ f\left( {{x_1},{x_2},{x_3}} \right) = {{\rm{e}}^{ - \frac{{\left( {x_1^2 + x_2^2 + x_3^2} \right)}}{{27}}}},\left| {{x_i}} \right| \le 1,\;\;\;i = 1,2,3. $ |
试按本文分层模糊系统(1) 给出逼近过程.
事实上, 有0<f(x1, x2, x3)≤1, 且函数f的左右偏导数均存在, 并有
| $ \frac{{\partial {f_ - }}}{{\partial {x_i}}} = \frac{{\partial {f_ + }}}{{\partial {x_i}}} = - \frac{2}{{27}}{x_i}f\left( {{x_1},{x_2},{x_3}} \right),\;\;\;\;i = 1,2,3. $ |
针对变量x1依据逼近算法第1步,得
| $ \begin{array}{l} \left| {\frac{{\partial f}}{{\partial {x_1}}}} \right| = \left| { - \frac{2}{{27}}{x_1}f\left( {{x_1},{x_2},{x_3}} \right)} \right| \le \frac{2}{{27}} \Rightarrow \\ \;\;\;\;\;{H_1}\left( f \right) = \mathop {\sup }\limits_{\left( {{x_1},{x_2},{x_3}} \right) \in {{\left[ { - 1,1} \right]}^3}} \left| {\frac{{\partial f}}{{\partial {x_1}}}} \right| = \frac{2}{{27}}. \end{array} $ |
类似地, 关于输入变量x2, x3,有
| $ {H_2}\left( f \right) = {H_3}\left( f \right) = \frac{2}{{27}}. $ |
故有 DH(f)=
依据逼近算法第2步, 对ε=0.1>0, 可计算m>
| $ {B_{1,0}}\left( {{x_1}} \right) = \left\{ \begin{array}{l} 1 - 9{x_1},\;\;\;\;0 \le {x_1} \le \frac{1}{9},\\ 1 + 9{x_1},\;\;\;\;\; - \frac{1}{9} \le {x_1} < 0,\\ 0,\;\;\;\;否则; \end{array} \right. $ |
| $ {B_{1, - 9}}\left( {{x_1}} \right) = \left\{ \begin{array}{l} - 8 - 9{x_1},\;\;\;\;\; - 1 \le {x_1} \le - \frac{8}{9},\\ 0,\;\;\;\;否则; \end{array} \right. $ |
| $ {B_{1,9}}\left( {{x_1}} \right) = \left\{ \begin{array}{l} - 8 + 9{x_1},\;\;\;\;\;\frac{8}{9} \le {x_1} \le 1,\\ 0,\;\;\;\;否则. \end{array} \right. $ |
现将模糊数B1, 0的隶属函数在[-1, 1]上逐次左(右)平移
同理, 若令B2, j(x2)=B1, j(x2), B3, j(x3)=B1, j(x3), j=0, ±1, ±2, …, ±9.则在x2, x3轴上也可获得模糊剖分{B2, j}和{B3, j}.此外, 在第1输出层选取后件模糊数的隶属度函数为
| $ \begin{array}{l} {C_q}\left( {{y_1}} \right) = \exp \left( { - \frac{1}{2}{{\left( {{y_1} - \frac{q}{9}} \right)}^2}} \right),q = 0, \pm 1,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; \pm 2, \cdots , \pm 8, \end{array} $ |
此时, 对调控参数η=
| $ {y_1} = \frac{{\sum\limits_{{j_1},{j_2} = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right)\left( {\frac{1}{3}d_0^1 + \frac{2}{3}{S_1}} \right)} }}{{\sum\limits_{{j_1},{j_2} = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right)} }}, $ |
| $ \begin{array}{l} {y_2} = \frac{{\sum\limits_{{j_1},{j_2},{j_3},q = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right){B_{3,{j_3}}}\left( {{x_3}} \right){C_q}\left( {{y_1}} \right)} }}{{\sum\limits_{{j_1},{j_2},{j_3},q = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right){B_{3,{j_3}}}\left( {{x_3}} \right){C_q}\left( {{y_1}} \right)} }} \times \\ \;\;\;\;\;\;\;\left( {\frac{1}{3}\left( {d_0^2 + \frac{1}{3}c_q^2d_0^1} \right) + \frac{2}{3}\left( {{S_2} + \frac{1}{3}c_q^2{S_1}} \right)} \right), \end{array} $ |
其中,
特别地, 经适当调节参数,若令cq2=1, d01=S1, d02=S2, 则有
| $ \begin{array}{l} \frac{1}{3}\left( {d_0^2 + \frac{1}{3}c_q^2d_0^1} \right) + \frac{2}{3}\left( {{S_2} + \frac{1}{3}c_q^2{S_1}} \right) = \\ \;\;\;\;\;\;{S_2} + \frac{1}{3}{S_1} = f\left( {\frac{{{j_1}}}{9},\frac{{{j_2}}}{9},\frac{{{j_3}}}{9}} \right) + \frac{1}{3}f\left( {\frac{{{j_1}}}{9},\frac{{{j_2}}}{9},0} \right). \end{array} $ |
此时, 第2层输出y2可进一步表示为
| $ \begin{array}{l} {y_2} = \frac{{\sum\limits_{{j_1},{j_2},{j_3},q = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right){B_{3,{j_3}}}\left( {{x_3}} \right){C_q}\left( {{y_1}} \right)} }}{{\sum\limits_{{j_1},{j_2},{j_3},q = - 9}^9 {{B_{1,{j_1}}}\left( {{x_1}} \right){B_{2,{j_2}}}\left( {{x_2}} \right){B_{3,{j_3}}}\left( {{x_3}} \right){C_q}\left( {{y_1}} \right)} }} \times \\ \;\;\;\;\;\;\;\left( {f\left( {\frac{{{j_1}}}{9},\frac{{{j_2}}}{9},\frac{{{j_3}}}{9}} \right) + \frac{1}{3}f\left( {\frac{{{j_1}}}{9},\frac{{{j_2}}}{9},0} \right)} \right). \end{array} $ |
对于调控参数η=

|
图 2 x3=0时函数f的曲面图 Fig. 2 Surface figure of f when x3=0 |

|
图 3 x3=0时分层混合模糊系统y2的曲面图 Fig. 3 Surface figure of layered hybrid system y2 when x3=0 |
|
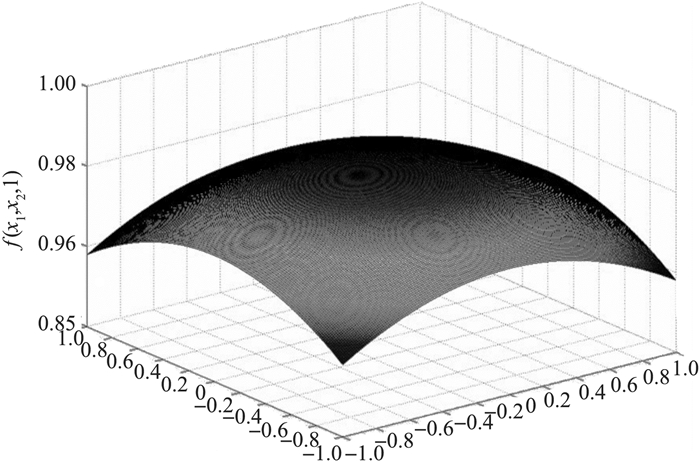
图 4 x3=0时Mamdani模糊系统的曲面图 Fig. 4 Surface figure of layered Mamdani system when x3=0 |
|
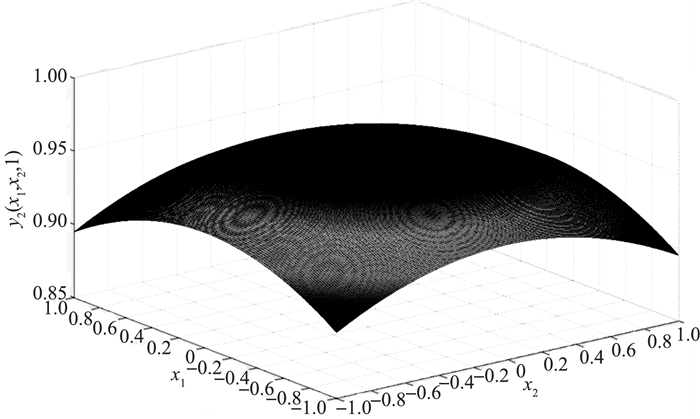
图 5 x3=0时T-S模糊系统的曲面图 Fig. 5 Surface figure of layered T-S system when x3=0 |
由图 2~5知,图 3更接近所给逼近函数f的值(见图 2), 亦即分层混合模糊系统具有更好的逼近性能.此外, 固定x3=0是为了在三维空间中画出各自分层模糊系统输出y2的图像.事实上, 模糊系统可以看作一个插值模型, 但它并不是一个简单的过程.这是因为现实中许多事物或现象其输入输出关系并不连续.因此, 研究模糊系统逼近对一般函数更具意义.
下面, 基于最后输出y2在论域[-1, 1]3上随机选取8个样本点, 并分别通过分层混合模糊系统、Mamdani模糊系统和T-S模糊系统比较其输出的误差, 详见表 2.
| 表 2 3类模糊系统在8个样本点处的输出和精度比较 Table 2 The comparison of the output and precision of three kinds of fuzzy system in eight sample points |
由统计推断中的t-假设检验可知,混合模糊系统均比Mamdani模糊系统和T-S模糊系统的逼近效果好.因此, 不妨设表 2数据D1(i)=Zi-Xi和D2(i)=Zi-Yi (i=1, 2, 3, …, 8) 均来自正态总体N(μD, σD2), 其中均值μD和方差σD2未知, 平均值Fλ和方差sDj(j=1, 2) 分别计算如下:
| $ \left\{ \begin{array}{l} {{\bar D}_1} = \frac{1}{8}\sum\limits_{i = 1}^8 {{D_1}\left( j \right)} = \frac{{0.078\;512\;1}}{8} \approx 0.009\;81,\\ {s_{{D_1}}} = \sqrt {\frac{1}{{8 - 1}}\sum\limits_{i = 1}^8 {{{\left( {{D_1}\left( i \right) - {{\bar D}_1}} \right)}^2}} } = \\ \;\;\;\;\;\;\;\;\sqrt {\frac{{0.001\;43}}{7}} \approx 0.014\;28, \end{array} \right. $ | (9) |
同理, 可得
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar D}_2} = \frac{1}{8}\sum\limits_{i = 1}^8 {{D_2}\left( i \right)} = \frac{{0.086\;02}}{8} \approx 0.010\;75,}\\ {{s_{{D_2}}} = \sqrt {\frac{1}{{8 - 1}}\sum\limits_{i = 1}^8 {{{\left( {{D_2}\left( i \right) - {{\bar D}_2}} \right)}^2}} } = }\\ {\;\;\;\;\;\;\;\;\sqrt {\frac{{0.001\;197\;223\;3}}{7}} \approx 0.013\;08.} \end{array}} \right. $ | (10) |
现对表 2中数据{D1(i)}在显著性水平α=0.05下检验假设{H0, H1}, 其中,
| $ {H_0}:{\mu _{{D_1}}} \le 0,\;\;\;{H_1}:{\mu _{{D_1}}} > 0. $ |
利用t-检验, 取检验统计量
| $ t = \frac{{{{\bar D}_1} - 0}}{{\frac{{{s_{{D_1}}}}}{{\sqrt n }}}} > {t_\alpha }\left( {n - 1} \right) = 1.894\;6. $ |
进而得到数据{D1(i)}的t-观察值为
| $ t = \frac{{{{\bar D}_1} - 0}}{{\frac{{{s_{{D_1}}}}}{{\sqrt n }}}} = \frac{{0.009\;81}}{{\frac{{0.014\;28}}{{\sqrt 8 }}}} \approx 1.953\;41 > 1.894\;6. $ |
可见上述观察值t落在拒绝域H1以内, 故在显著性水平α=0.05下拒绝H0.再由t-假设检验及数据{D1(i)}的含义知,分层混合模糊系统的输出y2比Mamdani模糊系统逼近性能好.
此外, 对数据{D2(i)}在α=0.05下检验假设{H0, H1}, 其中H0:μD2≤0, H1:μD2>0.
同理, 可得数据{D1(i)}的t-观察值满足
| $ t = \frac{{{{\bar D}_2} - 0}}{{\frac{{{s_{{D_2}}}}}{{\sqrt n }}}} = \frac{{0.010\;75}}{{\frac{{0.013\;08}}{{\sqrt 8 }}}} \approx 2.324\;24 > 1.894\;6. $ |
此时, 必须拒绝假设H0而接受H1, 根据统计推断的t-假设检验知,该分层混合模糊系统的输出y2也比T-S模糊系统逼近性能好.
综合上述2种情况, 认为分层混合模糊系统的输出y2均比Mamdani模糊系统和T-S模糊系统的逼近性能好.
| [1] | RAJU G V S, ZHOU J, KISNER R A. Hierarchical fuzzy control[J]. International J Control, 1991, 54(5): 1201–1216. DOI:10.1080/00207179108934205 |
| [2] | WANG L X. Universal approximation by hierarchical fuzzy systems[J]. Fuzzy Set and Systems, 1998, 93(1): 223–230. |
| [3] | LIU P Y, LI H X. Hierarchical T-S fuzzy system and its universal approximation[J]. Information Sciences, 2005, 169(3): 279–303. |
| [4] |
杜新宇, 张乃尧. 二叉树型分层模糊系统的等效性分析[J].
清华大学学报:自然科学版, 2004, 44(7): 33–36.
DU X Y, ZHANG N Y. Equivalence analysis of binary tree-type hierarchical fuzzy systems[J]. Journal of Tsinghua University:Natural Science, 2004, 44(7): 33–36. |
| [5] |
王贵君, 段晨霞. 广义分层混合模糊系统及其泛逼近性[J].
控制理论与应用, 2012, 29(5): 673–680.
WANG G J, DUAN C X. Generalized hierarchical hybrid fuzzy systems and their universal approximation[J]. Control Theory & Applications, 2012, 29(5): 673–680. |
| [6] |
朱晓东, 王杰. 一种新型分层模糊系统及其逼近性能[J].
控制与决策, 2013, 28(10): 1559–1563.
ZHU X D, WANG J. A new type of hierarchical fuzzy system and its approximation performance[J]. Control and Decision, 2013, 28(10): 1559–1563. |
| [7] |
王贵君, 宋巍巍, 韩权杰. 基于后件直联型分层的广义混合模糊系统及其积分模逼近[J].
控制与决策, 2015, 30(10): 1742–1750.
WANG G J, SONG W W, HAN Q J. Generalized hybrid fuzzy system based on consequent direct link type hierarchy and its integral norm approximation[J]. Control and Decision, 2015, 30(10): 1742–1750. |
| [8] |
索春凤, 王贵君. 最大交互数对非齐次T-S模糊系统的潜在影响[J].
山东大学学报:理学版, 2015, 50(8): 14–19.
SUO C F, WANG G J. The potential influence of maximum interactive number to non-homogeneous T-S fuzzy system[J]. Journal of Shandong University:Science Edition, 2015, 50(8): 14–19. |



