0 引 言
旋转曲面方程及其性质是高等数学教学的重要内容。高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] 。2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题。对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程。文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程。本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程。
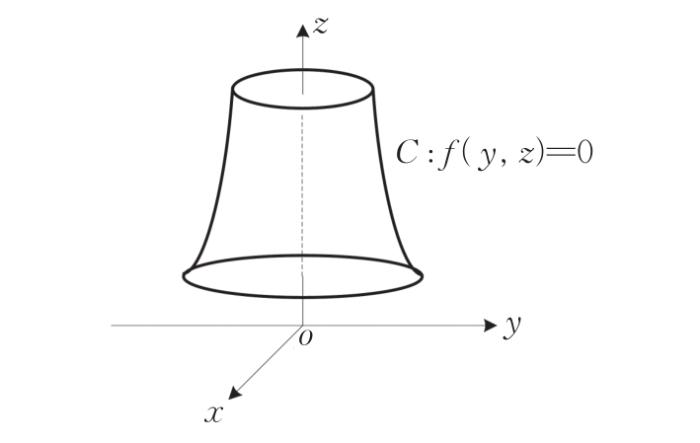
定义1 [1 -2 ] 平面上曲线C L
结论1 [1 -2 ] 若旋转曲面Σ y o z C : f ( y , z ) = 0 z 图1 所示),则该旋转曲面Σ f ( ± x 2 + y 2 , z ) = 0
图1
图1
平面曲线C z
Fig.1
Plane curve C z
1 主要结果及其推导
称空间曲线绕定直线旋转一周所成的曲面为旋转曲面,拓展了旋转曲面的概念。首先讨论空间曲线与定直线共面条件下,空间曲线绕定直线旋转一周所成的旋转曲面方程的求解问题(简称问题1),然后讨论更具一般性的旋转曲面方程求解问题(分别简称问题2和问题3)。
引理1 [6 ] 设坐标系o - x y z o - x ' y ' z ' o x ' o y ' o z ' o - x y z α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 p o - x y z o - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' )
x = x ' c o s α 1 + y ' c o s α 2 + z ' c o s α 3 , y = x ' c o s β 1 + y ' c o s β 2 + z ' c o s β 3 , x = x ' c o s γ 1 + y ' c o s γ 2 + z ' c o s γ 3 , (1)
x ' = x c o s α 1 + y c o s β 1 + z c o s γ 1 , y ' = x c o s α 2 + y c o s β 2 + z c o s γ 2 , z ' = x c o s α 3 + y c o s β 3 + z c o s γ 3 , (2)
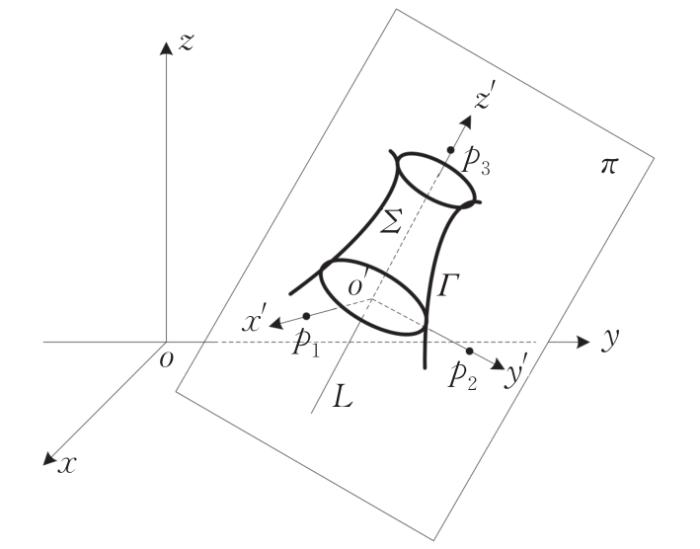
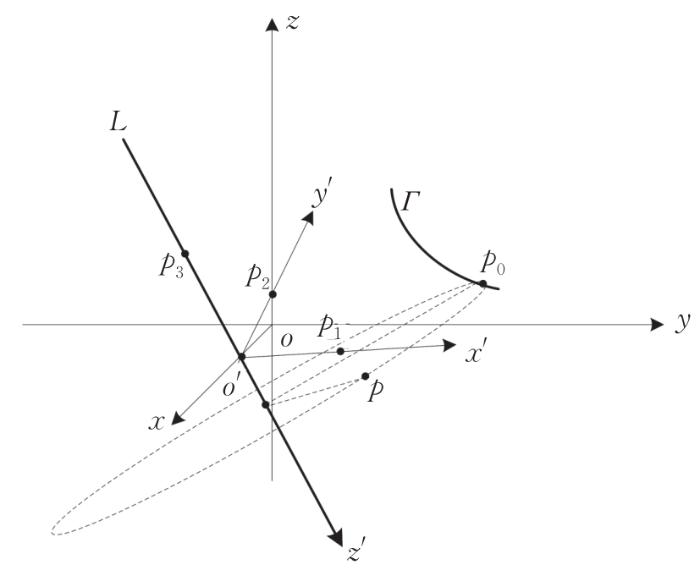
问题1 已知空间曲线Γ π : A x + B y + C z + D = 0 Σ 0 : f ( x , y , z ) = 0 L x - X 0 m = y - Y 0 n = z - Z 0 p L π Σ Γ L Σ
解 在直线L o ' o ' o - x y z ( x 0 , y 0 , z 0 ) π o ' L y ' x ' y ' z ' 图2 所示。为方便叙述,将文中新坐标系简记为o ' - x ' y ' z ' o - x y z x ' y ' z ' p 1 p 2 p 3 o ' p 1 ∥ x ' o ' p 2 ∥ y ' o ' p 3 ∥ z ' ∥ o ' p 1 o ' p 2 o ' p 3
( o ' p 1 ) 0 = { c o s α 1 , c o s β 1 , c o s γ 1 }
( o ' p 2 ) 0 = { c o s α 2 , c o s β 2 , c o s γ 2 }
( o ' p 3 ) 0 = { c o s α 3 , c o s β 3 , c o s γ 3 }
图2
图2
空间曲线Γ z '
Fig.2
Space curve Γ z '
由方向角和方向余弦的定义,知α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 x ' y ' z ' o - x y z
x = x ( x ' , y ' , z ' ) = x ' c o s α 1 + y ' c o s α 2 + z ' c o s α 3 + x 0 , y = y ( x ' , y ' , z ' ) = x ' c o s β 1 + y ' c o s β 2 + z ' c o s β 3 + y 0 , z = z ( x ' , y ' , z ' ) = x ' c o s γ 1 + y ' c o s γ 2 + z ' c o s γ 3 + z 0 , (3)
x ' = x ' ( x , y , z ) = ( x - x 0 ) c o s α 1 + ( y - y 0 ) c o s β 1 + ( z - z 0 ) c o s γ 1 , y ' = y ' ( x , y , z ) = ( x - x 0 ) c o s α 2 + ( y - y 0 ) c o s β 2 + ( z - z 0 ) c o s γ 2 , z ' = z ' ( x , y , z ) = ( x - x 0 ) c o s α 3 + ( y - y 0 ) c o s β 3 + ( z - z 0 ) c o s γ 3 。 (4)
将式(3)分别代入平面方程π : A x + B y + C z + D = 0 Σ 0 : f ( x , y , z ) = 0 x ' Γ y ' o ' z ' g ( y ' , z ' ) = 0 Σ Γ z ' L
g ( x ' 2 + y ' 2 , z ' ) = 0 (5)
g ( - x ' 2 + y ' 2 , z ' ) = 0 (6)
将式(4)代入式(5)或式(6),则得旋转曲面Σ o - x y z
g ( x ' 2 ( x , y , z ) + y ' 2 ( x , y , z ) , z ' ( x , y , z ) ) = 0 g ( - x ' 2 ( x , y , z ) + y ' 2 ( x , y , z ) , z ' ( x , y , z ) ) = 0
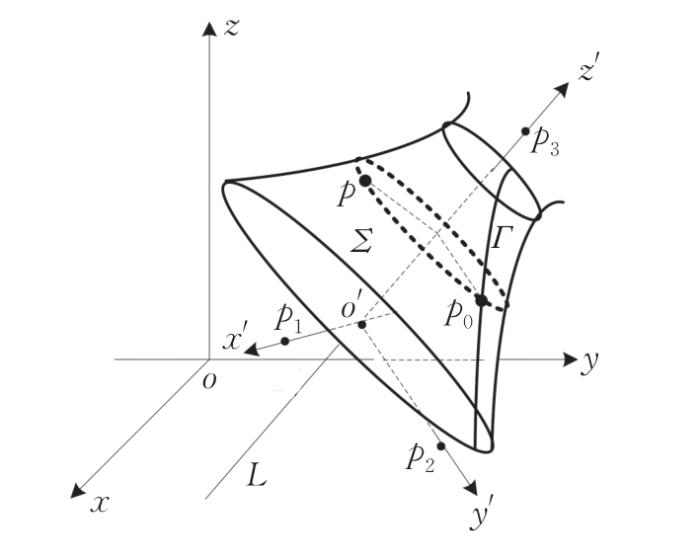
问题2 已知旋转曲面Σ Γ : x = f ( t ) y = g ( t ) z = h ( t ) ( a ≤ t ≤ b ) L x - X 0 m = y - Y 0 n = z - Z 0 p Σ
解 若空间曲线Γ L Σ Γ L
建立新坐标系o ' - x ' y ' z ' L o ' o ' o - x y z ( x 0 , y 0 , z 0 ) L z ' o ' L y ' x ' y ' z ' 图3 )。在x ' y ' z ' p 1 p 2 p 3 o ' p 1 o ' p 2 o ' p 3 o ' p 1 o ' p 2 o ' p 3
图3
图3
空间曲线Γ z '
Fig.3
Space curve Γ z '
( o ' p 1 ) 0 = { c o s α 1 , c o s β 1 , c o s γ 1 }
( o ' p 2 ) 0 = { c o s α 2 , c o s β 2 , c o s γ 2 }
( o ' p 3 ) 0 = { c o s α 3 , c o s β 3 , c o s γ 3 }
由方向角和方向余弦的定义,知α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 x ' y ' z ' o - x y z 式(4),可得到空间曲线Γ o ' - x ' y ' z '
x ' ( t ) = [ f ( t ) - x 0 ] c o s α 1 + [ g ( t ) - y 0 ] × c o s β 1 + [ h ( t ) - z 0 ] c o s γ 1 , y ' ( t ) = [ f ( t ) - x 0 ] c o s α 2 + [ g ( t ) - y 0 ] × c o s β 2 + [ h ( t ) - z 0 ] c o s γ 2 , z ' ( t ) = [ f ( t ) - x 0 ] c o s α 3 + [ g ( t ) - y 0 ] × c o s β 3 + [ h ( t ) - z 0 ] c o s γ 3 ,
a ≤ t ≤ b 。 (7)
空间直线L o - x y z x - X 0 m = y - Y 0 n = z - Z 0 p L o ' - x ' y ' z ' z ' L o ' - x ' y ' z ' x ' 0 = y ' 0 = z ' 1 o ' - x ' y ' z ' p ( x ' , y ' , z ' ) Σ Γ p 0 ( x ' ( t 0 ) , y ' ( t 0 ) , z ' ( t 0 ) ) L p 0 ( x ' ( t 0 ) , y ' ( t 0 ) , z ' ( t 0 ) ) 式(7)得到,即在坐标系o ' - x ' y ' z ' Σ
x ' = x ' 2 ( t 0 ) + y ' 2 ( t 0 ) c o s θ , y ' = x ' 2 ( t 0 ) + y ' 2 ( t 0 ) s i n θ , z ' = z ' ( t 0 ) ,
a ≤ t 0 ≤ b , 0 ≤ θ < 2 π , (8)
对参数t 0 , θ H ( x ' , y ' , z ' ) = 0 式(4),得到在坐标系o - x y z Σ
H ( x ' ( x , y , z ) , y ' ( x , y , z ) , z ' ( x , y , z ) ) = 0
问题3 已知旋转曲面Σ Γ : F ( x , y , z ) = 0 G ( x , y , z ) = 0 L x - X 0 m = y - Y 0 n = z - Z 0 p Σ
解 方法1 将空间曲线Γ F ( x , y , z ) = 0 G ( x , y , z ) = 0 Γ : x = f ( t ) y = g ( t ) z = h ( t ) ( a ≤ t ≤ b )
方法2 与问题2建坐标系方法类似,建立新坐标系o ' - x ' y ' z ' p o - x y z o ' - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' ) 式(3),得到空间曲线Γ o ' - x ' y ' z '
F ( x ( x ' , y ' , z ' ) , y ( x ' , y ' , z ' ) , z ( x ' , y ' , z ' ) ) = 0 , G ( x ( x ' , y ' , z ' ) , y ( x ' , y ' , z ' ) , z ( x ' , y ' , z ' ) ) = 0 , (9)
由空间直线L o ' - x ' y ' z ' z ' L o ' - x ' y ' z ' x ' 0 = y ' 0 = z ' 1 o ' - x ' y ' z ' p ( x ' , y ' , z ' ) Σ Γ p 0 ( x 0 ' , y 0 ' , z 0 ' ) L o ' - x ' y ' z ' Σ Γ z ' 图3 )。因为点p ( x ' , y ' , z ' ) p 0 ( x 0 ' , y 0 ' , z 0 ' ) z ' p 0 ( x 0 ' , y 0 ' , z 0 ' ) Γ Σ p o ' - x ' y ' z '
x ' 2 + y ' 2 = x 0 ' 2 + y 0 ' 2 , z ' = z 0 ' , F ( x ( x 0 ' , y 0 ' , z 0 ' ) , y ( x 0 ' , y 0 ' , z 0 ' ) , z ( x 0 ' , y 0 ' , z 0 ' ) ) = 0 , G ( x ( x 0 ' , y 0 ' , z 0 ' ) , y ( x 0 ' , y 0 ' , z 0 ' ) , z ( x 0 ' , y 0 ' , z 0 ' ) ) = 0 , (10)
消去参数x 0 ' , y 0 ' , z 0 ' x ' , y ' , z ' Σ o ' - x ' y ' z ' H ( x ' , y ' , z ' ) = 0 式(4)代入方程H ( x ' , y ' , z ' ) = 0 o - x y z
H ( x ' ( x , y , z ) , y ' ( x , y , z ) , z ' ( x , y , z ) ) = 0
2 应用举例
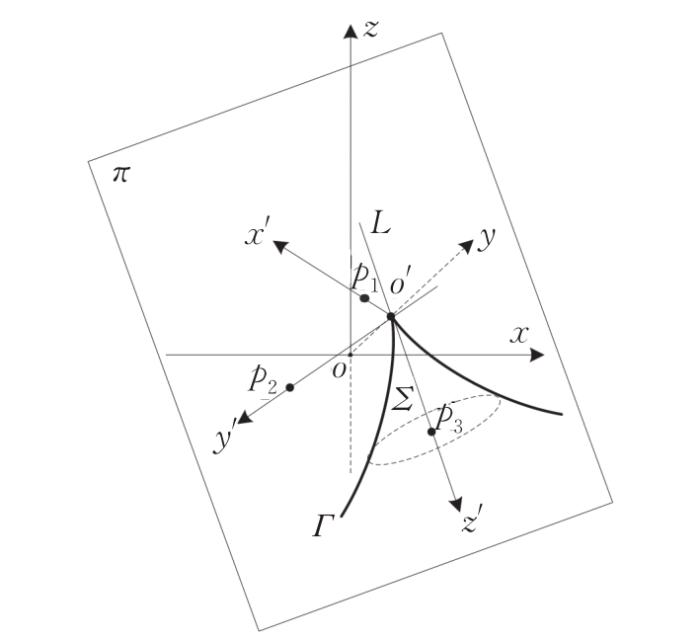
例1 旋转曲面由已知空间曲线Γ : x - 2 y + 2 z + 2 = 0 z - 2 y + 2 = ( y - 2 z - 1 ) 2 L : x - 0 2 = y - 1 - 1 = z - 0 - 2 Σ
解 由题中条件,可知空间直线L Γ π : x - 2 y + 2 z + 2 = 0 L p 0 ( 0,1 , 0 ) o ' z ' L π p 0 ( 0,1 , 0 ) L y ' x ' y ' z ' 图4 。
图4
图4
空间曲线Γ z '
Fig.4
Space curve Γ z '
方便起见,将新坐标系简记为o ' - x ' y ' z ' o - x y z x ' y ' z ' p 1 p 2 p 3 o ' p 1 ∥ x ' o ' p 2 ∥ y ' o ' p 3 ∥ z ' o - x y z o ' ( 0,1 , 0 )
o ' p 1 = { x 1 , y 1 - 1 , z 1 } ,
o ' p 2 = { x 2 , y 2 - 1 , z 2 } ,
o ' p 3 = { x 3 , y 3 - 1 , z 3 } ,
直线L s o - x y z s = { 2 , - 1 , - 2 }
因为o ' p 3 ∥ s { x 3 , y 3 - 1 , z 3 } = λ { 2 , - 1 , - 2 } λ λ = 1 x 3 = 2 y 3 = 0 z 3 = - 2 p 3 ( 2,0 , - 2 ) o ' p 3 = { 2 , - 1 , - 2 }
x 2 - 2 y 2 + 2 z 2 + 2 = 0 , 2 x 2 - ( y 2 - 1 ) - 2 z 2 = 0 ,
取x 2 = - 1 2 z 2 - 2 y 2 + 1 = 0 - 2 z 2 - y 2 - 1 = 0 y 2 = 0 z 2 = - 1 2 p 2 - 1,0 , - 1 2 o ' p 2 = - 1 , - 1 , - 1 2
因为o ' p 1 ⊥ o ' p 2 o ' p 1 ⊥ o ' p 3
- x 1 - ( y 1 - 1 ) - 1 2 z 1 = 0 , 2 x 1 - ( y 1 - 1 ) - 2 z 1 = 0 ,
取z 1 = 2 x 1 = 1 y 1 = - 1 p 1 = { 1 , - 1,2 } o ' p 1 = { 1 , - 2,2 }
设o ' x ' o ' y ' o ' z ' o - x y z α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 o ' p 1 = { 1 , - 2,2 } o ' p 2 = - 1 , - 1 , - 1 2 o ' p 3 = { 2 , - 1 , - 2 } x ' y ' z '
{ c o s α 1 , c o s β 1 , c o s γ 1 } = 1 3 , - 2 3 , 2 3 ,
{ c o s α 2 , c o s β 2 , c o s γ 2 } = - 2 3 , - 2 3 , - 1 3 ,
{ c o s α 3 , c o s β 3 , c o s γ 3 } = 2 3 , - 1 3 , - 2 3 。
设点p o - x y z o ' - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' ) 式(3)得到,为
x = 1 3 x ' - 2 3 y ' + 2 3 z ' , y - 1 = - 2 3 x ' - 2 3 y ' - 1 3 z ' , z = 2 3 x ' - 1 3 y ' - 2 3 z ' , (11)
将式(11)代入空间曲线方程 Γ : x - 2 y + 2 z + 2 = 0 z - 2 y + 2 = ( y - 2 z - 1 ) 2 Γ o ' - x ' y ' z ' Γ : x ' = 0 y ' = z ' 2 Σ Γ : x - 2 y + 2 z + 2 = 0 z - 2 y + 2 = ( y - 2 z - 1 ) 2 L : x - 0 2 = y - 1 - 1 = z - 0 - 2 o ' - x ' y ' z ' Γ : x ' = 0 y ' = z ' 2 z '
由结论1,得到旋转曲面Σ o ' - x ' y ' z ' x ' 2 + y ' 2 = z ' 2
设点p o - x y z o ' - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' ) 式(11)求逆变换得到,为
x ' = 1 3 x - 2 3 ( y - 1 ) + 2 3 z , y ' = - 2 3 x - 2 3 ( y - 1 ) - 1 3 z , z ' = 2 3 x - 1 3 ( y - 1 ) - 2 3 z , (12)
将式(12)代入旋转曲面Σ o ' - x ' y ' z ' x ' 2 + y ' 2 = z ' 2 Σ o - x y z
1 3 x - 2 3 ( y - 1 ) + 2 3 z 2 + - 2 3 x - 2 3 ( y - 1 ) - 1 3 z 2 1 2 = 2 3 x - 1 3 ( y - 1 ) - 2 3 z 2 (13)
例2 已知空间曲线Γ : x = t y = t z = t L : x - 0 2 = y - 1 - 1 = z - 0 - 2 Σ
解 以o ' ( 0,1 , 0 ) L z ' o ' - x ' y ' z ' 图4 所示。空间直线L o ' - x ' y ' z ' L : x ' 0 = y ' 0 = z ' 1 Γ o - x y z Γ : x = t y = t z = t 式(11),得到空间曲线Γ o ' - x ' y ' z '
t = 1 3 x ' - 2 3 y ' + 2 3 z ' , t - 1 = - 2 3 x ' - 2 3 y ' - 1 3 z ' , t = 2 3 x ' - 1 3 y ' - 2 3 z ' ,
化简后可得在直角坐标系o ' - x ' y ' z ' Γ
x ' = 1 3 t + 2 3 , y ' = - 5 3 t + 2 3 , z ' = - 1 3 t + 1 3 。 (14)
旋转曲面Σ Γ o ' - x ' y ' z ' L : x ' 0 = y ' 0 = z ' 1 Σ
x ' = 1 3 t + 2 3 2 + - 5 3 t + 2 3 2 c o s θ , y ' = 1 3 t + 2 3 2 + - 5 3 t + 2 3 2 s i n θ , z ' = - 1 3 t + 1 3 , (15)
x ' 2 + y ' 2 = ( 1 - z ' ) 2 + ( 1 - 5 z ' ) 2 (16)
由式(12),则可得旋转曲面Σ o - x y z
1 3 x - 2 3 ( y - 1 ) + 2 3 z 2 + 2 3 x + 2 3 ( y - 1 ) + 1 3 z 2 = 2 3 x - 1 3 ( y + 2 ) - 2 3 z 2 + 10 3 x - 1 3 ( 5 y - 2 ) - 10 3 z 2 。
例3 旋转曲面Σ Γ : x 2 + y - z 2 = 0 x - y + z + 1 = 0 L : x - 2 1 = y - 0 0 = z - 1 1 Σ [4 ] 。
解 以o ' ( 1,0 , 0 ) L z ' o ' - x ' y ' z ' 图5 ,将原坐标系记为o - x y z x ' y ' z ' p 1 p 2 p 3 p 1 p 2 p 3 o ' p 1 o ' p 2 o ' p 3 p 1 ( 1,1 , 0 ) p 2 ( 0,0 , 1 ) p 3 ( 2,0 , 1 ) o ' p 1 = { 0,1 , 0 } o ' p 2 = { - 1,0 , 1 } o ' p 3 = { 1,0 , 1 } o ' p 1 o ' p 2 o ' p 3 x ' y ' z ' { 0,1 , 0 } - 1 2 , 0 , 1 2 1 2 , 0 , 1 2 p o - x y z o ' - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' ) 式(3)和式(4)得到,分别为:
x - 1 = - 1 2 y ' + 1 2 z ' , y = x ' , z = 1 2 y ' + 1 2 z ' , (17)
x ' = y , y ' = - 1 2 ( x - 1 ) + 1 2 z , z ' = 1 2 ( x - 1 ) + 1 2 z 。 (18)
图5
图5
空间曲线Γ z '
Fig.5
Space curve Γ z '
空间曲线Γ o ' - x ' y ' z ' 式(17)得到,化简后为x ' = 2 + 2 z ' ( 2 + 2 z ' ) y ' = 3 + 2 2 z ' o ' - x ' y ' z ' p ( x ' , y ' , z ' ) Σ Γ p 0 ( x 0 ' , y 0 ' , z 0 ' ) L o ' - x ' y ' z ' Σ Γ z ' 图5 )。由点p ( x ' , y ' , z ' ) p 0 ( x 0 ' , y 0 ' , z 0 ' ) z ' p 0 ( x 0 ' , y 0 ' , z 0 ' ) Γ
x ' 2 + y ' 2 = x 0 ' 2 + y 0 ' 2 , z ' = z 0 ' , x 0 ' = 2 + 2 z 0 ' , ( 2 + 2 z 0 ' ) y 0 ' = 3 + 2 2 z 0 ' , (19)
消去变量x 0 ' , y 0 ' , z 0 ' o ' - x ' y ' z ' Σ
( 2 + 2 z ' ) 2 x ' 2 + ( 2 + 2 z ' ) 2 y ' 2 = ( 2 + 2 z ' ) 2 ( 2 + 2 z ' ) 2 + ( 3 + 2 2 z ' ) 2 (20)
将式(18)代入式(20),得到在坐标系o - x y z Σ
1 + 4 x + 5 x 2 + 6 x 3 + x 4 - 2 x 2 y 2 + 4 z + 10 x z + 14 x 2 z + 8 x 3 z - 4 x y 2 z + 5 z 2 + 10 x z 2 + 14 x 2 z 2 - 2 y 2 z 2 + 2 z 3 + 8 x z 3 + z 4 = 0
3 结 论
讨论了空间曲线Γ L Γ L
http://dx.doi.org/10.3785/j.issn.1008-9497.2022.06.001
参考文献
View Option
[1]
朱士信 , 唐烁 高等数学(下册) [M]. 北京 :高等教育出版社 , 2020 .
[本文引用: 4]
ZHU S X TANG S Advanced Mathematics (Volume Ⅱ) [M]. Beijing : Higher Education Press , 2020 .
[本文引用: 4]
[2]
同济大学数学系 高等数学(下册) [M].北京 :高等教育出版社 ,2019 .
[本文引用: 3]
Department of Mathematics , Tongji University Advanced Mathematics(Volume Ⅱ) [M]. Beijing : Higher Education Press , 2019 .
[本文引用: 3]
[3]
黄振华 ,祝秋文 ,胡清华 旋转曲面及其方程
[J].湖北师范大学学报(自然科学版) ,2017 ,37 (2 ):83 -86 .
[本文引用: 1]
HUANG Z H ZHU Q W HU Q H Rotation surface equation
[J]. Journal of Hubei University (Natural Science) ,2017 , 37 (2 ):83 -86 .
[本文引用: 1]
[5]
张树功 ,雷娜 ,刘停战 计算机代数基础:代数与符号计算的基本原理 [M]. 北京 :科学出版社 ,2005 :44 -50 .
[本文引用: 1]
ZHANG S G LEI N LIU T Z Fundamentals of Computer Algebra: Basic Principles of Algebra and Symbolic Computing [M]. Beijing : Science Press , 2005 :44 -50 .
[本文引用: 1]
[6]
刘绍学 , 朱元森 数学辞海 [M].北京 :中国科学技术出版社 , 2002 :85 -95 .
[本文引用: 1]
LIU S X ZHU Y S Mathematical Lexicon [M]. Beijing : China Science and Technology Press , 2002 :85 -95 .
[本文引用: 1]
4
2020
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... [1 -2 ].2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 定义1 [1 -2 ] 平面上曲线C L
... 结论1 [1 -2 ] 若旋转曲面Σ y o z C : f ( y , z ) = 0 z 图1 所示),则该旋转曲面Σ f ( ± x 2 + y 2 , z ) = 0 . ...
4
2020
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... [1 -2 ].2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 定义1 [1 -2 ] 平面上曲线C L
... 结论1 [1 -2 ] 若旋转曲面Σ y o z C : f ( y , z ) = 0 z 图1 所示),则该旋转曲面Σ f ( ± x 2 + y 2 , z ) = 0 . ...
3
2019
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 定义1 [1 -2 ] 平面上曲线C L
... 结论1 [1 -2 ] 若旋转曲面Σ y o z C : f ( y , z ) = 0 z 图1 所示),则该旋转曲面Σ f ( ± x 2 + y 2 , z ) = 0 . ...
3
2019
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 定义1 [1 -2 ] 平面上曲线C L
... 结论1 [1 -2 ] 若旋转曲面Σ y o z C : f ( y , z ) = 0 z 图1 所示),则该旋转曲面Σ f ( ± x 2 + y 2 , z ) = 0 . ...
旋转曲面及其方程
1
2017
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
旋转曲面及其方程
1
2017
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
关于旋转曲面方程的注记
2
2020
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 例3 旋转曲面Σ Γ : x 2 + y - z 2 = 0 x - y + z + 1 = 0 L : x - 2 1 = y - 0 0 = z - 1 1 Σ [4 ] . ...
关于旋转曲面方程的注记
2
2020
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
... 例3 旋转曲面Σ Γ : x 2 + y - z 2 = 0 x - y + z + 1 = 0 L : x - 2 1 = y - 0 0 = z - 1 1 Σ [4 ] . ...
1
2005
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
1
2005
... 旋转曲面方程及其性质是高等数学教学的重要内容.高等数学教材给出了平面曲线绕平面内定直线旋转一周所成的旋转曲面的定义及方程[1 ] ,主要给出的是旋转轴与坐标轴重合条件下的一类旋转曲面方程[1 -2 ] .2013年全国硕士研究生入学统一考试(数学一)试卷中出现旋转轴与坐标轴不重合条件下旋转曲面求解试题.对于空间曲线绕任意定直线旋转所成的旋转曲面方程,文献[3 ]将旋转曲面想象成由空间曲线上的动点围绕定直线旋转一周所成的一系列平行圆堆叠而成,并将平行圆方程和曲线方程联立推导出旋转曲面方程.文献[4 ]联立平行圆方程和空间曲线方程,并借助多项式理想的Groebner基理论方法对旋转曲面方程组进行去参数化处理[5 ] ,得到旋转曲面方程.本文以坐标平面上曲线绕坐标轴旋转所成的旋转曲面方程为基础,通过寻找2个坐标系之间的姿态和相对位置,利用方向角和转轴公式推导空间曲线绕定直线旋转所成的一般旋转曲面方程. ...
1
2002
... 引理1 [6 ] 设坐标系o - x y z o - x ' y ' z ' o x ' o y ' o z ' o - x y z α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 p o - x y z o - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' )
1
2002
... 引理1 [6 ] 设坐标系o - x y z o - x ' y ' z ' o x ' o y ' o z ' o - x y z α 1 β 1 γ 1 α 2 β 2 γ 2 α 3 β 3 γ 3 p o - x y z o - x ' y ' z ' ( x , y , z ) ( x ' , y ' , z ' )