一类具变指数的非线性椭圆方程在加权Sobolev空间中熵解的存在性

doi:10.3785/j.issn.1008-9497.2022.05.004

一类具变指数的非线性椭圆方程在加权Sobolev空间中熵解的存在性

代丽丽^,^,

通化师范学院数学学院, 吉林通化 134002

The existence of entropy solutions for the nonlinear elliptic problems with variable exponents in weighted Sobolev space

DAI Lili^,^,

Institute of Mathematics，Tonghua Normal University，Tonghua 134002，Jilin Province，China

收稿日期: 2020-12-02

基金资助:

吉林省教育厅科学研究项目. JJKH20210537KJ

Received: 2020-12-02

作者简介 About authors

代丽丽（1982—），ORCID：https：//orcid.org/0000-0002-6376-6949，女，博士，副教授，主要从事偏微分方程及其应用研究，E-mail：drx820115@126.com. , E-mail：drx820115@126.com

摘要

运用截断函数方法以及变指数在加权Sobolev空间中的嵌入关系，通过选取适当的检验函数，证明了一类非线性椭圆方程熵解的存在性。

关键词： 非线性椭圆方程 ; 截断函数 ; 加权Sobolev空间 ; 权函数

Abstract

In this paper, we utilize truncation method and some embedding of weighted Sobolev space with variable exponent to investigate the existence of entropy solutions for the nonlinear elliptic problems.

Keywords： the nonlinear elliptic equation ; truncation function ; weighted Sobolev space ; weighted functions

PDF (688KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

代丽丽. 一类具变指数的非线性椭圆方程在加权Sobolev空间中熵解的存在性. 浙江大学学报(理学版)[J], 2022, 49(5): 540-548 doi:10.3785/j.issn.1008-9497.2022.05.004

DAI Lili. The existence of entropy solutions for the nonlinear elliptic problems with variable exponents in weighted Sobolev space. Journal of Zhejiang University(Science Edition)[J], 2022, 49(5): 540-548 doi:10.3785/j.issn.1008-9497.2022.05.004

0　引言

在加权Sobolev空间中，考虑一般情形的非线性椭圆方程

\{\begin{array}{l} \begin{array}{l} - d i v (a (x, u, \nabla u)) + g (x, u, \nabla u) - \\ d i v φ (u) = μ, x \in Ω, \end{array} \\ u = 0, x \in \partial Ω, \end{array}

（1）

其中， $Ω \subset R^{N} (N \geq 2)$ 为具有Lipschitz边界 $\partial Ω$ 的有界区域， $μ = f - d i v F$ ， $f \in L^{1} (Ω)$ ， $F \in W^{- 1, p^{'} (x)} (Ω, ω^{*})$ ， $φ \in C^{0} (R, R^{N})$ ， $W_{0}^{1, p (x)} (Ω, ω)$ 为加权Sobolev空间， $ω (x)$ 为权函数，其范数形式为 ${‖\cdot‖}_{1, p (x), ω}$ 。此外，始终假设：

（H₁） $a (x, s, ξ) : Ω \times R \times R^{N} \to R^{N}$ 为Carathéodory的向量值函数，对几乎处处的 $x \in Ω$ ，所有的 $(s, ξ) \in R \times R^{N}$ ，满足

| a_{i} (x, s, ξ) | \leq β ω_{}^{\frac{1}{p (x)}} (x) [k (x) + ω_{}^{\frac{1}{p^{'} (x)}} | s |^{p (x) - 1} + ω_{}^{\frac{1}{p^{'} (x)}} | ξ |^{p (x) - 1}],

（2）

a (x, s, ξ) ξ \geq α ω (x) | ξ |^{p (x)},

（3）

[a (x, s, ξ) - a (x, s, η)] (ξ - η) > 0, ξ \neq η \in R^{N},

（4）

其中， $k (x)$ 为 $L^{p^{'} (x)} (Ω)$ 中的非负函数， $α$ ， $β$ 为正数。

（H₂） $g ： Ω \times R \times R^{N}$ →R为Carathéodory函数，且对几乎处处的 $x \in Ω$ 和任意的 $s \in R$ ，所有的 $ξ \in R^{N}$ ，满足

g (x, s, ξ) s \geq 0,

（5）

| g (x, s, ξ) | \leq b (|s|) [c (x) + ω {|ξ|}^{p (x)}],

（6）

其中， $b : R^{+} \to R^{+}$ 为连续非增函数， $c (x)$ 为 $L^{1} (Ω)$ 中的非负函数。

有关权函数 $ω (x)$ 的假设（H₃）为

（i） $ω \in L_{l o c}^{1} (Ω), ω_{}^{- \frac{1}{p (x) - 1}} \in L_{l o c}^{1} (Ω),$

\begin{array}{l} (i i) ω^{- s (x)} \in L^{1} (Ω), s (x) \in (\frac{N}{p (x)}, \infty) ⋂ \\ [\frac{1}{p (x) - 1}, \infty), \end{array}

（iii） $ω^{*} = \{ω_{i}^{*} = ω_{i}^{- \frac{p^{'} (x)}{p (x)}}\} ，$ 对所有的 $i = 1,2, \dots, N,$ 有 $p^{'} (x) = \frac{p (x)}{p (x) - 1} 。$

AHAROUCH等^［1］研究了在常指数情形下，当 $μ \in W^{- 1, p^{'}} (Ω), g = g (x, u)$ ，且 $φ \equiv 0$ 时，式（1）在Orlicz空间解的存在性结果。在变指数情形下，AZROUL等^［2］研究了椭圆方程

\begin{array}{l} - d i v ({|\nabla u|}^{p (x) - 2} \nabla u) + {|u|}^{p (x) - 2} u = μ \in \\ L^{1} (Ω) + W^{- 1, p^{'} (x)} (Ω) \end{array}

，

并得到熵解的存在性结果。ZHANG等^［3］在 $a (x, s, ξ) = {|ξ|}^{p (x) - 2} ξ$ ， $g = 0$ ， $φ = 0$ ，且 $μ \in$ $L^{1} (Ω) + W^{- 1, p^{'} (x)} (Ω)$ 的情形下，证明了重整化解和熵解的存在性。BOCCARDO等^［4］运用截断方法，证明了当 $p (x)$ 为常函数， $F = 0$ ， $f \in W^{- 1, p^{'}} (Ω)$ 时，式（1）在Sobolev空间中重整化解的存在性和正则性。此后，BOCCARDO等^［5］继续研究带有非线性导数项 $- d i v φ (u)$ 的非线性椭圆方程 $A (u) = f - d i v φ (u)$ ，并证明了其存在 ${W_{0}}^{1,1} (Ω)$ 解。

以上研究均在不加权的Sobolev空间进行。本文将在文献［2-3］等的基础上，引入权函数，扩展为加权变指数的Sobolev空间，并在此框架下，研究式（1）解的存在性。首先，带变指数的偏微分方程模型相较常指数优势显著，其可更精确地描述扩散过程，当 $p$ 不是常函数时，研究相关加权 $A_{p (\cdot)}$ 的文献较少，需特别关注 $L^{p (\cdot)} (Ω, ω)$ 空间的性质及嵌入。其次，权函数的引入增加了研究的难度，尤为困难的是空间的嵌入。最后，函数 $φ$ 无增加任何条件，即使作为一个分布，此项在方程中也可能无意义，且右端项可积性不高。因无法得到式（1）的弱能量解，所以考虑其熵解。本文主要借助截断函数方法对逼近方程做估计，运用加权变指数在Sobolev空间中的嵌入关系，选取合适的检验函数，令 $T_{k} (u_{n})$ 强收敛，并通过取极限，得到式（1）的熵解。

1　相关知识

给出加权变指数在Sobolev空间的相关知识^［6］。

（i） $L^{p (x)} (Ω, ω)$ 空间。设 $ω (x)$ 在 $R^{N}$ 上是一个正的可测函数且几乎处处有限函数，集合

C_{+} (\bar{Ω}) = {ς \in C (\bar{Ω}) : \underset{ς \in \bar{Ω}}{m i n} ς (x) > 1} 。

对任意的 $ς \in C_{+} (\bar{Ω})$ ，定义 $ς_{+} = \underset{x \in Ω}{s u p} ς (x)$ ， $ς_{-} = \underset{x \in Ω}{i n f} ς (x)$ 。对任意的 $p \in C_{+} (\bar{Ω})$ ，加权的变指数Lebesgue空间 $L^{p (x)} (Ω, ω)$ 由满足 $\int_{Ω} ω (x) {|u (x)|}^{p (x)} d x < \infty$ 的所有可测函数组成，赋予范数

{‖u‖}_{L^{p (x)} (Ω, ω)} = i n f \{λ > 0 : \int_{Ω} ω (x) {|\frac{u (x)}{λ}|}^{p (x)} \leq 1\} 。

（ii） $W^{k, p (x)} (Ω, ω)$ 空间。对任意正整数 $k$ ，记

W^{k, p (x)} (Ω, ω) = {u \in L^{p (x)} (Ω, ω) : D^{α} u \in L^{p (x)} (Ω, ω), |α| \leq k},

赋予范数

{‖u‖}_{W^{k, p (x)} (Ω, ω)} = \sum_{|α| \leq k} {‖D^{α} u‖}_{L^{p (x)} (Ω, ω)}

。

（iii）常用关系。如果记

ρ (u) = \int_{Ω} ω (x) {|u|}^{p (x)} d x, u \in L^{p (x)} (Ω, ω),

那么

m i n \{{‖u‖}_{L^{p (x)} (Ω, ω)}^{p_{-}}, {‖u‖}_{L^{p (x)} (Ω, ω)}^{p_{+}}\} \leq ρ (u) \leq m a x \{{‖u‖}_{L^{p (x)} (Ω, ω)}^{p_{-}}, {‖u‖}_{L^{p (x)} (Ω, ω)}^{p_{+}}\}

。

（iv）指标 $p_{s} (x)$ 与 $p_{s}^{*} (x)$ 。对任意的 $p, s \in C_{+} (\bar{Ω})$ ，设

p_{s} (x) : = \frac{p (x) s (x)}{1 + s (x)} < p (x),

其中， $s (x) \in (\frac{N}{p (x)}, \infty) ⋂ [\frac{1}{p (x) - 1}, \infty) 。$ 对任意的 $x \in Ω$ ，固定变指数的限制

p_{s}^{*} (x) : = \{\begin{array}{l} \frac{p (x) s (x) N}{[s (x) + 1] N - p (x) s (x)}, N > p_{s} (x), \\ + \infty, N \leq p_{s} (x) 。 \end{array}

（v）加权变指数在Sobolev空间中的连续嵌入定理。设 $p, s \in C_{+} (\bar{Ω})$ 满足 $l o g$ - $H \ddot{o} l d e r$ 连续性条件，若 $r \in C_{+} (\bar{Ω})$ 且 $1 < r (x) \leq p_{s}^{*}$ ，则有连续嵌入

$W^{1, p (x)} (Ω, ω)$ $L^{r (x)} (Ω)$ ，

当 $\underset{x \in Ω}{i n f} (p_{s}^{*} (x) - r (x)) > 0$ 时，嵌入是紧的。

（vi） $P o i n c a r e^{'}$ 型不等式。设 $p \in C_{+} (\bar{Ω})$ 满足 $l o g$ - $H \ddot{o} l d e r$ 连续性条件，则对任意的 $u \in C_{0}^{\infty} (Ω)$ ，有估计式

{‖u‖}_{L^{p (x)} (Ω, ω)} \leq C {‖\nabla u‖}_{L^{p (x)} (Ω, ω)}

，

其中，常数 $C > 0$ 且与 $u$ 无关。

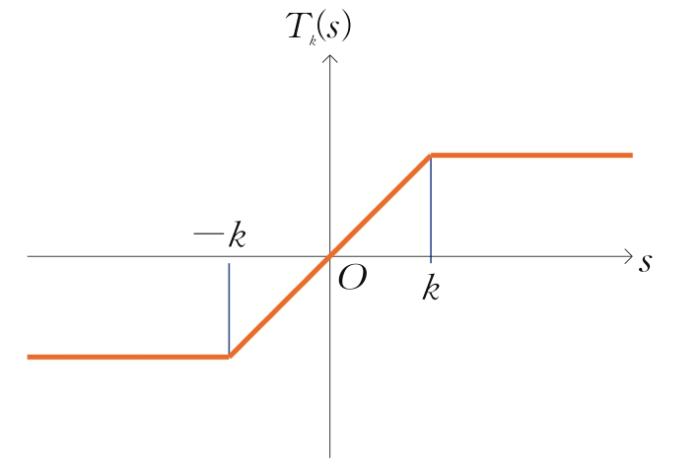
（vii）截断函数 $T_{k} (s)$ 。一般情形下，对于在 $R$ 中的 $s, k$ ，其中 $k \geq 0$ ，高度为 $k$ 的截断函数^［7-8］定义为

T_{k} (s) = m a x (- k, m i n (k, s)) = \{\begin{array}{l} s, |s| < k, \\ k, s \geq k, \\ - k, s \leq - k 。 \end{array}

鉴于其重要性以及直观起见，给出了 $T_{k} (s)$ 的简图，见图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 T_k （s）

Fig.1 T_k （s）

引理1 设 $a$ 和 $b$ 是2个非负实数，

ϕ (s) = s e^{θ s^{2}},

其中， $θ = \frac{b^{2}}{4 a^{2}}$ ，则

a ϕ^{'} (s) - b |ϕ (s)| \geq \frac{a}{2}, s \in R 。

（7）

引理2 对任意的 $u \in L^{p (x)} (Ω)$ 和 $v \in L^{q (x)} (Ω) ，$ $\frac{1}{p (x)} + \frac{1}{q (x)} = 1$ ，有

|\int_{Ω} u v d x| \leq (\frac{1}{p_{-}} + \frac{1}{q_{-}}) {|u|}_{L^{p (x)} (Ω)} {|v|}_{L^{q (x)} (Ω)} \leq 2 {|u|}_{L^{p (x)} (Ω)} {|v|}_{L^{q (x)} (Ω)} 。

（8）

引理3 假设 $（ H_{1} ）$ 和（ $H_{2}$ ）成立，设 $u_{n}$ 在 ${W_{0}}^{1, p (x)} (Ω, ω)$ 中弱收敛于 $u$ 且满足

\begin{array}{l} \underset{n \to \infty}{l i m} \int_{Ω} [a (x, u_{n}, \nabla u_{n}) - a (x, u, \nabla u)] \times \\ \nabla (u_{n} - u) d x = 0 ， \end{array}

则 $u_{n} \to u$ 在 ${W_{0}}^{1, p (x)} (Ω, ω)$ 中强收敛。

2　熵解的存在性

定义1 若 $T_{k} (u) \in W_{0}^{1, p (x)} (Ω, ω)$ ，且对任意的 $ψ \in W_{0}^{1, p (x)} (Ω, ω) ⋂ L^{\infty} (Ω)$ ，均有

\begin{array}{l} \int_{Ω} a (x, u, \nabla u) \nabla T_{k} (u - ψ) d x + \int_{Ω} g (x, u, \nabla u) T_{k} (u - ψ) d x + \\ \int_{Ω} φ (x, u, \nabla u) \nabla T_{k} (u - ψ) d x = \int_{Ω} f T_{k} (u - ψ) d x + \int_{Ω} F \nabla T_{k} (u - ψ) d x ， \end{array}

（9）

则称可测函数 $u$ 为式（1）的一个熵解。

定理1 若 $（ H_{1} ） ~ （ H_{3} ）$ 成立， $f \in L^{1} (Ω),$ $F \in W^{- 1, p^{'} (x)} (Ω, ω^{*})$ ，则式（1）至少存在1个熵解。

证明分5步完成证明过程^［9-11］。

第1步逼近问题及先验估计。

首先，设 $φ_{n} (s) = φ (T_{n} (s)),$

g_{n} (x, s, ξ) = \frac{g (x, s, ξ)}{1 + \frac{1}{n} |g (x, s, ξ)|},

建立关于式（1）的逼近方程

\{\begin{array}{l} \begin{array}{l} - d i v (a (x, u_{n}, \nabla u_{n})) + g (x, u_{n}, \nabla u_{n}) - \\ d i v φ (u_{n}) = f_{n} - d i v F, x \in Ω, \end{array} \\ u_{n} = 0, x \in \partial Ω, \end{array}

（10）

其中， $f_{n}$ 为 $L^{\infty} (Ω)$ 的函数序列，在 $L^{1} (Ω)$ 中强收敛于 $f$ ，对几乎处处的 $x \in Ω$ 和任意的 $s \in R$ ， $g_{n} (x, s, ξ)$ 满足式（5）和式（6），且 $|g_{n} (x, s, ξ)| \leq n, n \in N^{*}$ （ $N^{*}$ 为正整数集）。

由文献［12-13］的伪单调算子理论，可知式（10）至少存在1个弱解 $u_{n} \in W_{0}^{1, p (x)} (Ω, ω)$ ，即对任意的 $v \in W_{0}^{1, p (x)} (Ω, ω) ⋂ L^{\infty} (Ω),$ 有

\int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla v d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) v d x + \int_{Ω} φ_{n} (u_{n}) \nabla v d x = \int_{Ω} f_{n} v d x + \int_{Ω} F \nabla v d x 。

（11）

然后，对逼近解序列 $u_{n}$ 做先验估计。对任意的 $k > 0$ ，取 $T_{k} (u_{n})$ 为式（10）的检验函数，有

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n}) d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) T_{k} (u_{n}) d x + \\ \int_{Ω} φ_{n} (u_{n}) \nabla T_{k} (u_{n}) d x = \\ \int_{Ω} f_{n} T_{k} (u_{n}) d x + \int_{Ω} F \nabla T_{k} (u_{n}) d x 。 \end{array}

（12）

令 $Φ_{n} (t) = \int_{0}^{t} φ_{n} (τ) d τ$ ，有 $Φ_{n} (T_{k} (u_{n})) \in$ $[W_{0}^{1, p (x)} {(Ω, ω)]}^{N}$ 。注意到在 $\partial Ω$ 上， $u_{n} = 0$ ，且 $Φ_{n} (t) = 0$ ，由散度定理，有

\begin{array}{l} \int_{Ω}^{} φ_{n} (u_{n}) \nabla T_{k} (u_{n}) d x = \\ \int_{Ω}^{} φ_{n} (T_{k} (u_{n})) \nabla T_{k} (u_{n}) d x = \int_{Ω}^{} d i v Φ_{n} (T_{k} (u_{n})) d x = \\ \int_{\partial Ω}^{} Φ_{n} (0) n d x = 0 。 \end{array}

（13）

由式（3）、式（5）、式（19）及Young不等式，式（12）可整理为

\begin{array}{l} α \int_{Ω}^{} ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} d x \leq \\ \int_{Ω}^{} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n}) d x \leq \int_{Ω}^{} f_{n} T_{k} (u_{n}) d x + \int_{Ω}^{} F \nabla T_{k} (u_{n}) d x \leq k {‖f_{n}‖}_{L^{1} (Ω)} + C \int_{Ω}^{} {|F ω^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x + \\ \frac{α}{2} \int_{Ω} ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} d x 。 \end{array}

其中， $C = {(\frac{2}{α p_{-}})}^{\frac{p_{+}^{'}}{p_{-}}}$ 。由于 $F \in W^{- 1, p^{'} (x)} (Ω, ω^{*})$ ，所以对任意的 $k > 0$ ，有

\frac{α}{2} \int_{Ω}^{} ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} d x \leq k {‖f_{n}‖}_{L^{1} (Ω)} + C_{1},

即

\int_{Ω}^{} ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} d x \leq C_{2} k {‖f_{n}‖}_{L^{1} (Ω)},

（14）

其中， $C_{1}, C_{2}$ 为与 $k$ 无关的常数。

由加权变指数在Sobolev空间的嵌入定理，有

$W_{0}^{1, p (x)} (Ω, ω)$ $L^{p_{s}^{*} (x)} (Ω)$ ${L^{(p_{s}^{*})}}^{-} (Ω)$ ，

其中，

\{\begin{array}{l} p_{s}^{*} (x) : = \frac{p (x) s (x) N}{[s (x) + 1] N - p (x) s (x)}, \\ p_{s}^{*} {(x)}^{-} : = \frac{p^{-} s^{-} N}{(s^{-} + 1) N - p^{-} s^{-}}, \\ p_{s}^{*} {(x)}^{+} : = \frac{p^{+} s^{+} N}{(s^{+} + 1) N - p^{+} s^{+}} 。 \end{array}

由式（14），对任意的 $k \geq 1$ ，有

{‖\nabla T_{k} (u_{n})‖}_{{L^{(p_{s}^{*})}}^{-} (Ω, ω)} \leq C {‖\nabla T_{k} (u_{n})‖}_{L^{p (x)} (Ω, ω)} \leq C {[\int_{Ω} ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} d x]}^{\frac{1}{β}} \leq C {[k {‖f‖}_{L^{1} (Ω)}]}^{\frac{1}{β}},

其中，

β = \{\begin{array}{l} p^{-}, {‖\nabla T_{k} (u_{n})‖}_{L^{p (x)} (Ω, ω)} \geq 1, \\ p^{+}, {‖\nabla T_{k} (u_{n})‖}_{L^{p (x)} (Ω, ω)} < 1 。 \end{array}

因 ${|u_{n}| \geq k} = {|T_{k} (u_{n})| \geq k}$ ，故有

\begin{array}{l} m e a s {|u_{n}| \geq k} \leq {[\frac{{‖T_{k} (u_{n})‖}_{L^{(p_{s}^{*})^{-}} (Ω, ω)}}{k}]}^{^{(p_{s}^{*})^{-}}} \leq \\ \frac{C {‖f‖}_{L^{1} (Ω)}^{(p_{s}^{*})^{-}}}{k^{^{(p_{s}^{*})^{-} (1 - \frac{1}{β})}}} \leq \frac{C {‖f‖}_{L^{1} (Ω)}^{(p_{s}^{*})^{-}}}{k^{^{(p_{s}^{*})^{-} (1 - \frac{1}{p^{-}})}}} ， \end{array}

（15）

其中， $C$ 为常数。

第2步 $u_{n}$ 在 $Ω$ 上几乎处处收敛。即证明 $u_{n}$ 是一个依测度收敛的柯西序列。

对每个固定的 $ε > 0$ 和任意的正整数 $k$ ，有集合关系

\begin{array}{l} {|u_{n} - u_{m}| > ε} \subset {|u_{n}| > k} ⋃ {|u_{m}| > k} ⋃ \\ {|T_{k} (u_{n}) - T_{k} (u_{m})| > ε}, \end{array}

即

\begin{array}{l} m e a s {|u_{n} - u_{m}| > ε} \leq \\ m e a s {|u_{n}| > k} + m e a s {|u_{m}| > k} + m e a s {|T_{k} (u_{n}) - T_{k} (u_{m})| > ε} \end{array}

。

由加权变指数在Sobolev空间中的嵌入定理，知 $W_{0}^{1, p (x)} (Ω, ω)$ $L^{q} (Ω)$ 是紧的，其中 $q < (p_{s}^{*})^{-}$ 。于是有 $T_{k} (u_{n})$ 在 $L^{q} (Ω)$ 中收敛。由式（15），有

\underset{n, m \to \infty}{l i m} s u p m e a s {|u_{n} - u_{m}| > ε} \leq C k^{- γ},

其中， $γ = (p_{s}^{*})^{-} (1 - \frac{1}{p^{-}}) > 0$ ，常数 $C$ 依赖于 $p (\cdot),$ $s (\cdot) ， {‖f‖}_{L^{1} (Ω)}$ 。由于 $k \geq 1$ ，可得

\underset{n, m \to \infty}{l i m} s u p m e a s {|u_{n} - u_{m}| > ε} = 0 。

当 $0 < k < 1$ 时， $m e a s {|u_{n}| > k} \leq |Ω|$ 。这暗示 $u_{n}$ 是依测度收敛的，且由Riesz定理，知存在 $u_{n}$ 的一个子序列（仍记作本身）以及一个可测函数 $u$ ，使得

u_{n} \to u

在

Ω

上几乎处处收敛。（16）

结合式（14），可断言能抽取 $T_{k} (u_{n})$ 的子列（仍记作本身），使得

T_{k} (u_{n}) \to T_{k} (u)

在

W_{0}^{1, p (x)} (Ω, ω)

中弱收敛。（17）

第3步 $T_{k} (u_{n})$ 在 $W_{0}^{1, p (x)} (Ω, ω)$ 中强收敛。

设 $k > 0$ ，在式（10）中选取检验函数

\{\begin{array}{l} v_{n} = ϕ (z_{n}), \\ z_{n} = T_{2 k} (u_{n} - T_{h} (u_{n}) + T_{k} (u_{n}) - T_{k} (u)), \end{array}

其中， $h > k > 0$ ， $ϕ (s)$ 引理1已定义，则有

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) ϕ^{'} (z_{n}) \nabla z_{n} d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) ϕ (z_{n}) d x + \int_{Ω} φ_{n} (u_{n}) ϕ^{'} (z_{n}) \nabla z_{n} d x = \\ \int_{Ω} f_{n} ϕ (z_{n}) d x + \int_{Ω} F ϕ^{'} (z_{n}) \nabla z_{n} d x 。 \end{array}

（18）

令 $M = 4 k + h$ ，可知在 ${|u_{n}| > M}$ 上， $\nabla z_{n} = 0$ ，且在集合 ${|u_{n}| > k}$ 上，有

g_{n} (x, u_{n}, \nabla u_{n}) ϕ (z_{n}) \geq 0 。

于是可将式（18）整理为

\begin{array}{l} \int_{Ω} a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n})) ϕ^{'} (z_{n}) \nabla z_{n} d x + \int_{|u_{n}| \leq k} g_{n} (x, u_{n}, \nabla u_{n}) ϕ (z_{n}) d x \leq \\ - \int_{Ω} ϕ_{n} (T_{M} (u_{n})) φ^{'} (z_{n}) \nabla z_{n} d x + \int_{Ω} f_{n} φ (z_{n}) d x + \int_{Ω} F φ^{'} (z_{n}) \nabla z_{n} d x ， \end{array}

（19）

方便起见，写为

(A) + (B) \leq (C) + (D) + (E)

。

在 ${|u_{n}| \leq k}$ 和 ${|u_{n}| > k}$ 上将（A）分解为

\begin{array}{l} \int_{Ω} a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n})) ϕ^{'} (z_{n}) \nabla z_{n} d x = \int_{{|u_{n}| \leq k}} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) ϕ^{'} (z_{n}) \times \\ \nabla T_{2 k} [u_{n} - T_{k} (u)] d x + \\ \int_{{|u_{n}| > k}} a (x, T_{k} (u_{n}), \nabla T_{M} (u_{n})) φ^{'} (z_{n}) \nabla z_{n} d x = \\ (A_{1}) + (A_{2}) 。 \end{array}

对于 $(A_{2})$ ，由式（3），有

(A_{2}) \geq - ϕ^{'} (2 k) \int_{{|u_{n}| > k}} |a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n})) \times| |\nabla T_{k} (u)| d x 。

由于 $a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n}))$ 在 $(L^{p^{'} (x)} (Ω, ω^{*} {))}^{N}$ 中有界，且 $\nabla T_{k} (u) χ_{{|u_{n}| > k}} \to 0$ （其中 $χ_{{|u_{n}| > k}} = 1$ ）在 $(L^{p (x)} {(Ω, ω))}^{N}$ 中强收敛，所以

(A_{2}) = ε (n) 。

（20）

对于 $(A_{1})$ ，由式（3）以及在 ${|u_{n}| \leq k}$ 上 $|u_{n} - T_{k} (u)| \leq 2 k$ ，可得

\begin{array}{l} (A_{1}) = \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) \times |\nabla T_{k} (u_{n}) - \nabla T_{k} (u)| ϕ^{'} (z_{n}) d x = \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - \\ a (x, T_{k} (u_{n}), \nabla T_{k} (u)) \times \\ |\nabla T_{k} (u_{n}) - \nabla T_{k} (u)| ϕ^{'} (z_{n})] d x + \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) \nabla T_{k} (u_{n}) \times ϕ^{'} (T_{k} (u_{n}) - T_{k} (u)) d x - \\ \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) ϕ^{'} (z_{n}) \nabla T_{k} (u) d x 。 \end{array}

（21）

由Nemytskii算子的连续性，可知 $\nabla T_{k} (u_{n}) \to \nabla T_{k} (u)$ 在 $(L^{p (x)} {(Ω, ω))}^{N}$ 中弱收敛，同时 $a (x, T_{k} (u_{n}), \nabla T_{k} (u)) ϕ^{'} (\nabla T_{k} (u_{n}) - \nabla T_{k} (u)) \to$ $a (x, T_{k} (u_{n}), \nabla T_{k} (u)) ϕ^{'} (0)$ 在 $（ L^{p^{'} (x)} (Ω, ω^{*}) ）^{N}$ 中强收敛，所以

\int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) \nabla T_{k} (u_{n}) \times ϕ^{'} (T_{k} (u_{n}) - T_{k} (u)) d x = \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) \nabla T_{k} (u) ϕ^{'} (0) d x + ε (n) 。

类似地，有

\int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) ϕ^{'} (z_{n}) \nabla T_{k} (u) d x = \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u)) ϕ^{'} (0) \nabla T_{k} (u) d x + ε (n) 。

于是，

(A_{1}) = \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - a (x, T_{k} (u_{n}), \nabla T_{k} (u))] [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] ϕ^{'} (z_{n}) d x + ε (n) 。

（22）

联合式（14）和式（22），有

(A) \geq \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - a (x, T_{k} (u_{n}), \nabla T_{k} (u))] [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] ϕ^{'} (z_{n}) d x + ε (n) 。

（23）

对于 $(B)$ ，由式（3）和式（6），有

\begin{array}{l} |(B)| = |\int_{{|u_{n}| \leq k}} g_{n} (x, u_{n}, \nabla u_{n}) ϕ (z_{n}) d x| \leq \\ \int_{{|u_{n}| \leq k}} b (k) [c (x) + \\ ω (x) {|\nabla T_{k} (u_{n})|}^{p (x)} |ϕ (z_{n})|] d x \leq b (k) \int_{{|u_{n}| \leq k}} c (x) |ϕ (z_{n})| d x + \\ \frac{b (k)}{α} \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) \times \nabla T_{k} (u_{n}) |ϕ (z_{n})| d x = \\ (B_{1}) + (B_{2}) 。 \end{array}

（24）

对于 $(B_{1})$ ，考虑 $c (x) \in L^{1} (Ω)$ ，有

(B_{1}) = ε (n) 。

（25）

对于 $(B_{2})$ ，可分解为

\begin{array}{l} (B_{2}) = \frac{b (k)}{α} \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) \times \\ \nabla T_{k} (u_{n}) |ϕ (z_{n})| d x = \\ \frac{b (k)}{α} \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - \\ a (x, T_{k} (u_{n}), \nabla T_{k} (u))] \times \\ [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] |ϕ (z_{n})| d x + \\ \frac{b (k)}{α} \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) \nabla T_{k} (u) \times \\ |ϕ (z_{n})| d x + \frac{b (k)}{α} \int_{Ω} a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) \times \\ [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] |ϕ (z_{n})| d x 。 \end{array}

（26）

对于 $(B_{2})$ 右端后2项，易知当 $n \to \infty$ 时为 $ε (n)$ ，由式（25）和式（26）， $(B)$ 可化为

\begin{array}{l} |(B)| = |\int_{{|u_{n}| \leq k}} g_{n} (x, u_{n}, \nabla u_{n}) ϕ (z_{n}) d x| \leq \frac{b (k)}{α} \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - \\ a (x, T_{k} (u_{n}), \nabla T_{k} (u))] [\nabla T_{k} (u_{n}) - \\ \nabla T_{k} (u)] |ϕ (z_{n})| d x + ε (n) 。 \end{array}

（27）

对于 $(D)$ ，易知在 $W_{0}^{1, p (x)} (Ω, ω)$ 中， $z_{n} \to T_{2 k} (u - T_{h} (u))$ ，且 $f_{n}$ 在 $L^{1} (Ω)$ 中是强紧的，于是有

\int_{Ω} f_{n} ϕ (z_{n}) d x = \int_{Ω} f_{n} ϕ (T_{2 k} (u - T_{h} (u))) d x + ε (n) 。

（28）

对于 $(E)$ ，由 $F \in W^{- 1, p^{'} (x)} (Ω, ω^{*})$ ，可知

\int_{Ω} F \nabla ϕ (z_{n}) d x = \int_{Ω} F \nabla T_{2 k} (u - T_{h} (u)) \times ϕ^{'} (T_{2 k} (u - T_{h} (u))) d x + ε (n) 。

（29）

对于 $(C)$ ，令 $n > M$ ，当 $n \to \infty$ 时，有

\begin{array}{l} (C) = \int_{Ω} φ_{n} (T_{M} (u)) ϕ^{'} (z_{n}) \nabla z_{n} d x = \int_{{|u_{n}| \leq M}} φ_{n} (T_{M} (u_{n})) ϕ^{'} (z_{n}) \nabla z_{n} d x = \int_{Ω} φ_{n} (T_{M} (u)) ϕ^{'} (T_{2 k} (u - T_{h} (u))) \times \\ \nabla T_{2 k} (u - T_{h} (u)) d x + ε (n) 。 \end{array}

（30）

综上，由式（23）和式（27），可将式（19）左端整理为

(A) + (B) \geq \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - a (x, T_{k} (u_{n}), \nabla T_{k} (u))] [(z_{n}) - \frac{b (k)}{α} |(z_{n})|] \times [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] d x 。

由引理1，取a=1，b= $\frac{b (k)}{α}$ ，结合式（28）~式（30），且当 $n \to \infty$ 时，对式（19）取极限，有

\begin{array}{l} \underset{n \to \infty}{l i m s u p} \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - a (x, T_{k} (u_{n}), \nabla T_{k} (u))] [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] d x \leq 2 \int_{Ω} f φ (T_{2 k} (u - T_{h} (u))) d x - \\ 2 \int_{Ω} ϕ (T_{M} (u)) φ^{'} (T_{2 k} (u - T_{h} (u))) \times \nabla T_{2 k} (u - T_{h} (u)) d x + \\ 2 \int_{Ω} F φ^{'} (T_{2 k} (u - T_{h} (u))) \times \\ \nabla T_{2 k} (u - T_{h} (u)) d x 。 \end{array}

（31）

现证当 $h$ →+∞时，式（31）右端3项均趋于0。

事实上，对于右端第1项，应用Lebesgue控制收敛定理便可得到结果。

对于右端第2项，不妨设

Ψ (t) = \int_{0}^{t} ϕ (τ) φ^{'} (τ - T_{h} (τ)) χ_{{h < | τ | \leq 2 k + h}} d τ,

于是， $Ψ (u) \in (W_{0}^{1, p (x)} {(Ω, ω))}^{N}$ ，用证明式（19）同样的方法，有

\begin{array}{l} \int_{Ω} ϕ (T_{M} (u)) φ^{'} (T_{2 k} (u - T_{h} (u))) \times \nabla T_{2 k} (u - T_{h} (u)) d x = \int_{Ω} ϕ (u) φ^{'} (u - T_{h} (u)) \times \\ \nabla u χ_{{h < | u | \leq 2 k + h}} d x = \int_{Ω} d i v Ψ (u) d x = 0 。 \end{array}

(32)

对于右端第3项，选取 $φ (T_{2 k} (u_{n} - T_{h} (u_{n})))$ 作为式（10）的检验函数，有

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + \int_{Ω} ϕ_{n} (u_{n}) \nabla φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x = \\ \int_{Ω} f_{n} φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + \\ \int_{Ω} F \nabla φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x 。 \end{array}

（33）

用证明式（19）类似的方法，可得

\int_{Ω} ϕ_{n} (u_{n}) \nabla φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x = 0 。

由式（3）、式（5）及Young不等式，有

\begin{array}{l} α \int_{{h \leq | u_{n} | \leq 2 k + h}} ω (x) | \nabla u_{n} |^{p (x)} φ^{'} (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x \leq \\ \int_{Ω} f_{n} φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + \\ C \int_{{| u_{n} | \geq h}} {|F ω {(x)}^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x + \frac{α}{2} \int_{{h \leq | u_{n} | \leq 2 k + h)} ω (x) | \nabla u_{n} |^{p (x)} \times \\ φ^{'} (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x ， \end{array}

即

\frac{α}{2} \int_{{h \leq | u_{n} | \leq 2 k + h)} ω (x) | \nabla u_{n} |^{p (x)} \times φ^{'} (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x \leq \int_{Ω} f_{n} φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + C \int_{{| u_{n} | \geq h}} {|F ω {(x)}^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x 。

（34）

进而，由于 $ρ_{p (x)}$ 是弱下半连续的，且 $ϕ^{'} \geq 1$ ，所以

\begin{array}{l} \int_{Ω} ω (x) {|\nabla T_{2 k} (u - T_{h} (u))|}^{p (x)} ϕ^{'} (T_{2 k} (u - T_{h} (u))) d x \leq \\ C \int_{Ω} ω (x) {|\nabla T_{2 k} (u - T_{h} (u))|}^{p (x)} d x \leq C \underset{n \to \infty}{l i m} i n f \int_{Ω} ω (x) {|\nabla T_{2 k} (u_{n} - T_{h} (u_{n}))|}^{p (x)} d x \leq \\ C \underset{n \to \infty}{l i m} i n f \int_{Ω} ω (x) {|\nabla T_{2 k} (u_{n} - T_{h} (u_{n}))|}^{p (x)} \times \\ φ^{'} (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x \leq \\ C_{1} \underset{n \to \infty}{l i m} i n f \int_{Ω} f_{n} φ (T_{2 k} (u_{n} - T_{h} (u_{n}))) d x + \\ C_{1} \underset{n \to \infty}{l i m} i n f \int_{{|u_{n}| \geq h}} {|F ω {(x)}^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x ， \end{array}

其中， $C, C_{1}$ 为常数。当 $n \to \infty$ ， $h \to \infty$ 时，对式（34）按顺序依次取极限，有

\underset{h \to \infty}{l i m} s u p \int_{{h \leq |u| \leq 2 k + h}} ω (x) {|\nabla u|}^{p (x)} \times ϕ^{'} (T_{2 k} (u - T_{h} (u))) d x = 0,

\underset{h \to \infty}{l i m s u p} \int_{Ω} F \nabla T_{2 k} (u_{n} - T_{h} (u_{n})) \times φ^{'} (T_{2 k} (u - T_{h} (u))) d x = 0 。

因此，当 $h \to \infty$ 时，对式（31）取极限，可得

\begin{array}{l} \underset{n \to \infty}{l i m} \int_{Ω} [a (x, T_{k} (u_{n}), \nabla T_{k} (u_{n})) - a (x, T_{k} (u_{n}), \nabla T_{k} (u))] \times \\ [\nabla T_{k} (u_{n}) - \nabla T_{k} (u)] d x = 0 。 \end{array}

由引理3，有

$T_{k} (u_{n}) \to T_{k} (u) 在 W_{0}^{1, p (x)} (Ω, ω)$ 中强收敛。

第4步非线性项 $g_{n} (x, u_{n}, \nabla u_{n})$ 在 $L^{1} (Ω)$ 中强收敛。

用Vitali定理证明 $g_{n} (x, u_{n}, \nabla u_{n})$ 在 $L^{1} (Ω)$ 中强收敛于 $g (x, u, \nabla u)$ 。

由式（16），可知 $g_{n} (x, u_{n}, \nabla u_{n})$ → $g (x, u, \nabla u)$ 在 $Ω$ 上几乎处处收敛，因此只需证明 ${g_{n} (x, u_{n}, \nabla u_{n})}$ 在 $Ω$ 上等度积分。

对任一可测集 $E \subset Ω$ 以及实数 $m \geq 0$ ，由式（6），有

\begin{array}{l} \int_{E} | g_{n} (x, u_{n}, \nabla u_{n}) | d x = \\ \int_{E ⋂ {| u_{n} | \leq m}} | g_{n} (x, u_{n}, \nabla u_{n}) | d x + \int_{E ⋂ {| u_{n} | > m}} | g_{n} (x, u_{n}, \nabla u_{n}) | d x \leq \\ b (m) \int_{E} [c (x) + ω (x) | \nabla u_{n} |^{p (x)}] d x + \int_{E ⋂ {| u_{n} | > m}} | g_{n} (x, u_{n}, \nabla u_{n}) | d x \leq \\ b (m) \int_{E ⋂ \{|u_{n}| \leq m\}} [c (x) + ω (x) {|\nabla T_{m} (u_{n})|}^{p (x)}] d x + \int_{E ⋂ \{|u_{n}| > m\}} |g_{n} (x, u_{n}, \nabla u_{n})| d x = I_{1} + I_{2} 。 \end{array}

对于 $I_{1}$ ，注意到 $c (x) \in L^{1} (Ω)$ 以及 ${T_{k} (u_{n})}$ 在 $W_{0}^{1, p (x)} (Ω, ω)$ 中是紧的，设 $ε$ 为任意小的正数，则至少存在1个 $δ^{'} > 0$ ，使得当 $m e a s (E) < δ^{'}$ 时，有

I_{1} \leq \frac{ε}{2} ， n \in N^{*}

。（35）

对于 $I_{2}$ ，设 $ϑ_{m}$ 为满足下列条件的函数：

\{\begin{array}{l} ϑ_{m} (s) = 0, | s |\leq m - 1, \\ ϑ_{m} (s) = s i g n (s), | s |\geq m, \\ ϑ_{m}^{'} (s) = 1, m - 1 < | s | < m 。 \end{array}

令 $m > 1$ ，选取 $ϑ_{m} (u_{n})$ 作为式（10）的检验函数，有

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) ϑ_{m}^{'} (u_{n}) d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) ϑ_{m} (u_{n}) d x + \int_{Ω} ϕ_{n} (u_{n}) ϑ_{m}^{'} (u_{n}) d x = \\ \int_{Ω} f_{n} ϑ_{m} (u_{n}) d x + \int_{Ω} F ϑ_{m}^{'} (u_{n}) d x 。 \end{array}

由符号条件式（5），可知

\begin{array}{l} \int_{{m - 1 < |u_{n}| \leq m}} a (x, u_{n}, \nabla u_{n}) \nabla u_{n} d x + \int_{{| u_{n} | > m - 1}} g_{n} (x, u_{n}, \nabla u_{n}) d x + \int_{{m - 1 < | u_{n} | \leq m}} ϕ_{n} (u_{n}) \nabla u_{n} d x = \\ \int_{{| u_{n} | > m - 1}} f_{n} d x + \int_{{m - 1 < | u_{n} | \leq m}} F \nabla u_{n} d x 。 \end{array}

用证明式（19）类似的方法，可得

\int_{{m - 1 < | u_{n} | \leq m}} ϕ_{n} (u_{n}) \nabla u_{n} d x = \int_{Ω} ϕ_{n} (T_{m} (u_{n})) \nabla T_{m} (u_{n}) d x - \int_{Ω} ϕ_{n} (T_{m - 1} (u_{n})) \nabla T_{m - 1} (u_{n}) d x = \int_{Ω} d i v Φ (T_{m} (u_{n})) d x - \int_{Ω} d i v Φ (T_{m - 1} (u_{n})) d x = 0 。

由式（3）和Young不等式，可得

\begin{array}{l} ɑ \int_{{m - 1 < | u_{n} | \leq m}} ω (x) | \nabla u_{n} |^{p (x)} d x + \int_{{| u_{n} | > m - 1}} g_{n} (x, u_{n}, \nabla u_{n}) d x \leq \\ \int_{{m - 1 < | u_{n} | \leq m}} a (x, u_{n}, \nabla u_{n}) \nabla u_{n} d x + \\ \int_{{| u_{n} | > m - 1}} g_{n} (x, u_{n}, \nabla u_{n}) d x \leq \\ \int_{{| u_{n} | > m - 1}} | f_{n} | d x + \int_{{m - 1 < | u_{n} | \leq m}} F \nabla u_{n} d x \leq \\ \int_{{| u_{n} | > m - 1}} | f | d x + \\ C \int_{{m - 1 < | u_{n} | \leq m}} {|F ω {(x)}^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x + \\ \frac{α}{2} \int_{{m - 1 < | u_{n} | \leq m}} ω (x) | \nabla u_{n} |^{p (x)} d x 。 \end{array}

(36)

移项后去掉非负项，可得

\int_{{| u_{n} | > m - 1}} g_{n} (x, u_{n}, \nabla u_{n}) d x \leq \int_{{| u_{n} | > m - 1}} | f | d x + C \int_{{m - 1 < | u_{n} | \leq m}} {|F ω {(x)}^{- \frac{1}{p (x)}}|}^{p^{'} (x)} d x 。

于是，有

\underset{n \to \infty}{l i m} \underset{n \in N}{s u p} \int_{{| u_{n} | > m - 1}} g_{n} (x, u_{n}, \nabla u_{n}) d x = 0 。

（37）

由式（35）和式（37），可知当m充分大时，至少存在1个 $δ^{'} > 0$ ，使得当 $m e a s (E) < δ^{'}$ 时，有

\int_{E} | g_{n} (x, u_{n}, \nabla u_{n}) | d x < ε ，

因此 ${g_{n} (x, u_{n}, \nabla u_{n})}$ 是等度可积的。由Vitali定理，知 $g_{n} (x, u_{n}, \nabla u_{n}) \to g (x, u, \nabla u)$ $在 L^{1} (Ω)$ 中强收敛。

第5步取极限。

设 $ψ \in W_{0}^{1, p (x)} (Ω, ω) ⋂ L^{\infty} (Ω)$ ，选取 $T_{k} (u_{n} - ψ)$ 作为式（10）的检验函数，令 $M = k + ∥ ψ ∥_{L^{\infty} (Ω)}$ ，有

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n} - ψ) d x + \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) T_{k} (u_{n} - ψ) d x + \int_{Ω} ϕ_{n} (u_{n}) \nabla T_{k} (u_{n} - ψ) d x = \int_{Ω} f_{n} T_{k} (u_{n} - ψ) d x + \\ \int_{Ω} F \nabla T_{k} (u_{n} - ψ) d x 。 \end{array}

（38）

一方面，由 $| u_{n} | > M$ ，可知 $| u_{n} - ψ | \geq | u_{n} | - ∥ ψ ∥_{L^{\infty} (Ω)} > k$ 。因此， ${| u_{n} - ψ | \leq k} \subseteq {| u_{n} | \leq M}$ ，于是式（38）左端第1个积分项可化为

\begin{array}{l} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n} - ψ) d x = \int_{Ω} a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n})) [\nabla T_{M} (u_{n}) - \nabla ψ] χ_{{| u_{n} - ψ | \leq k}} d x = \int_{Ω} [a (x, T_{M} (u_{n}), \nabla T_{M} (u_{n})) - \\ a (x, T_{M} (u_{n}), \nabla ψ)] [\nabla T_{M} (u_{n}) - \nabla ψ] χ_{{| u_{n} - ψ | \leq k}} d x + \int_{Ω} a (x, T_{M} (u_{n}), \nabla ψ) \times [\nabla T_{M} (u_{n}) - \nabla ψ] χ_{{| u_{n} - ψ | \leq k}} d x 。 \end{array}

由Fatou引理，有

\begin{array}{l} \underset{n \to \infty}{l i m i n f} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n} - ψ) d x \geq \int_{Ω} [a (x, T_{M} (u), \nabla T_{M} (u)) - \\ a (x, T_{M} (u), \nabla ψ)] [\nabla T_{M} (u) - \\ \nabla ψ] χ_{{| u - ψ | \leq k}} d x + \underset{n \to \infty}{l i m} \int_{Ω} a (x, T_{M} (u), \nabla ψ) [\nabla T_{M} (u) - \\ \nabla ψ] χ_{{| u - ψ | \leq k}} d x 。 \end{array}

且

\begin{array}{l} \underset{n \to \infty}{l i m i n f} \int_{Ω} a (x, u_{n}, \nabla u_{n}) \nabla T_{k} (u_{n} - ψ) d x \geq \\ \int_{Ω} a (x, T_{M} (u), \nabla T_{M} (u)) [\nabla T_{M} (u) - \\ \nabla ψ] χ_{{| u - ψ | \leq k}} d x = \\ \int_{Ω} a (x, u, \nabla u) (\nabla u - \nabla ψ) χ_{{| u - ψ | \leq k}} d x = \\ \int_{Ω} a (x, u, \nabla u) (\nabla u - \nabla ψ) d x 。 \end{array}

另一方面， $T_{k} (u_{n} - ψ)$ 在 $L^{\infty} (Ω)$ 中弱收敛于 $T_{k} (u - ψ)$ ，且 $g_{n} (x, u_{n}, \nabla u_{n})$ 在 $L^{1} (Ω)$ 中强收敛于 $g (x, u, \nabla u)$ ，所以

\begin{array}{l} \int_{Ω} g_{n} (x, u_{n}, \nabla u_{n}) T_{k} (u_{n} - ψ) d x \to \\ \int_{Ω} g (x, u, \nabla u) T_{k} (u - ψ) d x ， n \to \infty 。 \end{array}

（39）

同时， $T_{k} (u_{n} - ψ)$ 在 $W_{0}^{1, p (x)} (Ω, ω)$ 中弱收敛于 $T_{k} (u - ψ)$ ，且当 $n \geq M$ 时，在 ${| u_{n} - ψ | \leq k}$ 中，

ϕ_{n} (u_{n}) = ϕ (T_{m} (u_{n}))

，

于是有

\begin{array}{l} \int_{Ω} ϕ_{n} (u_{n}) \nabla T_{k} (u_{n} - ψ) d x \to \\ \int_{Ω} ϕ (u) \nabla T_{k} (u - ψ) d x ， n \to \infty \end{array}

。

由于 $F \in W^{- 1, p^{'} (x)} (Ω, ω^{*})$ 以及 $f_{n}$ 在 $L^{1} (Ω)$ 中强紧，有

\int_{Ω} F \nabla T_{k} (u_{n} - ψ) d x \to \int_{Ω} F \nabla T_{k} (u - ψ) d x ， n \to \infty ，

\int_{Ω} f_{n} T_{k} (u_{n} - ψ) d x \to \int_{0} f T_{k} (u - ψ) d x ， n \to \infty 。

综上，对式（10）取极限 $（ n \to \infty ）$ ，可得式（9），即u是式（1）的1个熵解。

定理1得证。

http://dx.doi.org/10.3785/j.issn.1008-9497.2022.05.004

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

AHAROUCH

， BENNOUNA

， TOUZANI

Existence of renormalized solution of some elliptic problems in Orlicz space

［J］. Revista Matematica Complutense， 2009， 22：91-110. doi:10.5209/rev_rema.2009.v22.n1.16319

[本文引用: 1]

[2]

AZROUL

， BENBOUBKER

M B

， RHOUDAF

On some p（x） -quasilinear problem with right-hand side measure

［J］. Mathematics and Computers in Simulation， 2014， 102： 117-130. DOI：10.1016/j.matcom.2013.09.009

[本文引用: 2]

[3]

ZHANG

， ZHOU

S L

Entropy and renormalized solutions for the p（x）-Laplacian equation with measure data

［J］. Bulletin of the Australian Mathematical Society， 2010， 82（3）： 459-479. DOI：10.1017/S0004972710000432

[本文引用: 2]

[4]

BOCCARDO

， GIACHETTI

， DIAZ

1， et al.

Existence and regularity of renormalized solutions for some elliptic problems involving derivatives of nonlinear terms

［J］. Journal of Differential Equations， 1993， 106（2）： 215-237. DOI：10.1006/jdeq.1993.1106

[本文引用: 1]

[5]

BOCCARDO

， CROCE

， ORSINA

Existence of solutions for some noncoercive elliptic problems involving derivatives of nonlinear terms

［J］. Differential Equations and Applications， 2012， 4（1）： 3-9. DOI：10.7153/dea-04-02

[本文引用: 1]

[6]

GOLDSHTEIN

， UKHLOV

Weighted Sobolev spaces and embedding theorems

［J］. Transactions of the American Mathematical Society， 2009， 361（7）： 3829-3850. DOI：10.48550/arXiv.math/0703725

[本文引用: 1]

[7]

BLANCHARD

Truncations and monotonicity methods for parabolic equations

［J］. Nonlinear Analysis： Theory， Methods & Applications， 1993， 21（10）： 725-743. DOI：10.1016/0362-546X（93）90120-H

[本文引用: 1]

[8]

BLANCHARD

， MURAT

， REDWANE

Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems

［J］. Journal of Differential Equations， 2001， 177（2）： 331-374. DOI：10.1006/jdeq.2000. 4013

[本文引用: 1]

[9]

BENBOUBKER

M B

， CHRAYTEH

， MOUMNI

M E

， et al.

Entropy and renormalized solutions for nonlinear elliptic problem involving variable exponent and measure data

［J］. Acta Mathematica Sinica， 2015， 31（1）： 151-169. DOI：10.1007/s10114-015-3555-7

[本文引用: 1]

[10]

DAl

L L

， GAO

W J

， LI

Z Q

Existence of solutions for degenerate elliptic problems in weighted Sobolev space

［J］. Journal of Function Spaces， 2015， 2015： 1-9. DOI：10.1155/2015/265127

[11]

代丽丽

一类具退化强制的椭圆方程熵解的存在性

［J］. 华东师范大学学报（自然科学版）， 2019（4）： 52-61. DOI：10.3969/j.issn.1000-5641.2019.04.006

[本文引用: 1]

DAI

L L

Existence of entropy solutions for an elliptic equation with degenerate coercivity

［J］. Journal of East China Normal University（Natural Science）， 2019（4）： 52-61. DOI：10.3969/j.issn.1000-5641. 2019.04.006

[本文引用: 1]

[12]

LIONS

J L

. Quelques Méthodes de Résolution des Problemes Aux Limites Nonlinéaires［M］. Paris： Dunod， 1969.

[本文引用: 1]

[13]

SCHWARTZ

J T

. Nonlinear Functional Analysis［M］. Boca Raton： CRC Press， 1969.

[本文引用: 1]

Existence of renormalized solution of some elliptic problems in Orlicz space

2009

... AHAROUCH等^［1］研究了在常指数情形下，当

μ \in W^{- 1, p^{'}} (Ω), g = g (x, u)

，且

φ \equiv 0

时，式（1）在Orlicz空间解的存在性结果.在变指数情形下，AZROUL等^［2］研究了椭圆方程 ...

On some p（x） -quasilinear problem with right-hand side measure

2014

... AHAROUCH等^［1］研究了在常指数情形下，当

μ \in W^{- 1, p^{'}} (Ω), g = g (x, u)

，且

φ \equiv 0

时，式（1）在Orlicz空间解的存在性结果.在变指数情形下，AZROUL等^［2］研究了椭圆方程 ...

... 以上研究均在不加权的Sobolev空间进行.本文将在文献［2-3］等的基础上，引入权函数，扩展为加权变指数的Sobolev空间，并在此框架下，研究式（1）解的存在性.首先，带变指数的偏微分方程模型相较常指数优势显著，其可更精确地描述扩散过程，当

p

不是常函数时，研究相关加权

A_{p (\cdot)}

的文献较少，需特别关注

L^{p (\cdot)} (Ω, ω)

空间的性质及嵌入.其次，权函数的引入增加了研究的难度，尤为困难的是空间的嵌入.最后，函数

φ

无增加任何条件，即使作为一个分布，此项在方程中也可能无意义，且右端项可积性不高.因无法得到式（1）的弱能量解，所以考虑其熵解.本文主要借助截断函数方法对逼近方程做估计，运用加权变指数在Sobolev空间中的嵌入关系，选取合适的检验函数，令

T_{k} (u_{n})

强收敛，并通过取极限，得到式（1）的熵解. ...

Entropy and renormalized solutions for the p（x）-Laplacian equation with measure data

2010

... 并得到熵解的存在性结果.ZHANG等^［3］在

a (x, s, ξ) = {|ξ|}^{p (x) - 2} ξ

，

g = 0

，

φ = 0

，且

μ \in

L^{1} (Ω) + W^{- 1, p^{'} (x)} (Ω)

的情形下，证明了重整化解和熵解的存在性.BOCCARDO等^［4］运用截断方法，证明了当

p (x)

为常函数，

F = 0

，

f \in W^{- 1, p^{'}} (Ω)

时，式（1）在Sobolev空间中重整化解的存在性和正则性.此后，BOCCARDO等^［5］继续研究带有非线性导数项

- d i v φ (u)

的非线性椭圆方程

A (u) = f - d i v φ (u)

，并证明了其存在

{W_{0}}^{1,1} (Ω)

解. ...

p

不是常函数时，研究相关加权

A_{p (\cdot)}

的文献较少，需特别关注

L^{p (\cdot)} (Ω, ω)

空间的性质及嵌入.其次，权函数的引入增加了研究的难度，尤为困难的是空间的嵌入.最后，函数

φ

T_{k} (u_{n})

强收敛，并通过取极限，得到式（1）的熵解. ...

Existence and regularity of renormalized solutions for some elliptic problems involving derivatives of nonlinear terms

... 并得到熵解的存在性结果.ZHANG等^［3］在

a (x, s, ξ) = {|ξ|}^{p (x) - 2} ξ

，

g = 0

，

φ = 0

，且

μ \in

L^{1} (Ω) + W^{- 1, p^{'} (x)} (Ω)

的情形下，证明了重整化解和熵解的存在性.BOCCARDO等^［4］运用截断方法，证明了当

p (x)

为常函数，

F = 0

，

f \in W^{- 1, p^{'}} (Ω)

时，式（1）在Sobolev空间中重整化解的存在性和正则性.此后，BOCCARDO等^［5］继续研究带有非线性导数项

- d i v φ (u)

的非线性椭圆方程

A (u) = f - d i v φ (u)

，并证明了其存在

{W_{0}}^{1,1} (Ω)

解. ...

Existence of solutions for some noncoercive elliptic problems involving derivatives of nonlinear terms

2012

... 并得到熵解的存在性结果.ZHANG等^［3］在

a (x, s, ξ) = {|ξ|}^{p (x) - 2} ξ

，

g = 0

，

φ = 0

，且

μ \in

L^{1} (Ω) + W^{- 1, p^{'} (x)} (Ω)

的情形下，证明了重整化解和熵解的存在性.BOCCARDO等^［4］运用截断方法，证明了当

p (x)

为常函数，

F = 0

，

f \in W^{- 1, p^{'}} (Ω)

时，式（1）在Sobolev空间中重整化解的存在性和正则性.此后，BOCCARDO等^［5］继续研究带有非线性导数项

- d i v φ (u)

的非线性椭圆方程

A (u) = f - d i v φ (u)

，并证明了其存在

{W_{0}}^{1,1} (Ω)

解. ...

Weighted Sobolev spaces and embedding theorems

2009

... 给出加权变指数在Sobolev空间的相关知识^［6］. ...

Truncations and monotonicity methods for parabolic equations

1993

... （vii）截断函数

T_{k} (s)

.一般情形下，对于在

R

中的

s, k

，其中

k \geq 0

，高度为

k

的截断函数^［7-8］定义为 ...

Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems

2001

... （vii）截断函数

T_{k} (s)

.一般情形下，对于在

R

中的

s, k

，其中

k \geq 0

，高度为

k

的截断函数^［7-8］定义为 ...

Entropy and renormalized solutions for nonlinear elliptic problem involving variable exponent and measure data

2015

... 证明分5步完成证明过程^［9-11］. ...

Existence of solutions for degenerate elliptic problems in weighted Sobolev space

2015

一类具退化强制的椭圆方程熵解的存在性

2019

... 证明分5步完成证明过程^［9-11］. ...

一类具退化强制的椭圆方程熵解的存在性

2019

... 证明分5步完成证明过程^［9-11］. ...

1969

... 由文献［12-13］的伪单调算子理论，可知式（10）至少存在1个弱解

u_{n} \in W_{0}^{1, p (x)} (Ω, ω)

，即对任意的

v \in W_{0}^{1, p (x)} (Ω, ω) ⋂ L^{\infty} (Ω),

有 ...

1969

... 由文献［12-13］的伪单调算子理论，可知式（10）至少存在1个弱解

u_{n} \in W_{0}^{1, p (x)} (Ω, ω)

，即对任意的

v \in W_{0}^{1, p (x)} (Ω, ω) ⋂ L^{\infty} (Ω),

有 ...

〈

〉