使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

转速受限条件下TBM刀盘混合驱动系统控制器设计

王飞
龚国芳
秦永峰

浙江大学流体动力与机电系统国家重点实验室，浙江杭州 310027

中图分类号： TU 43

最近更新：2020-01-19

DOI：10.3785/j.issn.1006-754X.2019.00.002

摘要

传统全断面硬岩隧道掘进机（tunnel boring machine, TBM）刀盘转速同步控制方法是针对变频电机单一驱动源进行设计的，直接应用于混合驱动型TBM刀盘驱动系统易导致齿轮齿圈发生严重的偏载，显著降低TBM刀盘传动系统的使用寿命和TBM设备完好率。考虑到实际掘进过程中对刀盘转速的限制和系统参数漂移，采用自适应控制策略，针对电液混合驱动型TBM刀盘驱动系统设计基于驱动源力矩控制的转速控制方法。建立了齿轮齿圈传动系统模型，系统的参数不确定性得到充分考虑。通过MATLAB/AMESim联合仿真表明，该自适应控制系统对参数漂移具有补偿作用，在精确控制刀盘转速的同时，实现了不同类型驱动源间的负载力矩分配，原系统中的偏载问题得到了解决。电液混合驱动型TBM刀盘驱动系统通过液压马达和变频电机两种驱动源驱动特性的互补，有效提高了其地质适应性，并对提高掘进速度有着重要的作用。

关键词

刀盘驱动; TBM; 自适应控制; 负载力矩分配

全断面硬岩隧道掘进机（tunnel boring machine, TBM）凭借其环境友好、隧道施工安全高效等特点，被广泛应用于输水洞渠，公路和铁路隧道等长、大隧道的施工中^[

1,2,3,4,5,6,7]。TBM主机前部是装有若干滚刀的刀盘，由刀盘驱动系统驱动刀盘旋转，滚刀与掌子面接触产生切削作用剥离岩石。剥离下来的石渣通过TBM刀盘上的产渣斗和渣槽滑落到主皮带机上，通过后配套系统输送至隧道外。在不同地质条件下，刀盘转速需要实时调节以达到最高的岩石切削效率。由此可见，TBM刀盘转速控制系统的性能对TBM掘进性能有着至关重要的影响。

电液混合驱动型TBM刀盘驱动系统由若干变频电机和液压马达组成，通过齿轮齿圈传动系统将驱动单元进行刚性连接，如图1所示^[

8,9]。传统单一驱动源TBM刀盘转速控制系统采用的是多轴同步系统的相同转速并联控制策略，即作为驱动单元的电机接收相同的转速指令信号，通过自闭环控制方式分别对转速指令信号进行跟踪^{[参考文献 10
百度学术}10,11]。但齿轮齿圈传动系统和多轴同步系统有着明显的差别，多轴同步系统中的驱动单元通常不进行刚性连接，且各驱动单元的负载并不相关。而齿轮齿圈传动系统通过机械连接将各驱动单元的转速进行强制同步，且驱动单元负载之和为刀盘所受之负载。由于传统TBM刀盘转速控制系统缺乏对负载分配的控制，在实际使用中，特别是在刀盘转速发生变化的过程中，易导致部分小齿轮出现极大的偏载，从而使得主轴承侧向力加大，降低轴承使用寿命。这种现象在电液混合驱动型刀盘驱动系统中尤其明显^{[参考文献 7
百度学术}7]。

本文提出一种基于驱动单元力矩控制的自适应控制方法，通过对TBM动力学参数的在线估计，对掘进过程中的系统参数漂移进行补偿，从而对刀盘转速进行精确控制的同时，实现对负载力矩分配的控制。

1 非线性刀盘混合驱动系统建模

由于制造误差、安装误差和机构件磨损，齿轮齿圈传动系统存在随时间变化的齿隙^[

9,12]。在考虑时变齿隙的条件下，建立刀盘混合驱动系统的非线性数学模型。考虑到一般性，电液混合驱动系统由

$m$ 台电机和

$n$ 台液压马达组成。

根据牛顿第二定律，刀盘的动力学方程可以表示为：

$T_{c} = J_{c} {\ddot{θ}}_{c}^{} + b_{c} {\dot{θ}}_{c}^{} + D$

(1)

式中： $J_{c}$ 为刀盘转动惯量， $b_{c}$ 为刀盘等效黏性阻尼系数， $D$ 为集总参数模型下刀盘混合驱动系统受到的外负载和其他外干扰， ${\dot{θ}}_{c}^{}$ 和 ${\ddot{θ}}_{c}^{}$ 分别为刀盘的角速度和角加速度， $T_{c}$ 为刀盘总驱动力矩。

$T_{c}$ 可以表示为：

$T_{c} = i_{g} \overset{m + n}{\sum_{i = 1}} M_{i, p}$

(2)

式中： $i_{g}$ 为齿轮齿圈系统传动比， $M_{i, p}$ 为第i个驱动单元行星齿轮减速机的输出力矩。行星齿轮减速机输出端与小齿轮刚性连接，通过齿轮齿圈传动系统向刀盘输送力矩。

如前所述，齿隙是不可避免的。齿轮齿隙的简化模型如图2所示，第 $i$ 个小齿轮的啮合力矩可以表示为：

$M_{i, p} = b_{m} R_{g} Δ \dot{x} + k_{m} R_{g} F (Δ x)$

(3)

式中： $b_{m}$ 为啮合过程中的等效黏性阻尼系数，用以表示啮合过程中因摩擦等原因导致的能量损失； $k_{m}$ 为啮合刚度； $R_{g}$ 为大齿圈半径； $F (Δ x)$ 为齿轮齿圈传动系统的时变齿隙； $Δ {\dot{x}}_{i}^{}$ 和 $Δ x_{i}$ 分别为啮合过程中大齿圈与小齿轮的相对速度差和相对位移差， $Δ {\dot{x}}_{i}^{} = R_{p} {\dot{θ}}_{i, p}^{} - R_{r} {\dot{θ}}_{c}^{}$ ， $Δ x_{i} = R_{p} θ_{i, p} - R_{r} θ_{c}$ ，其中 $R_{p}$ 为小齿轮的半径，齿轮齿圈传动系统中所有小齿轮的半径相同， ${\dot{θ}}_{i, p}^{}$ 为大齿圈的角速度。

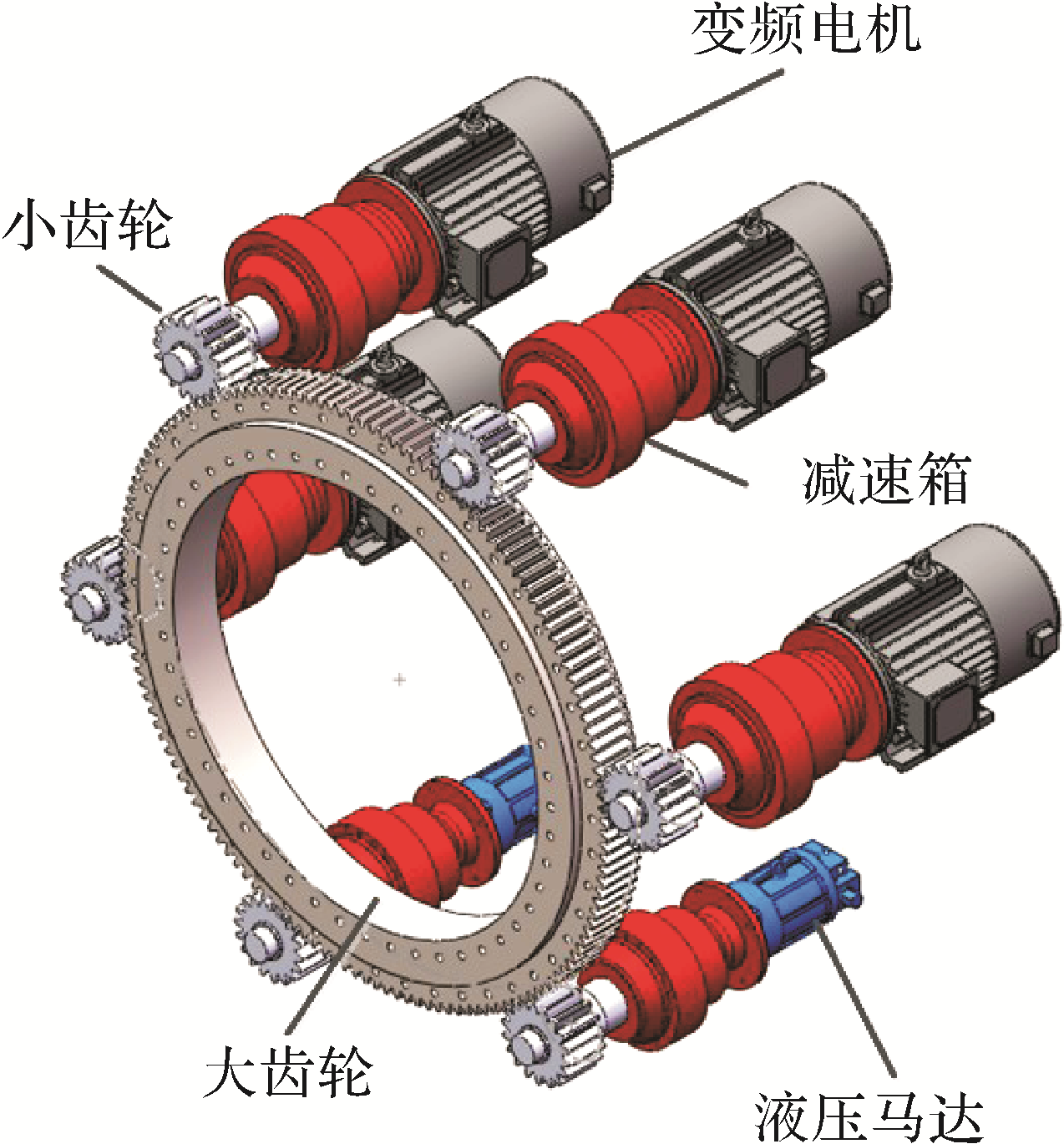
图 1 TBM齿轮齿圈传动系统简图

Fig. 1 Schematic diagram of the gear-ring transmission system of TBM

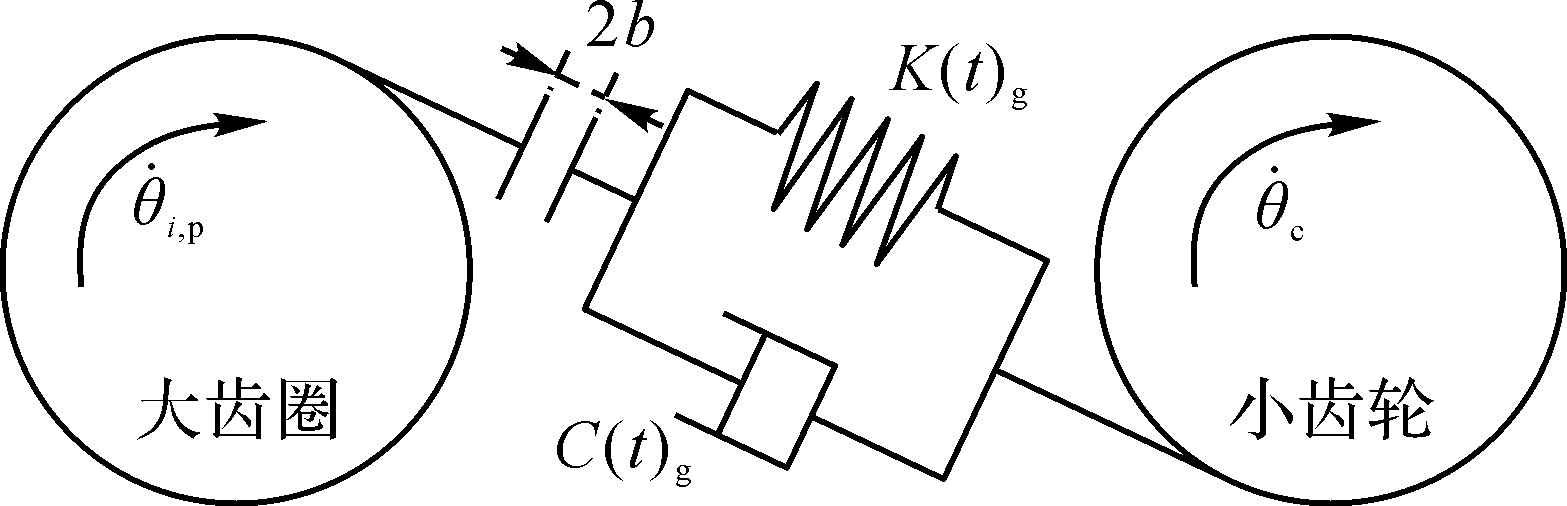
图 2 齿轮齿隙简化模型

Fig. 2 Schematic diagram of backlash of gear

以 $2 b (t)$ 表示与机构件磨损相关的时变齿隙，则齿轮齿圈传动系统的时变齿隙可以表示为：

$F (Δ x) = \{\begin{matrix} \begin{matrix} Δ x - b (t), \\ 0, \\ b (t) + Δ x, \end{matrix} & \begin{matrix} b (t) < Δ x \\ |Δ x| \leq b (t) \\ Δ x < - b (t) \end{matrix} \end{matrix}$

(4)

由于行星齿轮减速机与驱动单元固连，其转动惯量等物理参数可与驱动单元相应的物理参数进行综合，故刀盘传动可以视为理想传动过程，以 $M_{i, r}$ 表示第i个行星齿轮减速机的输入力矩，则 $M_{i, r}$ 可以表示为：

$M_{i, r} = \frac{1}{i_{r}} M_{i, p}$

(5)

式中： $i_{r}$ 为行星齿轮减速机的减速比。

在本系统当中，电机与液压马达均使用其自身的控制器以保证力矩跟踪性能，于是无论是将电机还是液压马达作为驱动单元，均可看做是理想驱动单元，其输出力矩与指令信号成线性关系。根据牛顿第二定律，获得驱动单元动力学方程如下：

$T_{i} = J_{i} {\ddot{θ}}_{i}^{} + b_{i} {\dot{θ}}_{i}^{} + M_{i, r}$

(6)

式中： $J_{i}$ 为驱动单元i的等效转动惯量； ${\dot{θ}}_{i}^{}$ 和 ${\ddot{θ}}_{i}^{}$ 分别为驱动单元i的角速度和角加速度； $b_{i}$ 为驱动单元i的等效黏性阻尼系数； $T_{i}$ 为驱动单元i的驱动力矩，可以表示为 $T_{i} = K_{T} u_{i}$ ，其中 $K_{T}$ 为力矩系数,u_i 为驱动单元i的输入信号。

2 负载力矩观测器设计

采用龙贝格观测器^[

13,14]对负载力矩进行观测，设计观测器为：

$\hat{D} = k_{1} (\hat{ω} - {\dot{θ}}_{c}^{})$

(7)

$\dot{\hat{ω}} = \frac{1}{J_{c}} [- \hat{D} + T_{c} - k_{2} (\hat{ω} - {\dot{θ}}_{c}^{}) - b_{c} {\dot{θ}}_{c}^{}]$

(8)

式中： $\hat{ω}$ 为对刀盘转速 ${\dot{θ}}_{c}^{}$ 的估计值； $k_{1}$ 为观测器增益， $k_{2}$ 为观测器辅助增益，且 $k_{1} > 0, k_{2} > 0$ ； $\hat{D}$ 为对干扰项 $D$ 的估计。

由于 $D = T_{c} - J_{c} {\ddot{θ}}_{c}^{} - b_{c} {\dot{θ}}_{c}^{}$ ，结合式(8)，则干扰观测误差 $\tilde{D}$ 可以表示为：

$\begin{array}{l} \tilde{D} = D - \hat{D} = J_{c} (\dot{\hat{ω}} - {\ddot{θ}}_{c}) + k_{2} (ω - {\dot{θ}}_{c}) = \\ - J_{c} \dot{\tilde{ω}} - k_{2} \tilde{ω} \end{array}$

(9)

式中： $\tilde{ω}$ 为转速误差， $\tilde{ω} = {\dot{θ}}_{c} - \hat{ω}$ 。

通过Lyapunov稳定性定理对观测器的稳定性进行验证，定义Lyapunov函数为：

$V_{1} = \frac{1}{2 k_{1}} {\tilde{D}}^{2} + \frac{1}{2} {\tilde{ω}}^{2}$

(10)

则式（10）可以进行如下化简：

$\begin{array}{l} {\dot{V}}_{1} = \frac{1}{k_{1}} \tilde{D} \dot{\tilde{D}} + \tilde{ω} \dot{\tilde{ω}} = \\ \frac{1}{k_{1}} \tilde{D} (\dot{D} - \dot{\hat{D}}) + \tilde{ω} ({\ddot{θ}}_{c} - \dot{\hat{ω}}) \end{array}$

(11)

若干扰相对于控制器响应时间变化较慢，且 $k_{1}$ 取值较大时，则可认为：

$\frac{1}{k_{1}} \dot{D} \approx 0$

(12)

将式（7）、（8）和（12）代入式（11），可得：

$\begin{array}{l} V_{1}^{̇} = \frac{1}{k_{1}} \tilde{D} (\dot{D} - \dot{\hat{D}}) + J_{c} \tilde{ω} ({\ddot{θ}}_{c} - \dot{\hat{ω}}) = \\ \frac{1}{k_{1}} \tilde{D} \dot{D} - \tilde{D} (\hat{ω} - {\dot{θ}}_{c}) + J_{c} \tilde{ω} [- D + \hat{D} + \\ k_{2} (\hat{ω} - {\dot{θ}}_{c})] = \\ \frac{1}{k_{1}} \tilde{D} \dot{D} + \tilde{D} \tilde{ω} + J_{c} \tilde{ω} (- \tilde{D} - k_{2} \tilde{ω}) = \\ \frac{1}{k_{1}} \tilde{D} \dot{D} - J_{c} k_{2} {\tilde{ω}}^{2} = \\ - J_{c} k_{2} {\tilde{ω}}^{2} \end{array}$

(13)

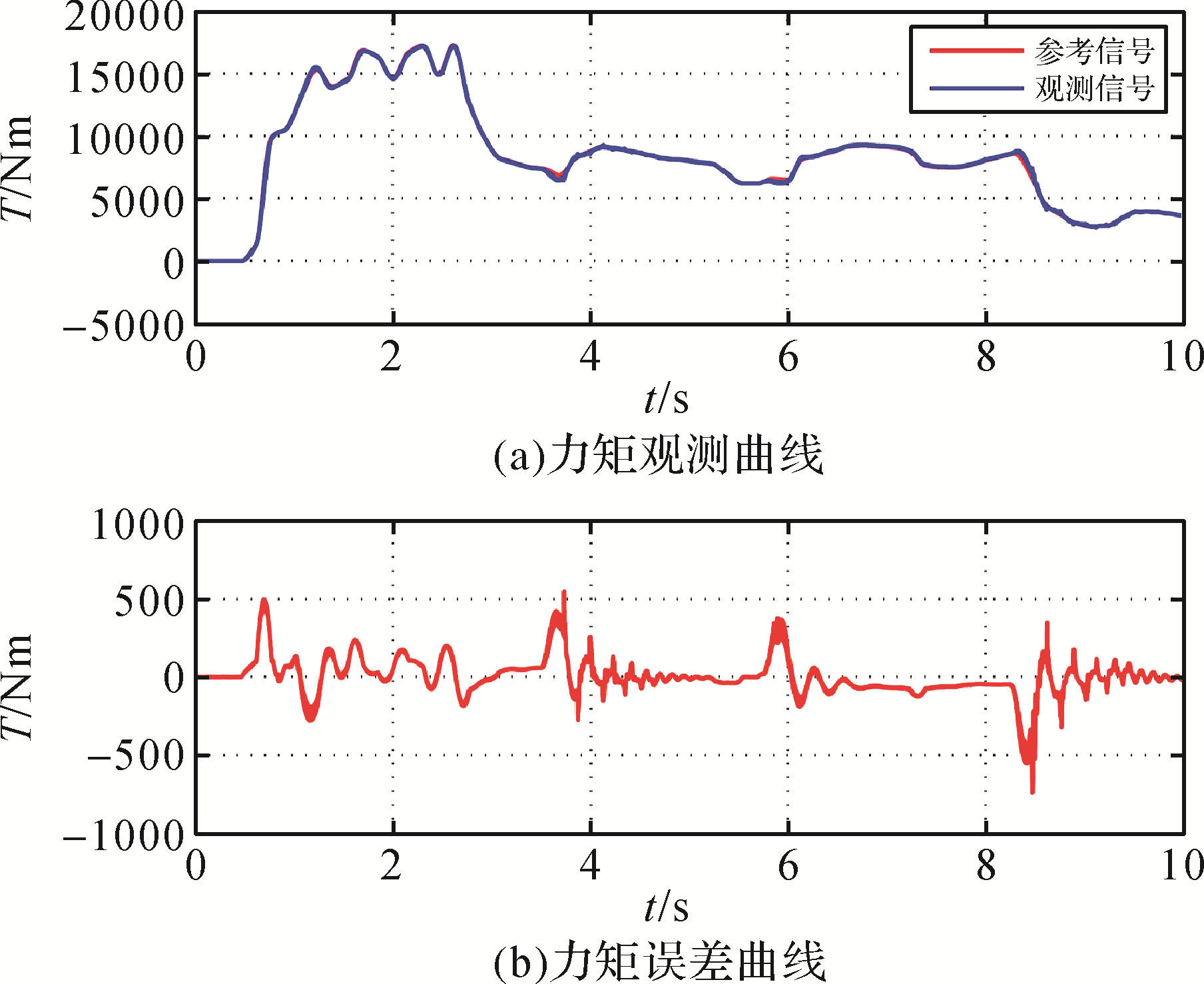
由于 ${\dot{V}}_{1}^{} = - k_{2} {\tilde{ω}}^{2} \leq 0$ ，即 $V_{1}^{̇}$ 为负定函数，根据LaSalle不变集定理，可知该观测器是稳定的，能够实现对干扰观测值的有效观测。线性观测器观测效果如图3所示，可见龙贝格观测器能够对负载力矩进行有效跟踪，观测器的最大误差为500 Nm，最大偏差为3.3%。

图 3 龙贝格观测器负载力矩观测效果

Fig. 3 Observation effect of load torque of the Luenberger observer

3 基于驱动单元力矩控制的刀盘转速自适应控制器设计

在TBM掘进过程中，由于地质条件实时发生变化，刀盘驱动系统动力学模型的物理参数实时发生改变，故需要设计相应的自适应控制方法对其物理参数的变化进行追踪和补偿^[

15]。同时由于TBM刀盘转速具有最高值限制以保证系统安全，在控制器设计当中也应予以考虑^{[参考文献 3
百度学术}3,16,17]。

通过刀盘转速自适应控制器对黏性阻尼系数和外干扰进行实时估计，获得当前所需驱动力矩值，即各个驱动单元力矩的总和。通过负载力矩分配器按照需要将力矩分配给各个驱动单元，从而实现在保证TBM刀盘转速跟踪精度的同时保证均载或其他所要求的力矩分配。刀盘转速自适应控制器的控制如图4所示。

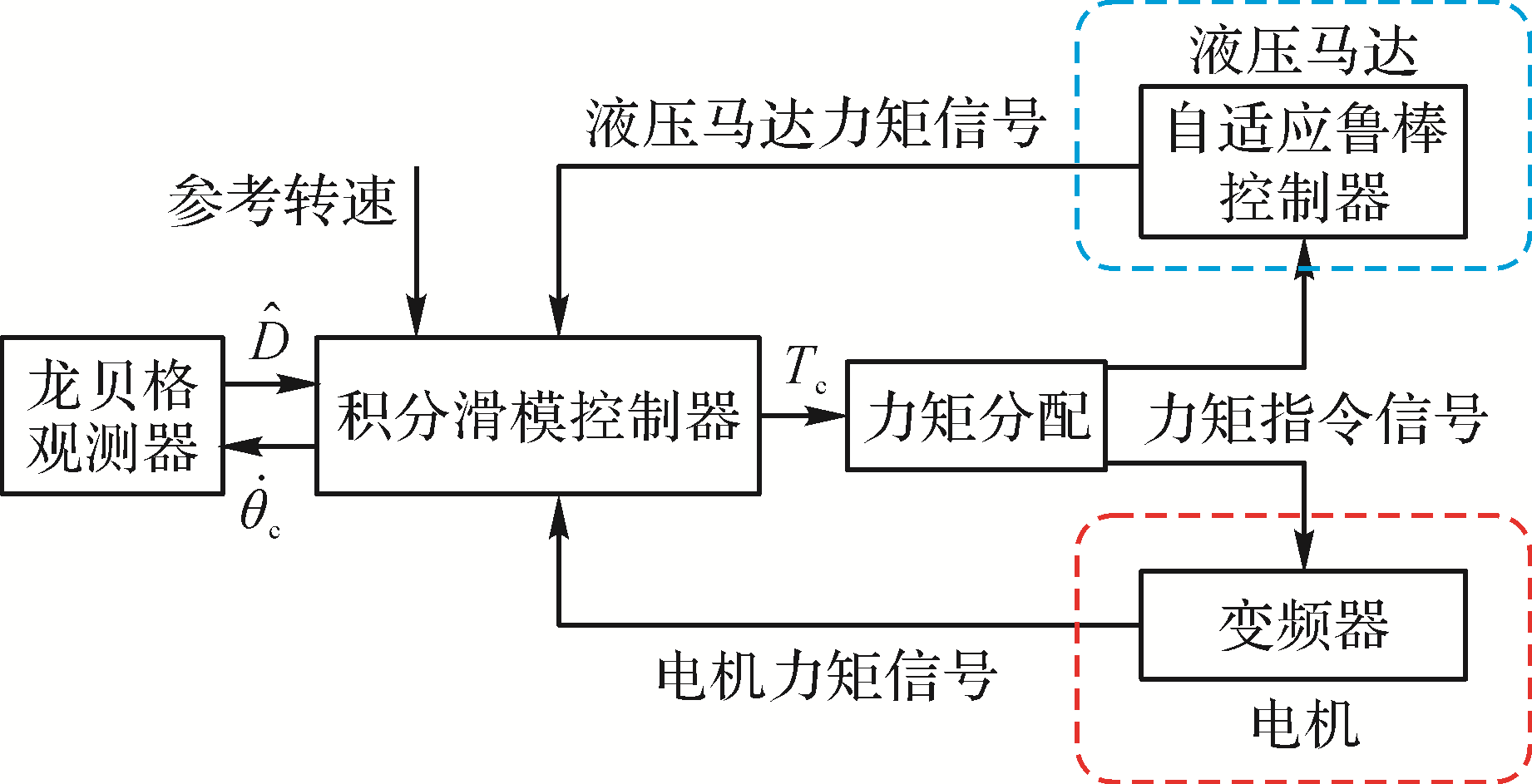
图4 刀盘转速自适应控制器的控制示意图

Fig. 4 Control diagram of rotational speed adaptive controller of cutterhead

基于Lyapunov稳定性定理的自适应控制器设计方法如下：

假设1：系统物理参数均是有界的，且上界已知，系统参数满足线性化参数条件。

设 $x_{1} = [{\dot{θ}}_{c}^{}]$ ，刀盘动力学系统输入为驱动系统中驱动单元输出的合力矩 $T_{c} = \overset{m + n}{\sum_{i = 1}} i_{r} i_{g} K_{T} u_{i}$ ，则将系统重写为状态空间的形式：

$\{\begin{array}{l} {\dot{x}}_{1}^{} = \frac{1}{J_{c}} (T_{c} - b_{c} {\dot{θ}}_{c}^{} - D) \\ y = x_{1} \end{array}$

(14)

刀盘角速度跟踪误差 $z_{1}$ 可表示为：

$z_{1} = x_{1} - x_{1 d}$

(15)

自适应控制器的设计目的是在有效估计系统参数的同时，使系统误差渐进收敛至零，同时使得控制状态 $x_{1} \leq γ_{1} = {\dot{θ}}_{m a x}^{}, γ_{1} > 0$ ，即 $γ_{1} = {\dot{θ}}_{m a x}^{}$ 为刀盘转速的最大值。为了达到这样的设计目的，将对称barrier函数引入控制系统李雅普诺夫候选函数的设计当中。设参数估计矩阵为：

$θ = [θ_{1} θ_{2}]^{T} = {[\frac{b_{c}}{J_{c}} \frac{D}{J_{c}}]}^{\begin{array}{l} T \end{array}}$

(16)

通过确定性等价原理，原系统可以表示为：

$\{\begin{array}{l} {\dot{x}}_{1}^{} = K_{T} u - {\overset{̑}{θ}}_{1}^{} {\dot{θ}}_{c}^{} - {\overset{̑}{θ}}_{2}^{} \\ y = x_{1} \end{array}$

(17)

式中： $u = T_{c}$ ，为刀盘动力学系统输入。

为了保证自适应控制器稳定，其控制律可依据李雅普诺夫定理进行推导，设计正定的李雅普诺夫候选函数为：

$V_{1} = \frac{1}{2} l o g \frac{γ_{z}^{2}}{γ_{z}^{2} - z_{1}^{2}} + \frac{1}{2} {\tilde{θ}}^{T} Γ^{- 1} \tilde{θ}$

(18)

式中； $γ_{z} > 0$ ，γ_z 为误差 $z_{1}$ 的最大值，即 $z_{1} \leq |γ_{z}|$ ； $\tilde{θ} = \hat{θ} - θ$ ,为系统估计误差矩阵; $Γ$ 为对称且正定的参数自适应速率矩阵。

则李雅普诺夫函数的微分可以表示为：

${\dot{V}}_{1}^{} = \frac{z_{1} {\dot{z}}_{1}^{}}{γ_{z}^{2} - z_{1}^{2}} + {\tilde{θ}}^{T} Γ^{- 1} \dot{\hat{θ}}$

(19)

对 $z_{1} = x_{1} - x_{1 d}$ 进行微分，得到：

$\begin{array}{l} {\dot{z}}_{1}^{} = {\dot{x}}_{1}^{} - {\dot{x}}_{1 d}^{} = \\ K_{T} u - θ_{1} {\dot{θ}}_{c}^{} - θ_{2} - {\dot{x}}_{1 d}^{} \end{array}$

(20)

将式（20）代入式(19)，可得：

${\dot{V}}_{1}^{} = \frac{z_{1} (K_{T} u - θ_{1} {\dot{θ}}_{c}^{} - θ_{2} - {\dot{x}}_{1 d}^{})}{γ_{z}^{2} - z_{1}^{2}} + {\tilde{θ}}^{T} Γ^{- 1} \dot{\hat{θ}}$

(21)

设计自适应控制器控制律为：

$u = \frac{1}{K_{T}} [{\overset{̑}{θ}}_{1}^{} {\dot{θ}}_{c}^{} + {\overset{̑}{θ}}_{2}^{} + {\dot{x}}_{1 d}^{} - (γ_{z}^{2} - z_{1}^{2}) κ_{1} z_{1}]$

(22)

令刀盘动力学系统参数矩阵 $φ_{1} = [- {\dot{θ}}_{c}^{} {, - 1]}^{T}$ ，将式(22)代入式(21)，得到：

$\begin{array}{l} {\dot{V}}_{1}^{} = \frac{z_{1} ({\tilde{θ}}_{1}^{} {\dot{θ}}_{c}^{} + {\tilde{θ}}_{2}^{} - (γ_{z}^{2} - z_{1}^{2}) κ_{1} z_{1})}{γ_{z}^{2} - z_{1}^{2}} + {\tilde{θ}}^{T} Γ^{- 1} \dot{\hat{θ}} = \\ - κ_{1} z_{1}^{2} - \frac{{\tilde{θ}}^{T} φ_{1} z_{1}}{γ_{z}^{2} - z_{1}^{2}} + {\tilde{θ}}^{T} Γ^{- 1} \dot{\hat{θ}} = \\ - κ_{1} z_{1}^{2} + {\tilde{θ}}^{T} (Γ^{- 1} \dot{\hat{θ}} - \frac{φ_{1} z_{1}}{γ_{z}^{2} - z_{1}^{2}}) \end{array}$

(23)

根据李雅普诺夫稳定性定理获得自适应控制器参数更新率为：

$\dot{\hat{θ}} = \frac{Γ φ_{1} z_{1}}{γ_{z}^{2} - z_{1}^{2}}$

(24)

对于驱动单元本身的动力学系统，由于物理参数较为稳定，易通过离线辨识得到相应参数的准确值，进而设计内模控制器对其进行补偿。针对液压马达的非线性控制特性，可采用鲁棒控制器对其进行控制。

负载力矩分配是根据实际的工程要求进行优化，优化方程可表示为：

$m i n J = \int λ f (x) d t$

(25)

式中： $J$ 为设计的代价方程； $λ$ 为 $m + n$ 个元素的行矩阵，表示每个驱动单元贡献的驱动力矩在总驱动力矩当中的占比； $f (x)$ 为代价函数，与TBM的状态值有关。

每个驱动单元的驱动力矩指令信号可以表示为：

$\begin{array}{l} T_{i} = λ_{i} T_{c} \\ s . t . λ_{1} + λ_{2} + \dots + λ_{n + m} = 1 \\ T_{c} > 0 N m \end{array}$

式中 $λ_{i}$ 为行矩阵 $λ$ 中第 $i$ 个元素，从而实现力矩的最优分配。

4 刀盘转速跟踪性能仿真及分析

通过AMESim（Advanced Modeling Environment for performing Simulation of engineer system）和MATLAB/Simulink软件联合仿真的方式进行控制器有效性的验证。AMESim被广泛应用于工程机械、车辆的原理设计和验证^[

18]。借助AMESim软件对液压系统进行建模，同时使用MATLAB/Simulink进行控制系统设计，在使用MATLAB/Simulink求解器的基础上，搭建仿真模型进行联合仿真。同时，为了不失一般性，并减轻计算机的计算负担，仿真系统中包含1台变频电机和1台液压马达。在该联合仿真系统中，进行以下2种控制器的对比仿真：1) 传统转速并联控制器；2）新型TBM刀盘转速自适应控制器。

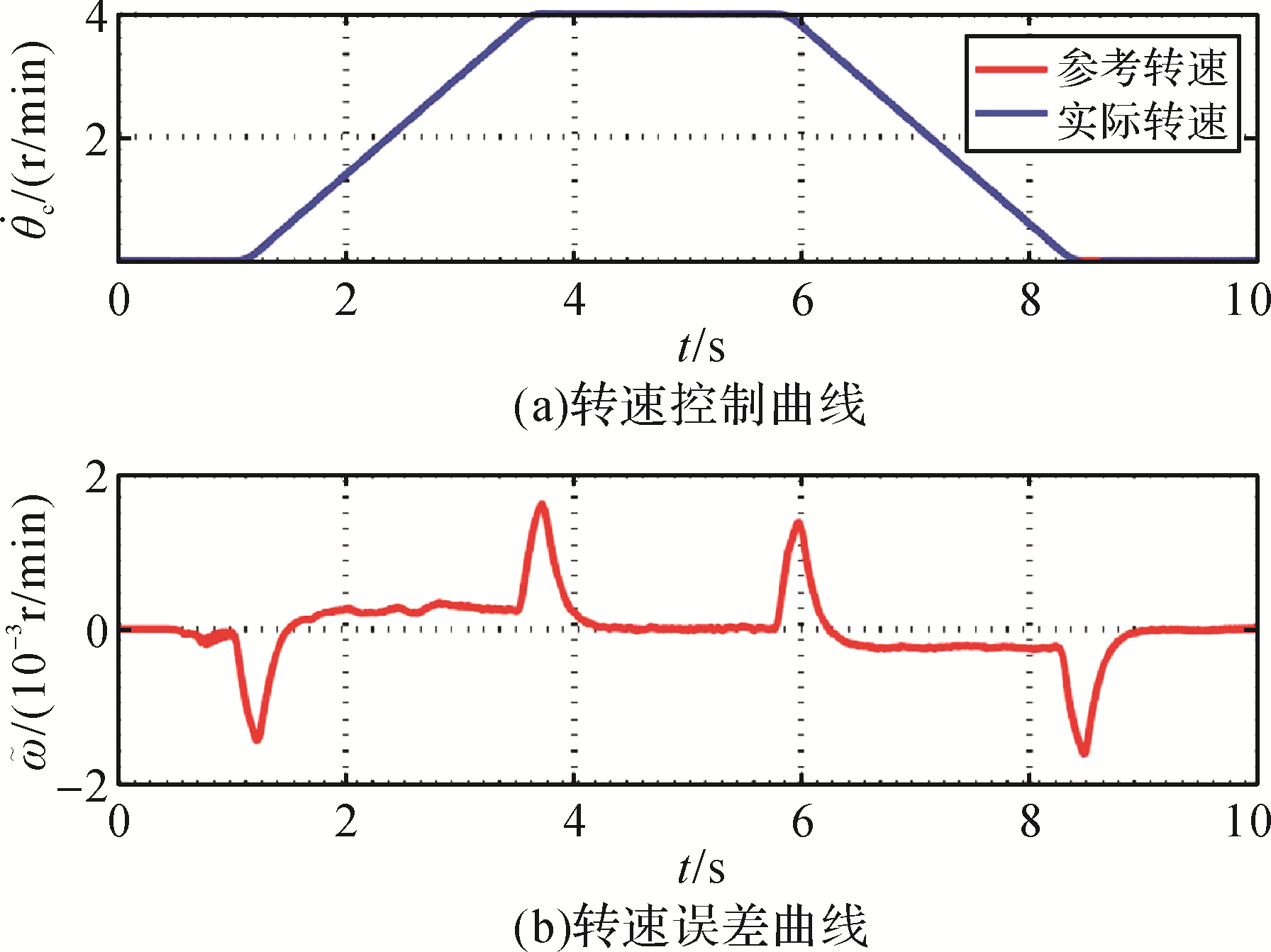
对于传统转速并联控制器，其转速跟踪性能如图5所示。转速并联控制器虽然可以获得较好的转速跟踪效果，但是由于其开环特性，转速跟踪误差无法收敛到零值，导致在刀盘转动过程中稳态误差始终存在。同时，由于转速并联控制器依靠驱动源自身对转速进行控制，驱动源间驱动力矩没有进行有效的调配，导致驱动力矩不同步，甚至出现一类驱动源成为另一类驱动源负载的情况。如图6所示，由于电机之间不均载现象不明显，为了说明问题，仅给出1台电机与1台液压马达驱动时的驱动力矩曲线。不均载的力矩分配特性与实际施工中驱动力矩分配相似，仿真结果复现了实际TBM驱动系统中出现的情况。

图5 传统转速并联控制器刀盘转速控制和误差曲线

Fig. 5 Cutterhead rotational speed control and error curves of traditional speed parallel controller

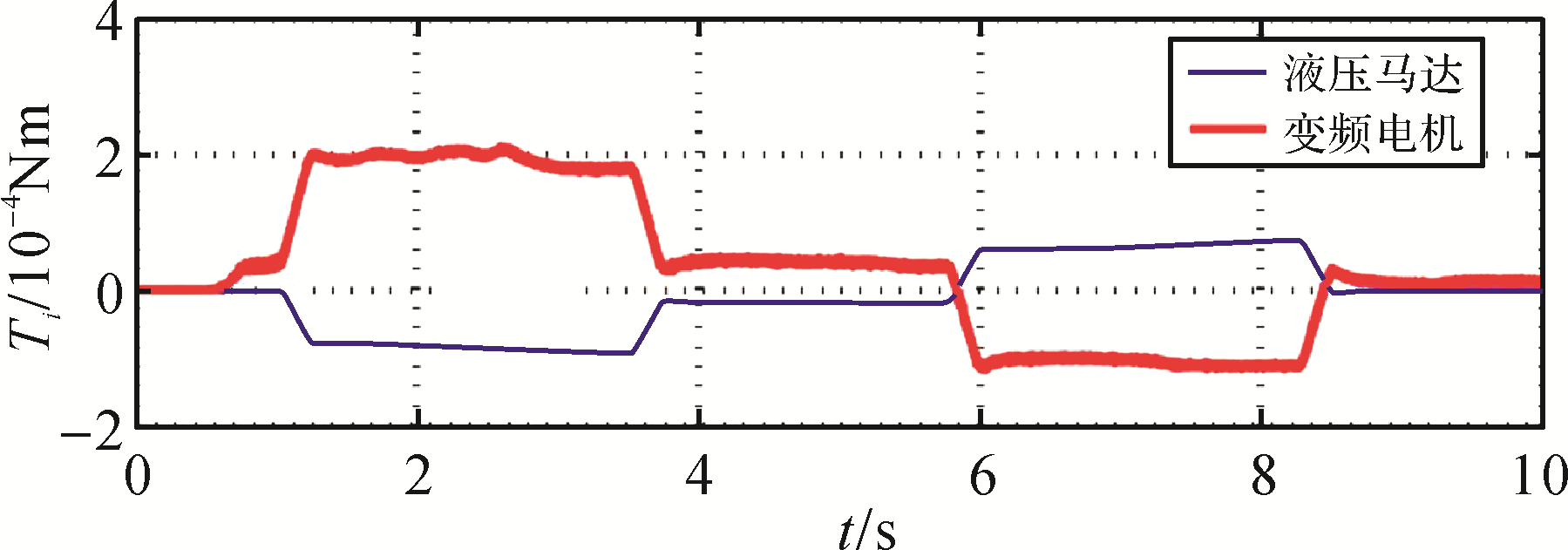
图6 传统转速并联控制下驱动单元的驱动力矩曲线

Fig. 6 Drive torque curve of the driving unit under traditional speed parallel control

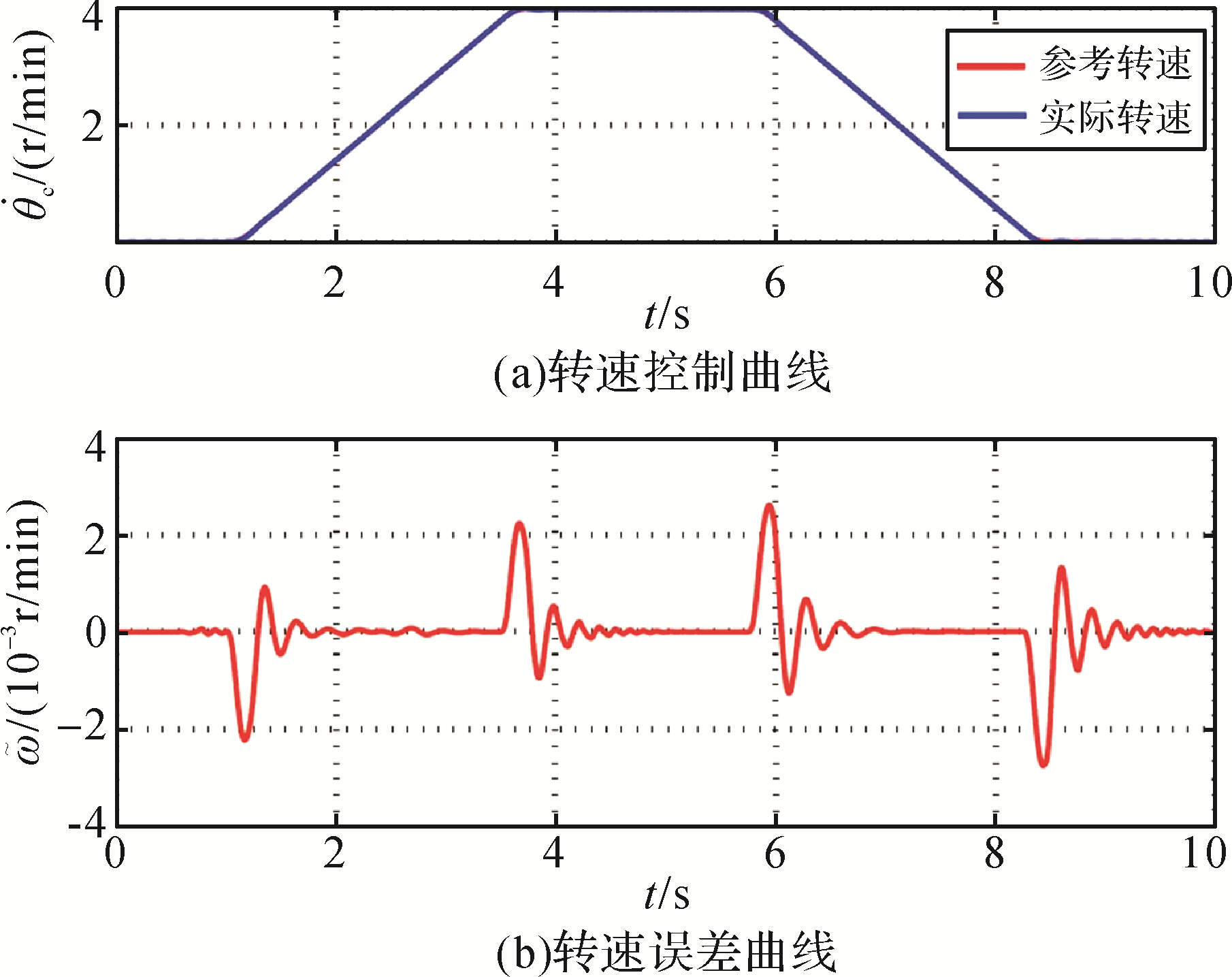
使用新型TBM刀盘转速自适应控制器，其转速跟踪性能与转速并联控制器相比，由于自适应控制器的作用，刀盘转速跟踪消除了稳态跟踪误差，提升了转速跟踪精度，如图7所示。同时，通过自适应控制器的干扰观测，实现转速和力矩的控制，通过力矩分配实现驱动单元输出力矩的可调。而由于液压马达由正转变为反转的过程中会造成液压系统受到冲击导致其转速波动，且液压马达作为TBM刀盘驱动源只有在低速重载才会接入系统，没有反向旋转的必要，故在刀盘减速时（6—8.5 s）液压马达的压力指令为零，即不为TBM刀盘系统提供减速力矩，如图8所示。由于液压马达刚性连接入系统，在刀盘减速过程中作为负载，故存在一定的正向压力。

图7 新型自适应控制器刀盘转速控制和误差曲线

Fig. 7 Cutterhead rotational speed control and error curves of new adaptive controller

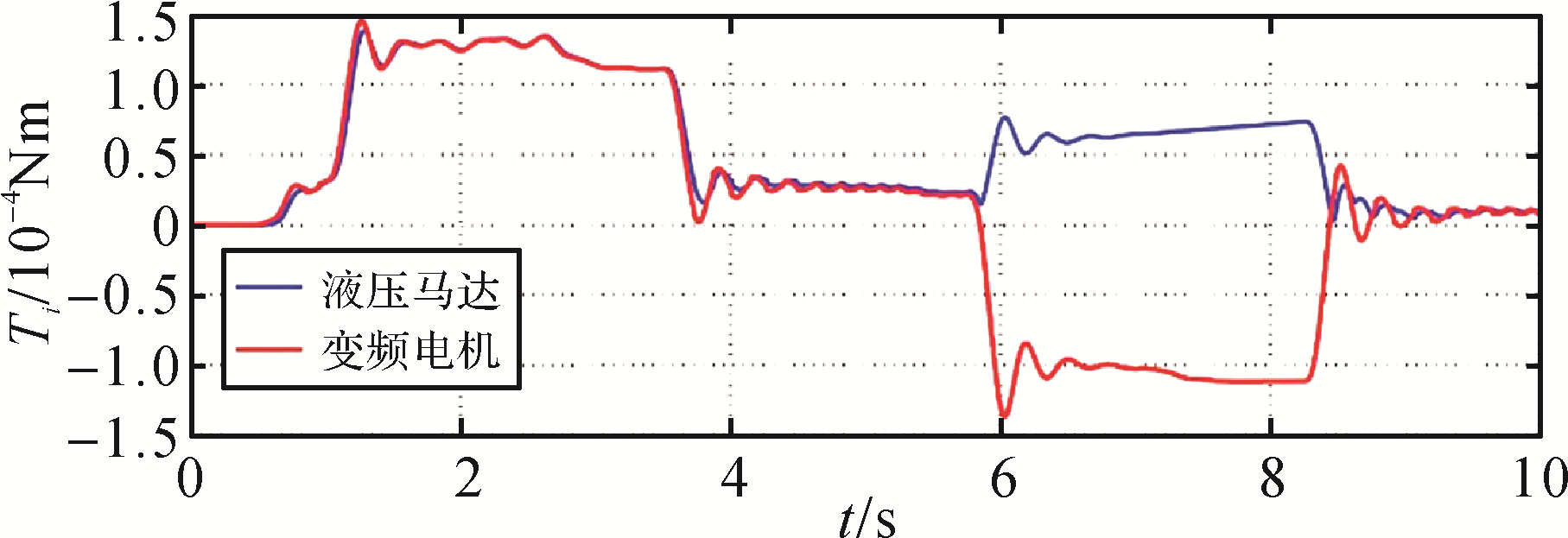
图8 自适应控制下驱动单元的驱动力矩曲线

Fig. 8 Drive torque curve of the driving unit under adaptive control

5 结论

本文在已有TBM刀盘转速控制器的基础上，针对混合驱动型刀盘驱动系统驱动单元偏载严重的问题，设计新型转速自适应控制器进行刀盘转速控制和力矩同步，通过联合仿真验证了该方法的有效性。

1) TBM刀盘混驱系统可提高整机的地质适应能力，但由于多驱动源驱动特性的差异，传统转速并联的开环转速控制方式会导致其驱动单元存在严重偏载，在转速变化过程中尤其明显。

2) 通过设计新型刀盘转速自适应控制器，实现对刀盘负载的观测和负载力矩的分配，从而实现多驱动源条件下的力矩同步。与传统转速并联控制器相比，驱动单元仅对自身的驱动力矩进行控制，刀盘转速控制由自适应控制器完成。

3) AMESim和MATLAB软件联合仿真的结果与预期一致，证明了自适应控制器的有效性。

参考文献

周赛群 .全断面硬岩掘进机（TBM）驱动系统研究[D]. 杭州:浙江大学机械工程学院, 2008：10-17. [百度学术]

ZHOU Sai-qun . Sudy on drive system of tunnel boring machine[D]. Hangzhou：Zhejiang University, School of Mechanical Engineering， 2008： 10-17. [百度学术]

MAIDL Bernhard, SCHMID Leonhard, RITZ Willy, et al . Hardrock tunnel boring machines[M]. Hamburg： John Wiley & Sons, 2008：17-29. [百度学术]

LIAO Jian-feng, CHEN Zheng, YAO Bin . High-performance adaptive robust control with balanced torque allocation for the over-actuated cutter-head driving system in tunnel boring machine[J]. Mechatronics, 2017, 46: 168-176. doi:10.1016/j.mechatronics.2017.08.007 [百度学术]

JAMSHIDI A . Prediction of TBM penetration rate from brittleness indexes using multiple regression analysis[J]. Modeling Earth Systems and Environment, 2018, 4 (1): 383-394. doi:10.1007/s40808-018-0432-2 [百度学术]

XIE Hai-bo, GONG Hua-sheng, HU Liang, et al . Improving the extricating performance of TBM cutter-head driving system with hydro-viscous clutch[C]// 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland，Aug. 29-31， 2016. doi:10.1109/MESA.2016.7587188 [百度学术]

WU Han-yang, HUO Jun-zhou, ZHANG Wei, et al . An electromechanical coupling model of TBM's main driving system[C]// 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland，Aug. 29-31， 2016. doi:10.1109/MESA.2016.7587111 [百度学术]

GONG Qiu-ming, YIN Li-jun, MA Hong-su, et al . TBM tunnelling under adverse geological conditions: an overview[J]. Tunnelling and Underground Space Technology, 2016, 57：4-17. doi:10.1016/j.tust.2016.04.002 [百度学术]

LIU Tong,GONG Guo-fang,PENG Zuo, et al . Modeling and intelligent synchronous control for parallel-connected motor-gear driving system of TBM cutterhead[C]//Mechanics and Mechanical Engineering: Proceedings of the 2015 International Conference (MME2015)， Chengdu， Dec. 25-27， 2015. doi:10.1142/9789813145603_0111 [百度学术]

SHAO Cheng-jun, LIAO Jian-feng, LI Xiu-liang, et al . An adaptive robust control for hard rock tunnel boring machine cutterhead driving system[C]// ASME 2015 Dynamic Systems and Control Conference, Columbus， Oct. 28-30， 2015. doi:10.1115/DSCC2015-9697 [百度学术]

SUN Dong, SHAO Xiao-yin, FENG Gang . A model-free cross-coupled control for position synchronization of multi-axis motions: theory and experiments[J]. IEEE Transactions on Control Systems Technology, 2007, 15 (2): 306-314. doi:10.3182/20050703-6-cz-1902.00400 [百度学术]

ZHANG Cheng-hui, SHI Qing-sheng, CHENG Jin . Synchronization control strategy in multi-motor systems based on the adjacent coupling error[J]. Proceedings of the Chinese Society of Electrical Engineering, 2007（15）: 59-63. doi:10.1360/aas-007-0331 [百度学术]

ZHANG Kai-zhi, YU Hai-dong, LIU Zhong-po, et al . Dynamic characteristic analysis of TBM tunnelling in mixed-face conditions[J]. Simulation Modelling Practice and Theory, 2010, 18 (7): 1019-1031. doi:10.1016/j.simpat.2010.03.005 [百度学术]

KAWAMURA Atsuo, ITOH Hiroshi, SAKAMOTO Kiyoshi . Chattering reduction of disturbance observer based sliding mode control[J]. IEEE Transactions on Industry Applications, 1994, 30 (2): 456-461. doi:10.1109/28.287509 [百度学术]

LI Hong-yi, SHI Peng,YAO De-yin, et al . Observer-based adaptive sliding mode control for nonlinear Markovian jump systems[J]. Automatica, 2016, 64： 133-142. doi:10.1016/j.automatica.2015.11.007 [百度学术]

LIAO Jian-feng, YAO Bin, ZHU Xiao-cong . Adaptive robust coordinated control for over-actuated cutter-head driving systems of hard rock tunnel boring machines[J]. IFAC-PapersOnLine, 2016, 49 (21): 611-616. doi:10.1016/j.ifacol.2016.10.668 [百度学术]

YAO Bin, TOMIZUKA Masayoshi . Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form[J]. Automatica, 1997, 33 (5): 893-900. doi:10.1016/s0005-1098(96)00222-1 [百度学术]

CHEN Shan, CHEN Zheng, YAO Bin, et al . Adaptive robust cascade force control of 1-DOF hydraulic exoskeleton for human performance augmentation[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22 (2): 589-600. doi:10.1109/TMECH.2016.2614987 [百度学术]

LYNN Alfred, SMID Edzko, ESHRAGHI Moji, et al . Modeling hydraulic regenerative hybrid vehicles using AMESim and Matlab/Simulink[C]// Enabling Technologies for Simulation Science IX, 2005: 24-41. doi:10.1117/12.603712 [百度学术]