使用Chrome浏览器效果最佳，继续浏览，你可能不会看到最佳的展示效果，

确定继续浏览么?

复制成功，请在其他浏览器进行阅读

基于模糊RBF神经网络的水下机械臂控制研究

袁凯 ^1,2
刘延俊 ^1,2,3
孙景余 ^1,2
罗星 ³

1. 山东大学海洋研究院，山东青岛 266237 ； 2. 山东大学深圳研究院，广东深圳 518057 ； 3. 山东大学高效洁净机械制造教育部先进制造重点实验室，山东济南 250061

中图分类号： TP 241

最近更新：2020-01-19

DOI：10.3785/j.issn.1006-754X.2019.00.007

摘要

针对水下复杂工作环境下机械臂控制性能易受影响，而传统控制方法效果不佳的问题，提出了一种基于模糊RBF（radial basis function，径向基函数）神经网络的智能控制器，用于精确、稳定地控制水下机械臂。考虑到在水扰动环境下，机械臂通常受到附加质量力、水阻力和浮力的影响，运用拉格朗日法和Morison方程，建立包含水动力项的二杆机械臂动力学模型，通过模糊RBF神经网络对水下机械臂动力学方程中的水动力不确定项进行总体识别并拟合，利用模糊系统启发式搜索和RBF神经网络推理速度较快的优点，使水下机械臂系统具有较高的控制精度和较强的自适应性。考虑到水动力项，采用Lyapunov稳定性理论验证了水下机械臂系统的稳定性。最后利用MATLAB对二杆机械臂进行轨迹跟踪控制仿真实验，并对比模糊RBF神经网络与常规RBF神经网络识别方法和传统模糊控制方法的控制效果。仿真结果表明：与常规RBF神经网络识别方法相比，模糊RBF神经网络控制下二杆机械臂关节1的响应时间缩短了91%，相对误差减小了88%，关节2的响应时间缩短了92%，相对误差降低了77%；与传统模糊控制方法相比，关节1的相对误差减小了65%，关节2的相对误差减小了10%。研究结果表明模糊RBF神经网络的控制效果优于常规RBF神经网络识别方法和传统模糊控制方法，可为水下机械臂的控制提供一种精度较高、较有效的方法。

关键词

模糊控制; RBF神经网络; 水下机械臂; 控制特性

水下机械臂是许多水下航行器的重要设备，它在水下资源取样、装置维修、平台搭建等应用中起着至关重要的作用。与常见的工业机械臂不同的是，水下机械臂通常在存在不确定参数，如在水动力扰动、外部噪声和干扰（例如水下电流）的情况下操纵任务^[

1]。这要求水下机械臂控制系统在补偿水动力干扰和噪声方面应更加稳健，并且采用信息执行反馈控制实时监测系统状态。

Yuh^[

2]针对水下机器人提出了一种神经网络控制系统，该系统使用了基于批评函数的递归自适应算法（加强学习方法）；Yang等^{[参考文献 3
百度学术}3,4]针对并联机器人与混联机器人分别设计了鲁棒控制器，均取得了较好的控制效果，但是该类机器人与水下机器人在外部载荷上有较大的差别；李敏等^{[参考文献 5
百度学术}5]采用模糊RBF神经网络对机器人中LuGre动态摩擦项进行补偿；袁伟杰等^{[参考文献 6
百度学术}6]采用遗传算法识别水下机器人的水动力参数；Gong等^{[参考文献 7
百度学术}7]针对不确定因素对机械臂系统的影响，提出了一种自适应RBF神经网络与参数可调复合非线性反馈控制（composite nonlinear feedback，CNF）相结合的控制方法；肖凡等^{[参考文献 8
百度学术}8]利用以遗传算法优化RBF神经网络参数的控制方法来实现机械臂的轨迹跟踪控制；俞建成等^{[参考文献 9
百度学术}9]提出了一种水下机器人神经网络直接自适应控制方法，但是在采用Lyapunov稳定性理论证明系统稳定性时，忽略了系统中的附加质量力。

鉴于神经网络的并行计算能力可使整个网络的推理大大加快，模糊系统的启发式搜索又能使整个网络的推理结果更为准确^[

10]，因此针对非线性且复杂的水下机械臂系统，笔者提出了一种基于模糊RBF神经网络的智能控制器，用于精确、稳健地控制水下机械臂。在模糊RBF神经网络中，神经网络的输入、输出层用来表示模糊系统的输入、输出信号，隐含层用来表示隶属函数关系和模糊规则，RBF作为模糊系统的隶属函数。首先，通过模糊RBF神经网络对水下机械臂水动力方程中的不确定项进行识别并拟合；然后，采用Lyapunov稳定性理论来验证包含水动力项的机械臂系统的稳定性。最后，对二杆机械臂进行仿真分析，以证明模糊RBF神经网络控制方法较常规RBF神经网络识别方法和传统模糊控制方法更有效。

1 水下机械臂动力学模型建立

基于拉格朗日方法，建立传统机械臂（共n个关节）的动力学方程^[

11]：

$M_{R B} (q) \ddot{q} + C (q, \dot{q}) \dot{q} + G (q) + F_{f} (\dot{q}) + τ_{d} = τ$

（1）

式中： $M_{R B} (q)$ 为n×n阶加速度惯性矩阵， $C (q, \dot{q})$ 为n×n阶向心力和科氏力矩阵， $G (q)$ 为重力矩阵， $F_{f} (\dot{q})$ 为关节摩擦力矩阵， $τ_{d}$ 为未知外部干扰， $τ$ 为关节驱动力矩阵， $\ddot{q} 、 \dot{q} 、 q$ 分别为关节的角加速度、角速度、角度矩阵。

对于水下机械臂，由于水下工作环境复杂，深海情况多变，其工作稳定性会受到多种因素（如洋流、温度等）的影响，因此，在建立水下机械臂动力学模型时，必须考虑水流的影响。影响水下机械臂工作稳定性的水动力主要包括水阻力、浮力、附加质量力及水流在加速运动过程中产生的力^[

12]。假设：水流无加速运动，即不考虑因水流加速而产生的力；机械臂各部件的重心和浮心重合，且重力和浮力方向相反，则：将水动力划分为3种力，分别为水阻力、附加质量力以及包含浮力的等效重力。

考虑3种水动力，则水下机械臂（n个关节）的动力学方程为：

$\begin{array}{l} M (q) \ddot{q} + C (q, \dot{q}) \dot{q} + D (q, \dot{q}) \dot{q} + G^{'} (q) + \\ F_{f} (\dot{q}) + τ_{d} = τ \end{array}$

（2）

式中： $M (q) = M_{R B} (q) + M_{A} (q)$ ，为包括附加质量力的n×n阶加速度惯性矩阵， $M_{A} (q)$ 为n×n阶附加质量力矩阵， $D (q, \dot{q})$ 为n×n阶水阻力矩阵， $G^{'} (q)$ 为包含浮力的等效重力矩阵。

根据Morison方程^[

13]，包含阻力项和惯性力项的水动力可以表示为：

$\begin{array}{l} d F = d F_{d} + d F_{m} = \\ \frac{1}{2} ρ C_{d} V (x) ‖V (x)‖ D d l + ρ C_{m} A \frac{d V (x)}{d t} d l \end{array}$

（3）

式中： $F_{d}$ 、 $F_{m}$ 分别为结构物单位长度上的水阻力和附加质量力， $ρ$ 为流体密度， $C_{d}$ 为水阻力系数， $C_{m}$ 为附加质量力系数， $V (x)$ 为速度函数， $D$ 为结构物的等效直径， $d l$ 为结构物单元厚度， $A$ 为结构物在垂直于水流速度方向上的投影面积^[

14]。

由于实际的水阻力系数 $C_{d}$ 和附加质量力系数 $C_{m}$ 很难测量，且这2个系数在水下机械臂工作环境中的变化很小，基本可以当作常数，根据经验，本文取 $C_{d} = 1.1$ ， $C_{m} = 1$ ^[

15]。

基于Morison方程，计算二杆机械臂的水阻力矩和附加质量力矩^[

16]。二杆机械臂运动模型示意图如图1所示。

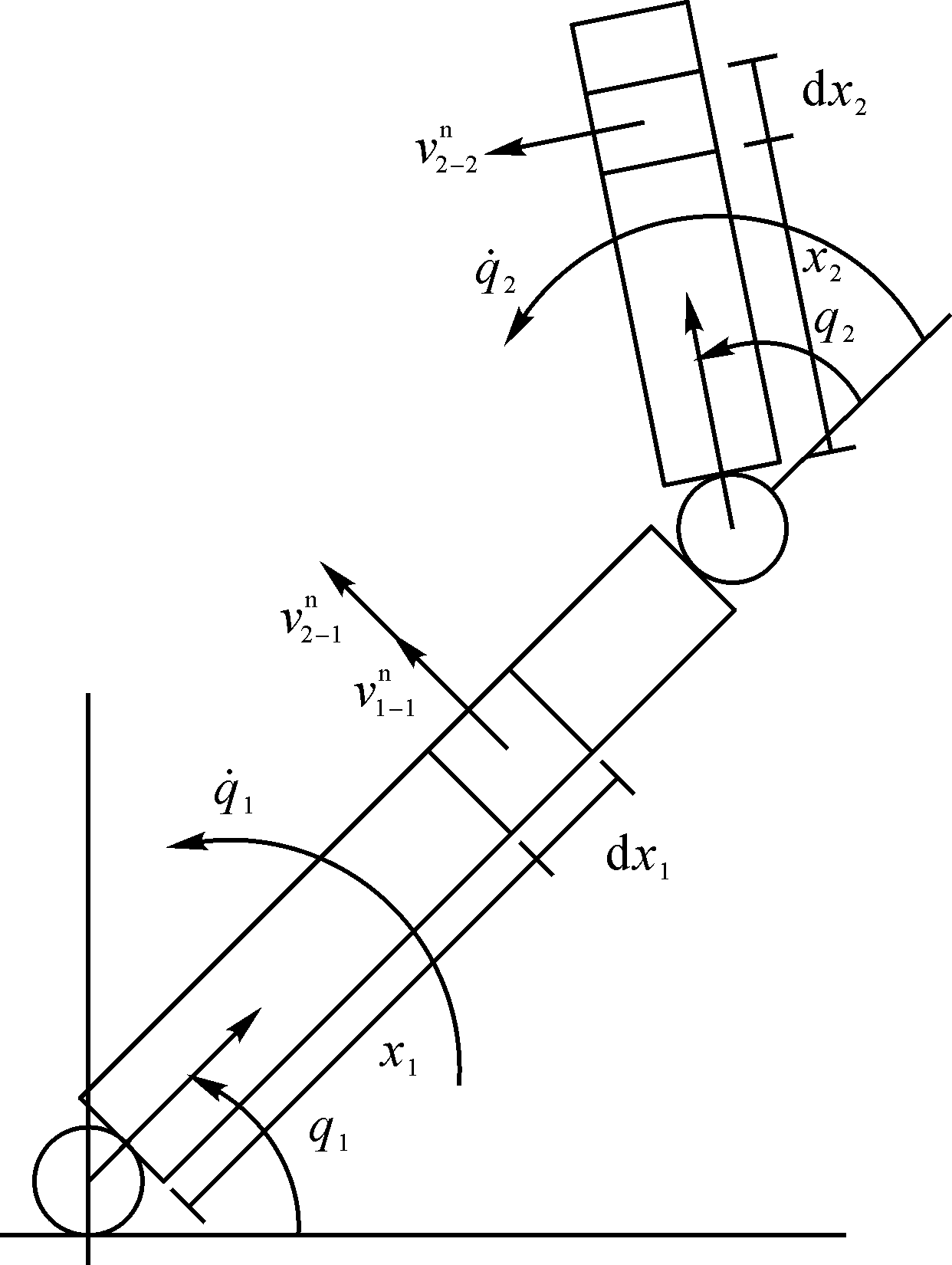
图1 二杆机械臂运动模型示意图

Fig. 1 Schematic diagram of two-link manipulator motion model

对于连杆1，水阻力矩 $τ_{D 1}$ 是由关节1的角速度 ${\dot{q}}_{1}$ 和关节2的角速度 ${\dot{q}}_{2}$ 使连杆1产生的法向速度引起的，根据运动学分析可知，此法向速度为：

$\{\begin{array}{l} v_{1 - 1}^{n} = {\dot{q}}_{1} x_{1} c o s q_{1} \\ v_{2 - 1}^{n} = {\dot{q}}_{1} l_{1} c o s q_{2} + ({\dot{q}}_{1} + {\dot{q}}_{2}) x_{2} \end{array}$

（4）

式中： $v_{1 - 1}^{n}$ 、 $v_{2 - 1}^{n}$ 分别为单元长度上关节1和关节2的角速度 ${\dot{q}}_{1}$ 、 ${\dot{q}}_{2}$ 使连杆1产生的法向速度， $q_{1}$ 、 $q_{2}$ 分别为关节1和关节2的转动角度，x ₁为单元dx ₁到连杆1底端的距离，x ₂为单元dx ₂到连杆2底端的距离， $l_{1}$ 为连杆1的长度。

则连杆1的水阻力矩为：

$\begin{array}{l} τ_{D 1} = \frac{1}{2} ρ D_{1} C_{d} \int_{0}^{l_{1}} {\dot{q}}_{1}^{} x_{1} c o s q_{1} |{\dot{q}}_{1}^{} x_{1} c o s q_{1}| x_{1} d x_{1} + \\ \frac{1}{2} ρ D_{2} C_{d} \int_{0}^{l_{2}} [{\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}] \\ |q_{1}^{̇} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}| (l_{1} c o s q_{2} + x_{2}) d x_{2} \end{array}$

（5）

式中： $D_{1}$ 、 $D_{2}$ 分别为连杆1,2的等效直径。

同理可得，连杆1的附加质量力矩为：

$\begin{array}{l} τ_{A 1} = \frac{π}{4} ρ D_{1}^{2} C_{m} \int_{0}^{l_{1}} \frac{d ({\dot{q}}_{1}^{} x_{1} c o s q_{1})}{d t} x_{1} d x_{1} + \\ \frac{π}{4} ρ D_{2}^{2} C_{m} \int_{0}^{l_{2}} \frac{d [{\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}]}{d t} \\ (l_{1} c o s q_{2} + x_{2}) d x_{2} \end{array}$

（6）

式中： $l_{2}$ 为连杆2的长度。

对于连杆2，水阻力矩 $τ_{D 2}$ 是关节2的角速度 ${\dot{q}}_{2}^{}$ 使连杆2产生的法向速度，根据运动学分析可知，此法向速度为：

$v_{2 - 2}^{n} = {\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}$

（7）

则连杆2的水阻力矩为：

$\begin{matrix} τ_{D 2} = \frac{1}{2} ρ D_{2} C_{d} \int_{0}^{l_{2}} [{\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}] \\ |{\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}| x_{2} d x_{2} \end{matrix}$

（8）

同理可得，连杆2的附加质量力矩为：

$τ_{A 2} = \frac{π}{4} ρ D_{2}^{2} C_{m} \int_{0}^{l_{2}} \frac{d [{\dot{q}}_{1}^{} l_{1} c o s q_{2} + ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) x_{2}]}{d t} x_{2} d x_{2}$

（9）

根据 $τ_{D} = {[\begin{matrix} τ_{D 1} & τ_{D 2} \end{matrix}]}^{T} = D {[\begin{matrix} {\dot{q}}_{1}^{} & {\dot{q}}_{2}^{} \end{matrix}]}^{T}$ ，求得水阻力矩阵 $D$ 为：

$D = [\begin{array}{l} [a_{1} l_{1}^{3} c_{1}^{2} + a_{2} (4 l_{1}^{3} c_{2}^{3} + 6 l_{1}^{2} l_{2} c_{2}^{2} + 4 l_{1} l_{2}^{2} c_{2} + l_{2}^{3})] {\dot{q}}_{1}^{} a_{2} (2 l_{1}^{2} l_{2} c_{2}^{2} + \frac{8}{3} l_{1} l_{2}^{2} c_{2} + l_{2}^{3}) {\dot{q}}_{1}^{} \\ a_{2} (4 l_{1}^{2} l_{2} c_{2}^{2} + \frac{16}{3} l_{1} l_{2}^{2} c_{2} + 2 l_{2}^{3}) {\dot{q}}_{1}^{} + a_{2} (\frac{4}{3} l_{1} l_{2}^{2} c_{2} + l_{2}^{3}) {\dot{q}}_{2}^{} a_{2} (\frac{8}{3} l_{1} l_{2}^{2} c_{2} + 2 l_{2}^{3}) {\dot{q}}_{1}^{} + a_{2} l_{2}^{3} {\dot{q}}_{2}^{} \end{array}]$

（10）

式中： $a_{1} = \frac{1}{8} ρ D_{1} l_{1} C_{d}$ ， $a_{2} = \frac{1}{8} ρ D_{2} l_{2} C_{d}$ , $c_{1} = c o s q_{1}$ , $c_{2} = c o s q_{2}$ 。

根据 $τ_{A} = {[\begin{matrix} τ_{A 1} & τ_{A 2} \end{matrix}]}^{T} = M_{A} {[\begin{matrix} {\ddot{q}}_{1}^{} & {\ddot{q}}_{2}^{} \end{matrix}]}^{T}$ ，求得附加质量力矩阵 $M_{A}$ 为：

$M_{A} = [\begin{array}{l} a_{3} l_{1}^{2} c_{1} + a_{4} (3 l_{1}^{2} c_{2}^{2} + 3 l_{1} l_{2} c_{2} + l_{2}^{2}) a_{4} (\frac{3}{2} l_{1} l_{2} c_{2} + l_{2}^{2}) \\ a_{4} (\frac{3}{2} l_{1} l_{2} c_{2} + l_{2}^{2}) a_{4} l_{2}^{2} \end{array}]$

（11）

式中： $a_{3} = \frac{1}{3} \frac{ρ}{ρ_{1}} m_{1} C_{m}$ ， $a_{4} = \frac{1}{3} \frac{ρ}{ρ_{2}} m_{2} C_{m}$ ， $ρ_{1}$ 为连杆1的平均密度， $ρ_{2}$ 为连杆2的平均密度， $m_{1}$ 为连杆1的质量， $m_{2}$ 为连杆2的质量。

2 基于模糊RBF神经网络的控制器设计

2.1　水下机械臂动力学模型分析

设目标位置为 $q_{d} (t)$ ，实际位置为 $q (t)$ ，则定义跟踪误差为：

$e (t) = q_{d} (t) - q (t)$

（12）

设计滑模函数为：

$r = \dot{e} + Λ e$

（13）

式中： $Λ$ 为滑模系数，为正定矩阵。

联立式（12）和（13）可得：

$\dot{r} = {\ddot{q}}_{d}^{} - \ddot{q} + Λ \dot{e}$

（14）

结合式（2）可得：

$\begin{array}{l} M \dot{r} = M ({\ddot{q}}_{d}^{} - \ddot{q} + Λ \dot{e}) = M ({\ddot{q}}_{d}^{} + Λ \dot{e}) - M \ddot{q} = \\ M ({\ddot{q}}_{d}^{} + Λ \dot{e}) + C \dot{q} + D \dot{q} + G + F_{f} + τ_{d} - τ = \\ - (C + D) r + τ_{d} - τ + f (15) \end{array}$

式中：

$f = M ({\ddot{q}}_{d}^{} + Λ \dot{e}) + (C + D) ({\dot{q}}_{d}^{} + Λ e) + G + F_{f}$

（16）

在实际中， f 是不确定的，本文用模糊RBF神经网络对 f 进行总体逼近。

2.2　模糊RBF神经网络设计

本文设计的模糊RBF神经网络的结构如图2所示，该神经网络由输入层、模糊化层、模糊推理层和输出层组成^[

17]。

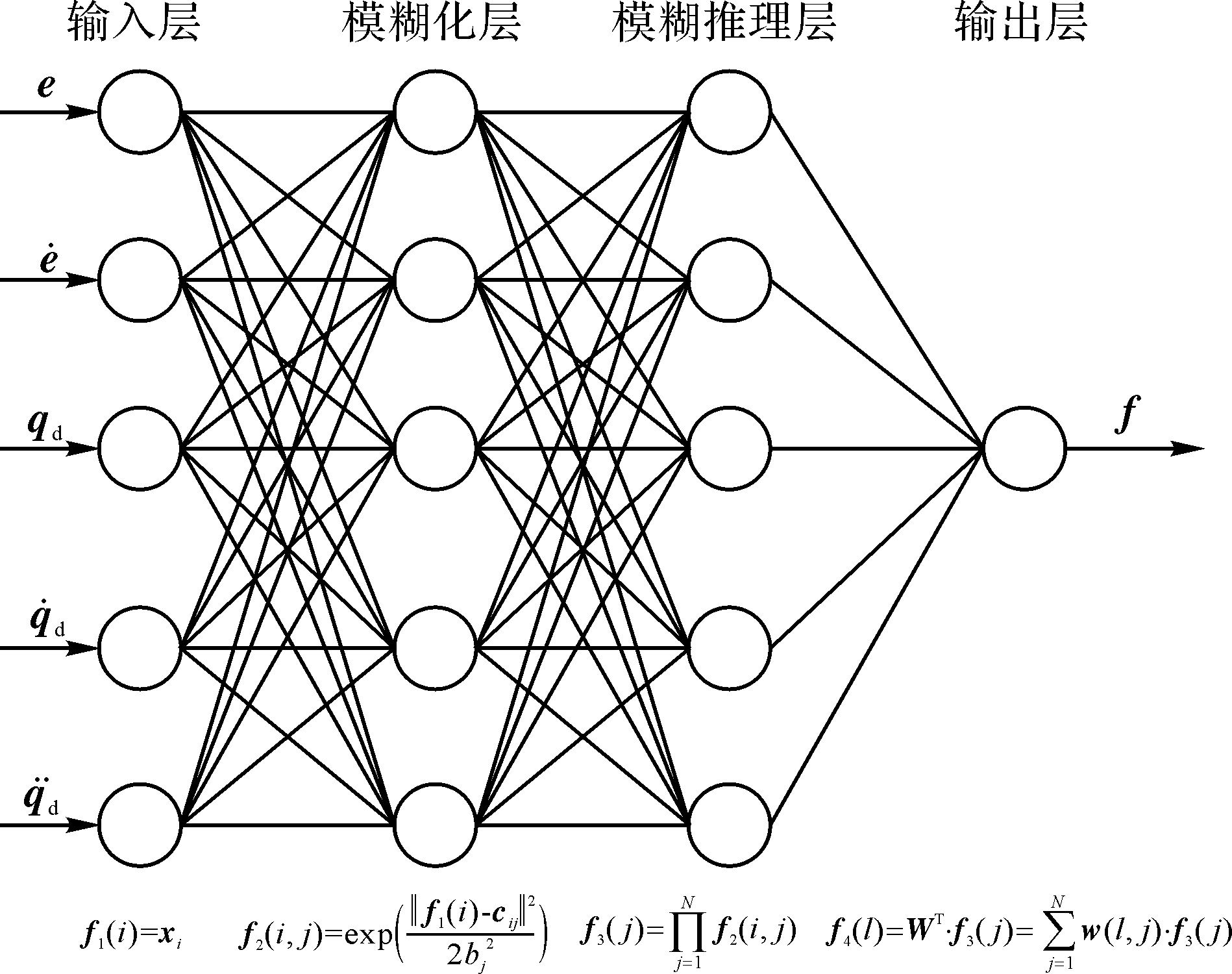
图2 模糊RBF神经网络结构

Fig. 2 Structure of fuzzy RBF neural network

该模糊RBF神经网络的信号传递及结构功能如下：

第1层：输入层。输入层的不同节点直接连入需要总体逼近的 f 的输入量，根据式（16），网络输入取：

$x = [\begin{matrix} e^{T} & {\dot{e}}^{T} & q_{d}^{T} & {\dot{q}}_{d}^{T} & {\ddot{q}}_{d}^{T} \end{matrix}]$

输入层中第i个节点的连接函数表示为：

$f_{1} (i) = x_{i}$ ，

$i = 1, 2, \dots, 5$

（17）

第2层：模糊化层，即隶属函数层。隶属函数层中所有节点的输出都可当作一个隶属函数，由于是RBF神经网络，故采用常用的高斯函数作为隶属函数。

输入层第i个节点与模糊化层第j个节点的连接函数表示为：

$f_{2} (i, j) = e x p (\frac{{‖f_{1} (i) - c_{i j}‖}^{2}}{2 b_{j}^{2}})$

（18）

式中： $c_{i j}$ 为第i个输入信号的第j个模糊集合高斯函数的均值， $b_{j}$ 为每个输入信号的第j个模糊集合高斯函数的均值， $j = 1, 2, \dots, 5$ 。

第3层：模糊推理层，即规则层。规则层通过与隶属函数层连接来完成模糊规则的匹配，隶属函数层中各个节点之间进行模糊运算，从而得到相应的点火强度。规则层节点个数与隶属函数层节点个数相等，因此规则层中第j个节点的输出为该节点所有输入信号的乘积，即：

$f_{3} (j) = \overset{N}{\prod_{j = 1}} f_{2} (i, j)$

（19）

式中： $N = \overset{n}{\prod_{i = 1}} N_{i}$ ， $N_{i}$ 为输入层中第i个节点输入隶属函数的个数。

第4层：输出层。输出层中每个节点的输出为该节点所有输入信号的加权和，即：

$f_{4} (l) = W^{T} \cdot f_{3} (j) = \overset{N}{\sum_{j = 1}} w (l, j) \cdot f_{3} (j)$

（20）

式中：l为输出层节点的个数，本文l=1， $W$ 为输出层节点与规则层节点的连接权值矩阵。

2.3　控制律设计

得到模糊RBF神经网络的输出 f 后，设计其控制律，为：

$τ = \hat{f} + K_{v} r - v$

（21）

式中： $\hat{f}$ 为模糊RBF神经网络对 $f$ 的逼近值， $K_{v}$ 为对称正定矩阵， $v$ 为克服模糊RBF神经网络逼近误差 $ε$ 的鲁棒项。

将式（21）代入式（15），得：

$\begin{array}{l} M \dot{r} = - (C + D) r + τ_{d} - \hat{f} - K_{v} r + v + f = \\ - (C + D + K_{v}) r + \tilde{f} + ε + v + τ_{d} \end{array}$

（22）

式中： $\tilde{f} + ε = f - \hat{f}$ 。

2.4　控制系统稳定性分析

定义Lyapunov函数为：

$L = \frac{1}{2} r^{T} M r + \frac{1}{2} t r ({\tilde{W}}^{T} Γ^{- 1} \tilde{W})$

（23）

对于二杆机械臂，令：

$M_{R B} = [\begin{matrix} l_{2}^{2} m_{2} + 2 l_{1} l_{2} m_{2} c_{2} + l_{1}^{2} (m_{1} + m_{2}) & l_{2}^{2} m_{2} + l_{1} l_{2} m_{2} c_{2} \\ l_{2}^{2} m_{2} + l_{1} l_{2} m_{2} c_{2} & l_{2}^{2} m_{2} \end{matrix}] = [\begin{matrix} B_{1} & B_{2} \\ B_{2} & B_{4} \end{matrix}]$

$M_{A} = [\begin{matrix} a_{3} l_{1}^{2} c_{1} + a_{4} (3 l_{1}^{2} c_{2}^{2} + 3 l_{1} l_{2} c_{2} + l_{2}^{2}) & a_{4} (\frac{3}{2} l_{1} l_{2} c_{2} + l_{2}^{2}) \\ a_{4} (\frac{3}{2} l_{1} l_{2} c_{2} + l_{2}^{2}) & a_{4} l_{2}^{2} \end{matrix}] = [\begin{matrix} A_{1} & A_{2} \\ A_{2} & A_{4} \end{matrix}]$

由 $M = M_{R B} + M_{A} = [\begin{matrix} A_{1} + B_{1} & A_{2} + B_{2} \\ A_{2} + B_{2} & A_{4} + B_{4} \end{matrix}]$ 可得：

$\begin{array}{l} |M_{1}| = A_{1} + B_{1} = a_{3} l_{1}^{2} c_{1} + a_{4} (3 l_{1}^{2} c_{2}^{2} + 3 l_{1} l_{2} c_{2} + l_{2}^{2}) + \\ l_{2}^{2} m_{2} + 2 l_{1} l_{2} m_{2} c_{2} + l_{1}^{2} (m_{1} + m_{2}) = \\ m_{1} l_{1}^{2} (1 + \frac{1}{3} \frac{ρ}{ρ_{1}} C_{m} c_{1}) + a_{4} [3 l_{1}^{2} {(c_{2} + \frac{l_{2}}{2 l_{1}})}^{2} + \\ \frac{1}{4} l_{2}^{2}] + m_{2} [{(l_{1} - l_{2})}^{2} + 2 l_{1} l_{2} (c_{2} + 1)] \end{array}$

因为 $- 1 < c_{1}, c_{2} < 1$ ， $C_{m} = 1$ ， $\frac{ρ}{ρ_{1}} < 1$ ，所以 $1 + \frac{1}{3} \frac{ρ}{ρ_{1}} C_{m} c_{1} > 0$ ， $l_{1}^{2} + l_{2}^{2} + 2 l_{1} l_{2} c_{2} > 0$ ，即 $|M_{1}| > 0$ 。

$\begin{array}{l} |M_{2}| = A_{1} A_{4} + B_{1} B_{4} + A_{1} B_{4} + B_{1} A_{4} - A_{2}^{2} - B_{2}^{2} - \\ 2 A_{2} B_{2} = l_{1}^{2} l_{2}^{2} m_{2}^{2} (1 - c_{2}^{2}) + \frac{3}{4} a_{4}^{2} l_{1}^{2} l_{2}^{2} c_{2}^{2} + \\ a_{4} l_{1}^{2} l_{2}^{2} m_{2} + (l_{1}^{2} l_{2}^{2} m_{1} m_{2} + a_{3} l_{1}^{2} l_{2}^{2} m_{2} c_{1} + \\ a_{4} l_{1}^{2} l_{2}^{2} m_{1} + a_{1} a_{2} l_{1}^{2} l_{2}^{2} c_{1}) = l_{1}^{2} l_{2}^{2} m_{2}^{2} (1 - c_{2}^{2}) + \\ \frac{3}{4} a_{4}^{2} l_{1}^{2} l_{2}^{2} c_{2}^{2} + a_{4} l_{1}^{2} l_{2}^{2} m_{2} + \\ l_{1}^{2} l_{2}^{2} (m_{2} + a_{4}) (m_{1} + a_{3} c_{1}) = l_{1}^{2} l_{2}^{2} m_{2}^{2} (1 - c_{2}^{2}) + \\ \frac{3}{4} a_{4}^{2} l_{1}^{2} l_{2}^{2} c_{2}^{2} + a_{4} l_{1}^{2} l_{2}^{2} m_{2} + \\ l_{1}^{2} l_{2}^{2} m_{1} m_{2} (1 + \frac{C_{m} ρ}{3 ρ_{2}}) (1 + \frac{C_{m} ρ}{3 ρ_{1}} c_{1}) \end{array}$

因为 $- 1 < c_{1}, c_{2} < 1$ ， $C_{m} = 1$ ， $\frac{ρ}{ρ_{1}} < 1$ ，所以 $1 + \frac{C_{m} ρ}{3 ρ_{1}} c_{1} > 1 - \frac{C_{m} ρ}{3 ρ_{1}} > \frac{1}{3}$ ，即 $|M_{2}| > 0$ 。

由 $|M_{1}| > 0$ ， $|M_{2}| > 0$ 得到 $M$ 是正定矩阵，即 $r^{T} M r > 0$ 。

取 $Γ$ 为对称正定矩阵， $t r ({\tilde{W}}^{T} Γ^{- 1} \tilde{W}) > 0$ ，故 $L > 0$ 。

对Lyapunov函数求导可得：

$\begin{array}{l} \dot{L} = r^{T} M \dot{r} + \frac{1}{2} r^{T} \dot{M} r + t r ({\tilde{W}}^{T} Γ^{- 1} \dot{\tilde{W}}) = \\ r^{T} [- (K_{v} + C + D) r + {\tilde{W}}^{T} f_{3} + (ε + τ_{d}) + v] + \\ \frac{1}{2} r^{T} \dot{M} r + t r ({\tilde{W}}^{T} Γ^{- 1} \dot{\tilde{W}}) = \\ - r^{T} (K_{v} + D - \frac{1}{2} {\dot{M}}_{A}) r + \frac{1}{2} r^{T} ({\dot{M}}_{R B} - 2 C) r + \end{array}$

$\begin{array}{l} r^{T} (ε + τ_{d} + v) + t r {\tilde{W}}^{T} (Γ^{- 1} \dot{\tilde{W}} + f_{3} r^{T}) = \\ - r^{T} (K_{v} + D - \frac{1}{2} {\dot{M}}_{A}) r + r^{T} (ε + τ_{d} + v) + \\ t r {\tilde{W}}^{T} (Γ^{- 1} \dot{\tilde{W}} + f_{3} r^{T}) \end{array}$

（24）

鲁棒项 $v$ 设计为：

$v = - (ε_{N} + b_{d}) s a t (r)$

（25）

式中： $‖ε‖ \leq ε_{N}$ ， $‖τ_{d}‖ \leq b_{d}$ ， $ε_{N}$ 、 $b_{d}$ 为常数, $s a t (r)$ 为饱和函数。

自适应律设计为：

$\dot{\hat{W}} = Γ \cdot f_{3} \cdot r^{T}$

（26）

由此可得 $\dot{\tilde{W}} = - Γ \cdot f_{3} \cdot r^{T}$ ，则有：

$\dot{L} \leq - (D_{m i n} + K_{v m i n} - \frac{1}{2} {\dot{M}}_{A m i n}^{}) {‖r‖}^{2} + r^{T} (ε + τ_{d}) - ‖r‖ (ε_{N} + b_{d})$

（27）

式中： $D_{m i n}$ 为矩阵 $D$ 的最小特征值， $K_{v m i n}$ 为矩阵 $K_{v}$ 的最小特征值， ${\dot{M}}_{A m i n}^{}$ 为矩阵 ${\dot{M}}_{A}$ 的最小特征值。

为使 $\dot{L} \leq 0$ ，则必有：

$D_{m i n} + K_{v m i n} - \frac{1}{2} {\dot{M}}_{A m i n}^{} > 0$

实际中， $K_{v m i n}$ 远大于 ${\dot{M}}_{A m i n}^{}$ ，从而可证 $\dot{L} \leq 0$ 。

根据Lyapunov稳定性分析法^[

18]可知，当

$\dot{L} \equiv 0$ 时，

$r \equiv 0$ ；当

$t \to \infty$ 时，

$r \to 0$ ，闭环系统渐近稳定。

根据设计的滑模函数、控制律、鲁棒项、自适应律以及滑模控制项，本文水下机械臂的控制原理框图如图3所示。

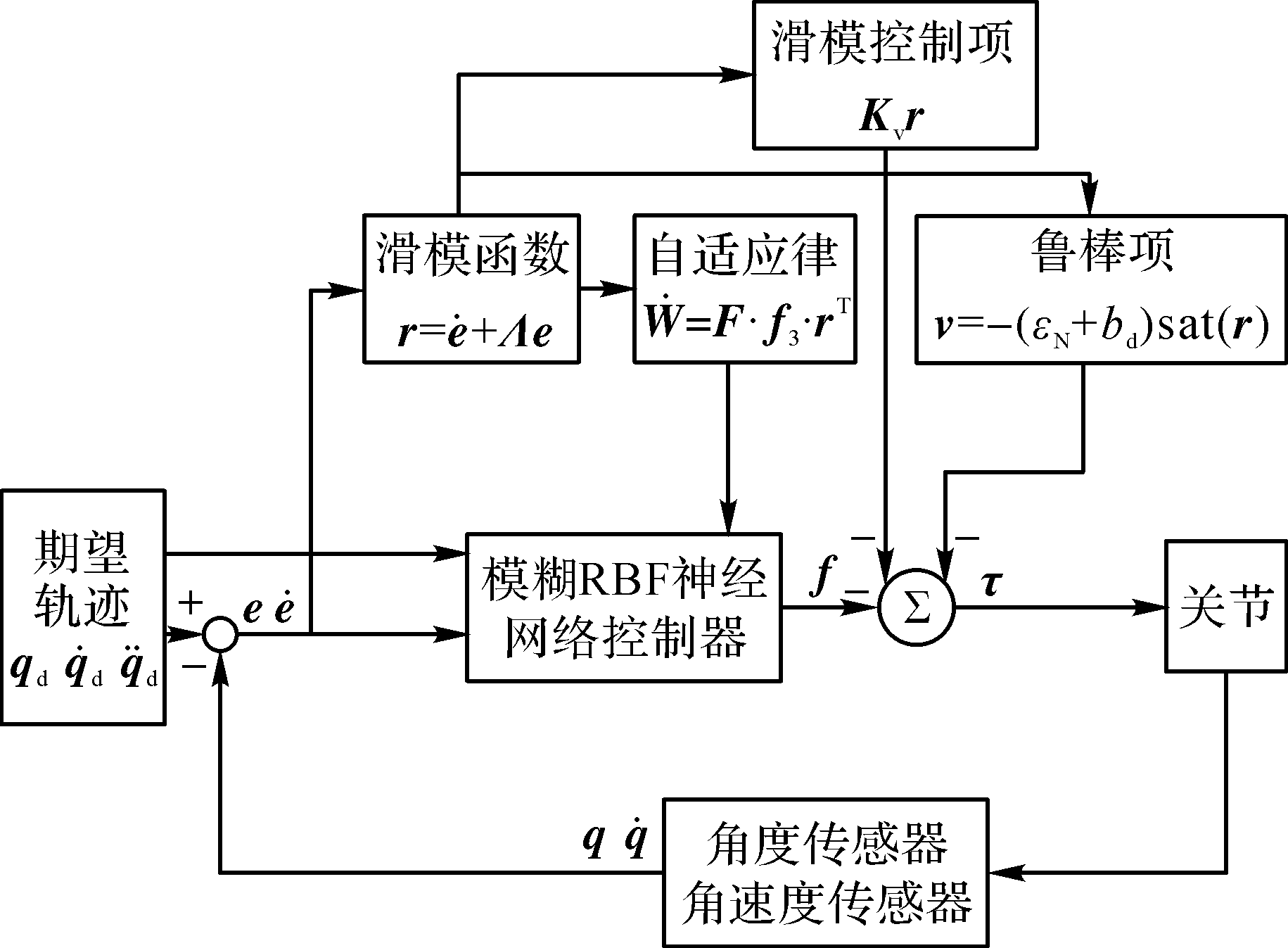
图3 水下机械臂控制原理框图

Fig. 3 Block diagram of underwater manipulator control principle

3 二杆机械臂仿真分析

本文研究的二杆机械臂的尺寸为：连杆1的长度l ₁=0.45 m，等效直径D ₁=0.1 m，质量m ₁=6 kg，密度ρ ₁=1 698 kg/m³；连杆2的长度l ₂=0.275 m，等效直径D ₂=0.1 m，质量m ₂=4 kg，密度ρ ₂=1 852 kg/m³。

设置二杆机械臂关节角度及角速度的初始值： $[q_{1} (0) {\dot{q}}_{1}^{} (0) q_{2} (0) {\dot{q}}_{2}^{} (0)] = [0.09 0 - 0.09 0]$ ，2个关节角度的期望值为 $q_{1 d} = q_{2 d} = 0.1 s i n t$ 。

根据式（2）所示的水下机械臂动力学方程，对于二杆机械臂，有：

1）带有附加质量矩阵的惯性矩阵为：

$M (q) = M_{R B} (q) + M_{A} (q)$

2）离心力和哥氏力矩阵 $C (q, \dot{q})$ 为：

$C (q, \dot{q}) = [\begin{matrix} - l_{1} l_{2} m_{2} {\dot{q}}_{2}^{} s_{2} & - l_{1} l_{2} m_{2} ({\dot{q}}_{1}^{} + {\dot{q}}_{2}^{}) s_{2} \\ l_{1} l_{2} m_{2} {\dot{q}}_{1}^{} s_{2} & 0 \end{matrix}]$

其中： $s_{1} = s i n q_{1}$ ， $s_{2} = s i n q_{2}$ 。

3）水阻力矩矩阵 $D (q, \dot{q})$ 由式（10）求得。

4）等效重力矩阵 $G (q)$ 为：

$G (q) = [\begin{matrix} m_{2} l_{2} g (1 - \frac{ρ}{ρ_{2}}) c_{12} + m_{1} l_{1} g (1 - \frac{ρ}{ρ_{1}}) c_{1} + m_{2} l_{1} g (1 - \frac{ρ}{ρ_{2}}) c_{1} \\ m_{2} l_{2} g (1 - \frac{ρ}{ρ_{2}}) c_{12} \end{matrix}]$

式中： $c_{12} = c o s (q_{1} + q_{2})$ 。

5）水下机械臂摩擦模型简化为库仑摩擦模型，则摩擦力矩阵 $F_{f} (\dot{q})$ 为:

$F_{f} (\dot{q}) = [\begin{matrix} k_{1} s g n ({\dot{q}}_{1}^{}) \\ k_{2} s g n ({\dot{q}}_{2}^{}) \end{matrix}]$

其中： $k_{1}$ 、 $k_{2}$ 为摩擦系数，本文取 $k_{1} = k_{2} = 0.2$ 。

6）取干扰项与输入的期望运动轨迹相同，则外加干扰 $τ_{d}$ 为:

$τ_{d} = [\begin{matrix} 0.1 s i n t \\ 0.1 s i n t \end{matrix}]$

二杆机械臂控制参数设置为：高斯函数中均值 $c = 0.1 [\begin{matrix} - 1 & - 0.5 & 0 & 0.5 & 1 \\ - 1 & - 0.5 & 0 & 0.5 & 1 \\ - 1 & - 0.5 & 0 & 0.5 & 1 \\ - 1 & - 0.5 & 0 & 0.5 & 1 \\ - 1 & - 0.5 & 0 & 0.5 & 1 \end{matrix}]$ ，标准差 $b = 1$ ，权值矩阵中任意元素初值取0.1，滑模系数 $Λ = d i a g (2.3,2.3)$ ， $K_{v} = d i a g (200,200)$ ，鲁棒项中 $ε_{N} = 0.2$ ， $b_{d} = 0.1$ ，自适应律中 $Γ = d i a g (1.5,1.5)$ 。

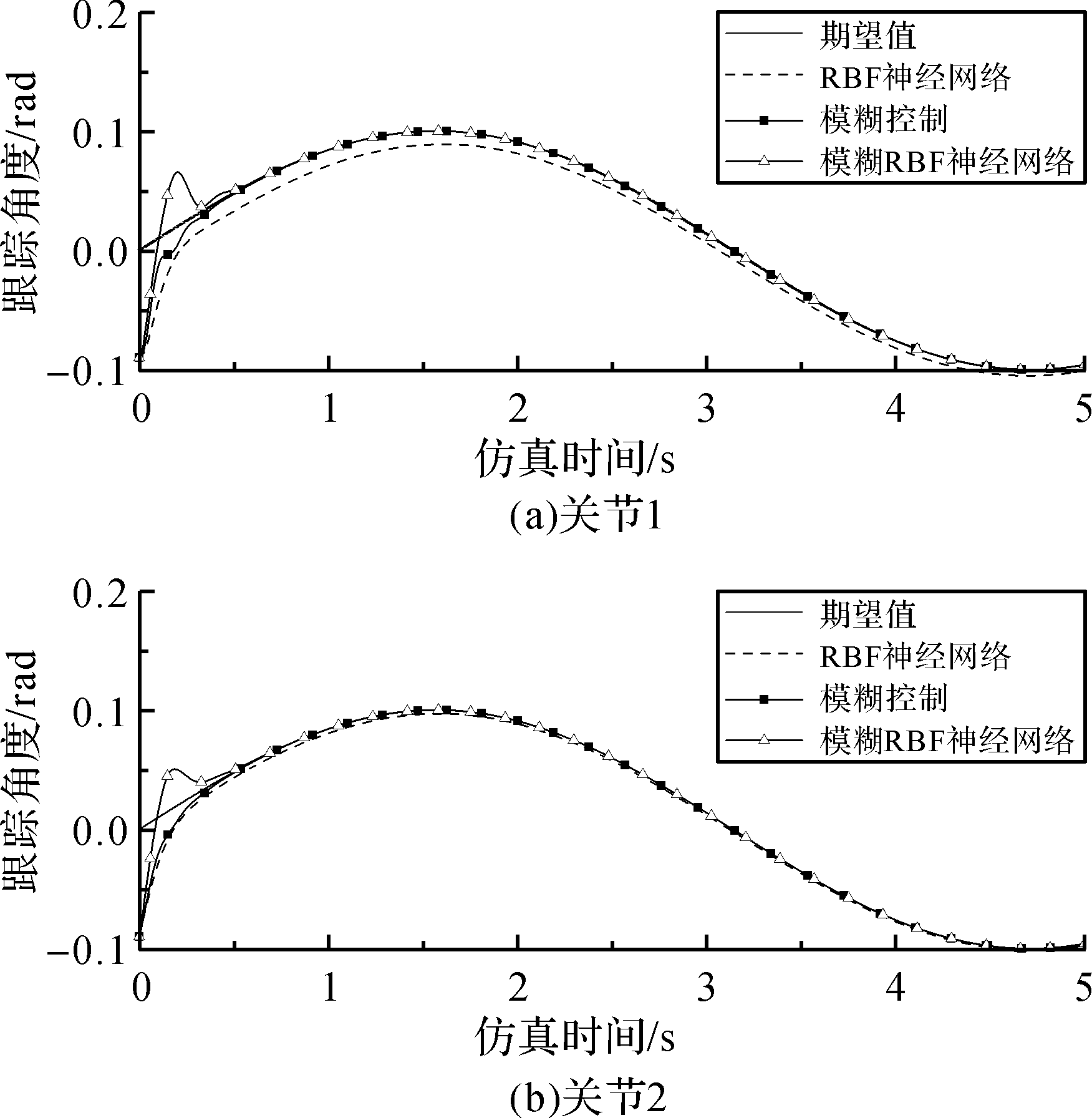
不同控制方法下二杆机械臂2个关节的角度跟踪曲线及稳态时角度跟踪误差曲线仿真结果分别如图4和图5所示。其中，常规RBF神经网络识别方法的隐层数为31层，其他参数与模糊RBF神经网络基本相同；传统模糊控制方法的隶属函数 $μ_{i} = e x p [- (x + \frac{- i + 3 π}{12}) / {(\frac{π}{24})}^{2}]$ $(i =$ $1,2, \dots, 5)$ ，其他参数与模糊RBF神经网络基本相同。

图4 二杆机械臂各关节的角度跟踪曲线

Fig. 4 Angle tracking curve of each joint of two-bar manipulator

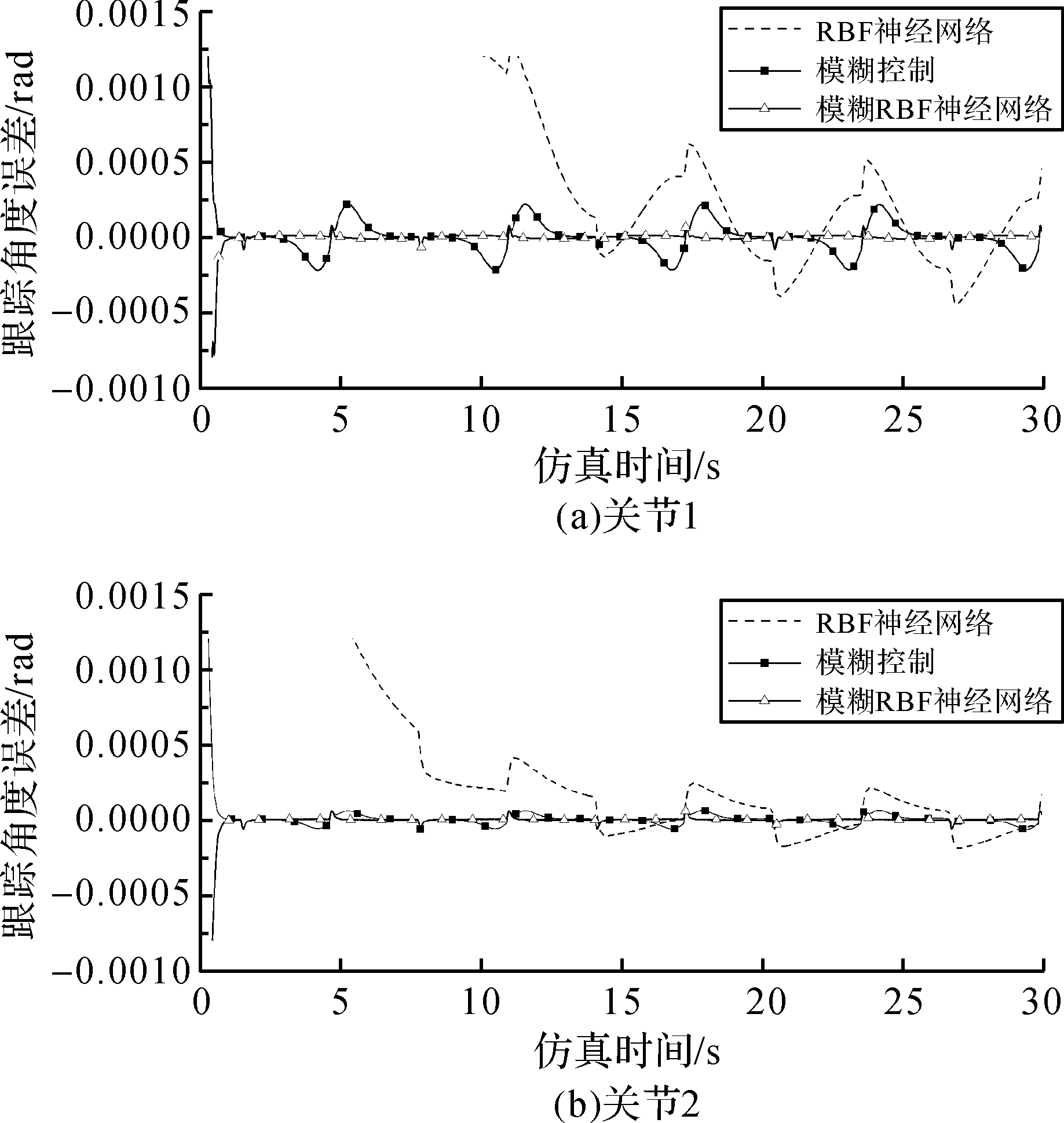
图5 二杆机械臂各关节的角度跟踪误差曲线

Fig. 5 Angle tracking error curve of each joint of two-bar manipulator

基于图4、图5结果，对二杆机械臂2个关节的角度跟踪误差进行分析，结果如表1所示。

表1 二杆机械臂各关节的角度跟踪误差分析

Table 1 Angle tracking error analysis of each joint of two-bar manipulator

控制方法	关节	响应时间/s	均方差/rad	最大稳态误差/rad	平均稳态误差/rad	相对误差/%
常规RBF神经网络	关节1	15	2.66× $10^{- 4}$	6.20× $10^{- 4}$	7.42× $10^{- 5}$	0.620
常规RBF神经网络	关节2	15	1.22× $10^{- 3}$	2.41× $10^{- 4}$	3.35× $10^{- 5}$	0.240
传统模糊控制	关节1	1.3	9.92× $10^{- 5}$	2.18× $10^{- 4}$	$-$ 8.47× $10^{- 6}$	0.218
传统模糊控制	关节2	1.2	3.01× $10^{- 5}$	6.32× $10^{- 5}$	$-$ 2.56× $10^{- 6}$	0.063
模糊RBF神经网络	关节1	1.3	1.49× $10^{- 5}$	7.55× $10^{- 5}$	6.34× $10^{- 7}$	0.076
模糊RBF神经网络	关节2	1.2	1.10× $10^{- 5}$	5.74× $10^{- 5}$	$-$ 4.58× $10^{- 9}$	0.057

由表1可知，在控制系统的响应时间上，常规RBF神经网络控制下的响应时间较长，关节1和关节2的响应时间均为15 s，传统模糊控制和模糊RBF神经网络控制下的响应时间较短，关节1的响应时间均为1.3 s，关节2的响应时间均为1.2 s；在控制系统的控制精度上，当系统达到稳定后，常规RBF神经网络控制下的最大稳态误差较大，关节1的最大稳态误差为6.20× $10^{- 4}$ rad，相对误差为0.620%，关节2的最大稳态误差为2.41× $10^{- 4}$ rad，相对误差为0.240%；传统模糊控制下的最大稳态误差较小，关节1的最大稳态误差为2.18× $10^{- 4}$ rad，相对误差为0.218%，关节2的最大稳态误差为6.32× $10^{- 5}$ rad，相对误差为0.063%；模糊RBF神经网络控制下的最大稳态误差最小，关节1的最大稳态误差为7.55× $10^{- 5}$ rad，相对误差为0.076%，关节2的最大稳态误差为5.74× $10^{- 5}$ rad，相对误差为0.057%。由此可得，与常规RBF神经网络识别方法相比，模糊RBF神经网络控制下关节1的响应时间缩短了91%，相对误差降低了88%，关节2的响应时间缩短了92%，相对误差降低了77%；与传统模糊控制方法相比，关节1的相对误差降低了65%，关节2的相对误差降低了10%。结果表明本文设计的模糊RBF神经网络的控制效果要优于常规RBF神经网络识别方法和传统模糊控制方法。

4 结论

针对水下机械臂提出了一种基于模糊RBF神经网络的控制方法，利用模糊系统启发式搜索和RBF神经网络推理速度较快的特点，实现了水下机械臂的高精度轨迹跟踪，并采用Lyapunov稳定性理论验证了水下机械臂系统的稳定性。通过对比分析模糊RBF神经网络、常规RBF神经网络识别方法和传统模糊控制方法控制下的二杆机械臂的角度跟踪曲线及角度跟踪误差发现，模糊RBF神经网络控制的响应时间更短，稳态误差更小，控制性能更有效。本研究为水下机械臂的控制提供了一种精度较高、较有效的方法。

参考文献

MOHAN Santhakumar, KIM Jinwhan . Indirect adaptive control of an autonomous underwater vehicle-manipulator system for underwater manipulation tasks[J]. Ocean Engineering, 2012, 54(4): 233-243. doi:10.1016/j. oceaneng.2012.07. 022 [百度学术]

YUH J . A neural net controller for underwater robotic vehicles[J]. IEEE Journal of Oceanic Engineering, 1990, 15(3): 161-166. doi:10.1109/48.107144 [百度学术]

YANG Xu, LIU Hai-tao, XIAO Ju-liang, et al . Continuous friction feedforward sliding mode controller for a Trimule hybrid robot[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(4): 1673-1683. doi: 10. 1109/TMECH.2018. 2853764 [百度学术]

YANG X, ZHU L M, NI Y, et al . Modified robust dynamic control for a diamond parallel robot[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(3): 959-968. doi:10.1109/TMECH.2019.2914165 [百度学术]

李敏, 王家序, 肖科, 等 . 基于模糊RBF神经网络动态摩擦分块补偿的机器人数字鲁棒滑模控制算法[J].中国机械工程,2012,23(23):2792-2796. doi:10.3969/j.issn. 1004-132X.2012.23.005 [百度学术]

LI Min, WANG Jia-xu, XIAO Ke, et al . Digital robust sliding mode control of robot manipulator with dynamic friction block compensation using fuzzy RBF neural network[J]. China Mechanical Engineering, 2012, 23(23): 2792-2796. [百度学术]

袁伟杰, 刘贵杰, 朱绍锋 . 基于遗传算法的自治水下机器人水动力参数辨识方法[J].机械工程学报,2010,46(11): 96-100. doi:10.3901/JME.2010.11.096 [百度学术]

YUAN Wei-jie, LIU Gui-jie, ZHU Shao-feng . Identification method of hydrodynamic parameters of autonomous underwater vehicle based on genetic algorithm[J]. Journal of Mechanical Engineering, 2010, 46(11): 96-100. [百度学术]

GONG Cheng-long, JIANG Yuan, LU Ke . RBF neural network control based on parameter adjustable CNF for robot manipulators behaviors[C]//Chinese Automation Congress (CAC), Xi'an: IEEE, 2018: 2859-2864. [百度学术]

肖凡, 李光, 周鑫林 . 多连杆机械臂GA-RBF神经网络轨迹跟踪控制[J].机械科学与技术,2018,37(5):669-674. doi:10.13433/j.cnki.1003-8728.2018.0503 [百度学术]

XIAO Fan, LI Guang, ZHOU Xin-lin . GA-RBF neural network control for trajectory tracking of multilink robot arm[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(5): 669-674. [百度学术]

俞建成, 李强, 张艾群，等 . 水下机器人的神经网络自适应控制[J].控制理论与应用,2008,25(1):9-13. doi:10.1038/cgt.2008.5 [百度学术]

YU Jian-cheng, LI Qiang, ZHANG Ai-qun, et al . Neural network adaptive control for underwater vehicles[J]. Control Theory & Applications, 2008, 37(5): 669-674. [百度学术]

余胜威 . MATLAB优化算法案例分析与应用[M].北京:清华大学出版社,2014:138-144. [百度学术]

YU Sheng-wei . Case analysis and application of MATLAB optimization algorithm[M]. Beijing: Tsinghua University Press, 2014: 138-144. [百度学术]

刘金琨 . 机器人控制系统的设计与MATLAB仿真[M]. 北京:清华大学出版社,2008:27-42. [百度学术]

LIU Jin-kun . Robot control system design and MATLAB simulation[M]. Beijing: Tsinghua University Press, 2008: 27-42. [百度学术]

魏循中 . 水下机械手结构设计及动力学研究[D].青岛：中国海洋大学工程学院,2014:44-45. [百度学术]

WEI Xun-zhong . Structure design and dynamic research of underwater manipulator[D]. Qingdao: Ocean University of China, School of Engineering, 2014: 44-45. [百度学术]

MORISON J R, JOHNSON J W, SCHAAF S A . The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. doi:10.2118/950149-g [百度学术]

高涵, 张明路, 张小俊, 等 . 水下机械手动力学模型及力矩影响研究[J]. 机械设计与制造, 2017 (3): 68-71. doi: 10.3969/j.issn.1001-3997.2017.03.018 [百度学术]

GAO Han, ZHANG Ming-lu, ZHANG Xiao-jun, et al . Research on underwater manipulator dynamics model and torque influence[J]. Machinery Design & Manufacture, 2017 (3): 68-71. [百度学术]

陈萍 . 水下机械手阻抗控制技术研究[D].哈尔滨:哈尔滨工程大学机电工程学院,2009:26. [百度学术]

CHEN Ping . Research on impedance control of underwater manipulator[D]. Harbin: Harbin Engineering University, College of Mechanical and Electrical Engineering, 2009: 26. [百度学术]

王华, 孟庆鑫, 王立权 . 基于切片理论的水下灵巧手手指动力学分析[J].机器人,2007,29(2):160-166. doi:10.3321/j.issn:1002-0446.2007.02.012 [百度学术]

WANG Hua, MENG Qing-xin, WANG Li-quan . Analysis on finger dynamics of dexterous underwater hand based on strip theory [J]. Robot, 2007, 29(2): 160-166. [百度学术]

李忠秋, 赵春雨, 洪洋, 等 . 基于模糊RBF网络补偿的控制输入受限滑模控制[J]. 电子世界,2018(12):8-10. doi: 10.19353/j.cnki.dzsj.2018.12.002 [百度学术]

LI Zhong-qiu, ZHAO Chun-yu, HONG Yang, et al . Control of input limited sliding mode based on fuzzy RBF network compensation[J]. Electronics World, 2018(12): 8-10. [百度学术]

WOLF A, SWIFT J B, SWINNEY H L, et al . Determining Lyapunov exponents from a time series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317. doi:10.1016/0167-2789(85)90011-9 [百度学术]

基于模糊RBF神经网络的水下机械臂控制研究

摘要

关键词

1 水下机械臂动力学模型建立

2 基于模糊RBF神经网络的控制器设计

2.1 水下机械臂动力学模型分析

2.2 模糊RBF神经网络设计

2.3 控制律设计

2.4 控制系统稳定性分析