2. 金策工业综合大学 机械工程系, 平壤 朝鲜 999093
2. Department of Mechanical Engineering, Kim Chaek University of Technology, Pyongyang 999093, Democratic People's Republic of Korea
液压阻尼器等被动式阻尼器常常被用来减缓振动和冲击,从而避免航空航天器件、桥梁建筑等遭到损坏,也能使汽车等交通工具具有更加舒服的乘坐环境。但是,由于被动式液压阻尼器不具有动态可调的特性,其往往只适用于特定的激励条件和一个有效载荷重量。
作为一种性能优良的智能结构,磁流变阻尼器具有反应快速、功耗低、阻尼力连续可调等优异性能,其可以作为一种应用前景良好的半主动作动装置,安装在电子控制和机械系统之间来提供简单和快速反应的接口。磁流变阻尼器[1-5]可以用来减缓隔振系统的振动和冲击作用,适用于不同的激励条件和载荷重量,近年来,其被广泛应用于机械、土木、航空航天等领域。但是,传统磁流变阻尼器往往不能在一定体积的限制条件下提供较大的可控阻尼力,这将限制磁流变阻尼器的应用。因此,研究具有新型结构的磁流变阻尼器来改善磁流变阻尼器的阻尼特性是十分有必要的。
近年来,一些学者研究并设计了具有混合模式的磁流变阻尼器,其被证实具有比单一模式更好的阻尼力特性。Sung等[6]对3种形式的磁流变阻尼器的特性进行了比较,设计和制作了一种具有剪切和流动混合模式的磁流变阻尼器,并进行了阻尼特性实验。Yazid等[7]设计了一种由剪切和挤压模式相结合的磁流变阻尼器,并通过有限元分析模拟由磁流变阻尼器的激励线圈产生的磁场,分别在剪切模式、挤压模式以及混合模式下测试了磁流变阻尼器的阻尼特性。
区别于常规磁流变阻尼器的节流通道形式,具有新型节流通道形式的磁流变阻尼器引起了学者的关注。这些磁流变阻尼器节流通道的结构形式包括旁路式、折叠式以及蜿蜒式。Robinson等[8]设计了一种具有多孔旁通阀的磁流变阻尼器,评估了多孔介质对磁流变阻尼器最大可控阻尼力和阻尼系数的影响。Kim等[9]设计并制造了一种具有折叠流动模式的磁流变阻尼器,通过数学建模和有限元分析对磁流变阻尼器的性能进行了预测,并通过实验证明了所设计的磁流变阻尼器具有比传统阻尼器更大的可控阻尼力和等效阻尼。Bai等[10]研制了一种具有环形-径向节流通道的磁流变阻尼器,建立了考虑磁流变液非线性流动效应的数学模型,并通过实验测试验证了数学模型的准确性。胡国良等[11-13]设计了不同形式节流通道的磁流变阀,建立了磁流变阀的数学模型并进行了有限元分析。张进秋等[14]提出了一种叶片式磁流变液减振器,并通过有限元分析对其结构进行了优化。
通常情况下,节流通道形式上的改变可以增大磁流变阻尼器的最大可控阻尼力,然而并不能增大磁流变阻尼器的动态范围,因为流动通道的延展可以提升在磁场作用下的剪切强度引起的压降,但同时在无磁场作用下的黏性压降和次要压降损失也会增大。为了提高磁流变阻尼器的效率,同时增大其最大可控阻尼力和动态范围,一些学者对磁流变阻尼器的磁路进行改进。Bai等[15]设计并制作了一个具有多级励磁线圈的内旁路式磁流变阻尼器,提高了磁流变阻尼器节流通道的利用效率。Senkal等[16]通过利用导磁和非导磁单元的堆叠形成蜿蜒磁路,设计并制作了用于触觉应用的紧凑型磁流变制动器。
本文设计了一种多级蜿蜒磁路式磁流变阻尼器来提高节流通道利用效率,从而使磁流变阻尼器具有更大的可控阻尼力和动态范围。为了显示所设计的磁流变阻尼器的合理性和优点,通过电磁有限元分析对磁流变阻尼器的原理和电磁特性进行了验证和分析。另外,比较了所设计的磁流变阻尼器和传统磁流变阻尼器的阻尼特性,包括不同激励条件下的阻尼力、等效阻尼和动态范围。
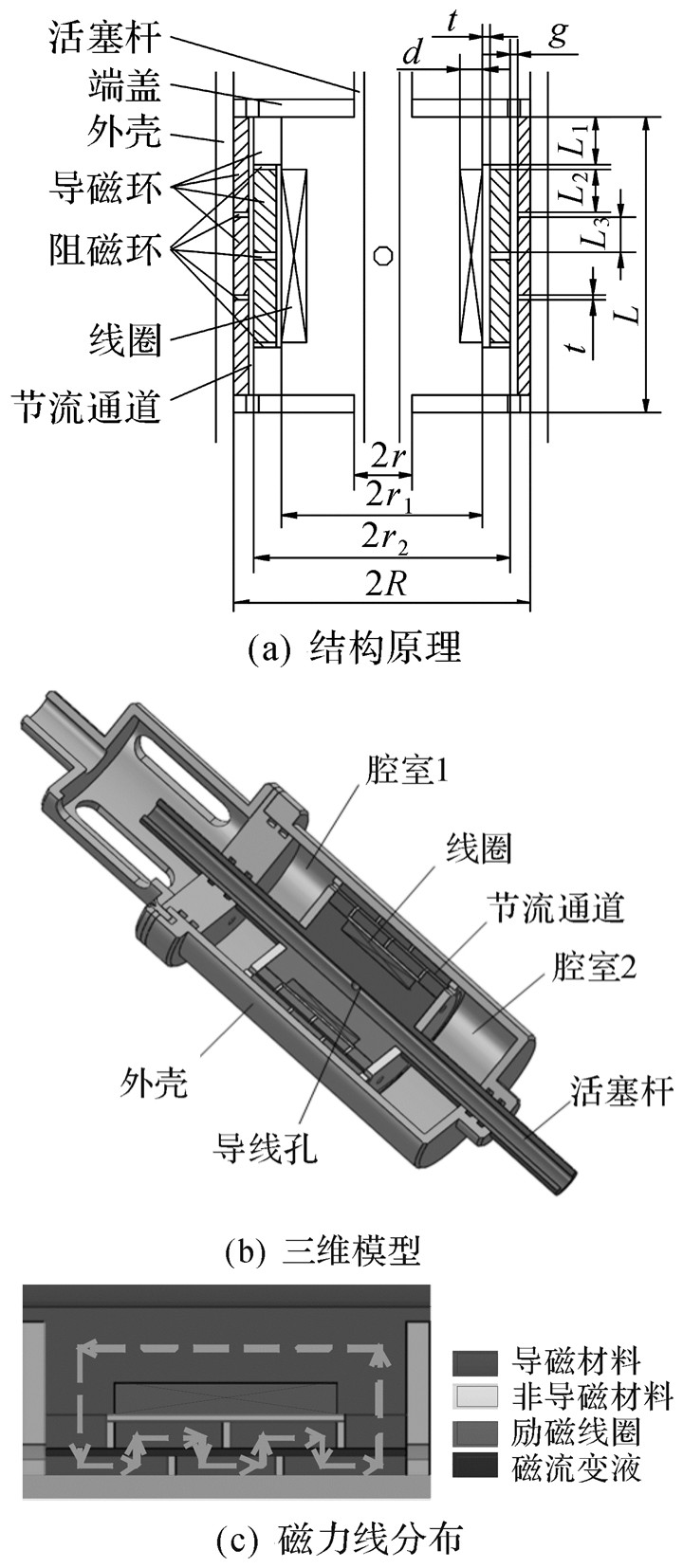
1 多级蜿蜒磁路式磁流变阻尼器的结构和原理图 1(a)和(b)分别为多级蜿蜒磁路式磁流变阻尼器的结构原理图和三维模型图。该磁流变阻尼器由阻尼器外壳、活塞单元以及活塞杆组成。活塞单元由端盖、阻磁环、导磁环以及励磁线圈组成。外壳、端盖和阻磁环的材料为不锈钢,活塞杆和导磁环为10号钢。活塞单元的零部件轴向通过端盖进行固定,径向利用过渡配合进行定位,零部件之间涂少量密封胶来增强密封性。导磁环和阻磁环之间形成环形节流通道,磁流变液通过节流通道在活塞壳体的腔室1和腔室2中交换流动。磁流变阻尼器的结构形式为双出杆结构,在活塞杆相对外壳的滑动过程中腔室1和腔室2的总体积不变,因此不用补偿磁流变液,即可省去蓄能器。活塞杆与外壳之间通过密封圈实现滑动密封,线圈的引线通过活塞杆上的导线孔以及活塞杆的轴心引出。
|
| 图 1 多级蜿蜒磁路式磁流变阻尼器结构原理 Fig.1 Structure principle of the MR damper with multistage serpentine magnetic circuit |
所设计的磁流变阻尼器具有蜿蜒磁路,如图 1(c)所示。通过策略地布置导磁和非导磁单元,迫使磁场数次通过节流通道并形成蜿蜒的磁路,提高节流通道的利用效率。从活塞杆的中心轴线开始,由通电的励磁线圈产生的磁路径向穿过节流通道,随后沿外圈的导磁环轴向前进,置于外圈的阻磁环迫使它径向穿越节流通道,沿内圈导磁环轴向前进后在阻磁环的作用下再次径向穿越节流通道,最后径向穿越节流通道形成闭合的电磁回路。
当线圈中不通入电流时,即在无磁场的作用下,磁流变阻尼器仅产生与磁流变液的黏度相关的黏滞阻尼力。然而,当通入电流后,磁流变液将被磁场激活,磁流变阻尼器将提供一个与磁流变液的剪切强度相关的可控阻尼力。随着电流的增大,在磁路的磁通密度达到饱和状态之前,磁流变液的剪切强度也将逐渐增大。因此,可以通过调节输入电流值来控制磁流变阻尼器产生的阻尼力。
2 磁流变阻尼器阻尼力的数学建模为了证明本文所设计的磁流变阻尼器的原理可行,将其阻尼特性与传统磁流变阻尼器进行比较,基于考虑磁流变液非线性流动特性的Bigaham塑性流体模型,结合具体的磁流变结构,分别建立了多级蜿蜒磁路式磁流变阻尼器和传统磁流变阻尼器的动力模型。
2.1 多级蜿蜒磁路式磁流变阻尼器的阻尼力从图 1可以看出,多级蜿蜒磁路式磁流变阻尼器的磁流变液的工作模式是流动式,该磁流变阻尼器的阻尼力大小可以表示为:
| $ F = (\Delta {P_{\rm{a}}} + \Delta {P_{{\rm{ml}}}}){A_{\rm{p}}} $ | (1) |
式中:ΔPa为通过节流通道的压降;ΔPml为磁流变液流经节流通道时因突然膨胀或收缩而造成的次要压降损失;Ap为活塞的有效面积。
Ap可以表示为:
| $ {A_{\rm{p}}} = \pi {R^2} - \pi [{({r_2} + g)^2} - r_2^2] - \pi {r^2} $ | (2) |
式中:R为活塞半径,r2为导磁环半径,r为活塞杆半径,g为节流通道的宽度。
通过节流通道的压降ΔPa可以表示为:
| $ \Delta {P_{\rm{a}}} = \Delta {P_\eta } + \Delta {P_\tau } $ | (3) |
式中:ΔPη和ΔPτ分别是黏性压降和屈服压降[17],它们可以表示为:
| $ \Delta {P_\eta } = \frac{{6\eta QL}}{{\pi {g^3}({r_2} + g/2)}} $ | (4) |
| $ \Delta {P_\tau } = \frac{{2c\tau ({L_1} + {L_2} + {L_3})}}{g} $ | (5) |
式中:η为无磁场作用下磁流变液的黏度,Q为磁流变液通过节流通道的体积流量,L为节流通道的长度,L1为外导磁环的长度,L2为外阻磁环的长度,τ为节流通道中磁流变液的剪切强度,c为与体积流量和屈服应力相关的系数。
如果活塞的速度用vp表示,则体积流量Q和系数c[18]分别可以表示为:
| $ Q = {A_{\rm{p}}}{v_{\rm{p}}} $ | (6) |
| $ c = 2.07 + \frac{{12Q\eta }}{{12Q\eta + 0.8\pi ({r_2} + g/2){g^2}\tau }} $ | (7) |
公式(1) 中的次要压降损失ΔPml[10]可以表示为:
| $ \Delta {P_{{\rm{ml}}}} = \frac{\rho }{2}\cdot2v_{\rm{d}}^2{K_{{\rm{ml}}}} $ | (8) |
式中:ρ为磁流变液的密度;vd为磁流变液通过节流通道的平均流速,
联合式(1) 至式(8),磁流变阻尼器的阻尼力可表示为:
| $ F = {A_{\rm{p}}}\left[ {\frac{{6\eta QL}}{{\pi {g^3}({r_2} + g/2)}} + \frac{{2c\tau ({L_1} + {L_2} + {L_3})}}{g})} \right] + {A_{\rm{p}}}\rho v_{\rm{d}}^2{K_{{\rm{ml}}}} $ | (9) |
如果E是正弦位移激励下1个周期内消耗的能量,那么等效阻尼[19]可表示为:
| $ {C_{{\rm{eq}}}} = \frac{E}{{\pi \omega {X^2}}} $ | (10) |
式中:ω为激励频率,X为正弦激励的幅值。
E可以表示为:
| $ E = \oint {F{\rm{d}}x} = \int_0^{\frac{{2\pi }}{\omega }} {F\dot x{\rm{d}}t} $ | (11) |
式中:x为在正弦位移激励下磁流变阻尼器活塞的位置,
动态范围是磁场作用下等效阻尼Ceq与无外加磁场下等效黏滞阻尼C0的比值,常常被用来评估磁流变阻尼器的阻尼特性,该比值表示为:
| $ D = \frac{{{C_{{\rm{eq}}}}}}{{{C_0}}} $ | (12) |
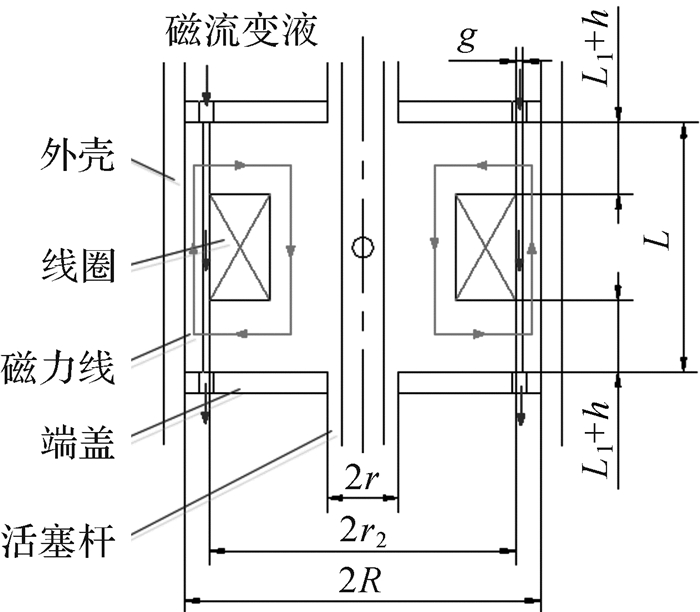
与多级蜿蜒磁路式磁流变阻尼器具有相同体积的传统磁流变阻尼器的结构如图 2所示。
|
| 图 2 传统磁流变阻尼器结构原理 Fig.2 Structural principle of the traditional MR damper |
类似于式(1) 至式(8),可以得到传统磁流变阻尼器的阻尼力:
| $ {F_{\rm{t}}} = {A_{\rm{p}}}\left[ {\frac{{6\eta QL}}{{\pi {g^3}({r_2} + g/2)}} + \frac{{2c\tau ({L_1} + {L_2} + {L_3})}}{g})} \right] + {A_{\rm{p}}}\Delta {P_{{\rm{ml}}}} $ | (13) |
式(13) 中活塞的有效面积Ap、体积流量Q、系数c以及次要压降损失ΔPml分别参见式(2)、式(6) 至式(8)。h在数值上等于本文所设计的磁流变阻尼器的绝磁环的厚度。
等效阻尼以及动态范围的定义分别参见式(10) 和式(12)。
3 磁流变阻尼器电磁特性的有限元分析为了验证方案原理的可行性,并获得磁流变阻尼器的电磁特性,利用Maxwell 2D软件分别对多级蜿蜒磁路式磁流变阻尼器和传统磁流变阻尼器进行电磁有限元分析[20]。考虑到磁流变阻尼器的结构是对称分布的,分析过程中取其一半活塞模型进行分析。
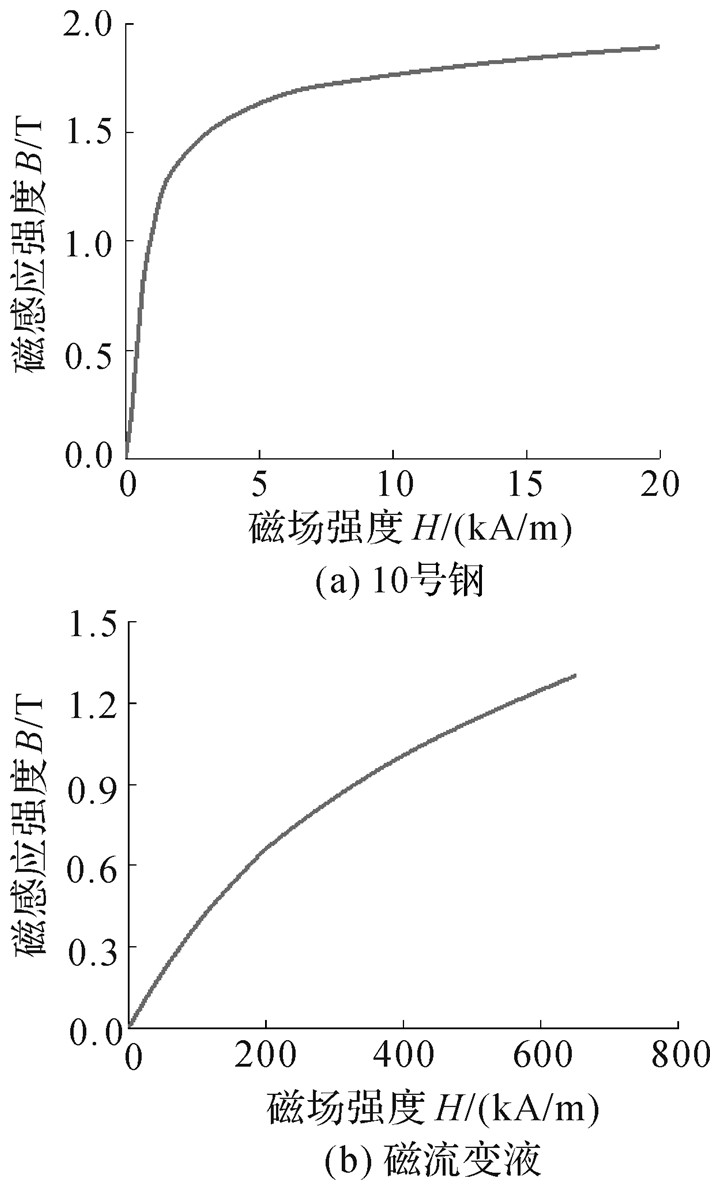
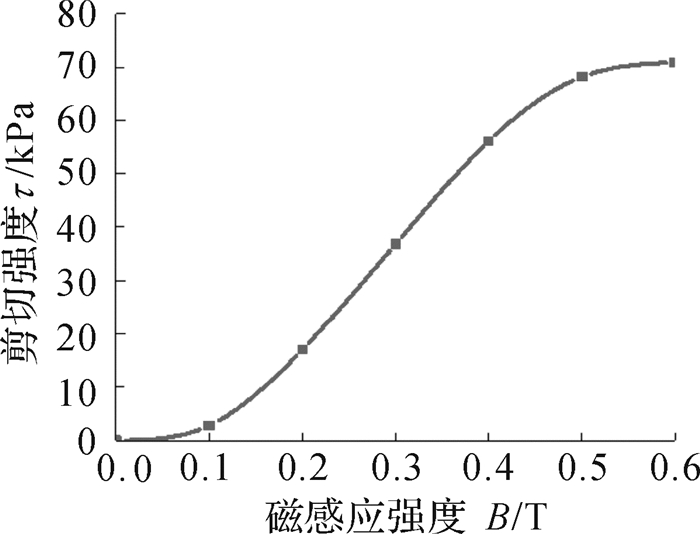
表 1列出了多级蜿蜒磁路式磁流变阻尼器的主要尺寸和相关参数。该磁流变阻尼器的工作介质采用重庆材料研究所生产的MRF-J01T磁流变液[13]。10号钢和磁流变液的磁化曲线如图 3所示,磁流变液的剪切强度与磁感应强度的关系曲线[13]如图 4所示。
| 参数 | 符号 | 数值 |
| 活塞杆半径 | r | 5 mm |
| 线圈外圈半径 | r1 | 17 mm |
| 内导磁环半径 | r2 | 21.5 mm |
| 活塞半径 | R | 25 mm |
| 通道1长度 | L1 | 8 mm |
| 通道2长度 | L2 | 6 mm |
| 通道3长度 | L3 | 7 mm |
| 绝磁环厚度 | h | 1 mm |
| 活塞长度 | L | 47 mm |
| 线圈宽度 | d | 4 mm |
| 节流通道宽度 | g | 1 mm |
| 磁流变液黏度 | η | 0.8 Pa·s |
| 磁流变液密度 | ρ | 2.65 g·cm-3 |
| 线圈匝数 | N | 500匝 |
|
| 图 3 磁化曲线 Fig.3 Magnetization curve |
|
| 图 4 磁流变液的剪切强度与磁感应强度的关系曲线 Fig.4 Relationship between shear strength and magnetic flux density of MRF |
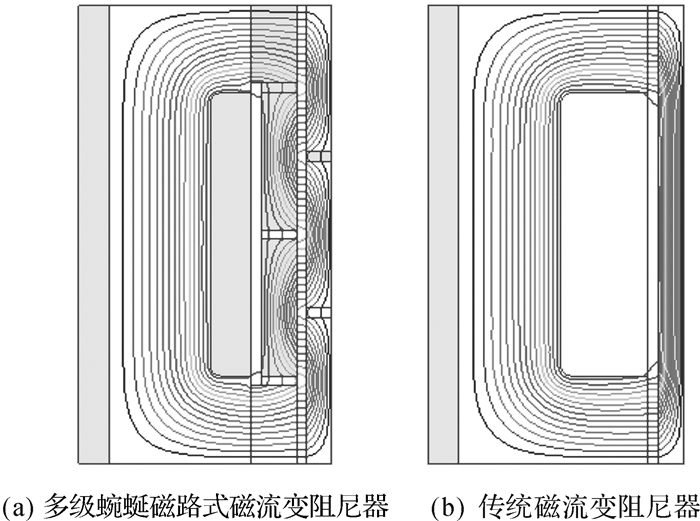
在1.5 A电流的激励下,多级蜿蜒磁路式磁流变阻尼器和传统磁流变阻尼器的磁力线分布如图 5所示,结构的磁感应强度分布云图如图 6所示。从图 5(a)中可以看出,磁力线是按照预期设计穿过节流通道形成蜿蜒的闭合回路。由于阻磁环较薄,且不能完全隔绝磁场,有少许磁力线没有穿过节流通道,而是直接通过阻磁环形成回路。相比于传统磁流变阻尼器的磁力线分布,多级蜿蜒磁路式磁流变阻尼器的磁力线多次穿越节流通道,节流通道几乎是全通道有效。
|
| 图 5 磁流变阻尼器的磁力线分布 Fig.5 Magnetic lines distribution of the MR damper |

|
| 图 6 磁感应强度分布云图 Fig.6 Nephogram magnetic flux density distribution |
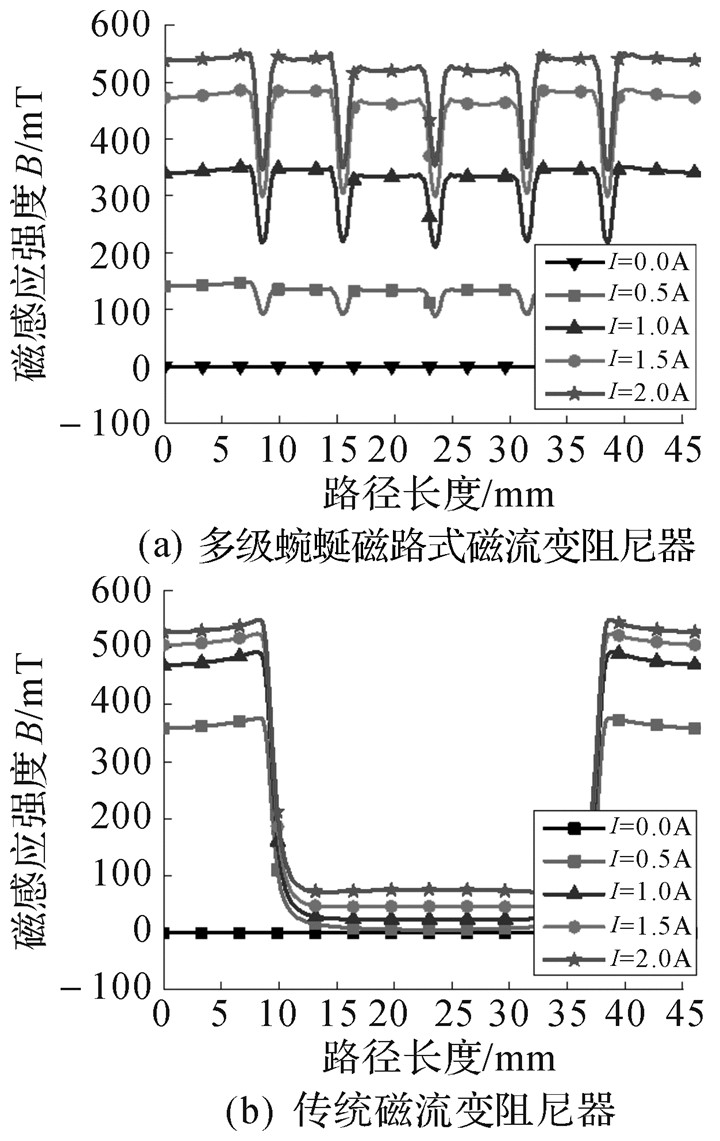
在不同电流的作用下,所设计的磁流变阻尼器和传统磁流变阻尼器沿节流通道路径的磁感应强度如图 7所示。比较可知,所设计的磁流变阻尼器的节流通道的有效长度比传统磁流变阻尼器大得多。由于传统磁流变阻尼器磁路的总磁阻比所设计的磁流变阻尼器的小,传统磁流变阻尼器更容易达到饱和状态,由图 7(b)可知,传统磁流变阻尼器在通入1.0 A电流时,磁流变液便有达到饱和状态的趋势。结合图 4和图 7可知,所设计的磁流变阻尼器和传统的磁流变阻尼器都能最大化利用磁流变液的磁特性,在通入2.0 A电流时达到磁饱和状态,表明结构设计合理。
|
| 图 7 磁流变阻尼器沿节流通道路径的磁感应强度 Fig.7 Magnetic flux density along the gap length of the MR dampers |
将有限元分析得到的有效节流通道中磁流变液的平均磁感应强度B代入磁流变液的剪切强度与其磁感应强度的关系式[13](由图 4中的曲线经过最小二乘法拟合得到)中,得到磁流变液在线圈通入不同电流时的剪切强度τ。然后将得到的剪切强度τ分别代入建立的数学模型(9) 和(13),并结合表 1中列出的参数以及计算得到磁流变液的平均流速等参数,得到所设计的磁流变阻尼器和传统磁流变阻尼器在不同电流下的阻尼力大小,并且依据式(10) 和(12) 可以计算出等效阻尼和动态范围。
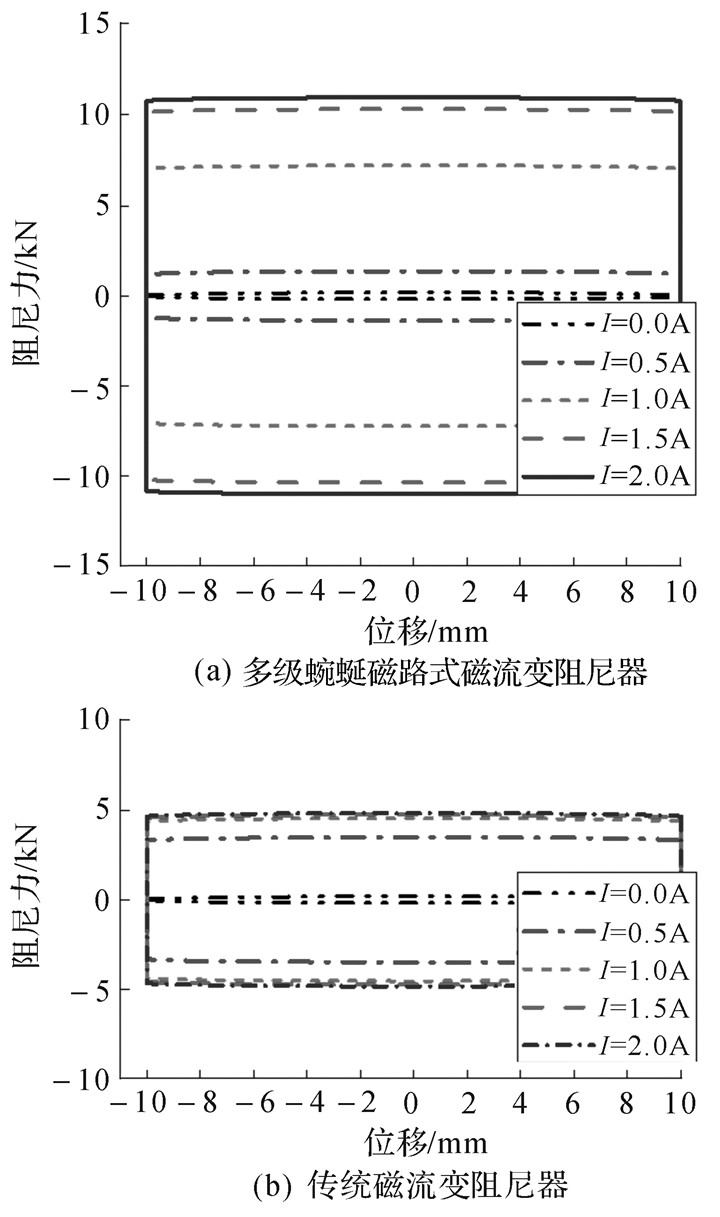
图 8和图 9所示分别为在频率为2 Hz、幅值为10 mm的正弦激励下,磁流变阻尼器的阻尼力与激励位移和速度的关系。虽然Bingham模型不能捕捉非线性滞后行为,但是能够较好描述阻尼力与激励位移的关系,并能够准确预测阻尼力的大小。并且,Bingham模型具有模型简洁、物理意义明显、便于理解和分析等优点,其被广泛应用于磁流变阻尼器的设计阶段来准确预测阻尼力。
|
| 图 8 阻尼力与位移的关系 Fig.8 The relationship between damping force and displacement |
|
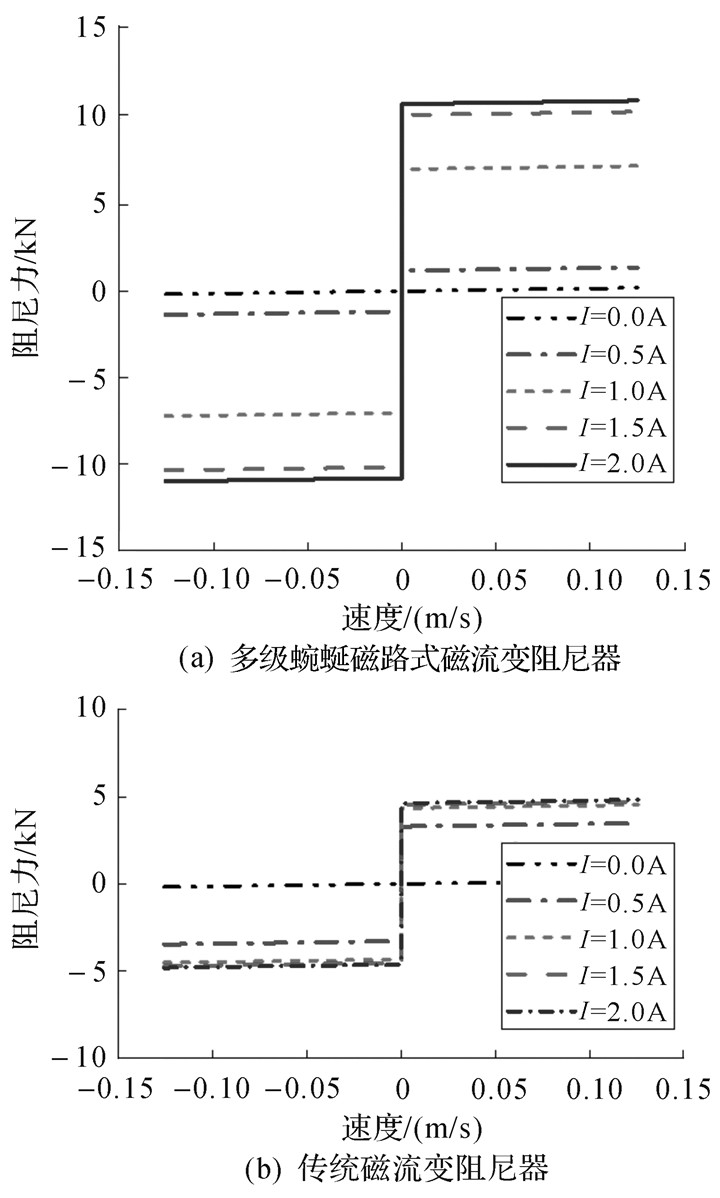
| 图 9 阻尼力与速度的关系 Fig.9 The relationship between damping force and velocity |
由图 8和图 9可知,无电流输入即无磁场作用的情况下,所设计的磁流变阻尼器和传统磁流变阻尼器输出的最大阻尼力相同,都为189 N,这是由于2种磁流变阻尼器具有相同形式和尺寸的节流通道,在无磁场作用下,阻尼器产生的阻尼力即黏性阻尼力相同。输入1.5 A电流时,所设计的磁流变阻尼器输出的最大阻尼力包括黏性阻尼力和剪切阻尼力,为11 000 N,远远大于传统磁流变阻尼器输出的4 823 N。因此,所设计的磁流变阻尼能够提供更大的可控阻尼力。
对比图 8(a)和(b)可以发现,在通入0.5 A电流时,所设计的磁流变阻尼器的阻尼力是要小于传统磁流变阻尼器的。由图 7可知,在通入0.5 A电流时,所设计的磁流变阻尼器的有效节流通道中磁流变液的磁感应强度约为0.142 T,小于传统磁流变阻尼器的0.369 T,而图 4显示磁流变液的剪切强度在磁感应强度0~0.15 T阶段的增长速度非常缓慢,因此,此时所设计的磁流变阻尼器的有效节流通道中的磁流变液的剪切强度比传统磁流变阻尼器的要小很多,小电流时其有效长度更长的优势没有体现出来。
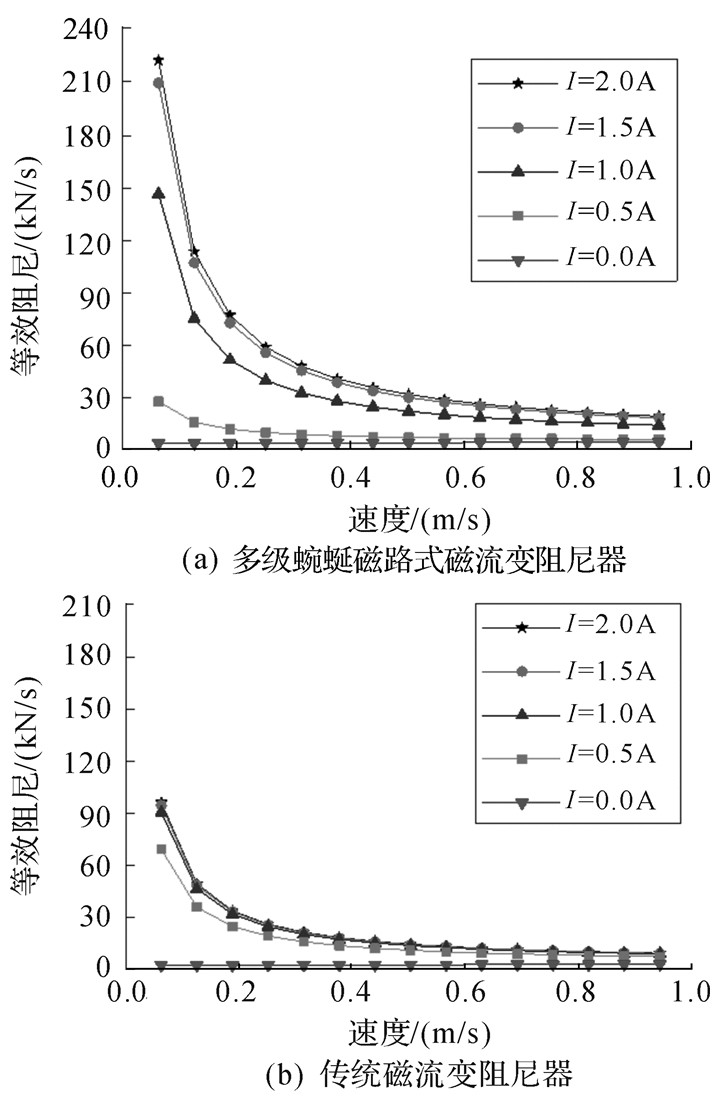
图 10显示在幅值为10 mm、不同频率(转换为不同频率对应的速度)的正弦激励下,磁流变阻尼器的等效阻尼特性。在相同激励频率(特定速度)下,随着输入电流的增大,磁流变阻尼器的等效阻尼增大;在相同输入电流下,随着激励频率的增大(速度的增大),磁流变阻尼器的等效阻尼减小。如图 10所示,当输入电流大于1.0 A时,在整个频率范围内,所设计的磁流变阻尼器的等效阻尼远大于传统磁流变阻尼器。
|
| 图 10 磁流变阻尼器的等效阻尼 Fig.10 Equivalent damping of the MR dampers |
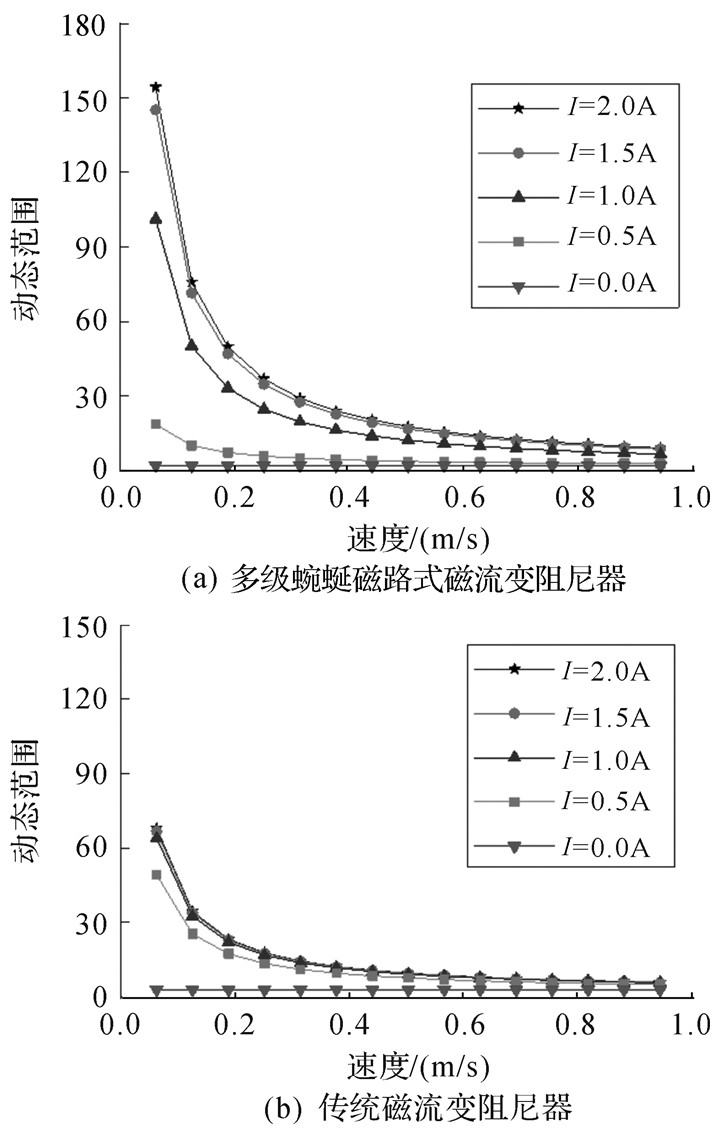
相应地,图 11为仿真得到的磁流变阻尼器的动态范围与激励频率和输入电流的关系。随着输入电流增大,磁流变阻尼器的阻尼系数增大;随着激励频率增大,磁流变阻尼器的阻尼系数减小。如图 11所示,在输入电流大于1.0 A时,所设计的阻尼器的阻尼系数远大于传统磁流变阻尼器。这是由于所设计的磁流变阻尼器与传统磁流变阻尼器具有相同形式的节流通道,在无磁场作用下,具有相同的等效阻尼,而所设计的磁流变阻尼器具有更高的通道利用效率,在磁场的作用下其等效阻尼远大于传统阻尼器。
|
| 图 11 磁流变阻尼器的动态范围 Fig.11 Dynamic range of the MR dampers |
同时需要指出的是,在小电流情况下,所设计的磁流变阻尼器的等效阻尼和动态范围比传统磁流阻尼器的小。这是由于传统磁流变阻尼器的总磁阻较小,在磁路达到饱和状态前,在小电流情况下其节流通道中磁流变液的磁感应强度相对较大,进而,其磁流变液的剪切应力相对较大,导致在小电流时其输出的阻尼力较大。但随着电流的增大,传统磁流变阻尼器的磁路更容易达到饱和状态,而所设计的磁流变阻尼器是缓慢达到饱和状态时,且能够更加高效地利用节流通道,节流通道有效长度上的优势便逐渐体现出来,其等效阻尼和动态范围在通入1.0 A电流时已超越了传统磁流变阻尼器。航空航天器件、土木建筑、汽车等往往需求很大的阻尼力和动态范围,因此,所设计的磁流变阻尼器具有良好的工程应用价值。为了适应不同的工程应用,可以对所设计的磁流变阻尼器的结构尺寸进行相应的优化。
4 结论1) 设计了一种具有多级蜿蜒磁路特性的磁流变阻尼器,通过策略地堆叠导磁环和阻磁环来引导磁路。该磁流变阻尼器活塞的直径为50 mm,长度为47 mm,在保证外形结构尺寸相等的前提下,本设计扩展了磁流变阻尼器节流通道的有效面积,使磁流变阻尼器的阻尼特性得到了改善。
2) 对所设计的磁流变阻尼器的工作原理进行了理论分析,同时基于Bingham流体模型推导了其阻尼力模型。利用Maxwell 2D软件对其电磁场进行了仿真分析,有限元仿真结果验证了所设计的磁流变阻尼器的原理可行,并得到了通入不同电流时沿节流通道路径的磁感应强度。相比于传统磁流变阻尼器,所设计的磁流变阻尼器的节流通道几乎是全通道有效。通入2.0 A电流时,所设计的磁流变阻尼器的有效节流通道中磁流变液的磁感应强度约为0.53 T。
3) 结合建立的数学模型与有限元分析结果,对所设计的磁流变阻尼器的动态特性进行了数值求解,并将其与传统磁流变阻尼器的动态特性进行了对比分析。分析结果显示,在正弦激励速度为0.125 m/s,并通入2.0 A电流的情形下,所设计的磁流变阻尼器的最大可控阻尼力为11 000 N,约为传统磁流变阻尼器的2.3倍。此外,不通入电流时,即在零场作用下,所设计的磁流变阻尼器的阻尼力是与传统磁流变阻尼器相等的。分析表明所设计的磁流变阻尼器具有更大的阻尼力可控范围。
| [1] | ZHU X C, JING X J, CHENG L. Magnetorheological fluid dampers: a review on structure design and analysis[J]. Journal of Intelligent Material Systems, 2012, 23(8): 839–873. DOI:10.1177/1045389X12436735 |
| [2] |
李忠献, 徐龙河.
新型磁流变阻尼器及半主动控制设计理论[M]. 北京: 科学出版社, 2012: 1-25.
LI Zhong-xian, XU Long-he. Novel magneto-rheological dampers and semi-active control design theory[M]. Beijing: Science Press, 2012: 1-25. |
| [3] | MUHAMMAD A, YAO X L, DENG Z C. Review of magnetorheological (MR) fluids and its applications in vibration control[J]. Journal of Marine Science and Application, 2006, 5(3): 17–29. DOI:10.1007/s11804-006-0010-2 |
| [4] | IMADUDDIN F, MAZLAN S A, ZAMZURI H. A design and modelling review of rotary magnetorheological damper[J]. Materials and Design, 2013, 51: 575–591. DOI:10.1016/j.matdes.2013.04.042 |
| [5] | WANG D H, LIAO W H. Magnetorheological fluid dampers: a review of parametric modelling[J]. Smart Materials and Structures, 2011, 20(2): 023001. DOI:10.1088/0964-1726/20/2/023001 |
| [6] | SUNG K G, CHOI S B. Preformance comparison of MR damper with three differernt working modes: shear, flow and mixed mode[J]. International Journal of Modern Physics B, 2005, 19(7/8/9): 1556–1562. |
| [7] | YAZID I I M, MAZLAN S A, KIKUCHI T, et al. Design of magnetorheological damper with a combination of shear and squeeze modes[J]. Materials and Design, 2014, 54: 87–95. DOI:10.1016/j.matdes.2013.07.090 |
| [8] | ROBINSON R, HU W, WERELYN M. Linking porosity and tortuosity to the performance of a magneto-rheological damper employing a valve filled with porous media[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2156–2159. DOI:10.1109/TMAG.2010.2043648 |
| [9] | KIM K, CHEN Z B, YU D, et al. Design and experiments of a novel magnetorheological damper featuring bifold flow mode[J]. Smart Materials and Structures, 2016, 25(7): 075004. DOI:10.1088/0964-1726/25/7/075004 |
| [10] | BAI X X, WANG D H, FU H. Principle, modeling, and testing of an annular-radial-duct magnetorheological damper[J]. Sensors and Actuators A: Physical, 2013, 201: 302–309. DOI:10.1016/j.sna.2013.07.028 |
| [11] |
胡国良, 李海燕, 李卫华.
径向流和圆环流磁流变阀压降性能分析与试验[J]. 农业机械学报, 2016, 47(4): 364–371, 405.
HU Guo-liang, LI Hai-yan, LI Wei-hua. Comparison and experiment of pressure drop of radial and annular type magnetorheological valves[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4): 364–371, 405. DOI:10.6041/j.issn.1000-1298.2016.04.048 |
| [12] |
胡国良, 李海燕, 张海云.
圆环流磁流变阀压降性能分析与试验[J]. 农业机械学报, 2016, 47(3): 381–388.
HU Guo-liang, LI Hai-yan, ZHANG Hai-yun. Performance analysis and experimental tests of pressure drop of annular type magnetorheological valve[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 381–388. DOI:10.6041/j.issn.1000-1298.2016.03.054 |
| [13] |
胡国良, 钟芳, 张海云, 等.
两级径向流蜿蜒式磁流变阀结构设计及动态性能分析[J]. 农业机械学报, 2016, 47(3): 381–388.
HU Guo-liang, ZHONG Fang, ZHANG Hai-yun, et al. Structure design and dynamic performance analysis of a two-stage radial type magnetorheological valve with meandering fluid flow paths[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 381–388. DOI:10.6041/j.issn.1000-1298.2016.03.054 |
| [14] |
张进秋, 彭志召, 张建, 等.
叶片式磁流变液减振器结构设计与优化[J]. 振动、测试与诊断, 2013, 33(1): 132–137.
ZHANG Jing-qiu, PENG Zhi-zhao, ZHANG Jian, et al. Design and optimization of vane magneto-rheological fluid damper[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1): 132–137. |
| [15] | BAI X X, HU W, WERELEY N M. Magnetorheological damper utilizing an inner bypass for ground vehicle suspensions[J]. IEEE Transactions on Magnetics, 2013, 49(7): 3422–3425. DOI:10.1109/TMAG.2013.2241402 |
| [16] | SENKAL D, GUROCAK H. Compact MR-brake with serpentine flux path for haptics applications [C]//Proceeding Third Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems. Salt Lake City, Mar. 18-20, 2009. |
| [17] | NGUYEN Q H, CHOI S B, WERELEY N M. Optimal design of magneto-rheological valves via a finite element method considering control energy and a time constant[J]. Smart Materials and Structures, 2008, 17(2): 025024. DOI:10.1088/0964-1726/17/2/025024 |
| [18] | NGUYEN Q H, CHOI S B, WERELEY N M. Optimal design of magneto-rheological valves via a finite element method considering control energy and a time constant[J]. Smart Materials and Structures, 2008, 17(2): 025024. DOI:10.1088/0964-1726/17/2/025024 |
| [19] |
邬思敏, 孟文俊, 李淑君.
双线圈旁置式新型磁流变制动器的设计与优化[J]. 工程设计学报, 2016, 23(5): 453–459.
WU Si-min, MENG Wen-jun, LI Shu-jun, et al. Design and optimization of a novel magnetorheological brake with double coils placed on the side housing[J]. Chinese Journal of Engineering Design, 2016, 23(5): 453–459. |
| [20] | SNYDER R A, KAMATH G M, WERELEY N M. Characterization and analysis of magneto-rheological damper behavior under sinusoidal loading[J]. AIAA Journal, 2001, 39(7): 1240–1253. DOI:10.2514/2.1466 |


