随着我国人民生活水平的提高和汽车工业的迅速发展,我国私家车的数量迅速上升,停车难的矛盾日益突出。随着对立体停车位研究的不断深入,我国的立体停车设备行业发展迅速[1]。简易升降式立体停车位具有以下特点:1) 结构简单可靠,整机重量轻,占地空间小,加工制造成本低;2) 自动化程度高,升降平稳,泊车时间短,操作简单;3) 整机与地面多点接触,机构受力状态好,具有防风、防震和防腐性能[2-6]。另外考虑到城市车库容量和占地面积有限等因素,因此智能升降式立体停车位具有广阔的应用前景。目前一些人口较为密集的城市对智能立体停车位的需求量逐年上升[7-10],这对智能立体停车位设备的稳定性和可靠性提出了更高的要求。
智能停车设备在载车上升过程中,负载力对设备的整体结构和传动控制系统产生了巨大冲击。由于液压传动具有易于控制并且控制精确、传动平稳、冲击小、增力系统理想、简单、安全、经济等特点,所以设计了智能立体停车位液压传动控制系统,并进行理论分析和试验研究,以实现智能立停车位稳定、准确控制和平稳运行。
本文首先对智能立体停车位工作原理进行阐述,然后分别介绍智能立体停车位行走、回转和升降调速液压控制系统,最后对设计的液压系统进行分析,为优化控制系统提供一定的参考。
1 工作原理本文研究的智能立体停车位设备由轨道、框架主体、回转升降立柱、台板和驱动控制系统组成。单臂式智能立体停车位的模型如图 1所示。

|
| 图 1 单臂式智能立体停车位模型 Fig.1 Single arm type intelligent stereo parking lot model |
运动原理采用的是无避让型车位的横移、旋转、升降三个动作。工作过程:首先,由液压马达带动链轮使链轮获得动力,行走轮沿轨道把车位运到一层停车位外端,利用液压缸推动回转轴实现立柱和台板回转,载车板与立柱在回转过程中不存在相对运动;其次,利用液压缸实现台板升降调速,该运动为直线运动;最后,使台板实现提升和下降两个动作,完成取放车工作。
2 液压控制系统设计液压控制系统是立体停车位的主要部分,它可使立体车位实现框架行走、立柱回转、载车板升降等各种动作。该设备的液压系统主要由行走系统、回转系统、升降系统三大部分组成,液压系统可实现锁紧、制动、调速等功能。设计的液压系统要适应环境要求,因为油液受温度影响较大;在设备行走、提升、回转过程中,整机运动要平稳,设备不能产生较大摇晃、振动,防止出现较大的液压冲击;换向阀换向过程中不能产生大的振动与噪声;在启动、制动状态速度发生改变的情况下要减小冲击。根据工作过程提出设备液压控制系统的技术要求,如表 1所示。
| 参数 | 数值 |
| 提升高度/m | 2.1 |
| 提升时间/s | 30 |
| 提升速度/(m/s) | 0.12 |
| 单程行走距离/m | 3.3 |
| 行走时间/s | <20 |
| 行走速度/(m/s) | 0.15 |
| 回转角度/(°) | 90 |
| 回转时间/s | <25 |
| 公称承载/kg | 3 000 |
行走回路中马达输出轴与链轮采用键连接,马达带动主动链轮转动,主动链轮带动3个从动链轮在导轨上行走。行走回路需满足运行平稳的要求,设定时间范围内要求完成动作且停在要求的位置,在负载变化时速度不可出现较大波动。立体停车位行走回路液压原理图如图 2所示。行走马达的运动方向由三位四通换向阀控制,换向阀在中位时液压泵不给行走回路供油。通过梭阀与压力补偿器集成,将比例换向阀转换为双向可调的调速阀,补偿压力装置可以用来填补由于设备与轨道摩擦等因素使负载变化而产生的压力损失,从而在一定程度上消除负载变化对速度产生的影响。通过调整连接换向阀与梭阀的溢流阀可达到补偿压力的目的。当选择的压力需要的补偿值不高时,比例换向阀具有不大的流量增益,相反如果选用的压力需要较高的补偿值时,比例换向阀则具有较大的流量增益。这样可以保证行走马达运行速度平稳,防止速度变化时出现较大的冲击力,也进一步保证了设备不会产生较大晃动。

|
| 图 2 行走回路液压原理图 Fig.2 Hydraulic principle diagram of walking circuit |
回转结构中立柱的下端采用一个推力球轴承、向心球轴承、轴套、下回转轴组合回转,下回转轴与摆臂、油缸液压站连接,上回转轴采用调心轴承。立柱回转是通过液压缸推动下回转轴来实现的,载车板与立柱在回转过程中不存在相对运动。该部分可通过液压缸的直线运动转换为机架的旋转运动。回转回路液压系统如图 3所示。通过三位四通电磁阀的电铁的切换实现油缸的伸出与收回。油缸的伸出与收回能控制立柱回转的方向,回转回路中设有叠加式双向节流阀。回转部分的液压缸采用双向可调节缓冲结构,以减缓接触冲击。在回转回路中添加双液控单向阀,能够对液压缸实现锁紧,防止液压油倒流。在回路中使用溢流阀,当对液压油缸施加背压时,可将下降速度控制在合理范围内。

|
| 图 3 回转回路液压原理图 Fig.3 Hydraulic principle diagram of rotary circuit |
升降调速回路液压原理如图 4所示,利用液压缸活塞杆的伸出与缩回实现台板的上升与下降。台板上升与下降的过程不仅对速度有一定的要求,而且对运动的平稳性也有要求,不能因为液压缸动作速度过快而使台板产生较大的冲击。液压缸采用单作用液压缸,在液压缸进出口采用节流阀与定差减压阀的组合来实现对其速度的控制。其中定差减压阀具有补偿阀功能,可以使节流阀口处于稳定状态。流量控制系统具有多种功能,包括自动低压卸荷、负载感应反馈以及流量匹配。通过节流阀开度来控制输入执行元件的流量,并保证负载对输给油缸无任何影响和输出速度的稳定性[11];通过改变节流阀口开度来控制工作压力;通过在液压缸进油管路中设置单向阀来防止液压缸中的液压油回流。升降液压缸回油油路采用出口节流的方式,该方式通过节流阀和换向阀的组合实现,并选择在液压缸进油管路中添加单向阀。下降动作的实现可以通过自重使液压缸缩回,下降过程中速度有一定的限制,要防止速度过快产生大的冲击力,并保证在升降回路不工作时锁紧,同时防止出现其他可能的回流现象。
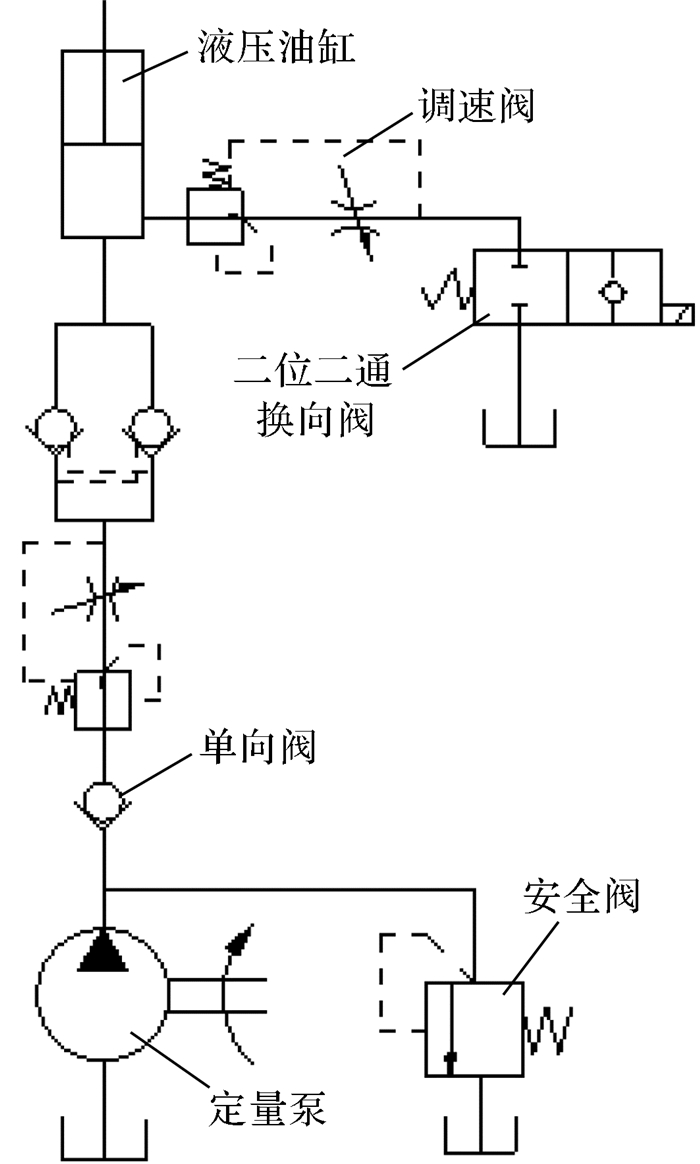
|
| 图 4 升降回路液压原理图 Fig.4 Hydraulic principle diagram of lifting circuit |
升降调速系统是智能立体停车位最主要的运动系统之一,其液压系统控制的精确性和可靠性是智能立体停车位工作稳定性的前提,因此需对升降调速系统的控制性能进行仿真分析。分析过程中忽略压泵的流量脉动、回转油缸的泄漏、管道动态特性及管道压力损失的影响。下面建立升降调速系统的数学模型并分析其动态特性。
升降调速回路中定差减压型压力补偿阀的节流阀口与弹簧腔出口相通,节流阀进油口与阀芯下腔相通。液压泵输出液压油压力为p1,经过减压阀后压力降为p2,p2经过节流阀后变为p3,同时作用在减压阀阀芯上,进行压力补偿。
数学模型模拟的是液压缸速度从初始状态到稳定状态的过渡过程。此时回转油缸活塞的受力方程为[12]:
| $ {{A_1}{p_{\rm{L}}} = m\ddot x + C\dot x + {F_{\rm{L}}} + {F_{\rm{s}}}} $ | (1) |
| $ {{p_{\rm{L}}} = {p_4} - n{p_5}} $ | (2) |
式中:A1——液压缸无杆腔有效工作面积;
m——液压缸运动部件及负载折算到运动部件上的质量;
x——活塞运动的位移;
C——阻尼系数;
FL——外负载;
Fs——系统阻力;
pL——负载压力;
p4——液压缸无杆腔工作压力;
p5——液压缸有杆腔工作压力;
n——活塞与活塞杆面积比。
液压缸无杆腔流量方程为:
| $ Q = {A_1}\dot x + {C_{\rm{i}}}{p_{\rm{L}}} + \frac{{{V_1}}}{{{\beta _{\rm{e}}}}}\frac{{{\rm{d}}{p_4}}}{{{\rm{d}}t}} $ | (3) |
式中:Q——液压缸进液腔流量;
Ci——液压缸内泄漏系数;
V1——液压缸进液腔容积;
βe——有液体积弹性模量;
由于液压缸内泄漏量很小,对系统分析影响不大,所以式(3) 中的CipL项可以视为零,因此(3) 式可化简为:
| $ Q = {A_1}\dot x + \frac{{{V_1}}}{{{\beta _{\rm{e}}}}}\frac{{{\rm{d}}{p_4}}}{{{\rm{d}}t}} $ | (4) |
若不考虑管道泄漏、压力损失等因素,那么通过节流阀的流量应等于进入液压缸无杆腔的流量,所以有流量连续方程,对其作线性化处理后得:
| $ \Delta Q = \frac{{\partial Q}}{{\partial a}}\Delta a + \frac{{\partial Q}}{{\partial {p_1}}}\Delta {p_1} = {K_{\rm{q}}}\Delta a - {K_{\rm{c}}}\Delta {p_1} $ | (5) |
式中:Kq——流量增益,
Kc——流量压力系数,
ΔQ——流量增量;
a——节流通流面积;
Δa——节流通流变化面积;
Δp1——压力增量。
其中ΔQ,Δa,Δp1可表示为:
| $ \left\{ \begin{array}{l} \Delta Q = Q\left( t \right) - Q\left( 0 \right)\\ \Delta a = a\left( t \right) - a\left( 0 \right)\\ \Delta {p_4} = {p_4}\left( t \right) - {p_4}\left( 0 \right) \end{array} \right. $ | (6) |
式中Q(0),a(0),p1(0) 分别为Q(t),a(t),p1(t)的初始值。
在初始值为零的情况下对式(1),(4) 和(5) 作拉氏变换,得出:
| $ \left\{ \begin{array}{l} {p_{\rm{L}}}\left( s \right) = \frac{m}{{{A_1}}}s\dot x\left( s \right) + \frac{B}{{{A_1}}}\dot x\left( s \right) + \frac{{{F_{\rm{L}}}\left( s \right)}}{{{A_1}}}\\ Q\left( s \right) = {A_1}\dot x\left( s \right) + \frac{{{V_0}}}{{{\beta _{\rm{e}}}}}s{p_4}\left( s \right)\\ \Delta Q\left( s \right) = {K_{{\rm{q}}0}}a\left( s \right) - {K_{{\rm{c}}0}}{p_4}\left( s \right) \end{array} \right. $ | (7) |
根据式(7) 绘制系统方块图,如图 5所示。
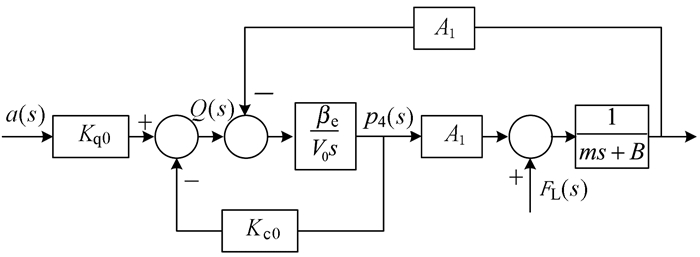
|
| 图 5 调速系统方块图 Fig.5 Block diagram of the speed regulating system |
分别以节流阀开口面积和负载力为输入量,液压缸活塞杆运动速度为输出量的传递函数为:
| $ G\left( s \right) = \frac{{\dot x\left( s \right)}}{{a\left( s \right)}} = \frac{{{K_{{\rm{q}}0}}{A_1}}}{{{{\left( {\frac{s}{{{\omega _{\rm{n}}}}}} \right)}^2} + 2{\xi _{\rm{n}}}\left( {\frac{s}{{{\omega _{\rm{n}}}}}} \right) + 1}} $ | (9) |
| $ H\left( s \right) = - \frac{{\frac{1}{{A_1^2}}\left( {{V_0}s/{\beta _{\rm{e}}} + {K_{{\rm{c}}0}}} \right)}}{{{{\left( {\frac{s}{{{\omega _{\rm{n}}}}}} \right)}^2} + 2{\xi _{\rm{n}}}\left( {\frac{s}{{{\omega _{\rm{n}}}}}} \right) + 1}} $ | (10) |
式中:ωn为液压缸固有频率;ξn为阻尼比。
4 仿真分析与试验验证利用MATLAB/Simulink[13]建立升降变速调速系统的仿真模型,模型如图 6所示,仿真主要参数如表 2所示。
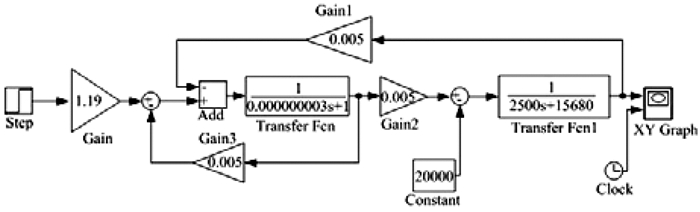
|
| 图 6 调速系统仿真模型 Fig.6 Simulation model of speed regulating system |
| 参数 | Kq0/(m3/s·m) | Kc0/(m3/s·Pa) | B/(N·s/m) | V0/m3 | βe/MPa |
| 数值 | 19 | 12.3 | 15 680 | 0.005 5 | 1.6×103 |
图 6所示仿真模型初始化参数按照表 2设置。分别施加25 000 N和30 000 N的负载力,仿真时间设置为5 s,使用变步长ODE15s求解器,选取液压缸速度从零达到稳态值的过程。仿真结果如图 7所示。
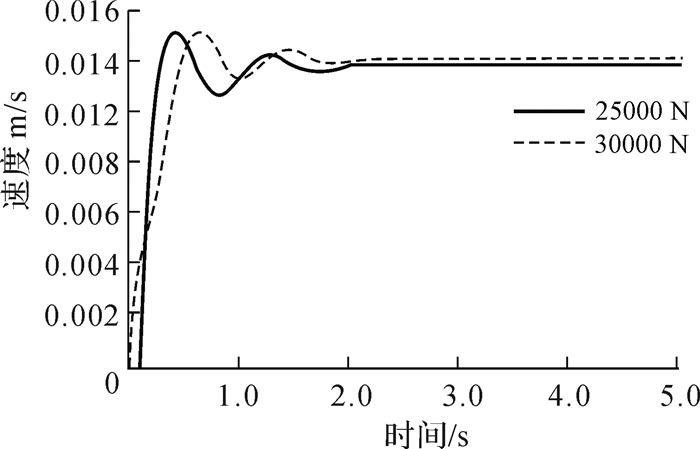
|
| 图 7 不同负载时活塞杆速度仿真曲线 Fig.7 Simulation curves of piston rod speed under different loads |
从图 7中看出负载大时液压缸达到稳定速度的用时要比负载小时长;且液压缸输出速度具有更好的动态特性,调速系统速度响应较快,是一个稳定系统。
由于智能立体停车位在工作过程中需要高稳定性和高可靠性,所以需要通过试验来验证仿真结果的正确性和操作机液压系统的可靠性。因此建立试验样机,其液压控制系统如图 8所示。

|
| 图 8 样机液压控制系统 Fig.8 Hydraulic control system of prototype |
在样机台板施加同样的25 000 N和30 000 N的负载力进行试验测试,观察并记录液压控制试验台液压缸的压力变化和液压缸活塞杆的伸缩速度。记录结果如9所示。
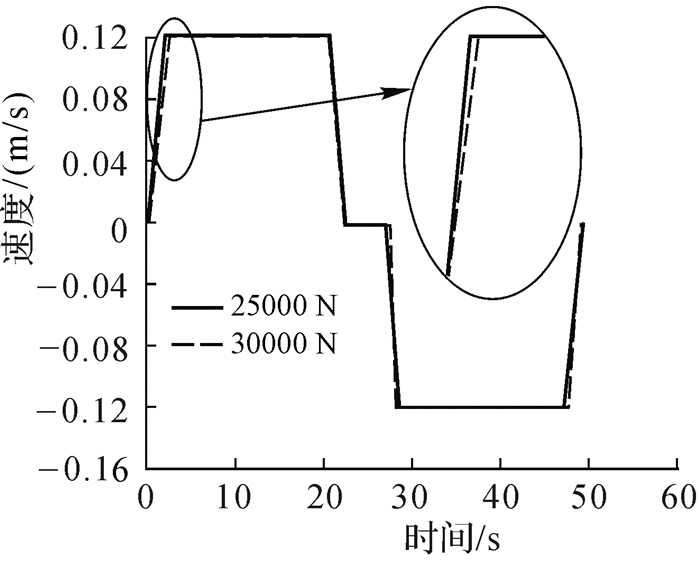
|
| 图 9 不同负载时活塞杆速度试验测试曲线 Fig.9 Test curves of piston rod speed under different loads |
从图 9中看出在负载相同的条件下,当液压缸达到稳定速度时,样机测试比仿真分析用时长。调速系统速度响应较快,是一个稳定系统。升降调速回路中使用的由定差减压阀、节流阀组成的流量阀起到压力补偿作用,从而使节流阀开口度稳定,从图中可以看出在负载变化时,液压缸输出速度基本不发生变化,由此看出调速回路设计的合理性。
5 结论1) 根据技术要求,设计出了智能立体停车位行走、回转、升降调速液压控制系统。建立了升降调速液压控制系统的数学模型和仿真模型。
2) 系统仿真模型仿真结果表明:升降调速回路系统不仅实现了台板升降过程中对速度的要求,而且满足了智能立体停车位的设计要求。
3) 通过产品试验测试,验证了升降调速回路设计方案和仿真模型的正确性,实现了智能立体停车位液压控制系统稳定、准确、快速控制。
| [1] |
刘延利. 后悬臂升降横移式立体车库虚拟样机设计[D]. 济南: 山东大学机械工程学院, 2012: 3-9.
LIU Yan-li. Virtual prototype design for the rear-cantilever and lift-sliding stereo garage[D]. Jinan: Shandong University, School of Mechanical Engineering, 2012: 3-9. |
| [2] |
毛君, 谢苗, 陈红月, 等. 框架平移回转式智能泊车设备: 201110256469. 8[P]. 2012-03-21.
MAO Jun, XIE Miao, CHEN Hong-yue, et al. Intelligent parking equipment rotated and translated by frame: 201110256469.8[P].2012-03-21. |
| [3] |
毛君, 谢苗, 陈红月, 等. 载车板回转立体停车位装备: 201220183739. 7[P]. 2012-11-21.
MAO Jun, XIE Miao, CHEN Hong-yue, et al. Rotating stereoscopic parking equipment worked with a plate: 201220183739.7[P]. 2012-11-21. |
| [4] |
毛君, 谢苗, 陈红月, 等. 单边液压驱动式立体框架停车位: 201210553685. 3[P]. 2013-04-24.
MAO Jun, XIE Miao, CHEN Hong-yue, et al. Unilateral stereoscopic framework parking space driven by hydraulic power: 201210553685.3[P]. 2013-04-24. |
| [5] |
毛君, 谢苗, 陈红月, 等. 伸缩式智能立体停车位: 201220624936. 8 [P]. 2013-06-05.
MAO Jun, XIE Miao, CHEN Hong-yue, et al. Telescopic intelligent stereo parking: 201220624936.8 [P]. 2013-06-05. |
| [6] |
毛君, 谢苗, 陈红月, 等. 单边电动式立体框架停车位: 201220705248. 4[P]. 2013-06-12.
MAO Jun, XIE Miao, CHEN Hong-yue, et al.Unilateral stereoscopic framework parking equipment driven by electronic power: 201220705248.4[P]. 2013-06-12. |
| [7] |
刘爽. PJSC型立体停车设备研究[D]. 阜新: 辽宁工程技术大学机械工程学院, 2012: 2-5.
LIU Shuang. Study on PJSC type stereo parking equinpment[D]. Fuxin: Liaoning Technical University, School of Mechanical Engineering, 2012: 2-5. |
| [8] |
毛君, 佟阳, 谢苗, 等.
智能立体车位防坠落系统动力学特性仿真[J]. 计算机系统应用, 2012, 21(11): 80–83.
MAO Jun, TONG Yang, XIE Miao, et al. Dynamic characteristics simulation of intelligent three-dimensional parking spaces falling protection system[J]. Computer Systems & Applications, 2012, 21(11): 80–83. DOI:10.3969/j.issn.1003-3254.2012.11.018 |
| [9] |
郑宝举, 袁永康, 员超.
智能立体停车库控制系统的设计与实现[J]. 计算机测量与控制, 2003, 11(6): 426–429.
ZHENG Bao-ju, YUAN Yong-kang, YUAN Chao. Design and realization of the control system of intelligent stereo garage[J]. Computer Measurement & Control, 2003, 11(6): 426–429. |
| [10] |
刘小华. 带环箍层钢框架立体停车结构静力及动力性能研究[D]. 长沙: 湖南大学土木工程学院, 2013: 1-3.
LIU Xiao-hua. Research on static and dynamic performance of steel-framed tridimensional parking structures with hoop-storeys[D]. Changsha: Hunan University, School of Civil Engineering, 2013: 1-3. |
| [11] |
王维东, 陈忠强, 黄新年.
压力补偿器在液压调速系统中的应用[J]. 流体与传动控制, 2005, 12(5): 18–20.
WANG Wei-dong, CHEN Zhong-qiang, HUANG Xin-nian. The applications of pressure compensator in velocity regulating hydraulic systems[J]. Fluid Power Transmission and Control, 2005, 12(5): 18–20. |
| [12] |
许益民.
电液比例控制系统分析与设计[M]. 北京: 机械工业出版社, 2005: 17-18.
XU Yi-min. Analysis and design of electro-hydraulic proportional control system[M]. Beijing: China Machine Press, 2005: 17-18. |
| [13] |
张志涌.
精通MATLABR2011a[M]. 北京: 北京航空航天大学出版社, 2013: 486-506.
ZHANG Zhi-yong. Master MATLABR2011a[M]. Beijng: Beihang University Press, 2013: 486-506. |



