2. 河南科技大学 机电工程学院, 河南 洛阳 471000;
3. 机械装备先进制造河南省协同创新中心, 河南 洛阳 471000
2. School of Mechatronics Engineering, Henan University of Science and Technology, Luoyang 471000, China;
3. Collaborative Innovation Center of Machinery Equipment Advanced Manufacturing of Henan Province, Luoyang 471000, China
盾构法因其具有开挖效率高、安全环保、人力节省等优点,逐渐取代了传统隧道施工法,目前盾构法已成为交通、市政、矿山等工程施工的首选方法[1]。推进系统是盾构机的重要组成部分,主要完成转弯、曲线顶进、姿态纠偏以及同步直线行进等任务,其中推进油缸的协调控制是盾构机在掘进过程中保持正确姿态的关键。
施工过程中刀盘面部承受的负载呈现不均匀性和时变性,导致盾构机推进油缸在实际工况下的协调控制变得十分复杂。盾构机推进油缸同步控制性能的好坏直接关乎隧道施工的质量[2]。因此,推进系统的同步控制是一个关键的技术问题,周如林等[3-4]将专家系统和PID控制相结合,设计出推进系统区间内同步控制器,并提出了压力同步和流量同步混合控制的思路。胡国良等[5]通过PLC编译主从式同步PID控制程序,并在试验台进行了实验验证。以上的研究主要集中在区间内推进油缸的同步控制,对各分组之间的同步控制没有进行研究。本文结合南昌1号线艾溪湖东站至艾溪湖西站区间隧道施工的实际问题,将单神经元PID控制应用于推进系统的速度控制中,并分析在变载荷工况下各组推进油缸的同步控制性能。
1 工程概况 1.1 工程背景南昌地铁1号线艾溪湖东站至艾溪湖西站区间隧道起于南昌市南昌县紫阳大道与创新一路交叉口(艾溪湖东站),沿紫阳大道向西下穿昌东大道、艾溪湖东路、艾溪湖大桥,穿越艾溪湖湖底,途径南昌人才大厦、海洋公园等,到达北京东路与艾溪湖南路交叉口(艾溪湖西站)[6]。整个区间总长度约为1 710.11 m,其中穿越艾溪湖湖底段为900 m。该标段存在3处平曲线,曲线半径分别为1 200 m,1 200 m和2 000 m,线间距为13.4 m。区间隧道线路纵坡设计为双向坡,最大坡度为17‰;竖曲线半径为5 000 m,区间覆土厚度为10.4~19.4 m。
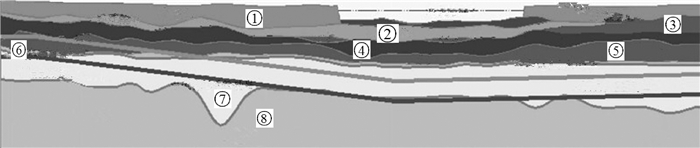
1.2 地质条件艾溪湖东站至艾溪湖西站区间隧道主要穿越砾砂层、砂质泥岩、圆砾层及部分黏土。该隧道工程区间砂层的最大渗透系数3.14×10-2 m/d,属于强渗透性地层,图 1所示为工程区间地质纵断面图,土体自上而下依次为:① 杂填土、② 粉质黏土、③ 中砂、④ 圆砾、⑤ 砾砂、⑥ 强风化粉砂质泥岩、⑦ 中风化粉砂质泥岩、⑧ 微风化粉砂质泥岩[7]。地面标高为18.07~23.89 m,水位埋深为6.8~7.4 m,高程为12.6~11.8 m。
|
| 图 1 工程区间地质纵断面图 Fig.1 Geologic profile of engineering interval |
本工程区间由中铁隧道集团承建,采用2台S553型“英雄号”海瑞克土压平衡盾构机进行施工作业,前盾直径为6 250 mm,刀盘开挖直径为6 280 mm,整机总长为80 m,装机功率为1 269 kW。管片外径为6 000 mm,内径为5 400 mm,厚为300 mm,环宽为1.2 m,盾构机最小曲线半径为600 m,最大纵坡为25‰,主驱动最高转速为4.5 r/min,总重为520 t。
本区间穿过的地层为风化泥质粉砂层及部分砂砾地层土质,具有软硬不均、渗透系数较大等特点,导致工程技术复杂、施工难度大[8]。在南昌1号线施工中曾出现以下问题:管片与盾尾间隙控制不当,导致管片拼装困难;遇到地质条件突变的地层时,盾构偏离设计轴线出现“蛇形现象”,局部出现掘进面土体失稳、地面隆起变形的情况。经分析发现,盾构推进油缸速度同步控制的不理想是导致上述现象产生的主要因素,现针对该施工问题进行研究。
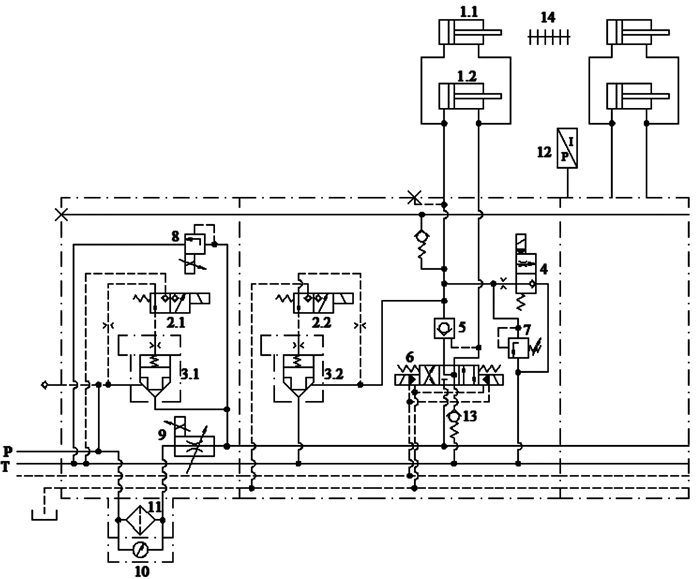
2 盾构推进系统工作原理以该施工区间采用的“英雄号”土压平衡盾构机为例,其推进系统单组区间的液压工作原理如图 2示。
|
| 1.1,1.2—推进油缸;2.1,2.2—电磁换向阀;3.1,3.2—插装阀;4—比例换向阀;5—液控单向阀;6—三位四通电液换向阀;7—溢流阀;8—比例溢流阀;9—比例调速阀;10—油压表;11—过滤器;12—压力传感器;13—单向阀;14—位移传感器 图 2 盾构机液压推进系统工作原理 Fig.2 Work principle of hydraulic propulsion system of shield machine |
推进系统通过控制各区推进油缸的协调和同步动作,使盾构机实时保持正确的掘进姿态并沿着设定轴线准确地向前推进[9]。针对推进系统推进油缸数量多、控制复杂等特点,采用分区操作的控制方式,将推进油缸分为上、下、左、右可单独控制的4组,这既能保证直线行进的同步性,又能满足曲线施工的协调性。
推进系统采用压力和流量复合控制技术,保证盾构机在变负载、非线性的工况下,其各区油路能够提供与外界环境变化相匹配的压力和流量[10]。压力传感器检测当前的负载压力,反馈信号与设定信号的偏差,作用于比例溢流阀,构成压力闭环。位移传感器反馈速度信号,作用于比例调速阀,形成速度闭环。
3 推进系统单神经元PID控制由于施工过程中土质环境的时变性和刀盘受力的不均匀性,PID控制器不能根据盾构机施工环境的变化实时调整控制规律,难以保证各分组推进油缸之间同步运动[11]。针对以上问题,本文将传统PID与神经元结合,实现了控制参数的实时调整,有效解决了盾构推进系统时变性、非线性、强耦合性等问题。单神经元PID控制原理如图 3所示。

|
| 图 3 单神经元PID控制原理 Fig.3 Single neuron PID control principle |
增量式PID控制器的控制表达式为[12]:
| $ u\left( k \right) = u\left( {k - 1} \right) + \Delta u\left( k \right) $ | (1) |
| $ u\left( k \right) = {k_{\rm{p}}}e\left( k \right) + {k_{\rm{i}}}T\sum\limits_{j = 1}^k {e\left( j \right)} + \frac{{{k_{\rm{d}}}}}{T}\left( {e\left( k \right) - e\left( {k - 1} \right)} \right) $ | (2) |
式中:kp,ki,kd为PID控制器的比例、积分、微分系数,T为采样周期。
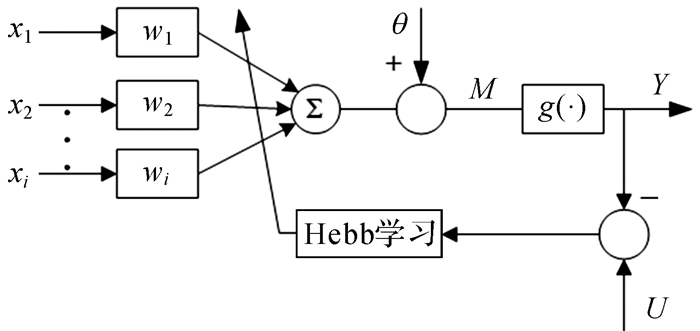
3.2 单神经元PID控制器单神经元是人工网络中的基本组成单元,图 4是单神经元模型。其中:U为设定值,Y为系统输出量,X=(x1,x2,…,xi)是单神经网络输入向量,W=(w1,w2,…,wi)是网络连接权值向量,θ为网络阈值,g(·)为神经元活化函数。
|
| 图 4 单神经元模型 Fig.4 Single neuron model |
加权器输出为:
| $ M = \sum\limits_i {{w_{\rm{i}}}{x_i}} + \theta $ | (3) |
活化函数取:
| $ g\left( x \right) = \frac{{1 - {{\rm{e}}^{ - x}}}}{{1 + {{\rm{e}}^{ - x}}}} $ | (4) |
单神经元连接权值wi采用有监督的学习规则,可表示为:
| $ \Delta {w_i}\left( k \right) = \eta \left( {u\left( k \right) - Y\left( k \right)} \right){x_i}\left( k \right) $ | (5) |
加权器处理后的信号M经活化函数g(·)作用,得出神经元的输出:
| $ Y = g\left( M \right) $ | (6) |
神经元有3个输入量,阈值为0,由式(3) 得,加权器处理过的输出为:
| $ M\left( k \right) = {w_1}\left( k \right){x_1}\left( k \right) + {w_2}\left( k \right){x_2}\left( k \right) + {w_3}\left( k \right){x_3}\left( k \right) $ | (7) |
本文将单神经元网络与PID控制相结合,由式(1)、(2) 和(7) 对xi(k)进行赋值:
| $ \left\{ \begin{array}{l} {w_1}\left( k \right) = {k_{\rm{p}}}\\ {w_2}\left( k \right) = {k_{\rm{i}}}\\ {w_3}\left( k \right) = {k_{\rm{d}}}\\ {x_1}\left( k \right) = e\left( k \right)\\ {x_2}\left( k \right) = T\sum\limits_{j = 1}^k {e\left( j \right)} \\ {x_3}\left( k \right) = \frac{1}{T}\left( {e\left( k \right) - e\left( {k - 1} \right)} \right) \end{array} \right. $ | (8) |
综上所述,由于连接权值具有实时性和自学性,将权重赋值PID控制参数,即可实现单神经元PID控制器在线调整参数[13]。
采用有监督的Hebb学习算法,权重的公式调整为[14]:
| $ {w_i}\left( {k + 1} \right) = {w_i}\left( k \right) + \eta e\left( k \right)u\left( k \right){x_i}\left( k \right) $ | (9) |
其中e(k)为教师信号,通过此信号的指导,单神经元控制器根据外界环境的变化,不断地进行学习重新组合,使得控制器的比例、积分、微分系数kp,ki,kd实时调整[15]。为了使训练过程神经网络收敛性提高,将上述算法规范化:
| $ \left\{ \begin{array}{l} u\left( k \right) = u\left( {k - 1} \right) + K\sum\limits_{j = 1}^3 {{w_i}\left( k \right){x_i}\left( k \right)} \\ {w_i}\left( k \right) = \frac{{{w_i}\left( k \right)}}{{\sum\limits_{i = 1}^3 {\left| {{w_i}\left( k \right)} \right|} }}\\ {w_1}\left( {k + 1} \right) = {w_1}\left( k \right) + {\alpha _{\rm{p}}}e\left( k \right)u\left( k \right){x_1}\left( k \right)\\ {w_2}\left( {k + 1} \right) = {w_2}\left( k \right) + {\alpha _{\rm{i}}}e\left( k \right)u\left( k \right){x_2}\left( k \right)\\ {w_3}\left( {k + 1} \right) = {w_3}\left( k \right) + {\alpha _{\rm{d}}}e\left( k \right)u\left( k \right){x_3}\left( k \right) \end{array} \right. $ | (10) |
式中:αp,αi,αd为学习速率。
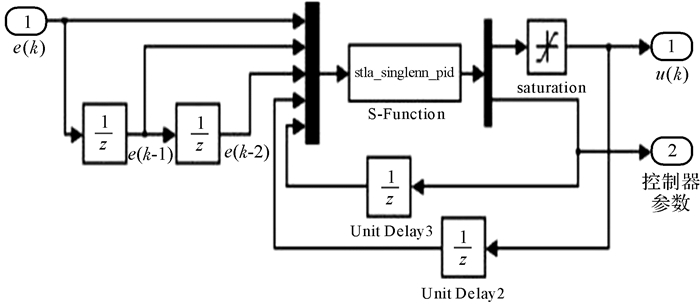
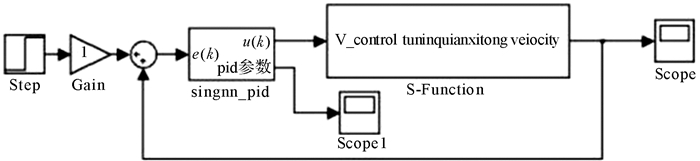
4 推进系统模型 4.1 单神经元PID控制器模型在MATLAB环境下使用S函数编写单神经元PID控制算法,利用Simulink建立单神经元PID控制器模型,如图 5所示。将B,C,D组推进油缸的位移与A组推进油缸位移的偏差量作为输入信号e(k),经过控制器的实时分析处理,在模型的输出端得出控制信号u(k)和控制规律参数。
|
| 图 5 单神经元PID控制器模型 Fig.5 Model of single neuron PID controller |
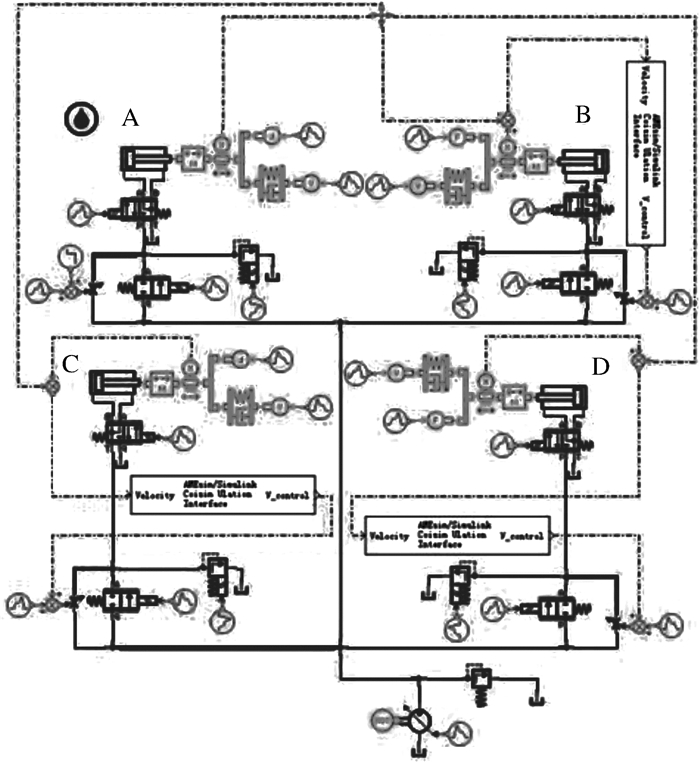
建立推进系统单神经元PID控制器模型后,利用AMEsim软件建立盾构推进系统AMESim仿真模型,如图 6所示。并在AMESim中创建与Simulink的接口模块[16],实现液压系统AMESim模型与Simulink模型的连通。图 7所示为推进系统联合仿真模型,通过联合仿真,综合利用AMESim和MATLAB各自的突出优势,为盾构机推进系统提供一个完善的仿真环境[17]。
|
| 图 6 推进系统AMESim仿真模型 Fig.6 AMESim simulation model of propulsion system |
|
| 图 7 推进系统联合仿真模型 Fig.7 Combined simulation model of propulsion system |
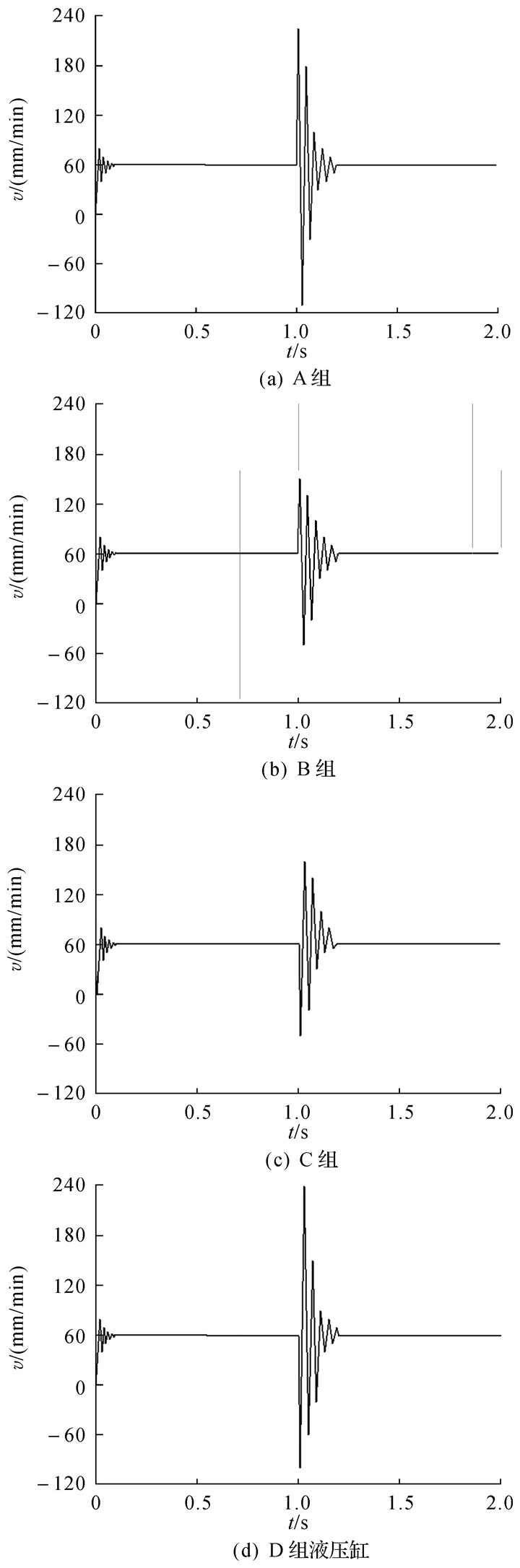
本文主要研究盾构机在实际施工过程中遇到外界负载变化时,推进系统推进油缸呈现出的同步特性。该系统仿真参数设置:推进系统主油路流量为8.496 L/min,仿真时间设置为2 s,采样时间为0.02 s,在0—1 s内,A,B,C,D各组的推进油缸负载均为650 N,1—2 s内,4组推进油缸负载分别为500,600,700,800 kN。图 8是当外负载发生变化时,采用常规PID控制时4组推进油缸的速度仿真曲线。
|
| 图 8 常规PID控制时推进油缸的速度曲线 Fig.8 Velocity curve of propulsion cylinder under the control of conventional PID |
由图 8可看出,当外负载发生变化时,各分组推进油缸的推进速度经过波动后,在0.3 s时又回到稳态值60 mm/min,通过比较A,B,C,D各组推进油缸速度曲线发现:负载变化越大,速度波动越明显,由此说明采用常规PID控制策略时的自适应能力差。在实际工况下,为满足盾构机推进系统各组推进油缸同步控制的精度要求,需对推进油缸同步控制策略作进一步改进。
5.2 单神经元PID控制仿真取神经网络学习速率为0.5,0.4,0.5,网路初始连接值均为0.1,其他参数设定与常规PID仿真一样。参数设定完成后,对推进系统进行联合仿真。图 9是当外负载发生变化时,在单神经元PID控制下各组推进油缸的速度仿真曲线。

|
| 图 9 单神经元PID控制时推进油缸的速度曲线 Fig.9 Velocity curve of propulsion cylinder under the control of single neuron PID |
由图 9可知,外界负载变化时,各组推进油缸速度经过较小波动后,快速恢复到60 mm/min。相比于常规PID控制下的速度仿真曲线发现:采用单神经元PID控制策略使得推进控制系统自适应能力提高、鲁棒性增强。
5.3 仿真结果对比分析A,B,C,D四组推进油缸采用不同控制算法在软硬不均匀地层外界突变负载工况下所得的推进速度的响应特性,如表 1所示。
| 推进油缸 | 稳态值v/(mm/min) | 常规PID | 单神经元PID | ||
| 峰值v/(mm/min) | 调节时间t/s | 峰值v/(mm/min) | 调节时间t/s | ||
| A组 | 60 | 228 | 0.30 | 123 | 0.2 |
| B组 | 60 | 150 | 0.25 | 96 | 0.1 |
| C组 | 60 | 164 | 0.27 | 95 | 0.1 |
| D组 | 60 | 247 | 0.32 | 135 | 0.2 |
采用单神经元PID控制算法时,各区间速度的最大峰值由原来的228,150,164,247 mm/min减少至改进后的123,96,95,135 mm/min。调节时间由改进前的0.25~0.3 s,减少至改进后的0.1~0.2 s,即:调节时间缩短0.1 s左右,振荡幅值减小至原来的1/2内。结果表明该系统稳定性好,适应性强,调节时间短,大大提高了推进油缸的同步特性。A,B,C,D四组推进油缸的速度基本保持一致,表明此控制策略可以提高盾构机推进油缸的同步控制精度。
6 结论本文针对盾构机在南昌地铁1号线的不良地质区间施工时推进油缸速度同步性差的问题,提出单神经元PID控制策略。研究其在不均变载荷的施工环境下推进油缸速度同步控制的性能,并利用AMESim和Simulink对该系统进行联合仿真。从仿真结果可以看出:负载突变时,系统稳定性好,调节时间短,各区推进油缸速度控制基本同步。这从根本上解决了管片拼装困难、盾构偏离设计轴线、地面隆起变形等因速度不同步导致的工程实际问题。
| [1] |
陈馈, 洪开荣, 吴学松, 等.
盾构施工技术[M]. 北京: 人民交通出版社, 2008: 91-93.
CHEN Kui, HONG Kai-rong, WU Xue-song. Shield construction technology[M]. Beijing: China Communication Press, 2008: 91-93. |
| [2] |
候典清. 盾构推进系统顺应特性及掘进姿态控制研究[D]. 杭州: 浙江大学机械工程学院, 2013: 81-97.
HOU Dian-qing. Research on compliance characteristics and attitude control of shield propulsion system[D]. Hangzhou: Zhejiang University, College of Mechanical Engineering, 2013: 81-97. |
| [3] |
周如林, 龚国芳, 汪慧, 等.
盾构推进系统专家PID同步控制分析[J]. 中国机械工程, 2010, 21(18): 2202–2206.
ZHOU Ru-lin, GONG Guo-fang, WANG Hui, et al. Expert-PID synchronization control of thrust hydraulic system[J]. China Mechanical Engineering, 2010, 21(18): 2202–2206. |
| [4] |
周如林, 龚国芳, 施虎, 等.
盾构推进系统液压缸的同步协调控制[J]. 工程设计学报, 2009, 16(6): 457–461.
ZHOU Ru-lin, GONG Guo-fang, SHI Hu, et al. Synchronization coordinated control of the hydraulic cylinder of the thrust system on shield machines[J]. Chinese Journal of Engineering Design, 2009, 16(6): 457–461. |
| [5] |
胡国良, 刘乐平, 龚国芳, 等.
盾构推进系统同步控制仿真与试验研究[J]. 中国机械工程, 2008, 19(10): 1197–1201.
HU Guo-liang, LIU Le-ping, GONG Guo-fang, et al. Simulation and experimental analyses of synchronization control for shield thrust system[J]. China Mechanical Engineering, 2008, 19(10): 1197–1201. DOI:10.3321/j.issn:1004-132X.2008.10.016 |
| [6] |
王欣一. 南昌地铁一号线的地下空间形态研究[D]. 南昌: 南昌大学经济管理学院, 2013: 32-35.
WANG Xin-yi. Underground space's exploitation and research[D]. Nanchang: Nanchang University, School of Economics Management, 2013: 32-35. |
| [7] |
李小明. 土压平衡盾构掘进引起地面沉降研究: 以南昌地铁为例[D]. 南京: 南京大学地球科学与工程学院, 2014: 13-16.
LI Xiao-ming. Study on ground subsidence induced by earth pressure balanced shield tunneling: a Nanchang subway respective[D]. Nanjing: Nanjing University, School of Earth Sciences and Engineering, 2014: 13-16. |
| [8] |
白廷辉, 刘树佳, 廖少明, 等.
软土地区盾构掘进速度对地层扰动现场试验研究[J]. 岩土力学, 2016, 37(7): 2040–2045.
BAI Ting-hui, LIU Shu-jia, LIAO Shao-ming, et al. Experimental study of disturbance caused by the advancing speed of shield tunneling in soft soil[J]. Rock and Soil Mechanics, 2016, 37(7): 2040–2045. |
| [9] |
刘峰, 龚国芳, 石元奇, 等.
基于自适应控制技术的盾构掘进监控系统[J]. 工程设计学报, 2010, 17(4): 302–306.
LIU Feng, GONG Guo-fang, SHI Yuan-qi, et al. Monitoring system of shield tunneling machine based on adaptive control technology[J]. Chinese Journal of Engineering Design, 2010, 17(4): 302–306. |
| [10] | YANG Hua-yong, SHI Hu, GONG Guo-fang, et al. Electro-hydraulic proportional control of thrust system for shield tunneling machine[J]. Automation in Construction, 2009, 18(7): 950–956. DOI:10.1016/j.autcon.2009.04.005 |
| [11] |
刘国斌, 龚国芳, 朱北斗, 等.
基于BP神经网络的盾构推进速度自适应PID控制[J]. 工程设计学报, 2010, 17(6): 454–458.
LIU Guo-bin, GONG Guo-fang, ZHU Bei-dou, et al. Adaptive PID control of thrust speed of the shield based on BP networks[J]. Chinese Journal of Engineering Design, 2010, 17(6): 454–458. |
| [12] | DUAN X M, XIE H B, LIU Z B, et al. Precise control of thrust force on the shield tunneling machine[J]. Applied Mechanics & Materials, 2011(48/49): 834–839. |
| [13] |
王昕, 赵丁选, 尚涛, 等.
基于单神经元的液压挖机自适应PID节能控制[J]. 吉林大学学报(工学版), 2005, 35(4): 377–380.
WANG Xin, ZHAO Ding-xuan, SHANG Tao, et al. Adaptive PID control for energy-saving of hydraulic excavator based on single neuron[J]. Journal of Jilin University (Engineering and Technology Edition), 2005, 35(4): 377–380. |
| [14] |
严骏, 黎波, 郭刚, 等.
基于单神经元PID的挖掘机铲斗位姿自适应控制[J]. 解放军理工大学学报(自然科版), 2012, 13(3): 316–319.
YAN Jun, LI Bo, GUO Gang, et al. Adaptive control for bucket position of excavator based on single neuron PID[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2012, 13(3): 316–319. |
| [15] |
王秀君, 胡协和.
一种改进的单神经元PID控制策略[J]. 浙江大学学报(工学版), 2011, 45(8): 1499–1501.
WANG Xiu-jun, HU Xie-he. An improved control strategy of single neuron PID[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(8): 1499–1501. |
| [16] | LYNN A, SMID E. Modeling hydraulic regenerative hybrid vehicles using AMESim and MATLAB Simulink[J]. Proceedings of Spie the International Society for Optical Engineering, 2005(5805): 24–40. |
| [17] |
刘统, 龚国芳, 张振, 等.
TBM试验台刀盘混合驱动系统设计与仿真分析[J]. 工程设计学报, 2015, 22(5): 438–444.
LIU Tong, GONG Guo-fang, ZHANG Zhen, et al. Design and simulation analysis of hybrid cutterhead driving system for TBM test bed[J]. Chinese Journal of Engineering Design, 2015, 22(5): 438–444. |


