2. 大连理工大学 机械工程学院, 辽宁 大连 116024
2. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
全断面隧道掘进机(tunnel boring machine,TBM)是利用回转刀具开挖岩石隧道,形成完整隧道断面的大型高端隧道装备。刀盘是TBM的核心工作部件,具有破岩、支撑掌子面等功能,其性能直接影响整机掘进性能及工作效率[1]。通过对国内实际隧道工程的调研发现,由于地质环境、施工参数的复杂性及多变性,TBM刀盘系统的振动问题较为突出,常常诱发刀具异常磨损,刀盘面板、焊缝开裂及主轴承密封失效等各种难以修复的损伤。强振动问题导致的关键部件失效,不仅降低了施工效率,延误了工期,甚至致使整条隧道报废,后果十分严重。因此,有必要建立有效的TBM刀盘系统动力学模型,研究其动态特性,并分析不同参数对刀盘振动的影响规律,为刀盘系统的设计及参数匹配提供理论依据。
目前,关于TBM刀盘的研究工作主要集中在刀盘结构静力学性能、布局优化、振动特性等分析上。夏毅敏等[2-3]应用数值模拟方法模拟某供水工程TBM刀盘的掘进过程,分析刀盘的静态响应特性,并提出刀盘边缘滚刀布置方法。赵振威等[4]基于有限元软件建立3种类型的刀盘,分析了相同工况下不同刀盘结构的静力学性能。李震等[5]以提高静力学性能为目标,对刀盘结构主参数进行了优化设计。Huo等[6]提出基于协同进化遗传算法的滚刀平面布置设计方法,并分析了额定工况下盘体结构的应力及变形分布。韩美东等[7-8]基于ABAQUS/Explicit环境模拟刀盘的掘进过程,得到了刀盘的动态掘进载荷及推进临界速度。Zhang,Li等[9-10]建立了多体耦合的盾构机掘进动力学模型及刀盘主驱动模型,研究复杂地质条件下回转系统的动态特性及参数影响规律。谢启江[11]基于集中质量法建立了TBM推进系统动力学模型,分析系统载荷传递规律,研究变约束条件下刀盘载荷与支撑界面刚度的耦合关系。近年来,大连理工大学孙伟团队在TBM刀盘系统及主机系统振动特性方面做了一定的研究工作,同时结合仿真和实测手段研究了刀盘的振动及系统力流传递规律[12-14]。在国外,Yagiz,Yazdani-Chamzini等[15-16]采用非线性多元回归模型及模糊多准则决策方法模型建立了TBM的性能评价模型,为TBM选型及性能预测提供理论基础。Zare, Rostami等[17-18]基于理论模型及工程数据对TBM的性能进行了评价,为整机的地质适应性设计提供参考。
综上所述,国内外学者在TBM刀盘结构设计、整机设计及性能分析等方面已经做了大量的研究工作,但有关刀盘结构参数及掘进参数对振动的影响涉及较少,相关的研究工作对刀盘的结构设计及参数选择还不能给予直接的参考。为此,本文在前期建立的刀盘系统动力学模型基础上[12],以某供水工程的TBM刀盘系统为研究对象,分析系统结构参数及掘进参数对刀盘振动响应的影响,进而为刀盘的结构设计及系统参数匹配提供参考。
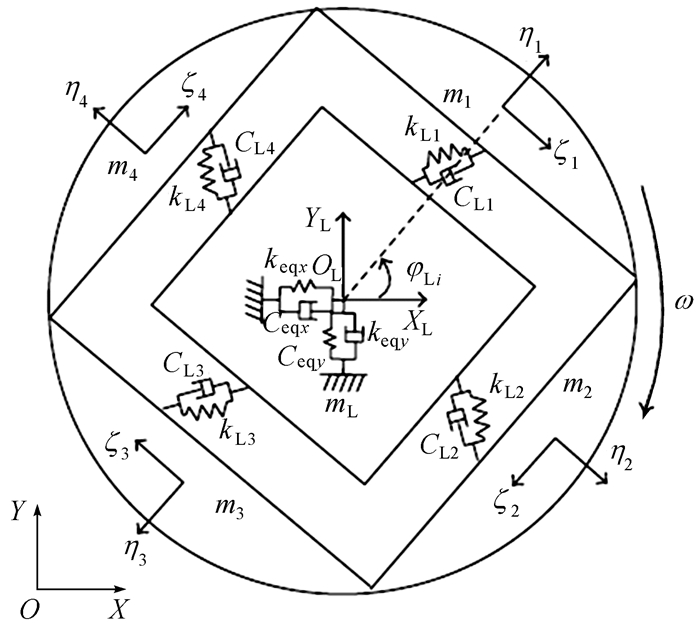
1 TBM刀盘系统动力学模型基于集中参数质量法建立分体式刀盘系统多自由度耦合动力学模型[12],如图 1所示,并采用拉格朗日方程得到系统各构件运动微分方程,整理成标准的振动微分方程如式(1) 所示,模型中M,C,K及F分别为系统的质量矩阵、阻尼矩阵、刚度矩阵及载荷向量。其中前三者与系统内部结构参数有关,载荷向量主要是各分体刀盘的外部激励。对中方五分式刀盘而言,将刀盘划分为5个质量结点(如图 1所示),每个结点均承受3个力和3个力矩,这些力和力矩与各分体上的滚刀载荷有关。整个刀盘载荷呈现空间多点分布[12]。
| $ \boldsymbol{M\ddot X} + \boldsymbol{C\dot X} + \boldsymbol{KX} = \boldsymbol{F} $ | (1) |
|
| 图 1 分体式刀盘系统耦合动力学模型 Fig.1 Coupled dynamics model of split-cutterhead system |
以国内某供水工程的TBM刀盘系统为研究对象,开展刀盘振动响应的影响因素分析。该工程隧洞横断面型式为圆型,TBM掘进段洞径净断面直径为7.51 m,开挖直径为8.53 m,系统参数如表 1所示。
| 参数 | 滚刀数量 | 驱动电机功率/kW | 刀盘额定转速/(r/min) | 刀盘脱困扭矩/kN·m | 刀盘额定推力/kN | 齿轮模数/mm | 大齿圈齿数/个 | 小齿轮齿数/个 |
| 数值 | 54 | 3 440 | 5.6 | 10 500 | 18 600 | 22 | 174 | 14 |
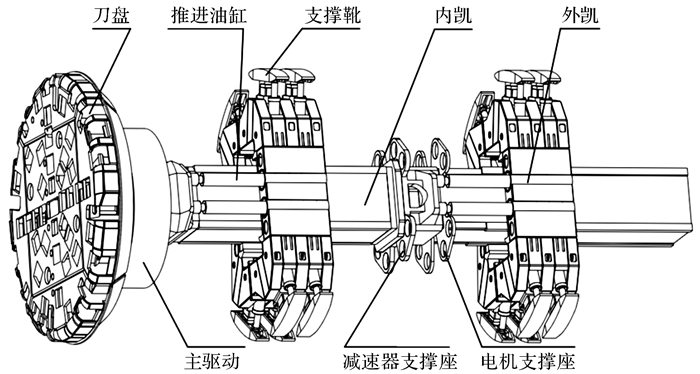
TBM主机主要由刀盘刀具、主驱动系统、内凯、外凯、支撑靴及油缸等部件组成,整体结构示意图如图 2所示。掘进机工作部件主要包含2种动力传递路径:一种是回转运动,由主驱动系统提供;另一种是平移运动,由支撑-推进-换步系统供给。刀盘由刀盘轴承支撑,通过液压张紧膨胀螺栓将刀盘与主轴承的旋转部件相连,以控制要求的预紧力,再由主驱动系统提供扭矩,驱动刀盘回转,进而带动滚刀达到开挖岩石的目的。内凯与主轴承外圈座刚性联接,由外凯提供支撑,可以沿TBM掘进方向滑动。外凯则通过支撑靴和支撑油缸固定在洞壁上,伸出推进油缸向刀盘传递推力,推动整机前进,同时外凯承受由刀盘系统传递过来的反推力、反扭矩及因前端部件重量而产生的倾覆力矩。
|
| 图 2 TBM主机结构示意图 Fig.2 The structure schematic of TBM mainframe |
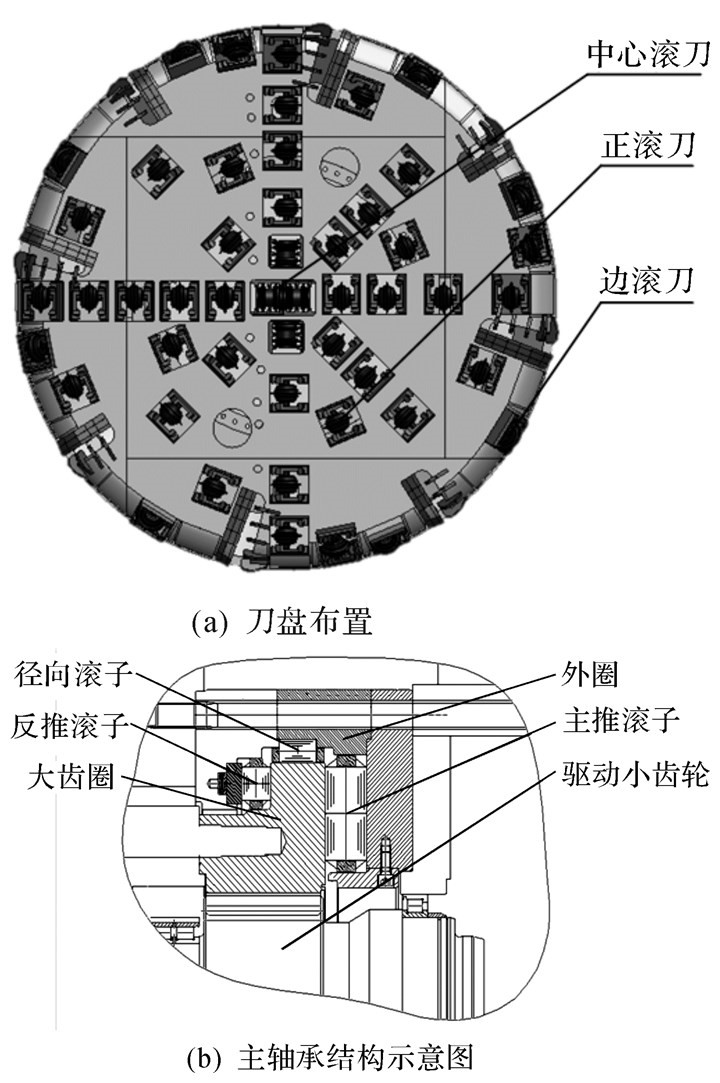
该供水工程8#标段采用的是X型支撑机型的TBM,刀盘结构采用中方五分式,直径为8.53 m,滚刀布置如图 3(a)所示,各滚刀同时承受破岩冲击载荷,且呈现空点多点分布。TBM主驱动采用内啮合结构型式,主轴承结构示意图如图 3(b)所示。刀盘工作时,驱动扭矩由8个变频电机经过行星齿轮减速器后,通过联轴器传至小齿轮,小齿轮驱动大齿圈,大齿圈再通过螺栓连接传力环及刀盘法兰,进而带动刀盘旋转。
|
| 图 3 刀盘布置及主轴承结构 Fig.3 The cutterhead layout and main bearing structure |
影响刀盘振动的因素很多,如地质参数、结构参数及掘进参数等,地质参数往往无法改变,只能根据勘探结果,调整掘进参数,实现刀盘的地质适应性。而刀盘的结构参数及掘进参数则可根据掘进状态进行设计或调整。为此,本文主要分析这2种参数对刀盘振动的影响,包括刀盘分体质量、转速及齿轮布置参数。
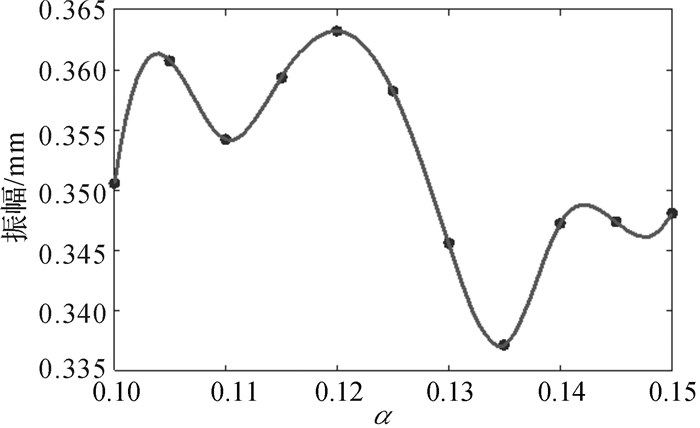
3.1 刀盘分体质量对于中方五分式刀盘而言,假设各刀盘分体质量占整个刀盘质量的比例是α,则刀盘中心块质量分数为1-4α,分析刀盘分体质量对刀盘振动的影响,进而确定比较合理的分体质量分数分布区间。据工程数据统计,刀盘中心块质量分数通常占刀盘总质量的40%~60%,因此这里取α=0.10~0.15。改变α值,通过基于Newmark-β数值方法求解得到不同α值对应的刀盘中心块轴向平移(沿隧道掘进方向)的振动幅值[13]。并采用样条曲线拟合,得到刀盘轴向振动幅值随质量分数α的变化规律,如图 4所示。
|
| 图 4 刀盘分体质量对其轴向振动响应的影响 Fig.4 The influence of cutterhead piece mass on axial vibration response |
由图 4结果可知,刀盘分体质量对刀盘轴向振动影响显著,呈现强烈的非线性变化规律。当α=0.135时,刀盘振动幅值最小,且属于全局最优点。由此可知,中方五分式刀盘在设计制造时,建议将分体质量比例控制在13%~14%之间,使得刀盘振动能处于最佳的波动范围,有利于降低振动噪音,减小由振动造成的结构损伤,延长装备的服役寿命。
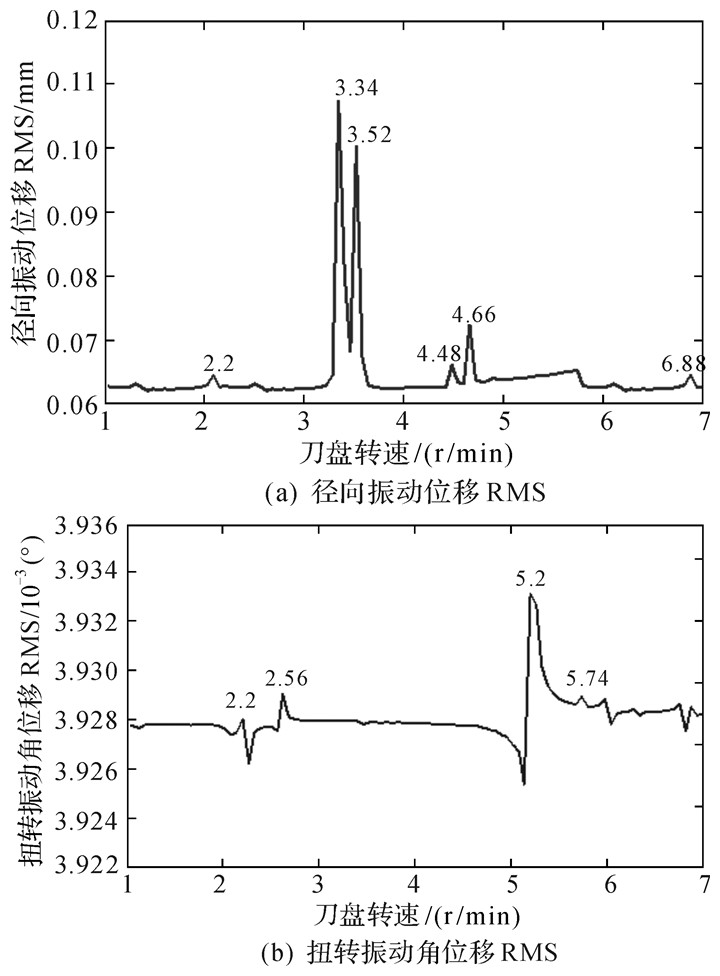
3.2 刀盘转速在一定的施工地质环境下,合理选择TBM掘进时的刀盘转速,研究刀盘系统在不同运行速度下的动态特性具有重要的工程意义。鉴于本文研究的TBM刀盘直径为8.53 m,参考国内外各型掘进机的刀盘转速及实际工程实例,刀盘常用的转速有:1.44,2.7,4,5.44及6.85 r/min等。根据这几种转速,可选择刀盘正常工作转速在1~7 r/min之间,保持其他参数不变,基于数值计算,分析刀盘系统的振动响应,得到刀盘振动位移有效值即均方根值(root mean square, RMS)与转速之间的关系曲线,如图 5所示。
|
| 图 5 不同转速下的刀盘振动位移RMS Fig.5 Vibration displacement RMS of cutterhead under different rotational speeds |
由图 5可知,刀盘转速对径向振动位移RMS影响较大,这里引入振动波动率概念,定义振动波动率η为响应波动幅度A与振动最大值xmax之比,即:
| $ \eta {\rm{ = }}\frac{A}{{{x_{\max }}}} $ | (2) |
通过式(2) 可计算刀盘不同方向振动位移RMS的波动率大小,其中径向振动位移RMS的波动率可达36%左右,而扭转振动角位移RMS的波动率不到1%。当刀盘转速在2 r/min以下时,刀盘振动位移RMS响应曲线较平稳,波动很小;当刀盘转速高于2 r/min时,径向振动位移和扭转振动角位移的RMS曲线波动较为明显,且某些转速时会出现峰值突变,如刀盘在2.2,2.56,3.34,3.52,4.48,4.66,5.2,5.74及6.88 r/min等转速下的振动位移RMS会明显增大,应尽可能避免刀盘长时间在这些转速下工作。
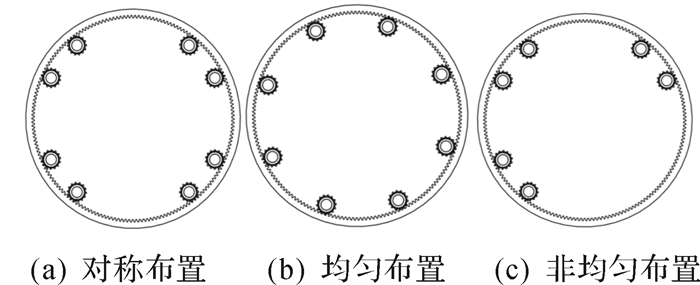
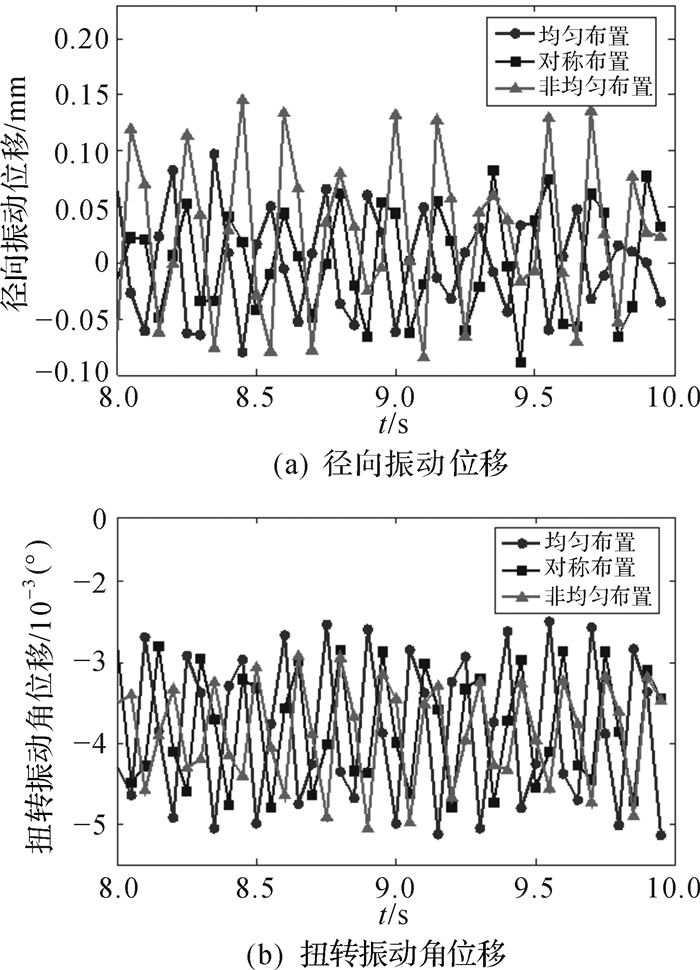
3.3 齿轮布置参数在本文研究的刀盘系统方案中,采用的是以8个小齿轮对称布置的方式驱动,而目前在掘进机中较常使用的小齿轮布置方式也多为对称布置或者均匀布置。针对不同的布置方式分析刀盘的振动响应变化,对系统的驱动和控制具有实际的工程意义。对比于设计方案中的对称布置,本文还假定了另外两种齿轮布置方式进行对比分析,分别是均匀布置和非均匀布置(即8个小齿轮中,其中一个象限内的2个小齿轮处于不工作情况),3种布置方式的齿轮具体分布如图 6所示,分析得到的刀盘振动响应如图 7所示。
|
| 图 6 齿轮的3种布置形式 Fig.6 Three arrangement forms of gear |
|
| 图 7 不同齿轮布置形式下的刀盘振动响应 Fig.7 Cutterhead vibration response under different arrangement forms of gear |
由图 7可以明显看出,稳定后,3种齿轮布置方式的刀盘振动响应的变化规律一致,径向振动幅度相差较大,尤其是当小齿轮为非均匀布置时,刀盘径向振动幅度要比其他两种布置方式大30%左右,但对刀盘扭转振动影响不大。而均匀布置和对称布置时的刀盘径向振动幅度相差不大,均匀布置的振动稍微小些。因此,在主驱动内部安装空间足够的情况下,小齿轮应尽量采用均匀布置,有时候为了兼顾其他设备的布置与安装,可以采用对称布置,尽可能避免采用非均匀布置方式,以免造成结构振动过大,从而导致刀盘系统构件发生故障或失效(如轴承损坏、密封失效等)。
4 结论1) 对于中方五分式刀盘而言,当设计的分体质量分数比例控制在13%~14%时,刀盘轴向振动处于最佳的波动范围,有利于减小由于振动造成的结构损伤,延长装备的服役寿命。
2) 当TBM刀盘转速小于2 r/min时,刀盘振动响应较平稳;当转速高于2 r/min时,刀盘径向振动位移及扭转振动角位移RMS曲线波动较为明显,且得到了一系列峰值突变的转速,工作时应尽可能避免刀盘长时间在这些转速下工作。
3) 当刀盘主驱动系统的某些小齿轮出现故障无法工作时,刀盘径向振动幅度比正常情况大30%左右;而小齿轮均匀布置时,有利于降低刀盘振动,在主驱动系统内部安装空间允许的情况下,小齿轮应尽量采用均匀布置。
以上结论是假定刀盘上每把滚刀同时承受额定冲击载荷的工况下得到的,实际上刀盘在掘进时会遇到多种工况,如岩体为上软下硬,需纠偏等,下一步将对不同工况下的刀盘振动进行分析,得到更详尽的参数对刀盘振动的影响规律。
| [1] |
水利部科技推广中心.
全断面岩石掘进机(TBM)[M]. 北京: 石油工业出版社, 2005: 95-96.
Promotion Center for Science & Technology Achievements of Ministry of Water Resources. Full face rock tunnel boring machine (TBM)[M]. Beijing: Petroleum Industry Press, 2005: 95-96. |
| [2] |
夏毅敏, 陈卓, 林赉贶, 等.
某供水工程TBM刀盘破岩过程动静态响应特性[J]. 哈尔滨工程大学学报, 2016, 37(5): 1–6.
XIA Yi-min, CHEN Zhuo, LIN Lai-kuang, et al. Static and dynamic response characteristics of TBM cutterhead's rock-breaking process: case study of a diversion project[J]. Journal of Harbin Engineering University, 2016, 37(5): 1–6. |
| [3] |
林赉贶, 郭金成, 夏毅敏, 等.
全断面岩石掘进机边缘滚刀优化布置研究[J]. 现代隧道技术, 2016, 53(4): 90–96.
LIN Lai-kuang, GUO Jin-cheng, XIA Yi-min, et al. Layout optimization of TBM gauge disc cutters[J]. Modern Tunnelling Technology, 2016, 53(4): 90–96. |
| [4] |
赵振威, 郑康泰, 李楠, 等.
不同几何结构的TBM刀盘静力学性能对比分析[J]. 隧道建设, 2016, 36(1): 102–107.
ZHAO Zhen-wei, ZHENG Kang-tai, LI Nan, et al. Analysis on static mechanical performances of TBM cutterhead with different geometries[J]. Tunnel Construction, 2016, 36(1): 102–107. DOI:10.3973/j.issn.1672-741X.2016.01.016 |
| [5] |
李震, 霍军周, 孙伟, 等.
全断面岩石掘进机刀盘结构主参数的优化设计[J]. 机械设计与研究, 2011, 27(1): 83–86, 90.
LI Zhen, HUO Jun-zhou, SUN Wei, et al. Cutterhead structure optimal design of the full-face rock tunnel boring machine[J]. Machine Design & Research, 2011, 27(1): 83–86, 90. |
| [6] | HUO Jun-zhou, SUN Wei, CHEN Jing, et al. Disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on different layout patterns[J]. Computers & Industrial Engineering, 2011, 61(4): 1209–1225. |
| [7] |
韩美东, 蔡宗熙, 曲传咏.
基于动力稳定性的全断面岩石隧道掘进机刀盘临界推进速度研究[J]. 机械工程学报, 2014, 50(21): 10–16.
HAN Mei-dong, CAI Zong-xi, QU Chuan-yong. Study on the critical driving speed of the tunnel boring machine cutterhead based on the dynamic stability[J]. Journal of Mechanical Engineering, 2014, 50(21): 10–16. |
| [8] |
韩美东, 曲传咏, 蔡宗熙, 等.
刀盘掘进过程动态仿真[J]. 哈尔滨工程大学学报, 2015, 36(8): 1098–1102.
HAN Mei-dong, QU Chuan-yong, CAI Zong-xi, et al. Dynamic numerical simulation of tunneling by the TBM cutter head[J]. Journal of Harbin Engineering University, 2015, 36(8): 1098–1102. |
| [9] | ZHANG Kai, YU Hai-dong, LIU Zhong-po, et al. Dynamic characteristic analysis of TBM tunnelling in mixed-face conditions[J]. Simulation Modelling Practice & Theory, 2010, 18(7): 1019–1031. |
| [10] | LI Xian-hong, YU Hai-bin, YUAN Ming-zhe, et al. Dynamic modeling and analysis of shield TBM cutterhead driving system[J]. Journal of Dynamic Systems Measurement & Control, 2010, 132(4): 1–14. |
| [11] |
谢启江. 变约束条件下硬岩掘进机动力学建模及特性研究[D]. 上海: 上海交通大学机械与动力工程学院, 2015: 10-16.
XIE Qi-jiang. Research on modeling and dynamic behavior of tunnel boring machines with variable constraints[D].Shanghai: Shanghai Jiaotong University, School of Mechanical Engineering, 2015: 10-16. |
| [12] | SUN Wei, LING Jing-xiu, HUO Junz-hou, et al. Dynamic characteristics study with multidegree-of-freedom coupling in TBM cutterhead system based on complex factors[J]. Mathematical Problems in Engineering, 2013, 2013(3): 657–675. |
| [13] | HUO Jun-zhou, WU Hang-yang, YANG Jing, et al. Multi-directional coupling dynamic characteristics analysis of TBM cutterhead system based on tunnelling field test[J]. Journal of Mechanical Science & Technology, 2015, 29(8): 3043–3058. |
| [14] |
霍军周, 欧阳湘宇, 王亚杰, 等.
重载冲击激励下TBM主机系统动力学建模与振动特性分析[J]. 机械科学与技术, 2015, 34(9): 1322–1327.
HUO Jun-zhou, OUYANG Xiang-yu, WANG Ya-jie, et al. Modeling and vibration analysis of TBM mainframe under impact heavy loads[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(9): 1322–1327. |
| [15] | YAGIZ S, GOKCEOGLU C, SEZER E, et al. Application of two non-linear prediction tools to the estimation of tunnel boring machine performance[J]. Engineering Applications of Artificial Intelligence, 2009, 22(4/5): 808–814. |
| [16] | YAZDANI-CHAMZINI A, YAKHCHALI S H. Tunnel boring machine (TBM) selection using fuzzy multicriteria decision making methods[J]. Tunnelling and Underground Space Technology, 2012, 30(4): 194–204. |
| [17] | ZARE S, BRULAND A, ROSTAMI J. Evaluating D & B and TBM tunnelling using NTNU prediction models[J]. Tunnelling & Underground Space Technology, 2016(59): 55–64. |
| [18] | ROSTAMI J. Performance prediction of hard rock tunnel boring machines (TBMs) in difficult ground[J]. Tunnelling & Underground Space Technology, 2016(57): 173–182. |


