2. 中南大学 高性能复杂制造国家重点实验室, 湖南 长沙 410083
2. State Key Laboratory of High Performance and Complex Manufacturing, Central South University Changsha 410083, China
硬岩掘进机(tunnel boring machine,TBM)是集机械、液压、电气和控制等多学科技术于一体的大型工程机械设备,被广泛应用于隧道施工中。TBM主要应用于硬岩地质岩层的掘进作业,工作时刀具向岩层顶进和破碎岩石的过程中机体会产生强烈的振动[1-2]。比例控制元件由于性能优良,在TBM上大量应用。作为电液比例控制的关键元件,比例电磁铁在振动环境下的特性及工作可靠性,对电液比例控制系统和元件具有十分重要的影响。对比例电磁铁的主要要求就是要具有水平的力—位移特性、良好的线性度、稳定性且响应快[3]。国内外对比例电磁铁研究的主要目的是改善比例电磁铁的输出特性,实现尽可能大的恒力输出和工作行程范围[4]。主要方法包括:对比例电磁铁的结构进行优化,采用磁路解析法、有限元法对电磁铁的输出特性进行综合优化[5-8];新原理、新材料的应用[9-12]。在强振动作用下,由于壳体和衔铁的相对运动,气隙磁阻的变化将由壳体和衔铁的共同运动引起。目前,对强振动作用下比例电磁铁的研究鲜见报道。针对振动对比例电磁铁的输出力特性的影响,以一单向比例电磁铁为研究对象,采用理论与仿真结合的方法分析其影响规律,为提高振动环境下比例控制元件的工作稳定性提供一定的理论参考。
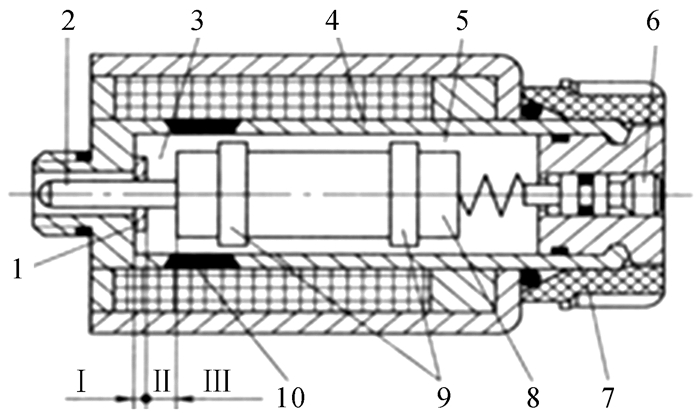
1 比例电磁铁的动态数学模型图 1为单向比例电磁铁的典型结构示意图,包含衔铁、导套、极靴、线圈、推杆等组成部分。导套由隔磁环和前后两段导磁材料焊接而成,导套前段与极靴组合形成带锥形端部的盆形极靴。螺线管线圈安置于导套和壳体之间,通电时产生磁场。与衔铁相连的推杆用于输出力或位移,电磁铁后端有一调零机构,用于调节弹簧初始位移。当给线圈通有一定电流时,在隔磁环附近比例电磁铁形成Φ1和Φ2两条磁路[13],磁路Φ1从极靴底部沿轴向通过工作气隙形成电磁力F1,磁路Φ2从极靴外周沿径向通过工作气隙形成电磁力F2,2个力的合力即为比例电磁铁的输出力。
|
| 1—限位片;2—推杆;3—工作气隙;4—导套;5—非工作气隙;6—应急手动推杆;7—橡胶螺母;8—衔铁;9—轴承环;10—隔磁环 图 1 单向比例电磁铁的结构示意图 Fig.1 Structure sketch of the unidirectional proportional solenoid |
根据麦克斯韦电磁场理论和强迫振动理论,可建立强振动环境下比例电磁铁的动态数学模型。
强振动环境下的控制线圈电压方程:
| $ {u_0}\left( t \right) - {u_{\rm{c}}}\left( t \right) = \left( {{R_{\rm{c}}} + {r_{\rm{d}}}} \right)i\left( t \right) + {L_{\rm{c}}}\frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} $ | (1) |
式中:u0(t)为放大器输出电压;Lc为线圈电感;uc(t)为衔铁运动和壳体振动时在线圈上产生的动生感应电动势;i(t)为线圈电流;Rc为线圈电阻;rd为放大器内阻。
根据电磁感应理论可知衔铁和壳体的相对运动会产生感应电动势,强振动环境下的线圈动生感应电动势为:
| $ {u_{\rm{c}}}\left( t \right) = {K_{\rm{c}}}\frac{{{\rm{d}}\left( {x\left( t \right) + {x_{\rm{p}}}\left( t \right)} \right)}}{{{\rm{d}}t}} $ | (2) |
式中:Kc为动生感应电动势系数;x(t)为衔铁位移;xp(t)为壳体在振动作用下的位移。
比例放大器通过取样电阻形成反馈电压,其过程可看作一比例环节,即:
| $ {u_{\rm{f}}}\left( t \right) = {K_{\rm{f}}}i\left( t \right) $ | (3) |
式中:uf(t)为反馈电压;Kf为电流负反馈系数。
比例放大器的输出电压u0(t)与输入电压ug(t)之间呈线性关系,可认为是一个比例环节,即:
| $ {u_0}\left( t \right) = {K_{\rm{e}}}\left( {{u_{\rm{g}}}\left( t \right) - {u_{\rm{f}}}\left( t \right)} \right) $ | (4) |
式中:Ke为放大器的放大系数;ug(t)为放大器的输入电压。
强振动环境下衔铁的输出力方程:
| $ {f_{\rm{e}}}\left( t \right) = \frac{{{{\left( {i\left( t \right)N} \right)}^2}}}{{2{R_{\rm{g}}}l}} $ | (5) |
式中:fe(t)为衔铁的输出力;N为线圈匝数;Rg为气隙磁阻,Rg=l/μ0A;l为气隙长度,l=x0-x(t)-xp(t),x0为初始气隙长度;μ0为真空磁导率;A为气隙部位垂直于磁力线的面积。
衔铁运动时需要克服惯性力、阻尼力、弹簧力和液压力。强振动环境下其平衡方程为:
| $ f\left( t \right) = m\frac{{{{\rm{d}}^2}x\left( t \right)}}{{{\rm{d}}{t^2}}} + B\frac{{{\rm{d}}\left( {x\left( t \right) + {x_{\rm{p}}}\left( t \right)} \right)}}{{{\rm{d}}t}} + k\left( {x\left( t \right) + {x_{\rm{p}}}\left( t \right)} \right) + F $ | (6) |
式中:m为衔铁质量;B为阻尼系数;k为刚度系数;F为负载作用力。
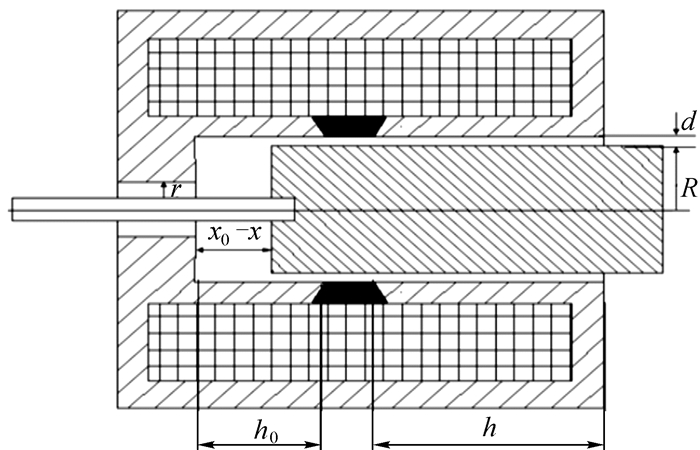
比例电磁铁结构简图如图 2所示。应用磁路分析[14]的方法结合基础振动的作用,不计漏磁通和磁饱和的影响,利用等效磁路计算其强振动环境下的磁阻。
|
| 图 2 比例电磁铁结构简化图 Fig.2 The structure simplified diagram of proportional solenoid |
| $ {\mathit{\Lambda }_0} = \frac{{2\pi Rh{\mu _0}}}{d} $ | (7) |
| $ {\mathit{\Lambda }_{\rm{g}}} = \frac{{2\pi R({h_0} - {x_0} + x + {x_{\rm{p}}}){\mu _0}}}{d} $ | (8) |
| $ {\mathit{\Lambda }_{\rm{b}}} = 2\pi {\mu _0}\frac{{({R^2} - {r^2})}}{{{x_0} - x - {x_{\rm{p}}}}} $ | (9) |
总磁导为:
| $ \mathit{\Lambda } = \frac{{{\mathit{\Lambda }_0}{\mathit{\Lambda }_\delta }}}{{{\mathit{\Lambda }_0} + {\mathit{\Lambda }_\delta }}} $ | (10) |
其中:Λδ=Λg+Λb。
则磁阻为:
| $ {R_{\rm{g}}}{\rm{ = }}\frac{1}{\mathit{\Lambda }} $ | (11) |
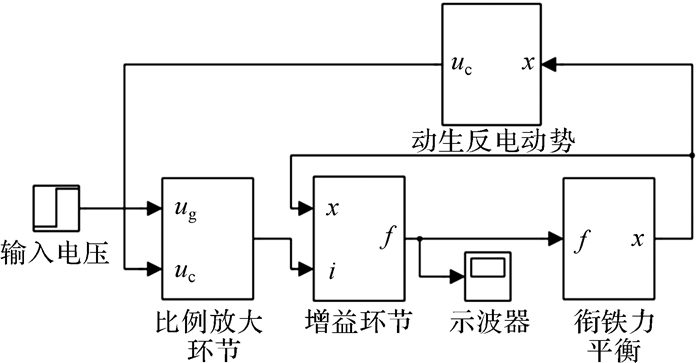
强振动环境下,比例电磁铁的工作气隙和动生感应电动势发生了改变,进而影响到比例电磁铁力输出特性。已有大量文献研究了结构参数对比例电磁铁的力输出特性的影响规律,本文主要研究振动干扰情况下比例电磁铁的输出力特性。根据上文方程(1) 至(11),建立如图 3所示的强振动环境下比例电磁铁的仿真模型。仿真参数如表 1所示,主要结构参数为:R=17.6 mm,r=7.6 mm,h=18 mm,h0=6.25 mm,d=0.2 mm。
|
| 图 3 强振动下比例电磁铁仿真模型 Fig.3 Proportional solenoid simulation model under the strong vibration |
| 参数 | 数值 |
| 衔铁质量m/kg | 0.012 |
| 阻尼系数B/(N·s/m) | 3 |
| 弹簧刚度k/(N/m) | 2 921 |
| 负载作用力F/N | 35 |
| 气隙初始长度x0/mm | 3 |
| 比例放大器电压ug(t)/V | 5 |
| 线圈电感Lc/H | 0.2 |
| 动生感应电动势系数Kc/(V·s/m) | 0.049 4 |
| 电阻Rc+rd/Ω | 19 |
| 电流负反馈系数Kf/(V/A) | 6 |
| 放大器电压放大系数Ke | 3.5 |
| 线圈匝数N | 400 |
影响比例电磁铁输出力特性的主要因素有磁阻、工作副摩擦、材料的非线性及结构参数等。由于强振动作用会导致衔铁与壳体的相对位移变化,进而改变气隙磁阻和动生感应电动势的大小。故本文主要研究在阶跃电压作用下,振动参数(幅值和频率)和结构参数(衔铁质量、阻尼系数和弹簧刚度)对振动环境下比例电磁铁动态响应的影响规律。
2.2.1 振动参数对气隙磁阻的影响无振动时气隙磁阻随着衔铁的运动而减小,当衔铁接触到限位片时气隙磁阻稳定,此时电磁铁的输出力也将保持恒定。图 4为振动作用下振动幅值对气隙磁阻波动幅值的影响,振动作用下气隙磁阻不再稳定而是产生波动,振动幅值与气隙磁阻波动幅值呈线性正相关。这主要是由于强振动会导致衔铁与限位片之间产生相对运动,打破了之前的稳定,振动幅值越大,则相对运动的距离越大即气隙磁阻越大。而仿真结果表明振动频率的大小变化对气隙磁阻的波动幅值影响不大,限于篇幅,本文未给出其关系曲线。

|
| 图 4 气隙磁阻波动幅值与振动幅值关系曲线 Fig.4 The relation curve of gap reluctance fluctuation amplitude and vibration amplitude |
动生感应电动势的大小与衔铁和壳体之间的相对运动速度有关,振动的幅值和频率都将影响电动势的波动幅值。如图 5所示,动生感应电动势的变化曲线是衔铁运动速度规律的一种体现,由无振动时动生感应电动势曲线的变化可以看出,动生感应电动势经历了“增大—降低—增大—降低”的过程,与之对应的是:在开始通电时衔铁在空行程阶段的运动负载力为零,所以速度增大,随后空行程阶段结束,衔铁受到的负载作用力速度下降,同时由于气隙磁阻的减小,衔铁运动速度再次增大,最后衔铁与限位片接触,速度降低至零。在振动作用下,由于衔铁与壳体的相对速度的大小和方向发生了改变,所以动生反电动势的大小和方向也将发生改变,如图 5中振动环境下的动生感应电动势变化曲线所示。在无振动时,当衔铁静止后动生感应电动势为零;而在振动环境下,由于衔铁与壳体之间的相对运动,动生反电动势不为零,而存在周期性的波动。

|
| 图 5 动生感应电动势变化曲线 Fig.5 The variation curves of motional induction electromotive force |
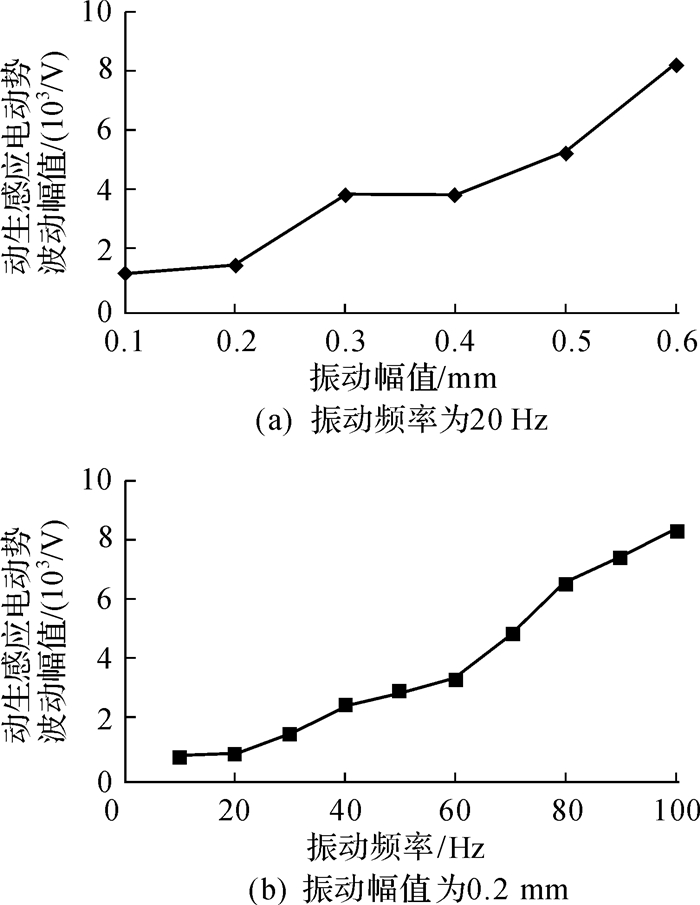
如图 6所示为振动幅值和频率对动生感应电动势波动幅值的影响曲线,振动幅值和频率与动生感应电动势波动幅值正相关,且变化趋势相似。这是因为随着强振动的幅值和频率的增加,衔铁与壳体之间的相对速度会加大,所以动生感应电动势会增大。
|
| 图 6 动生感应电动势波动幅值与振动参数关系曲线 Fig.6 The relation curve of motional induction electromotive force fluctuation amplitude and vibration parameters |
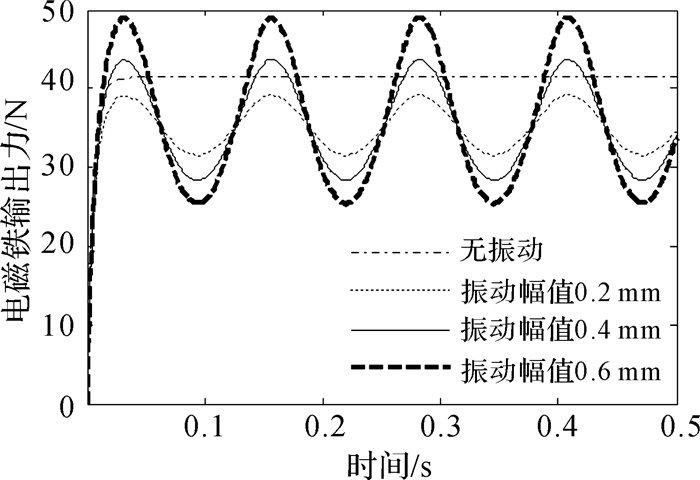
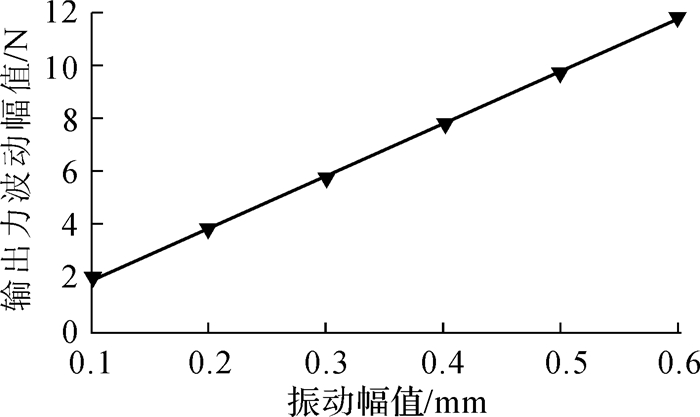
图 7是振动频率为50 Hz,振动幅值分别为0.2,0.4,0.6 mm时比例电磁铁的输出力曲线与无振动时的对比,由图可知在振动环境下比例电磁铁的输出力将产生周期性波动。仿真分析了不同的振动幅值和频率对比例电磁铁输出力的影响,结果表明,振动频率对输出力的波动幅值影响不大,而与输出力的波动频率直接相关。振动幅值的影响如图 8所示,从图中可以看出,输出力的波动幅值与振动幅值呈线性正相关,相关比例约为20 N/mm。
|
| 图 7 比例电磁铁输出力变化曲线 Fig.7 The variation curves of the proportional solenoid output force |
|
| 图 8 输出力波动幅值与振动幅值关系曲线 Fig.8 The relation curve of output force fluctuation amplitude and vibration amplitude |
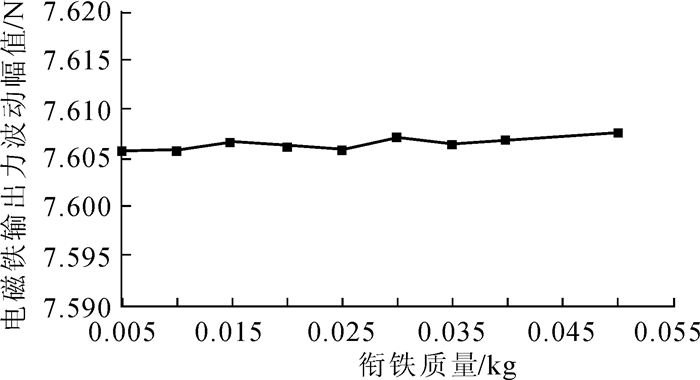
强振动下的比例电磁铁系统认为是一个弹簧-质量-阻尼系统,因此有必要分析衔铁的质量大小对电磁铁输出力的影响。由于比例电磁铁本身体积的限制,其衔铁质量不可能太大,所以仿真分析了振动频率为50 Hz,振动幅值为0.4 mm,衔铁质量在0.005~0.05 kg范围内变化时的比例电磁铁的输出力波动大小,结果如图 9所示。由图可知随衔铁质量的增加,比例电磁铁输出力的波动幅值有较小的增大。这主要是由于衔铁的质量大则惯性大,从而在振动作用下衔铁运动状态变化缓慢,使得壳体与衔铁之间的相对运动更加剧烈。
|
| 图 9 输出力波动幅值与衔铁质量关系曲线 Fig.9 The relation curve of output force fluctuation amplitude and the armature quality |
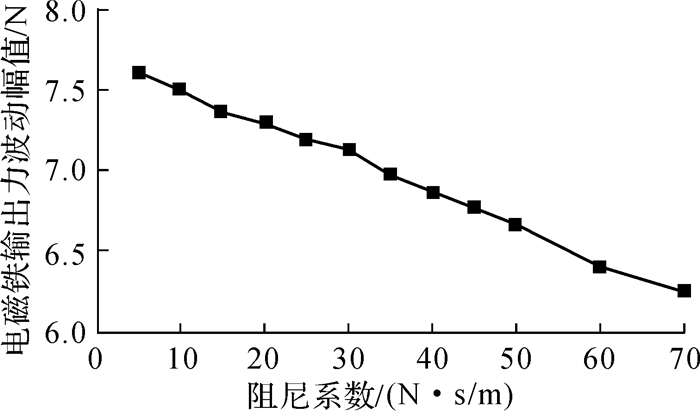
在弹簧-质量-阻尼系统中,阻尼系数的大小影响着系统的阻尼率,因此,有必要分析阻尼系数的大小与比例电磁铁输出力的关系。为研究振动环境下阻尼系数对电磁磁铁输出力的影响规律,仿真分析了振动频率为50 Hz,振动幅值为0.4 mm,阻尼系数在5~70 N·s/m范围内变化时的电磁铁输出力的波动幅值大小,结果如图 10所示。由图可知,随着阻尼系数的增加,电磁铁输出力的波动幅值线性减小,这是由于随着阻尼的增大,衔铁与壳体之间的相对运动受到了阻碍。
|
| 图 10 输出力波动幅值与阻尼系数关系曲线 Fig.10 The relation curve of output force fluctuation amplitude and the damping coefficient |
在弹簧-质量-阻尼系统中,弹簧刚度的大小影响着系统的固有频率,同时衔铁与壳体之间由弹簧相连,其对电磁铁的输出力有重要影响。为探究振动环境下弹簧刚度对电磁磁铁输出力的影响规律,仿真分析了振动频率为50 Hz,振动幅值为0.4 mm,弹簧刚度在20 000~100 000 N/m范围内变化时电磁铁输出力的波动幅值大小,结果如图 11所示。由图可知:当弹簧刚度小于20 000 N/m时,随着弹簧刚度的增加,电磁铁输出力的波动幅值下降迅速;当弹簧刚度大于20 000 N/m时,随着弹簧刚度的增加,电磁铁输出力的波动幅值下降缓慢。这是由于随着弹簧刚度的增加,衔铁与壳体之间的相对运动有所减弱,所以电磁铁输出力的波动幅值有所下降。

|
| 图 11 输出力波动幅值与弹簧刚度关系曲线 Fig.11 The relation curve of output force fluctuation amplitude and the spring stiffness |
1) 强振动的幅值与比例电磁铁输出力的波动幅值正相关,相关比例约为20 N/mm。在强振动下比例电磁铁输出力的稳定性会受到破坏。
2) 强振动主要通过直接影响气隙磁阻的大小进而影响比例电磁铁的输出力。
3) 增大阻尼有利于降低比例电磁铁输出力的波动幅值;在弹簧刚度低于20 000 N/m范围内增大弹簧刚度能有效降低比例电磁铁输出力的波动幅值。
| [1] |
陈立和.
浅析机械应用中的TBM与液压系统[J]. 吉林省教育学院学报(学科版), 2011, 40(2): 138–139.
CHEN Li-he. A brief analysis of TBM and hydraulic system in mechanical applications[J]. Journal of Jilin Institute of Education (Science Edition), 2011, 40(2): 138–139. |
| [2] | LI X H, YU H B, YUAN M Z, et al. Study on the linear dynamic model of shield TBM cutter head driving system[C]//IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society. Melbourne, Nov.7-10, 2011. |
| [3] |
许益民.
电液比例控制系统分析与设计[M]. 北京: 机械工业出版社, 2005: 26-50.
XU Yi-ming. Electro-hydraulic proportional control system analysis and design[M]. Beijing: China Machine Press, 2005: 26-50. |
| [4] |
路甬祥, 胡大紘.
电液比例控制技术[M]. 北京: 机械工业出版社, 1988: 12-40.
LU Yong-xiang, HU Da-yong. Electro-hydraulic proportional control technology[M]. Beijing: China Machine Press, 1988: 12-40. |
| [5] |
申屠胜男, 徐龙稳, 孟彬, 等.
双向比例电磁铁的设计及仿真分析[J]. 机械设计与研究, 2015, 31(1): 27–30.
SHENTU Sheng-nan, XU Long-wen, MENG Bing, et al. Design and simulation analysis of bidirectional proportional electromagnet[J]. Journal of Mechanical Design and Research, 2015, 31(1): 27–30. |
| [6] |
孟彬, 阮健, 李胜.
低惯量旋转电磁铁的动态特性研究[J]. 中国机械工程, 2011, 22(20): 2407–2410.
MENG Bing, RUAN Jian, LI Sheng. Research on dynamic characteristics of rotary electromagnet with low inertia[J]. China Mechanical Engineering, 2011, 22(20): 2407–2410. |
| [7] | SCHULTZ A. Design of valve solenoids using the method of finite elements[J]. Power Transmission and Motion Control, 2005, 56(12): 243–254. |
| [8] | YONG Li, FAN Ding, JIAN Cui, et al. Low power linear actuator for direct drive electrohydraulic valves[J]. Journal of Zhejiang University-SCIENCE A, 2008, 9(7): 940–943. DOI:10.1631/jzus.A0820028 |
| [9] | ENCICA L, PAULIDES J J H, LOMONOVA E, et al. Electromagnetic and thermal design of a linear actuator using output polynomial space mapping[J]. IEEE Transactions on Industry Applications, 2008, 44(2): 534–542. DOI:10.1109/TIA.2008.916604 |
| [10] | KARUNANIDHI S, SINGAPERUMAL M. Mathematical model and experimental characterization of a high dynamic servo valve integrated with piezoelectric actuator[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2010, 224(4): 419–435. DOI:10.1243/09596518JSCE899 |
| [11] |
王传礼. 基于GMM转换器喷嘴挡板伺服阀的研究[D]. 杭州: 浙江大学机械工程学院, 2005: 1-26.
WANG Chuan-li. Research on the nozzle flapper servo valve driven by GMM actuator[D]. Hangzhou: Zhejiang University, College of Mechanical Engineering, 2005: 1-26. |
| [12] | MAJID Ghassemi, YASSER Molayi Barsi, MOHAMMAD Hossein Hamedi. Effect of armature design on thermal and electromagnetic distribution of an electromagnetic launcher[J]. Heat Transfer Engineering, 2008, 29(9): 839–844. DOI:10.1080/01457630802053934 |
| [13] |
杨征瑞, 花克勤, 徐轶.
电液比例与伺服控制[M]. 北京: 冶金工业出版社, 2009: 150-155.
YANG Zheng-rui, HUA Ke-qing, XU Yi. Electro-hydraulic proportional and servo control[M]. Beijing: Metallurgical Industry Press, 2009: 150-155. |
| [14] |
王淑红, 肖旭亮, 熊光煜.
直流恒力电磁铁特性[J]. 机械工程学报, 2008, 44(2): 244–248.
WANG Shu-hong, XIAO Xu-liang, XIONG Guang-yu. Direct current electromagnets with constant traction characteristic[J]. Journal of Mechanical Engineering, 2008, 44(2): 244–248. |



