2. 太原理工大学 精密加工山西省重点实验室, 山西 太原 030024
2. Shanxi Key Laboratory of Precision Machining, Taiyuan University of Technology, Taiyuan 030024, China
超声铣削、超声研磨和超声抛光等旋转超声加工工艺在硬脆材料加工中具有加工精度高、加工表面质量好、材料去除率高、加工成本低等优点,已应用于生物制造工程和航空航天等领域复合材料、精密仪器、半导体和光学元件等的制造中[1-4]。旋转超声加工设备的核心是超声谐振系统,而多环盘结构作为超声谐振系统中一个典型的负载结构,其动力学分析具有重要意义。
超声振动系统的振动模式已经从基本的纵向振动模式向其他多种振动模式发展,其中纵弯谐振系统是一种较为典型的复合振动模式。Gallego-Juárez等[5-7]设计了一种利用压电陶瓷产生纵振激励的阶梯矩形板或阶梯圆板作横向弯曲振动的新型超声换能器。张小丽[8]设计了纵弯及纵径振动模式的超声换能器。李华等[9]设计了一种纵弯谐振模式的超声振动雾化系统。在旋转超声加工中,纵弯谐振模式通常是换能器和变幅杆的纵向振动与环盘或多环盘结构负载的横向弯曲振动发生耦合的一种振动模式,因此多环盘负载的横向弯曲耦合振动频率分析对于功率超声纵弯谐振系统的设计具有重要意义。
盘形铣刀、砂轮、珩磨轮和研磨轮等刀具多为环盘或多环盘组合结构,但各个环盘的材料不尽相同。此外,由于上述负载的厚径比通常不在经典薄板理论的适用范围中,所以需要对各个环盘应用中厚板理论进行横向弯曲振动频率的求解。He等[10-11]基于Mindlin理论推导了厚圆盘弯曲振动时的径向位移和横向位移的解析式,以及不同边界条件下的频率方程。李向鹏等[12]基于Mindlin理论推导了自由边界条件下中厚圆环板横向振动频率方程,并将理论求解结果与有限元仿真和模态实验结果进行了对比验证。佘银柱等[13]将齿轮简化为一阶梯变厚度环板,推导了其横向弯曲振动频率方程,并分析了中厚板理论的适用范围。秦慧斌等[14-15]提出了带有轮毂、辐板和轮缘结构的齿轮横向弯曲振动的统一求解模型。Hosseini-Hashemi等[16-17]研究了密度连续变化的阶梯圆盘和环盘的梯度功能板自由振动的解析解。上述文献虽然对圆盘、环盘和多环盘结构的横向弯曲振动的求解问题进行了研究,但这些研究都是基于特定材料的振动单元,不适用于多种材料组成的多环盘。
本文以三环盘横向弯曲耦合振动为例,基于Mindlin厚板动力学理论推导了横向弯曲振动的频率方程,设计了三环盘横向弯曲耦合振动频率计算软件,运用计算软件对12种不同结构、材料的多环盘进行了振动频率求解,并与有限元模态分析和模态实验结果进行了比较分析,验证了频率计算模型的准确性。
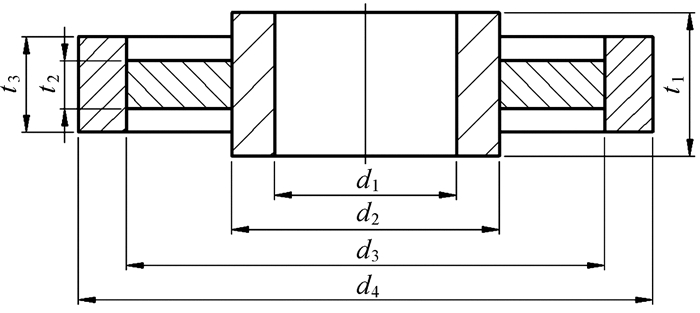
1 多环盘横向弯曲耦合振动模型的建立 1.1 多环盘物理模型与理论分析盘形铣刀、砂轮、抛光轮以及如图 1所示的珩磨轮、研磨轮等负载均可简化为如图 2所示的多环盘分析模型,其中:键槽、减重孔、工艺圆角和倒角等微小结构对振动的影响可忽略;t1,t2,t3分别为内、中、外环盘的厚度;d1为内环盘内径,即轴孔孔径;d2为内环盘外径、中环盘内径;d3为中环盘外径、外环盘内径;d4为外环盘外径。各环盘单元材料不同,分别以ρ1,ρ2,ρ3表示内、中、外环盘的密度,E1,E2,E3表示内、中、外环盘的弹性模量,μ1,μ2,μ3表示内、中、外环盘的泊松比。

|
| 图 1 珩磨轮和研磨轮的实物图 Fig.1 Physical pictures of honing wheel and grinding wheel |
|
| 图 2 多环盘分析模型 Fig.2 The analysis model of multi annular plate |
单环盘自由振动时,环盘内外边界均为自由边界。而多环盘是由多个环盘单元组合而成的集合体,当多环盘横向弯曲振动时,内、中环盘之间和外、中环盘之间的连接面上的挠度、转角、弯矩、剪力是连续的,仅有内环盘的内径和外环盘的外径是自由边界。因此多环盘横向弯曲耦合振动模型可由连续条件与自由边界条件的联合方程表示。
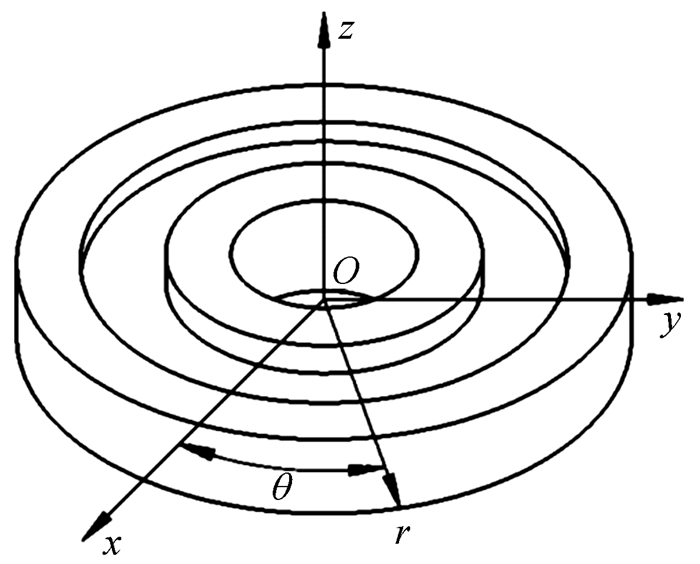
1.2 多环盘横向弯曲耦合振动的数学模型建立如图 3所示柱坐标系(r,θ,z),坐标系原点与多环盘中性面的中心重合。
|
| 图 3 三环盘分析模型及柱坐标系 Fig.3 The analysis model of 3-annular plate and cylindrical coordinate |
根据Mindlin理论,中厚环盘的动力学平衡方程为:
| $ \left\{ \begin{array}{l} \frac{{\partial M_r^i}}{{\partial r}} + \frac{1}{{{r_i}}}\frac{{\partial M_{r\theta }^i}}{{\partial \theta }} + \frac{{M_r^i-M_\theta ^i}}{{{r_i}}}-Q_r^i = \frac{{{\rho _i}t_i^3}}{{12}}\frac{{{\partial ^2}\beta _r^i}}{{\partial {t^2}}}\\ \frac{{\partial M_{r\theta }^i}}{{\partial r}} + \frac{1}{{{r_i}}}\frac{{\partial M_{r\theta }^i}}{{\partial \theta }} + \frac{{2M_{r\theta }^i}}{{{r_i}}}-Q_\theta ^i = \frac{{{\rho _i}t_i^3}}{{12}}\frac{{{\partial ^2}\beta _\theta ^i}}{{\partial {t^2}}}\\ \frac{{\partial Q_r^i}}{{\partial r}} + \frac{1}{{{r_i}}}\frac{{\partial Q_\theta ^i}}{{\partial \theta }} + \frac{{Q_r^i}}{{{r_i}}} = {\rho _i}{t_i}\frac{{{\partial ^2}{\omega _t}}}{{\partial {t^2}}} \end{array} \right. $ | (1) |
式中:i=1,2,3,分别表示内、中、外环盘;ri表示各环盘的外径,即r1=0.5d2,r2=0.5d3,r3=0.5d4,r0表示轴孔半径,即r0=0.5d1;ti表示环盘i的厚度;βri和βθi分别表示环盘i的中性面沿径向和圆周的转角。环盘i的弯矩分量Mri,Mθi,Mrθi和剪力分量Qri,Qθi的表达式为[18]:
| $ \left\{ \begin{array}{l} M_r^i = {D_i}\left[{\frac{{\partial \beta _r^i}}{{\partial r}} + \frac{{{\mu _i}}}{{{r_i}}}\left( {\beta _r^i + \frac{{\partial \beta _\theta ^i}}{{\partial \theta }}} \right)} \right]\\ M_\theta ^i = {D_i}\left[{{\mu _i}\frac{{\partial \beta _r^i}}{{\partial r}} + \frac{1}{{{r_i}}}\left( {\beta _r^i + \frac{{\partial \beta _\theta ^i}}{{\partial \theta }}} \right)} \right]\\ M_{r\theta }^i = \frac{{1 - {\mu _i}}}{2}{D_i}\left[{\frac{1}{{{r_i}}}\left( {\frac{{\partial \beta _r^i}}{{\partial \theta }}-\beta _\theta ^i} \right) + \frac{{\partial \beta _\theta ^i}}{{\partial r}}} \right]\\ Q_r^i = \frac{{{G_i}{t_i}}}{{{k_\tau }}}\left( {\beta _r^i + \frac{{\partial {w_i}}}{{\partial r}}} \right)\\ Q_\theta ^i = \frac{{{G_i}{t_i}}}{{{k_\tau }}}\left( {\beta _\theta ^i + \frac{1}{{{r_i}}}\frac{{\partial {w_i}}}{{\partial \theta }}} \right) \end{array} \right. $ | (2) |
式中:
| $ {D_i} = \frac{{{E_i}t_i^3}}{{12\left( {1-\mu _i^2} \right)}}, {G_i} = \frac{{{E_i}}}{{2\left( {1 + {\mu _i}} \right)}}, {k_\tau } = \frac{{12}}{{{\pi ^2}}} $ |
其中Di,Gi,kτ分别为环盘i的弯曲刚度、剪切弹性模量和剪切影响因子。将式(2) 代入式(1),可求得环盘i的振型基本方程为:
| $ \left\{ \begin{array}{l} {w_i} = w_1^i + w_2^i\\ \beta _r^i = \left( {\sigma _1^i-1} \right)\frac{{\partial w_1^i}}{{\partial r}} + \left( {\sigma _2^i-1} \right)\frac{{\partial w_2^i}}{{\partial r}} + \frac{1}{{{r_i}}}\frac{{\partial {H_i}}}{{\partial \theta }}\\ \beta _\theta ^i = \frac{{\left( {\sigma _1^i-1} \right)}}{{{r_i}}}\frac{{\partial w_1^i}}{{\partial \theta }} + \frac{{\left( {\sigma _2^i - 1} \right)}}{{{r_i}}}\frac{{\partial w_2^i}}{{\partial r}} - \frac{{\partial {H_i}}}{{\partial r}} \end{array} \right. $ | (3) |
式中:wi为环盘i的横向位移振型,βri,βθi为环盘i的中性面法线的挠度和转角,w1i,w2i,Hi为环盘i的振型函数。在式(3) 中:
| $ \sigma _1^i = \frac{{{{\left( {\delta _2^i} \right)}^2}}}{{{R_i}{{\left( {\delta _0^i} \right)}^4}-S_i^{-1}}}, \sigma _2^i = \frac{{{{\left( {\delta _1^i} \right)}^2}}}{{{R_i}{{\left( {\delta _0^i} \right)}^4}-S_i^{ - 1}}} $ |
其中:
| $ \left\{ \begin{array}{l} {R_i} = \frac{{t_i^2}}{{12}}, {S_i} = \frac{{{k_\tau }{D_i}}}{{{G_i}{t_i}}}\\ {\left( {\delta _0^i} \right)^4} = \frac{{{\rho _i}{t_i}}}{{{D_i}}}{\omega ^2}\\ {\left( {\delta _1^i} \right)^2} = \frac{1}{2}{\left( {\delta _0^i} \right)^4}\left\{ {\left( {{R_i} + {S_i}} \right) + {{\left[{{{\left( {{R_i}-{S_i}} \right)}^2} + 4{{\left( {\delta _0^i} \right)}^4}} \right]}^{\frac{1}{2}}}} \right\}\\ {\left( {\delta _2^i} \right)^2} = \frac{1}{2}{\left( {\delta _0^i} \right)^4}\left\{ {\left( {{R_i} + {S_i}} \right) - {{\left[{{{\left( {{R_i}-{S_i}} \right)}^2} + 4{{\left( {\delta _0^i} \right)}^{-4}}} \right]}^{\frac{1}{2}}}} \right\}\\ {\left( {\delta _H^i} \right)^2} = \frac{{2\left[{{R_i}{{\left( {\delta _0^i} \right)}^4}-S_i^{-1}} \right]}}{{1 -\mu }} \end{array} \right. $ |
当环盘自由振动时,振型函数w1i,w2i,Hi满足方程:
| $ \left\{ \begin{gathered} \left[{\;\blacksquare + {{\left( {\delta _j^i} \right)}^2}} \right]w_j^i = 0 \hfill \\ \left[{\;\blacksquare + {{\left( {\delta _H^i} \right)}^2}} \right]{H_i} = 0 \hfill \\ \end{gathered} \right. $ | (4) |
其中
| $ \blacksquare \left( \cdot \right) = \frac{{{\partial ^2}\left( \cdot \right)}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial \left( \cdot \right)}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}\left( \cdot \right)}}{{\partial {\theta ^2}}} $ |
式(4) 为Bessel方程,故可设式(3) 的一般解为:
| $ \left\{ \begin{gathered} w_1^i = \left[{A_{1m}^i{J_m}\left( {\delta _1^ir} \right) + B_{1m}^i{Y_m}\left( {\delta _1^ir} \right)} \right]\cos \left( {m\theta } \right) \hfill \\ w_2^i = \left[{A_{2m}^i{J_m}\left( {\delta _2^ir} \right) + B_{2m}^i{Y_m}\left( {\delta _2^ir} \right)} \right]\cos \left( {m\theta } \right) \hfill \\ {H_i} = \left[{A_{3Hm}^i{J_m}\left( {\delta _H^ir} \right) + B_{3Hm}^i{Y_m}\left( {\delta _H^ir} \right)} \right]\sin \left( {m\theta } \right) \hfill \\ \end{gathered} \right. $ | (5) |
式中:Ajmi,Bjmi,A3Hmi, B3Hmi(i=1,2,3;j=1,2) 为待定系数,由环盘边界条件或连接面的连续条件所确定,Jm(·),Ym(·)是m阶第一类和第二类Bessel函数,m(m=1,2,…,∞)为环盘横向弯曲振动的节径数。对于旋转超声加工,要求节径数m=0,即环盘作节圆型横向弯曲振动,此时加工效果最为理想[14]。因此式(5) 中的Hi≡0,环盘i的振型函数方程可进一步表示为:
| $ \left\{ \begin{matrix} {{w}_{i}}=w_{1}^{i}+w_{2}^{i} \\ \beta _{r}^{i}=(\sigma _{1}^{i}-1)\frac{\partial w_{1}^{i}}{{{\partial }_{r}}}+\left( \sigma _{2}^{i}-1 \right)\frac{\partial w_{2}^{i}}{{{\partial }_{r}}} \\ \beta _{\theta }^{i}=\frac{(\sigma _{1}^{i}-1)}{{{r}_{i}}}\frac{\partial w_{1}^{i}}{\partial \theta }+\frac{\sigma _{2}^{i}-1}{{{r}_{i}}}\frac{\partial w_{2}^{i}}{{{\partial }_{r}}} \\ \end{matrix} \right. $ | (6) |
由于环盘负载通常安装在变幅杆振幅最大处,只有环盘负载的切削点受到高频脉冲切削力。经加工实验验证,高频脉冲切削力对环盘负载振动频率的影响不大,因此可忽略切削力,认为外环盘外边界为自由边界。此时,多环盘的边界条件可表示为:
| $ \left\{ \begin{matrix} M_{r}^{1}{{\left| _{r\text{=}{{r}_{0}}}\text{=0, }\ M_{r}^{3} \right|}_{r\text{=}{{r}_{3}}}}=0 \\ Q_{r}^{1}{{\left| _{r\text{=}{{r}_{0}}}\text{=0, }\ Q_{r}^{3} \right|}_{r\text{=}{{r}_{3}}}}=0 \\ \end{matrix} \right. $ | (7) |
多环盘结构负载发生横向弯曲耦合振动时,环盘单元之间连接面的位移、转角、剪力和弯矩是连续的,即在环盘单元的连接面处有以下连续条件:
| $ \left\{ \begin{matrix} {{w}_{1}}{{\left| _{r\text{=}{{r}_{1}}}\text{=}{{w}_{2}} \right|}_{r\text{=}{{r}_{1}}}}~, {{w}_{2}}{{\left| _{r\text{=}{{r}_{2}}}\text{=}{{w}_{3}} \right|}_{r\text{=}{{r}_{2}}}} \\ \beta _{r}^{1}{{\left| _{r\text{=}{{r}_{1}}}\text{=}\beta _{r}^{2} \right|}_{r\text{=}{{r}_{1}}}}, \text{ }\beta _{r}^{2}{{\left| _{r\text{=}{{r}_{2}}}\text{=}\beta _{r}^{3} \right|}_{r\text{=}{{r}_{2}}}} \\ Q_{r}^{1}{{\left| _{r\text{=}{{r}_{1}}}\text{=}Q_{r}^{2} \right|}_{r\text{=}{{r}_{1}}}}, \text{ }Q_{r}^{2}{{\left| _{r\text{=}{{r}_{2}}}\text{=}Q_{r}^{3} \right|}_{r\text{=}{{r}_{2}}}} \\ M_{r}^{1}{{\left| _{r\text{=}{{r}_{1}}}\text{=}M_{r}^{2} \right|}_{r\text{=}{{r}_{1}}}}~, \text{ }M_{r}^{2}{{\left| _{r\text{=}{{r}_{2}}}\text{=}M_{r}^{3} \right|}_{r\text{=}{{r}_{2}}}} \\ \end{matrix} \right. $ | (8) |
每个环盘的振动位移和内力都可由包含待定系数Ajmi,Bjmi(i=1,2,3;j=1,2) 的函数表示。将式(2)、式(5) 和式(6) 代入边界条件式(7) 和环盘连续条件式(8),经整理可得三环盘横向弯曲耦合振动的频率方程为:
| $ {\mathit{\boldsymbol{K}}_{12 \times 12}}{\zeta _{12 \times 1}} = {{\bf{0}}_{12 \times 1}} $ | (9) |
式中:K是多环盘的刚度矩阵,ζ为振型向量。
由于待定系数包含振动圆频率ω,则待定系数不全为零,因此频率方程的解不全为零的充要条件为|K|=0。采用数值法进行求解,以固定的步长在振动圆频率ω的求解区间内搜索求解。当ω的取值满足|K|=0,此时的ω取值即为频率方程的数值解。
若某一多环盘的尺寸参数仅有一个为未知,而其横向弯曲耦合振动频率已知为ω0,亦可以以固定的步长在求解区间内搜索求解多环盘的未知尺寸参数。当尺寸参数的取值满足|K|=0,此时的尺寸参数取值即为该尺寸的数值解,能使多环盘在频率ω0发生横向弯曲耦合振动,即利用振动频率求解多环盘某一未知尺寸。
当环盘之间的某些尺寸和材料相同时,多环盘结构会发生变化或者是退化。当三环盘满足:
| $ {t_i} = {t_{i + 1}}, {E_i} = {E_{i + 1}}, {\rho _i} = {\rho _{i + 1}}, {\mu _i} = {\mu _{i + 1}} $ |
其中i=1或i=2,此时三环盘结构退化为双环盘结构;当三环盘满足:
| $ \begin{gathered} {t_1} = {t_2} = {t_3}, {E_1} = {E_2} = {E_3} \hfill \\ {\rho _1} = {\rho _2} = {\rho _3}, {\mu _1} = {\mu _2} = {\mu _3} \hfill \\ \end{gathered} $ |
此时,三环盘结构退化为单环盘结构。结构退化后,上述振动频率求解方法仍可适用于退化后结构的横向弯曲耦合振动频率求解。
2 多环盘横向弯曲耦合振动频率计算程序根据上述的多环盘横向弯曲耦合振动频率的求解过程,利用MATLAB开发了频率计算程序。该程序主要分为人机交互界面和求解函数两部分。人机交互界面可输入、读取多环盘的几何尺寸及材料参数,并进行参数变换和函数调用;求解函数则是基于上述三环盘横向弯曲耦合振动频率的求解方法所编写的,可根据输入的参数计算谐振频率并给出求解曲线。该程序的流程图如图 4所示。

|
| 图 4 多环盘横向弯曲耦合振动频率求解程序流程图 Fig.4 The flow chart of the solving program for transverse flexure coupled vibration of multi annular plate |
MATLAB的GUI模块提供用户一个图形用户界面开发环境,利用其开发的人机交互界面能提供软件用户一个简单直观的操作平台。由于GUI模块与所编写的函数同在MATLAB环境下,所以能够直接进行函数调用,降低了软件的设计难度。
开发的三环盘横向弯曲耦合振动频率求解的人机交互界面如图 5所示,其中主要包括三环盘尺寸示意图、材料性能参数、尺寸参数、频率区间选择及求解、谐振频率求解结果五个部分。

|
| 图 5 三环盘横向弯曲耦合振动频率求解的人机交互界面 Fig.5 Human-computer interface for solving frequency of transverse flexure coupled vibration of 3-annular plate |
输入参数并计算后,软件将给出如图 6所示的ω-|K|曲线,并将前三阶节圆型横向弯曲耦合振动频率求解结果显示在如图 7所示的求解结果显示框中;若无解,则会弹出提示框提示用户无解。

|
| 图 6 振动频率求解曲线 Fig.6 The solving curve of vibration frequency |

|
| 图 7 横向弯曲耦合振动频率求解结果 Fig.7 Results of transverse flexure coupled vibration frequency |
环盘组成材料的材料性能参数如表 1所示。为验证该频率计算程序的准确性,取如表 2所示的不同材料、不同结构和不同尺寸的环盘进行横向弯曲耦合振动频率求解。
| 材料 | 密度/(kg/m3) | 弹性模量/GPa | 泊松比 |
| 45钢 | 7 800 | 210 | 0.3 |
| Al | 2 700 | 68.5 | 0.34 |
| CBN | 3 500 | 720 | 0.3 |
| 参数 | 单环盘 | 双环盘 | 三环盘 | |||||||||||
| 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | 11号 | 12号 | |||
| t1/卖萌 | 30 | 25 | 32 | 32 | 40 | 40 | 25 | 25 | 25 | 20 | 20 | 20 | ||
| t2/卖萌 | 30 | 25 | 32 | 32 | 40 | 40 | 10 | 10 | 10 | 12 | 12 | 12 | ||
| t3/卖萌 | 30 | 25 | 13 | 13 | 23 | 23 | 20 | 20 | 20 | 20 | 20 | 20 | ||
| d1/卖萌 | 63.5 | 26 | 32 | 32 | 35 | 35 | 38 | 38 | 38 | 38 | 38 | 38 | ||
| d2/卖萌 | 63.5 | 26 | 32 | 32 | 35 | 35 | 55 | 55 | 55 | 56 | 56 | 56 | ||
| d3/卖萌 | 63.5 | 26 | 50 | 50 | 52 | 52 | 130 | 130 | 130 | 192 | 192 | 192 | ||
| d4/卖萌 | 220.5 | 101.2 | 84 | 84 | 92 | 92 | 162 | 162 | 162 | 225 | 225 | 225 | ||
| 内圆环盘 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | ||
| 中圆环盘 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | 45钢 | Al | 45钢 | 45钢 | Al | ||
| 外圆环盘 | 45钢 | 45钢 | 45钢 | CBN | 45钢 | CBN | 45钢 | CBN | CBN | 45钢 | CBN | CBN | ||
将尺寸参数、材料性能参数输入交互界面中,并设定合适的求解频率区间,可得到如表 3中fMk的计算结果,其中k表示横向弯曲耦合振动的阶数。
| 参数 | 单环盘 | 双环盘 | 三环盘 | |||||||||||
| 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | 11号 | 12号 | |||
| fM1/Hz | 4 665 | 15 805 | 22 585 | 31 585 | 22 035 | 33 135 | 4 195 | 6 335 | 5 255 | 2 205 | 3 075 | 2 845 | ||
| fM2/Hz | 21 035 | 55 965 | 55 615 | 50 285 | 74 925 | 109 225 | 15 235 | 19 115 | 19 055 | 8 775 | 10 295 | 19 425 | ||
| fA1/Hz | 4 671 | 64 355 | 21 880 | 31 329 | 21 470 | 33 519 | 4 074 | 6 164 | 5 231 | 2 191 | 3 057 | 2 844 | ||
| fA2/Hz | 20 248 | 15 877 | 55 970 | 49 442 | 70 817 | 112 919 | 14 840 | 19 114 | 19 168 | 8 729 | 10 315 | 19 607 | ||
| Δ1/% | 0.13 | 0.45 | 3.22 | 0.82 | 2.63 | 1.15 | 2.97 | 2.77 | 0.46 | 0.64 | 0.59 | 0.04 | ||
| Δ2/% | 3.89 | 1.68 | 0.63 | 1.71 | 5.80 | 3.27 | 2.66 | 0.01 | 0.59 | 0.53 | 0.19 | 0.93 | ||
对频率求解结果进行有限元模态分析,在ANSYS下对上述环盘直接进行建模,单元类型选用20节点的SOLID 95,按照表 1中的材料性能参数设置3种材料的属性参数,网格划分时采用4级精度的智能网格,选择不同材料对不同环盘单元进行划分,分析类型设置为模态分析,模态分析方法选择Block Lanczos法,模态提取数目为80个。多环盘的1,2阶横向弯曲耦合振动频率的有限元模态分析结果如表 3中fAk所示,表中Δk表示MATLAB与有限元模态分析求解出的第k阶谐振频率之间的相对偏差。由有限元模态分析得到的1,6,12号模型的前2阶节圆型振动模态和频率分别如图 8所示。

|
| 图 8 1,6,12号模型的前2阶振动模态及对应频率 Fig.8 The first two order vibrating modals and corresponding frequencies of model 1, 6 and 12 |
由MATLAB数值计算结果与ANSYS有限元模态分析结果之间的对比可知,2种求解结果的最大相对偏差为5.80%,最小相对偏差为0.01%。
文献[11]通过理论模型与实验研究,验证了在横向弯曲耦合振动频率计算中将等厚度齿轮简化为直径等于分度圆的中厚环盘模型的可行性。因此对于1,2,3,7,10号模型,选取了对应的齿轮进行了模态实验。
实验采用单点激振、多点拾振的锤击法以获得齿轮的1,2阶横向弯曲耦合振动频率。齿轮竖直悬挂于支架上,4个CA-YD-125型加速度传感器均布于齿轮外圈。传感器与YE5850B型电荷放大器相连,电荷放大器又与信号采集系统相连,最后信号采集系统通过数据线将信号采集结果传送给电脑。其实验系统如图 9所示。

|
| 图 9 模态实验装置 Fig.9 Devices of modal experiments |
模态实验的结果如表 4所示,其中,fMk表示MATLAB求解出的第k阶横向弯曲耦合振动频率,fEk表示模态实验求得的第k阶谐振频率,Δk表示理论值与模态实验结果之间的相对偏差,“*”表示受实验条件所限无法测得相应的2阶频率,“—”表示由于无法测得2阶频率而无法求得相对偏差。由表 4可知,多环盘横向弯曲耦合振动分析模型的理论值与模态实验结果之间的最大相对偏差为4.95%,最小相对偏差为0.26%。
| 比较项 | 1号 | 2号 | 3号 | 7号 | 10号 |
| fM1/Hz | 4 665 | 15 805 | 22 585 | 4 195 | 2 205 |
| fM2/Hz | 21 035 | 55 965 | 55 615 | 15 235 | 8 775 |
| fE1/Hz | 4 653 | 15 875 | 23 678 | 4 032 | 2 101 |
| fE2/Hz | 20 086 | * | * | 15 475 | 8 685 |
| Δ1/% | 0.26 | 0.44 | 4.62 | 4.04 | 4.95 |
| Δ2/% | 4.72 | — | — | 1.55 | 1.04 |
综上所述,三环盘横向弯曲耦合振动频率计算程序能较准确地求解出不同材料组成的三环盘结构负载的低阶横向弯曲耦合振动频率,验证了多环盘横向弯曲耦合振动分析模型的正确性,能够满足旋转超声加工系统设计的工程需要。
振动模型的理论值、有限元分析结果和模态实验结果之间的偏差存在原因主要有以下三点:
1) 当环盘厚径比越大,振动模型的理论计算结果与有限元模态分析结果和模态实验结果的偏差越大,当厚径比超过0.5时,Mindlin理论计算偏差较大。
2) 振动频率求解时采用的是数值法,因而计算结果存在求解误差。
3) 由于多环盘模型忽略了轮齿、键槽、倒角等结构,因此多环盘分析模型与齿轮模态实验的结果之间存在偏差。
4 结论1) 建立了多种材料构成的多环盘的横向弯曲耦合振动的分析模型,推导了谐振频率方程,并基于MATLAB设计了相应的频率计算函数和人机交互界面。
2) 利用该软件计算了不同材料、结构和尺寸的多环盘横向弯曲耦合振动频率。与有限元模态分析结果比较的最大相对偏差为5.80%,最小相对偏差为0.01%;与模态实验结果比较的最大相对偏差为4.95%,最小相对偏差为0.26%。验证了求解模型的准确性。
3) 基于MATLAB设计的频率计算程序能够简化耦合振动频率或几何尺寸的计算过程,降低了谐振系统设计对技术人员的设计理论要求,缩短了设计时间,为旋转超声加工谐振的设计提供了技术参考。
| [1] |
秦慧斌, 吕明, 王时英, 等.
齿轮超声加工纵向振动系统的设计与实验研究[J]. 工程设计学报, 2013, 20(2): 140–145.
QIN Hui-bin, LV Ming, WANG Shi-ying, et al. Design and experiment research of longitudinal vibration system in gear ultrasonic machining[J]. Chinese Journal of Engineering Design, 2013, 20(2): 140–145. |
| [2] | WANG Y, LIN B, CAO X, et al. An experimental investigation of system matching in ultrasonic vibration assisted grinding for titanium[J]. Journal of Materials Processing Technology, 2014, 214(9): 1871–1878. DOI:10.1016/j.jmatprotec.2014.04.001 |
| [3] | NING F D, CONG W L, PEI Z J, et al. Rotary ultrasonic machining of CFRP: a comparison with grinding[J]. Ultrasonics, 2016, 66: 125–132. DOI:10.1016/j.ultras.2015.11.002 |
| [4] | JATINDER K. Ultrasonic machining-a comprehensive review[J]. Machining Science & Technology, 2013, 17(3): 325–379. |
| [5] | GALLEGO-JUAREZ J A, RODRIGUEZ G, ACOSTA V, et al. Power ultrasonic transducers with extensive radiators for industrial processing[J]. Ultrasonics Sonochemistry, 2010, 17(6): 953–964. DOI:10.1016/j.ultsonch.2009.11.006 |
| [6] | GALLEGO-JUAREZ J A, RORiGUEZ G, ACOSTA-APARICIO V M, et al. Power ultrasonics: applications of high-Intensity ultrasound[M]. Oxford: Woodhead Publishing, 2014: 159-193. |
| [7] | GALLEGO-JUAREZ J A. High-power ultrasonic processing: recent developments and prospective advances[J]. Physics Procedia, 2010, 3(1): 35–47. DOI:10.1016/j.phpro.2010.01.006 |
| [8] |
张小丽. 纵弯及纵径振动模式转换功率超声换能器的研究[D]. 西安: 陕西师范大学物理学与信息技术学院, 2014: 67-103.
ZHANG Xiao-li. Analysis of power ultrasonic transducers for longitudinal-flexural and longitudinal-radial mode-conversion vibration[D]. Xi'an: Shaanxi Normal University, School of Physics and Information Technology, 2014: 67-103. |
| [9] |
李华, 任坤, 殷振, 等.
纵弯转换超声振动雾化系统的雾化特性研究[J]. 中国机械工程, 2015, 26(4): 446–451.
LI Hua, REN Kun, YIN Zhen, et al. Study on atomization property of an ultrasonic vibration atomization system based on longitudinal and flexural vibration conversion[J]. China Mechanical Engineering, 2015, 26(4): 446–451. |
| [10] | HE X P, ZHU T, PAN X J. Analytical and experimental investigation on thick plates in flexural vibration[J]. Acta Acustica United with Acustica, 2014, 100(3): 411–417. DOI:10.3813/AAA.918720 |
| [11] |
潘晓娟, 贺西平.
厚圆盘弯曲振动研究[J]. 物理学报, 2010, 59(11): 7911–7916.
PAN Xiao-juan, HE Xi-ping. Analysis of flexural vibration thick disk[J]. Acta Physica Sinica, 2010, 59(11): 7911–7916. DOI:10.7498/aps.59.7911 |
| [12] |
李向鹏, 张春辉, 王时英.
基于Mindlin理论的齿轮横向振动模型[J]. 振动与冲击, 2011, 30(12): 230–234.
LI Xiang-peng, ZHANG Chun-hui, WANG Shi-ying. Models of transverse vibration of gear based on Mindlin's theory[J]. Journal of Vibration and Shock, 2011, 30(12): 230–234. DOI:10.3969/j.issn.1000-3835.2011.12.045 |
| [13] |
佘银柱, 吕明, 王时英.
阶梯变厚度齿轮的横向弯曲振动[J]. 机械科学与技术, 2013, 32(1): 116–119.
SHE Yin-zhu, LÜ Ming, WANG Shi-ying. Transverse bending vibration of gear with stepped variable thickness[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(1): 116–119. |
| [14] | QIN H B, LÜ M, SHE Y Z, et al. Modeling and solving for transverse vibration of gear with variational thickness[J]. Journal of Central South University, 2013, 20(8): 2124–2133. DOI:10.1007/s11771-013-1716-3 |
| [15] |
吕明, 王时英, 秦慧斌.
非谐振设计理论与齿轮超声加工[M]. 北京: 科学出版社, 2014: 36-70.
LÜ Ming, WANG Shi-ying, QIN Hui-bin. Nonresonant design theory and ultrasonic gear machining[M]. Beijing: Science Press, 2014: 36-70. |
| [16] | HOSSEINI-HASHEMI S, DERAKHSHANI M, FADAEE M. An accurate mathematical study on the free vibration of stepped thickness circular/annular Mindlin functionally graded plates[J]. Applied Mathematical Modelling, 2013, 37(6): 4147–4164. DOI:10.1016/j.apm.2012.08.002 |
| [17] | HOSSEINI-HASGEMI S, BEDROUD M, NAZEMNEZHAD R. An exact analytical solution for free vibration of functionally graded circular/annular Mindlin nanoplates via nonlocal elasticity[J]. Composite Structures, 2013, 103(9): 108–118. |
| [18] | LIEW K M, WANG C M, XIANG Y, et al. Vibration of Mindlin Plates[M]. Oxford: Elsevier Science Ltd., 1998: 27-88. |



