可靠性预计是在产品设计阶段对系统可靠性进行定量的估计，根据产品的历史可靠性数据、系统的构成和结构特点、系统的工作环境等因素估计组成系统的部件及系统的可靠性。通过可靠性预计可以找出设计方案的薄弱环节，从而采取改进措施，提高系统可靠性^[1-4]。

目前，可靠性预计新方法的研究更多集中在电子器件领域，而机械产品的可靠性预计仍主要依赖于传统的方法，如相似产品法、故障率统计法、失效机理分析法等^[5-9]，或对这些传统方法进行一定程度的改进。例如，郝庆波等^[10]提出了一种基于区间层次分析的可靠性预计方法；陈云霞等^[11]建立了功能分析与失效机理结合的可靠性预计方法；针对高复杂度系统，王树清^[12]采用高效实用的ITEM ToolKi可靠性平台对其可靠性预计进行了研究；杜丽等^[13]将模糊相似产品法与综合评判法相结合进行可靠性预计；周真等^[14]提出了基于BP神经网络的可靠性预计方法；严博等^[15]提出了一种应用随机进程代数的网络系统可靠性预计方法。这些方法多数是从数学的角度进行研究，没有充分考虑机械产品的功能、结构、运动以及产品内部更细致的动作，如零件的转动、移动，缺少对机械产品的针对性。文献[10]虽然考虑了结构，但其考虑的层次为部件级，且部件级相似产品的相似度不好把握，比较笼统，不够细致。

基于以上分析，本文试图从“功能—运动—动作(function-movement-action，FMA)”结构化分解的角度，充分考虑产品的功能、内部结构、运动等特点，并综合成熟参考结构的可靠性数据和专家经验来实现可靠性预计。

对机械产品而言，如数控机床，其各大功能是通过各部件的运动实现的，而部件的运动则是由组成部件的零件的基本动作完成的^[16-18]。FMA结构化分解方法就是根据机械产品的这一特点，将产品按照“功能—运动—动作”进行自上而下地分解，其核心思想就是将实现产品功能的复杂的综合运动拆分成一系列基本的动作单元，将产品各功能看成一系列相互关联的动作。如图 1所示，首先明确产品的各大功能，即功能1，功能2，…，功能n₁，建立功能层。以功能2为例，功能2的实现需要相应部件的机械运动，由此可确定与功能2相关的n₂个运动，建立运动层。再以运动2为例，运动2的实现需要组成部件的零件的基本动作来完成，如零件的转动、移动，由此得到元动作1，元动作2，…，元动作n₃，建立元动作层。实际中的产品比较复杂，经过分解之后会得到很多层次，因此把功能层和元动作层之间的层次称为过程层。

图 1 机械产品的FMA结构化分解 Fig.1 FMA structure decomposition of mechanical product

图选项

产品经过FMA结构化分解至不能再分解的元动作层后，可得最小动作单元——元动作运动单元(meta-action units，MU)。元动作运动单元是结构相对独立且能够实现目标动作，可控可分析且不能再细分的动作单元，如蜗杆转动元动作。虽然产品的结构往往很复杂，但通过FMA结构化分解得到的元动作一般是机械结构的2种基本动作形式：直线移动和转动，这样有利于选择与元动作单元相似的参考结构。

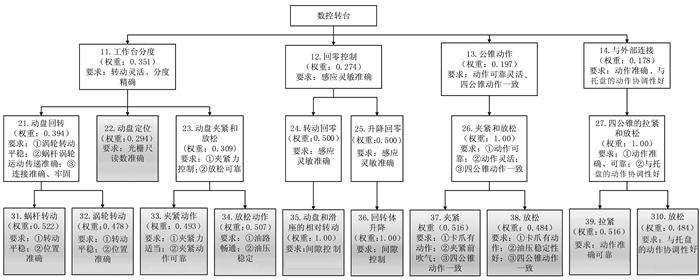
为了更好地说明结构化分解方法，以数控机床的功能部件(数控转台)为例进行分析。首先，要明确产品的各大运动功能，数控转台的四大运动功能分别是：工作台分度、回零控制、公锥动作和与外部连接。各大运动功能都有其相应的要求，工作台要分度精确，回零控制要灵敏，公锥动作要灵活一致，与外部连接要准确协调。按照上节的基本思路，将数控转台层层分解至不能再分解，即分解至元动作层，如图 2所示。

图 2 数控转台运动功能结构化分解 Fig.2 Structure decomposition of numerical control rotary table's movement function

图选项

为研究方便，如果某一运动单元由n_z(n_z≥1) 个下一层次的运动单元来实现，则称该运动单元为这n_z个运动单元的父代运动单元，称这n_z个运动单元为该运动单元的子代运动单元。例如在图 2中，“31蜗杆转动”和“32涡轮转动”为“21动盘回转”的子代运动单元，反之，“21动盘回转”为“31蜗杆转动”和“32涡轮转动”的父代运动单元。

通过运动功能分解可以确定产品运动功能的最小机械结构——元动作运动单元。元动作到整个产品的运动功能具有严格的层次关系，因此，只要知道元动作单元的可靠性就可以自下而上预计整个产品的可靠性，而元动作运动单元的可靠性可通过选择与其相似的参考结构来预计。

选取参考结构就是通过评价待选结构与元动作运动单元的相似度，将相似度高的待选结构作为参考结构。相似度“高”是一个模糊概念，且人为判断的过程也具有一定的模糊性，因此，本文采用一种基于区间数正态云模型的综合评价方法。

相似度评价就是要综合许多专家的评价意见得出一个评价值，亦即需要通过一定的算法将各位专家给出的区间数形式的评价结果汇总形成一个评价值。问题是如何将区间数转化为云评价值，其中关键的一步是将正态分布区间数转换成有界闭区间正态模糊数^[19]。文献[19]中给出，普通的实数为模糊数，区间数为模糊数，闭区间为有界闭模糊数。由此，正态分布区间数逆向云算法设计如下：

1) 对于n个正态分布区间数v_k=[v_k^-，v_k⁺]，每个区间数可看作一个正态模糊数的α-水平截集，其中α的大小可以由实际问题的估计区间大小判定，本文中取α=0.5，因为隶属度为0.5的这一点是最模糊的点。于是有：

并得到模糊隶属函数曲线为：

其中：k=1，2，…，n；α用于衡量模糊度。

2) 输入经过模糊化处理的n个区间数样本，根据模糊运算法则和模糊扩张原理得到评价云的期望曲线方程：

3) 将n个模糊数的模糊隶属曲线平移成一个曲线簇，则这个曲线簇可以看作云的近似。由此可将均值t作为所求评价云的期望值Ex，方差σ_k的期望和标准差作为评价云的熵En和超熵He，即：

相似度的评价是以评价云的期望值Ex为主要指标，兼顾熵En和超熵He，期望值越大相似度越高，则待选结构越容易被选为参考结构，如熵和超熵值异常则需要重新计算评价云。

待选结构的相似度有4个等级，即“很相似”“较相似”“一般”和“不相似”。以期望值为衡量指标建立评语集：

对所有的待选结构进行相似度评价，根据评价云的期望值Ex和评语集，将“很相似”的待选结构定为预计元动作运动单元可靠性的参考结构。

影响评价的因素有很多，其中主要因素有功能差异、组成结构、尺寸大小、组成材料、制造装配、复杂程度、运动速度以及运动幅度等，为在评价过程中综合考虑这些因素，建立因素集C，即：

而每个因素对评价的影响并不相同，故需要确定每个因素的影响权重。聘请专家对各因素的权重进行打分评价，分值范围为0~10分，以区间数形式给出，分值越高表明权重越大，即该因素对评价结果的影响越大，如表 1所示。利用逆向云算法，计算出每个因素的权重云a₁′，a₂′，…，a₈′。为使各权重云的均值相加为1，根据云运算法则^[20]作如下处理：

令：

其中i=1，2，…，8。从而可得影响因素的权重矩阵A，即:

假设某元动作运动单元有n_d个待选结构，对于第i(1≤i≤n_d)个待选结构，聘请m位专家对其与元动作运动单元的相似度进行打分评价，打分范围为0~100分。为充分考虑判断的模糊性，以区间数[r_gh^-，r_gh⁺]的形式给出，其表示第g位专家在第h个影响因素方面给出的相似度评价值，g=1，2，…，m，h=1，2，…，8，如表 2所示。

由2.1节的逆向云发生器算法可得出第i个待选结构的相似度评价矩阵为：

由此可以得出第i个待选结构的相似度综合评价值：

根据公式(2)，可以得到全部待选结构的相似度综合评价值B₁，B₂，…，B_nd。

根据综合云评价值和评语集，可把所有的待选结构区分开来，即对每个参考结构作出“很相似”“较相似”“一般”和“不相似”的判断，并将判定为“很相似”的待选结构确定为元动作运动单元可靠性预计的参考结构。

元动作运动单元是将产品进行FMA结构化分解之后的最小单元，是产品可靠性预计的基础，其可靠性预计的依据是所选参考结构的可靠性水平。尽管参考结构与元动作运动单元很相似，但仍然存在不同，所以直接把参考结构的可靠性看作元动作运动单元的可靠性是不可取的。由2.2节待选结构相似度的评价过程可知，评价云的期望值${{\rm{\hat Ex}}} $是在百分制打分的基础上得出的，因此，可以用相似度修正参考结构的可靠性数据来预计元动作运动单元的可靠性。

假设某产品经过分解之后得到n_y个元动作运动单元，第j(1≤j≤n_y)个元动作运动单元有n_c个参考结构，每个参考结构的平均故障率为$\overline {{\lambda _i}} $，相应的综合评价云期望值为$ {\rm{\hat E}}{{\rm{x}}_i}\left( {1 \le i \le {n_{\rm{c}}}} \right)$，则该元动作运动单元平均故障率的预计值为：

式中：$\overline {{\lambda _{{\rm{y}}j}}} $表示第j个元动作运动单元的平均故障率预计值。同理可得n_y个元动作运动单元的可靠性预计值分别为${{\bar \lambda }_{{\rm{y1}}}}, {{\bar \lambda }_{{\rm{y2}}}}, ..., {{\bar \lambda }_{{\rm{y}}{{\rm{n}}_{\rm{y}}}}} $。

如图 3所示，假设某父代运动单元按照FMA结构化分解方法分解出n_z(n_z≥1) 个子代运动单元，则完成相应功能的父代运动单元与子代运动单元的可靠性关系为：

图 3 父代运动单元分解图 Fig.3 Decomposition of the parent movement unit

图选项

式中：R_f(t)为父代运动单元的可靠度；R_zi(t)为第i个子代运动单元的可靠度，1≤i≤n_z。

由于$R\left( t \right) = {{\rm{e}}^{-\int_0^t {\lambda \left( t \right){\rm{d}}t} }} $，所以式(4) 可以转化为：

式中：λ_f(t)父代运动单元的故障率；λ_zi(t)为第i个子代运动单元的故障率。

由此可以得出：

即：父代运动单元的故障率等于各子代运动单元的故障率之和。但由于各子代运动单元的故障时间不一定服从同一种分布，所以可以用运动单元的平均故障率代替故障率函数。

当t=T时，即试验时间截止到T时，运动单元在时间区间[0，T]内的平均故障率为：

将式(7) 代入式(6)，得：

式中：${{\bar \lambda }_{\rm{f}}} $为父代运动单元的平均故障率；${{{\bar \lambda }_{{\rm{z}}i}}} $为第i个子代运动单元的平均故障率，1≤i≤n_z。

由式(8) 可知，父代运动单元的平均故障率等于各子代运动单元的平均故障率之和。因此，可从元动作运动单元开始，层层预计父代运动单元的可靠性，最终可预计整个产品的可靠性。然而，每个子代运动单元对其父代运动单元可靠性的影响程度不同，所以，还需确定子代运动单元对父代单元的影响权重以修正公式(8)。

将子代运动单元对父代运动单元可靠性影响的重要度进行比较，构建比较矩阵。考虑到判断过程具有模糊性，根据专家建议，对每一个子代运动单元按照1~9的标度以区间数${{\tilde d}_{kl}} = \left[{d_{kl}^-, d_{kl}^ + } \right] $进行相对重要度的赋值，从而构造比较判断矩阵${\mathit{\boldsymbol{\tilde D}}} $，即：

式中：${{\tilde d}_{kl}} = \left[{d_{kl}^-, d_{kl}^ + } \right] $表示第k个子代运动单元与第l个子代运动单元对其父代运动单元可靠性影响的重要度比值，可选取1~9范围内的任意区间数(或其倒数)表示；1≤k≤n_z，1≤l≤n_z，D^-=(d_kl^-)_nz×nz，D⁺=(d_kl⁺)_nz×nz。

采用区间数特征向量法(interval eigenvector method，IEM)^[21]来求解各子代运动单元的影响权重。首先利用特征向量法分别求出D^-和D⁺的权重向量，记为x^-，x⁺，然后由式(10)、式(11) 求出比较判断矩阵${\mathit{\boldsymbol{\tilde D}}} $的区间数权重向量，即：

一般来讲，0 < α′ < 1 < β′时，区间判断矩阵${\mathit{\boldsymbol{\tilde D}}} $的一致性较好，可以采用。

此时得到的${{\tilde \omega }_k} = \left[{\omega _k^-, \omega _k^ + } \right] $是一个区间数，令：

取

式中：γ是专家选中的权值，0≤γ≤1。当γ=0时，ω_k=ω_k^-，决策者持谨慎态度；当γ=0.5时，ω_k=(ω_k^-+ω_k⁺)/2，决策者持中庸态度；当γ=1时，ω_k=ω_k⁺，此时决策者持激进态度。

用由式(12) 得到的ω_k修正公式(8)，得：

根据公式(13)，可以从元动作运动单元开始层层预计父代运动单元的可靠性，最终预计整个产品的可靠性水平。

以数控转台为例，进一步说明基于FMA结构化分解的可靠性预计方法。首先将研究对象进行运动功能结构化分解，如图 2所示，由图可知，标号为31，32，22，33，34，35，36，37，38，39和310运动功能为元动作，其对应的机械结构为元动作运动单元。为进行可靠性预计，首先要确定各影响因素的权重，并对每一个元动作运动单元评价和选出合适的参考结构。

聘请10位专家以区间数的形式进行打分评价，10位专家对各影响因素的评价值如表 3所示。

根据逆向云发生器，计算各影响因素的权重，以因素c₁为例，取α=0.5：

则因素“功能差异”的权重云为a′₁=(7.75，0.55，0.27)，同理可得a′₂=(7.96，0.62，0.31)，a′₃=(5.28，0.66，0.38)，a′₄=(6.50，0.64，0.33)，a′₅=(5.58，0.62，0.32)，a′₆=(5.95，0.34，0.15)，a′₇=(5.73，0.49，0.36)，a′₈=(4.75，0.68，0.26)。

由公式(1) 可得影响因素权重矩阵A：

下面预计元动作运动单元的可靠性，以标号为“35”的运动单元为例。首先确定一定数量的待选结构，本文取10个，元动作单元“35”的10个待选结构的平均故障率如表 4所示。聘请10位专家从各个影响因素出发对每一个待选结构进行相似度评价。以表 4中第1个待选结构为例，其专家评价值汇总如表 5所示。根据逆向云发生器算法，取α=0.5，得第1个参考结构在各因素方面的平价云值：r₁₁=(79.65，3.7，1.59)，r₁₂=(72.95，3.96，1.95)，r₁₃=(64.15，5.23，2.10)，r₁₄=(63.85，4.21, 1.09)，r₁₅=(68.20，4.26，1.27)，r₁₆=(80.95，4.38，1.64)，r₁₇=(70.35，4.21，1.60)，r₁₈=(60.15，3.87，1.52)。

于是有综合评价矩阵R₁，即:

根据公式(2) 有B₁=A·R₁=(70.77，2.86，1.41)。

采用同样的方法可得其他待选结构的相似度综合评价值，如表 6所示。

由表 6和评语集可知，待选结构4，6，7和8属于“很相似”的结构，可作为参考结构。根据公式(3)，标号为“35”的“动盘和滑座的相对转动”元动作运动单元的平均故障率预计值为：

同理可得：

要进行产品的可靠性预计，还需确定子代运动单元对父代运动单元可靠性影响的重要度权重。如图 2所示，以子代“动盘回转”“动盘定位”“动盘夹紧和放松”运动单元对父代“工作台分度”运动单元的影响为例。首先构建比较矩阵，父代单元“11”的各子代单元的权重矩阵如表 7所示。

根据IEM方法得区间数权重向量$\tilde \omega $=[[0.367，0.420]，[0.283，0.305]，[0.292，0.326]]，取γ=0.5，代入(12) 式得权重ω=(0.394，0.294，0.309)。同理，可得出所有子代运动单元的权重，如图 2所示。

将元动作运动单元的可靠性预计值以及各子代运动单元的权重代入公式(13)，层层预计父代运动单元的可靠性：

根据第2层次运动单元的可靠性预计值来预计第1层次运动单元的可靠性：

根据第1层次运动单元的平均故障率预计数控转台的平均故障率：

即数控转台的平均故障率预计值为2.96×10^-4/h^-1。

将该预计值和用传统方法得到的预计值分别与数控转台的平均故障率真实值进行对比，得出误差，其中误差为预计值与真实值差值的绝对值与真实值的比值。如表 8所示，可知本文方法具有相对较小的误差。

本文提出了基于“功能—运动—动作”结构化分解的可靠性预计新方法。首先根据FMA结构化分解的方法将产品分解得到较简单的元动作运动单元，从而将可靠性预计工作建立在细致分析机械结构及其运动功能的基础上，使得预计过程更加精确。然后通过评价和选取与元动作运动单元相似的参考结构，并通过确定评价系数和参考结构的数据预计元动作运动单元的可靠性及整个产品的可靠性水平。该方法适用于机械产品(如数控机床等)的可靠性预计，也为机械产品其他性能的分析提供了新的思路。