2. 华南理工大学 安全科学与工程研究所, 广东 广州 510640;
3. 北京科技大学 土木与环境工程学院, 北京 100083
2. Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640, China;
3. School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China
地下开采是金属矿床开采的主要方式,在开采过程中,如果空区得不到及时有效处理,将遗留大小不等的采空区。为了提高资源回收率,需要对间柱、顶柱等残矿资源进行爆破回采。频繁爆破作业不可避免地侵扰了采空区群的应力平衡,造成空区群内部累积损伤效应,导致关键区域间柱、顶柱的承载力下降,降低整个空区群落的整体安全度,严重时会引发大面积顶板冒落、覆岩滑移、地表塌陷等工程地质灾害[1-5]。动荷载激励下采空区群的动力响应问题是矿业界关注的焦点,对此开展研究,对于降低工程地质灾害发生概率,具有十分重要的意义。
金属矿地下开采是一个长期的受到爆破荷载作用的过程,空区群失稳的动荷载分析通常以爆炸应力波为激励源,研究方法主要以数值分析法和现场监测法[6-14]为主。鲁文妍等[10]结合ABAQUS隐式和显式分析,对在地震作用下洞室群的动力时程响应进行了仿真研究;李新平等[11]应用FLAC3D数值软件模拟爆破振动对相邻洞室的影响,得到了爆破振动作用下相邻洞室振动速度、应力和位移的分布规律。宗琦等[12]以某矿山深孔爆破和城市基坑爆破工程为例,对爆破振动速度和爆破振动频率进行了监测,研究了爆破地震波的传播和衰变规律;Nick等[13]监测了爆破振动对邻近洞室的扰动,提出了控制爆破振动的方法。但是,数值分析法和现场监测法都存在一定的不足:1) 数值计算法存在建模繁琐、计算工程量大且耗时长等问题;2) 现场监测则存在监测成本高、监测周期长和监测环境恶劣等问题。
结构层间剪切模型分析法是一种从结构动力学的角度出发,研究高层建筑结构动力响应特性问题的方法。该方法具有自由度少、计算量小、计算效率高、耗时少等特点,能较好反映结构内部各层的受力、变形情况[15-18]。考虑地下采空区群与地表构筑物空间结构上的相似性,本文提出地下采空区群类层间剪切模型分析法。针对采空区群上覆岩层及周边围岩作用,探索性地引入“虚拟间柱群”和剪切力影响因子,研究采空区群内岩体介质的动力响应特性。以某大型金矿5个中段组成的采空区群为例,构建爆炸应力波动力响应的类层间剪切模型,在动力平衡微分方程的基础上,求解外部激励下关键质点的位移和速度值,揭示采空区群内质点的动力响应规律。
1 类层间剪切模型构建 1.1 采空区群赋存环境处理采空区群主要受上覆岩层压力、周边围岩水平地应力等共同作用。为了反映上覆岩层和周边围岩在动力计算过程中的力学效应,本文对上覆岩层和周边围岩分别进行等效处理。
1) 上覆岩层。
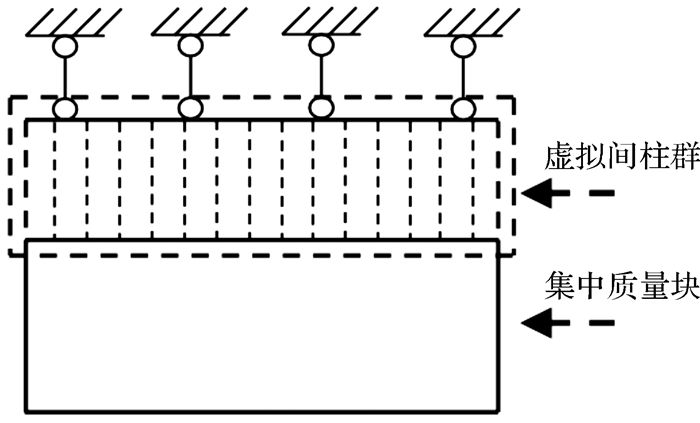
上覆岩层是具有非连续自应力构造特性的块系岩体[19],将上覆岩层等效为由“虚拟间柱群”和集中质量块组成的体系,如图 1所示。上覆岩层上部不作处理,中部等效为“虚拟间柱群”,下部等效为集中质量块,块体质量为mn。
|
| 图 1 上覆岩层等效体系 Fig.1 Overburden equivalent system |
2) 周边围岩。
在爆炸应力波激励下,采空区群岩体与周边围岩产生相对运动,二者的接触面发生剪切作用。因此,可将周边围岩对采空区群的水平地应力等效为剪切力Q。考虑到采空区所处中段埋深和单元采空区形状特征,引入剪切力影响因子δ对剪切力进行修正。
1.2 基本假设1) 采空区群赋存围岩岩体构造完整,忽略断层和节理对采空区群稳定性的影响。
2) 忽略采矿过程中大量的采准、切割巷道对采空区群稳定性的影响。
3) 研究范围内,假定采空区群岩体为均质、各向同性的弹塑性材料,岩体材料破坏符合摩尔-库仑(Mohr-Coulomb)强度准则。
4) 采场是具有相似形状的空间结构体,单元采空区暴露面积相等,顶(间)柱的尺寸规格相同。
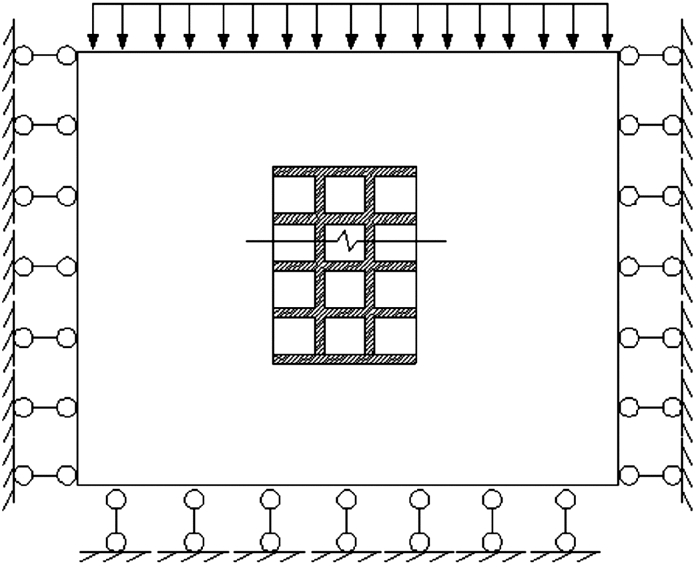
1.3 模型构建采空区群由间柱、顶柱、空区、上覆岩层和周边围岩组成,为便于理论分析,规则化处理复杂采空区群。周边围岩采用铰接处理,上覆岩层等效为均布荷载,等效处理后,采空区群围岩静载力学模型如图 2所示。
|
| 图 2 采空区群围岩静载力学模型 Fig.2 The static mechanical model of goaf group |
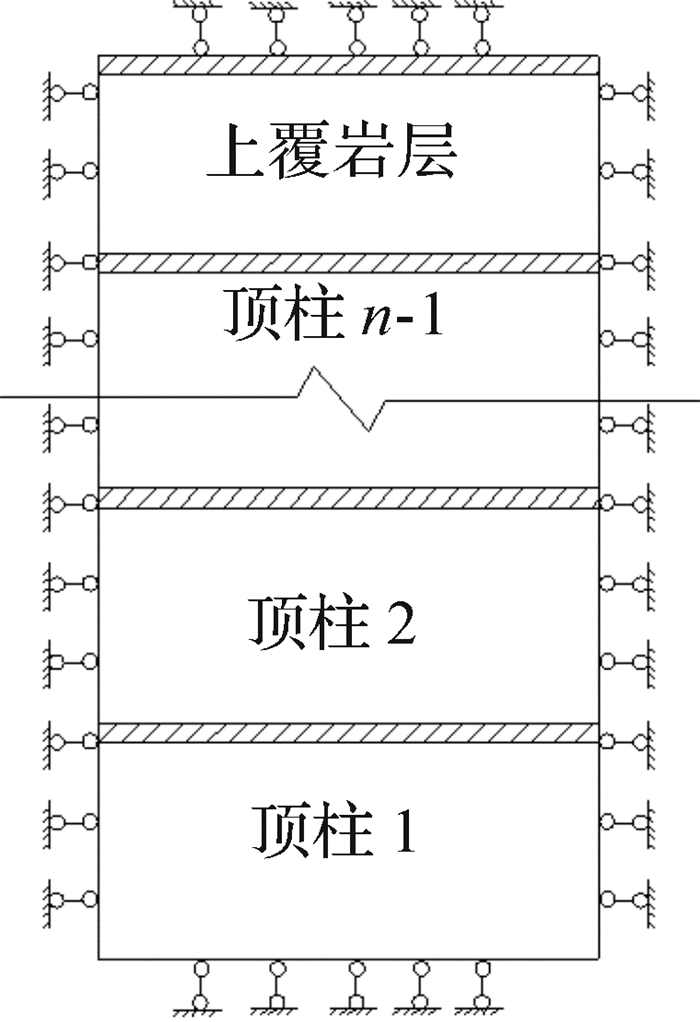
采空区群内各中段顶(底)柱岩体呈连续性分布,为无限自由度系统。在动荷载激励下,不同段位顶柱的质点的动力响应特性参数(位移、速度)相互独立。基于文献[20]的研究结果,作连续体的离散化处理。可以将采空区群围岩静载力学模型近一步简化为类层间剪切模型(图 3),从而进行动力分析,将无限自由度问题转化为有限自由度问题进行求解。
|
| 图 3 采空区群类层间剪切模型 Fig.3 Similar layer model of goaf group |
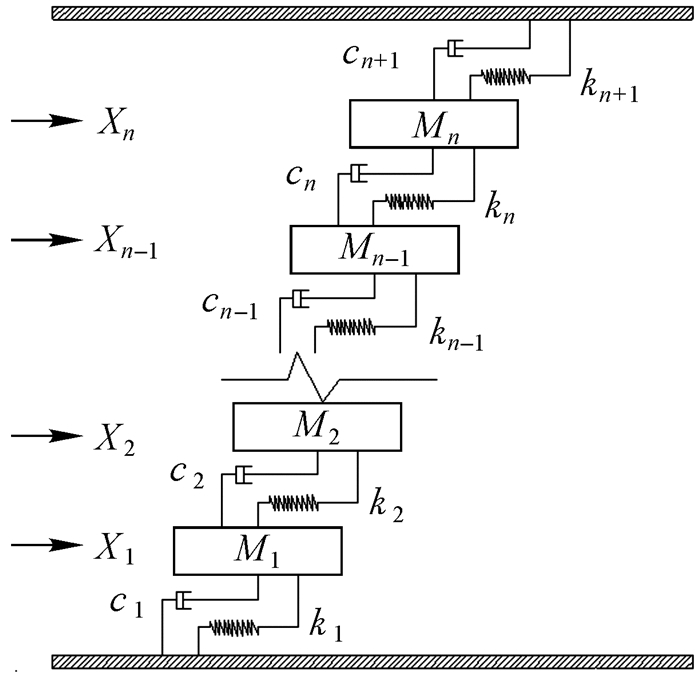
岩体是弹塑性介质,在外部荷载激励作用下,组成岩体的微小颗粒之间相互作用,不断消耗内部储存的能量。以弹簧作为反映岩体弹性变形的元件,以黏性阻尼作为反映岩体能量耗散的元件。根据结构动力学理论分析方法,构建采空区群类层间剪切模型的动力响应计算模型(图 4),爆炸应力波激励下的动力响应方程满足式(1)。
|
| 图 4 采空区群动力响应计算模型 Fig.4 Dynamic calculation model of goaf group |
| $ \mathit{\boldsymbol{M}}\left\{ {\ddot x} \right\} + \mathit{\boldsymbol{C}}\left\{ {\dot x} \right\} + \mathit{\boldsymbol{K}}\left\{ x \right\} + \delta \mathit{\boldsymbol{Q = F}} $ | (1) |
式中:M,C,K,Q,F分别为质量矩阵、阻尼矩阵、刚度矩阵、剪切力矩阵及爆破载荷矩阵;
由达朗贝尔(D’Alembert)原理知,采空区群的质量矩阵M、阻尼矩阵C和刚度矩阵K分别为:
| $ \mathit{\boldsymbol{M = }}\left[\begin{array}{l} {M_1}\\ \;\;\;\;\;\;\;\;{M_2}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M_{n-1}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M_n}\;\;\; \end{array} \right] $ | (2) |
| $ \mathit{\boldsymbol{C = }}{\mathit{\boldsymbol{C}}_{\rm{j}}} + {\mathit{\boldsymbol{C}}_{\rm{w}}} $ | (3) |
| $ \mathit{\boldsymbol{K = }}\left[\begin{array}{l} {k_1} + {k_2}\;\;-{k_2}\\ \;-{k_2}\;\;{k_2} + {k_3}\;\;-{k_3}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {k_{n - 2}}\;\;{k_{n - 2}} + {k_{n - 1}}\;\; - {k_{n - 1}}\;\;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {k_{n - 1}}\;\;\;\;{k_{n - 1}} + {k_n}\;\; \end{array} \right] $ | (4) |
1) 各层顶柱质量M。
根据结构动力学理论,采用集中质量法对顶柱进行处理,即将采空区层间1/2高度范围内的全部质量集中到各自相应的顶柱上,如式(5):
| $ \left\{ \begin{array}{l} {M_j} = \frac{1}{2}\left( {{m_j} + {m_{j-1}}} \right)\;\;\left( {j \ne 1} \right)\\ {M_1} = \frac{1}{2}{m_1} \end{array} \right. $ | (5) |
2) 层间刚度k。
将整个采空区群视为剪切型振动体系,根据力法,采空区群层间刚度为:
| $ {k_j} = \sum\limits_{i = 1}^n {{{\left( {\frac{{{h^3}}}{{12EI}} + \frac{{\mu h}}{{GA}}} \right)}^{-1}}} $ | (6) |
式中:i为各中段间的间柱个数,kj指采空区群各中段的层间刚度,h为采空区层间高度,E为顶柱岩体的弹性模量,I为间柱的截面惯性矩,μ为形状系数,G为岩体的剪切模量,A为截面积。
3) 层间阻尼C。
为了综合考虑岩体内多种耗能因素的影响,在分析过程中,需考虑层间岩体阻尼Cj作用及层间围岩对爆炸应力波能量的耗散作用Cw。
其中,层面间阻尼采用岩土工程界常用的Rayleigh阻尼进行表征,表达式为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{C}}_{\rm{j}}} = \alpha \mathit{\boldsymbol{M + }}\beta \mathit{\boldsymbol{K}}\\ {\mathit{\boldsymbol{C}}_{\rm{w}}} = \gamma {\mathit{\boldsymbol{C}}_{\rm{j}}} \end{array} \right. $ | (7) |
式中:α,β分别为不依赖于频率的质量比例因子和刚度比例因子;γ为能量耗损因子,根据文献[20]的方法对其赋值。
为了精确确定α,β的大小,需对采空区群系统进行模态分析[21]。根据模态分析结果,采用“贡献”最大、与模态相应的自振圆频率ω和阻尼比ξ来计算α和β。这里,取工程中常用的岩体阻尼比ξi=ξj=0.05。
| $ \left\{ \begin{array}{l} \alpha = \frac{{2{\omega _i}{\omega _j}\left( {{\omega _i}{\xi _j}-{\omega _j}{\xi _i}} \right)}}{{\left( {{\omega _i} + {\omega _j}} \right)\left( {{\omega _i}-{\omega _j}} \right)}}\\ \beta = \frac{{2\left( {{\omega _i}{\xi _j}-{\omega _j}{\xi _i}} \right)}}{{\left( {{\omega _i} + {\omega _j}} \right)\left( {{\omega _i} - {\omega _j}} \right)}} \end{array} \right. $ | (8) |
1) 爆破荷载F。
依据矿山实际爆破炸药当量及文献[22-23]的方法,对爆破荷载大小进行取值,单位面积爆破等效荷载如式(9):
| $ F\left( t \right) = 32000 \times \left( {{{\rm{e}}^{-115.53t}}-{{\rm{e}}^{-231.05t}}} \right) $ | (9) |
2) 剪切力Q。
由广义胡克定律可知,周边围岩对采空区群岩体的剪切力大小为:
| $ {Q_j} = \frac{{GS}}{L}{x_j} $ | (10) |
式中:G为顶柱或间柱岩体的剪切模量;S为顶柱或间柱与围岩的有效接触面积;L为顶柱的高度或间柱的宽度;xj为顶柱或间柱在某时刻的位移,方向与运动方向相反。采空区群岩体与围岩剪切力矩阵为:
| $ \mathit{\boldsymbol{Q = }}{\left[{{Q_1}\;\;{Q_2}\;\;...\;\;{Q_n}} \right]^{\rm{T}}} $ | (11) |
3) 剪切力影响因子δ。
目前,工程界尚无地下空间结构体剪切力影响因子δ的定量取值方法,这里参照地表构筑物的分析方法进行取值,主要应考虑以下2个制约因素:
① 各中段单元采空区赋存深度。由于采空区群周边上下围岩岩性基本相同,各中段高度为50 m左右,各中段采空区群单元所受剪切力具有相近的数量级,因此各中段岩层间剪切力修正系数δ的取值应在同一数量级,彼此差值波动较小。
② 单元采空区形状特征。单元采空区外形不同,与周边围岩的接触面积不同,所受周边围岩的剪切力大小也将存在差异。为了提高回采效率,在条件允许的情况下,尽可能将采场设计成具有相似形状的空间结构体。因此,各单元空区围岩剪切力影响因子δ应在一定范围内选取。
综上,剪切力影响因子δ的取值范围为[1, 10],相邻段位差值不超过4。修正后剪切力矩阵为:
| $ \mathit{\boldsymbol{Q = }}\delta {\left[{{Q_1}\;\;{Q_2}\;\;...\;\;{Q_n}} \right]^{\rm{T}}} $ | (12) |
采用MATLAB工具包对式(1) 进行求解,可得采空区群系统内各中段顶柱的位移矩阵
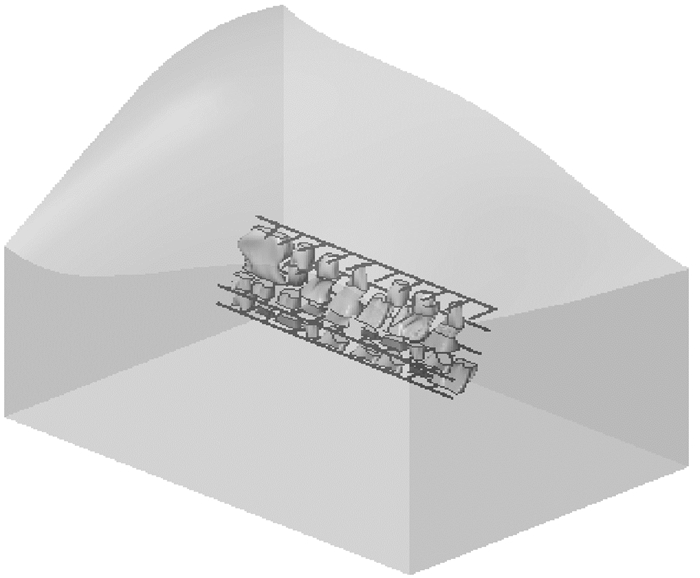
某金矿为大型地下开采矿山,位于秦岭褶皱系南秦岭印支褶皱带凤县-镇安褶皱束的北缘,含金角砾岩带(AnKsb)主要分布于泥盆系中统古道岭组地层中,矿床赋存于该含金角砾岩带。KT5矿体连续分布于矿床东部43-77勘探线之间,矿体形态大致呈陡立的不规则板状体(图 5)。上覆岩层及围岩主要由泥盆系中统的王家楞组(D2W)和古道岭组(D2g)的碎屑岩和碳酸岩组成。矿体和围岩基本上为渐进接触,无明显边界。
|
| 图 5 KT5三维模型 Fig.5 KT5 three-dimensional model |
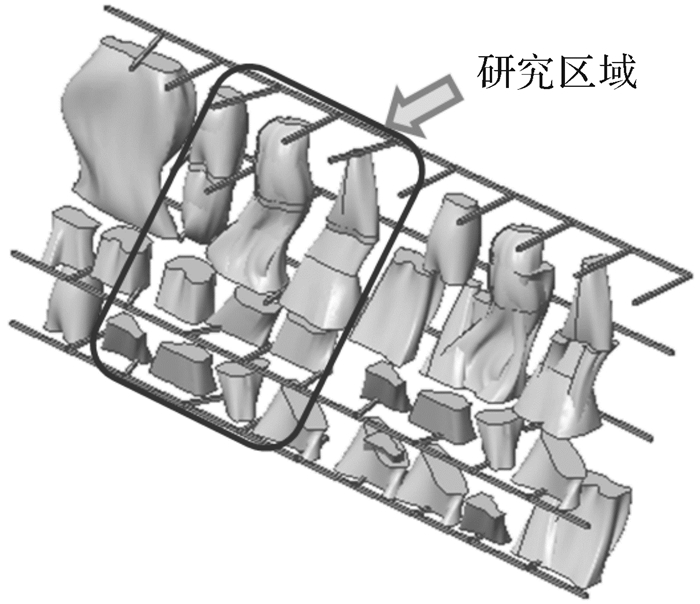
选取该矿山1 420~1 620 m中段的63-69勘探线间采空区群为研究对象(图 6),采用类层间剪切模型法,研究爆破回采间柱过程中采空区内质点动力响应规律,利用数值分析法比对分析结果。
|
| 图 6 某矿山KT5矿体1 420~1 620 m中段采空区群 Fig.6 Goaf group of a mine KT5 orebody 1 420~1 620 m layer |
1) 岩体物理力学参数。
依据矿山实测数据,所研究区域矿体、围岩的物理力学参数如表 1所示。
| 类型 | 弹性模 量/GPa |
抗拉强 度/MPa |
内摩擦 角/(°) |
黏聚力/ MPa |
容重/ kN·m-3 |
泊松 比 |
| 矿体 | 28 | 6.5 | 40 | 14 | 27.2 | 0.26 |
| 围岩 | 35 | 8.8 | 45 | 18 | 25.5 | 0.24 |
2) 结构参数。
由式(2)、(3)、(4),分别计算类层间剪切模型的质量矩阵M、刚度矩阵K和阻尼矩阵C。
3) 外力荷载。
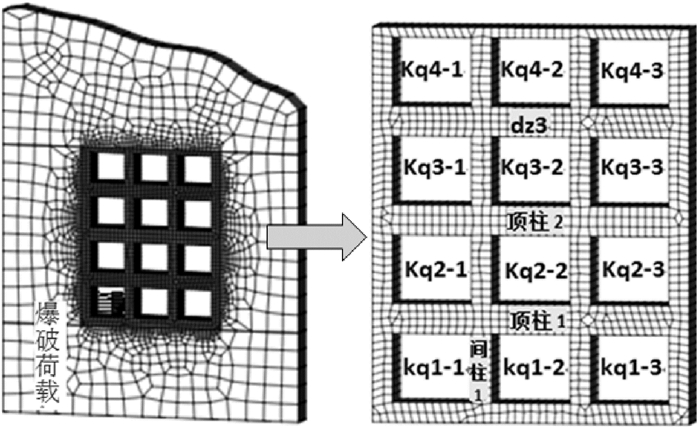
① 爆破荷载。爆破荷载大小由式(9) 确定,爆破荷载时程曲线如图 7所示,爆破作业位置为底层间柱,爆破荷载集中施加在间柱左侧临空面上(图 8)。
|
| 图 7 爆破荷载时程曲线 Fig.7 Time history curve of blasting load |
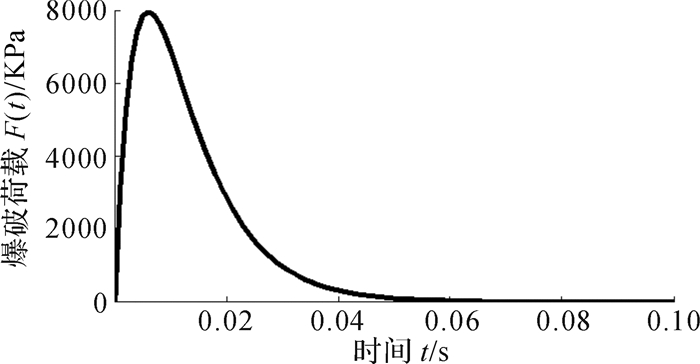
|
| 图 8 采空区群动力响应数值模型及采空区群分布图 Fig.8 Dynamic response numerical model and distribution of Goaf group |
② 剪切力。依据表 1和式(10) 至(12) 及2.2节中模型参数,计算可得剪切力分别为:Q1=3.888 5×1011N,Q2=Q3=Q4=1.749 825×1012N,Q5=3.781 85×1012 N;根据2.2节对剪切力影响因子两个制约因素的分析,可以确定δ的取值范围和采空区群各岩体δ的取值规律,因此,类剪切模型中各中段剪切力影响因子δ的取值分别选取为1,2,4,8,10。
3.2 数值计算法根据圣维南原理,在对边界进行合理简化的基础上,构建研究区域数值模型(图 8)。该模型长为340 m,宽为90 m,左侧高为450 m,右侧高为350 m。单元采空区跨度为30 m,宽度为40 m,高度为35 m,顶柱厚度为15 m,间柱宽度为10 m,围岩厚度为90 m。
设定岩体破坏服从摩尔-库仑(Mohr-Coulomb)准则,初始地应力为岩体的自重应力。为了避免由爆破波的反射作用产生的较大误差,在模型周边设置黏性边界,并对前后边界进行位移约束。同时,为了提高数值模拟结果精度,对采空区群体系进行了网格细分[24],如图 8所示。
爆破荷载集中施加在间柱左侧临空面上,爆破作业位置为间柱1(图 8),爆破荷载时程曲线如图 7所示。
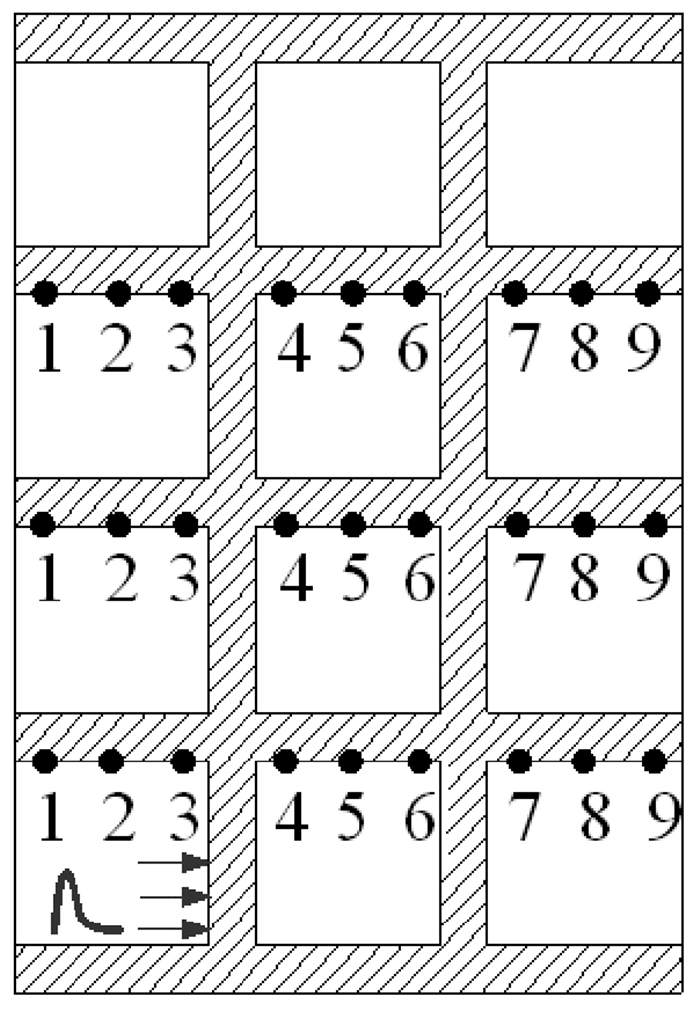
3.3 动力响应分析采空区群单元空区位置分布如图 9所示。为了对比分析,在数值分析法中,分别选取各中段单元空区顶柱位置的3个质点作为记录点,记录质点的位移与速度时程响应数据,再进行加权平均处理,作为对应单元采空区岩体质点的动力响应数据。将计算结果与类层间剪切模型法进行对比分析。
|
| 图 9 监测点布置图 Fig.9 Layout of monitoring points |
1) 位移结果分析。
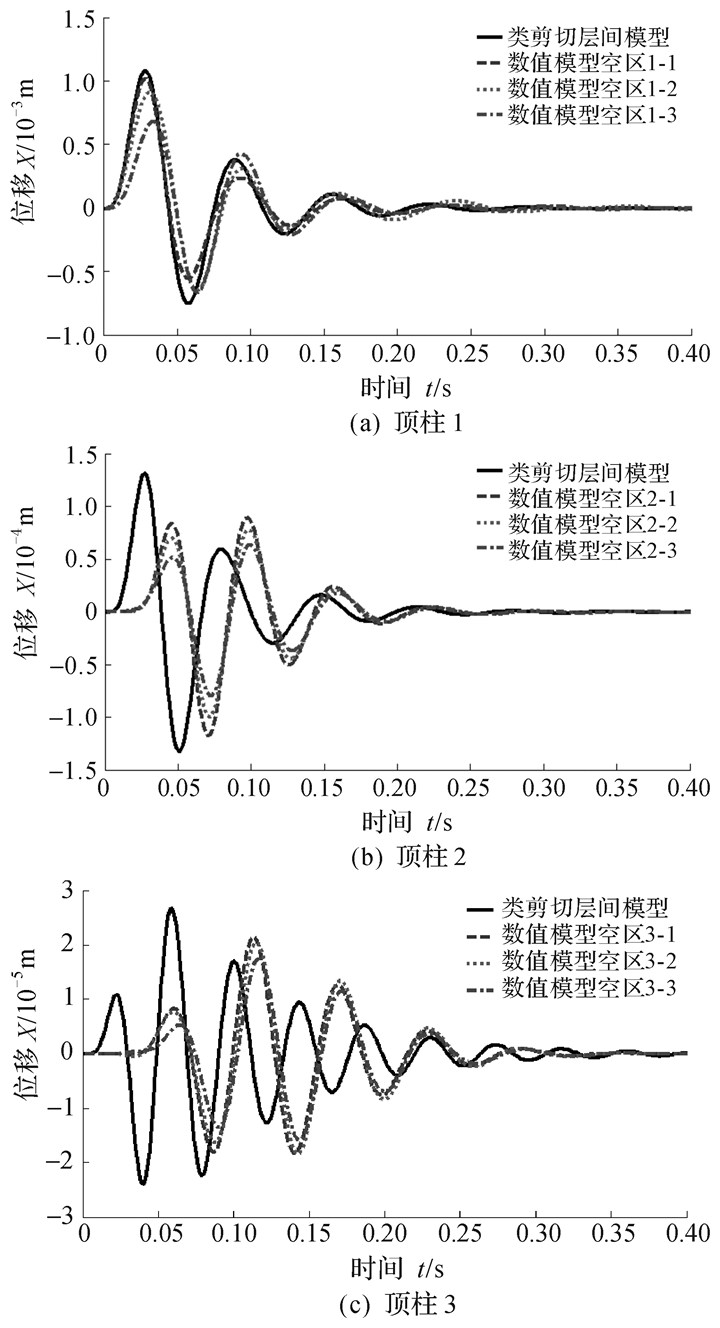
由采空区群内各中段顶柱位移响应时程曲线(图 10)可知,类层间剪切模型法与数值分析法所得结果处于同一量级且变化趋势相近。在爆破荷载激励下,由于时空效应,距离爆破荷载的顶柱越远,动力响应强度越弱(位移峰值表征),振动开始时间越晚(起振时间表征)。顶柱1距离爆破位置较近,在爆破瞬间作出响应,其位移峰值最大;顶柱2和顶柱3分别在相隔一段时间后,开始出现滞后响应,位移响应的峰值依次减少1个数量级。在采空区群岩体内部阻尼及外部围岩剪切应力的双重作用下,各中段顶柱振幅逐渐衰减至零,采空区群系统最终恢复平衡。
|
| 图 10 各中段顶柱位移响应时程曲线 Fig.10 Time history curve of displacement response of the pillar of each layer |
2) 速度结果分析。
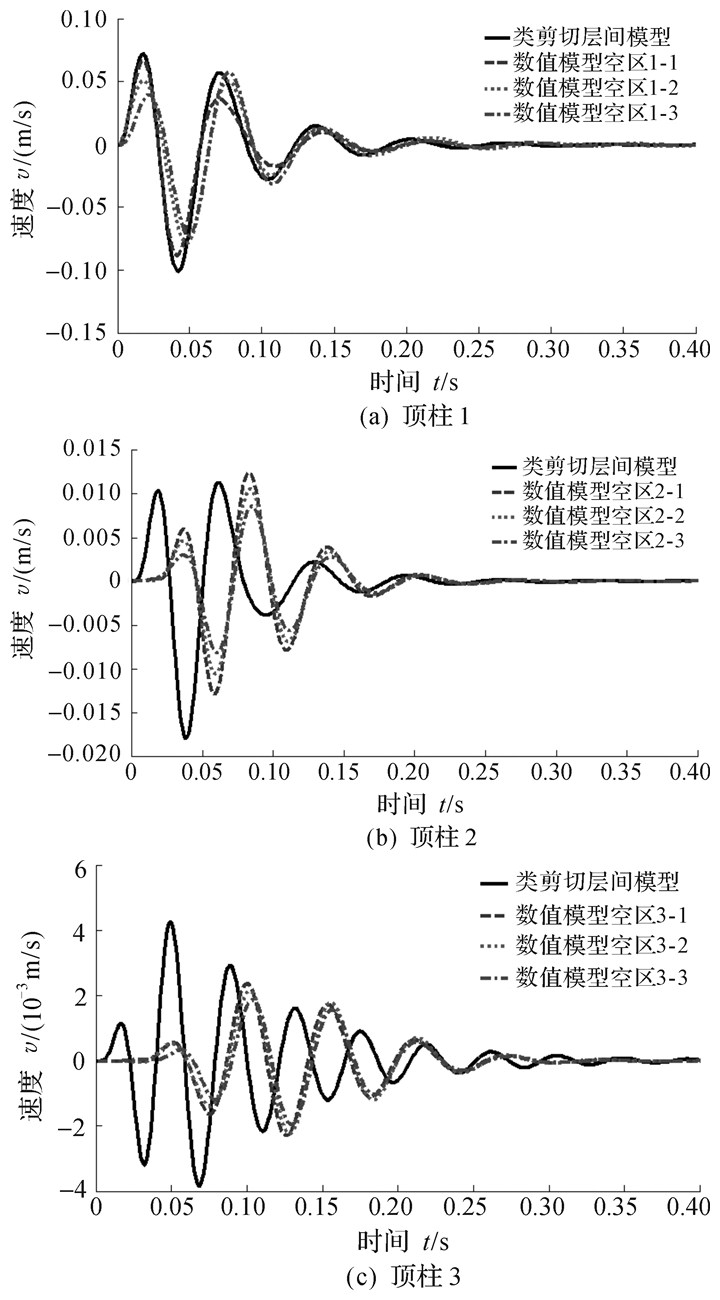
由图 11可知,2种方法得到各顶柱的速度响应时程曲线变化趋势一致、彼此振动幅值相近,各顶柱的速度曲线与位移曲线呈相似的衰减规律。
|
| 图 11 各中段顶柱速度响应时程曲线 Fig.11 Time history curve of velocity response of the pillar of each layer |
由图 10和图 11知,类层间剪切模型法和数值分析法相比,顶柱2和顶柱3动力响应超前。究其原因:1) 采空区群赋存环境复杂,各中段顶柱层面相距50 m,单元采空区跨度为30 m,存在响应步差。2) 在数值计算过程中,考虑了爆炸应力波的传播时间效应;为了简化计算过程,类剪切模型法忽略了爆炸应力波的传播时间效应。
为了弥补类层间剪切模型法的不足,需估算各中段顶柱与爆破荷载位置的距离,计算岩体中爆炸应力波的剪切波速[25],如式12所示:
| $ {C_s} = \sqrt {\frac{G}{\rho }} $ | (12) |
由此可以通过计算类层间剪切模型法中各中段顶柱响应的超前时间,对位移及速度响应时程曲线进行修正。
4 结论1) 提出采空区群动力响应的类层间剪切模型法,研究采空区群内岩体介质的位移和速度响应规律。该方法将上覆岩层等效为由“虚拟间柱群”和集中质量块组成的系统,将周边围岩作用等效为剪切力作用,具有可行性。
2) 爆破激励下,由于时空效应,距离爆破荷载的顶柱越远,其动力响应强度越弱,振动开始时间越晚。采空区群岩体在其内部阻尼及外部围岩剪切力的双重作用下,作振幅衰减振动,且最大变形峰值发生在体系达到稳定状态之前。
3) 参照地表构筑物的动力响应分析方法,考虑单元空区的赋存深度和构成形状特征,引入剪切力影响因子δ,拟定其取值范围,修正了围岩的剪切力作用。采空区群赋存环境不同,空区间顶(间)柱岩体及周边围岩力学性质也存在差异,导致剪切力影响因子δ的取值具有较大的经验性。因此,δ的取值与校验方法有待深入研究。
4) 与数值计算法相比,类层间剪切模型法在研究采空区群内质点动力响应时,所得的位移、速度时程曲线趋势一致、幅值相近,但运算时间更短、运算效率更高。该方法为研究采空区群动力响应特性提供了一种新思路。
| [1] |
付华, 陈从新, 夏开宗, 等.
金属矿山地下开采引起岩体变形规律浅析[J]. 岩石力学与工程学报, 2015, 34(9): 1860–1868.
FU Hua, CHEN Cong-xin, XIA Kai-zong, et al. Analysis of rock deformation caused by underground mining of metal mines[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(9): 1860–1868. |
| [2] | KONICEK P, SOUCEK K, STAS L, et al. Long-hole distress blasting for rock burst control during deep underground coal mining[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 61: 141–153. |
| [3] | WANG Fang-tian, ZHANG Cun, ZHANG Xiao-gang, et al. Overlying strata movement rules and safety mining technology for the shallow depth seam proximity beneath a room mining goaf[J]. International Journal of Mining Science and Technology, 2015, 25(1): 139–143. DOI:10.1016/j.ijmst.2014.12.007 |
| [4] | MA Hai-tao, WANG Ji-nan, WANG Yun-hai. Study on mechanics and domino effect of large-scale goaf cave-in[J]. Safety Science, 2012, 50(4): 689–694. DOI:10.1016/j.ssci.2011.08.050 |
| [5] | ZHOU Jian, LI Xi-bing, MITRI Hani S, et al. Identification of large-scale goaf instability in underground mine using particle swarm optimization and support vector machine[J]. International Journal of Mining Science and Technology, 2013, 23(5): 701–707. DOI:10.1016/j.ijmst.2013.08.014 |
| [6] | YASITLI N E, UNVER B. 3D numerical modeling of longwall mining with top-coal caving[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(2): 219–235. |
| [7] | XIAO Chao, ZHENG Huai-chang, HOU Xiao-lin, et al. A stability study of goaf based on mechanical properties degradation of rock caused by rheological and disturbing loads[J]. International Journal of Mining Science and Technology, 2015, 25(5): 741–747. DOI:10.1016/j.ijmst.2015.07.007 |
| [8] | YAN Guo-chao, MA Zhong-hui, HU Yao-qing. Study on numerical simulation of the arrangement about mining roadway with short distance[J]. Procedia Engineering, 2011, 26: 301–310. DOI:10.1016/j.proeng.2011.11.2172 |
| [9] | FEI Hong-lu, YANG Wei-feng, ZHANG Guo-hui, et al. Surrounding rock stability of mined out area under blast loading in mental mine pillar robbing[J]. Explosion and Shock Waves, 2013, 33(4): 344–350. |
| [10] |
鲁文妍, 钟登华, 佟大威, 等.
基于三维地质模型的地下洞室群地震动力响应分析[J]. 岩土力学, 2012, 33(3): 919–924.
LU Wen-yan, ZHONG Deng-hua, TONG Da-wei, et al. Dynamic response analysis of underground cavern group based on 3D geologic model[J]. Rock and Soil Mechanics, 2012, 33(3): 919–924. |
| [11] |
李新平, 陈俊桦, 李友华, 等.
溪洛渡电站地下洞室群爆破地震效应的研究[J]. 岩石力学与工程学报, 2010, 29(3): 493–501.
LI Xin-ping, CHEN Jun-hua, LI You-hua, et al. Study of blasting seismic effects of underground chamber group in Xiluodu hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 493–501. |
| [12] |
宗琦, 汪海波, 周胜兵.
爆破地震效应的监测和控制技术研究[J]. 岩石力学与工程学报, 2008, 27(5): 938–945.
ZONG Qi, WANG Hai-bo, ZHOU Sheng-bing. Research on monitoring and controlling techniques considering effects of seismic shock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(5): 938–945. |
| [13] | NICK Yugo, WOO Shin. Analysis of blasting damage in adjacent mining excavations[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2015, 7(3): 282–290. DOI:10.1016/j.jrmge.2014.12.005 |
| [14] | DAI Feng, LI Biao, XU Nu-wen. Deformation forecasting and stability analysis of large-scale underground powerhouse caverns from microseismic monitoring[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 86: 269–281. |
| [15] |
曹征良, 李爱群.
多高层建筑结构地震反应非线性分析统一算式[J]. 深圳大学学报(理工版), 2003, 20(4): 108–115.
CAO Zheng-liang, LI Ai-qun. Analysis of nonlinear unified formula of high-rise building structure seismic response[J]. Journal of Shengzhen University (Science & Engineering), 2003, 20(4): 108–115. |
| [16] |
严东晋, 孙传怀, 张海明.
框架结构水平振动简化分析模型的准确性[J]. 振动与冲击, 2011, 30(12): 191–194.
YAN Dong-jin, SUN Chuan-huai, ZHANG Hai-ming. Accuracy of simplified models for frame structure horizontal vibration analysis[J]. Journal of Vibration and Shock, 2011, 30(12): 191–194. DOI:10.3969/j.issn.1000-3835.2011.12.037 |
| [17] |
韩博, 熊琛, 许镇, 等.
城市区域建筑物震害预测剪切层模型及其参数确定方法[J]. 工程力学, 2014, 31(Supplement): 73–78.
HAN Bo, XIONG Chen, XU Zhen, et al. A multi-story concentrated-mass shear model for urban regional seismic damage prediction and associated parameter determination[J]. Engineering Mechanics, 2014, 31(Supplement): 73–78. |
| [18] | LU Xin-zheng, HAN Bo, MUNEO Hori, et al. A coarse-grained parallel approach for seismic damage simulations of urban areas based on refined models and GPU/CPU cooperative computing[J]. Advances in Engineering Software, 2014, 70: 90–103. DOI:10.1016/j.advengsoft.2014.01.010 |
| [19] |
唐治, 潘一山, 王凯兴.
冲击地压巷道围岩支护作用动力学分析[J]. 岩土工程学报, 2015, 37(8): 1532–1538.
TANG Zhi, PAN Yi-shan, WANG Kai-xing. Dynamic analysis of support for surrounding rock of rockburst roadway[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1532–1538. DOI:10.11779/CJGE201508025 |
| [20] |
姜立春, 曾俊佳, 王国伟.
水平采空区群离散多自由度动力响应模型[J]. 岩石力学与工程学报, 2016, 35(1): 59–67.
JIANG Li-chun, ZENG Jun-jia, WANG Guo-wei. A discrete dynamic response model with multiple degrees of freedom for horizontal goaf group[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1): 59–67. |
| [21] | CHOPRA A K. Dynamics of structures[M]. 4th ed. New Jersey: Prentice-Hall, 2012: 342-349. |
| [22] | LU Wen-bo, YANG Jian-hua, CHEN Ming, et al. An equivalent method for blasting vibration simulation[J]. Simulation Modelling Practice and Theory, 2011, 19(9): 2050–2062. DOI:10.1016/j.simpat.2011.05.012 |
| [23] |
张玉成, 杨光华, 刘鹏, 等.
爆破荷载在数值计算中的等效施加方法研究[J]. 地下空间与工程学报, 2012, 8(1): 56–64.
ZHANG Yu-cheng, YANG Guang-hua, LIU Peng, et al. An equivalent approach for acting blasting load in dynamic numerical simulation of blasting vibration[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(1): 56–64. |
| [24] |
张雨霆, 肖明, 张志国.
大型地下洞室群地震响应分析的动力子模型法[J]. 岩石力学与工程学报, 2011, 30(supplement 2): 3392–3400.
ZHANG Yu-ting, XIAO Ming, ZHANG Zhi-guo. Dynamic sub-model method of earthquake response analysis of large-scale underground caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(supplement 2): 3392–3400. |
| [25] |
宋波, 李悦, 单宏兰, 等.
爆破作用对地下金属矿山围岩稳定性的影响[J]. 岩石力学与工程学报, 2007, 26(supplement 1): 3461–3467.
SONG Bo, LI Yue, SHAN Hong-lan, et al. Study on effects of blasting on stability of surrounding rockmass in underground metallic mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(supplement 1): 3461–3467. |



