2. 北京交通大学 机械与电子控制工程学院, 北京 100044
2. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China
负载模拟系统,用于地面实验室条件下模拟飞行器控制舵面在飞行时所受空气铰链力矩载荷谱[1]。其中,电动负载模拟系统 (electric load simulation system, ELSS) 因响应快、控制灵活、加载精度高等特点,在高精度、中小力矩模拟中得到了广泛应用[2]。
电动负载模拟系统的加载是通过加载电机与舵机的相互扭转来实现的,是典型的被动式扭矩伺服系统。舵机的转动会对加载力矩产生显著影响,由此而产生的力矩为多余力矩。ELSS的控制系统存在的一个亟需解决的问题就是系统多余力矩的抑制。目前,国内外学者对于多余力矩的抑制进行了很多研究,其中较为有效的是利用结构不变性原理在系统中引入前馈控制器[3-7]。但是这种补偿完全依赖于干扰环节精确的数学模型,对于一些工况改变的系统无法实现有效的抑制[8]。此外,还有诸如位置同步法、神经网络控制、模糊控制等许多方法[9-15],但是这些方法都具有一定的局限性,难以在实际工程中得到有效应用。
本文基于前馈控制原理与自适应控制原理,设计了一种自适应抑制位置干扰力矩的控制方法。该方法可以在实际系统参数改变或部分未知的条件下,系统自适应地调节控制器参数,抑制多余力矩的干扰,进而提高系统力矩的输出精度。运用计算机仿真与试验结合的方法,验证了该自适应控制方法的有效性。
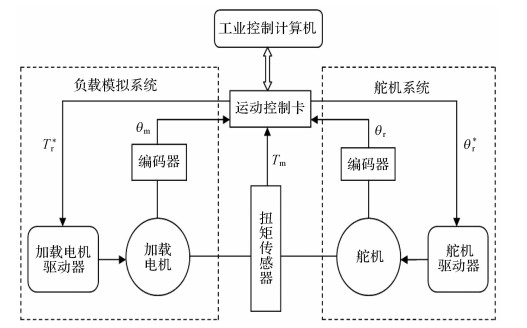
1 ELSS工作原理及其数学模型在对舵机加载的过程中,扭矩传感器采集实际加载到承载舵机轴上的力矩值,编码器采集加载电机转角以及承载舵机偏转角。控制计算机根据被采集的实际力矩值和舵机转角计算出加载电机给定力矩值并输出至电机执行机构。图 1所示为电动负载模拟系统工作原理图。
|
| 图 1 电动负载模拟系统工作原理图 Fig.1 Working principle diagram of ELSS |
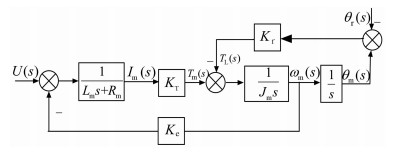
通过分析加载伺服电机的工作原理及多余力矩产生的机理,得到负载模拟系统的数学模型,如图 2所示。其中U(s) 为控制器输出电压控制量,Lm,Rm分别为加载电机工作电感和电阻,Im为电枢电流,KT为电机扭转系数,Tm为加载电机电磁转矩,TL为加载系统实际输出转矩,Jm为折算到加载电机轴上的等效转动惯量,ωm为加载电机转速,θm为加载电机转角,θr为舵机转角,Kf为扭矩传感器扭转刚度,Ke为电机反电动势常数。
|
| 图 2 电动负载模拟系统数学模型 Fig.2 Mathematical model of ELSS |
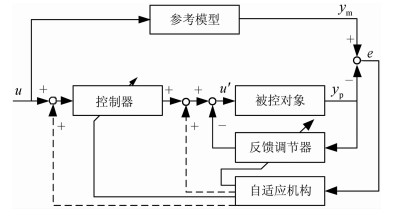
自适应控制是一种适应性控制策略,自20世纪50年代末由Mit教授提出以来,出现了多种不同的自适应控制方案[16-18]。本次研究基于模型参考自适应系统 (model reference adaptive system, MRAS),结合前馈控制补偿原理设计了一种新的控制方法。图 3为模型参考自适应控制系统基本结构。控制目标的实际输出yp与参考模型的输出ym的偏差e=0。当控制器与被控对象发生变化,系统实际输出与目标输出偏离,即偏差e≠0。偏差信号将被输入到自适应机构,自适应机构按照预先制定的适应律产生调节方案,改变控制器的参数,使得主回路与参考模型趋于一致,实际输出yp逼近参考输出ym。
|
| 图 3 模型参考自适应控制系统基本结构 Fig.3 The basic structure of MRAS |
针对ELSS被控对象的特点,参考模型的状态空间数学模型为:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_{\rm{m}}} = {\mathit{\boldsymbol{A}}_{\rm{m}}}{\mathit{\boldsymbol{x}}_{\rm{m}}} + {\mathit{\boldsymbol{B}}_{\rm{m}}}{\mathit{\boldsymbol{u}}_{\rm{r}}}\\ {y_{\rm{m}}} = {\mathit{\boldsymbol{C}}_{\rm{m}}}{\mathit{\boldsymbol{x}}_{\rm{m}}} \end{array} \right. $ | (1) |
实际控制系统的状态空间描述为:
| $ \left\{ \begin{array}{l} \dot x = \boldsymbol{Ax} + \boldsymbol{Bu}\\ {y_{\rm{p}}} = \boldsymbol{Cx} \end{array} \right. $ | (2) |
式中:Am,Bm分别为n×n和n×m理想常数矩阵,xm为n维模型状态向量,ur为m维输入向量,Cm为1×n常数输出矩阵,A, B分别为与Am,Bm同行列的常数矩阵,x为n维状态向量,u为m维控制变量,C为与Cm对应的同行列常数矩阵。
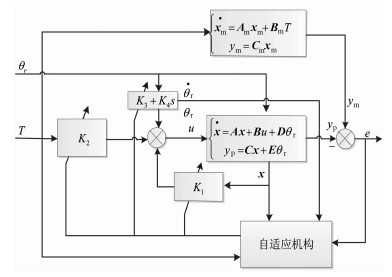
图 4所示为本文设计的自适应控制系统示意图。在该系统中,由于加载电机处存在舵机的位置干扰,故将舵机运动扰动项作为系统被控对象的一部分后,再设计控制器。并且针对承载电机位置扰动设计单独的控制环节。同时在常规模型参考自适应控制系统的基础上,引入前馈控制器。由于引入了位置运动的角速度这一参数,为了有相应的可调控制器去适应这种变化,在系统的前馈控制器中加入微分项,引入新的控制器参数。然后自适应机构根据电机轴角速度去调节该微分项控制器的系数,从而产生一个补偿量来削弱多余力矩。由于多余力矩与轴转动角速度、角加速度等有关,且系统在中低频段由角速度引起的多余力矩占大多数,所以引入的微分项将针对角速度进行补偿。最终主控制器设计为比例控制器,前馈补偿控制器为比例微分控制器。
|
| 图 4 自适应控制系统示意图 Fig.4 Schematic diagram of adaptive control system |
此时系统的控制量为:
| $ u = {K_1}\boldsymbol{x} + {K_2}\boldsymbol{T} + {K_3}{\theta _r} + {K_4}{{\dot \theta }_r} $ | (3) |
系统输出误差为:
| $ e = {y_{\rm{m}}}-{y_{\rm{p}}} $ | (4) |
对系统误差一求阶导,得:
| $ \dot e = {\mathit{\boldsymbol{C}}_\rm{m}}{{\mathit{\boldsymbol{\dot x}}}_\rm{m}}-\mathit{\boldsymbol{C\dot x}}-\mathit{\boldsymbol{E}}{{\dot \theta }_\rm{r}} $ | (5) |
令矩阵可逆,将状态空间方程 (1)、(2) 及控制量方程 (3) 代入式 (5),得系统误差微分方程为:
| $ \begin{array}{l} \dot e = {\mathit{\boldsymbol{C}}_{\rm{m}}}{\mathit{\boldsymbol{A}}_{\rm{m}}}{\mathit{\boldsymbol{C}}^{-1}}_{\rm{m}}e + ({\mathit{\boldsymbol{C}}_{\rm{m}}}{\mathit{\boldsymbol{A}}_{\rm{m}}}{\mathit{\boldsymbol{C}}^{-1}}_{\rm{m}}\mathit{\boldsymbol{C}}-\mathit{\boldsymbol{CB}}{K_1} - \mathit{\boldsymbol{CA}})\mathit{\boldsymbol{x}} + \\ ({\mathit{\boldsymbol{C}}_{\rm{m}}}{\mathit{\boldsymbol{B}}_{\rm{m}}} - \mathit{\boldsymbol{CB}}{K_2})\mathit{\boldsymbol{T}} + ({\mathit{\boldsymbol{C}}_{\rm{m}}}{\mathit{\boldsymbol{A}}_{\rm{m}}}{\mathit{\boldsymbol{C}}^{ - 1}}_{\rm{m}}\mathit{\boldsymbol{E}} - \mathit{\boldsymbol{CB}}{K_3} - \\ \mathit{\boldsymbol{CD}}){\theta _{\rm{r}}} + ( - \mathit{\boldsymbol{E}} - \mathit{\boldsymbol{CB}}{K_4}){{\dot \theta }_{\rm{r}}} \end{array} $ | (6) |
式中:D,E为维数适当的常数矩阵,T为输出力矩,θr为舵机转角。
令CmAmCm-1=Φ, CmAmCm-1C-CBK1-CA=Φ1, CmBm-CBK2=Φ2, (CmAmCm-1E-CBK3-CD)θr=Φ3, -E-CBK4=Φ4,则上式变成:
| $ \dot e = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}e + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}x + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2}\mathit{\boldsymbol{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3}{\theta _r} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_4}{{\dot \theta }_{\rm{r}}} $ | (7) |
从式 (7) 可以看出,通过增加对角速度的控制,可构造比较简单的Lyapunov函数,就能使得广义误差e渐进收敛,并由此得到控制器参数K1,K2,K3及K4的自适应律。
定义系统Lyapunov函数为:
| $ V = \frac{1}{2}(P{e^2} + {(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1^{\rm{T}})^2} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^2}_2 + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^2}_3 + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^2}_4) $ | (8) |
其中P是Lyapunov方程PAm+AmP=-Q的解,Q为正定矩阵,一般取单位阵。P>0,则V>0,Lyapunov函数正定。
Lyapunov函数V的一阶导数为:
| $ \dot V = Pe\dot e + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}_1^{\rm{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_2} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_3} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_4}{{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_4} $ | (9) |
将系统误差微分方程 (6) 代入式 (9),得:
| $ \begin{array}{l} \dot V = P\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{e^2} + [(Pe\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}_1^{\rm{T}}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1} + (Pe\mathit{\boldsymbol{T}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_2}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2} + \\ (Pe{\theta _{\rm{r}}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_3} + (Pe{{\dot \theta }_{\rm{r}}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_4}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_4}] \end{array} $ | (10) |
令式 (10) 中最后一项等于0,即:
| $ \begin{array}{l} (Pe\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}_1^{\rm{T}}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1} + (Pe\mathit{\boldsymbol{T}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_2}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2} + \\ (Pe{\theta _{\rm{r}}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_3}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3} + (Pe{{\dot \theta }_{\rm{r}}} + {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_4}){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_4} = 0 \end{array} $ | (11) |
由于系统参考模型稳定,则理想常数矩阵Am特征值小于0,由此可知Φ < 0,故
Lyapunov函数正定,其一阶导数
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_1} =-Pe{\mathit{\boldsymbol{x}}^{\rm{T}}} $ | (12) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_2} =-Pe\mathit{\boldsymbol{T}} $ | (13) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_3} =-Pe{\theta _{\rm{r}}} $ | (14) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }}}_4} =-Pe{{\dot \theta }_{\rm{r}}} $ | (15) |
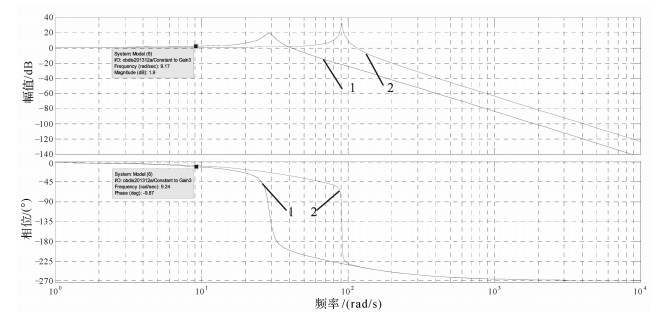
利用建立的系统数学模型,可得系统频率特性。如图 5所示为系统无扰时的开环频率特性。图中显示的2条曲线分别是系统在没有扰动条件下不同传递刚度时系统的开环频率特性曲线。曲线1是传递刚度为6.487×104 N·m/rad时的开环频率特性,曲线2为传递刚度增大10倍后的系统开环频率特性。从图中可知,根据双十特性指标,系统频宽达到20 Hz,相位裕度接近60°,系统稳定。同时从图中可知系统的无扰加载频宽受传递刚度影响较大,刚度增大使得系统频宽相应增大,且系统的谐振峰值也会增大。这将对系统的稳定性产生影响。
|
| 图 5 系统无扰时的开环频率特性Bode图 Fig.5 Open loop frequency Bode diagram of system without disturbance |
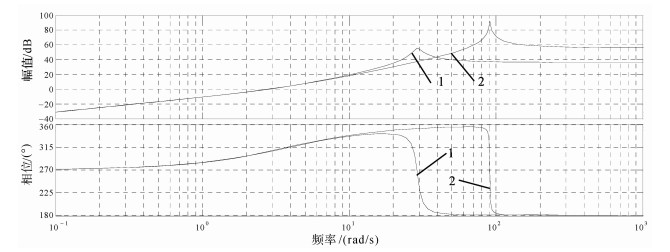
存在位置扰动时的频率响应曲线如图 6所示。系统位置扰动在不同频段呈现了不同特性。位置干扰在低频段时表现为1阶微分特性,此时主要影响因素为角速度;在中频段时表现为2阶微分特性,此时主要影响因素为角加速度;高频段时表现为比例环节特性,此时主要影响因素为位置弹性力。同时传递刚度对频率特性的影响与图 5相似。
|
| 图 6 存在位置干扰力矩时的频率特性Bode图 Fig.6 Frequency Bode diagram with position disturbance |
为了验证上述自适应控制系统的有效性,利用Simulink搭建了系统结构框图,并针对该系统分别在舵机运动频率为1,5,10 Hz正弦信号条件下进行计算机仿真。系统相关参数设置如下:比例因子P=1 000;输入、输出初始值均设为0;状态向量xm初始值设为0;可调增益K1,K2,K3及K4初始值均为0;转动惯量为0.01 kg·m2;输入力矩指令幅值6 N·m;舵机运动位置幅值取为π/6 rad;仿真步长为0.001。
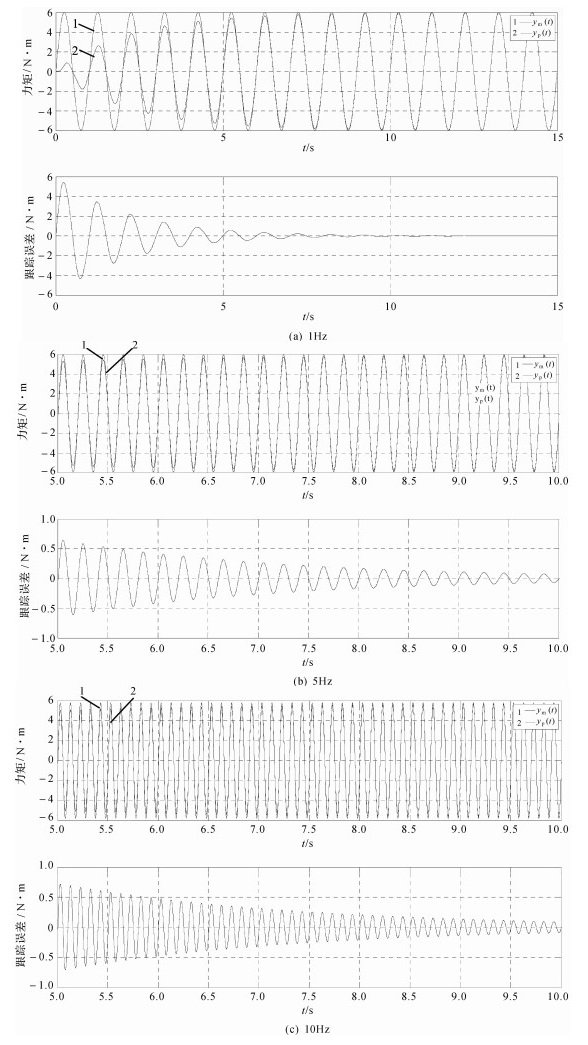
图 7表示自适应控制系统输出力矩及跟踪误差曲线。曲线1为参考模型的理想输出,曲线2为系统实际输出。由图 7(a)可知,当舵机运动频率为1 Hz,调节刚开始时,由于初始值设置均为0,所以初始跟踪误差很大。随着自适应律的不断采样调整,跟踪误差不断减小,最终趋于0。此时系统调节至误差为0所用时间约为10 s。
|
| 图 7 自适应控制系统力矩输出及跟踪误差曲线 Fig.7 The torque output and tracking error curve of adaptive control system |
舵机运动频率为5 Hz与10 Hz时,系统的跟踪误差变化规律与1 Hz时相同:误差慢慢减小,最终趋于0,但是5 Hz时系统的调节时间约为11 s,10 Hz时系统的调节时间约为12 s,如图 7(b)和图 7(c)所示。通过对比可知,随着舵机运动频率的增加,系统调节时间越长。
自适应系统的仿真结果,证明了自适应控制系统抑制加载误差的有效性,能够在实际系统参数未知或改变时通过参考模型的输出变化将系统稳定在理想输出状态,有较强的自适应性和鲁棒性。
4 试验验证试验采用的电机为科尔摩根公司生产的交流永磁同步伺服电机,其型号为B-206-D,配合S700系列的全数字式交流伺服驱动器使用。扭矩传感器选用北京三晶公司生产的JN338-5AG高转速扭矩传感器。电机的尾端装有2500线制标准光学编码器,检测转子的位置并进行反馈,可以作为电机的转速测量元件。根据系统的抗干扰需求和传感器信号的采集匹配,选用的运动控制卡包括PCI-1711U和PCI-1784U,以此实现数据的实时交换。该系统的控制软件在.NET Framework平台上,采用Visual Studio 2010集成开发环境,选用C#语言进行控制软件界面程序编写。在软件界面程序编写过程中为实现人机交互友好、开发简单,软件使用第三方工业仪表控件Locomp ActiveX。三相220 V交流供电,使用时需要设置变压器,将380 V交流电转换为220 V交流电。图 8与9分别为试验台实物图和控制柜实物图。

|
| 1—承载电机; 2—扭矩传感器; 3—防护罩; 4—加载电机; 5—试验台架; 6—绝缘联轴器 图 8 电动负载模拟系统试验台实物图 Fig.8 The practicality picture of ELSS plant |

|
| 图 9 电动负载模拟系统控制柜实物图 Fig.9 The praticality picture of ELSS control box |
在不同舵机运动频率及运动幅值情况下进行试验,验证系统自适应抑制多余力矩的能力。为了达到该目的,在试验过程中让加载电机加载一个恒定力矩,承载电机以不同的运动幅值和运动频率进行运动,观察不同运动情况下系统的跟踪精度和加载能力。
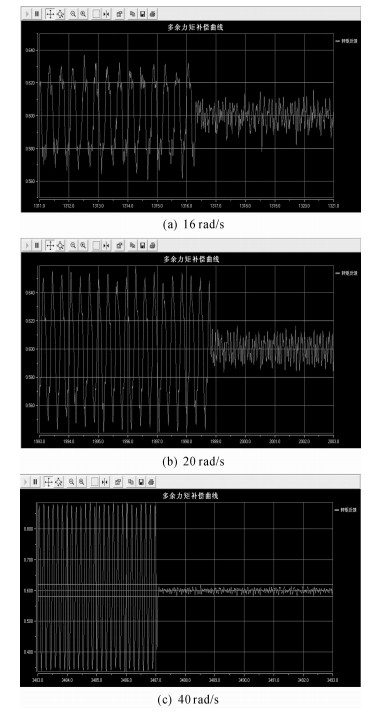
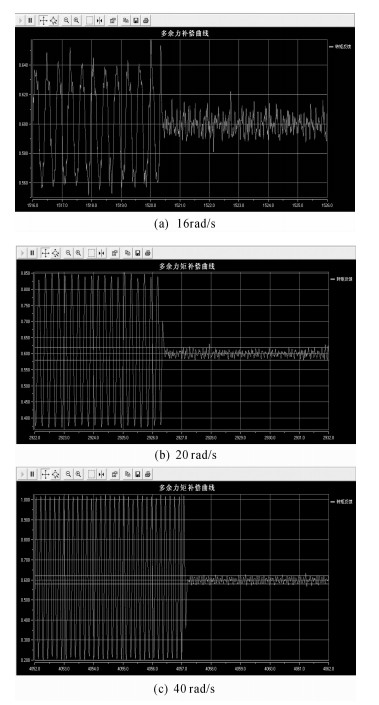
如图 10所示是加载电机在恒定加载力矩为3 N·m,承载舵机运动幅值为2π rad条件下,舵机运动频率分别为16,20,40 rad/s时多余力矩在自适应补偿前后的效果曲线。从图中可以看出补偿效果明显。其中在运动频率为16 rad/s下抑制多余力矩百分比约为60%,在20 rad/s时抑制多余力矩百分比约为71%,在40 rad/s时抑制多余力矩百分比为90%以上。
|
| 图 10 恒定加载力矩为3 N·m,运动幅值为2π rad条件下自适应补偿前后的多余力矩曲线 Fig.10 Surplus torque curve before and after adaptive compensation with constant loading turque of 3 N·m and motion amplitude phase of 2π rad |
如图 11所示是加载电机在恒定加载力矩为3 N·m,承载舵机运动幅值为4π rad条件下,舵机运动频率分别为16,20,40 rad/s时多余力矩在自适应补偿前后的效果曲线。从图中可以看出补偿效果明显。其中运动频率为16 rad/s时抑制多余力百分比约为76%,在20 rad/s时抑制多余力百分比为约90%,在40 rad/s时抑制多余力百分比为95%以上。
|
| 图 11 恒定加载力矩为3 N·m,动幅值为4π rad条件下自适应补偿前后的多余力矩曲线 Fig.11 Surplus torque curve before and after adaptive compensation with constant loading turque of 3 N·m and motion amplitude phase of 4π rad |
通过对比这2组曲线发现,随着运动幅值的增加,抑制效果会有所提升。这是因为在系统模型参考自适应的自适应律中引入了角度和角度微分项,试验过程中角度微分项通过加载电机编码器测得值取微分后获得。在承载电机作大幅值运动时,运行更加平稳,产生的角速度波动较小,对系统运行稳定性更有利,通过自适应律调节效果更加明显。
5 结论本文分析了电动负载模拟系统的结构组成及工作原理,给出了ELSS的数学模型,并设计了一种能够跟踪力矩输入且有效抑制多余力矩的自适应控制系统,得出了该系统的自适应律。通过计算机仿真,证明了自适应控制系统抑制加载误差的有效性,并且舵机运动频率越高,系统调节误差所需时间越长。最后通过试验,佐证了该控制方法的实用性,并且通过2组试验的对比可知,随着运动幅值的增加,该控制方法对多余力矩抑制效果有所提升。
| [1] |
牛国臣, 王巍, 宗光华.
基于迭代学习的电动负载模拟器复合控制[J]. 控制理论与应用, 2015, 31(12): 1470–1477.
NIU Guo-chen, WANG Wei, ZONG Guang-hua, et al. Composite control for electric load simulator based on iterative learning[J]. Control Theory & Applications, 2015, 31(12): 1470–1477. |
| [2] |
王鑫, 冯冬竹.
引入弹簧杆的电动负载模拟器实验研究[J]. 电机与控制学报, 2012, 16(9): 91–94.
WANG Xin, FENG Dong-zhu. Experimental research on DC load simulator test bed with elastic rod[J]. Journal of Electric Machines and Control, 2012, 16(9): 91–94. |
| [3] | KABOLI S, ZOLGHADRI M R, HAGHBIN S, et al. Effects of the flux value on the torque ripple of the direct torque controlled induction motor drives determination[J]. A Power Electronics and Drive Systems, 2003(1): 439–444. |
| [4] |
符文星, 孙力, 于云峰, 等.
电动负载模拟器控制系统设计[J]. 西北工业大学学报, 2008, 26(5): 621–622.
FU Wen-xing, SUN Li, YU Yun-feng, et al. Improving design of control system for DC motor-driven torque control simulator[J]. Journal of Northwestern Polytechnical University, 2008, 26(5): 621–622. |
| [5] | QUANG Truong-dinh, KYOUNG Kwan-ahn, JONG Il Yoon. Introduction to quantitative feedback theory for robust force control of load simulator[C]//Proceedings of the Second International Conference on Communications and Electronics. Hoian, Vietnam, Jun. 4-6, 2008: 42-47. |
| [6] | WANG X, FENG D Z. A study on dynamics of electric load simulator using spring beam and feedforward control technique[C]. Chinese Control and Decision Conference. Guilin: IEEE Computer Society, 2009:301-306. |
| [7] |
李成功, 靳红涛, 焦宗夏.
电动负载模拟器多余力矩产生机理及抑制[J]. 北京航空航天大学学报, 2006, 32(2): 204–208.
LI Cheng-gong, JIN Hong-tao, JIAO Zong-xia. Mechanism and suppression of extraneous torque of motor driver load simulator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(2): 204–208. |
| [8] |
郭行, 陈康, 孙力, 等.
一种引入位置比例控制提高电动负载模拟器性能的控制系统设计方法[J]. 西北工业大学学报, 2014, 32(2): 235–239.
GUO Xing, CHEN Kang, SUN Li, et al. An effective method for designing control system of motor-driven torque control simulator by introducing position proportional control[J]. Journal of Northwestern Polytechnical University, 2014, 32(2): 235–239. |
| [9] |
汪成文, 焦宗夏, 罗才瑾.
基于改进的速度同步控制的电液负载模拟器[J]. 航空学报, 2012, 33(9): 1717–1725.
WANG Cheng-wen, JIAO Zong-xia, LUO Cai-jin. An improved velocity synchronization control on electro-hydraulic load simulator[J]. Acta Aeronautica ET Astronautica Sinica, 2012, 33(9): 1717–1725. |
| [10] |
王刚, 李建府, 朱荣刚.
CMAC改进算法在电动负载模拟器的应用[J]. 电光与控制, 2011, 18(4): 72–76.
WANG Gang, LI Jian-fu, ZHU Rong-gang. Application of an improved arithmetic based on CMAC in electrical load simulator[J]. Electronics Optics & Control, 2011, 18(4): 72–76. |
| [11] |
刘晓琳, 王春婷, 袁昆.
电液负载模拟器的多余力抑制方法研究[J]. 计算机仿真, 2015, 32(7): 23–27.
LIU Xiao-lin, WANG Chun-ting, YUAN Kun. Research of strategy to restrain surplus force of electro-hydraulic loading simulator system[J]. Computer Simulation, 2015, 32(7): 23–27. |
| [12] |
杨钢, 刘迎雨, 杜经民, 等.
基于模糊PID控制器的电液负载模拟系统[J]. 华中科技大学学报 (自然科学版), 2012, 40(4): 59–62.
YANG Gang, LIU Ying-yu, DU Jing-min, et al. Electro-hydraulic load systems based on fuzzy PID controller[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(4): 59–62. |
| [13] | HAN S S, JIAO Z X, YAO J Y, et al. Compound velocity synchronizing control strategy for electro-hydraulic load simulator and its engineering applications[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(5): 1–13. |
| [14] | SHANG Y, JIAO Z, WANG X. Study on friction torque loading with an electro-hydraulic load simulator[J]. Chinese Journal of Aeronautics, 2009, 22(6): 691–699. DOI:10.1016/S1000-9361(08)60160-0 |
| [15] | KARIM Khayati. Force control loop affected by bounded uncertainties and unbounded inputs for pneumatic actuator systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(1): 1–8. |
| [16] |
刘彦呈, 刘厶源, 王川, 等.
UUV推进电机在线参数辨识自适应控制方法研究[J]. 电机与控制学报, 2016, 20(4): 34–40.
LIU Yan-cheng, LIU Si-yuan, WANG Chuan, et al. Research on online parameter identification and adaptive control of UUV propulsion motor[J]. Electric Machines and Control, 2016, 20(4): 34–40. |
| [17] |
杨雪松, 李长春, 延皓, 等.
基于矢量匹配的扰动力矩消除方法[J]. 兵工学报, 2016, 37(2): 348–356.
YANG Xue-song, LI Chang-chun, YAN Hao, et al. Vector matching-based disturbance torque elimination method[J]. Acta Armamentarii, 2016, 37(2): 348–356. |
| [18] |
董雪仰, 戈新生.
航天器太阳帆板展开过程最优控制的自适应Gauss伪谱法[J]. 应用数学与力学, 2016, 37(6): 655–664.
DONG Xue-yang, GE Xin-sheng. The adaptive Gauss pseudospectral method for the optimal control of spacecraft solar array deployment[J]. Applied Mathematics and Mechanics, 2016, 37(6): 655–664. |




