近年来,随着风电装机总容量的提高,风电功率的随机性及不稳定性使得风电大规模并网对电力系统的安全稳定运行、电能质量、调度计划等提出了新的挑战[1-2]。实践证明,精确的风电功率预测有利于电力系统调度部门制定风电并网计划,降低电网旋转备用容量,提高电网运行的安全性、可靠性、经济性及其市场竞争力[2]。
在对风电功率数据进行预测建模时,大部分研究是直接将已去噪的风电功率数据作为模型的输入数据,这会使数据样本之间所存在的相似性被忽略,从而导致预测结果不稳定。文献[3]表明了风电功率数据存在相似的变化趋势,提出基于相似理论的聚类分析方法对实时风电功率进行预测。传统的K-means等聚类算法[4-5]的计算复杂,容易出现局部最优,而谱聚类 (spectral clustering,SC)[6]计算简单,能适应大规模数据集,能在任意样本空间进行分析,具有可识别非凸分布能力,且不受样本维数的影响,能收敛于全局最优解。因此,在研究超短期风电功率预测时,应用SC可以提高样本之间的相似性,降低预测模型的计算复杂性,提高预测的准确性。
目前,风电功率预测的方法有持续时间法[7]、卡尔曼滤波法[8]、人工神经网络法[9]、Volterra自适应预测法[10]、小波分析法[11]和支持向量机法 (support vector machine,SVM)[12]等。其中SVM具有非线性拟合能力较强和训练时间短等优点,故在风电功率预测研究中得到了广泛的应用。文献[13]指出选择合适的模型参数和核参数对SVM模型的学习和泛化能力尤为重要,会对预测模型的准确性产生直接的影响。在SVM的参数寻优研究中,已有学者提出了遗传算法[14]、粒子群算法[15]和引力搜索算法[16]等方法。研究结果证实参数寻优有助于提高SVM模型的预测准确性。因此采用智能算法对SVM的参数寻优,能够提高风电功率预测精度。
本文使用一种改进型引力搜索算法 (AGSA) 对SVM进行参数优化。在预测前,通过经验模态分解 (EMD) 对风电原始数据进行去噪处理,剔除不规则的数据;然后应用谱聚类 (SC) 对经验模态分解后的子序列进行聚类分析,增强模型的稳定性。在基本的引力搜索算法上,引入混沌时间序列机制,解决初始种群产生时粒子寻优位置重复率高的问题;引入具有全局记忆性的惯性权重系数;引入高斯决策,解决算法出现的早熟问题,提高算法的收敛速度和收敛精度。以某风电场的实际数据为算例,对所提模型进行了仿真。结果表明:EMD-SC-AGSA-SVM模型能提高风电功率预测的精度,且预测效果较好,证明了所采用方法的合理性。
1 风电功率时间序列的经验模态分解由于风电功率时间序列具有较强的非线性、非平稳性与随机性,而EMD是一种适用于非线性、非平稳性自适应信号的分解方法,将EMD应用到风电功率时间序列上,可以把实际存在不同时间尺度或趋势分量的风电功率时间序列数据逐级分解,从而得到一系列具有相同特征尺度的风电功率序列,分解出来的时间序列要比原来的规律性强,且平稳性能更高,可提升风电功率预测效果。EMD基本理论[17]就是将复杂信号分解成多个简单的固有模态函数 (intrinsic mode function,IMF),且每个IMF是相互独立存在的。其分解过程为:
1) 确定风电功率时间序列{x(t)}上的所有极值点和上、下包络线Emax,Emin。数据x(t) 与上、下包络线的均值m(t)=(Emax+Emin)/2的差记为h1,则:
| $ {h_1} = x\left( t \right)-m\left( t \right) $ | (1) |
将h1视作新的x(t),重复步骤1),直到hi满足IMF的条件,则其成为从原始信号筛选出的第1阶IMF,记为C1(t)。
2) 将C1(t) 从x(t) 中分离,得到差值信号r1(t):
| $ {r_1}\left( t \right) = x\left( t \right)-{C_1}\left( t \right) $ | (2) |
把r1(t) 作为“新”信号,重复公式 (1) 的筛分步骤,直到第n阶的残余信号rn(t) 为单调函数,不再筛分出新的IMF分量。
| $ {r_n}\left( t \right) = {r_{n-1}}\left( t \right)-{C_n}\left( t \right) $ | (3) |
3) 最终结果是风电功率时间序列,可表示为n个IMF分量和1个残余项的和,即:
| $ x\left( t \right) = \sum\limits_{i = 1}^n {{C_i}\left( t \right) + {r_n}\left( t \right)} $ | (4) |
谱聚类是一种新型的谱图聚类划分方法,它将需要聚类的数据样本看作图谱上的顶点,用样本之间的相似度表示图谱边上的权重值,从而把数据集合的聚类问题转变为图形的最优划分[18]。图谱的划分准则直接影响聚类结果的好坏,较常见的准则有SM算法、NJW算法和K-means算法等。
谱聚类算法基本步骤为:
1) 输入需要聚类的样本集和聚类数目;
2) 根据相似性测度对给定样本数据集建立相似矩阵A;
3) 计算相似矩阵A的前z个特征值和特征向量,并构建特征向量空间B;
4) 采用SM算法或其他传统聚类算法对空间B的特征向量聚类,输出聚类结果。
3 支持向量机相关理论SVM模型的基本思路如下:设已给定的风电功率训练样本集为{(x1,y1),(x2,y2),…,(xn,yn)}∈Rn×R,引入一个非线性映射Φ(x),且利用结构风险最小原则构造最优型回归决策目标函数:
| $ f\left( x \right) = \boldsymbol{w}\cdot\Phi \left( x \right) + b $ | (5) |
式中:w代表权向量值,b代表偏差值。
再引入结构风险函数Rreg:
| $ {R_{{\rm{reg}}}} = \frac{1}{2}||w|{|^2} + \gamma {R_{{\rm{emp}}}} $ | (6) |
式中:||w||2是叙述函数;γ是常数且大于0,其作用是平衡经验风险和模型复杂度。
式 (5) 中的回归决策函数可转化为以下优化问题:
| $ \left\{ \begin{array}{l} {\rm{min}}f\left( x \right) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + \gamma \sum\limits_{i = 1}^m {({\xi _i} + {\xi ^*}_i)} \\ {\rm{s}}{\rm{.t}}.{y_i}-{\mathit{\boldsymbol{w}}^{\rm{T}}}\Phi \left( x \right)-b \le \varepsilon + {\xi _i}\\ \;\;{\mathit{\boldsymbol{w}}^{\rm{T}}}\Phi \left( x \right) + b-{y_i} \le \varepsilon + {\xi ^*}_i\\ \;\;{\xi _i}, {\xi ^*}_i \ge 0 \end{array} \right. $ | (7) |
式中:ε是预测估计精度值,ξi*,ξi是引入的松弛变量。
通过引入非负Lagrange乘子构造Lagrange函数,式 (7) 的线性规划问题求解可转化为以下优化问题:
| $ \left\{ \begin{array}{l} {\rm{min}}f\left( x \right) = \frac{1}{2}\sum\limits_{i, j = 1}^m {({\alpha _i}- {\alpha ^*}_i)({\alpha _j}- {\alpha ^*}_j)} K({x_i}, {x_j})- \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^m {{y_i}({\alpha _i} - {\alpha ^*}_i) + \varepsilon ({\alpha _i} - {\alpha ^*}_i)} \\ {\rm{s}}{\rm{.t}}.\sum\limits_{i = 1}^m {{y_i}({\alpha _i} - {\alpha ^*}_i) = 0} \\ \;\;\;{\alpha _i}, {\alpha ^*}_i \in \left[{0, \gamma } \right] \end{array} \right. $ | (8) |
式中:αi,αi*是引入的非负Lagrange乘子。
引入已定义的核函数:
| $ K({x_i}, {x_j}) = \Phi ({x_i})\cdot\Phi ({x_j}) $ | (9) |
则非线性回归函数可表示为:
| $ f\left( x \right) = \sum\limits_{i = 1}^m {({\alpha _i}-{\alpha ^*}_i)K({x_i}, {x_j}) + b} $ | (10) |
文献[19-20]指出采用径向基核函数 (radial basis function,RBF) 对SVM的性能优化有所帮助,对空间繁杂性影响较小,更容易实现SVM的优化过程。因此,选取径向基核函数 (RBF) 作为SVM模型的核函数,即:
| $ K({x_i}, {x_j}) = \exp \left( {-\frac{{||x-{x_i}|{|^2}}}{{2{\sigma ^2}}}} \right) $ | (11) |
由上述分析可知,在利用SVM模型进行预测时,需要对参数γ和核参数σ进行优化选择,所以本文采用AGSA算法对这2个参数进行寻优,从而得到更好的预测模型。
4 基于EMD-SC和AGSA优化支持向量机的风电功率预测模型 4.1 基于AGSA的SVM参数优化 4.1.1 基本的引力搜索算法理论假设在一个S维的搜索空间,N个粒子集合种群为X=(X1,X2,…,XN),第i个粒子在S维搜索空间的位置是Xi=(Xi1,Xi2,…,Xis,…,XiS),依据牛顿万有引力定理,第i个粒子与第j个粒子的相互作用力为:
| $ F_{ij}^s\left( t \right) = G\left( t \right)\frac{{{M_i}\left( t \right) \times {M_j}\left( t \right)}}{{{x_i}\left( t \right), {x_j}{{\left( t \right)}_2} + e}}({x^s}_j\left( t \right)-{x^s}_i\left( t \right)) $ | (12) |
式中:Mj和Mi分别是第j个粒子和第i个粒子的万有引力质量,e是非零常数,G(t) 是t时刻的万有引力常量。
G(t) 的计算公式如下:
| $ G\left( t \right) = {G_0}{{\rm{e}}^{-\alpha \frac{t}{{{\psi _{{\rm{max}}}}}}}} $ | (13) |
式中:G0,α是常数,ψmax是程序的最大迭代次数。
假设万有引力质量与惯性质量是一致的,根据适应度函数得到粒子质量,定义为:
| $ \left\{ \begin{array}{l} {m_i}\left( t \right) = \frac{{{\rm{fitnes}}{{\rm{s}}_i}\left( t \right)-{\rm{worst}}\left( t \right)}}{{{\rm{best}}\left( t \right)-{\rm{worst}}\left( t \right)}}\\ {M_i}\left( t \right) = \frac{{{m_i}\left( t \right)}}{{\sum\limits_{j = 1}^N {{m_j}\left( t \right)} }}, \;\;i = 1, 2, \ldots, N \end{array} \right. $ | (14) |
式中:fitnessi(t) 是粒子适应度函数值,best (t) 是群体最优适应度函数值,worst (t) 是群体最差适应度函数值。
在S维的空间中,个体i所受的作用力总和FiS(t) 的定义如下:
| $ \sum\limits_{j \in {k_{best}}, j \ne i} {{\rm{rand}} \times G\left( t \right)\frac{{{M_i}\left( t \right) \times {M_j}\left( t \right)}}{{||{x_i}\left( t \right), {x_j}\left( t \right)|{|_2}}}({x^s}_j\left( t \right)-{x^s}_i\left( t \right))} $ | (15) |
式中:rand是[0,1]之间的随机变量,kbest是刚开始适应值最好的个体的数集。
根据牛顿第二定律,t时刻粒子i在第s维的万有引力的加速度定义如下:
| $ {a^s}_i\left( t \right) = \frac{{{F^s}_i\left( t \right)}}{{{M_i}\left( t \right)}} $ | (16) |
种群里粒子个体的万有引力速度和位置表达式如下:
| $ {v^s}_i\left( {t + 1} \right) = {d_1} \times {v^s}_i\left( t \right) + {a^s}_i\left( t \right) $ | (17) |
| $ {X^s}_i\left( {t + 1} \right) = {X^s}_i\left( t \right) + {v^s}_i\left( {t + 1} \right) $ | (18) |
式中d1是权重系数。
4.1.2 改进1——混沌序列初始种群分析基本的GSA可知,GSA寻优时的初始种群是随机产生的,对初始值的依赖十分敏感,容易产生粒子位置重复和分布不均匀,以致基本的万有引力搜索算法的寻优效果不理想。因此,考虑到混沌运动具有常见性、随机性和具有丰富的内部层次的有序结构等优点,在GSA的初始种群产生时,引入混沌序列策略,可以减小粒子寻优位置的重复率。
混沌序列产生的方法很多,本文采用最为常见的Logistic映射。初始种群的产生步骤如下:
1) 在算法的S维搜索空间中,产生一组随机向量x=[x1,x2,…,xs,…,xS],xs∈[0,1]且各分量不相等;
2) 利用Logistic映射,得到关于xs的映射方程:xk+1s=u×xks×(1-xks),当u=4时,映射方程产生完全混沌序列;
3) 对得到的混沌序列,利用公式 (19) 将混沌运动的遍历范围映射到优化参数变量的搜索范围:
| $ {x^s}_{k + 1} = {x^s}_{k + 1,{\rm{min}}} + {x^s}_{k + 1} \times {x^s}_{k + 1,{\rm{min}}} - {x^s}_{k + 1,{\rm{max}}} $ | (19) |
式中,xk+1,mins和xk+1,maxs分别代表取值的最小值和最大值。
4.1.3 改进2——全局记忆性的速度权重系数在速度的迭代过程中,万有引力速度公式 (17) 中的权重系数d1对算法的收敛性能起决定性作用,权重系数变大,收敛速度就相应地变快,对全局搜索有利,但对精确结果不利;权重系数变小,对全局搜索和精确结果有利,但收敛速度会逐渐变慢。
因此,借鉴PSO中关于动态惯性权重的思想[21],对速度公式 (17) 中的速度权重d1进行修正,其表达式如下:
| $ {d_1} = {d_{1{\rm{max}}}}-{d_{1{\rm{min}}}}\frac{{{\psi _{{\rm{max}}}}-\psi }}{{{\psi _{{\rm{max}}}}}} + {d_{1{\rm{min}}}} $ | (20) |
式中:d1max和d1min为d1的权重上、下限,ψ和ψmax分别为算法当前迭代数和最大迭代数。
GSA算法本身是无记忆性的,可通过引入粒子群算法 (PSO) 中的全局记忆功能和群体交流功能,来改进GSA的速度表达式,使粒体更快达到最优解。即最终速度更新表达式为:
| $ \begin{array}{c} {v^s}_i\left( {t + 1} \right) = \left( {\left( {{d_{{\rm{1max}}}}-{d_{{\rm{1min}}}}} \right)\frac{{{\psi _{{\rm{max}}}}-\psi }}{{{\psi _{{\rm{max}}}}}} + {d_{{\rm{1min}}}}} \right) \times {v^s}_i + \\ {b_1} \times {c_1} \times ({p^s}_{{\rm{best}}}-{x^s}_i\left( t \right) + {b_2} \times {c_2} \times \\ ({g^s}_{{\rm{best}}} - {x^s}_i\left( t \right)) + {a^s}_i\left( t \right) \end{array} $ | (21) |
式中:c1,c2为[0,1]区间内的随机数;b1,b2为正常系数;pbests为粒子i经历过的历史最优位置;gbests为种群最优粒子位置。
4.1.4 改进3——高斯扰动由文献[22]的结果可知,虽然GSA的优化性能与其他智能算法相比有较大的提高,但在大多数情况下,GSA算法也只能收敛到某区域最优值,存在局部化最优问题。因此,为增强算法跳出局部最优问题的能力,提高算法的收敛速度,在基本算法中引入高斯扰动优化策略。高斯扰动表示式如下:
| $ {f_{{\rm{Gauss}}}} = {\rm{exp}}(-{\mu ^2}/\delta ) $ | (22) |
式中:μ是均值,δ是代表高斯核的参数。文献[23]指出高斯参数δ的取值越小,对系统的扰动会越强,因此在本文中,选δ=0.87。
使用高斯扰动操作后的粒子位置Xis(t+1) 为:
| $ {X^s}_i\left( {t + 1} \right) = {f_{{\rm{Gauss}}}} + 1 \times {X^s}_i\left( t \right) + {v^s}_i\left( {t + 1} \right) $ | (23) |
综上所述,SVM参数的优化过程如下:
1) 设置种群规模大小为Na,粒子维数S,最大进化迭代次数为ψmax,利用混沌序列机制初始化SVM参数 (参数γ和核参数σ),形成初始化种群,随机给定个体速度初始值。
2) 计算每个粒子的目标函数值F(xi) 作为适应度值,目标函数为:
| $ F({x_i}) = {\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({{\bar y}_i}-{y_i})}^2}} $ | (24) |
式中:yi和yi分别为训练的数值和实际的数值;n是样本的数目值。MSE越小,则表示经过算法选择出来的这组参数的效果越好。
3) 记录每个粒子的历史最优位置和种群最优粒子位置。
4) 按式 (14) 计算粒子的万有引力质量,按式 (15) 计算每个粒子的万有引力总和,按式 (16) 计算粒子加速度。
5) 按式 (21) 和式 (23) 更新每个粒子的速度值和位置值。
6) 若满足最大迭代次数,则该算法程序运行结束;若不满足,则转入步骤2) 继续循环。
4.2 EMD-SC-AGSA-SVM预测模型的建立 4.2.1 数据的归一化处理由于风电功率数据值存在较大的波动性,因此在训练与预测之前,要对原始数据进行处理,采用以额定功率49.3 kW为基值进行归一化处理,公式如下所示:
| $ {{\hat x}_i} = {x_i}/{P_{{\rm{cap}}}}{\rm{, }}\;\;\;i = 1, 2, \ldots, n $ | (25) |
式中:xi是原始数据值;Pcap是风机的额定容量;
风电功率本身具有随机性、波动性,如果想利用预测模型得到风电功率的变化规律,就需要大量训练样本集的支持,而对经EMD的各子序列加入SC,可以保证各分解的子序列均有足够大的空间,从而保证了样本训练的有效性。
4.2.3 EMD-SC-AGSA-SVM风电功率预测建模流程首先应用EMD对原始风电功率数据进行分解,然后应用SC进行空间聚类,而后将已经聚类好的各子序列分别建立AGSA-SVM预测模型,最后把各个分解序列的预测结果叠加求和得到最终预测结果,建模过程如图 1。

|
| 图 1 EMD-SC-AGSA-SVM模型框架 Fig.1 Framework of EMD-SC-AGSA-SVM model |
以某风电场2010年4月1日到2010年4月26日发电功率时间序列为例,该机组由58台G58-850 kM机组组成,总的装机容量为49.3 MW,每15 min采一次样,以小时为单位将其平均化处理后选择其中的500个数据,如图 2所示。选前450个数据作为SVM模型训练集,余下的50个数据作为SVM模型的预测集。

|
| 图 2 风电功率的原始实测数据 Fig.2 The original actual data of wind power |
采用EMD对风电原始数据分解得到6个风电功率子序列IMF1至IMF6和一个剩余序列r6,分解结果如图 3所示。

|
| 图 3 EMD处理后的风电功率 Fig.3 Wind power after EMD treatment |
AGSA算法的粒子种群规模均设置为30,最大迭代次数T=500,万有引力常数G0=100,α=20;权重系数d1max和d1min分别取1.5和0.9,b1和b2分别为0.78和0.88,高斯参数δ=0.87。算法ADPSO的参数设置参照文献[24]。SC初始分类设置为5,选用Nyström采样算法[25],最小样本空间设置为800。对上述算法各进行100次模拟实验,确保实验得到最优解。
5.3 预测模型效果评价和各模型之间的对比评价预测误差采用的指标为:绝对平均误差EMAE、均方根误差ERMSE、最大相对误差Emax和时间成本Tmax。这4种指标具体表达式如下:
| $ {E_{{\rm{MAE}}}} = \frac{1}{N}\cdot\sum\limits_{k = 1}^N {\left| {\tilde y\left( k \right)-y\left( k \right)} \right|} $ | (26) |
| $ {E_{{\rm{RMSE}}}} = \frac{1}{N}\cdot\sum\limits_{k = 1}^N {\sqrt {\frac{1}{N}{{\left( {\tilde y\left( k \right)-y\left( k \right)} \right)}^2}} } $ | (27) |
| $ {E_{{\rm{max}}}} = \mathop {{\rm{max}}\left( {|\tilde y\left( k \right)-y\left( k \right)|} \right)}\limits_{k = 1, 2, \ldots, N} $ | (28) |
| $ {T_{{\rm{max}}}} = \mathop {{\rm{max}}}\limits_{i = 1, 2, \ldots, n} {t_i} $ | (29) |
式中:N为预测点个数,
依据《中华人民共和国能源行业标准:风电功率预测系统功能规范》(NB/T31046—2013) 和《风电场并网标准》相关规定,RMAE≤25%,RMSE≤15%。目前,研究文献中风电功率预测系统精度误差在3%左右[24]。
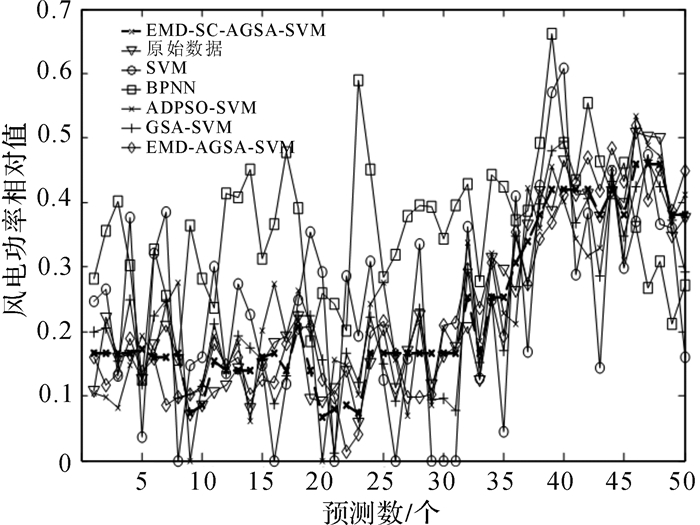
为了使预测结果更符合实际情况,对预测结果中的负功率按等于0处理,将预测相对值高于1(即超过额定功率49.5 kW) 按等于1处理。处理后,各预测模型的预测结果如图 4所示,各模型的预测误差指标对比如表 1所示。
|
| 图 4 各模型风电功率预测值的对比 Fig.4 Comparison of predicted wind power by different models |
| 预测模型 | EMAE/% | ERMSE/% | Emax/% | Tmax/s |
| BPNN | 11.928 8 | 13.984 6 | 23.697 6 | 109.755 2 |
| SVM | 6.088 7 | 7.037 9 | 11.588 6 | 81.296 3 |
| ADPSO-SVM | 5.471 3 | 6.338 9 | 10.946 5 | 66.880 5 |
| GSA-SVM | 4.717 6 | 5.530 6 | 9.372 1 | 35.826 3 |
| EMD-AGSA-SVM | 4.080 8 | 4.626 4 | 7.448 1 | 29.242 3 |
| EMD-SC-AGSA-SVM | 2.021 7 | 2.136 2 | 6.079 3 | 21.754 2 |
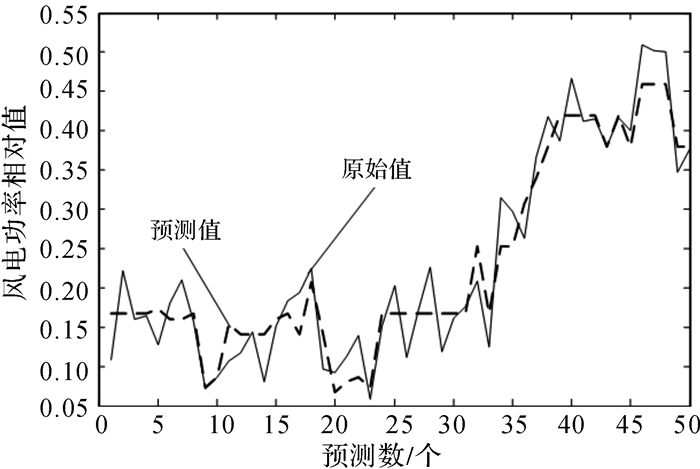
表 1中列举了多种组合算法,但是并不说明使用组合方法越多,算法的结果就越好,是需要根据各模型自身的特点,即通过各方法优势的相互补充来构建组合模型,以此达到提高预测准确性的目的。本文采用的EMD-SC-AGSA-SVM也是依照此理论依据进行组合的,其利用EMD吸取了小波变换多分辨和能克服小波变换时需要选择小波基及快速确定分解尺度等优点,对原始风电功率时间序列进行分解,可以将真实存在的不同时间尺度或趋势分量的风电功率时间序列数据逐级分解,从而得到一系列具有相同特征尺度的风电功率数据,分解后得到的数据比原始数据规律性强,可提升预测效果;采用谱聚类分析方法是因为风电功率数据存在相似的变化趋势,应用SC可以提高样本之间的相似性,降低预测模型的计算复杂性,提高预测的准确性;对EMD分解后的各子序列应用SC,可以保证各分解的子序列均有足够大的空间,从而保证了样本训练的有效性;而支持向量机模型在风电预测方面应用非常广泛,但是核函数及相关参数的选定是受限制的,且依赖于输入该模型的风电功率原始数据;通过EMD和SC对风电功率原始时间序列的处理,可以减少SVM模型对数据的依赖,也保证了风电功率样本训练的有效性;对于SVM模型的核函数及其参数则采用了更好的智能算法即改进后的引力搜索算法 (AGSA),该算法能够提高基本GSA算法的收敛速度、收敛精度和全局寻优能力。同时由表 1可以看出,在进行超短期风电功率预测时,EMD-SC-AGSA-SVM模型相对比BPNN,ADPSO-SVM,EMD-AGSA-SVM等模型,预测精度有明显的提高,其组合模型的EMAE=2.0217%,而ERMSE=2.1362%,在《中华人民共和国能源行业标准》的允许误差范围之內,在表 1的组合预测模型中是最低的,也表明本文所采用的风电功率预测组合模型是有效的,是根据EMD,SC,AGSA及SVM的优点互补来构建的,并非是随意搭建的组合预测模型。同时也验证了算法是有效、可行的,模型预测结果稳定,算法运行时间较短。由于EMD-SC-AGSA-SVM模型引入了SC聚类策略,使得输入数据的有效性大大提高,相对EMD-AGSA-SVM模型而言,本文模型的预测准确性有所提高。EMD-SC-AGSA-SVM的预测值输出如图 5所示。
|
| 图 5 EMD-SC-AGSA-SVM的风电功率预测值与原始实测数据的对比 Fig.5 Comparison between the predicted wind power of EMD-SC-AGSA-SVM and original actual data |
由图 5可以得到,EMD-SC-AGSA-SVM模型预测值与风电功率原始值是基本吻合的,可以有效地对风电功率进行相似跟踪和拟合,稳定性能较好。在原始值功率波动起伏较大时,预测效果也能较吻合。
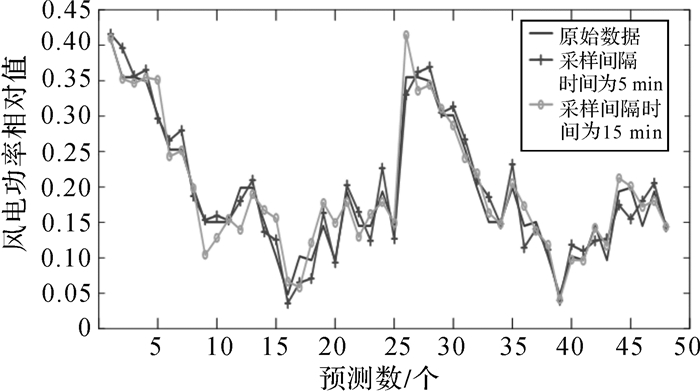
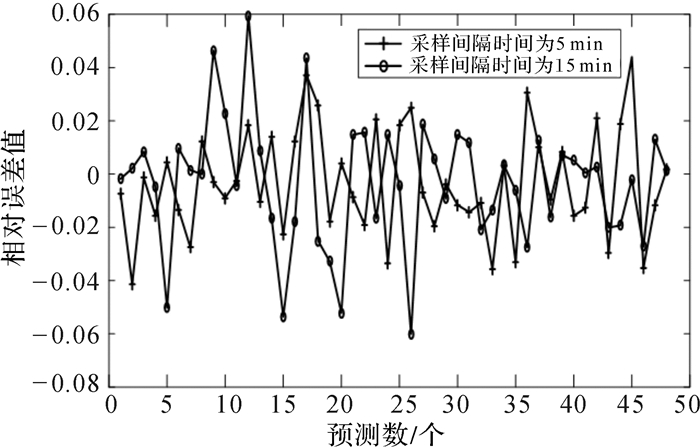
由于本文所使用的原始风电功率时间序列样本是以每15 min采样一次得到的,为了对比不同采样间隔的样本对风电功率预测精度的影响,分别使用采样间隔时间为5 min和15 min对同一时间段的风电功率数据进行预测,同时为避免采用样本数量带来影响,样本处理仍按照每小时为单位将其平均化处理,且选择相同的样本集作为训练集。例如:对2010年4月5,6号这2天的风电功率进行预测,其预测结果分别如图 6和图 7所示,预测误差性能见表 2。
|
| 图 6 不同采样频率的预测结果对比 Fig.6 Comparison of the predicted results with different sampling frequencies |
|
| 图 7 不同采样频率的风电功率预测误差曲线值 Fig.7 Curves of wind power prediction error with different sampling frequencies |
| 采样间隔/min | EMAE/% | ERMSE/% | Emax/% |
| 5 | 1.695 7 | 1.764 7 | 4.395 3 |
| 15 | 1.962 5 | 2.174 3 | 6.002 1 |
表 2列出了采样间隔时间分别为5 min和15 min的预测误差性能。可以看出选择采样间隔时间为5 min的预测模型较为准确,绝对平均误差EMAN=1.6957%,同采样间隔为15 min的模型相对比,降低了0.2668%;均方根误差ERMSE=1.7647%,对比采样间隔为15 min的模型,下降了0.4096%,这是由于风电功率采样间隔时间的增大,不能很好地跟随功率的变化轨迹。通过表 2可以得出样本的采样间隔时间对风电功率的预测精度有影响;采样间隔时间相对较短有助于提高风电功率预测精准性。
6 结论1) 在SVM参数寻优中,引入混沌时间序列机制、具有全局记忆性的惯性权重系数和高斯扰动,有效地提高了基本GSA算法的收敛速度、收敛精度和全局寻优能力。
2) EMD-SC-AGSA-SVM模型通过SC算法对原始数据聚类分析,有效地提高了预测值对原始值的相似跟踪,提高了预测的稳定性和准确性。
3) 以某一风电场实际数据为例,进行仿真分析。仿真结果表明,与常见的模型相比,EMD-SC-AGSA-SVM组合模型在超短期预测时均能获得可靠、准确、优质的预测结果,为超短期风电功率预测提供了一种有效、可靠的方法,同时也证明了所采用方法的合理性。
4) 样本的采样间隔时间对预测精度存在影响,采样间隔为5 min的预测性能要比采样间隔为15 min的优异,达到国家电网对风电场的风电功率预测的相应要求。
因此,从预测精度、搜索能力和计算时间等方面,可以看出本文提出的基于EMD-SC-AGSA-SVM模型能提高超短期风电功率预测的精度性,极具工程开发意义。
| [1] |
张宁宇, 高山, 赵欣.
一种考虑风电随机性的机组组合模型及其算法[J]. 电工技术学报, 2013, 28(5): 22–29.
ZHANG Ning-yu, GAO Shan, ZHAO Xin. An unit commitment model and algorithm with randomness of wind power[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 22–29. |
| [2] | MA Xi-yuan, SUN Yuan-zhang, FANG Hua-liang. Scenario generation of wind power based on statistical uncertainty and variability[J]. IEEE Transaction on Sustainable Energy, 2013, 4(4): 894–904. DOI:10.1109/TSTE.2013.2256807 |
| [3] | DONG L, WANG L J, SHAHNAWAZ F K, et al. Wind power day-ahead prediction with cluster analysis of NWP[J]. Renewable and Sustainable Energy Reviews, 2016, 60(6): 1206–1212. |
| [4] | HUANG Z X. Extensions to the K-means algorithm for clustering large data sets with categorical values[J]. Data Mining and Knowledge Discovery, 1998, 2(3): 283–304. DOI:10.1023/A:1009769707641 |
| [5] |
周林, 平西建, 徐森, 等.
基于谱聚类的聚类集成算法[J]. 自动化学报, 2012, 38(8): 1335–1342.
ZHOU Lin, PING Xi-Jian, XU Sen, et al. Cluster ensemble based on spectral clustering[J]. Acta Automatica Sinica, 2012, 38(8): 1335–1342. |
| [6] | BACH F R, JORDAN M I. Learning spectral clustering[J]. Advances in Neural Information Processing Systems, 2004, 16(2): 1–13. |
| [7] | PEIYUAN C, PEDERSEN T, BAK J B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667–676. DOI:10.1109/TPWRS.2009.2033277 |
| [8] | LOUKA P, GALANIS G, SIEBERT N, et al. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(12): 2348–2362. DOI:10.1016/j.jweia.2008.03.013 |
| [9] |
范高峰, 王伟胜, 刘纯, 等.
基于人工神经网络的风电功率预测[J]. 中国电机工程学报, 2008, 28(34): 118–123.
FAN Gao-feng, WANG Wei-sheng, LIU Chun, et al. Wind power prediction based on artificial neural network[J]. Proceedings of the CSEE, 2008, 28(34): 118–123. DOI:10.3321/j.issn:0258-8013.2008.34.019 |
| [10] |
江岳春, 张丙江, 邢方方, 等.
基于混沌时间序列GA-VNN模型的超短期风功率多步预测[J]. 电网技术, 2015, 39(8): 2160–2166.
JIANG Yue-chun, ZHANG Bing-jiang, XING Fang-fang, et al. Super-short-term multi-step prediction of wind power based on GA-VNN model of chaotic time series[J]. Power System Technology, 2015, 39(8): 2160–2166. |
| [11] |
杨琦, 张建华, 王向峰, 等.
基于小波-神经网络的风速及风力发电量预测[J]. 电网技术, 2009, 33(17): 44–48.
YANG Qi, ZHANG Jian-hua, WANG Xiang-feng, et al. Wind speed and generated wind power forecast based on wavelet-neural network[J]. Power System Technology, 2009, 33(17): 44–48. |
| [12] |
严欢, 卢继平, 覃俏云, 等.
基于多属性决策和支持向量机的风电功率非线性组合预测[J]. 电力系统自动化, 2013, 37(10): 29–34.
YAN Huan, LU Ji-ping, QIN Qiao-yun, et al. A nonlinear combined model for wind power forecasting based on multi-attribute decision-making and support vector machine[J]. Automation of Electric Power Systems, 2013, 37(10): 29–34. |
| [13] |
谢宏, 魏江平, 刘鹤立.
短期负荷预测中支持向量机模型的参数选取和优化方法[J]. 中国电机工程学报, 2006, 26(22): 17–22.
XIE Hong, WEI Jiang-ping, LIU He-li. Parameter selection and optimization method of SVM model for short-term load forecasting[J]. Proceedings of the CSEE, 2006, 26(22): 17–22. DOI:10.3321/j.issn:0258-8013.2006.22.004 |
| [14] |
肖白, 聂鹏, 穆钢, 等.
基于多级聚类分析和支持向量机的空间负荷预测方法[J]. 电力系统自动化, 2015, 39(12): 56–61.
XIAO Bai, NIE Peng, MU Gang, et al. A spatial load forecasting method based on multilevel clustering analysis and support vector machine[J]. Automation of Electric Power Systems, 2015, 39(12): 56–61. DOI:10.7500/AEPS20140520001 |
| [15] |
高昆仑, 刘建明, 徐茹枝, 等.
基于支持向量机和粒子群算法的信息网络安全态势复合预测模型[J]. 电网技术, 2011, 35(4): 176–182.
GAO Kun-lun, LIU Jian-ming, XU Ru-zhi, et al. A hybrid security situation prediction model for information network based on support vector machine and particle swarm optimization[J]. Power System Technology, 2011, 35(4): 176–182. |
| [16] | ZHANG W, NIU P, LI G, et al. Forecasting of turbine heat rate with online least squares support vector machine based on gravitational search algorithm[J]. Knowledge-Based Systems, 2013, 39(2): 34–44. |
| [17] | KUANG W, YANG Z, LING W K, et al. Nonlinear and adaptive undecimated hierarchical multiresolution analysis for real valued discrete time signals via empirical mode decomposition approach[J]. Digital Signal Processing, 2015, 45(10): 36–54. |
| [18] |
蔡晓妍, 戴冠中, 杨黎斌.
谱聚类算法综述[J]. 计算机科学, 2008, 35(7): 14–18.
CAI Xiao-yan, DAI Guan-zhong, YANG Li-bin. Survey on spectral clustering algorithms[J]. Computer Science, 2008, 35(7): 14–18. |
| [19] |
荣海娜, 张葛祥, 金炜东.
系统辨识中支持向量机核函数及其参数的研究[J]. 系统仿真学报, 2006, 18(11): 3204–3208.
RONG Hai-na, ZHANG Ge-xiang, JIN Wei-dong. Selection of kernel functions and parameters for support vector machines in system identification[J]. Journal of System Simulation, 2006, 18(11): 3204–3208. DOI:10.3969/j.issn.1004-731X.2006.11.050 |
| [20] | MOHANDES M A, HALAWANI T O, REHMAN S, et al. Support vector machines for wind speed prediction[J]. Renewable Energy, 2004, 29(6): 939–947. DOI:10.1016/j.renene.2003.11.009 |
| [21] |
刘刚, 彭春华, 相龙阳.
采用改进型多目标粒子群算法的电力系统环境经济调度[J]. 电网技术, 2011, 35(7): 139–144.
LIU Gang, PENG Chun-hua, XIANG Long-yang. Economic-environmental dispatch using improved multi-objective particle swarm optimization[J]. Power System Technology, 2011, 35(7): 139–144. |
| [22] | RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm[J]. Information Science, 2009, 179(13): 2232–2248. DOI:10.1016/j.ins.2009.03.004 |
| [23] |
李志刚, 吴文传, 张伯明, 等.
一种基于高斯罚函数的大规模无功优化离散变量处理方法[J]. 中国电机工程学报, 2013, 33(4): 68–76.
LI Zhi-gang, WU Wen-chuan, ZHANG Bo-ming, et al. A large-scale reactive power optimization method based on Gaussian penalty function with discrete control variables[J]. Proceedings of the CSEE, 2013, 33(4): 68–76. |
| [24] |
王贺, 胡志坚, 陈珍, 等.
基于集合经验模态分解和最小二乘向量机的短期风速组合预测[J]. 电工技术学报, 2014, 29(4): 237–245.
WANG He, HU Zhi-jian, CHEN Zhen, et al. A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 237–245. |
| [25] |
丁世飞, 贾洪杰, 史忠植.
基于自适应Nyström采样的大数据谱聚类算法[J]. 软件学报, 2014, 25(9): 2037–2049.
DING Shi-fei, JIA Hong-jie, SHI Zhong-zhi. Spectral clustering algorithm based on adaptive Nyström sampling for Big Data analysis[J]. Journal of Software, 2014, 25(9): 2037–2049. |


