2. 智能物流装备山西省重点实验室, 山西 太原 030024
2. Shanxi Key Laboratory of Intelligent Logistics Equipment, Taiyuan 030024, China
铁路隧道落煤吸尘装置主要用于吸收清理铁路隧道道床上的落煤,保障列车行车安全。以大秦铁路线为例,该铁路沿线上有将近50座隧道,隧道里程达67.196 km。大秦铁路线以运煤为主,列车密度大,约10 min一趟。列车高速穿梭于隧道中时,由于空气的扰动,列车上的煤料被卷起并下落到道床上,严重处落煤厚度已达10 cm以上,严重影响行车安全及铁路维修保养[1]。
对重载铁路线隧道落煤的清理,主要的方式为人工清理,其缺点是效率低、成本高。在现代化除尘设备领域,国内的研究方向主要为移动式除尘车,其中北京大学与铁路局工务段研发了一款除尘车,太原铁路局开发了适合于重载铁路隧道内使用的落煤清扫除尘设备[1];而国外由于没有运煤专用线,大部分为清扫铁路沿线垃圾的清扫车,例如法国SOCOFER公司开发了一款铁路除尘车[2]。但现有的移动式除尘车辆无法满足清扫宽度4 m及清理落煤量20 t/h的要求。
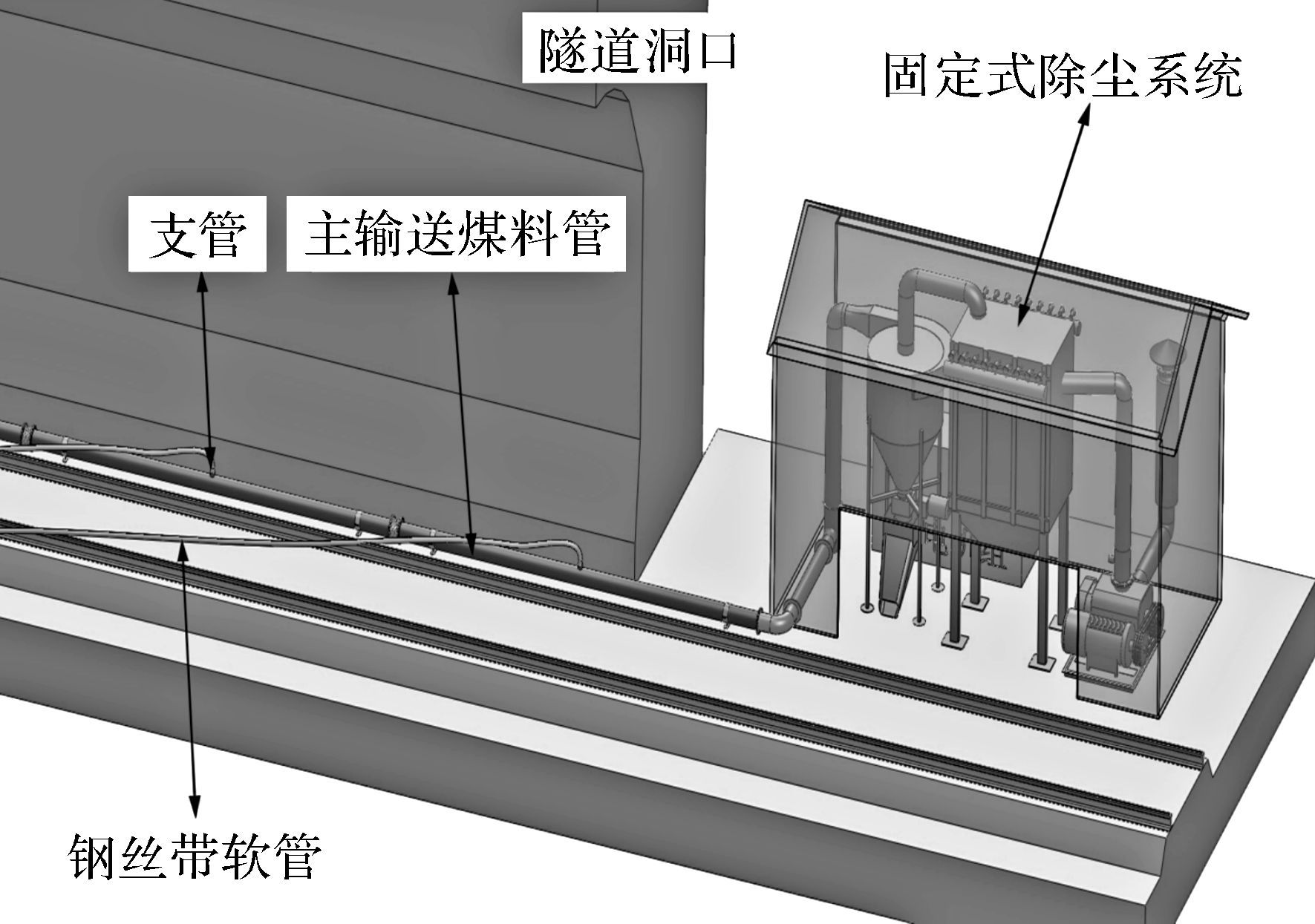
本文讨论的是由太原科技大学、太原融盛科技有限公司以及太原铁路局科研所联合研制的TY-RS型铁路隧道落煤吸尘装置,如图 1所示。其清扫宽度达到8 m,除尘量达到22 t/h。该装置为固定式除尘系统,除尘设备布置在隧道洞口,隧道内布置1个主输送煤料管,该主管上设计了多个连接钢丝带软管的支管,人工抓取钢丝带软管对落煤进行抽吸,最后采用负压气力输送的方式将落煤输送至洞口收集处理。在对主输送煤料管的设计研究中,支管的数量及布置形式对煤料的输送效率有很大影响。从理论上来讲,在不考虑主输送煤料管最大输送能力的情况下,固定长度的主输送煤料管上支管的数量越多,可使更多的作业人员参与吸尘,作业效率更高。肖益民等[3]对Y型喉管流场分析及结构优化中,以小麦输送为例得到了支管的最佳入射角为45°~75°,但其研究介质为小麦,与隧道落煤不同。邹杰[4]则通过对T型三通内的流场进行分析,得出最佳入射角为45°,但对多支管问题及其相互影响没有涉及。现有的研究中,并没有对铁路隧道内落煤相似环境作业下相邻支管间的影响及其落煤输送效率进行研究。
|
| 图 1 铁路隧道落煤吸尘装置三维示意图 Fig.1 The three-dimensional schematic diagram of the railway tunnel fallen coal dust collection device |
本文运用SolidWorks对铁路隧道落煤吸尘装置中的主输送煤料管进行优化设计,通过Fluent对影响输送效率的不同参数进行仿真计算,分析主输送煤料管上支管的最佳入射角α以及主输送煤料管上支管的间距H,并采用气固两相流颗粒轨道模型模拟验证,提出一种更为合理的主输送煤料管。加工制作后通过现场试验验证其合理性。
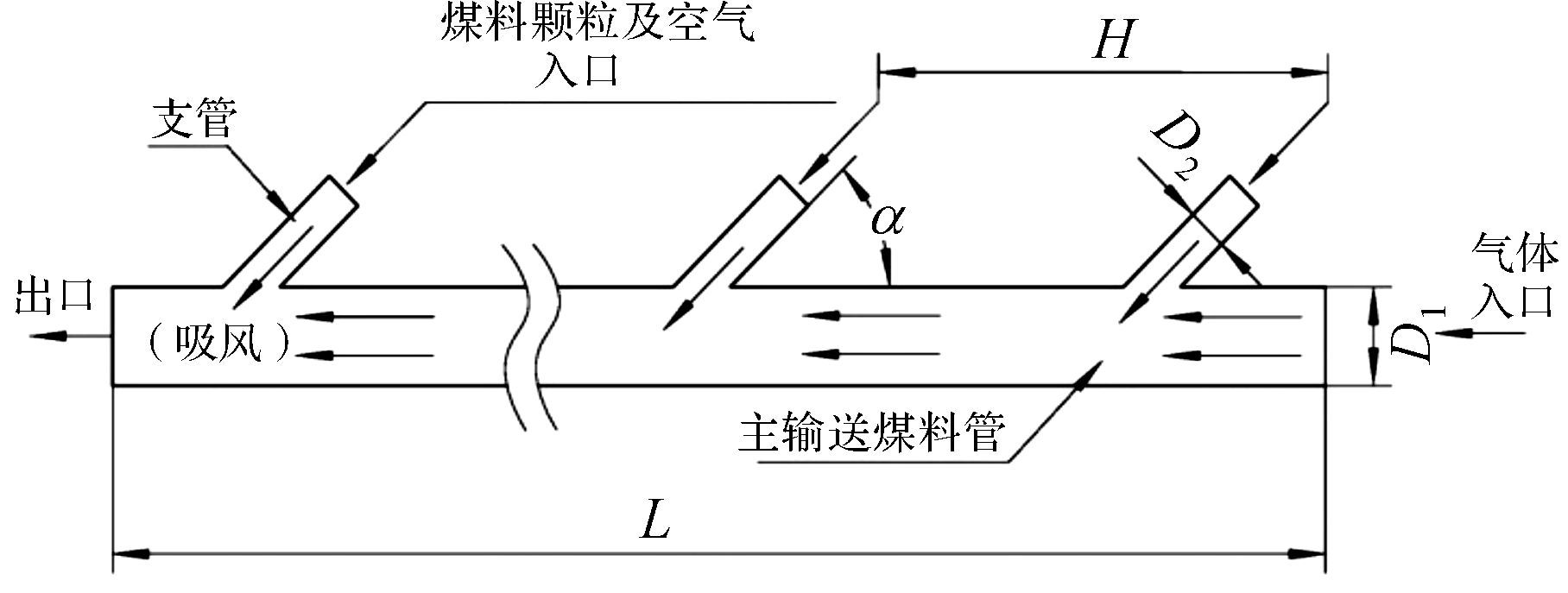
1 模型的建立 1.1 主输送煤料管几何模型图 2为铁路隧道落煤吸尘装置中主输送煤料管的结构示意图,在主输送煤料管上布置有n个支管,每2个支管之间的距离为H,支管与主输送煤料管之间的夹角即入射角为α,D1为主输送煤料管的直径,D2为支管直径,L为主输送煤料管的长度。
|
| 图 2 主输送煤料管结构示意图 Fig.2 Structure schematic diagram of the main coal conveying pipe |
在图 2所示的主输送煤料管的结构中,罗茨鼓风机在出口一侧产生负压,煤料颗粒及空气从支管进入主输送煤料管,在气固混合后从左边的出口输出。煤料入射角α及相邻支管之间的间距H会影响主输送煤料管内煤料的水平速度及煤料间的碰撞程度。
1.2 数学模型目前对气固两相流的数值模拟主要有欧拉法和欧拉-拉格朗日法[5-10],其中欧拉法将气体和固体颗粒均作为连续相进行处理,主要应用于密相流动,且不能反映固体颗粒的大小、密度等物理特性,而欧拉-拉格朗日法将固体颗粒作为离散相,将气体作为连续相处理,考虑了颗粒与颗粒、颗粒与气体间的相互作用,更能真实地反映固体颗粒在气体中的复杂变化[11-13]。Elbehery等[14]和Wang等[15]借助欧拉-拉格朗日法对弯管气固两相流进行分析并通过试验验证了欧拉-拉格朗日法的适用性。因此,本文采用欧拉-拉格朗日法来模拟落煤颗粒在吸尘装置管道中的运动。
欧拉-拉格朗日法由气体连续相的连续性方程、动量方程和颗粒离散相的质量方程、动量方程组成,其中气相连续性方程为[16-18]:
| ${\partial \over {\partial t}}({\alpha _{\rm{f}}}{\rho _{\rm{g}}}) + {\partial \over {\partial {x_{\rm{i}}}}}({\alpha _{\rm{f}}}{\rho _{\rm{g}}}{u_{\rm{i}}}) = 0$ |
气相动量方程为:
| $\eqalign{ & {\partial \over {\partial t}}({\alpha _{\rm{f}}}{\rho _{\rm{g}}}) + {\partial \over {\partial {x_{\rm{i}}}}}({\alpha _{\rm{f}}}{\rho _{\rm{g}}}{u_{\rm{i}}}) = - {\alpha _{\rm{f}}}{{\partial p} \over {\partial {x_{\rm{i}}}}} + {\partial \over {\partial {x_{\rm{i}}}}}({\alpha _{\rm{f}}}{\tau _{{\rm{ij}}}}) + \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {F_{\rm{f}}} + {\alpha _{\rm{f}}}{\rho _{\rm{g}}}g \cr} $ |
式中:ρg为气相密度;ui为气相速度;Ff为气相在气固两相流体中受离散相的作用力;αf是除去颗粒相体积后的空隙率,用Vk表示第k个颗粒相体积,V表示总体积,其表达式为:
| ${\alpha _{\rm{f}}} = 1 - {{\sum\limits_{k = 1}^{} {} {V_{\rm{k}}}} \over V}$ |
颗粒相质量方程为[19]:
| $\frac{{\partial {\rho _{\rm{s}}}}}{{\partial t}} + \frac{\partial }{{\partial {x_{\rm{i}}}}}\left( {{\rho _{\rm{s}}}{u_{\rm{j}}}} \right) = - \sum {{n_k}{m_k}} $ |
第k组颗粒相的动量方程为:
| ${{\partial {\rho _{\rm{s}}}} \over {\partial t}} + {\partial \over {\partial {x_{\rm{i}}}}}({\rho _{\rm{s}}}{u_{\rm{j}}}) = - \sum {n_{\rm{k}}}{m_{\rm{k}}}$ |
式中:ρs为颗粒相密度,uj为颗粒相速度,ukj为第k组颗粒相速度,mk为第k组颗粒相质量,Fk为第k组颗粒的Magnus力。
2 数值仿真过程通过Fluent软件对主输送煤料管内煤料的输送进行流场分析,需要对所分析模型进行基本的假设和网格的划分。
2.1 主输送煤料管几何模型在实际工程应用中,煤料的输送环境是十分复杂的,而在Fluent软件中对其进行仿真需要对其模型进行简化,提出以下基本假设:
1) 在管道入射口,其横截面上输送煤料分布均匀,为定常流;
2) 煤料颗粒假设为球形,粒径最大为0.003 m,最小为1×10-5 m;
3) 忽略颗粒间的碰撞力及Basset力,考虑重力影响及气固曳力。
2.2 几何参数设置在进行首次试验时,为方便起见,选取市场上现有的产品作验证性试验,主输送煤料管选用PVC管,支管选用钢丝带软管。首先选取主输送煤料管的直径D1=200 mm,煤料输入支管直径D2=90 mm,选取试验水平管道长度为2 500 mm,在该试验段水平管道上布置安装3组支管入口。
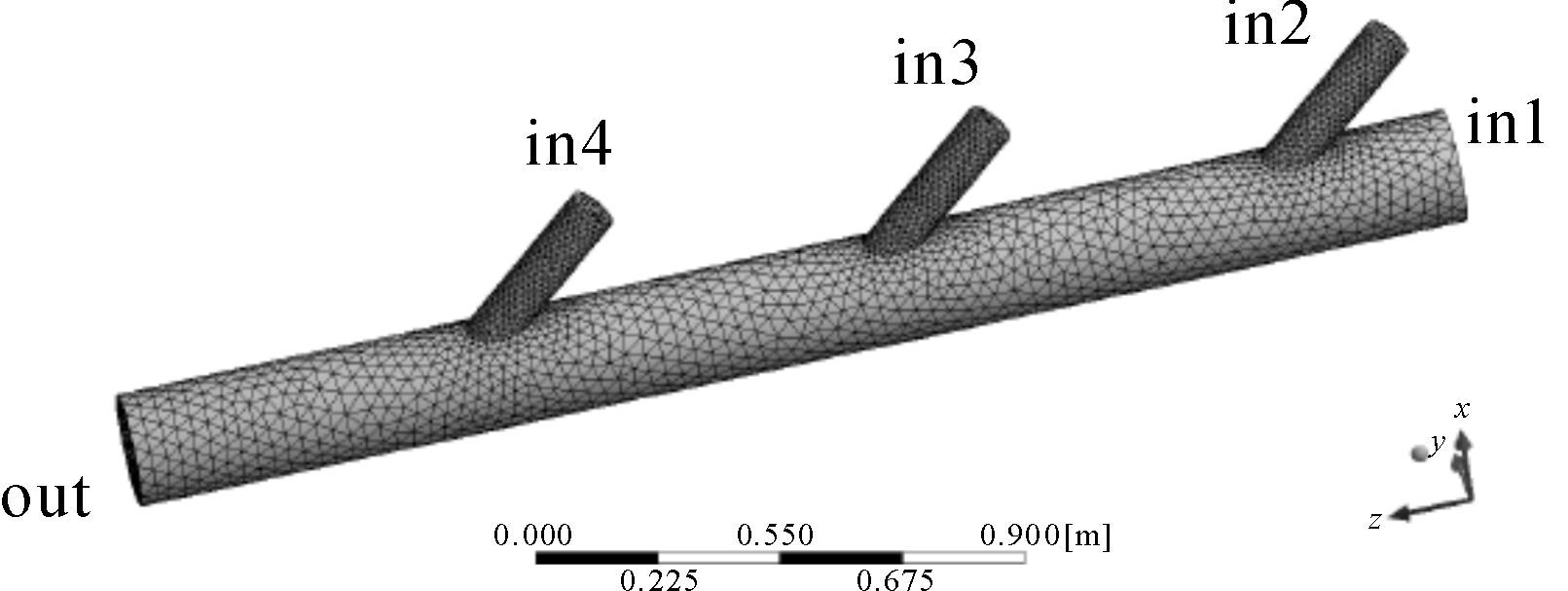
2.3 网格划分如图 3所示,该主输送煤料管道模型采用四面体非结构化网格进行划分,总网格为41 283个。在检查网格质量中,Skewness的数值最大为0.748 43,平均值为0.225 593,无超过0.75的单元,网格划分质量满足仿真需要。
|
| 图 3 主输送煤料管网格划分 Fig.3 Meshing of the main coal conveying pipe |
主输送煤料管入口 (in1) 采用速度入口边界条件,气相速度为20 m/s,颗粒相速度为20 m/s,颗粒相总流量为5 kg/s;3个支管入口 (in2,in3,in4) 同样采用速度入口边界条件,气相速度为20 m/s,颗粒相速度为2 m/s,颗粒相总流量0.5 kg/s;主输送煤料管出口 (out) 采用outflow边界条件,气相为空气,颗粒相为煤料。其中空气密度为1.225 kg/m3,煤料的密度为1 550 kg/m3。
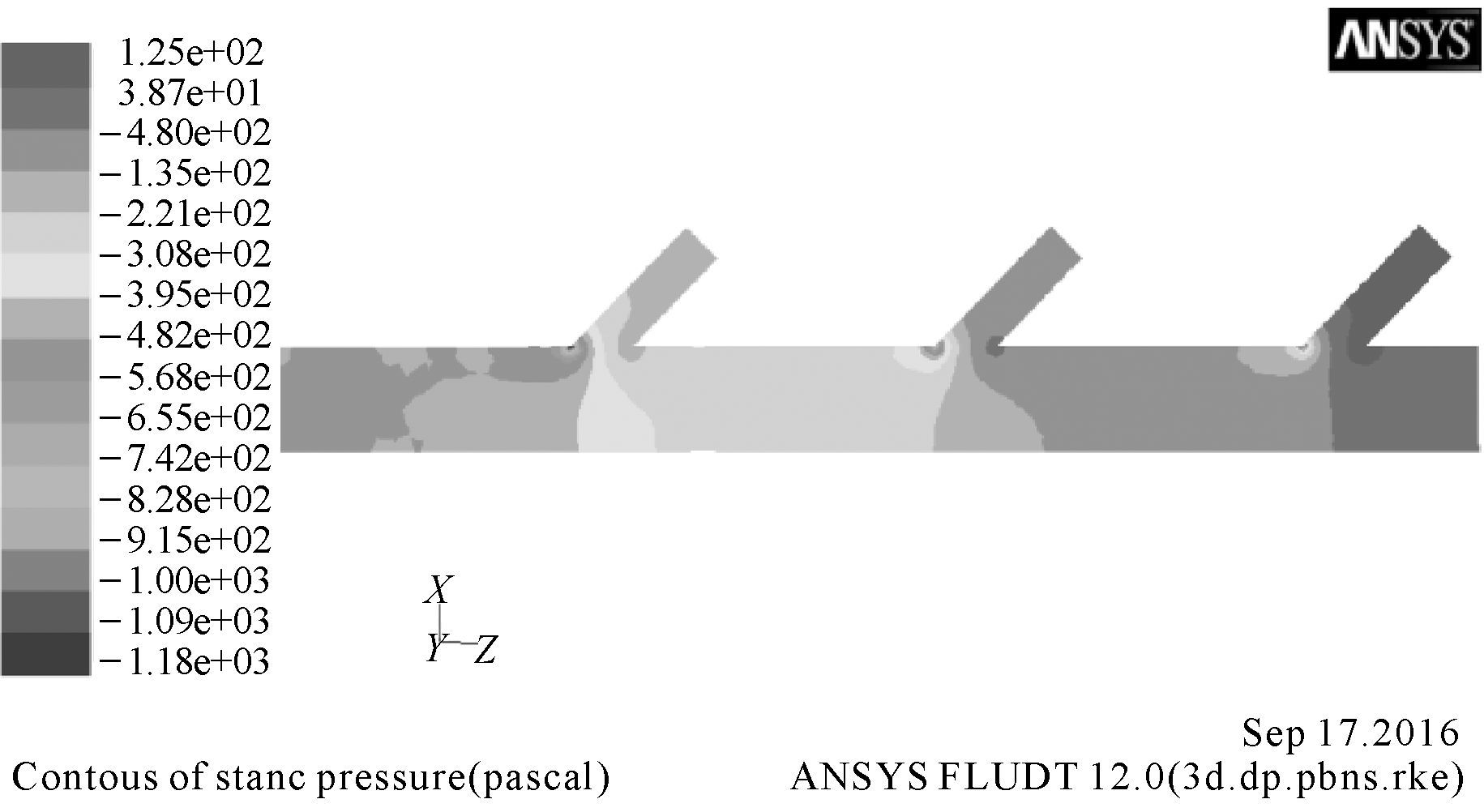
3 仿真结果及分析 3.1 主输送煤料管静压分析图 4所示为主输送煤料管中心剖切平面的静压力分布图,在支管与主输送煤料管连接处静压明显地下降。
|
| 图 4 主输送煤料管中心剖切平面的静压力分布图 Fig.4 The static pressure distribution of center section plane of the main coal conveying pipe |
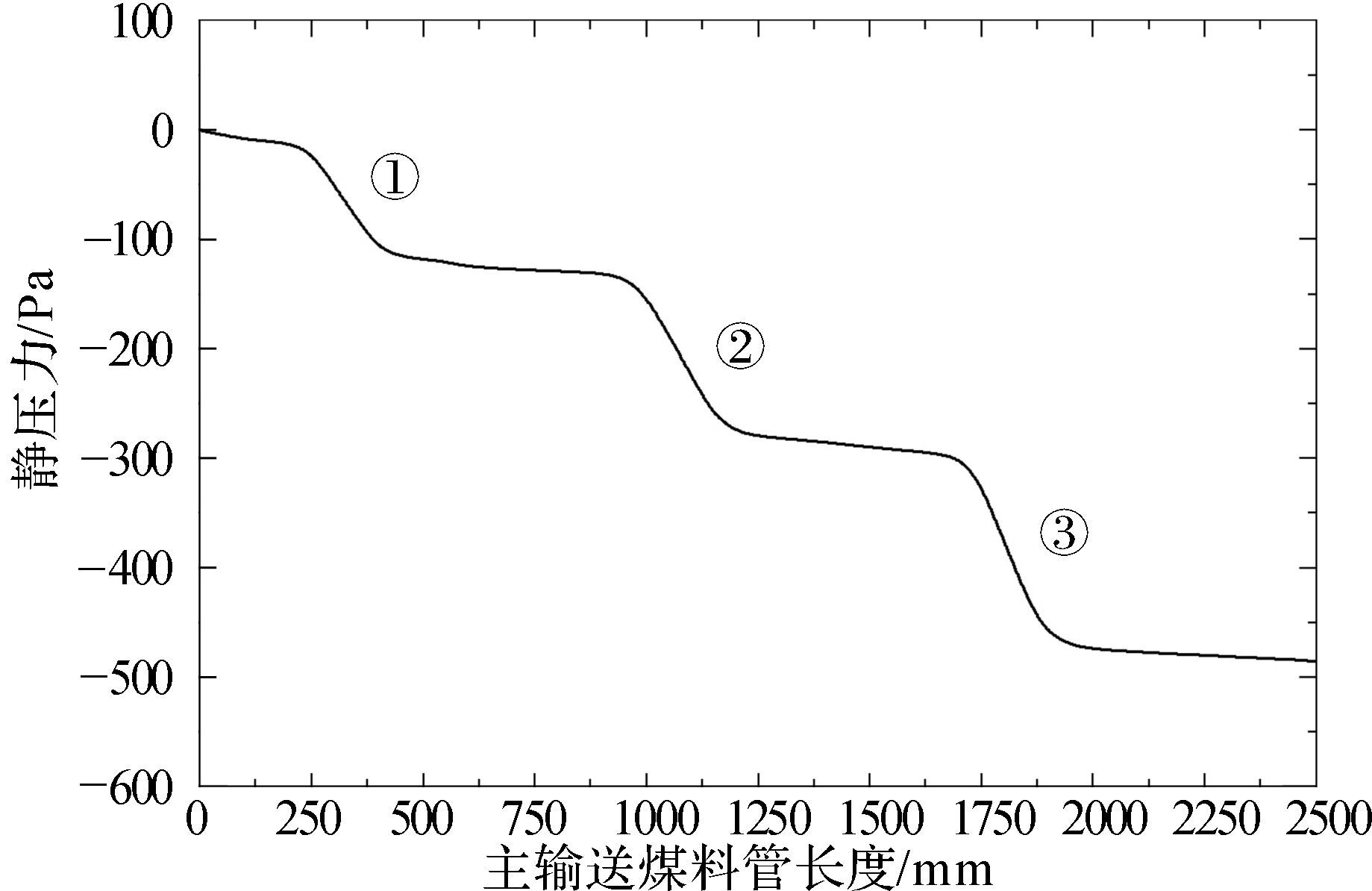
图 5所示为主输送煤料管沿中心轴线上的静压力曲线,图中有①、②、③ 三处静压下降明显区域,均为支管处煤料的混合区域。
|
| 图 5 主输送煤料管中心轴线静压力曲线 Fig.5 The static pressure curve of center axis of the main coal conveying pipe |
由图 4和图 5分析可知,气固两相流在主输送煤料管进口时压降较小,但在3个支管处压力下降明显,此时煤料从支管入口摄入,与主输送煤料管内流体发生较大的能量交换。分析图 4可知,在支管与主输送煤料管交叉处产生了涡流,支管流体与主输送煤料管流体发生充分混合。分析图 5可知,在主输送煤料管沿中心轴线上的静压力发生了3次下降,并且每次下降的幅度增大,这是由于主输送煤料管内流体颗粒与支管颗粒混合后其颗粒的动能逐次减小。
3.2 不同入射角α下流场分析在支管间的间距H=750 mm,其他参数一致的情况下,分析入射角α对流场的影响。入射角α的范围为0°~90°,选取15°,30°,45°,60°,75°,90°六种情况进行仿真,分析其流场情况。
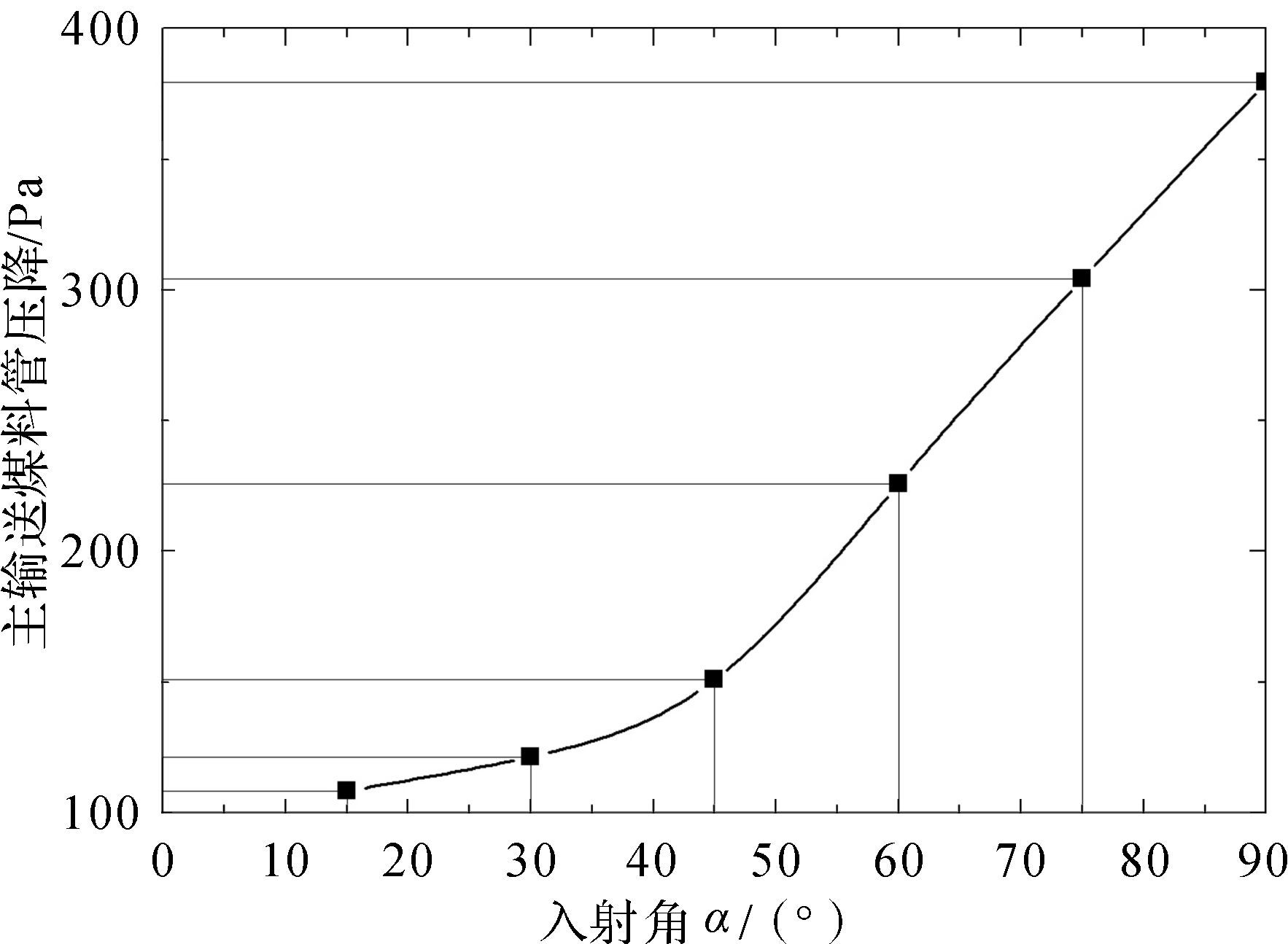
分析图 6可知,随着入射角α的增大,压降同样增大,为一条单调递增函数曲线。在入射角α<45°的情况下,压降变化幅度小,处于合理区间。在入射角α>45°的情况下,压降变化幅度大。这是由于入射角α越大,支管入射的颗粒流方向与主输送煤料管的方向偏差越大,交汇时会消耗更大的压力。
|
| 图 6 支管间距为750 mm时不同入射角下进出口压降曲线 Fig.6 The inlet and outlet pressure drop curve at different incident angles with branch pipe spacing of 750 mm |
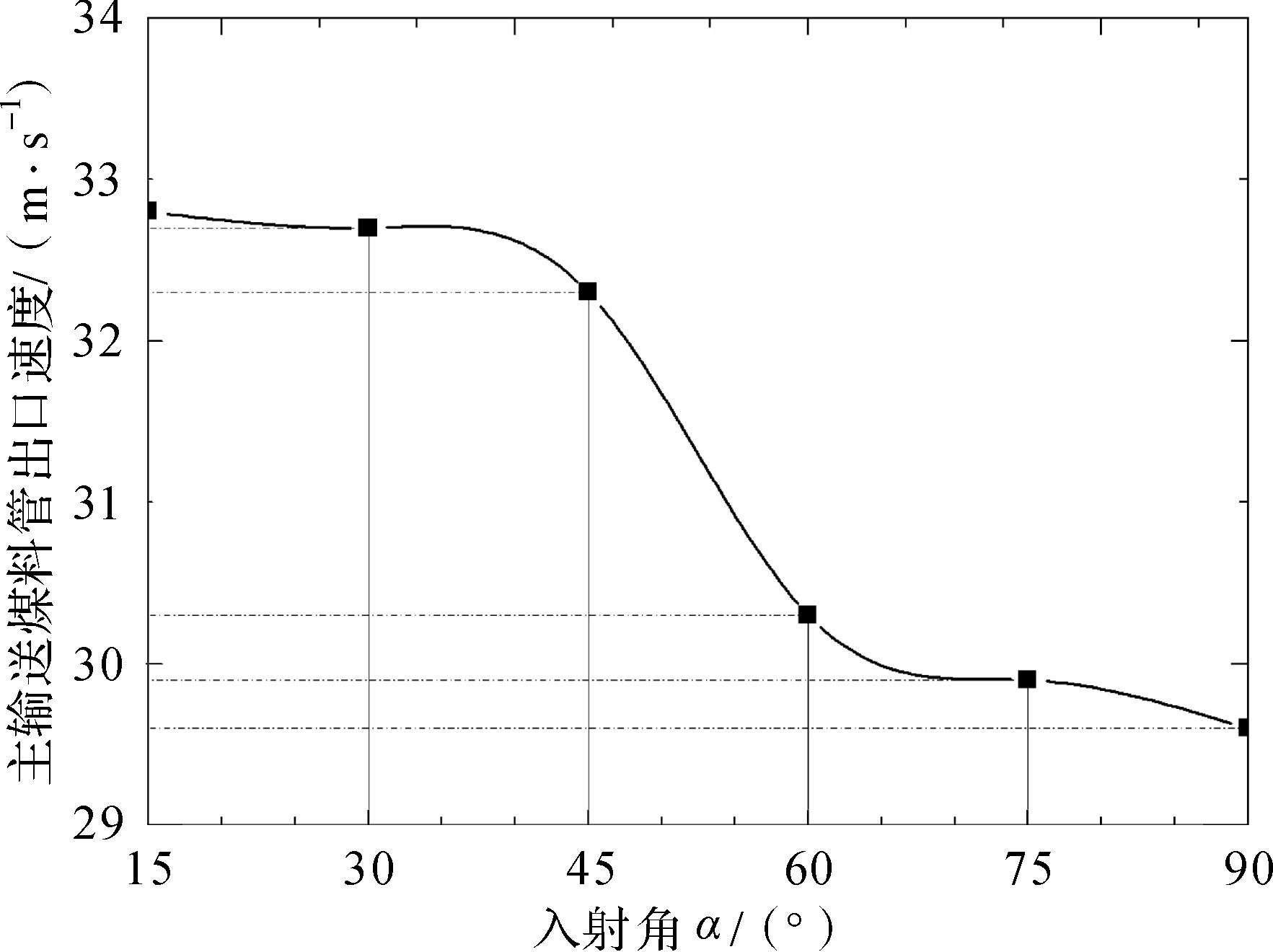
分析图 7可知,随着入射角α的增大,主输送煤料管出口速度下降。这是由于入射角α越大,煤料颗粒垂直于主输送煤料管的速度越大,沿其水平方向速度越小,支管射入的颗粒与主输送煤料管内的颗粒发生激烈碰撞与速度交换,对主输送煤料管内流体速度的影响较大。在入射角α<45°的情况下,速度下降较小,颗粒流可获得较大的水平输送速度。
|
| 图 7 支管间距为750 mm时不同入射角下出口速度曲线 Fig.7 The outlet velocity curve at different incident angles with branch pipe spacing of 750 mm |
综合压降与速度分析可知,当入射角α<45°的情况下,在该气力输送系统中可获得较好的煤料输送。
3.3 不同支管间距H下流场分析针对在设定固定管道长度下,分析相邻支管间距离对输送煤料效率的影响。本文采用欧拉-拉格朗日离散相 (DPM) 模型,假定支管入射角α=45°,分析支管间的间距分别为500,750,1 000 mm时煤料的碰撞情况。
分析比较图 8至图 10中颗粒的运动轨迹可以发现,从各个支管入射的颗粒在进入主输送煤料管后,部分质量轻的颗粒在极短的距离内获得较大的速度后随主输送煤料管内的流体运动;其余大部分颗粒会穿越主输送煤料管内的流体至管道底部,并发生聚集和反弹。在支管间距H=500 mm情况下,最右侧支管入口 (in2) 入射的颗粒流部分在碰触到管壁底部后反弹,反弹至上管道壁面时,其反弹区域对第2支管入口 (in3) 入射的颗粒流产生了干扰;支管间距H=1 000 mm情况下,最右侧支管入口 (in2) 入射的颗粒流完成与主输送煤料管内的流体内混合后距离第2支管入口 (in3) 还有一定间距;支管间距H=750 mm情况下,较前2组情况,颗粒运动轨迹良好。

|
| 图 8 支管间距为500 mm时颗粒运动轨迹 (α=45°) Fig.8 The particle trajectories with the branch pipe spacing of 500 mm |

|
| 图 9 支管间距为750 mm时颗粒运动的轨迹 (α=45°) Fig.9 The particle trajectories with the branch pipe spacing of 750 mm |

|
| 图 10 支管间距为1 000 mm时颗粒运动的轨迹 (α=45°) Fig.10 The particle trajectories with the branch pipe spacing of 1 000 mm |
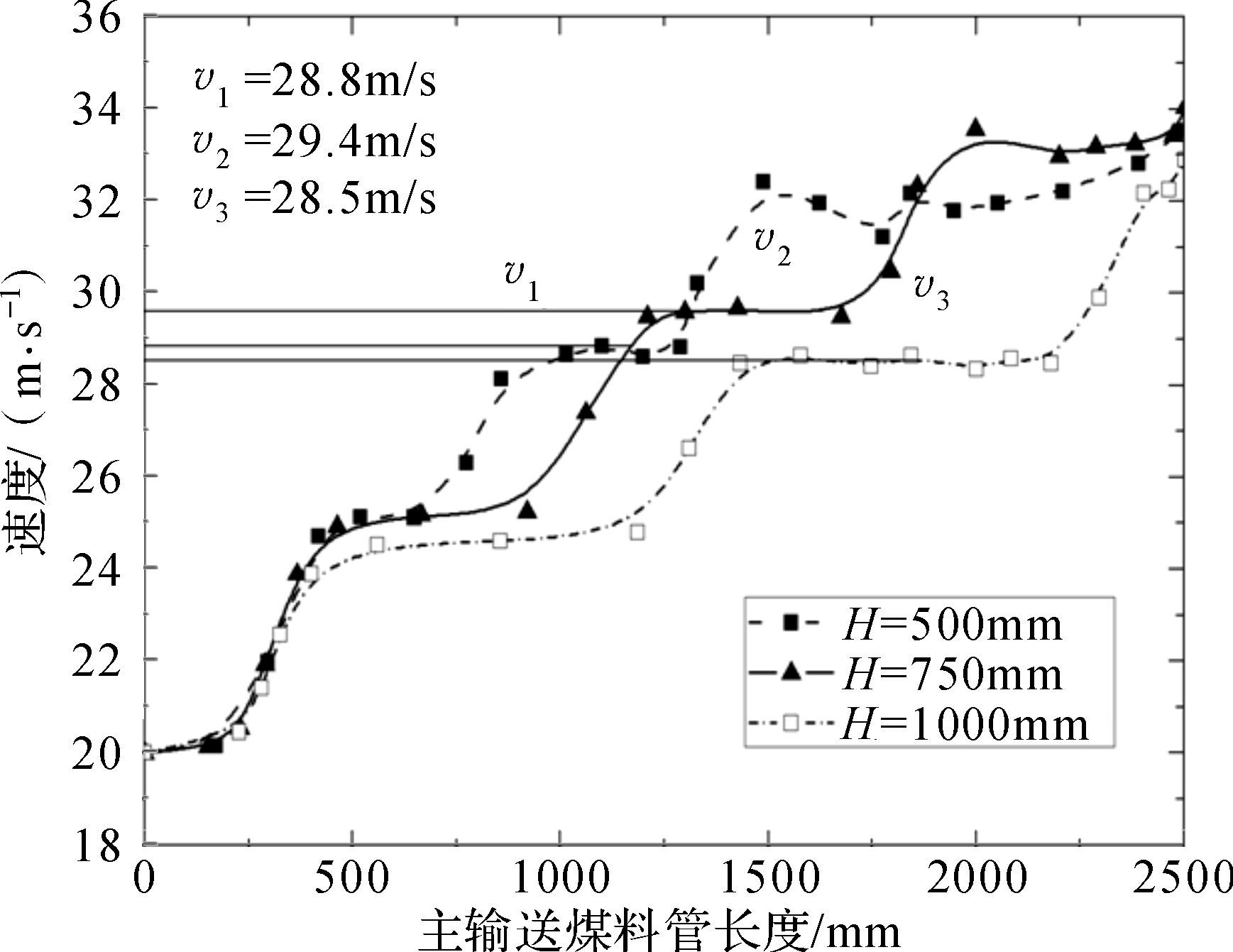
分析图 11至图 13可知,主输送煤料管内颗粒流的速度在逐渐增加,在支管入口处由于支管颗粒流的入射干扰了主输送煤料管内颗粒的运动,相应的速度增长会停滞。在支管间距为500,750,1 000 mm三种情况下,对主输送煤料管内颗粒流的速度进行对比分析,结果如图 14所示。由于在仿真中主输送煤料管的长度L是固定的,为2 500 mm,无法保证在不同的支管间距下出口处流体已经达到完全稳定的状态,因此只可将3组试验中第2支管入口 (in3) 入射的颗粒混合达到稳定状态后的速度作为分析依据。观察第2支管入口 (in3) 入射的颗粒流运动平稳后的平均速度可知,3组不同间距的支管粒子流平稳后的速度分别为v1=28.8 m/s,v2=29.4 m/s,v3=28.5 m/s,v2的平均速度要明显大于其余2组。

|
| 图 11 支管间距为500 mm时颗粒速度云图 (α=45°) Fig.11 The particle velocity nephogram with the branch pipe spacing of 500 mm |

|
| 图 12 支管间距为750 mm时颗粒速度云图 (α=45°) Fig.12 The particle velocity nephogram with the branch pipe spacing of 750 mm |

|
| 图 13 支管间距为1 000 mm时颗粒速度云图 (α=45°) Fig.13 The particle velocity nephogram with the branch pipe spacing of 1 000 mm |
|
| 图 14 主输送煤料管颗粒速度仿真结果 (α=45°) Fig.14 Simulation results of the particle velocity of the main coal conveying pipe |
根据流量与速度的关系式可知,在相同输送管截面积下,单位时间内支管间距H=750 mm情况下煤料的输送量要大于其余2组,输送效率更高。
4 试验验证如图 15、图 16所示,大秦铁路隧道落煤吸尘装置安装在铁路隧道洞口一侧,将主输送煤料管铺设在洞壁一侧。洞外安装有罗茨鼓风机、除尘器、螺旋落料器、控制器及发电机组等装置。罗茨鼓风机选用功率为55 kW,流量为6 000 m3/h,压力为0.045 MPa的机型,主输送煤料管采用市场上现有的PVC管道,直径选取200 mm。为方便试验及更换,主输送煤料管上的支管选用变径三通管道。根据仿真试验结果,选取了市面上现有的入射角α为45°,60°,90°的变径三通管道。为得到更精确的试验结果,在长度约100 m的主输送煤料管上选取一段长度为5 m的区域作为试验段,用热球式风速计测得该试验段的风速为20.1 m/s,满足试验要求。试验中布置2组共6个变径三通管道进行试验。每次试验分别组合3个角度的三通以及3组不同的距离进行试验,共进行9组试验,每组试验时间控制在10 min,支管进口的煤料采用喂料的方式,尽量保证试验结果的合理性及准确性。在螺旋落料器处称重落煤的量,记录试验结果。在第3支管入口 (in4) 前布置流速计,检测其平均流速,并与仿真分析的3组结果进行对比。

|
| 图 15 主输送煤料管试验现场 Fig.15 The experiment site of the main coal conveying pipe |

|
| 图 16 铁路隧道落煤吸尘装置 Fig.16 The railway tunnel fallen coal dust collection device |
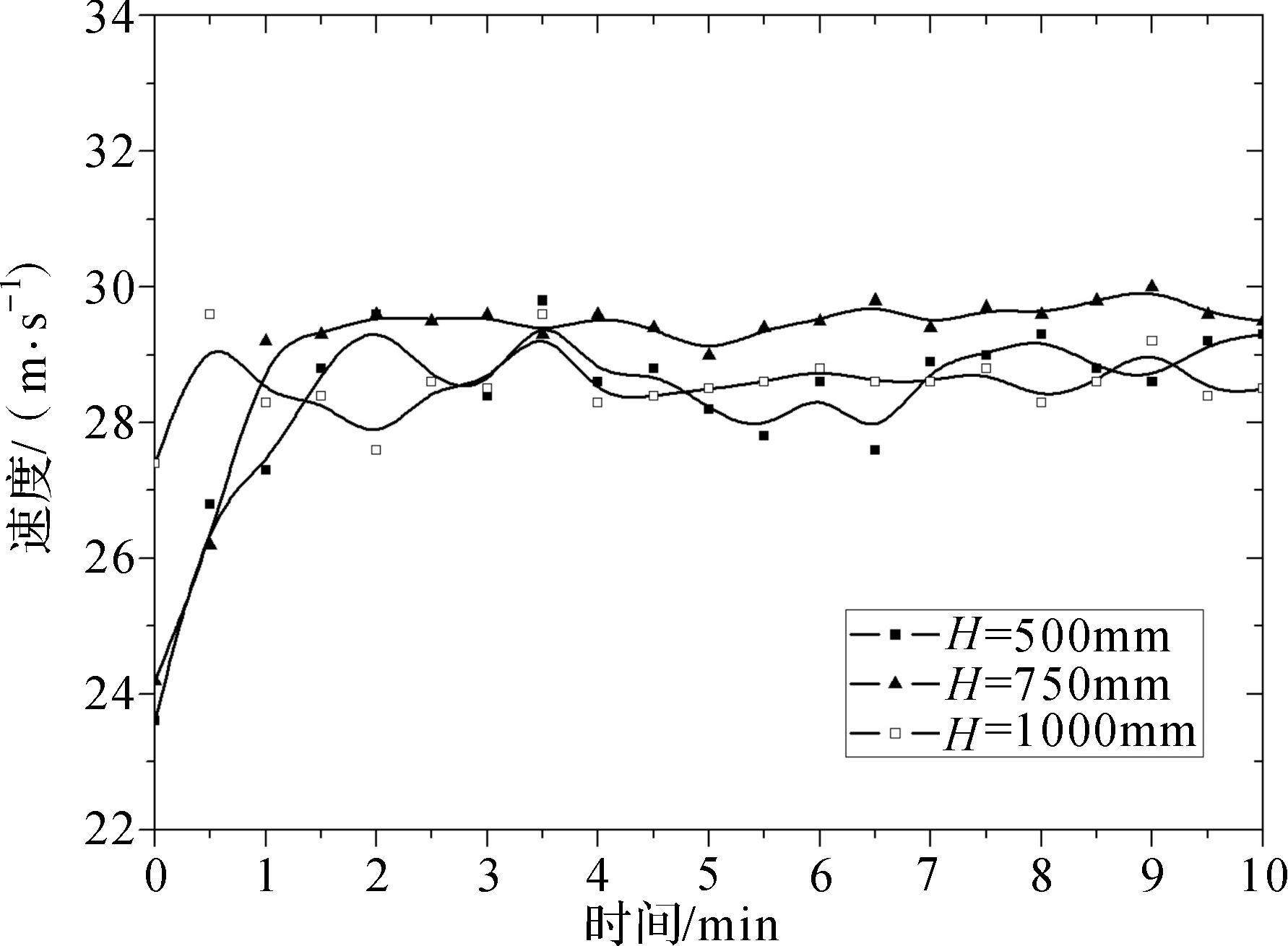
10 min内的流速检测数据如图 17所示,与仿真分析值v1=28.8 m/s,v2=29.4 m/s,v3=28.5 m/s结果相近。支管间距H=750 mm的情况下,其平均速度较大,稳定在29.5 m/s附近且波动幅度小;支管间距H=500 mm的情况下,其平均速度波动幅度大,各支管间速度影响较大;支管间距H=1 000 mm的情况下,其平均速度稳定在28.6 m/s附近。
|
| 图 17 主输送煤料管颗粒速度试验结果 (α=45°) Fig.17 Experimental results of particle velocity of the main coal conveying pipe |
隧道洞口输送煤料量试验结果如表 1所示,记录了在10 min内,相同主输送煤料管截面积下9组试验方案输送的煤料量。
| 支管间距/mm | 输送煤料量/kg | ||
| α=45° | α=60° | α=90° | |
| 500 | 1 432 | 1 325 | 1 190 |
| 750 | 1 643 | 1 525 | 1 420 |
| 1 000 | 1 580 | 1 480 | 1 310 |
分析表 1可得出,当支管间距H一定的情况下,随着入射角α的增大,出煤量减小;当入射角α一定时,支管间距H=500 mm的情况下出煤量最小,750 mm时出煤量最大,但与1 000 mm时相比相差较小。试验结果表明,当入射角α≈45°,支管间距H>750 mm时,煤料的输送量较大,即输送效率较高。
试验结果与仿真结果在优化选取支管间距H及入射角α时,所得结论相符。该结论对指导铁路隧道落煤吸尘装置的优化设计具有重要意义。
5 结论借助Fluent软件对新型铁路隧道落煤吸尘装置中特殊的管道进行数值模型分析,以指导主输送煤料管的优化及设计,并结合试验结果获得如下主要结论:
1) 对主输送煤料管静压进行分析,得到了支管与主输送煤料管交叉处的煤料颗粒的流动状况,结果表明,在该交叉处有涡流存在,支管流体与主输送煤料管流体发生充分混合,静压力下降。
2) 分析了不同入射角α下主输送煤料管流场,得到了不同入射角α与主输送煤料管进出口压降、颗粒出口速度的关系曲线,结果表明入射角α<45°时较为合理。
3) 分析了不同支管间距H下主输送煤料管流场,得到了颗粒的运动轨迹及不同支管间距H下主输送煤料管内颗粒速度的关系曲线,结果表明支管间距在750 mm附近时比较合理。
4) 通过实际隧道吸尘试验,分析比较不同入射角α及不同支管间距H下煤料的输送量,进一步验证了支管间距在750 mm附近以及入射角α在45°附近时煤料的输送量较大,为铁路隧道落煤吸尘装置管道的优化提供依据。
| [1] |
王旭荣.
重载铁路隧道清扫系统的研究与应用[J]. 科技情报开发与经济, 2011, 21(17): 192–194.
WANG Xu-rong. Research on and application of heavy haul railway's tunnel cleaning system[J]. Sci-Tech Information Development & Economy, 2011, 21(17): 192–194. DOI:10.3969/j.issn.1005-6033.2011.17.079 |
| [2] |
史天亮.
铁路道床吸污车吸尘机理分析及吸尘效果数值模拟[J]. 铁道建筑, 2014(4): 135–138.
SHI Tian-liang. Aspiration of railway solid pollution car mechanism analysis and numerical simulation of dust collection effect[J]. Railway Engineering, 2014(4): 135–138. |
| [3] |
肖益民, 柳波, 范永超.
Y型喉管流场分析及结构优化[J]. 计算机仿真, 2015, 32(5): 270–274.
XIAO Yi-min, LIU Bo, FAN Yong-chao. Analysis of flow field in Y-type pipe and optimization of its structure[J]. Computer Simulation, 2015, 32(5): 270–274. |
| [4] |
邹杰. 基于Fluent的三通内流体流场模拟分析研究[D]. 上海: 华东理工大学化工学院, 2014: 39-47.
ZOU Jie. Simulation and analysis on fluid folw field in tee based on Fluend soft[D]. Shanghai: East China University of Science and Technology, School of Chemical Engineering, 2014: 39-47. |
| [5] |
陶文铨.
数值传热学[M]. 西安: 西安交通大学出版社, 2001: 185-324.
TAO Wen-quan. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001: 185-324. |
| [6] | EL-BEHERY S M, HAMED M H, EL-KADI M A, et al. CFD prediction of air-solid flow in 180° curved duct[J]. Powder Technology, 2009, 191(1/2): 130–142. |
| [7] | EGHLIMI A, KOUZOUBOY A, FLETCHER C A J. A new RNG-based two-equation model for predicting turbulent gas-particle flows[C]//Proc Conf on CFD in Mineral & Metal Processing and Power Generation Industries. Melbourne, Jul. 3-4, 1997. |
| [8] | LIN K C, KENNEDY P, JACKSON T. Structures of water jets in a Mach 1.94 supersonic cross flow[C]// AIAA Meeting and Exhibit, Reno, NN, Jan. 5-8, 2004. |
| [9] | WU P K, KIRKENDALL K A, FULLER R P, et al. Breakup processes of liquid jets in subsonic cross flows[J]. Journal of Propulsion & Power, 2015, 13(1): 64–73. |
| [10] | OEVERRNANN M, GERBER S, BEHRENDT F. Euler-Lagrange/DEM simulation of wood gasification in a bubbling fluidized bed reactor[J]. Particuology, 2009, 7(4): 307–316. DOI:10.1016/j.partic.2009.04.004 |
| [11] |
袁竹林, 徐益谦.
用拉格朗日法对气固两相流动的数值模拟[J]. 发电设备, 1997(6): 27–29.
YUAN Zhu-lin, XU Yi-qian. Numerical simulation of gas-solid two phase flows with Lagrange's theorem[J]. Power Equipment, 1997(6): 27–29. |
| [12] | MURTHY B N, GHADGE R S, JOSHI J B. CFD simulations of gas-liquid-solid stirred reactor: prediction of critical impeller speed for solid suspension[J]. Chemical Engineering Science, 2007, 62(24): 7184–7195. DOI:10.1016/j.ces.2007.07.005 |
| [13] | TAMBURINI A, BRUCATO A, CIPOLLINA A, et al. CFD predictions of sufficient suspension conditions in solid-liquid agitated tanks[J]. International Journal of Nonlinear Sciences & Numerical Simulation, 2012, 13(6): 427–443. |
| [14] | ELBEHERY S M, HAMED M H, ELKADI M A, et al. Numerical simulation and CFD-based correlation of erosion threshold gas velocity in pipe bends[J]. CFD Letters, 2010, 2(1): 39–53. |
| [15] | WANG J. A CFD based correlation for erosion factor for long-radius elbows and bends[J]. Journal of Energy Resources Technology, 2003, 125(1): 26–34. DOI:10.1115/1.1514674 |
| [16] | CHUNG T J. Compuational fluid dynamics[M]. Cambridge: Cambridge University Press, 2002: 161-168. |
| [17] | CHEN P, SANYAL J, DUDUKOVIC M P. Numerical simulation of bubble columns flows: effect of different breakup and coalescence closures[J]. Chemical Engineering Science, 2005, 60(4): 1085–1101. DOI:10.1016/j.ces.2004.09.070 |
| [18] | SARTHOU A, VINCENT S, CALTAGIRONE J P, et al. Eulerian-Lagrangian grid coupling and penalty methods for the simulation of multiphase flows interacting with complex objects[J]. International Journal for Numerical Methods in Fluids, 2008, 56(8): 1093–1099. DOI:10.1002/(ISSN)1097-0363 |
| [19] |
张淼. 基于颗粒轨道模型的高速列车多相流数值模块和分析[D]. 杭州: 浙江大学航空航天学院, 2011: 7-19.
ZHANG Miao.Numerical simulation and analysis of high-speed train in multiphase flow based on particle orbit model scheme[D]. Hangzhou: Zhejiang University, School of Aeronautics and Astronautics, 2011: 7-19. |
| [20] | GIMBUN J, CHUAH T G, FAKHRU'L-RAZI A, et al. The influence of temperature and inlet velocity on cyclone pressure drop: a CFD study[J]. Chemical Engineering & Processing Process Intensification, 2005, 44(1): 7–12. |





