钛合金具有很高的比强度、较宽的工作温度范围、优异的腐蚀抗力等优点,在航天航空、原子能工业以及民用工业中得以广泛应用[1]。但在拥有优异综合性能的同时,钛合金材料也存在自身导热系数低、切削温度高、亲和力大、加工中粘刀和加工硬化现象严重的问题。这些缺陷使得钛合金成为一种典型的难加工材料。因此随着钛合金零件需求量的扩大,需寻求一种新的加工方法来满足钛合金加工生产的需要。
旋转超声磨削加工是将固结金刚石磨料工具的磨削加工与普通超声振动加工结为一体的复合加工[2-3]。旋转超声磨削相对于普通磨削有磨削力小、材料去除率高、加工表面质量好等优点,因此其应用越来越广泛。
自20世纪60年代起,国内外大量学者开始研究旋转超声加工技术,对脆性材料和韧性材料均开展了大量的研究[4-6],先后发表了许多关于该加工方法的理论模型和试验分析的研究成果。近几年随着计算机仿真技术的快速发展,使用有限元方法研究加工方法的机理相对于建立理论模型和开展试验研究而言有着独特的优势,因此越来越被广泛应用。Jiao等[7]通过建立旋转超声加工有限元模型研究了加工先进陶瓷过程中接触区应力应变分布和陶瓷材料边缘磨损情况;王艳等[8]建立了单颗磨粒超声辅助磨削有限元模型,研究了单颗磨粒磨削速度和磨削深度对磨削力和磨削温度的影响规律。然而,以上有限元模型要么将旋转超声磨削过程大大简化,要么只考虑了单颗磨粒对旋转超声磨削过程的影响,事实上,旋转超声磨削是固结磨粒磨具表面大量排列参差不齐、分布不规则且形状各异的磨粒共同在工件上耕犁、划擦以及高频超声振动下,工件表面层产生疲劳作用的结果,因此有限元模型中需要考虑多颗磨粒共同作用对旋转超声磨削过程的影响。
磨料粒度对旋转超声磨削材料去除率、磨具磨损均有显著影响[9],因此合理选择磨料粒度对加工效率与磨具寿命有较大意义。同时磨料粒度是本文虚拟磨具建模中的重要参数,其影响着固结磨粒磨具建模效果,因此本文基于磨具端面磨粒形貌建立了不同磨料粒度的多颗磨粒磨具模型。又因为磨削力是磨削过程中重要指标之一,在实践中又比较容易控制与测量,因此本文在Deform-3D中建立旋转超声磨削钛合金的有限元模型,研究固结磨粒磨具磨料粒度对旋转超声磨削力的影响规律,并通过开展旋转超声磨削钛合金试验验证多颗磨粒磨具模型与旋转超声磨削有限元模型的正确性。
1 固结磨粒磨具建模 1.1 磨粒密度使用光学显微镜 (OLYMPUS BX60M) 测量了磨料浓度为100%、磨料粒度为100#(125~150 μm) 的磨具端面形貌,如图 1所示。选取磨具端面不同区域拍摄磨粒形貌照片,并统计每张照片中金刚石磨粒的数目,得平均每张光镜照片中磨粒数为7.2个。每张光镜照片所对应的实际磨具端面面积是相同的,计算得固结磨粒磨具平均磨粒密度为6.313 1个/mm2。

|
| 图 1 磨具端面形貌 Fig.1 Topography of abrasive tool end surface |
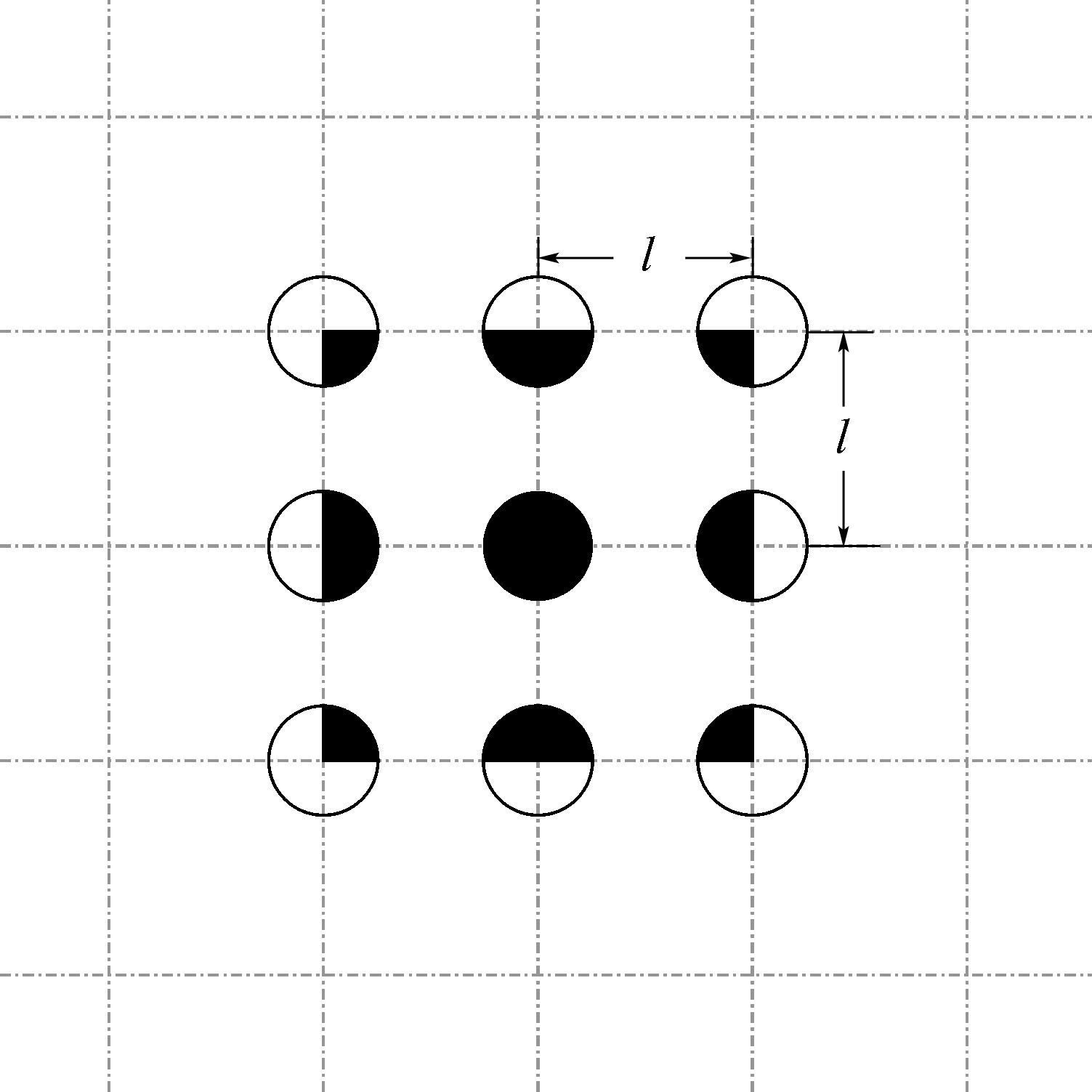
根据磨粒密度可以估算出磨粒平均间距[10]。如图 2所示,假设在正方形面上均匀分布的磨粒形状均为球体且粒径相等,球体磨粒中心与网格线交点重合。相邻网格线之间的长度为l,则在2l×2l面积上的等效磨粒数为4个 (图 2中黑色阴影部分)。根据1.1节中的磨粒密度就可以计算出磨料浓度为100%、磨料粒度为100#的固结磨粒磨具表面磨粒的平均间距为0.398 mm。
|
| 图 2 磨粒平均间距示意图 Fig.2 Sketch diagram of abrasive grain average interval |
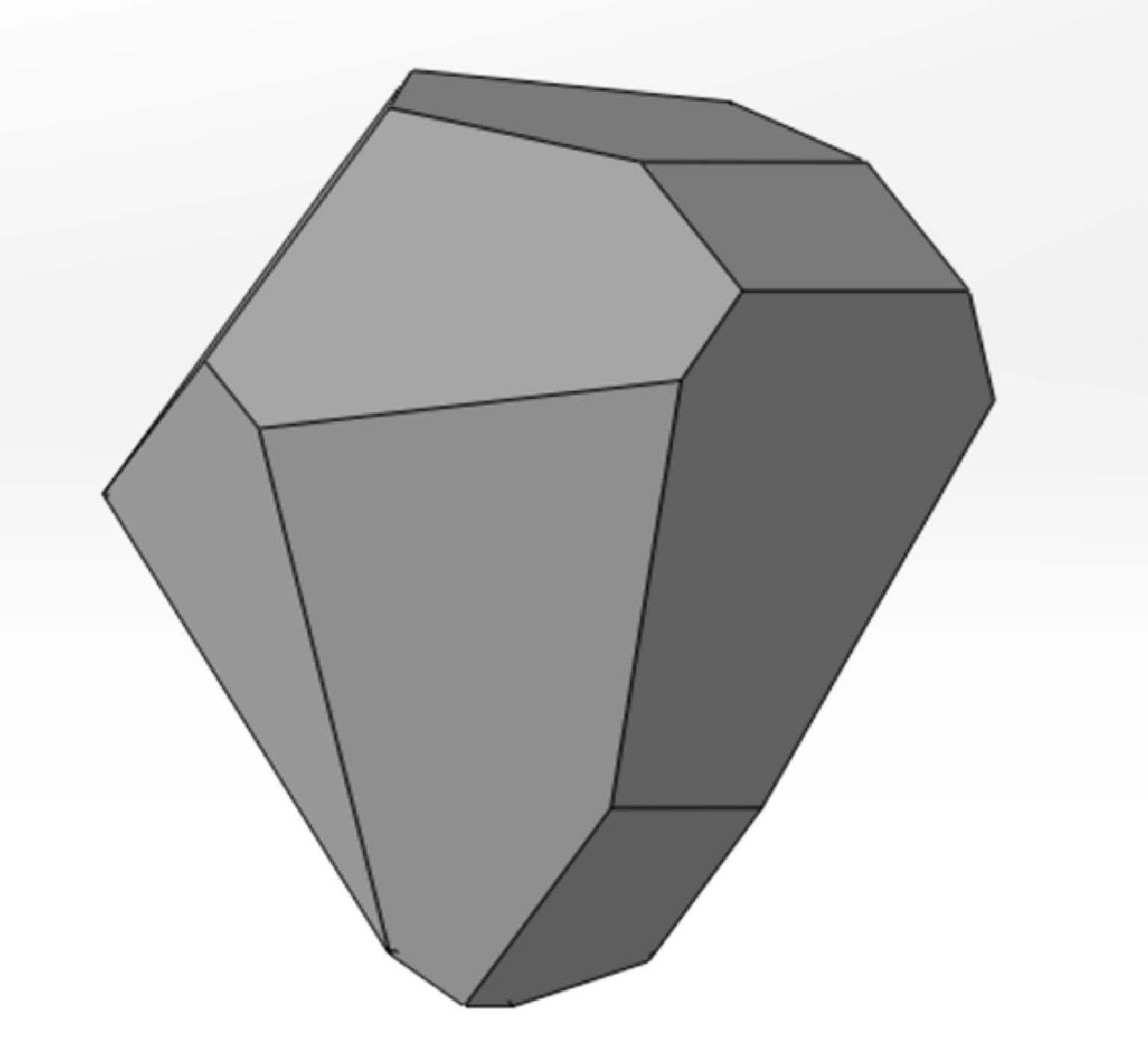
由磨粒光镜照片可以看出,磨粒的整体形状是不规则的,存在多个面、多个棱角。与球体磨粒、圆锥体磨粒和棱锥体磨粒相比,采用不规则多面体更能够准确描述磨粒的几何特征。本文采用随机空间平面切分正六面体来生成不规则多面体结构磨粒。随机切分平面与磨粒最小粒径的球面相切,保证切分之后的磨粒粒径在此粒度范围之内。随机平面切分磨粒次数随机,使得切分之后的磨粒满足磨粒形状随机的特点。单颗多面体磨粒如图 3所示。
|
| 图 3 多面体磨粒 Fig.3 Polyhedron abrasive grain |
在实际固结磨粒磨具表面,磨粒的分布是随机的,突出高度也各不相同,因此建立磨粒形状随机、分布随机的多颗磨粒磨具模型时必须考虑磨粒随机分布的特性。在磨粒随机分布方法中,磨粒的位置用其中心坐标表示,通过调节磨粒的中心坐标值控制磨粒在磨具端面随机分布,并通过磨粒绕其中心随机旋转来改变其姿态,实现位姿的随机。
在多颗磨粒磨具建模时为避免磨粒之间发生重叠,采用虚拟格子方法[11],即:将每一颗磨粒的位置约束在偏移区域内,每颗磨粒在偏移区域中的位置都通过随机坐标来控制。虚拟格子法中磨粒位置随机分布如图 4所示。为避免多颗磨粒互相重叠,考虑磨料粒度对随机分布的影响,磨粒之间的间距sg可表示为:

|
| 图 4 磨粒位置随机分布 Fig.4 Random distribution of abrasive grains position |
| ${s_{\rm{g}}} = l + {d_{\rm{m}}}$ | (1) |
式中dm为磨粒平均粒径。
则计算得磨粒之间的间距sg=0.535 5 mm。
1.5 建模过程多颗磨粒磨具由磨粒与磨具基体组成。本文只考虑磨粒与工件的接触,因此认为在旋转超声磨削钛合金的过程中,磨具基体把持着磨粒,当磨粒磨削工件时其并不与工件表面接触。本文建立与实验中固结磨粒磨具同等尺寸的虚拟多颗磨粒磨具模型,多颗磨粒磨具的外径、内径分别为10 mm和6 mm,具体实现步骤如下:
1) 在AutoCAD软件中生成正六面体磨粒模型。
2) 使用MATLAB软件生成磨粒位置偏移随机数和姿态角度随机数。将磨粒中心在偏移区域内进行随机偏移;以磨粒中心为旋转点,将偏移之后的磨粒绕旋转中心在X轴、Y轴、Z轴方向上随机旋转,实现磨粒姿态的随机。
3) 在Solidworks软件中使用随机平面切分正六面体磨粒,生成形状各异的多面体磨粒。
4) 建立磨具基体模型,将随机分布的磨粒装配到磨具基体中,磨粒顶端到基体表面的出刃高度随机。分别建立磨料浓度为100%,磨料粒度为60#(250~350 μm)、100#(125~150 μm)、150#(75~106 μm) 三种不同粒度的多颗磨粒磨具,其中磨料粒度为100#的磨具模型如图 5所示。

|
| 图 5 磨粒度为100#的多颗磨粒磨具模型 Fig.5 Model of multi grain abrasive tool with grain size of 100# |
Johnson-Cook (J-C) 材料模型能够反映材料应变率强化效应和温升软化效应,该模型利用变量乘积关系分别描述应变、应变率和温度的关系,本文采用J-C材料模型作为钛合金Ti6Al4V本构模型。该模型的具体表达式如下:
| $\sigma = (A + B{\varepsilon ^n})(1 + C{\rm{ln}}\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}})[1 - {(\frac{{T - {T_r}}}{{{T_m} - {T_r}}})^m}]$ | (2) |
式中:A为准静态下的屈服应力,MPa;B为硬化系数;n为应变硬化指数;ε为等效塑性应变;C为应变敏感系数;${{\rm{\dot \varepsilon }}}$为等效塑性应变率;${{\rm{\dot \varepsilon }}}$0为参考塑性应变率;m为温度敏感指数;T为材料的变形温度,℃;Tm,Tr分别为材料的熔点温度和室内温度 (20 ℃)。
| 参数 | A/MPa | B | n | C | m |
| 数值 | 968.88 | 567.17 | 0.375 | 0.039 4 | 1.3 |
将在Solidworks中建好的多颗磨粒磨具模型导入Deform-3D中进行前处理,为节约计算时间,在Deform-3D中建立内径为4 mm、外径为12 mm的圆环形工件模型。多颗磨粒磨具模型设置为刚体,圆环形钛合金工件设置为塑性体,采用相对方式划分网格,最小网格尺寸为0.09 mm。Deform-3D自带丰富的材料库,多颗磨粒磨具材料选择金刚石材料,工件材料选择钛合金Ti6Al4V。设置工件各表面为热交换面,模拟过程中的热传递系数设置为11 N/(s·mm·℃),磨具和工件材料的初始温度均为室温 (20 ℃)。工件的热容、热传导率[13]和杨氏模量[14]均随温度变化,杨氏模量随温度变化值如表 2所示。旋转超声磨削有限元模型如图 6所示。
| 温度/℃ | 0 | 200 | 400 | 600 | 800 | 1 000 |
| 杨氏模量/GPa | 112 | 104 | 92 | 76 | 56 | 32 |

|
| 图 6 旋转超声磨削有限元模型 Fig.6 Finite element model of rotary ultrasonic grinding |
本文仿真试验采用国际单位标准SI,仿真模式为热传递 (heat transfer) 和变形 (deform);采用拉格朗日增量算法 (Lagrangian incremental) 求解磨削力;求解器采用共轭梯度法,其为Deform-3D中最常用的求解器,此方法考虑了刀-屑摩擦及工件材料流动应力受应变、应变率和温度的影响。为避免网格严重畸变导致求解精度的降低或者计算不收敛,仿真试验中采用自适应网格重划分技术 (adapt remeshing)。设置多颗磨粒磨具绕固定轴线的转速实现磨具旋转运动。在Deform-3D中,设置磨具路径轨迹为空间中的任一轨迹,因此通过设置磨具运动方程实现磨具轴向超声振动,磨具轴向运动方程如下:
| $S = {f_{\rm{d}}} \times t + a{\rm{sin}}\left( {2\pi f \times t} \right)$ | (3) |
式中:S为磨具轴向位移,mm;a为超声振幅,mm;fd为超声频率,kHz;t为仿真时间,s。
2.3 旋转超声磨削有限元仿真分析使用3种不同磨料粒度的多颗磨粒磨具模型分别进行单因素仿真分析,研究磨料粒度对磨削力的影响。相关仿真参数如表 3所示。
| 仿真参数 | 主轴转速/(r·min) | 进给速度/(mm/s) | 超声振幅/μm | 超声频率/kHz |
| 数值 | 4 000 | 0.15 | 2 | 25 |
试验采用德国DMG ultrasonic 70超声振动机床,采用六因素 (主轴转速、进给速度、超声功率、磨料粒度、磨料浓度、超声频率) 三水平正交试验。本文主要针对不同磨料粒度对旋转超声磨削力的影响,因此磨料粒度每一水平的磨削力数值是除磨料粒度因素之外的所有因素取所有水平的平均磨削力。磨具结合剂类型为锡青铜基,所用磨具由郑州磨料磨具磨削研究所制备,磨具内径、外径分别为6 mm和10 mm。磨具振动频率为25 kHz,经测量,机床最大振幅约为3 μm,机床功率供给系统控制磨具振幅,超声功率设置为60%。工件材料为钛合金Ti6Al4V,工件尺寸为50 mm×50 mm×0.5 mm。试验系统冷却方式为外冷,采用钛合金专用切削液。固定在工件下面的三向测力仪和放大器获取试验磨削力信号。使用MATLAB软件分析磨削力的数据,每组试验重复3次,取3次试验数据的平均值作为试验磨削力数值。
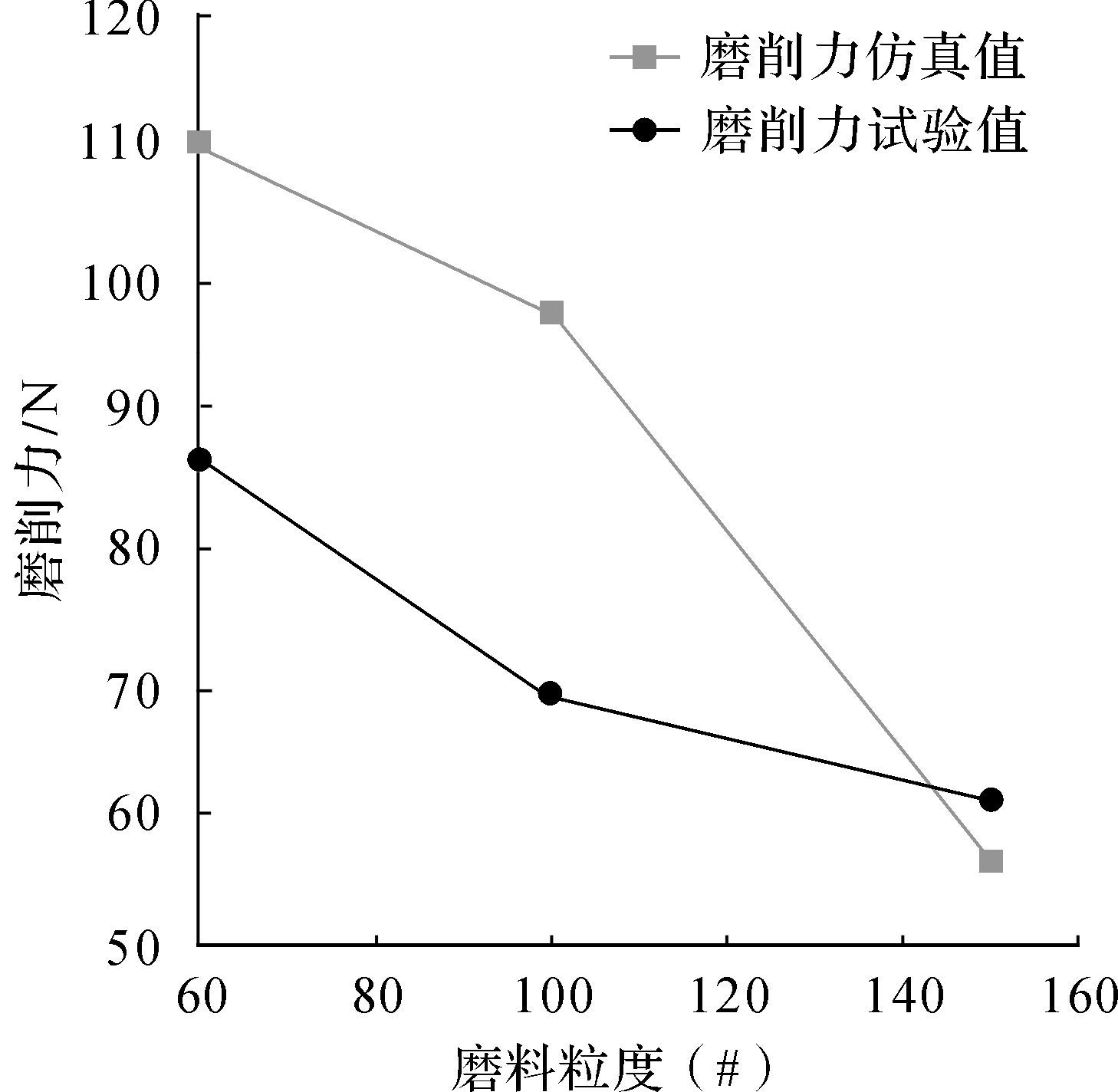
4 结果与分析取仿真和试验数据中稳定磨削阶段的磨削力作为最终磨削力数值,不同磨料粒度的多颗磨粒磨具磨削力的仿真值和试验值如表 4所示,多颗磨粒磨具磨料粒度对旋转超声磨削钛合金中磨削力的影响如图 7所示。
| 磨料粒度 | 60# | 100# | 150# |
| 磨削力仿真值/N | 110.35 | 97.60 | 56.38 |
| 磨削力试验值/N | 86.48 | 68.73 | 60.83 |
|
| 图 7 磨料粒度对磨削力的影响 Fig.7 The effect of the abrasive grain size on grinding force |
根据表 4和图 7的结果可知,磨料粒度增大,即磨粒半径减小,旋转超声磨削力减小,仿真结果和试验结果具有一致性。该结论与文献[15]中磨料粒度对旋转超声磨削钛合金磨削力的影响以及文献[16]中金刚石磨粒半径对旋转超声磨削制孔切削力的影响均一致,不同磨料粒度的仿真和试验,其一致的结果表明了本文中多颗磨粒磨具模型与旋转超声磨削有限元模型的正确性。
5 总结1) 基于磨料浓度为100%、磨料粒度为100#的固结磨粒磨具端面形貌和虚拟格子法建立了磨粒位置分布随机、形状大小随机的多颗磨粒磨具模型,也可以获得其他磨料浓度、磨料粒度的多颗磨粒磨具模型。
2) 基于多颗磨粒磨具模型建立旋转超声磨削钛合金有限元仿真模型,研究了不同磨料粒度对旋转超声磨削力的影响规律。结果表明:随着磨料粒度的增大,磨削力减小。
3) 使用不同磨料粒度磨具开展旋转超声磨削钛合金试验,验证有限元仿真模型中关于磨料粒度对磨削力的影响规律,试验结果和仿真结果具有一致性,说明多颗磨粒磨具模型与有限元模型的正确性,为多颗磨粒磨具旋转超声磨削的研究提供了新的思路。
| [1] |
金和喜, 魏克湘, 李建明, 等.
航空用钛合金研究进展[J]. 中国有色金属学报, 2015, 25(2): 280–292.
JIN He-xi, WEI Ke-xiang, LI Jian-ming, et al. Research development of titanium alloy in aerospace industry[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 280–292. |
| [2] |
房丰州, 倪浩, 宫虎.
硬脆材料的旋转超声辅助加工[J]. 纳米技术与精密工程, 2014, 12(3): 227–234.
FANG Feng-zhou, NI Hao, GONG Hu. Rotary ultrasonic machining of hard and brittle materials[J]. Nanotechnology and Precision Engineering, 2014, 12(3): 227–234. |
| [3] | WANG Y, LIN B, ZHANG X F. Research on the system matching model in ultrasonic vibration-assisted grinding[J]. International Journal of Advanced Manufacturing Technology, 2014, 70(1/4): 449–458. |
| [4] |
郑书友, 冯平法, 徐西鹏.
旋转超声加工技术研究进展[J]. 清华大学学报 (自然科学版), 2009, 49(11): 1799–1804.
ZHENG Shu-you, FENG Ping-fa, XU Xi-peng. Development trends of rotary ultrasonic machining technology[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(11): 1799–1804. |
| [5] |
张承龙, 冯平法, 吴志军, 等.
旋转超声钻削的切削力数学模型及试验研究[J]. 机械工程学报, 2011, 47(15): 149–155.
ZHANG Cheng-long, FENG Ping-fa, WU Zhi-jun, et al. Mathematical modeling and experimental research for cutting force in rotary ultrasonic drilling[J]. Journal of Mechanical Engineering, 2011, 47(15): 149–155. |
| [6] |
魏士亮, 赵鸿, 薛开, 等.
工程陶瓷脆性域旋转超声磨削加工切削力研究[J]. 哈尔滨工程大学学报, 2014, 35(8): 976–981.
WEI Shi-liang, ZHAO Hong, XUE Kai, et al. Investigation of the cutting force of rotary ultrasonic grinding machining in the brittle regime for engineering ceramics[J]. Journal of Harbin Engineering University, 2014, 35(8): 976–981. |
| [7] | JIAO Y, LIU W J, PEI Z J, et al. Study on edge chipping in rotary ultrasonic machining of ceramics: an integration of designed experiments and finite element method analysis[J]. Journal of Manufacturing Science & Engineering, 2005, 127(4): 752–728. |
| [8] |
王艳, 张省, 王帅, 等.
基于Deform-3D轴向超声辅助磨削仿真试验[J]. 系统仿真学报, 2015, 27(1): 104–111.
WANG Yan, ZHENG Sheng, WANG Shuai, et al. Simulation experiment of ultrasonic assisted grinding along axial direction on basis of Deform-3D[J]. Journal of System Simulation, 2015, 27(1): 104–111. |
| [9] |
荆君涛, 刘运凤, 李占杰, 等.
旋转超声磨削加工中影响磨具寿命的结构参数优化[J]. 光学精密工程, 2013, 21(4): 972–979.
JING Jun-tao, LIU Yun-feng, LI Zhan-jie, et al. Optimization of structure parameters of affecting tool life in rotary ultrasonic grinding machining[J]. Optics and Precision Engineering, 2013, 21(4): 972–979. |
| [10] |
张祥雷, 姚斌, 冯伟, 等.
基于多颗磨粒随机分布的虚拟砂轮建模及磨削力预测[J]. 航空学报, 2014, 35(12): 3489–3498.
ZHANG Xiang-lei, YAO Bin, FENG Wei, et al. Model of virtual grinding wheel based on random distribution of multi abrasive grains and prediction of grinding force[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3489–3498. |
| [11] |
宿崇, 许立, 李明高, 等.
磨粒建模方法与切削过程仿真研究[J]. 航空学报, 2012, 33(11): 2130–2135.
SU Chong, XU Li, LI Ming-gao, et al. Study on modeling and cutting simulation of abrasive grains[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2130–2135. |
| [12] |
刘东, 陈五一.
钛合金TC4切削过程流动应力模型研究[J]. 塑性工程学报, 2008, 15(1): 167–171.
LIU Dong, CHEN Wu-yi. Research on the flow stress model of titanium alloy TC4 during the cutting process[J]. Journal of Plasticity Engineering, 2008, 15(1): 167–171. |
| [13] |
黄旭.
先进航空钛合金材料与应用[M]. 北京: 国防工业出版社, 2012: 58-63.
HUANG Xu. Advanced aeronautical titanium alloys and applications[M]. Beijing: National Defence Industry Press, 2012: 58-63. |
| [14] |
周兆锋, 陈明和, 范平, 等.
钛合金TC4热应力校形的数值模拟[J]. 南京航空航天大学学报, 2009, 41(5): 620–625.
ZHOU Zhao-feng, CHEN Ming-he, FAN Ping, et al. Numerical simulation on hot sizing of titanium alloy TC4[J]. Journal of Nanjing University of Aeronautitics & Astronautics, 2009, 41(5): 620–625. |
| [15] | CHURI N J, PEI Z J, TREADWELL C. Rotary ultrasonic machining of titanium alloy (Ti6Al4V): effects of tool variables[J]. International Journal of Precision Technology, 2007, 1(1): 85–96. DOI:10.1504/IJPTECH.2007.015347 |
| [16] |
秦娜. 旋转超声波磨削制孔的切削力建模与试验研究[D]. 大连: 大连理工大学机械工程学院, 2011: 32-43.
QIN Na. Cutting force model and experimental study on core drilling by ultrasonic vibration assisted grinding[D]. Dalian: Dalian University of Technology, School of Mechanical Engineering, 2011: 32-43. |



