2. 中国西南电子技术研究所, 四川 成都 610036
2. Southwest China of Institute of Electronic Technology, Chengdu 610036, China
机电耦合是指机械结构位移场和电磁场相互作用、相互影响的物理现象[1]。随着信息技术的发展,复杂电子设备涉及精密机械、电磁学、热学等多学科,其电性能的实现不仅依赖于各学科领域的设计水平,更取决于多学科的有机结合。例如,随着天线向高频段、高增益、高密度方向发展,其机械结构、电磁场及热场之间的相互影响越来越明显。机电耦合常常导致高密度天线阵的性能难以提高。
近年来,机电耦合引起了众多学者的关注[2-6]。国外很早就在机电耦合及多物理场耦合问题上开展了研究,如:用边界元法研究耦合接触[7]及电子设备中不同场间的耦合问题[8];Zocchi研究了反射面天线测量的均方根误差问题[9];Steinberg对电子设备从器件级到系统级的力学特性进行了研究,提出了使电子设备在恶劣环境下仍能正常工作的方法[10];Voeller指出在未来25种新技术中,多场耦合问题将会受到高度重视[11]。在国内:段宝岩分析了国内电子装备机电耦合研究的现状与发展[12];余伟等研究了平板裂缝天线子阵形变后的方向图的变化[13];Liu对非线性机电耦合系统延时反馈进行了研究[14];彭博等研究了电子产品多物理场耦合,提出一种面向电子产品的多场耦合协同仿真方法[15]。在2013年召开的第94期“双清论坛”上,与会专家分析了电子装备机电耦合问题在国防、航空等领域及学科发展中面临的挑战,建议将该专题作为未来3~5年国家自然科学基金优先资助方向[16],可以看出我国在机电耦合研究方面的重视程度。
在电子产品机电耦合分析中,不同物理场间的数据传递方法是研究的重点和难点。本文针对微波天线的机电耦合问题,提出一种基于模型重构的机电耦合仿真方法并开发了相应的仿真平台。在仿真平台中,首先利用ANSYS Workbench进行力学分析;然后利用APDL语言编写相关的接口程序,获取并导出由结构分析产生的变形网格,利用NURBS (Non-Uniform Rational B-Spline) 曲面重构出变形几何体;最后将变形的几何实体导入电磁场分析软件HFSS中进行天线性能的计算,并与变形前天线的性能进行对比,实现微波天线的机电耦合分析。
1 结构变形对天线性能的影响平板裂缝天线是一种常见的微波天线,具有薄壁、多层腔体的结构,由激励、耦合及辐射波导组成,依靠众多裂缝辐射的能量在空间形成方向图。在实际工作中,由振动引起的结构变形可使裂缝位置、姿态及互耦效应发生变化,导致天线电性能变化[1, 17]。
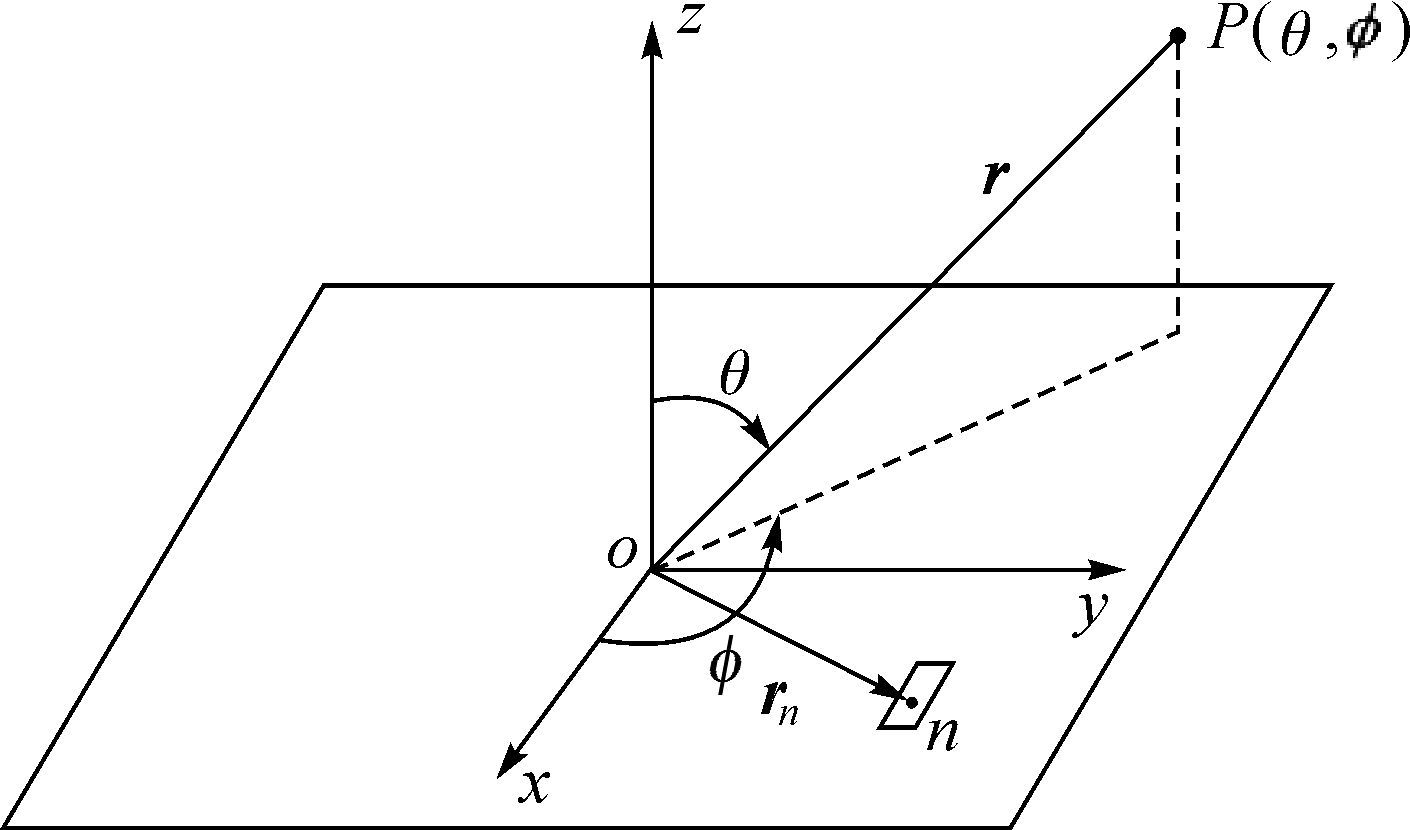
图 1所示为简化的平板裂缝天线模型,天线辐射阵面位于xoy平面,z轴正向为阵面法向,原点o为阵面几何中心。辐射阵面开有大量辐射缝,电磁能量通过辐射缝辐射到外部空间。为清晰描述天线坐标关系,图中只给出了第n条辐射缝,缝隙中心坐标rn=(xn,yn,0),n=1,2,…,N,N为阵面缝隙总数。在观察点P(θ,ø) 处,天线电场方向图为:
|
| 图 1 简化的平板裂缝天线模型 Fig.1 The simplified model of the slot array antenna |
| $\mathit{\boldsymbol{E}}\left( {\theta ,\phi } \right) = \sum\limits_{n = 1}^N {} {V_n}\cdot{\mathit{\boldsymbol{f}}_n}({l_n},{w_n},\theta ,\phi )\cdot{e^{{\rm{j}}{\eta _n} + {jk{\mathit{\boldsymbol{r}}_n} \cdot \mathit{\boldsymbol{\hat r}}}}}$ | (1) |
式中:Vn与ηn分别为第n个缝隙辐射电压的幅度和相位;fn(ln,wn,θ,ø) 为第n个缝隙的单元方向图;ln,wn分别为第n个缝隙的长度和宽度;θ和ø为点P的观察方向;k为传播常数,
fn(ln,wn,θ,ø) 的形式为:
| $\eqalign{ & {\mathit{\boldsymbol{f}}_n}({l_n},{w_n},\theta ,\phi ) = {\rm{j}}k({H_n}({l_n},{w_n},\theta ,v)sin{\rm{ }}\phi \times {{\mathit{\boldsymbol{\hat a}}}_\theta } + \cr & \quad \quad \quad \quad \quad \quad \quad \quad {H_n}({l_n},{w_n},\theta ,\phi )cos{\rm{ }}\phi cos{\rm{ }}\theta \times {{\mathit{\boldsymbol{\hat a}}}_\phi }) \cr} $ | (2) |
式中:
| $\eqalign{ & {H_n}({l_n},{w_n},\theta ,\phi ) = {{{{2\pi } \over {{l_n}}}\left( {{{{\rm{cos}}k{l_n}{\rm{sin }}\theta cos{\rm{ }}\phi } \over 2}} \right)} \over {{{\left( {{\pi \over {{l_n}}}} \right)}^2} - {{\left( {k{\rm{sin }}\theta {\rm{cos }}\phi } \right)}^2}}} \times \cr & \quad \quad \quad \quad \quad \quad \quad \quad {{{\rm{sin}}(k{\rm{sin }}\theta {\rm{sin }}\phi \times {w_n}/2)} \over {k{\rm{sin }}\theta {\rm{sin }}\phi \times {w_n}/2}} \cr} $ | (3) |
文献[18]研究了环境载荷对天线结构变形 (辐射缝位置和指向、缝腔变形) 的影响,并分析了上述结构变形所引起的天线口径面幅值和相位分布误差,建立了如下的机电耦合模型:
| $\eqalign{ & \mathit{\boldsymbol{E}}\left( {\theta ,\phi } \right) = \sum\limits_{n = 1}^N {} {A_n}\cdot{\mathit{\boldsymbol{f}}_n}({l_n},{w_n},\theta ,\phi ,\mathit{\boldsymbol{\delta }}\left( \mathit{\boldsymbol{\beta }} \right),\gamma ) \times \cr & \quad \quad \quad \quad {{V'}_n}\mathit{\boldsymbol{\delta }}\left( \mathit{\boldsymbol{\beta }} \right){e^{{\rm{j}}\eta {\prime _n}\left( {\mathit{\boldsymbol{\delta }}\left( \mathit{\boldsymbol{\beta }} \right),\gamma } \right)}}\cdot{{\rm{e}}^{{\rm{j}}{\varphi _n}(\mathit{\boldsymbol{\delta }}\left( \mathit{\boldsymbol{\beta }} \right),\gamma )}} \cr} $ | (4) |
式中:
式 (4) 的耦合模型是依据辐射缝电压受到缝腔内部变形和外部空间辐射互耦的影响而导致其幅度和相位发生变化,将结构位移场的参数和天线制造、装配过程中产生的随机误差,引入天线远场方向图的计算中,具有较强的理论意义,但在具体的应用中,天线实际的变形量及制造、装配过程的随机误差等参数很难确定,因此仅通过解析方法来研究天线机电耦合特性略显不足。为此,本文提出一种基于模型重构的机电耦合仿真方法。
2 基于模型重构的机电耦合仿真方法的实现 2.1 模型重构理论NURBS曲面是一种特殊形式的分片有理参数多项式曲面,其中每一个子曲面片定义在单位正方域中某个具有非零面积的子矩形域上。应用NURBS曲面重构变形后的模型时,首先需要对变形后的网格进行分块划分,然后对每个块域进行拟合和重构。其具体过程如下:
首先对网格中的每一个数据点pi (i=0,1,…,n) 实行参数化分割,采用福利 (Foley) 参数化 (又称修正弦长参数化) 方法进行。
| $\left\{ \matrix{ {\mu _0} = 0 \hfill \cr {\mu _i} = {\mu _{i - 1}} + {k_i}\left| {\Delta {p_{i - 1}}} \right| \hfill \cr} \right.$ | (5) |
式中:i=1,2,…,n,修正系数ki>1。
然后根据参数化结果,构造NURBS曲线与曲面。NURBS曲线可表示为:
| $p\left( u \right) = {{\sum\limits_{i = 0}^n {{\omega _i}{d_i}{N_{i,k}}\left( u \right)} } \over {\sum\limits_{i = 0}^n {} {\omega _i}{N_{i,k}}\left( u \right)}}$ | (6) |
式中:di,ωi(i=0,1,…,n) 分别为控制顶点及与控制顶点相联系的权因子;Ni,k(u) 为k次规范B样条基函数。可根据德布尔-考克斯递推公式求出:
| $\left\{ \matrix{ {N_{i,0}}\left( u \right) = \left\{ {\matrix{ {1,} & {{u_i} \le u \le {u_{i + 1}}} \cr {0,} & {其他} \cr } } \right. \hfill \cr {N_{i,k}}\left( u \right) = {{u - {u_i}} \over {{u_{i + k}} - {u_i}}}{N_{i,k - 1}}\left( u \right) + {{{u_{i + k + 1}} - u} \over {{u_{i + k + 1}} - {u_{i + 1}}}}{N_{i + 1,k - 1}}\left( u \right) \hfill \cr} \right.$ | (7) |
NURBS曲面类似NURBS曲线,一个k×l次的NURBS曲面可表示为:
| $p\left( {u,v} \right) = {{\sum\limits_{j = 0}^n {} \sum\limits_{m = 0}^n {} {\omega _{i,j}}{d_{i,j}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)} \over {\sum\limits_{j = 0}^n {} \sum\limits_{m = 0}^n {} {\omega _{i,j}}{N_{i,k}}\left( u \right){N_{j,l}}\left( v \right)}}$ | (8) |
式中:权因子ωi,j是附加的形状参数;k,l分别表示u,v的次数。
2.2 基于模型重构的天线机电耦合仿真方法的实现及仿真平台的开发基于模型重构的天线机电耦合仿真主要包括3个步骤:首先在ANSYS Workbench中进行天线的力学仿真;其次是对变形网格的提取、输出及基于变形网格的模型重构;最后将变形后的模型导入专业的天线仿真软件中进行计算,并与变形前的天线性能进行对比,得到天线的机电耦合特性。该仿真方法流程如图 2所示。

|
| 图 2 基于模型重构的天线机电耦合仿真方法流程图 Fig.2 Flow chart of simulation method of antenna electromechanical coupling based on model reconstruction |
在变形网格的获取与输出过程中,需要根据ANSYS提供的参数化设计语言APDL开发一种专用接口程序,其核心思想是将结构分析后的位移 (即受力后的变形) 加载到有限元模型的节点上,并更新有限元模型,获得天线变形后的网格模型。通过UPGEOM,FACTOR,LSTEP,SBSTEP,Fname,Ext等语句实现,其中FACTOR为节点位移,LSTEP为结果数据的载荷步编号,SBSTEP为结果数据的子步编号,Fname为文件名,Ext为文件扩展名。在对变形网格重构的过程中,其核心是对导入的变形网格进行表面检测并利用NURBS对表面网格进行填充,重构出变形后的几何实体。
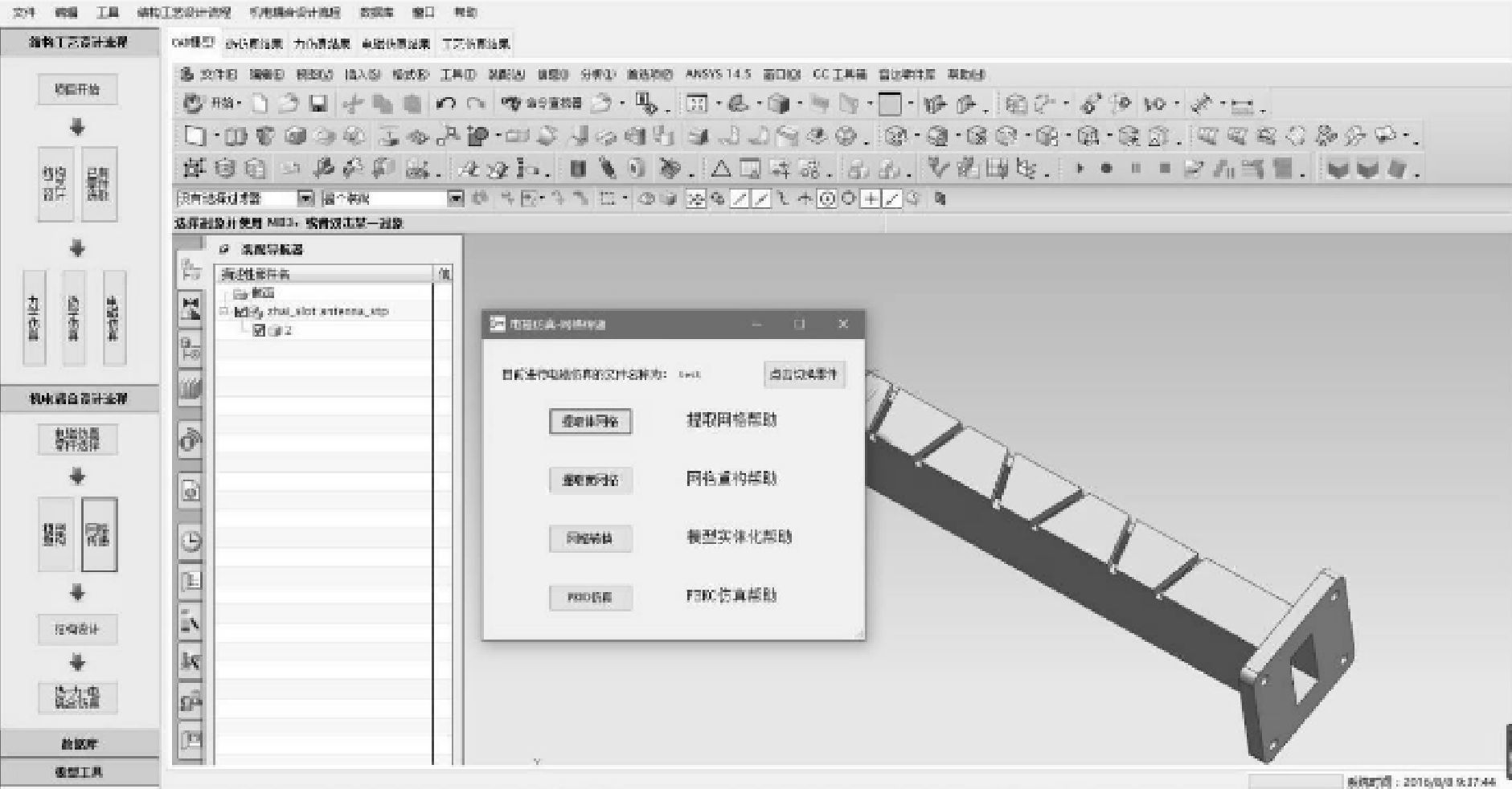
根据图 2的仿真流程,开发了一个基于模型重构的天线机电耦合仿真分析软件平台,在该平台上集成了力学分析软件ANSYS Workbench、模型重构软件Finite Element Modeler及电磁场分析软件HFSS,再对相应的接口进行设计,可非常方便地实现基于模型重构的天线机电耦合分析。仿真平台如图 3所示。
|
| 图 3 基于模型重构的天线机电耦合仿真平台 Fig.3 The simulation platform of antenna electromechanical coupling based on model reconstruction |
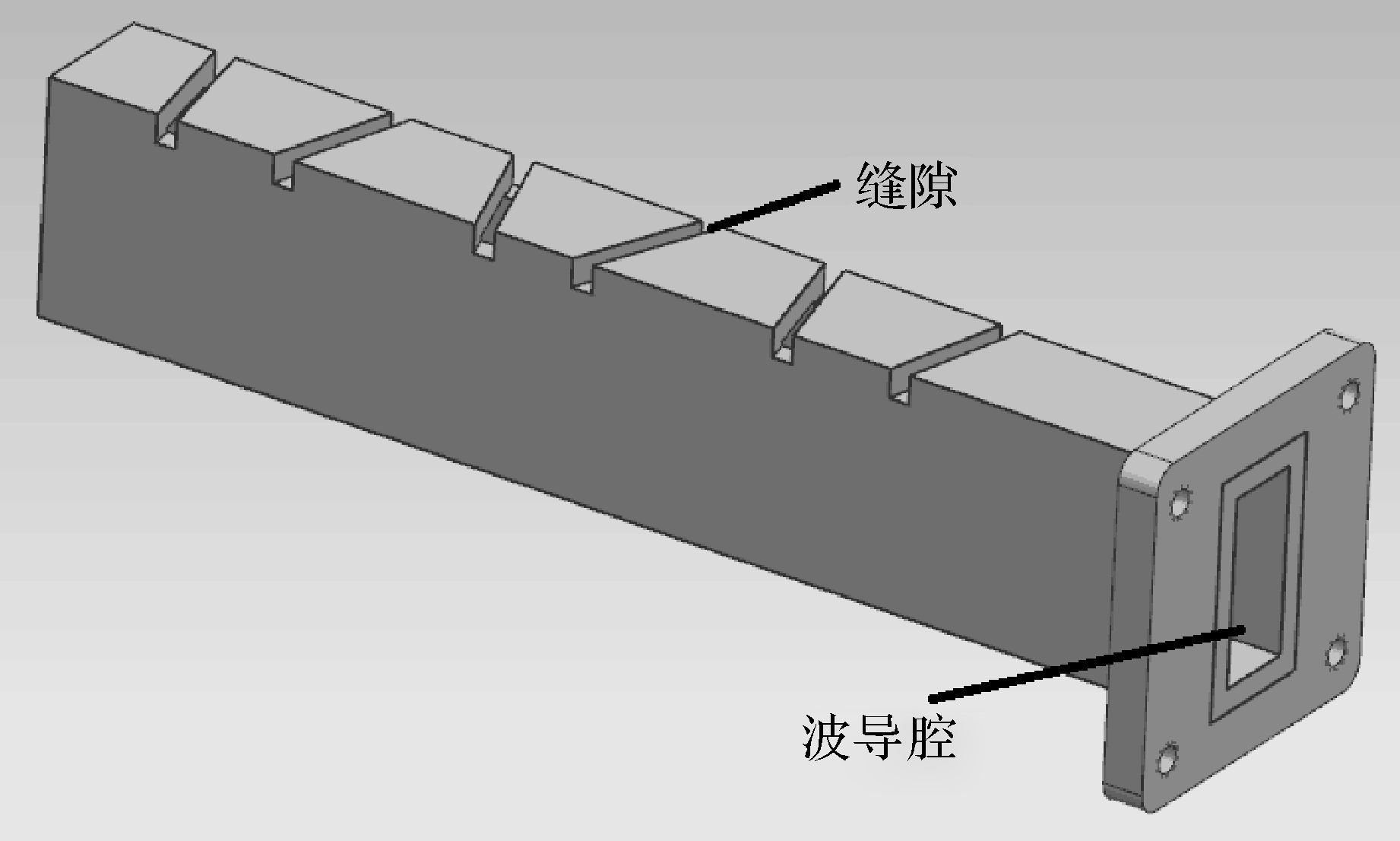
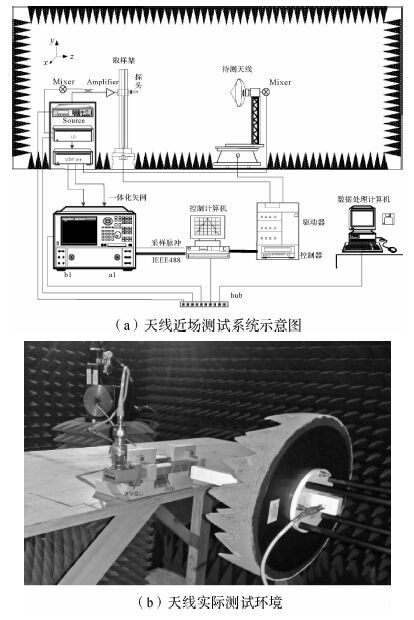
本节对窄边开缝的波导缝隙天线进行机电耦合仿真和测试,来验证本文方法的正确性。天线实体模型如图 4所示,天线近场测试系统示意图及实际测试环境如图 5所示。测试所加载的力为50 000 N,天线的最大变形为1.0 mm。
|
| 图 4 波导缝隙天线的实体模型 Fig.4 Solid model of waveguide slot antenna |
|
| 图 5 天线的近场测试系统和实际测试环境 Fig.5 The near-field measurement system and actual test environment for antenna |
在仿真平台中,首先利用ANSYS Workbench进行与测试环境相同的仿真,获得天线受力后的变形网格如图 6(a)所示。利用该变形网格重构的天线几何模型如图 6(b)所示。将该模型导入电磁分析软件HFSS进行仿真,结果如图 6(c)所示。在HFSS中计算天线电性能,变形前后天线性能的仿真与测试结果如表 1所示,天线增益的对比如图 7所示。
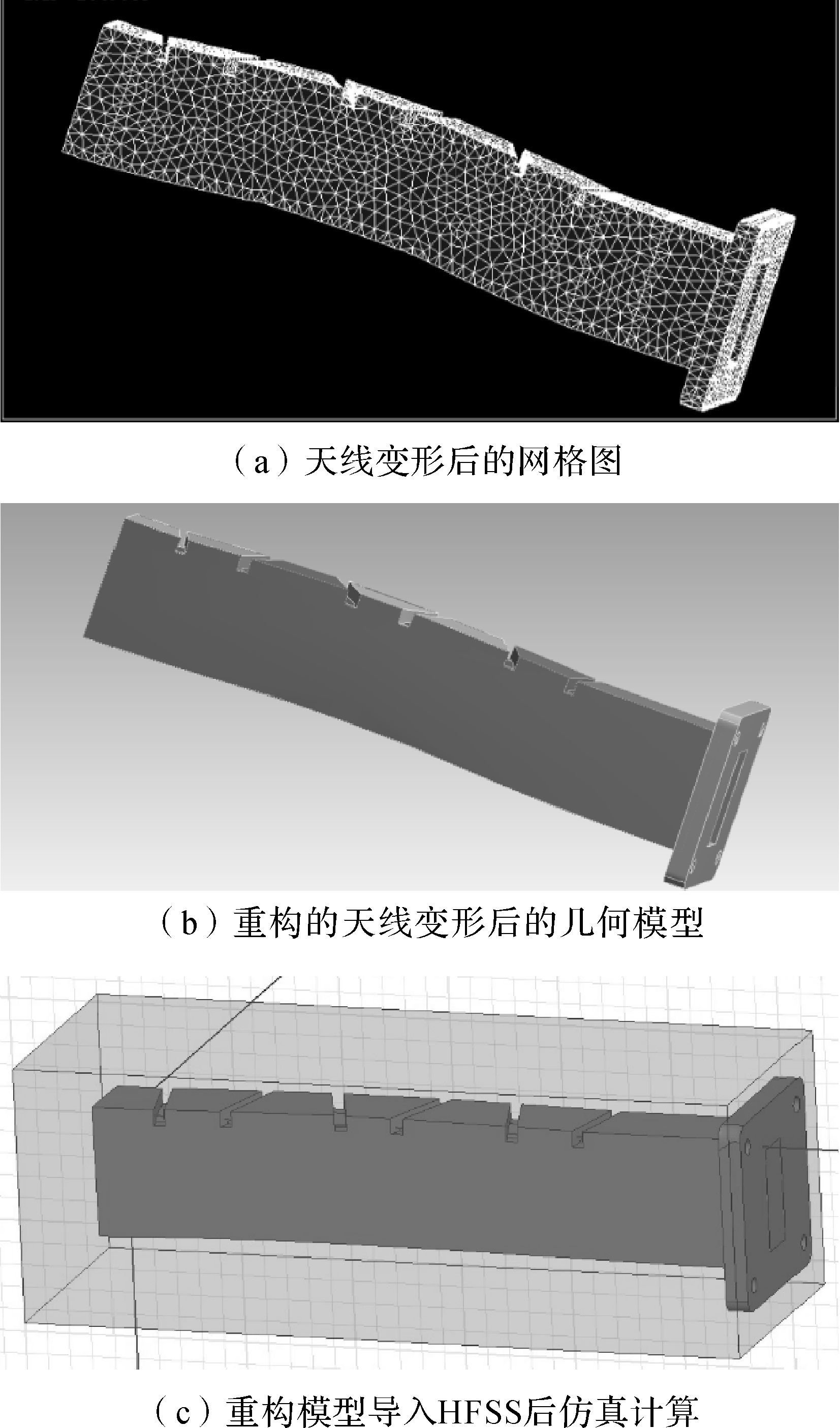
|
| 图 6 基于模型重构的天线机电耦合仿真分析过程 Fig.6 Simulation analysis process of antenna electromechanical coupling based on model reconstruction |
| 方式 | 天线的最大变形/mm | 天线的增益/dB | 最大增益变化/dB | |
| 变形前 | 变形后 | |||
| 仿真 | 1.007 | 13.397 | 13.104 | 0.293 |
| 测试 | 0.994 | 12.536 | 12.261 | 0.275 |
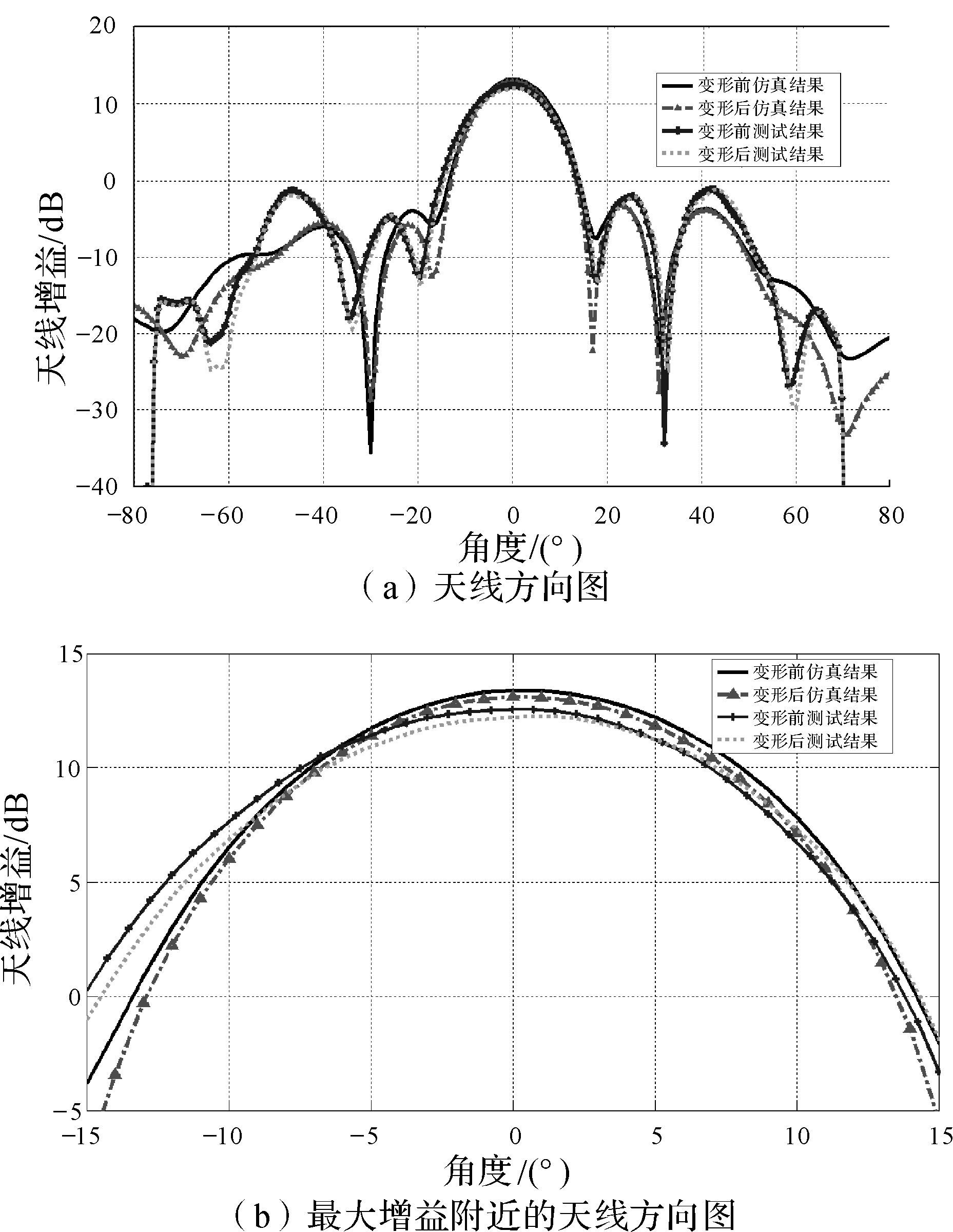
|
| 图 7 变形前后天线增益的仿真和测试结果对比 Fig.7 Comparison of simulation and measurement results of antenna gain before and after deformation |
对比图 4和图 6可以发现,变形后,天线的辐射缝隙和波导腔发生了变化,导致缝电压幅度及缝电压相位发生了相应的改变,可能会影响到天线的性能。从表 1和图 7可以看出,天线变形会导致天线增益下降,使天线性能降低。对比测试数据与本文基于模型重构的机电耦合仿真方法的数据可以看出,测试和仿真结果吻合较好,特别是变形对天线最大增益的影响上,2种方法得出的结果非常接近,表明本文方法具有较高的精度。
5 结束语本文针对微波天线的机电耦合问题,提出了一种基于模型重构的机电耦合仿真方法并开发了相应的仿真平台。在仿真平台中,集成了力学分析软件ANSYS Workbench、模型重构软件Finite Element Modeler及电磁场分析软件HFSS,开发了不同软件间的接口,可以非常方便地进行天线机电耦合仿真。以波导缝隙天线为例,将实验测试的结果与该平台的仿真结果进行对比,得到以下结论:1) 天线受力变形将导致天线的最大增益降低;2) 在天线性能的计算中,仿真结果比实际测试结果偏大约0.8 dB,但是在变形导致天线增益降低的计算中,仿真与测试的值相差很小。综上可以看出,本文基于模型重构的机电耦合仿真方法,可用于天线产品设计阶段的机电耦合研究。
| [1] |
段宝岩.
电子装备机电耦合理论、方法及应用[M]. 北京: 科学出版社, 2011: 10.
DUAN Bao-yan. Electromechanical coupling theory, method and application of electronic equipment[M]. Beijing: Science Press, 2011: 10. |
| [2] | STEPHAN R, ARNON L, GIL U, et al. Analysis of microstructural induced enhancement of electromechanical coupling in soft dielectrics[J]. Applied Physics Letters, 2013, 102(15): 151905. DOI:10.1063/1.4801775 |
| [3] | ERNESTO T, ANTONINO M, ROCCO R, et al. Numerical integration of coupled equations for high-speed electromechanical devices[J]. IEEE Transactions on Magnetics, 2015, 51(3): 7203404. |
| [4] | PETER T B, BELA L, JOZSEF P. A coupled analytical-finite element technique for the calculation of radiation form tilted rectangular waveguide slot antennas[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1666–1669. DOI:10.1109/TMAG.2007.915981 |
| [5] | WANG C S, DUAN B Y, ZHANG F S, et al. Coupled structural-electromagnetic-thermal modelling and analysis of active phased array antennas[J]. IET Microwaves, Antennas & Propagation, 2010, 4(2): 247–257. |
| [6] | AL-HATTAMLEH O, JEONG C, RICHARDS R F, et al. The effect of design and process parameters on electromechanical coupling for a thin-film PZT membrane[J]. Journal of Microelectromechanical Systems, 2006, 15(6): 1715–1725. DOI:10.1109/JMEMS.2006.883575 |
| [7] | RIEGER A, WRIGGERS P. Adaptive methods for thermomechanical coupled contact problems[J]. Journal of Numerical Methods in Engineering, 2004, 59(6): 871–894. DOI:10.1002/(ISSN)1097-0207 |
| [8] | MBARKI R, BACCAM N, DAYAL K, et al. Piezoelectricity above the curie temperature combining flexoelectricity and functional grading to enable high-temperature electromechanical coupling[J]. Applied Physics Letters, 2014, 104(12): 122904. DOI:10.1063/1.4869478 |
| [9] | ZOCCHI F E. Estimation of the accuracy of a reflector surface form the measured RMS error[J]. IEEE Transactions on Instrumentation & Measurement, 2005, 54(5): 2124–2129. |
| [10] | STEINBERG S D. Vibration analysis for electronic equipment[M]. New York: Wiley InterScience, 1988: 56-60. |
| [11] | VOELLER J. 25 technologies to watch[J]. Civil Engineering, 2001, 71(8): 64–69. |
| [12] |
段宝岩.
电子装备机电耦合研究的现状与发展[J]. 中国科学 (信息科学), 2015, 45(3): 299–312.
DUAN Bao-yan. Review of electromechanical coupling of electronic equipment[J]. Science China (information Science), 2015, 45(3): 299–312. |
| [13] |
余伟, 顾卫军, 郭先松.
平板裂缝天线子阵形变后的方向图分析[J]. 现代雷达, 2008, 28(12): 70–73.
YU Wei, GU Wei-jun, GUO Xian-song. Pattern analysis for deformed subarray of planar slotted antenna array[J]. Modern Radar, 2008, 28(12): 70–73. DOI:10.3969/j.issn.1004-7859.2008.12.019 |
| [14] | LIU Shuang, ZHAO Shuang-shuang, WANG Zhao-long, et al. Stability and Hopf bifurcation of a nonlinear electromechanical coupling system with time delay feedback[J]. Chinese Physics B, 2015, 24(1): 014501. DOI:10.1088/1674-1056/24/1/014501 |
| [15] |
彭博, 杜平安, 夏汉良, 等.
电子产品多物理场耦合仿真方法研究[J]. 系统仿真学报, 2010, 22(4): 853–857.
PENG Bo, DU Ping-an, XIA Han-liang, et al. Research on simulation method of electronics products multi-field coupling system[J]. Journal of System Simulation, 2010, 22(4): 853–857. |
| [16] |
王国彪, 段宝岩, 黎明, 等.
高精度电子装备机电耦合研究进展[J]. 中国科学基金, 2014, 28(4): 241–250.
WANG Guo-biao, DUAN Bao-yan, LI Ming, et al. Electromechanical coupling on high accuracy electronic equipments: a review[J]. Bulletin of National Natural Science Foundation of China, 2014, 28(4): 241–250. |
| [17] |
王从思, 王伟, 宋立伟.
微波天线多场耦合理论与技术[M]. 北京: 科学出版社, 2015: 152-155.
WANG Cong-si, WANG Wei, SONG Li-wei. The theory and technology of multi field coupling of microwave antennas[M]. Beijing: Science Press, 2015: 152-155. |
| [18] | SONG Li-wei, DUAN Bao-yan, ZHENG Fei, et al. Performance of planar slotted waveguide arrays with surface distortion[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(9): 3218–3223. DOI:10.1109/TAP.2011.2161537 |



