2. 浙江科技学院 机械与汽车工程学院, 浙江 杭州 310023;
3. 浙江大华技术股份有限公司, 浙江 杭州 310053
2. School of Mechanical and Automotive Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, China;
3. Zhejiang Dahua Technology Co., Ltd., Hangzhou 310053, China
减振器是现代车辆上必不可少的部件[1],它通过为车辆提供符合要求的阻尼力来发挥作用,吸收车辆行驶过程中来自路面的各种振动,避免发生严重的侧倾及俯仰,从而提高车辆的行驶平顺性和操控稳定性,提高乘坐的舒适性。减振器阻尼力异常会影响减振器与车辆悬架的匹配,最终影响行车安全性[2]。
现代车辆普遍采用筒式液压减振器,双筒式液压减振器因其工艺简单、性能稳定、成本低的优点,在乘用车中应用最为广泛,其阻尼力的产生是多个部件共同作用的结果,影响因素较多。国外学者从不同方面对筒式液压减振器的阻尼力建模方法进行了研究,如:Herr等[3]应用计算流体力学分析了液压阀件的液流特性、压力分布特性,建立了某减振器的物理模型;Duym等[4-5]针对油液可压缩性及气泡等因素,分析了减振器阻力滞环特性的建模方法,并且针对车辆系统进行动力学仿真,通过测试数据反推模型参数,来探讨减振器物理模型的建模方法;Lang及Besinger等[6-7]在建立的非参数化模型中将减振器阻尼力表达为包含多运动状态参数的函数;Sudarshan等[8]对一款摩托车用的液压减振器进行了有限元分析,并与试验结果对比,表明有限元仿真的正确性。国内部分学者对减振器进行实际结构简化后获得了许多实用性较强的物理参数模型、等效参数化模型、非参数化模型和数值模型[9-12]。陈轶杰等[13]研究了减振器节流阀片的变形对减振器阻尼力的影响情况,得出结构参数跟材料特性是影响阀片变形的因素。周长城等[14]进行了减振器阀片厚度的优化设计,提出了叠加阀片的等效厚度计算公式,并进行了整车试验。现有文献中很少有通过调整减振器阀组件的零件尺寸公差和尺寸链来提高减振器可靠性及使用寿命的方法。
目前国内外研究主要集中在减振器的数学建模、性能参数优化及跟悬架的匹配方面,较少针对减振器可靠性分析减振器尺寸参数、油液黏度等对阻尼力的影响,及其在预测分析减振器寿命方面的作用。本文以某型车辆使用的双筒式液压减振器为研究对象,根据减振器阻尼力的产生机理,建立阻尼力数学模型,并通过试验进行验证。根据减振器的尺寸及性能参数的分布,采用ANSYS中的Design Exploration模块,使用响应面法确定减振器各参数的灵敏度,并使用蒙特卡洛抽样方法,考虑主要影响因素的随机性,获得减振器的阻尼力分布情况,为减振器的可靠性设计提供依据。
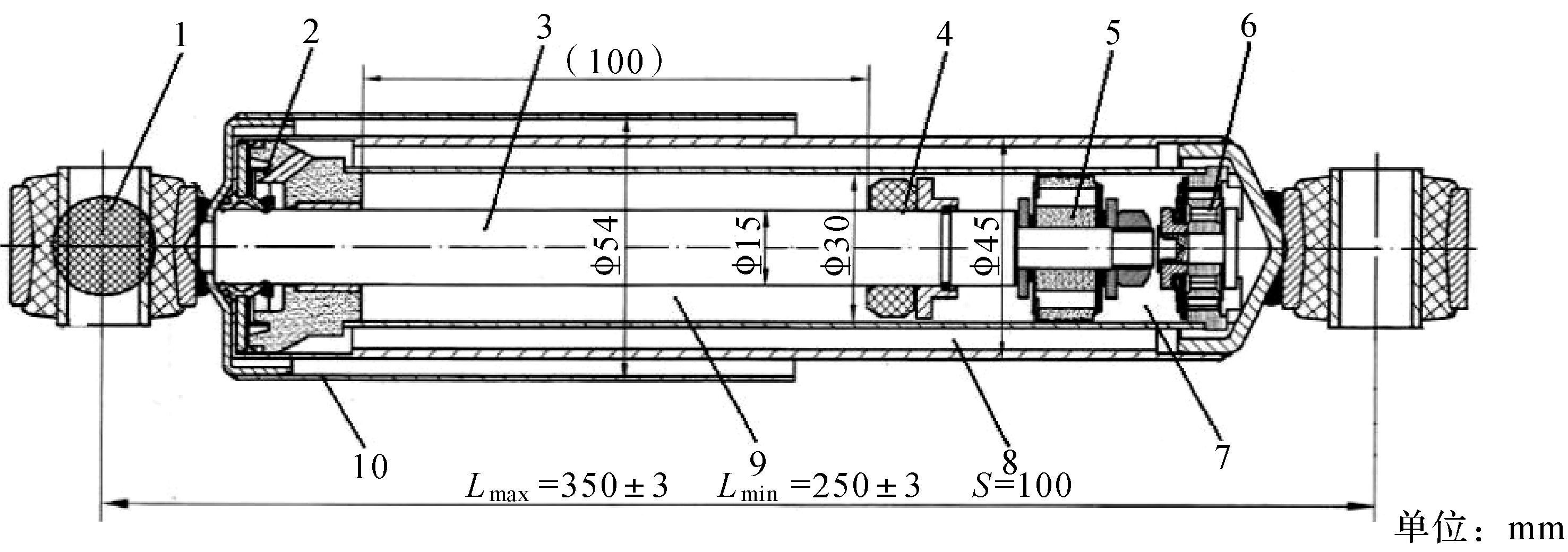
1 阻尼力模型的建立本文研究的双筒式液压减振器结构如图 1所示,图中L表示减振器长度,mm;S为可动行程,mm。活塞杆3的上端与导向器及油封总成2配合;活塞5把减振器的内腔分成上腔9和下腔7;在活塞5及底阀座6上各有2个供液体流通的阀,分别为复原阀、流通阀以及压缩阀、补偿阀;贮油缸筒和工作缸筒之间形成储油腔8。减振器的阻尼力按照复原和压缩工作行程可以分为复原力和压缩力。
|
| 1—橡胶衬套;2—导向器油封总成;3—活塞杆总成;4—限位块;5—活塞阀总成;6—底阀总成;7—压缩腔 (下腔);8—储油腔;9—复原腔 (上腔);10—金属垫盖 图 1 双筒式液压减振器结构图 Fig.1 Structure diagram of the double-tube hydraulic damper |
根据减振器活塞及底阀上的流通孔尺寸及形状,应用流体力学对油液流过阻尼孔产生的节流压差进行求解[15],并结合活塞受力平衡条件,得到减振器的阻尼力值。在定义复原阻尼力为正、压缩阻尼力为负的情况下,可以用式 (1) 计算减振器的总阻尼力:
| $F = ({A_{\rm{h}}} - {A_{\rm{g}}}){p_1} - {A_{\rm{h}}}{p_2} + {F_{\rm{f}}}{\rm{sign}}\;\dot x$ | (1) |
式中:Ah为活塞截面积;Ag为活塞杆截面积;p1为减振器上腔的瞬时压力;p2为下腔的瞬时压力;Ff为摩擦力;sign
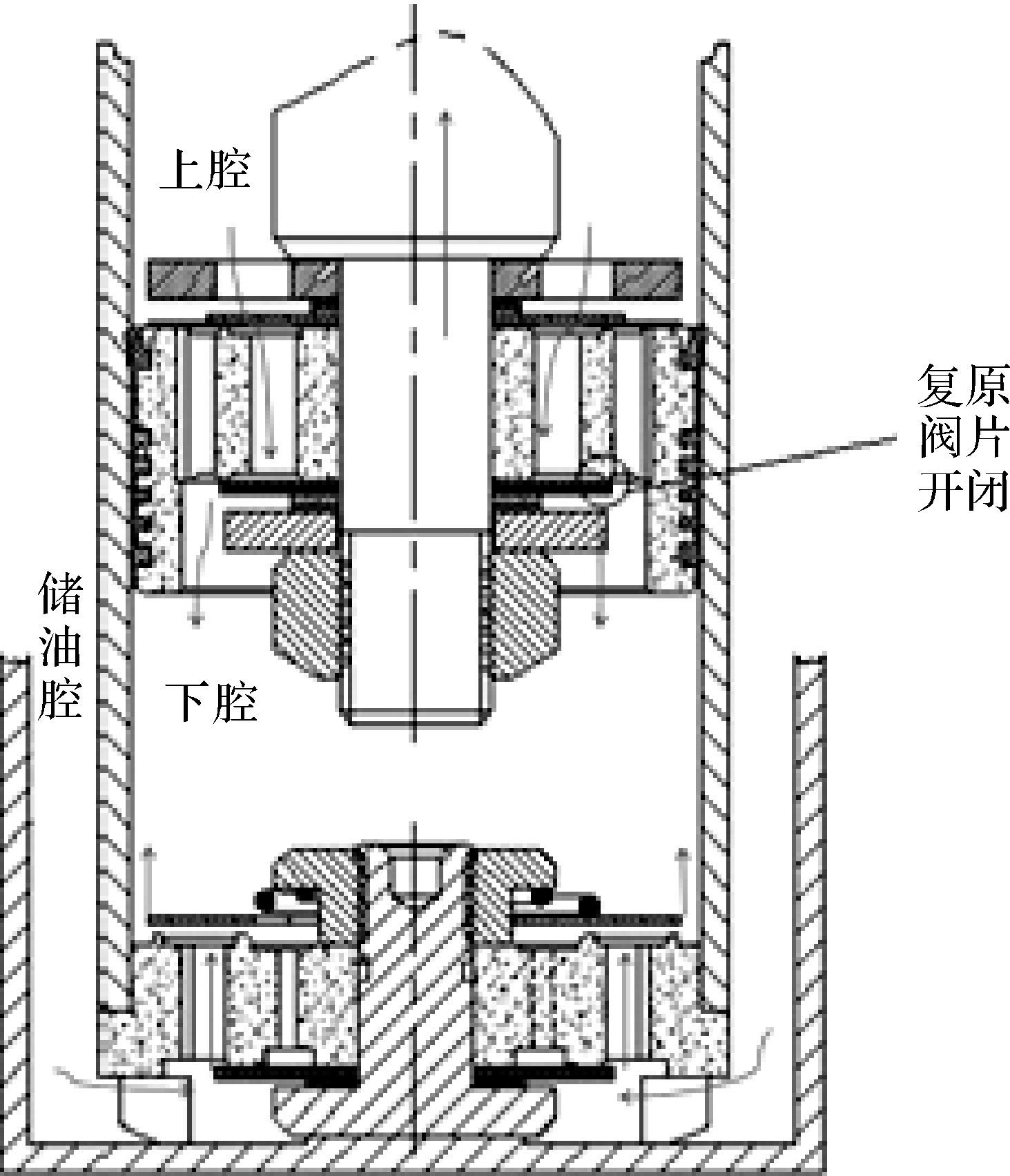
根据复原 (压缩) 阀是否开启,减振器的阻尼力又分为复原 (压缩) 阀开启前/后的复原 (压缩) 力。假设减振器复原阀和压缩阀的开启压力分别为p0,p′0,所对应的活塞速度分别为v0,v′0,当活塞的实际速度vh<v0时,复原力主要由活塞阀体上的通道、节流阀片与活塞形成的常通孔节流产生;当活塞的实际速度vh≥v0时,油液通过活塞阀体上的通道后,一部分从常通孔流出,另一部分从复原阀开启的缝隙中流出,复原行程中油液流动情况如图 2所示。压缩行程中的阻尼力主要通过压缩阀产生,其机理与复原行程相似。根据阻尼力的产生机理建立阻尼力数学模型[16]。
|
| 图 2 复原行程中油液流动示意图 Fig.2 Schematic diagram of fluid flow in the recovery stroke |
复原行程中,复原阀开启前油液流动情况如图 3所示,假设油液流过活塞阀座上的流量为q1-1,形成的压降为Δp1-1,用短孔流动理论进行求解;通过节流阀片上常通孔的流量为q1-2,形成的压降为Δp1-2,用缝隙流动理论求解。
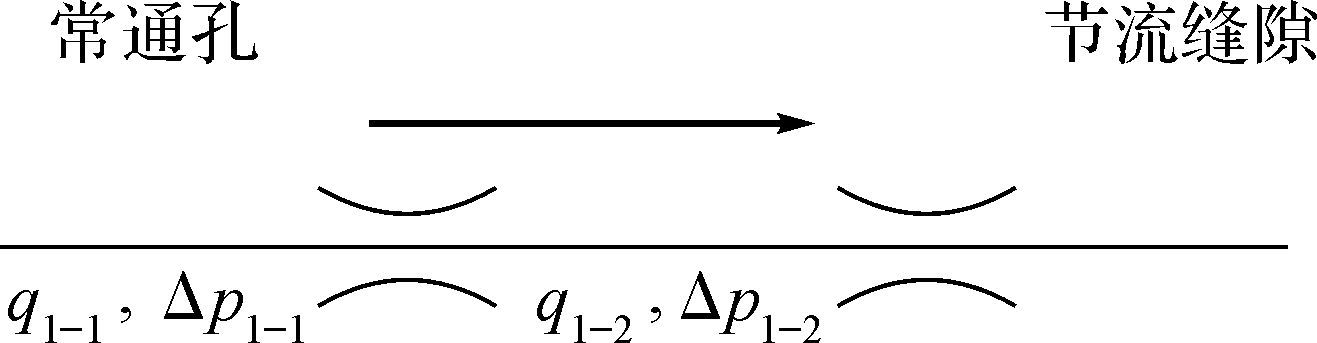
|
| 图 3 复原行程中复原阀开启前油液流动示意图 Fig.3 Schematic diagram of fluid flow in the recovery stroke before recovery valve opened |
| ${q_{1 - 1}} = {C_{\rm{q}}}{A_1}\sqrt {{2 \over \rho }\Delta {p_{1 - 1}}} = {C_{\rm{q}}}{{\pi d_1^2{N_1}} \over 4}\sqrt {{2 \over \rho }\Delta {p_{1 - 1}}} $ | (2) |
| ${q_{1 - 2}} = {{{b_1}\delta _1^3\Delta p} \over {12\mu {l_1}}} = {{{N_2}{b_{k1}}\delta _1^3\Delta {p_{1 - 2}}} \over {12\mu {l_1}}}$ | (3) |
| ${q_{1 - 1}} = {q_{1 - 2}} = \left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right){v_{\rm{h}}}$ | (4) |
由于p1-p2=Δp1-1+Δp1-2,可以得到复原阀开启前的复原力表达式为:
| $\eqalign{ & {F_{{\rm{fq}}}} = {{8\rho } \over {C_{\rm{q}}^{\rm{2}}N_1^2{\pi ^2}d_1^4}}{\left( {{A_{\rm{h}}} - A_{\rm{g}}^{}} \right)^3}v_{\rm{h}}^{\rm{2}} + \cr & \quad {{12\mu {l_1}} \over {{N_2}{b_{k1}}\delta _1^3}}{\left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right)^2}{v_{\rm{h}}} + f \cr} $ | (5) |
式中:ρ为油液密度;Cq为流通系数;N1,N2分别为常通孔及节流缝隙个数;d1为常通孔直径;μ为油液黏度;l1,bk1,δ1分别为缝隙流通长度、宽度及高度。
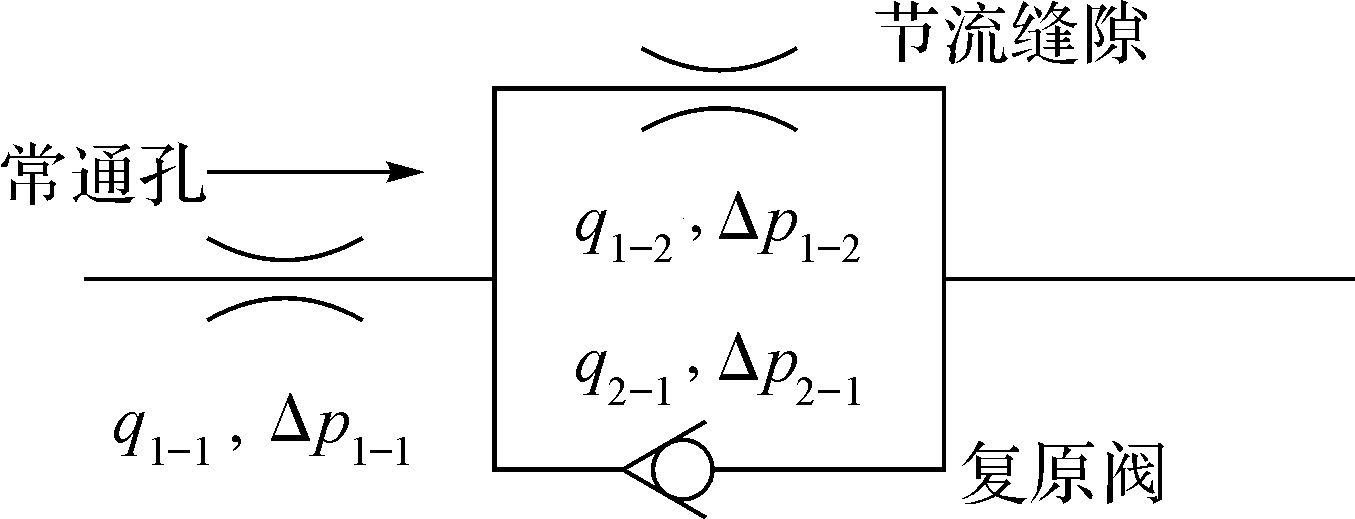
1.2 复原阀开启后的复原力复原行程中,复原阀开启后油液流动情况如图 4所示,假设通过复原阀片变形后产生的缝隙流量为q2-1,产生的压降为Δp2-1,用环形平面缝隙理论进行研究。
|
| 图 4 复原行程中复原阀开启后油液流动示意图 Fig.4 Schematic diagram of fluid flow in the recovery stroke after recovery valve opened |
| ${q_{2 - 1}} = {{\pi \delta _2^3\Delta {p_{2 - 1}}} \over {6\mu {\rm{ln}}\left( {{r_{{\rm{b1}}}}/{r_{{\rm{k1}}}}} \right)}}$ | (6) |
| ${p_1} - {p_2} = \Delta {p_{1 - 1}} + \Delta {p_{1 - 2}} = \Delta {p_{1 - 1}} + \Delta {p_{2 - 1}}$ | (7) |
| ${q_{1 - 1}} = {q_{1 - 2}} + {q_{2 - 1}} = \left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right){v_{\rm{h}}}$ | (8) |
联立各式求解,可以得到复原阀开启后的复原力表达式为:
| $\eqalign{ & {F_{{\rm{fh}}}} = {{8\rho } \over {{C_q}^2{N_1}^2{\pi ^2}{d_1}^4}}{\left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right)^3}v_{\rm{h}}^{\rm{2}} + \cr & {\left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right)^2}{v_{\rm{h}}}/\left[ {{{{N_2}{b_{{\rm{k}}1}}\delta _1^3} \over {12\mu {l_1}}} + {{\pi \delta _2^3} \over {6\mu {\rm{ln}}\left( {{r_{{\rm{b1}}}}/{r_{{\rm{k1}}}}} \right)}}} \right] + f \cr} $ | (9) |
式中:δ2为复原阀开启高度;rb1为复原阀片外半径;rk1为复原阀片节流半径。
由于阀片的开启高度跟上、下腔的压差有关,在进行模拟仿真的时候,需要对阀片开启高度δ2进行分析:
| ${\delta _2} = {{{A_{{\rm{r1}}}}\left( {\Delta {p_{2 - 1}} - {p_0}} \right)} \over {{k_1}}}$ | (10) |
代入式 (6) 可得:
| ${q_{2 - 1}} = {{\pi A_{{\rm{r1}}}^{\rm{3}}{{\left( {\Delta {p_{2 - 1}} - {p_0}} \right)}^3}\Delta {p_{2 - 1}}} \over {6\mu {\rm{ln}}\left( {{r_{{\rm{b1}}}}/{r_{{\rm{k}}1}}} \right)k_1^3}}$ | (11) |
又:
| ${q_{2 - 1}} = \left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right){v_{\rm{h}}} - {{{N_2}{b_{{\rm{k1}}}}\delta _1^3\Delta {p_{1 - 2}}} \over {12\mu {l_1}}}$ | (12) |
得到:
| $\Delta {p_{2 - 1}} = f\left( {{k_1},{A_{{\rm{r}}1}},{q_{2 - 1}},\mu ,{r_{{\rm{b1}}}},{r_{{\rm{k1}}}},{p_0}} \right)$ |
式中:Ar1为阀片的受力面积;k1为阀片特性系数;p0为复原阀开阀压差,可以通过对减振器进行多次试验并寻找开阀速度点得出。
最后得到开阀后复原力的精确表达式为:
| $\eqalign{ & {F_{{\rm{fq}}}} = {{8\rho } \over {{C_{\rm{q}}}^2{N_1}^2{\pi ^2}{d_1}^4}}{\left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right)^3}{v_{\rm{h}}}^2 + \left( {{A_{\rm{h}}} - {A_{\rm{g}}}} \right) \cr & f\left( {{k_1},{A_{{\rm{r1}}}},{q_{2 - 1}},\mu ,{r_{{\rm{b1}}}},{r_{{\rm{k1}}}},{p_0}} \right) + f \cr} $ | (13) |
分析方法与复原阀开启前相似,得到压缩阀开启前的压缩力表达式为:
| ${F_{{\rm{yq}}}} = {{8\rho } \over {{C_{\rm{q}}}^2{N_3}^2{\pi ^2}{d_2}^4}}{A_{\rm{g}}}^3{v_{\rm{h}}}^2 + {{12\mu {l_2}} \over {{N_4}{b_{{\rm{k2}}}}{\delta _3}^3}}{A_{\rm{g}}}^2{v_{\rm{h}}} + f$ | (14) |
分析方法与复原阀开启后相似,得到压缩阀开启后的压缩力为:
| $\eqalign{ & {F_{{\rm{yh}}}} = {{8\rho } \over {{C_{\rm{q}}}^{\rm{2}}{N_3}^2{\pi ^2}{d_2}^4}}{A_{\rm{g}}}^3{v_{\rm{h}}}^2 + \cr & \quad \quad {A_{\rm{g}}}^{\rm{2}}{v_h}/\left[ {{{{N_4}{b_{{\rm{k2}}}}{\delta _3}^3} \over {12\mu {l_2}}} + {{\pi {\delta _4}^3} \over {6\mu {\rm{ln}}\left( {{r_{{\rm{b2}}}}/{r_{{\rm{k2}}}}} \right)}}} \right] + f \cr} $ | (15) |
考虑到阀片开启程度与内部压强相关,得到压缩阀开启后的压缩力最终表达式为:
| $\eqalign{ & {F_{{\rm{yh}}}} = {{8\rho } \over {{C_{\rm{q}}}^{\rm{2}}{N_3}^2{\pi ^2}{d_2}^4}}{A_{\rm{g}}}^3{v_{\rm{h}}}^2 + \cr & \quad \quad g\left( {{k_2},{q_{4 - 2}},{A_{{\rm{r2}}}},\mu ,{r_{{\rm{b2}}}},{r_{{\rm{k2}}}},{p_0}} \right){A_{\rm{g}}} + f \cr} $ | (16) |
式中:N3,N4分别为常通孔及节流缝隙个数;d2为常通孔直径,l2,bk2,δ3分别为缝隙流通长度、宽度及高度;δ4为压缩阀开启高度,rb2为压缩阀片外半径;rk2为压缩阀片节流半径;k2为压缩阀片特性的系数。
2 阻尼力模型仿真及试验验证减振器建模过程中,涉及的参数主要分为3类:1) 结构参数,如活塞的直径等,可以根据实际测量得到;2) 油液特性参数,可以根据厂家提供的油液参数以及相关材料中公布的数值进行定义;3) 性能参数,主要包括各阀片的变形系数、压缩阀及复原阀开启压力、储油腔中充气气体的压力以及减振器的摩擦力等,可以查找设计值或通过实际试验及理论计算获得。表 1为测试减振器各参数的设计值以及通过分析计算获得的主要参数值。
测试减振器的油液特性参数为:密度ρ=858 kg/m3,动力黏度μ=9.61×10-3 N·s/m2[17]。减振器在专用设备上进行摩擦力试验,并根据绘得的摩擦力图判定该型号减振器复原行程的摩擦力约为30 N,压缩行程的摩擦力约为20.3 N;分析得到该减振器的复原阀开阀速度为0.146 m/s,压缩阀开阀速度为-0.39 m/s,换算得到该减振器的复原阀片的预压力为1.02 MPa,压缩阀片的预压力为4.96 MPa。
| 参数 | 名称 | 符号 | 量值 | 公差 |
| 减振器基本尺寸 | 活塞杆直径 | dg | 15 mm | 0.01 mm |
| 活塞杆截面积 | Ag | 176.6 mm2 | — | |
| 活塞直径 | dh | 30 mm | 0.021mm | |
| 活塞截面积 | Ah | 706.5 mm2 | — | |
| 活塞座小孔 | 直径 | d1 | 2 mm | 0.01 mm |
| 个数 | N1 | 6 | — | |
| 流通系数 | Cq | 0.82 | — | |
| 活塞阀片常通孔的尺寸 | 单条宽度 | bk1 | 2 mm | 0.01 mm |
| 条数 | N2 | 3 | — | |
| 高度 | δ1 | 0.1 mm | 0.005 mm | |
| 流通长度 | l1 | 0.8 mm | 0.004 mm | |
| 复原阀片变形后的尺寸 | 阀片外半径 | rb1 | 10.25 mm | 0.018 mm |
| 阀片节流半径 | rk1 | 9.75 mm | 0.015 mm | |
| 阀片变形系数 | k1 | 5.2×106 | — | |
| 压缩阀座小孔 | 直径 | d2 | 1.5 mm | 0.01 mm |
| 个数 | N3 | 3 | — | |
| 压缩阀片常通孔尺寸 | 单条宽度 | bk2 | 0.8 mm | 0.004 mm |
| 条数 | N4 | 1 | — | |
| 高度 | δ3 | 0.1 mm | 0.005 mm | |
| 流通长度 | l2 | 0.5 mm | 0.004 mm | |
| 压缩阀片变形后的尺寸 | 阀片外半径 | rb2 | 10.5 mm | 0.018 mm |
| 阀片节流半径 | rk2 | 7.5 mm | 0.015 mm | |
| 阀片变形系数 | k2 | 2.7×106 | — |
为了验证理论模型是否合理,需要进行试验验证。本试验在MTS849型减振器试验台上进行,如图 5所示,定义测试频率为2.4 Hz,振幅为40 mm的激励,通过安装在夹具上方的力传感器,得到该减振器的速度特性曲线。最后将仿真曲线与试验曲线进行对比,图 6的 (a) 和 (b) 分别表示复原、压缩行程中阻尼力仿真值与试验值的对比情况。图 7、图 8、图 9分别给出了频率为0.4,1.2,2.4 Hz时仿真与试验所得示功图的对比情况。试验结果表明该模型能够较好地描述减振器的实际工作情况。

|
| 图 5 MTS849型减振器试验台 Fig.5 MTS849 damper test bench |

|
| 图 6 减振器速度特性曲线 Fig.6 Velocity characteristic curve of damper |
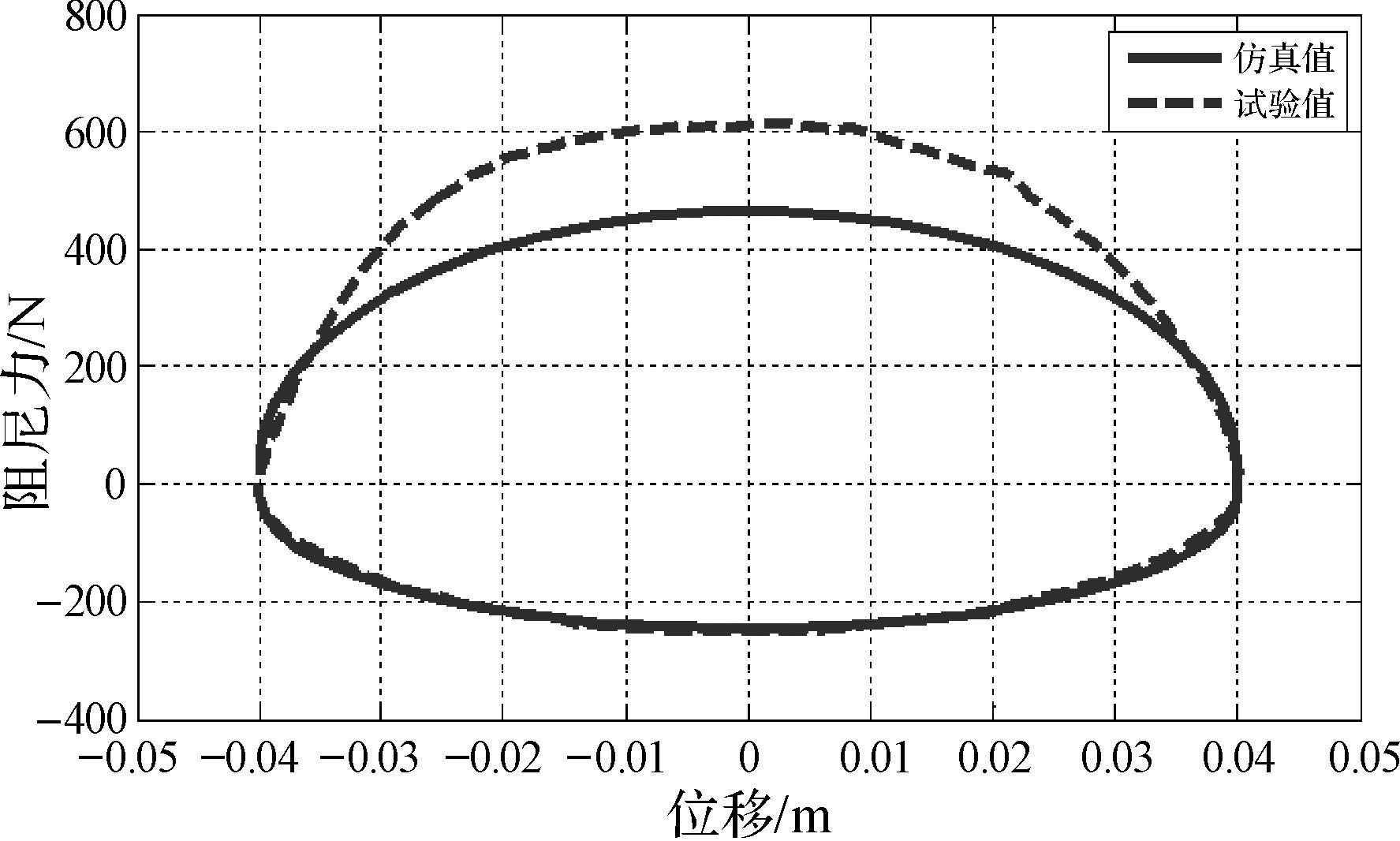
|
| 图 7 频率为0.4 Hz时的示功图对比 Fig.7 Comparison of indicator diagram with frequency of 0.4 Hz |
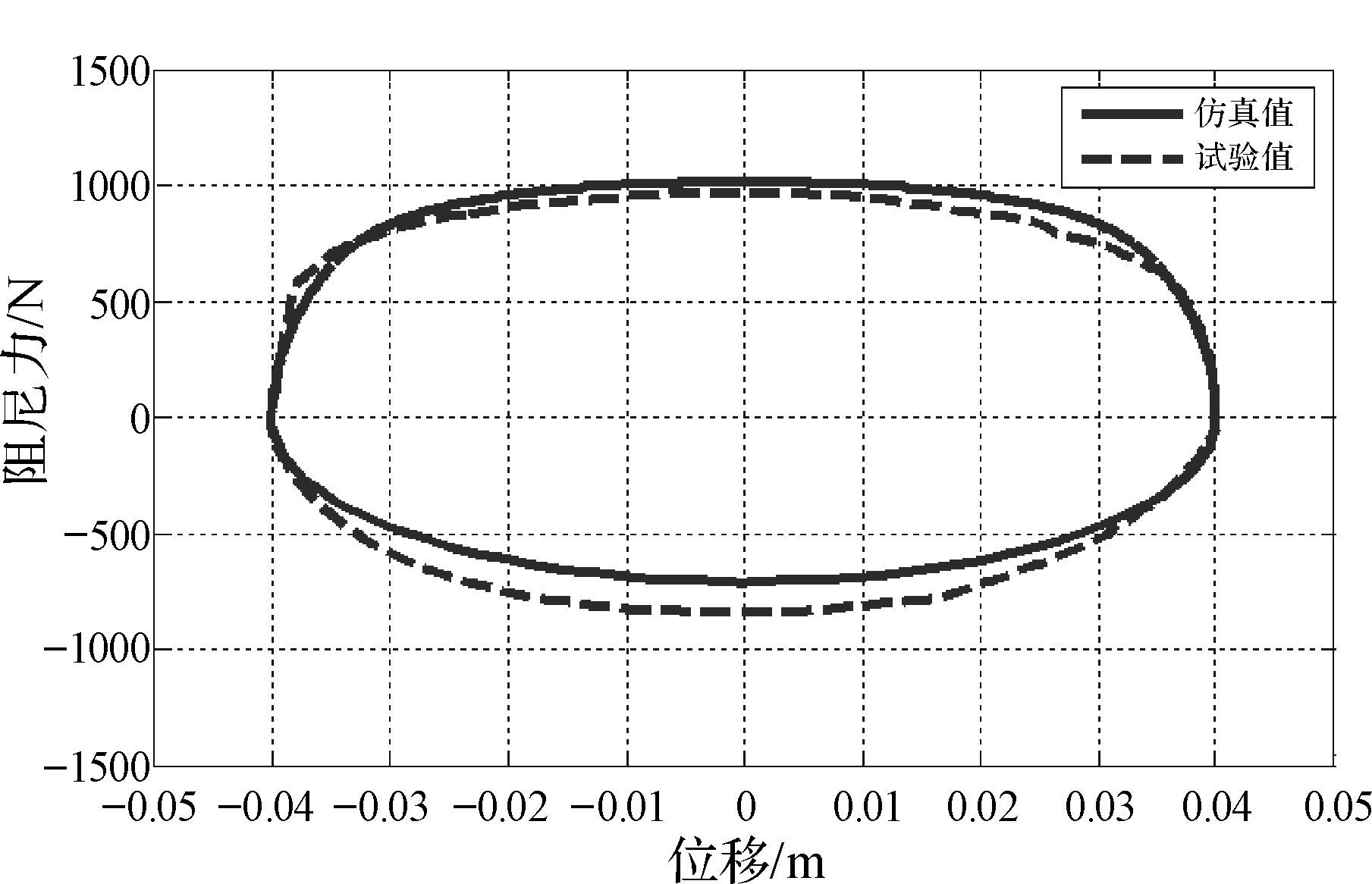
|
| 图 8 频率为1.2 Hz时的示功图对比 Fig.8 Comparison of indicator diagram with frequency of 1.2 Hz |
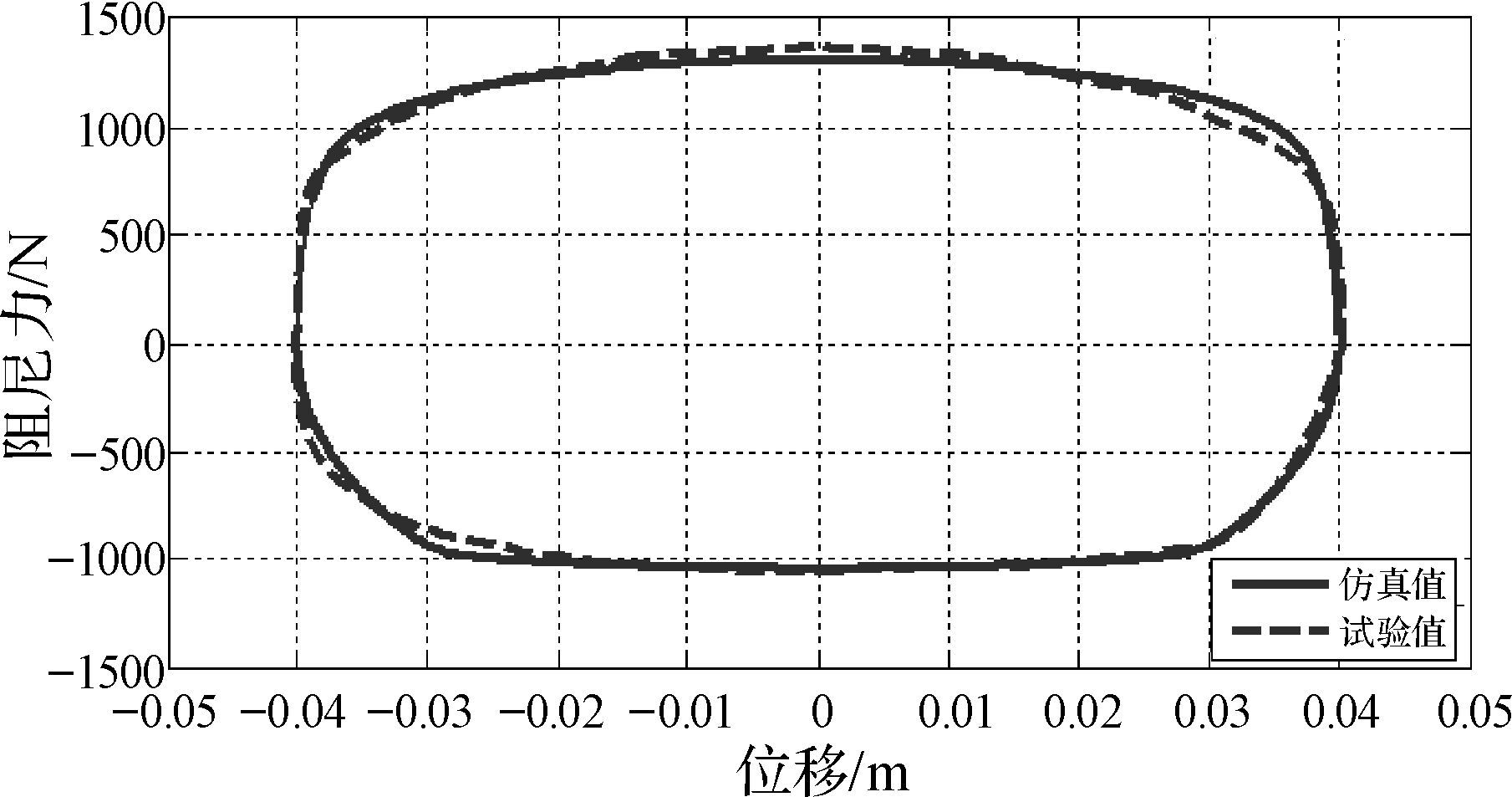
|
| 图 9 频率为2.4 Hz时的示功图对比 Fig.9 Comparison of indicator diagram with frequency of 2.4 Hz |
分析各参数对减振器阻尼力影响的灵敏度,可以针对性地制定技术措施,从而提高产品的可靠性。本文使用ANSYS Workbench中的Design Exploration模块研究不同的性能参数对阻尼力的影响。研究过程中,将结构尺寸参数假设为正态分布,根据实际设计公差,按照3δ原则计算标准差;将油液的密度及黏度假设为正态分布,变异系数设为5%。通过计算获得阻尼力模型各结构参数、性能参数、油液特性参数等的灵敏度值如表 2、表 3所示。
| 参数 | 概率分布 | 均值 | 标准差 | 灵敏度值 (开阀前) | 灵敏度值 (开阀后) |
| d1 | 正态分布 | 2 mm | 1.7×10-3 mm | 0.033 | 0.061 |
| dh | 正态分布 | 30 mm | 3.3×10-3 mm | -0.015 | -0.057 |
| dg | 正态分布 | 15 mm | 3.3×10-3 mm | 0.030 | -0.022 |
| l1 | 正态分布 | 0.8 mm | 1.7×10-3 mm | -0.015 | -0.040 |
| bk1 | 正态分布 | 2 mm | 1.7×10-3 mm | -0.021 | -0.168 |
| δ1 | 正态分布 | 0.1 mm | 8.3×10-4 mm | -0.918 | -0.396 |
| ρ | 正态分布 | 858 kg/m3 | 42.9 kg/m3 | 0 | 0 |
| μ | 正态分布 | 9.61×10-3N·s/m2 | 1.6×10-4N·s/m2 | 0.367 | 0.703 |
| δ2 | 正态分布 | 0.041 mm | 3.4×10-4 mm | — | -0.481 |
| rb1 | 正态分布 | 10.25 mm | 3×10-3 mm | — | 0.122 |
| rk1 | 正态分布 | 9.75 mm | 2.5×10-3 mm | — | -0.097 |
| 参数 | 概率分布 | 均值 | 标准差 | 灵敏度值 (开阀前) | 灵敏度值 (开阀后) |
| dg | 正态分布 | 15 mm | 3.3×10-3 mm | 0.007 | -0.021 |
| ρ | 正态分布 | 858 kg/m3 | 42.9 kg/m3 | 0 | 0 |
| μ | 正态分布 | 9.61×10-3N·s/m2 | 1.6×10-4N·s/m2 | 0.301 | 0.624 |
| d2 | 正态分布 | 1.5 mm | 1.7×10-3 mm | -0.030 | 0.000 5 |
| l2 | 正态分布 | 0.5 mm | 1.7×10-3 mm | 0.036 | 0.022 |
| bk2 | 正态分布 | 0.8 mm | 1.7×10-3 mm | -0.015 | -0.022 |
| δ3 | 正态分布 | 0.1 mm | 8.3×10-4 mm | -0.951 | -0.679 |
| δ4 | 正态分布 | 0.032 mm | 3.4×10-4 mm | — | -0.391 |
| rb2 | 正态分布 | 10.25 mm | 3×10-3 mm | — | 0.010 |
| rk2 | 正态分布 | 7.5 mm | 2.5×10-3 mm | — | -0.042 |
分析表 2可以发现,复原行程中复原阀开启前,跟阻尼力正相关的参数为:活塞座小孔直径d1、活塞杆直径dg及油液黏度μ;负相关的参数为:活塞直径dh、常通孔宽度bk1、流通长度l1及高度δ1;其影响程度由高到低依次排序为δ1, μ, d1, dg, bk1, l1, dh, ρ。随着复原阀的开启,各项参数的灵敏度值均有所变化,其中正相关的参数为:活塞座小孔直径d1、油液黏度μ及复原阀片外半径rb1;负相关的参数为:活塞直径dh、活塞杆直径dg、活塞阀片常通孔宽度bk1、流通长度l1及高度δ1、复原阀开启高度δ2、复原阀片节流半径rk1;其影响程度由高到低依次排序为μ, δ2, δ1, bk1, rb1, rk1, d1, dh, l1, dg, ρ。
分析表 3可以发现:压缩行程中压缩阀开启前,跟阻尼力正相关的参数为:压缩阀片常通孔流通长度l2、活塞杆直径dg及油液黏度μ;负相关的参数为:压缩阀座小孔直径d2、压缩阀片常通孔宽度bk2及高度δ3;其影响程度由高到低依次排序为δ3,μ,l2,d2,bk2,dg, ρ。随着压缩阀的开启,各参数的灵敏度值均有所变化,其中正相关的参数为:压缩阀片常通孔流通长度l2、油液黏度μ、压缩阀座小孔直径d2、压缩阀片外半径rb2;负相关的参数为:活塞杆直径dg、压缩阀片常通孔宽度bk2及高度δ3、压缩阀开启高度δ4及压缩阀片节流半径rk2;其影响程度由高到底依次排序为δ3,μ,δ4,rk2,bk2,l2,dg,rb2,d2,ρ。
综上分析,可以发现油液黏度、阀片常通孔的流通高度、各阀的开启高度对减振器阻尼力的影响较大。由于阀片常通孔的流通高度不容易发生大的变化,复原 (压缩) 阀的开启高度受偶然因素的影响较大,而油液黏度退化的过程较长且变化值较大,结合工程实际,认为油液黏度的退化可以造成阻尼力退化,而阀系开启高度的偶然变化会导致减振器阻尼力退化分布的离散系数较大。
4 阻尼力的先验分布估计由于阀片特性及其他结构参数的差异,导致批量生产的减振器的阻尼力表现值会在一定范围内波动。按照减振器的结构设计及尺寸公差要求,根据灵敏度分析结果,考虑对减振器阻尼力影响较大的参数,使用蒙特卡洛抽样方法,对减振器阻尼力的分布进行估计。
使用蒙特卡洛抽样法进行5万次抽样计算,获得减振器在各个速度点的阻尼力分布情况,如表 4所示。图 10展示了速度为0.1,0.3 m/s时复原力的分布情况,其余速度点有类似的分布。
| 参数 | 速度/(m/s) | 复原力/N | 压缩力/N |
| 均值 标准差 | 0.1 | 464.565 10.833 | 307.127 7.133 |
| 均值 标准差 | 0.3 | 1 028.348 20.786 | 882.662 21.468 |
| 均值 标准差 | 0.6 | 1 328.904 21.629 | 987.460 19.186 |
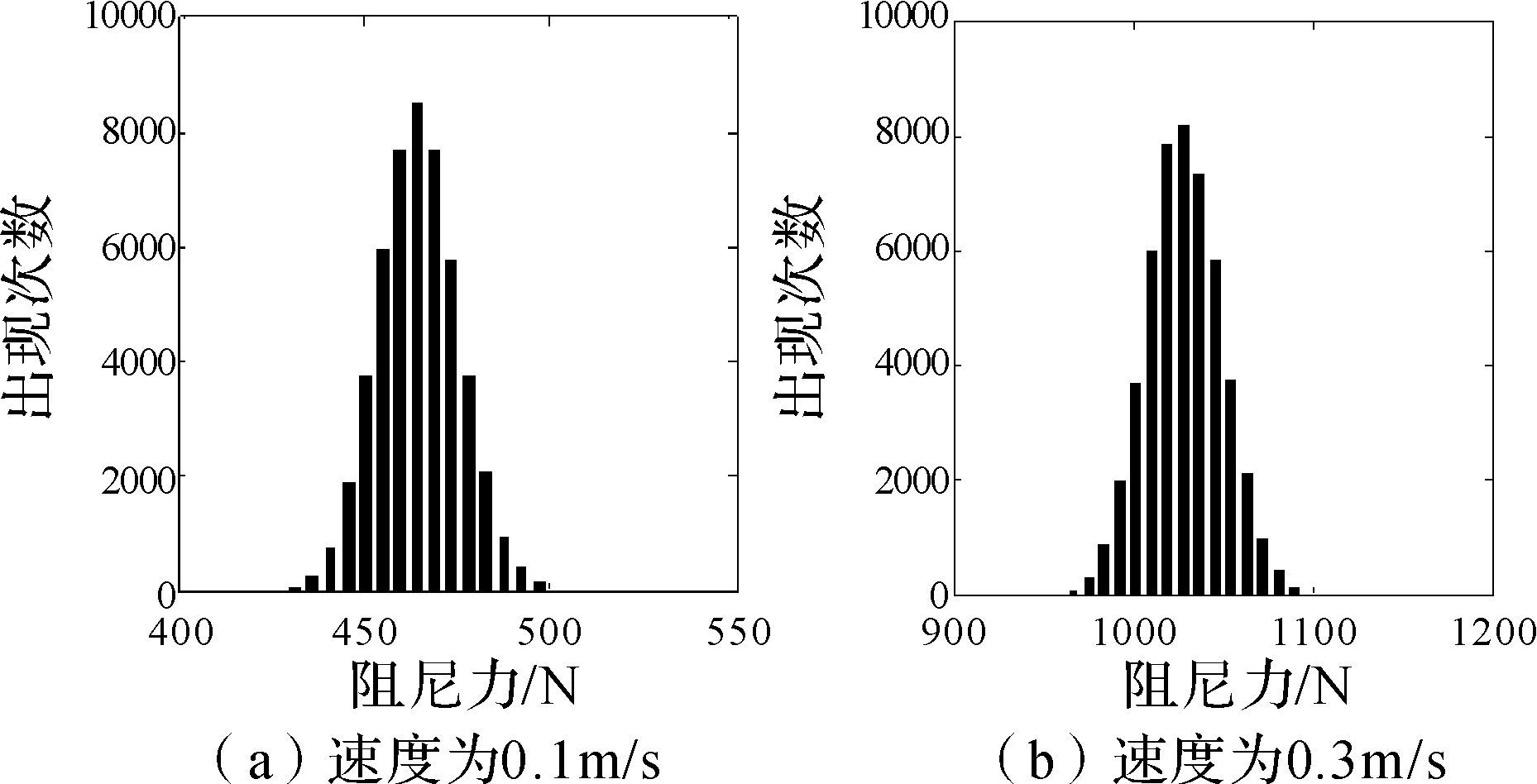
|
| 图 10 复原力的分布情况 Fig.10 The distribution of damping force |
1) 通过对某型双筒式液压减振器的结构、工作原理进行分析,根据减振器阻尼力产生的机理,建立了双筒式液压减振器阻尼力的数学模型,使用MATLAB工具进行计算,得到了仿真模型的速度特性曲线和示功图,并通过实际台架性能试验对仿真结果进行了验证,二者基本一致,表明仿真模型能够较好地描述减振器的实际工作情况,为减振器的设计提供了依据。
2) 对减振器阻尼力的数学模型进行了灵敏度分析,得到了油液黏度、常通孔尺寸及阀片的开启高度是影响减振器阻尼力变化的主要因素,为建立减振器的阻尼力退化模型提供了支撑。
3) 根据减振器的具体结构参数进行了阻尼力的分布估计,获得减振器在各个速度下的阻尼力分布情况,为减振器的性能预测和可靠性研究提供了依据。
| [1] |
周长城.
汽车液压筒式减振器设计及理论[M]. 北京: 北京大学出版社, 2012: 1-8.
ZHOU Chang-cheng. Automotive hydraulic shock absorber design and theory[M]. Beijing: Peking University Press, 2012: 1-8. |
| [2] |
杨明亮, 李人宪, 丁渭平, 等.
阀系参数对高速列车液压减振器阻力特性的影响[J]. 西南交通大学学报, 2014, 49(2): 291–296.
YANG Ming-liang, LI Ren-xian, DING Wei-ping, et al. Influence of valves parameters on damping characteristics of hydraulic shock absorber for high-speed trains[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 291–296. |
| [3] | HERR F, MALLIN T, LANE J, et al. A shock absorber model using CFD analysis and Easy5 [J]. SAE Paper, 1999-01-1322. |
| [4] | DUYM SW, STIENS R, BARON G V, et al. Physical modeling of the hysteretic behaviour of automotive shock absorbers [J]. SAE Paper, 970101. |
| [5] | DUYM SW R. Simulation tools, modeling and identification, for an automotive shock absorber in the context of vehicle dynamics[J]. Vehicle System Dynamics, 2000, 33(4): 261–285. DOI:10.1076/0042-3114(200004)33:4;1-U;FT261 |
| [6] | LANG H. A study of the characteristics of automotive hydraulic dampers at high stroking frequency[D]. Michigan: University of Michigan, Department of Mechanical Engineering, 1977: 65-118. |
| [7] | BESINGER F H, CEBON D, COLE D J. Damper models for heavy vehicle ride dynamics[J]. Vehicle System Dynamics, 1995, 24(1): 35–64. DOI:10.1080/00423119508969081 |
| [8] | SUDARSHAN Martande, JANGALE Y N, MOTGI N S. Design and analysis of shock absorber[J]. International Journal of Application or Innovation in Engineering & Management, 2013, 3(3): 195–199. |
| [9] |
刘荣胜. 减振器工作过程的数值模拟及其应用[D]. 北京: 清华大学汽车工程系, 1997: 35-65.
LIU Rong-sheng. Numerical simulation and its application on the working process of damper[D]. Beijing: Tsinghua University, Department of Automotive Engineering, 1997:35-65. |
| [10] |
檀润华, 陈鹰, 赵凡, 等.
汽车减震器新型数学模型的研究[J]. 汽车工程, 1998, 20(2): 113–117.
TAN Run-hua, CHEN Ying, ZHAO Fan, et al. A new mathematical model for shock absorbers in motor vehicles[J]. Automotive Engineering, 1998, 20(2): 113–117. |
| [11] |
吕振华, 高源, 王望予, 等.
汽车转向系减振器原理及其阻尼特性的试验分析[J]. 汽车技术, 1997(7): 26–30.
Lü Zhen-hua, GAO Yuan, WANG Wang-yu, et al. Experiment analysis on principle and its damping characteristic of automotive steering damper[J]. Automobile Technology, 1997(7): 26–30. |
| [12] |
马天飞, 崔泽飞, 张敏敏.
基于AMESim双筒叠加阀片式充气减振器建模与仿真[J]. 机械工程学报, 2013, 49(12): 123–130.
MA Tian-fei, CUI Ze-fei, ZHANG Min-min. Modeling and simulating of the gas-precharged dual-sleeve shock absorber with multiple valve plates using AMESim[J]. Journal of Mechanical Engineering, 2013, 49(12): 123–130. |
| [13] |
陈轶杰, 顾亮.
减振器节流阀片对阀门水击力的影响研究[J]. 振动与冲击, 2008, 27(2): 103–106.
CHEN Yi-jie, GU Liang. Study on influence of a shock absorber throttle slice on valve water hammer[J]. Journal of Vibration and Shock, 2008, 27(2): 103–106. |
| [14] |
周长城, 任传波.
最佳阻尼匹配减振器阀片厚度优化设计与特性试验[J]. 振动工程学报, 2009, 22(1): 54–59.
ZHOU Chang-cheng, REN Chuan-bo. Optimum design of throttle slice thickness and its characteristic test for telescopic damper with damping matching[J]. Journal of Vibration Engineering, 2009, 22(1): 54–59. |
| [15] |
林建忠, 阮晓东, 陈邦国, 等.
流体力学[M]. 北京: 清华大学出版社, 2013: 265-285.
LIN Jian-zhong, RUAN Xiao-dong, CHEN Bang-guo, et al. Fluid mechanics[M]. Beijing: Tsinghua University Press, 2013: 265-285. |
| [16] |
李仕生, 徐中明, 杨建国, 等.
带缓冲簧的汽车减振器外特性及其敏感度分析[J]. 中国机械工程, 2012, 23(5): 614–625.
LI Shi-sheng, XU Zhong-ming, YANG Jian-guo, et al. Outer characteristics and sensitivity analysis of automotive shock absorbers with buffer spring[J]. China Mechanical Engineering, 2012, 23(5): 614–625. |
| [17] |
上海海联润滑材料科技有限公司. 减振器油产品介绍[DB/OL]. [2016-10-30]. http://www.hirilube.com/.
Shanghai Hailian Lubricating Material Technology Ltd. Company. Introduction of damper oil product[DB/OL].[2016-10-30].http://www.hirilube.com/. |



