随着市场所需产品的结构、功能日趋复杂,产品开发过程中设计任务间的信息关系也越来越复杂,其原因主要有2个方面:一是由于产品的各项功能联系越来越紧密,导致设计任务间的信息耦合度越来越高,造成信息解耦困难;二是由于产品兼具的功能越来越多,设计任务间的信息集也越来越大,导致任务间的信息关系错综复杂。因此,企业为了获取竞争优势,在产品设计过程中,针对设计任务间复杂的信息依赖关系,对设计任务进行合理的分配就显得尤为重要。
近年来,国内外研究人员针对产品开发过程中设计任务间的信息关系作了很多研究,如:张广军等[1]提出了将公理设计矩阵与设计结构矩阵集成应用的方法,促进了产品设计过程中功能与结构设计的同步演化;Moustafa等[2]用动态规划法求解最佳的任务分配,使得劳动力成本最小;张金标[3]将设计活动间的信息关系分成了3种,即顺序型、并行型和耦合型,并提出了相对应的活动执行方式;贾军等[4]建立了一种复杂产品研发时间和研发团队交流的优化模型,得出了最优的产品研发时间和团队交流策略;刘伟等[5]提出了一种模仿生物原型的仿生设计方法,能够快速地将生物原型转换成所需的产品技术;陈卫明等[6]通过建立动态环境下基于混合迭代的耦合集求解模型,对任务执行过程中影响项目完成时间的任务执行工期的不确定性、任务输出分支的不确定性和资源分配的不确定性三个方面进行了分析;Krishnan等[7]针对多任务间的信息需求关系,提出了几种多任务间的任务执行方式:串行方式、重叠方式及并行方式;Amaresh等[8]提出了功能-结构映射的产品开发模型;张金标等[9]提出了并行设计耦合活动集混合迭代算法;包北方等[10]从任务间的信息流及任务的执行方式两个方面对设计任务类型作出了综合分析;徐亮亮等[11]提出了一种设计需求与方案求解协同演化的形式化表达模型;徐晓刚等[12]对设计任务间的迭代进行了研究,提出了设计任务间多种类型的设计迭代形式;包北方等[13]给出了任务适合度、任务协调效率的定义,并构建了一种产品定制协同开发任务多目标分配优化模型;Yang等[14]提出了一种基于本体论的多视角任务分解策略,为分布式制造环境下的资源合理分配提供了支持;黄瑾等[15]在应用网格系统的基础上,建立了一种具有层次化结构的资源分配与任务调度模型;郭希娟等[16]提出了一种多准则的动态任务分配算法,使得任务的分配更加均衡;叶菁等[17]提出了一种基于遗传算法的网格资源分配与调度方法,实现了更有效的任务资源分配;苏财茂等[18]扩展了有向图的建模方法,并将该方法与符号设计结构矩阵结合,提出了一种耦合任务集的自动解耦算法。总体来看,上述文献提出了产品开发过程中的多种设计方法,分析了任务间的多种信息关系,并针对这些信息关系提出了相应的任务分配策略,但没有明确提出信息关系复杂的多任务的合理分配方案。当多任务间同时出现上述文献中所提到的多种信息关系而导致任务间的信息集较大时,采用单阶段的任务执行方式很难理清任务间的信息依赖关系,致使难以达到合理分配设计任务的目的。
本文针对单输入多输出耦合设计任务间的复杂信息需求关系,通过研究单输入多输出耦合设计任务的二阶段迭代模型的信息处理策略,构建并求解二阶段任务分配方案执行时间的数学模型,以期得到二阶段任务执行方式的最佳任务分配方案。
1 单输入多输出耦合设计任务的单阶段迭代模型分析单输入多输出耦合设计任务迭代模型将任务分为上、下游两个阶段执行,上游任务为信息输入任务,下游任务为信息输出任务。下游为多个彼此之间信息独立的并行执行的子任务,上游任务与下游各个并行的子任务间存在信息耦合关系。因此下游并行的各个子任务间通过上游任务建立了一种间接的信息耦合关系。下游中任一子任务信息发生更改都会通过上游任务间接地对下游其他子任务产生影响。
上游任务在预估下游各子任务执行所需信息的基础上执行,并在任务执行过程中输出下游任务开始执行时所需的初始信息。下游任务中的某一子任务根据上游任务传递的信息开始执行,执行完成后得到输出信息,判断输出信息是否与预期结果相符并将信息反馈给上游任务。上游任务进行预估信息更正后迭代执行,并将新的信息传递给下游任务,下游任务中受到上游任务更改信息影响的其他子任务也将进行迭代返工,迭代完成后同样将信息反馈给上游任务,整个任务以这种迭代返工的方式不断更新信息,反复迭代直至下游所有子任务得到预期的输出结果为止。当下游并行子任务间的间接耦合关系较为复杂时,存在因不能对这种耦合关系进行解耦而导致任务执行过程不能收敛的风险。因此在进行任务迭代返工时,需要对任务迭代次数设定一个阈值[19],即当任务迭代次数达到一定程度时,下游任务的输出结果能够满足产品的性能需求,任务间就不再需要继续迭代返工。
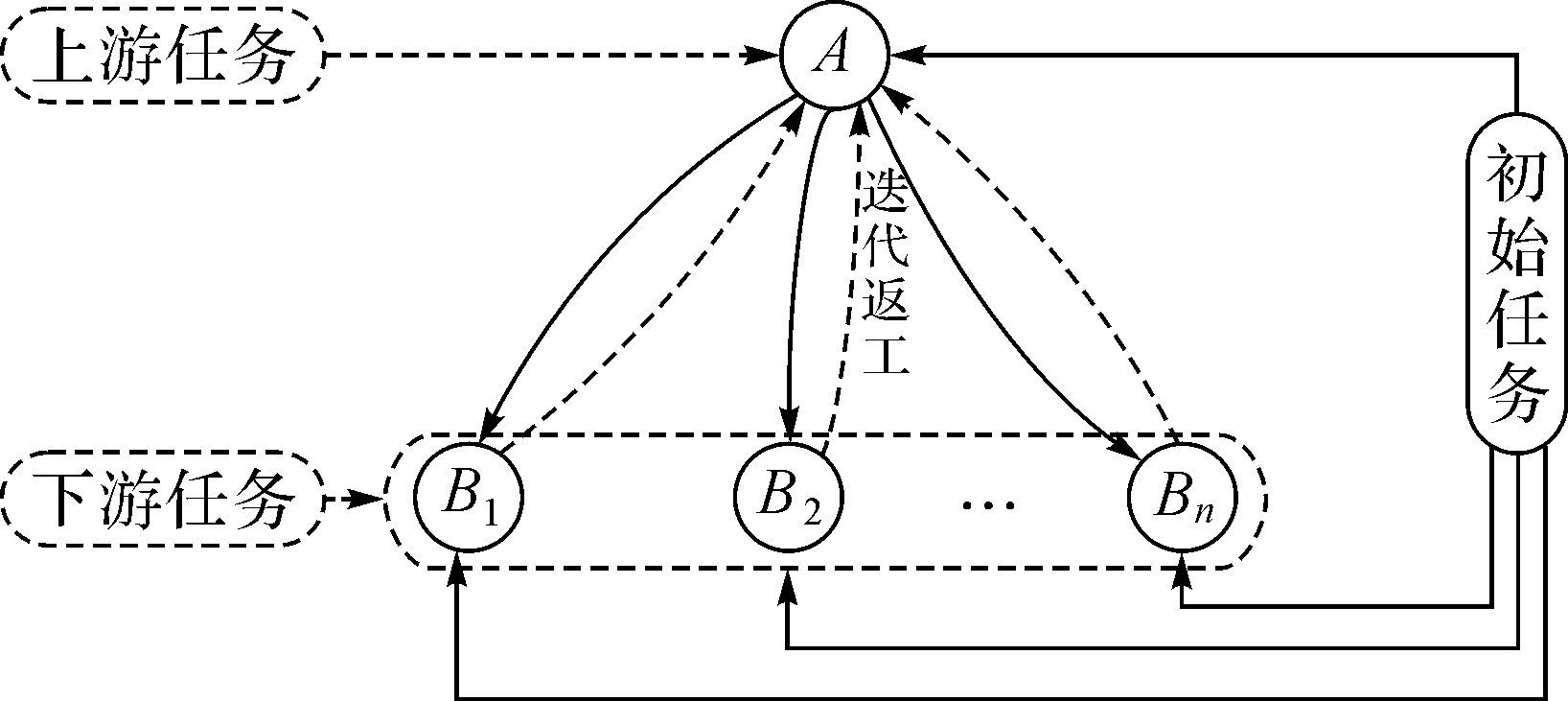
单输入多输出耦合设计任务采用单阶段迭代的任务执行模式,在上、下游任务组成串行任务的同时,下游任务又由多个并行执行的子任务组成,它们构成了一个简单的混合迭代任务模型,如图 1所示。
|
| 图 1 单输入多输出耦合设计任务单阶段迭代模型 Fig.1 The single-stage iteration model of coupling design task with single input and multiple output |
单输入多输出耦合设计任务由于下游并行子任务间存在间接的信息耦合关系,因此当下游并行执行子任务较多时,采用单阶段的任务执行方式执行任务时,下游并行执行的各个子任务存在因资源受限而无法同时执行的风险。同时,由于下游并行任务都与上游任务存在耦合关系,因此采用单阶段迭代的任务执行方式存在因任务分配不合理而导致任务间耦合信息集过大,以致在任务执行过程中产生虚假信息而造成任务间多余迭代返工的问题。对于资源受限以及任务分配不合理的问题,本文将寻求在二阶段迭代模式下的有效解决办法。
2 单输入多输出耦合设计任务二阶段迭代模型的信息优化处理单输入多输出耦合设计任务的上、下游两个阶段的任务间存在信息耦合关系,2个阶段任务中任一阶段的任务信息发生变化都会引起另一阶段任务所得信息发生变化,进而导致该阶段任务需要进行迭代返工。而由于任务执行初始信息是在预估的基础上得到的,并不能完全符合设计要求,所以在任务执行过程中必须不断地对信息进行修正,使最终的输出信息达到设计任务最初的预期目标。在这个信息修正过程中,就存在大量的迭代返工,进而延长了任务执行时间。
对于这种存在信息耦合关系的任务,执行过程中的迭代返工是不可避免的。要想尽可能缩短整个任务的执行时间,就必须加快任务间的信息交流并提高信息交流的正确率,尽可能保证任务间的每次迭代返工都是在获取的信息量最大、信息的正确度较高的基础上进行的,尽量减少每次迭代返工过程中所做的无用功,进而减少整个任务执行过程中的工作量,达到缩短整个任务执行时间的目的。
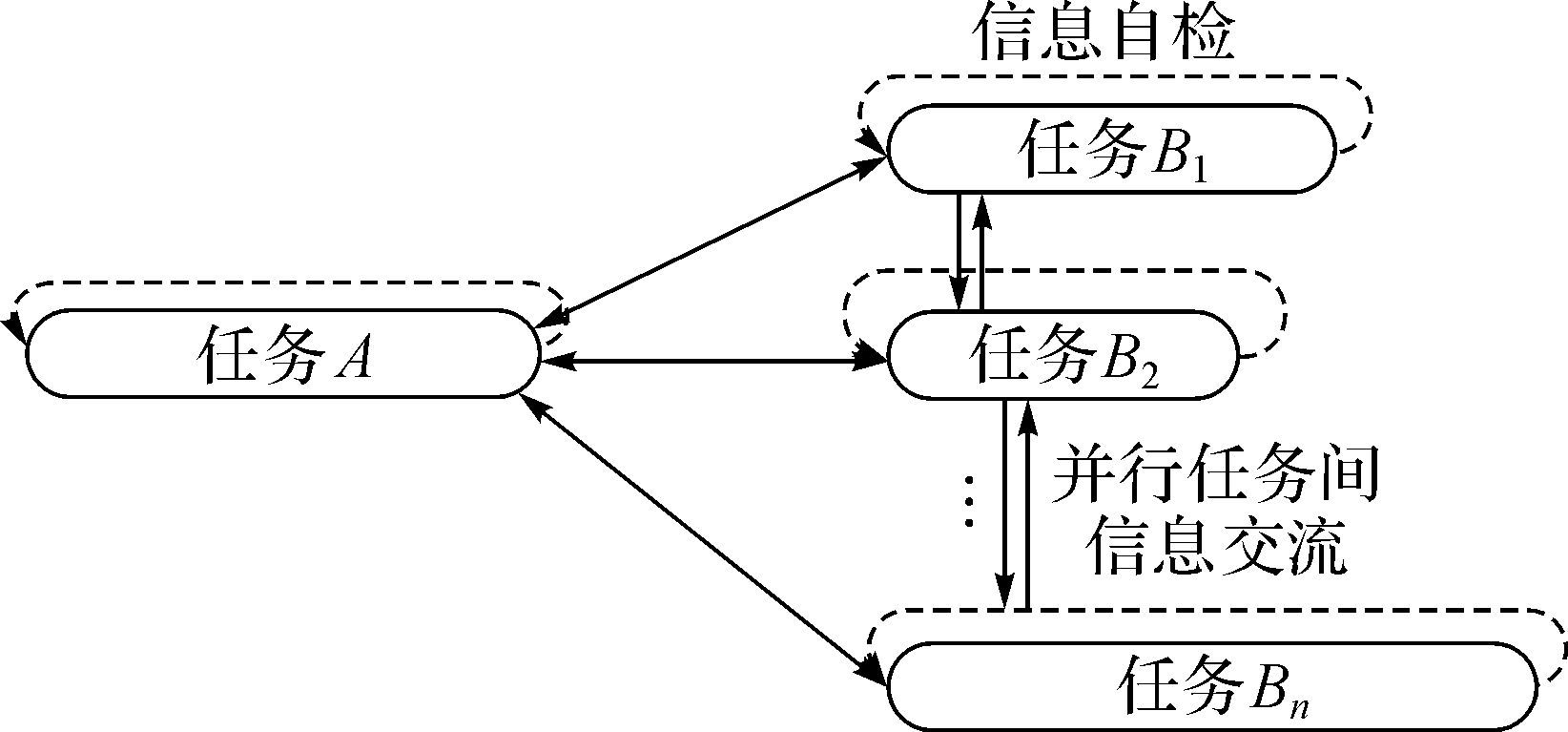
下游并行任务之间虽然不存在直接的耦合关系,彼此之间的直接信息关联度较小,但是彼此之间都可以通过上游任务产生相互的影响。因此要想通过加快任务间的信息传递来减少上、下游任务间的迭代次数,就必须寻求既能加快任务间的信息交流速度同时还能提高传递信息正确性的方法。本文针对单输入多输出耦合设计任务间的信息关系提出了如图 2所示的信息优化处理模式。
|
| 图 2 单输入多输出耦合设计任务间信息处理模式 Fig.2 The information processing mode of coupling design task with single input and multiple output |
图 2所示的信息处理模式分两部分:1) 下游任务在获取上游任务传递的信息后开始执行,执行过程中并行执行的子任务之间每隔一小段时间就进行一次信息交流,预估彼此之间通过上游任务间接产生的影响,及时对自身信息进行更正;2) 上、下游所有任务在完成一次迭代后对自身进行一次迭代评估,以保证各个任务在执行过程不会因执行过程出错而产生错误信息。
上、下游任务间的信息在经过上述处理以后再进行传递和反馈,通过这种任务自身信息自检以及任务间的信息及时交流来保证任务彼此间获取信息的正确性和快速性,能够尽量减少耦合设计任务间因获取信息错误而导致的无用迭代返工。
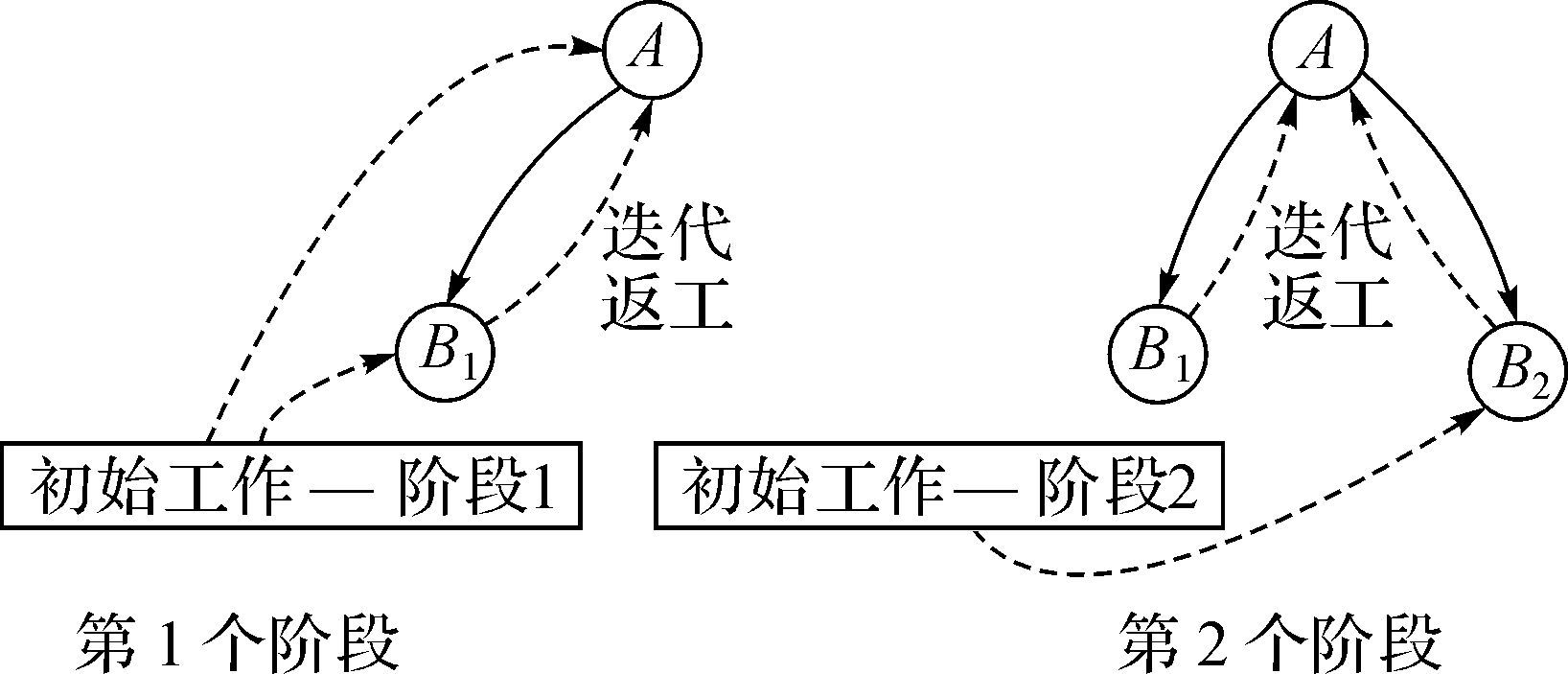
3 单输入多输出耦合设计任务的二阶段迭代模型的构建与求解 3.1 单输入二输出耦合设计任务的二阶段迭代模型二阶段迭代模型是将任务分2个阶段执行,每个阶段都包括初始任务和任务间的迭代返工。由于每个阶段执行的初始任务数和迭代返工的任务数都不确定,因此合理分配每个阶段的任务类型和任务数是二阶段迭代模型的核心。图 3所示为单输入二输出耦合设计任务的二阶段迭代模型。
|
| 图 3 单输入二输出耦合设计任务的二阶段迭代模型 Fig.3 The two-stage iteration model of coupling design task with single input and two output |
图 3所示的二阶段迭代模型,第1阶段执行的初始任务包括任务A和B1以及任务A,B1间的迭代返工,第2阶段执行的任务包括初始任务B2和任务A,B2之间的迭代返工。
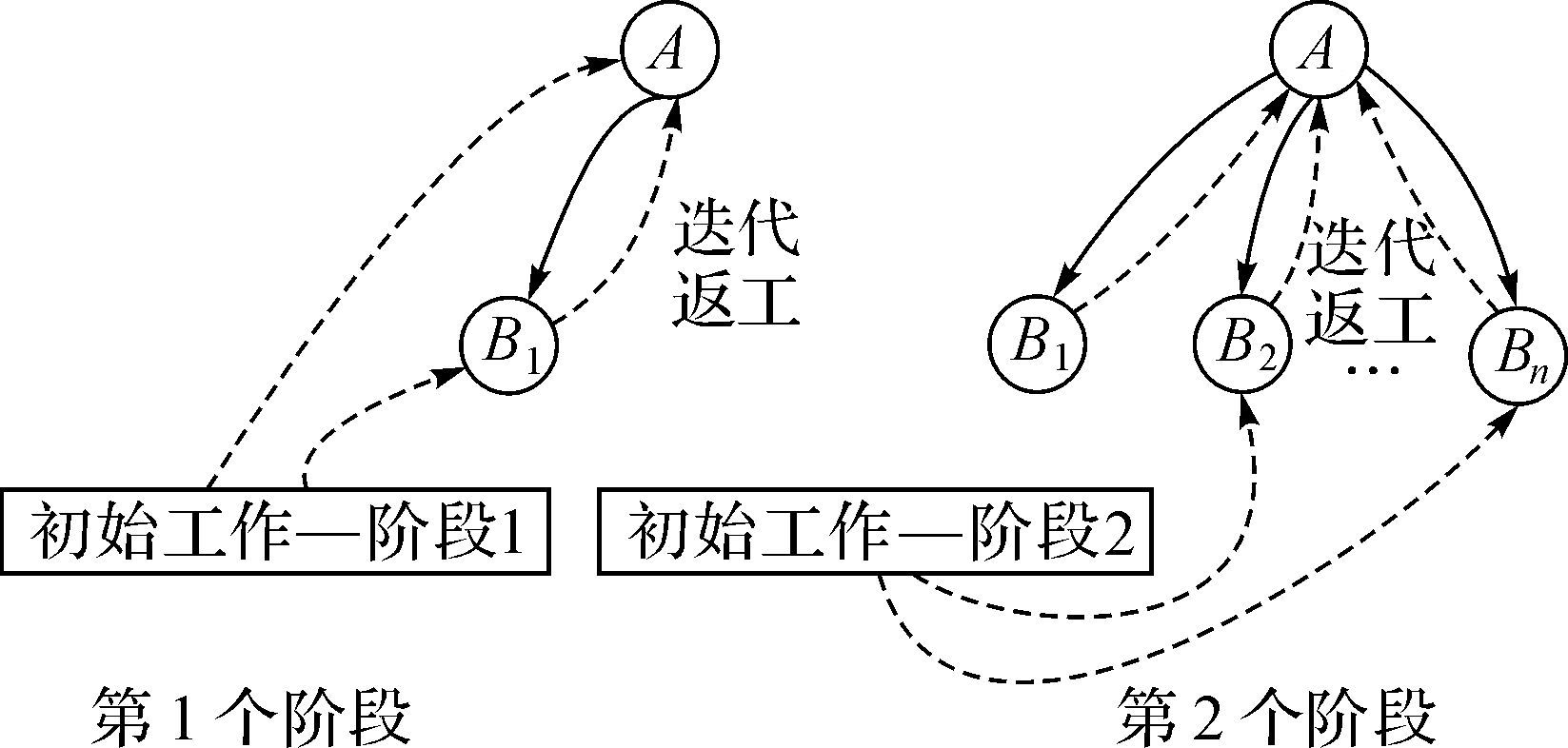
3.2 单输入多输出耦合设计任务的二阶段迭代模型单输入多输出耦合设计任务是在单输入二输出耦合设计任务的基础上增加了若干输出任务,其二阶段迭代模型如图 4所示。
|
| 图 4 单输入多输出耦合设计任务的二阶段迭代模型 Fig.4 The two-stage iteration model of coupling design task with single input and multiple output |
此时的二阶段迭代模型的执行策略是:第1阶段执行的任务包括初始任务即上游的输入任务A和下游的输出任务B1以及上、下游任务间的迭代返工;第2阶段执行的任务包括初始任务即下游还未执行的任务B2,B3,…,Bn,以及上、下游各个任务间的迭代返工。
采取二阶段迭代模型,每阶段任务分配数比单阶段迭代模型少,因此资源受限的可能性也比单阶段迭代模型小;同时二阶段迭代模型的任务分配方案考虑到任务间的信息耦合强度的大小以及任务间的返工概率的问题,通过合理选择第1阶段执行的任务以及延迟到第2阶段执行的任务,可以使多任务间的任务分配更为合理,能够有效缩短整个任务的执行时间。
3.3 二阶段迭代模型执行时间的数学模型二阶段迭代模型的整个任务执行时间需要分2个阶段计算,然后将这2个阶段的任务执行时间相加。在陈庭贵等[19]建立的完全并行耦合任务的二阶段迭代时间求解模型的基础上,构建单输入多输出耦合设计任务的二阶段迭代数学模型。
设有n个设计任务,第1个阶段任务执行所需时间为:
| ${T_1} = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{KAK}}} \right)^{ - 1}}\mathit{\boldsymbol{KU}}$ | (1) |
式中:W为任务工期矩阵,是一个1×n维的行矩阵;I为n×n维的单位矩阵;A为n×n维的任务返工量矩阵,由各个任务间的返工量确定;U为n×1维的初始工作矩阵,其元素ui定义为:
| ${u_i} = \left\{ {\matrix{ 1 & {第i个任务在当前阶段执行} \cr 0 & {其他} \cr } } \right.$ | (2) |
K为n×n维的任务分布矩阵,其元素ki定义如下:
| ${k_ij} = \left\{ {\matrix{ 1 & {第i个任务在第1阶段执行} \cr 0 & {其他} \cr } } \right.$ | (3) |
在第2个阶段,要完成的初始工作包括第1阶段没有执行的任务的初始工作,而要完成的迭代返工工作既包括第1阶段已经执行的任务即上游任务的迭代返工 (称为二次迭代返工),还包括第2阶段执行的所有任务的迭代返工。因此,该阶段所需时间可表示为:
| ${T_2} = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}} + \mathit{\boldsymbol{D}}} \right)\mathit{\boldsymbol{U}}$ | (4) |
式中:D为n×n维的二次迭代返工矩阵,用于求解参与第2阶段迭代返工的第1阶段已经完成迭代返工任务的迭代返工时间。矩阵D的元素定义如下:
| ${d_ij} = \left\{ {\matrix{ 1 & {i=j且第i个任务在第1,2阶段迭代执行} \cr 0 & {其他} \cr } } \right.$ | (5) |
则完成二阶段迭代模型所需的时间T为:
| $\eqalign{ & T = {T_1} + {T_2} = \cr & \quad \mathit{\boldsymbol{W}}{\left[( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{KAK}}} \right)^{ - 1}}\mathit{\boldsymbol{K}} + {\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}} \right)^{ - 1}}\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}} + \mathit{\boldsymbol{D}}} \right)]\mathit{\boldsymbol{U}} \cr} $ | (6) |
采用二阶段迭代模式执行单输入多输出耦合设计任务时,上游任务必须在第1阶段执行,而且在第2阶段任务执行过程中,上游任务还会参与第2阶段任务的迭代返工。每个阶段的任务分配方案不同,整个任务的执行时间也不同。在规划任务执行方案时,首先将所有可以执行的二阶段任务分配方案枚举出来,然后将各个任务分配方案的任务执行时间计算出来并进行对比,得出任务执行时间最短的任务分配方案。
4 实例分析以某企业汽车发动机开发项目为例,对上述二阶段迭代模型进行应用分析。该汽车发动机开发涉及零件数量多,且存在大量的耦合和非耦合关系。选取任务A(缸盖设计)、任务B(活塞设计)、任务C(带轮设计)、任务D(增压器设计)、任务E(消声器设计)、任务F(燃油供给系统设计) 为对象进行分析。任务A和任务B之间存在强耦合关系,任务A和任务D之间存在中等耦合关系,任务A和任务C,E,F之间存在弱耦合关系,任务B,C,D,E,F之间相互独立。任务A先执行,任务B,C,D,E,F在获取任务A的输出信息后才开始执行。
各任务的执行工期用工期矩阵W表示为:
W=[28 20 14 25 22 18]
各任务之间的返工量用返工量矩阵A表示,由于任务B,C,D,E,F之间相互独立,因此这些任务之间不存在返工量,即在矩阵A中对应位置元素的值为0。
| $\mathit{\boldsymbol{A = }}\left| {\matrix{ 0 \hfill & {0.32} \hfill & {0.10} \hfill & {0.22} \hfill & {0.08} \hfill \cr {0.32} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr {0.10} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr {0.22} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr {0.08} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr {0.14} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \cr } } \right.\left. {\underline {\, {\matrix{ {0.14} \hfill \cr 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr 0 \hfill \cr } } \,}}\! \right| $ |
每个阶段执行的任务数不同,任务分布矩阵K和初始工作矩阵U均不相同,可按照其定义分别来确定。下面以2个方案为例来说明任务分布矩阵K和初始工作矩阵U的定义。
若任务A在第1阶段执行,其他任务在第2阶段执行,则任务分布矩阵K1为:
| ${\mathit{\boldsymbol{K}}_1}=\left| {\matrix{ 1 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & 0 \hfill & {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & 0 \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill & 0 \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill & {} \hfill & 0 \hfill \cr {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \cr } } \right.\left. {\underline {\, {\matrix{ {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr 0 \hfill \cr } } \,}}\! \right| $ |
第1,2阶段的初始工作矩阵分别为:
U11=[1 0 0 0 0 0]T
U12=[0 1 1 1 1 1]T
若任务A,B在第1阶段执行,其他任务在第2阶段执行,则任务分布矩阵为:
| ${\mathit{\boldsymbol{K}}_2}=\left| {\matrix{ 1 \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & 1 \hfill & {} \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & 0 \hfill & {} \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill & 0 \hfill & {} \hfill \cr {} \hfill & {} \hfill & {} \hfill & {} \hfill & 0 \hfill \cr {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \cr } } \right.\left. {\underline {\, {\matrix{ {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr {} \hfill \cr 0 \hfill \cr } } \,}}\! \right| $ |
第1,2阶段的初始工作矩阵分别为:
U21=[1 1 0 0 0 0]T
U22=[0 0 1 1 1 1]T
将整个任务的执行工期矩阵W、返工量矩阵A、对应的任务分布矩阵K、初始工作矩阵U、二次迭代返工矩阵D分别代入式 (1) 和式 (4),再根据式 (6) 可计算得到二阶段与单阶段迭代任务分配方案执行时间的计算结果,如表 1所示。
| 任务序号 | 任务分布 | 任务执行总时间/d |
| 1 | A-BCDEF | 175.2 |
| 2 | AB-CDEF | 179.86 |
| 3 | AC-BDEF | 174.26 |
| 4 | AD-BCEF | 177.82 |
| 5 | AE-BCDF | 175.17 |
| 6 | AF-BCDE | 174.84 |
| 7 | ABC-DEF | 180.94 |
| 8 | ABD-CEF | 189.29 |
| 9 | ABE-CDF | 181.59 |
| 10 | ABF-CDE | 183.81 |
| 11 | ACD-BEF | 178.19 |
| 12 | ACE-BDF | 174.5 |
| 13 | ACF-BDE | 174.54 |
| 14 | ADE-BCF | 178.89 |
| 15 | ADF-BCE | 179.59 |
| 16 | AEF-BCD | 175.31 |
| 17 | ABCD-EF | 182.04 |
| 18 | ABCE-DF | 183.11 |
| 19 | ABCF-DE | 184.69 |
| 20 | ABDE-CF | 192.53 |
| 21 | ABDF-CE | 195 |
| 22 | ABEF-CD | 185.28 |
| 23 | ACDE-BF | 179.66 |
| 24 | ACDF-BE | 180.68 |
| 25 | ACEF-BD | 175.38 |
| 26 | ADEF-BC | 181.32 |
| 27 | ABCDE-F | 195.78 |
| 28 | ABCDF-E | 198.65 |
| 29 | ABCEF-D | 187.62 |
| 30 | ABDEF-C | 199.06 |
| 31 | ACDEF-B | 187.62 |
| 32 | ABCDEF | 203.25 |
表 1共有32个任务分配方案。其中,方案1(A-BCDEF) 表示任务A在第1阶段完成,任务B,C,D,E,F在第2阶段完成;方案2(AB-CDEF) 表示任务A,B在第1阶段完成,任务C,D,E,F在第2阶段完成;以此类推。方案1至31是二阶段迭代模型的任务分配方案,方案32是单阶段迭代模型的任务分配方案。方案1中第1阶段任务数为1个;方案2至6中第1阶段任务数为2个;方案7至16中第1阶段任务数为3个;方案16至26中第1阶段任务数为4个;方案26至31中第1阶段任务数为5个。本文所举的实例分析中,执行时间最短的任务分配方案为方案12,任务分布为ACE-BDF。
从表中数据可以看出,任一个二阶段任务分配方案都比单阶段任务迭代模式节省时间。选取任务数量分布不同的方案1,2,7,17,27进行对比分析,可以看出:在单输入多输出耦合任务二阶段迭代模型中,整个任务的执行时间随着第1阶段执行的任务数增多而增长,说明第1阶段执行的任务数越多,第2阶段所有任务间的迭代返工也越多,这也验证了本文所提出的下游并行任务间信息的间接耦合关系,下游信息输出任务的初始信息都来自上游任务,第1阶段任务执行过程中下游子任务执行越多,第2阶段任务执行过程中上、下游任务间的信息更新次数会越多,迭代返工次数也越多,所以整个产品开发任务的执行时间也就越长。再选取任务分配方案7至16进行对比,分析得出:下游任务与上游任务耦合关系强的任务放在第1阶段执行时,整个任务的执行时间就相对较长;反之,下游任务与上游任务耦合关系强的任务放在第2阶段执行时,整个任务执行时间就相对较短。因此,针对单输入多输出耦合设计任务采取二阶段迭代模型的执行策略时,在尽量减少第1阶段执行的任务数的同时,尽可能将下游与上游任务间耦合关系较强的任务放在第2阶段执行。
5 结束语本文通过分析产品设计开发过程中任务间的信息关系,根据任务间具有单输入多输出耦合信息关系的任务模型,提出了单输入多输出耦合二阶段迭代模型的信息处理优化策略。通过建立二阶段迭代模型的任务分配方案执行时间数学模型,求解得到了二阶段任务分配方案的执行时间。通过实例求解了不同的二阶段任务分配方案的执行时间并进行比较,得到了执行时间最短的二阶段任务分配方案,验证了本文方法的有效性。
与单阶段方法相比,采用二阶段方法能够有效地减少每个阶段任务间的信息积累量,有助于理清每个阶段任务间的信息依赖关系,进而得到更加合理的耦合设计任务分配方案,达到缩短产品开发时间的目的。
单输入多输出耦合设计任务二阶段迭代模型的上游只有1个输入任务,当上游有多个输入任务时,即任务模型为多输入多输出耦合任务模型时,任务间的信息交流和迭代返工更加复杂。为此,可以考虑采用三阶段甚至更多阶段的任务分配方法,将整个任务集进一步细分,构建多输入多输出耦合设计任务的时间求解模型,以获得最佳的设计任务分配方案。
| [1] |
张广军, 唐敦兵, 戴胜.
基于公理化设计矩阵与设计结构矩阵集成的研究[J]. 机械设计与研究, 2008, 24(5): 15–18.
ZHANG Guang-jun, TANG Dun-bing, DAI Sheng. Product design based on the co-evolution of axiomatic design matrix and design structure matrix[J]. Machine Design & Research, 2008, 24(5): 15–18. |
| [2] | MOUSTAFA E, HESHAM K A. A dynamic programming algorithm for days-off scheduling with sequence dependent labor costs[J]. Journal of Scheduling, 2008, 11(2): 85–93. DOI:10.1007/s10951-007-0040-x |
| [3] |
张金标.
一种改进的产品设计耦合活动迭代模型[J]. 山东大学学报 (工学版), 2008, 38(2): 37–41.
ZHANG Jin-biao. An improved iteration model for coupled activities in product design[J]. Journal of Shandong University (Engineering Science), 2008, 38(2): 37–41. |
| [4] |
贾军, 张卓.
复杂产品研发时间和研发团队交流优化模型及其应用研究[J]. 中国机械工程, 2013, 24(15): 2030–2035.
JIA Jun, ZHANG Zhuo. Research on optimized model of development cycle and R & D team communication strategies and its application to complex product[J]. China Mechanical Engineering, 2013, 24(15): 2030–2035. DOI:10.3969/j.issn.1004-132X.2013.15.009 |
| [5] |
刘伟, 曹国忠, 郭德斌, 等.
基于多元仿生的快速响应设计研究[J]. 工程设计学报, 2015, 22(1): 1–10.
LIU Wei, CAO Guo-zhong, GUO De-bin, et al. Research on rapid response design based on multiple bionic[J]. Chinese Journal of Engineering Design, 2015, 22(1): 1–10. |
| [6] |
陈卫明, 陈庭贵, 肖人彬.
动态环境下基于混合迭代的耦合集求解方法[J]. 计算机集成制造系统, 2010, 16(2): 271–309.
CHEN Wei-ming, CHEN Ting-gui, XIAO Ren-bin. Coupled sets solving method based on hybrid iteration under dynamic environment[J]. Computer Integrated Manufacturing Systems, 2010, 16(2): 271–309. |
| [7] | KRISHNAN V, EPPINGER S D, WHITNEY D E. Accelerating product development by the exchange of preliminary product design information[J]. Journal of Mechanical Design, 1995, 117(4): 491–498. DOI:10.1115/1.2826709 |
| [8] | AMARESH C, THOMAS P B. A scheme for functional reasoning in conceptual design[J]. Design Studies, 2001, 22(6): 493–517. DOI:10.1016/S0142-694X(01)00008-4 |
| [9] |
邢乐斌, 李君.
基于设计迭代的耦合任务动态分配策略研究[J]. 计算机工程与应用, 2012, 48(23): 219–223.
XING Le-bin, LI Jun. Dynamic assignment of coupled tasks based on design iteration[J]. Computer Engineering and Application, 2012, 48(23): 219–223. DOI:10.3778/j.issn.1002-8331.2012.23.048 |
| [10] |
包北方, 杨育, 李斐, 等.
产品定制协同开发任务分解模型[J]. 计算机集成制造系统, 2014, 20(7): 1537–1545.
BAO Bei-fang, YANG Yu, LI Fei, et al. Decomposition model in product customization collaborative development task[J]. Computer Integrated Manufacturing Systems, 2014, 20(7): 1537–1545. |
| [11] |
徐亮亮, 唐敦兵, 朱仁淼, 等.
设计需求与方案求解协同演化模型的形式化表达[J]. 工程设计学报, 2011, 18(1): 17–22.
XU Liang-liang, TANG Dun-bing, ZHU Ren-miao, et al. Formalization of co-evolution model of design requirement and solution solving[J]. Chinese Journal of Engineering Design, 2011, 18(1): 17–22. |
| [12] |
徐晓刚, 刘伟, 刘达斌, 等.
产品开发中的设计迭代及其解耦策略[J]. 组合机床与自动化加工技术, 2011, 38(9): 29–31.
XU Xiao-gang, LIU Wei, LIU Da-bin, et al. Design iteration and de-coupling method[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2011, 38(9): 29–31. |
| [13] |
包北方, 杨育, 李雷霆, 等.
产品定制协同开发任务分配多目标优化[J]. 计算机集成制造系统, 2014, 20(4): 739–746.
BAO Bei-fang, YANG Yu, LI Lei-ting, et al. Multi-objective optimization for task allocation of product customization collaborative development[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 739–746. |
| [14] | YANG W, ZHANG W, WANG Y, et al. Ontology-based multi-perspective task decomposition to support composite manufacturing service discovery[J]. International Journal of Digital Content Technology and its Application, 2011, 5(7): 290–296. DOI:10.4156/jdcta |
| [15] |
黄瑾, 金海, 谢夏, 等.
网格系统中的层次化资源分配与任务调度[J]. 华中科技大学学报 (自然科学版), 2006, 34(10): 51–54.
HUANG Jin, JIN Hai, XIE Xia, et al. Hierarchical resource allocation and task scheduling in grid environments[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2006, 34(10): 51–54. |
| [16] |
郭希娟, 李墨华.
基于多准则的动态任务分配算法[J]. 计算机应用, 2008, 28(10): 2507–2509.
GUO Xi-juan, LI Mo-hua. Dynamic task assigment algoritum based on multi-criteria[J]. Computer Application, 2008, 28(10): 2507–2509. |
| [17] |
叶菁, 谢丽聪.
基于遗传算法的网格资源分配与调度研究[J]. 计算机与现代化, 2010, 17(10): 4–7.
YE Jing, XIE Li-cong. Research on task allocation and scheduling in grid based on genetic algorithm[J]. Computer and Modernization, 2010, 17(10): 4–7. DOI:10.3969/j.issn.1006-2475.2010.10.002 |
| [18] |
苏财茂, 柯映林.
面向协同设计的任务规划与解耦策略[J]. 计算机集成制造系统, 2006, 12(1): 21–26.
SU Cai-mao, KE Ying-lin. Task planning and decoupling strategy for collaborative design[J]. Computer Integrated Manufacturing Systems, 2006, 12(1): 21–26. |
| [19] |
陈庭贵, 肖人彬.
基于内部迭代的耦合任务集求解方法[J]. 计算机集成制造系统, 2008, 14(12): 2375–2383.
CHEN Ting-gui, XIAO Ren-bin. Coupled task solving method based on inner iteration[J]. Computer Integrated Manufacturing Systems, 2008, 14(12): 2375–2383. |


