随着国家城市化进程的推进,城市人口集中,建筑向高空发展是目前各国城市建设中普遍存在的状况[1].建筑行业及建筑装饰行业[2]必将寻求建筑装配自动化[3]的生存之路,其中提高建筑装配自动化的稳定性和安全性成为当务之急[4].
自适应力控制方法[5]是在基本的力控制方法中加入了自适应策略,使得在机器人或环境参数未知的情况下[6],通过在线参数估计方法获得所需要的环境刚度系数以及相应的阻尼[7]、阻抗参数等.其中以Seul为代表,其根据Hogan基础阻抗控制算法[8]中存在不足之处,即:由于机器人动力学模型不够精确所带来的位置跟踪偏差.应该加入预先的期望力来直接控制对接触力的跟踪,以及控制器要求有足够的鲁棒性来处理未知环境下刚度和位置的不确定性,提出了自适应阻抗控制算法,有效改善了基础阻抗控制的不足和对未知环境的适应能力[9].
本文对采用自适应阻抗控制方法的幕墙安装机器人的柔顺操作策略进行研究[10],运用Seul的自适应阻抗控制方法,通过仿真分析和实验验证,最终得到适用于幕墙安装流程的力控制算法[10].
1 机器人本体及阻抗控制模型本文所研究的幕墙安装机器人[11]为六自由度串联机器人[12],主要用于大型大理石板材、玻璃板材等外饰幕墙的安装,质量约为400 kg,工作半径为1.5 m,最大吸取质量为50 kg.
1.1 幕墙安装机器人运动学正解模型根据D-H法则[13],采用后置坐标系法,幕墙安装机器人结构简图及各关节坐标系如图 1所示.
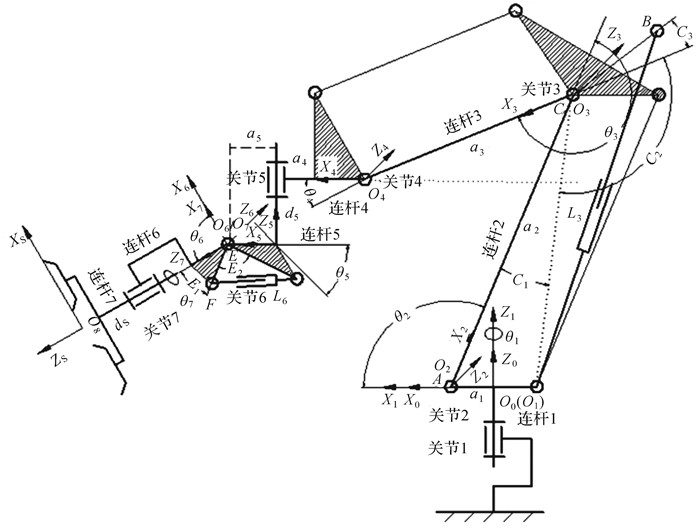
|
| 图 1 幕墙安装机器人结构简图 Fig.1 Slabstone-installation robot structure diagram |
各连杆坐标系建立后,可以通过各坐标系之间的平移、旋转来计算n-1系与n系间的变换关系,该变换过程可用一个总的变换矩阵来表示连杆n的齐次变换矩阵:
| $ {{\mathit{\boldsymbol{A}}}_{n}}=\left[\begin{matrix} \rm{cos}~{{\theta }_{n}} &-\rm{sin }\!\!~\!\!\rm{ }{{\theta }_{n}} & 0 & {{a}_{n-1}} \\ \rm{sin}~{{\theta }_{n}}\rm{cos}~{{\alpha }_{n-1}} & \rm{cos}~{{\theta }_{n}}\rm{cos}~{{\alpha }_{n-1}} &-\rm{sin}~{{\alpha }_{n-1}} &-{{d}_{n}}\rm{sin}~{{\alpha }_{n-1}} \\ \rm{sin}~{{\theta }_{n}}\rm{sin}~{{\alpha }_{n-1}} & \rm{cos}~{{\theta }_{n}}\rm{sin}~{{\alpha }_{n-1}} & \rm{cos}~{{\alpha }_{n-1}} & {{d}_{n}}\rm{cos }\!\!~\!\!\rm{ }{{\alpha }_{n-1}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] $ | (1) |
各个坐标系间的转换矩阵相乘便可以得到从基坐标系O0到末端坐标系O8的转换矩阵80T:
| $ {}_{8}^{0}\mathit{\boldsymbol{T}}={{\mathit{\boldsymbol{A}}}_{1}}{{\mathit{\boldsymbol{A}}}_{2}}{{\mathit{\boldsymbol{A}}}_{3}}{{\mathit{\boldsymbol{A}}}_{4}}{{\mathit{\boldsymbol{A}}}_{5}}{{\mathit{\boldsymbol{A}}}_{6}}{{\mathit{\boldsymbol{A}}}_{7}}{{\mathit{\boldsymbol{A}}}_{8}}=\left[\begin{matrix} {{n}_{X}} & {{o}_{X}} & {{a}_{X}} & {{p}_{X}} \\ {{n}_{Y}} & {{o}_{Y}} & {{a}_{Y}} & {{p}_{Y}} \\ {{n}_{Z}} & {{o}_{Z}} & {{a}_{Z}} & {{p}_{Z}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] $ | (2) |
为了最终计算各个伺服电机处的旋转或位移量θ1,θ2,θ3,θ5,θ6,θ7与机器人末端位姿矩阵[n,o,a,p]之间的关系,需推导出由L3,L6计算θ3,θ6的公式.
根据三角形的正弦定理和余弦定理求得:
| $ {{\theta }_{3}}=2\pi-{{C}_{1}}-{{C}_{2}} $ | (3) |
同理可得到关节6的求解方法,由此得到了幕墙安装机器人各个伺服电机处的旋转位移变量θ1,θ2,θ3,θ5,θ6,θ7与机器手末端位姿矩阵[n,o,a,p]之间的关系.
1.2 幕墙安装机器人阻抗控制模型为方便研究阻抗控制算法的特点与其实验仿真效果,以关节2和关节3为阻抗控制的研究模型,并将这2关节简化为连杆结构,方便模型的建立与计算.建立的幕墙安装机器人阻抗控制模型如图 2所示.
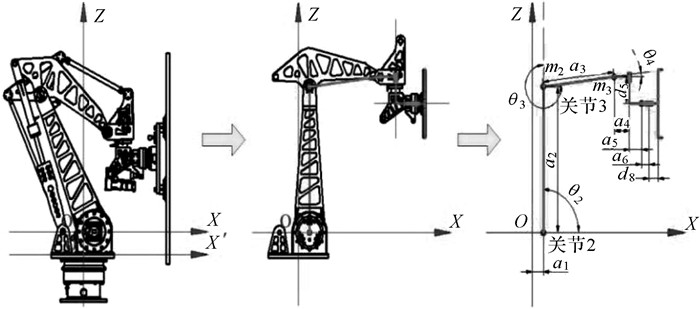
|
| 图 2 幕墙安装机器人阻抗控制模型 Fig.2 Impedance control model of slabstone-installing robot |
根据所建立的阻抗控制模型,假设各连杆的质量均集中在连杆的末端即旋转关节处,后面几处关节的位姿不发生变化(只对关节2和关节3进行研究),令L=a4+a5+a6+a8, 则研究模型的运动学方程为:
| $ \left\{ \begin{array}{*{35}{l}} X={{a}_{2}}\cos {{\theta }_{2}}+{{a}_{3}}\cos {{\theta }_{4}}+{{a}_{1}}+L \\ Y={{a}_{2}}\sin {{\theta }_{2}}+{{a}_{3}}\sin (-{{\theta }_{4}})-{{d}_{5}} \\ \end{array} \right. $ | (4) |
采用牛顿-欧拉递推方法[14],记:τ=(τ2,τ3)T,q=(θ2,θ3)T,得到该研究模型在关节空间中的动力学方程封闭形式的一般结构式为:
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) $ | (5) |
式中:D(q) 为惯性矩阵,
| $ \begin{align} & \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}})=\left[\begin{matrix} {{a}_{3}}^{2}{{m}_{3}}+2{{a}_{2}}{{a}_{3}}{{m}_{3}}\cos {{\theta }_{3}}+{{a}_{2}}^{2}({{m}_{2}}+{{m}_{3}}) & {{a}_{3}}^{2}{{m}_{3}}+{{a}_{2}}{{a}_{3}}{{m}_{3}}\cos {{\theta }_{3}} \\ {{a}_{3}}^{2}{{m}_{3}}+{{a}_{2}}{{a}_{3}}{{m}_{3}}\cos {{\theta }_{3}} & {{a}_{3}}^{2}{{m}_{3}} \\ \end{matrix} \right] \\ & \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot{q}}})=\left[\begin{matrix} -{{m}_{3}}{{a}_{2}}{{a}_{3}}{{{\dot{\theta }}}_{3}}^{2}\sin {{\theta }_{3}}-2{{m}_{3}}{{a}_{2}}{{a}_{3}}{{{\dot{\theta }}}_{2}}{{{\dot{\theta }}}_{3}}\sin {{\theta }_{3}} \\ {{m}_{3}}{{a}_{2}}{{a}_{3}}{{{\dot{\theta }}}_{2}}^{2}\sin {{\theta }_{3}} \\ \end{matrix} \right] \\ & \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})=\left[\begin{matrix} {{m}_{3}}{{a}_{3}}g\cos ({{\theta }_{2}}+{{\theta }_{3}})+({{m}_{2}}+{{m}_{3}}){{a}_{2}}g\cos {{\theta }_{2}} \\ {{m}_{3}}{{a}_{3}}g\cos ({{\theta }_{2}}+{{\theta }_{3}}) \\ \end{matrix} \right] \\ \end{align} $ |
其中大臂和小臂的质量m2和m3分别为:m2=39.431 kg,m3=25.478 kg.a1=0.090 m,a2=1.080 m,a3=0.640 m,L=a4+a5+a6+d8=0.412 1 m.
由此得到了幕墙安装机器人阻抗控制研究模型的数学方程及其相关参数.
2 幕墙安装机器人阻抗控制算法 2.1 自适应阻抗控制方程依据自适应阻抗控制算法的控制思想,在基础阻抗控制关系式中引入期望力[15],则阻抗方程可以改写为:
| $ {{F}_{e}}-{{F}_{d}}=\mathit{\boldsymbol{M}}\ddot{E}+\mathit{\boldsymbol{B}}\dot{E}+\mathit{\boldsymbol{K}}E, $ | (6) |
式中:Fe为与环境接触产生的作用力,Fd为系统预设的期望力, M为机器人末端质量惯性系数,B为机器人末端阻尼系数,K为机器人末端与环境端接触刚度系数,E为位置偏差.
当机器人末端处于未接触运动空间状态时,Fe=0,则阻抗方程为:
| $ \mathit{\boldsymbol{M}}\ddot{E}+\mathit{\boldsymbol{B}}\dot{E}+\mathit{\boldsymbol{K}}E=-{{F}_{\rm{d}}} $ | (7) |
当处于环境接触空间状态时,机器人末端与环境接触达到稳定状态,Fe=Fd≠0,Ė=Ë=0,由于接触力的存在,环境产生弹性形变,因此E≠0,所以由式(6) 可知刚度系数K在受到环境作用力的方向上为0,则式(6) 可改写为:
| $ \mathit{\boldsymbol{M}}\ddot{E}+\mathit{\boldsymbol{B}}\dot{E}={{F}_{\rm{e}}}-{{F}_{\rm{d}}} $ | (8) |
由于机器人在实际的幕墙安装工作中,一般得不到安装环境位置的准确值,只能得到环境位置的估计值L′e,则环境位置与真实值间存在的偏差δ为:
| $ \delta {{L}_{\text{e}}}={{L}_{\text{e}}}^{\prime }-{{L}_{\text{e}}} $ | (9) |
则机器人末端处于环境接触空间状态时,估计值与安装环境之间真实的位置偏差E′为:
| $ {E}'={{{{L}'}}_{\text{e}}}-{{L}_{0}}\text{=}{{L}_{\text{e}}}-{{L}_{0}}\text{+}\delta $ | (10) |
自适应阻抗控制的目的就是跟踪环境的位置,因而机器人末端的目标位置即安装环境的位置Le,得:
| $ E={{L}_{\text{e}}}-{{L}_{0}}\text{=}{E}'-\delta $ | (11) |
用E′代替E,得到:
| $ \mathit{\boldsymbol{M}}{\ddot{E}}'+\mathit{\boldsymbol{B}}{\dot{E}}'={{F}_{\rm{e}}}-{{F}_{\rm{d}}} $ | (12) |
为纠正机器人力控制中存在的误差,在方程中设置一个补偿项Ω来抵消产生的力误差[16],使控制系统的输出量稳定准确,其表达式为:
| $ \Omega (t)=\Omega (t-\lambda )+\eta \frac{{{F}_{\rm{d}}}(t-\lambda )-{{F}_{\rm{e}}}(t-\lambda )}{\mathit{\boldsymbol{B}}} $ |
其中:λ为控制器的采样周期,η为新周期的更新率且η>0.
由此得到最终的自适应阻抗方程,分别为未接触运动状态方程(13) 和环境接触运动状态方程(14):
| $ \mathit{\boldsymbol{M}}\overset{\bullet \bullet }{\mathop{E}}\, +\mathit{\boldsymbol{B}}\overset{\bullet }{\mathop{E}}\, +\mathit{\boldsymbol{K}}E=-{{F}_{\rm{d}}} $ | (13) |
| $ \mathit{\boldsymbol{M}}\overset{\bullet \bullet }{\mathop{E}}\, '+\mathit{\boldsymbol{B}}(\overset{\bullet }{\mathop{E}}\, '+\Omega )={{F}_{\rm{e}}}-{{F}_{\rm{d}}}. $ | (14) |
以阻抗控制研究模型为基础,将自适应阻抗控制规律代入其中,引入控制器的采样时间,则幕墙安装机器人动力学方程改写成时间的函数为:
| $ \mathit{\boldsymbol{\hat{D}}}(t)\mathit{\boldsymbol{\ddot{q}}}(t)+\bar{h}(t)=\tau (t)-{{\tau }_{\rm{e}}}(t) $ | (15) |
式中:
令
| $ \hat{\bar{h}}(t)=\bar{h}(t-\lambda )=\tau (t-\lambda )-{{\tau }_{\rm{e}}}(t-\lambda )-\mathit{\boldsymbol{\hat{D}}}(t)\mathit{\boldsymbol{\ddot{q}}}(t-\lambda ) $ | (16) |
用
| $ \tau (t)-{{\tau }_{\rm{e}}}(t)=\mathit{\boldsymbol{\hat{D}}}(t)\mathit{\boldsymbol{\ddot{q}}}(t)+\hat{\bar{h}}(t) $ | (17) |
其中
| $ \begin{align} & \tau \left( t \right)=\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right){{J}^{-1}}\left[{{{\ddot{L}}}_{0}}-\dot{J}\mathit{\boldsymbol{\dot{q}}} \right]+\tau \left( t-\lambda \right) \\ & -{{\tau }_{\rm{e}}}\left( t-\lambda \right)-\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right)\mathit{\boldsymbol{\ddot{q}}}\left( t-\lambda \right)+{{\tau }_{\rm{e}}}\left( t \right) \\ \end{align} $ | (18) |
其中:
通过对幕墙安装机器人阻抗控制研究模型的运动学和动力学计算以及幕墙安装流程分析,将自适应阻抗控制器分为未接触运动空间和环境接触空间两部分,运用MATLAB进行仿真分析.令采样频率为200 Hz (即λ=5ms),ρ=9.024, 在仿真过程中
当幕墙安装机器人末端处于自由运动状态时,不受外界环境作用力的影响,因此Fe, τe(t), τe(t-λ) 均为零,得到运动空间的自适应阻抗控制方程为
| $ \begin{align} & \tau \left( t \right)=\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right){{\mathit{\boldsymbol{J}}}^{-1}}\left[{{{\ddot{L}}}_{\rm{d}}}+{{\mathit{\boldsymbol{M}}}^{-1}}\left( {{F}_{\rm{d}}}+\mathit{\boldsymbol{B}}\dot{E}+\mathit{\boldsymbol{K}}E \right)-\mathit{\boldsymbol{\dot{J}\dot{q}}} \right] \\ & +\tau \left( t-\lambda \right)-\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right)\mathit{\boldsymbol{\ddot{q}}}\left( t-\lambda \right) \\ \end{align} $ | (19) |
采用固定步长和龙阁库塔(ode4) 算法,按照空间直线的信号进行位置跟踪.
采用给定阶跃信号

|
| 图 3 最终理想空间直线跟踪轨迹 Fig.3 Final ideal space linear tracking trajectory |
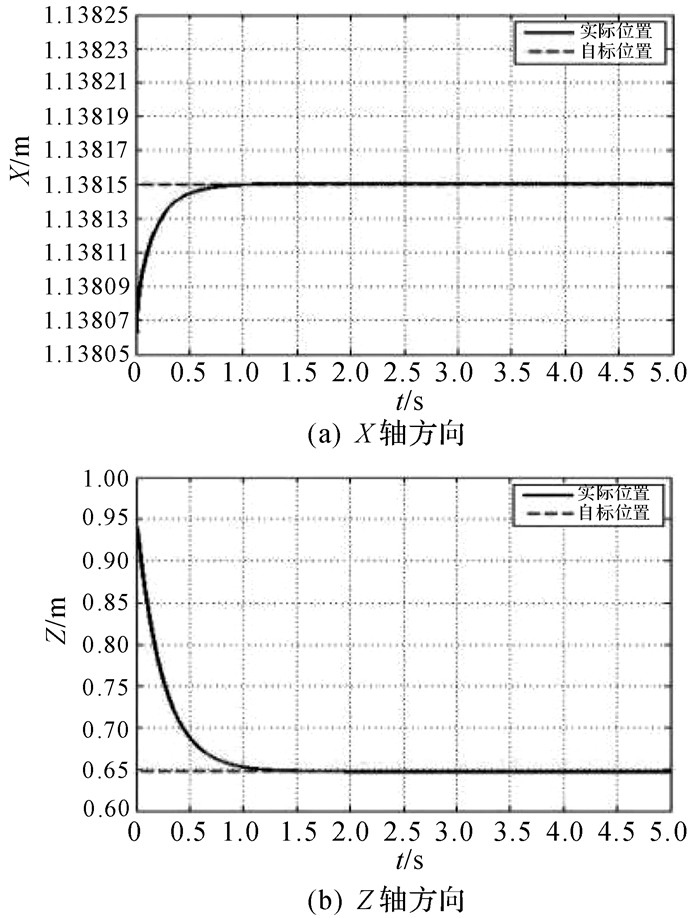
|
| 图 4 空间直线X轴和Z轴方向位置跟踪情况 Fig.4 Position tracking of spatial straight line at X axis and Z axis direction |
当机器人末端处于环境接触状态[17]时,其与安装环境产生相互作用力,因此Fe,τe(t),τe(t-λ) 均不为零,得环境接触空间的自适应阻抗控制方程为:
| $ \begin{align} & \tau \left( t \right)=\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right){{\mathit{\boldsymbol{J}}}^{-1}}\left[\ddot{L}_{\rm{e}}^{\rm{ }\!\!'\!\!\rm{ }}+{{\mathit{\boldsymbol{M}}}^{-1}}\left( {{F}_{\rm{d}}}-{{F}_{\rm{e}}}+\mathit{\boldsymbol{B}}\left( {{{\dot{E}}}^{'}}+\Omega \right) \right)-\mathit{\boldsymbol{\dot{J}\dot{q}}} \right] \\ & +\tau \left( t-\lambda \right)-{{\tau }_{\rm{e}}}\left( t-\lambda \right)-\overset{\mathit{\boldsymbol{ }}\!\!\hat{\ }\!\!\rm{ }}{\mathop{\mathit{\boldsymbol{D}}}}\, \left( t \right)\mathit{\boldsymbol{\ddot{q}}}\left( t-\lambda \right)+{{\tau }_{\rm{e}}}\left( t \right) \\ \end{align} $ | (20) |
设定环境接触为弹性形变,以机器人零位位置为起始位置,目标位置即为幕墙板材的安装环境位置(1.1381,0,0.94724) m,不再额外给定期望位置,同时给定期望的环境接触力,即Fd=3.3 N.
此为X方向上的单方向作用力.取更新率η=0.1,环境位置偏差值和环境刚度系数分别为:
δ=0.000 2 m,Ke=4 000N/m.
取出参数的最优值为:
| $ \mathit{\boldsymbol{M}}=\left[\begin{matrix} 0.8 & 0 \\ 0 & 0.8 \\ \end{matrix} \right], \mathit{\boldsymbol{B}}=\left[\begin{matrix} 500 & 0 \\ 0 & 2500 \\ \end{matrix} \right], \mathit{\boldsymbol{K}}=\left[\begin{matrix} 0 & 0 \\ 0 & 1600 \\ \end{matrix} \right] $ |
最终的环境接触空间跟踪轨迹如图 5,图中粗实线为需要进行安装的幕墙位置.
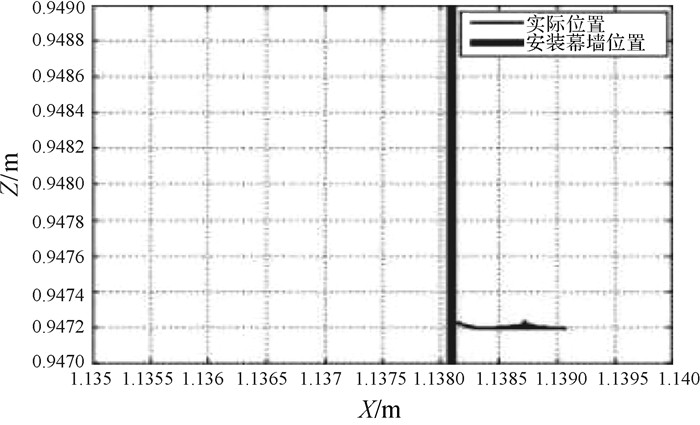
|
| 图 5 环境接触空间跟踪轨迹 Fig.5 Tracking trajectory of environmental contact space |
在环境接触空间X轴方向上的位置跟踪情况和机器人末端与环境接触力的变化情况如图 6和图 7所示.
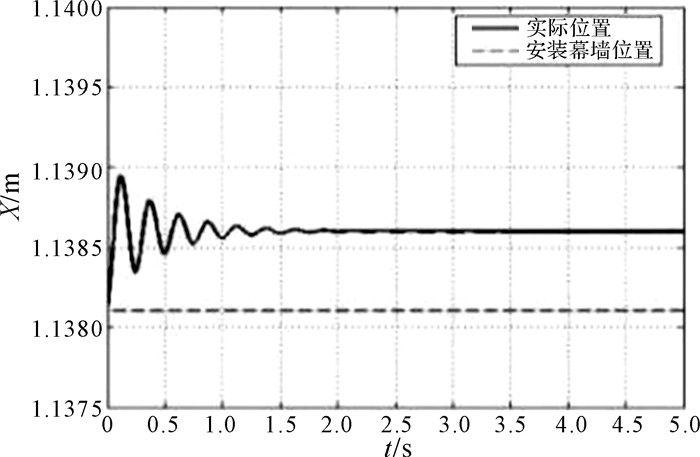
|
| 图 6 环境接触空间在X轴方向上的位置跟踪情况 Fig.6 Position tracking of environmental contact space at X axis direction |

|
| 图 7 自适应阻抗控制机器人末端接触力的变化情况 Fig.7 Changes of the end contact force of the adaptive impedance control robot |
可见机器人末端与环境接触力最终维持在一个稳定的状态下,且收敛于所给定期望力的值.
3.3 环境接触空间状态下参数的选取在环境接触空间状态下调整惯性矩阵估计值[17]和更新率大小同样可影响幕墙安装机器人末端的环境接触力和系统最终的稳定性,因此应在满足更新率和惯性矩阵估计值约束条件的情况下选取使控制性能最优的参数.
为使系统保持稳定,更新率η必须满足
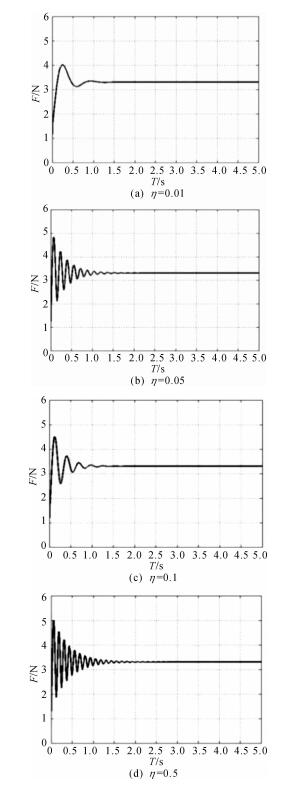
|
| 图 8 更新率η对环境接触力的影响 Fig.8 Influence of renewal rate on environmental contact force |
由对不同更新率η的仿真可知,随着η的增大,力跟踪信号的调整时间加长,力初始状态时的波动较大,振荡频率增加,超调量也比较大,说明幕墙安装机器人末端在起初与安装环境接触时,抖动会随着η的增大而加剧,应该予以避免.因此,为满足控制系统的稳定性和快速性,应选取一个较小的η值,但为了同时满足信号采集的实时性和误差补偿项的要求,更新率η不能过小,因此取η=0.01较为合适.
同理,对于惯性矩阵估计值
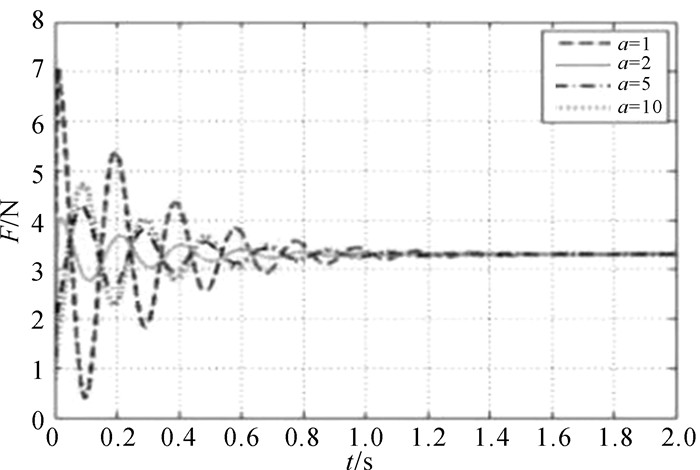
|
| 图 9 惯性矩阵预估值$ \mathit{\boldsymbol{\hat D}}(\mathit{\boldsymbol{t}}) $对环境接触力的影响 Fig.9 Influence of the inertia matrix estimation $ \mathit{\boldsymbol{\hat D}}(\mathit{\boldsymbol{t}}) $ on the environmental contact force |
由对不同预估值α的仿真可知,当α < 1时,接触位置会偏离环境位置,不能始终保持接触力,控制系统不能精确地跟踪给定的期望力.当预估值α在[1, 10]区间内时,由图 9可知,随着α的增大,控制系统最终收敛于期望力的最大超调量和调整时间都先逐渐减小再逐渐增大,当α=2时力的跟踪曲线较为平滑,超调量最小,有较好的力跟踪性能,由此可知,取预估值α=2是满足条件范围内较为合适的参数.
4 机器人柔顺操作实验研究相关柔顺操作实验主要依赖于幕墙安装机器人运动控制系统的搭建.基于上述阻抗控制的理论分析,对幕墙安装机器人本体进行柔顺操作的相关实验.将仿真程序应用到幕墙安装机器人本体当中,在机器人末端安装六维力传感器作为信号的输入端,通过人机协调的方式对幕墙安装机器人进行柔顺操作,如图 10所示.对在操作者端力传感器检测到的人力变化进行分解和判断,并在每个受力方向上设定阈值,当某个方向超过该阈值时,说明该方向为人力操作实际作用的方向,并采用运动控制板卡的速度控制模式和阻抗控制柔顺操作理论进行协调控制,最后随人力变化调节速度大小和方向以得到操作者所期望的轨迹路线.

|
| 图 10 幕墙安装机器人柔顺操作实验装置 Fig.10 Experimental device for compliant operation of slabstone-installation robot |
为验证幕墙安装机器人的柔顺性,用其在白板上绘制人力柔顺操作的直线,根据效果图可以看出,在机器人工作空间内描绘出的水平竖直直线较为理想,基本满足操作者人力的意图与安装移动需求,如图 11所示.

|
| 图 11 幕墙安装机器人柔顺操作绘制的空间直线 Fig.11 Slabstone-installing robot flexible operation drawing space straight line |
在实验中,为验证通过人机协调操作进行空间直线位移的精度,全程运用激光跟踪设备对幕墙安装机器人末端进行轨迹跟踪,测量得到的实时位置信息可以用来监控运动轨迹,并且计算出到每个测量点的误差[4].图 12所示为测得的力控制操作时机器人X方向和Z方向的末端位置误差图.将X轴和Z轴方向上各测量点与期望直线轨迹的偏差列于表 1中.
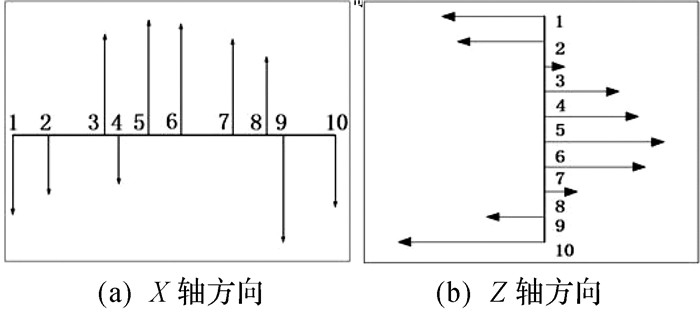
|
| 图 12 测得的机器人X轴和Z轴方向末端位置误差 Fig.12 The end position error measured of the robot at X axis and Z axis direction |
| 测量点 | X轴方向偏差值/mm | Z轴方向偏差值/mm |
| 1 | 0.688 | 1.002 |
| 2 | 0.500 | 0.833 |
| 3 | 0.899 | 0.100 |
| 4 | 0.403 | 0.703 |
| 5 | 1.030 | 0.922 |
| 6 | 0.998 | 1.211 |
| 7 | 0.850 | 1.002 |
| 8 | 0.686 | 0.234 |
| 9 | 0.950 | 0.507 |
| 10 | 0.618 | 1.494 |
在控制算法上对操作者的输入力进行滤波,以消除机器人末端在运动过程中的振动,通过操作者端六维力传感器的示数显示,分别得到了操作者在操控机器人末端水平和竖直方向上(即X轴方向和Z轴方向) 直线运动时所施加力的变化,如图 13所示.
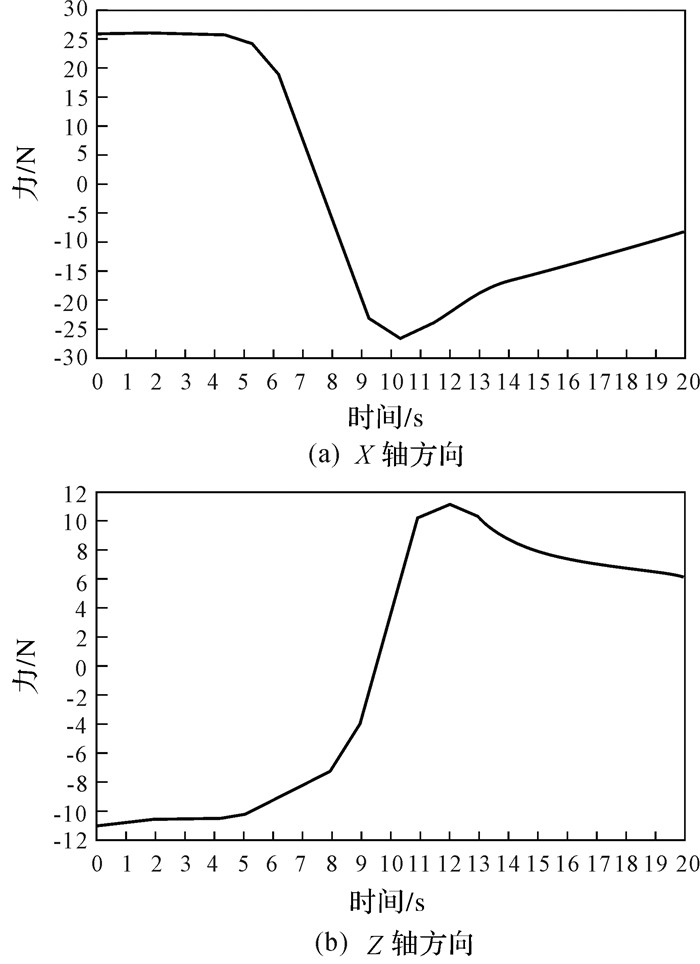
|
| 图 13 操作者在水平、竖直方向上施加力的变化情况 Fig.13 The force change situation at the horizontal and vertical direction exerted by operator |
仿真采用给定阶跃信号作为输入,通过参数调整,最终实现机器人末端理想的直线运动.仿真结果表明,实际跟踪位置和目标位置基本一致.在柔顺操作实验中,采用操作者在不同维度的力作为输入,施加力的方向与机器人末端运动的方向一致,同时施加力的大小决定了机器人末端运动的速度和位移大小,通过观察水平、竖直方向上施加力变化情况,结合激光跟踪设备得到的末端位置偏差图和轨迹偏差值大小,可知其运动过程中测量点与期望直线轨迹的的位置偏差稳定在1 mm左右,能够满足幕墙安装机器人在自由运动空间快速移动的稳定性和准确性以及人机协调的柔顺性要求.由此可知仿真和实验结果基本一致,证明了基于力控制的自适应阻抗方法的合理性和该方法应用于幕墙安装机器人的可行性.
5 结论以幕墙安装机器人为执行机构,采用自适应阻抗控制的方法,达到了良好的实验效果,并基本满足高空幕墙安装机器人的工作要求.本文建立了较为准确的自适应阻抗控制的物理模型与数学模型,分别在未接触空间和接触空间进行了分析,提出利用给定的输入信号和期望力得到了最终接触力和位置的跟踪曲线,仿真分析验证了基于自适应阻抗控制方法的可行性,并且通过柔顺操作实验验证了方法的合理性.基于幕墙安装机器人的自适应阻抗控制方法在实际应用中有较大的通用价值,对幕墙安装自动化的发展有较强的意义.
| [1] |
楚风华.
"十二五"中国建筑业发展展望[J]. 中国建设信息, 2011(4): 2–7.
CHU Feng-hua. Prospects for the development of China's construction industry in 12th Five-Year[J]. China Construction Information, 2011(4): 2–7. |
| [2] |
王亚娥.
试论建筑幕墙行业成本控制的有效策略[J]. 科技风, 2012(5): 154.
WANG Ya-e. On the effective strategy of cost control in construction curtain wall industry[J]. Science and Technology Wind, 2012(5): 154. |
| [3] | CHOI J H, LEE S Y, LEE K Y, et al. Automation system for curtain wall installation Ⅱ (ASCI Ⅱ)[2006-08-10].http://xueshu.baidu.com/s?wd=paperuri:(0daa6402150c05e186577ad325dd13f0)&filter=sc_long_sign&sc_ks_para=q%3DAutomation+system+for+curtain+wall+installation+II+%28ASCI+II%29&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_us=9036715237523179311. |
| [4] | KUSHIDA Daisuke, NAKAMURA Masatoshi, GOTO Satoru. Flexible motion of pull-out-work by articulated robot arm based on forcefree control[J]. IEEE International Conference on Industrial Electronics Society, 2000, 3: 1797–1802. |
| [5] |
刘楚辉.
自适应控制的应用研究综述[J]. 组合机床与自动化加工技术, 2007(1): 1–4.
LIU Chu-hui. Application research of adaptive control[J]. Combined Machine Tools and Automatic Processing technology, 2007(1): 1–4. |
| [6] | JUNG Seul, HSIA T C, BONITZ R G. Force tracking impedance control of robot manipulators under unknown environment[J]. IEEE International Conference on Control Systems Technology, 2004, 12(3): 474–483. DOI:10.1109/TCST.2004.824320 |
| [7] | JUNG Seul, HSIA T C. Force tracking impedance control of robot manipulators for environment with damping[J]. IEEE International Conference on Industrial Electronics Society, 2007: 2742–2747. |
| [8] | JUNG Seul, HSIA T C. Reference compensation technique of neural force tracking impedance control for robot manipulators[J]. Proceedings of the 8th World Congress on Intelligent Control and Automation, 2010, 20(1): 650–655. |
| [9] |
杨振.基于阻抗控制的机器人柔顺性控制方法研究[D].南京:东南大学机械工程学院, 2005:6-25.
YANG Zhen.Research on robot compliance control method based on impedance control[D].Nanjing:Southeast University, School of Mechanical Engineering, 2005:6-25. |
| [10] | JUNG Seul, HSIA T C. Neural network techniques for robust force control of robot manipulaitors[J]. IEEE International Symposium on Intelligent Control, 1995: 111–116. |
| [11] |
孙伟, 于永璋.
几种建筑机器人概介[J]. 建筑机械化, 1990, 6(6): 22–24.
SUN Wei, YU Yong-zhang. A few construction robots[J]. Construction Mechanization, 1990, 6(6): 22–24. |
| [12] |
李铁军, 王海玲, 赵海文.
串并联板材安装机器人结构设计与实现[J]. 机器人, 2011(1): 107–112.
LI Tie-jun, WANG Hai-ling, ZHAO Hai-wen. Design and implementation of a series parallel plate installation robot[J]. Robot, 2011(1): 107–112. |
| [13] | HSIA T C. Simple robust schemes for cartesian space control of robot manipulators[J]. IEEE International Conference on Robotics and Automation, 1994, 9(4): 167–174. |
| [14] | HOGAN Neville. Impedance control of industrial robots[J]. Robotics and Computer-Integrated Manufacturing, 1984, 1(1): 97–113. DOI:10.1016/0736-5845(84)90084-X |
| [15] | DAISUKE Kushida, GOTO Satoru, KYURA Nobuhiro. Flexible motion realized by forcefree control:pull-out-work by articulated robot arm[J]. IEEE International Conference on Robotics & Automation, 2001, 3: 2747–2752. |
| [16] | HOGAN Neville. Impedance control:an approach to manipulation. Ⅰ-Theory. Ⅱ-Implementation. Ⅲ-Applications[J]. Journal of Dynamic Systems, Measurement, and Control, 107(1):1-24. |
| [17] | KAZEROONI, SHERIDAN T B, HOUPT P K. Fundamentals of robust compliant motion for manipulators[J]. IEEE Transaction on Robotics and Automation, 1986, 2(2): 418–427. |


