鱼类在长期的自然选择进化过程中形成了依靠身体尾部波动推进(body caudal fin,BCF) 和依靠鱼鳍拍动或波动推进(medial paired fin,MPF) 两种主要运动模式[1].相对于BCF模式而言,采用MPF模式推进的鱼类具有更高的低速机动性和稳定性,具备在复杂水下环境中生存的能力.尤其是在运动过程中,身体几乎不参与任何的动作行为,为载人仿生推进器的研究提供了很好的参考.
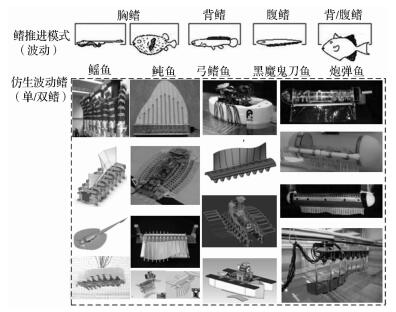
出于潜在的应用需求,近年来研究人员更多地关注MPF模式推进的机理分析及推进器的设计与实现.人们希望理解MPF模式高效、高机动性和高稳定性的推进机理,研制相应的水下推进器,进而替代人工从事诸如水下资源勘查、污染物探测、水下考古、军事侦测等工作[2].图 1给出了近年来研制的基于鱼鳍波动的水下仿生推进装置[3-18],这些装置大多由鳍条、覆盖于鳍条之间的柔性蒙皮以及驱动电机组成.电机往复或旋转运动的频率和幅度以及电机之间的运动相位差形成了不同的波形,产生不同的推进效果.
|
| 图 1 仿生波动鳍推进装置 Fig.1 Bionic undulating fin propulsion devices |
进一步分析发现,所有这些装置的鳍条运动可分为从仿生鳍根部至端部鳍条作等幅摆动和根部至端部鳍条作变幅摆动两种模式.后者为依靠鱼鳍波动推进的鱼类广泛采用的推进模式.初步实验测试显示鳍条在这2种运动模式下产生的游动效果(如平均推进力) 存在一定的差异.因此,深入研究相同运动学参数下鳍条2种运动模式产生的游动效果差异,并分析造成这种差异的原因是十分有意义的.
利用计算流体动力学原理,重点比较分析鳍条的2种运动模式在不同运动学参数下,鳍面的压力分布、横向截面速度矢量场和压力场、无量纲阻力系数以及尾迹涡街的结构形态.通过研究,得出了2种运动模式产生的推进力均随着频率、摆幅和波长的增大而增加,相同参数下鳍条等幅摆动产生的推进力始终小于变幅摆动,影响2种运动模式游动效果的主要原因之一来自于沿鳍条方向的差异.该数值计算方法广泛应用于水下生物体和仿生推进器的游动机理分析中,已被证明是非常可靠和有效的研究手段之一[19-31].
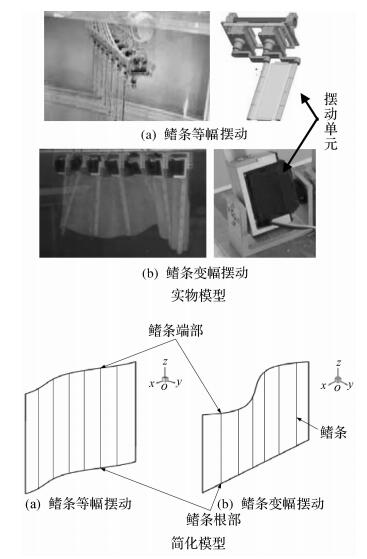
1 鳍条的2种运动模式鳍条的2种运动模式的实物模型和简化模型分别如图 2所示,实物长×宽均为0.7m×0.4 m.图 2(a)为鳍条等幅摆动,图 2(b)为鳍条变幅摆动.试验初步测量了不同运动学参数下2种运动模式产生的推进力大小.
|
| 图 2 鳍条2种运动模式的运动学建模 Fig.2 Kinematic modeling of two fin ray motion patterns |
如图 3所示,试验测试装置主要由试验系统和鱼鳍模型组成,其中,试验系统包括一个6 m×4 m×1.8 m的玻璃水槽以及置于其上方的气动导轨,导轨连接六分量测力计.鱼鳍模型通过连接杆与测力计固接.该试验主要探究鱼鳍在2种运动模式下产生的平均推进力随运动学参数变化的规律.

|
| 图 3 试验测试装置 Fig.3 The experiment equipment |
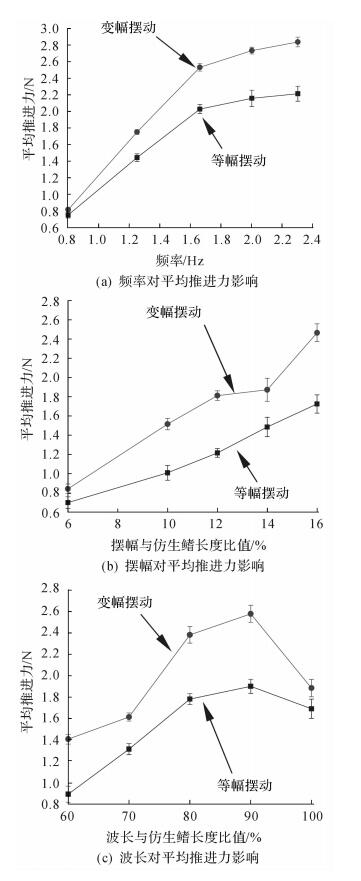
图 4所示为鳍条在2种运动模式下,不同运动学参数(频率、摆幅和波长) 对仿生鳍平均推进力影响的试验结果.总体而言,平均推进力随着运动学参数增加而增大.另一方面,相同运动学参数下鳍条变幅摆动产生的平均推进力始终大于鳍条等幅摆动.
|
| 图 4 鳍条2种模式下产生的平均推进力随运动学参数的变化情况 Fig.4 The change of averaged propulsion force with kinematic parameters under two motion patterns of fin ray |
为了深入探讨鱼鳍鳍条在2种运动模式下平均推进力存在差异的原因,利用流体动力学仿真软件Fluent (美国ANSYS软件开发公司,版本:Fluent 6.3.26) 对模型进行计算,通过绘制和分析形成的流场细节(如速度场、压力场和涡量场等分布情况),从流体动力学和涡动力学角度揭示其内在规律.
3 建模与定义 3.1 鳍面运动学建模首先建立鳍条在2种运动模式下的鳍面运动学方程.假定鳍条按照正弦规律作往复运动,则形成的鳍面呈现正弦波状运动,在图 2所示的直角坐标系中,等幅摆动形成的鳍面上任意一点P(x,y,z) 的运动学方程如式(1) 所示,变幅摆动形成的鳍面上任意一点Q(x,y,z) 的运动学方程如式(2) 所示:
| $ {y_P}({x_P}, {z_P}, t) = A \times {\rm{sin}}[2\pi (\frac{{{x_P}}}{\lambda }-\frac{t}{T})] $ | (1) |
| $ {y_Q}({x_Q}, {z_Q}, t) = \frac{{{z_Q}}}{k} \times {\rm{sin}}[2\pi (\frac{{{x_Q}}}{\lambda }-\frac{t}{T})] $ | (2) |
式中:A为摆幅,λ为波长,T为周期,t为时间,k为决定摆幅变化程度的常数.为探究运动学参数更宽范围内平均推动力变化的一般性规律,分析计算频率为2,4,6,8,10 Hz,λ/L(L为鱼鳍长度) 为2/3,9/10,1/1,7/4,2/1,常数k=7,6,5,3条件下的平均推动力的变化情况.
3.2 无量纲阻力系数定义无量纲阻力系数Cd综合体现了模型波动产生的推进力,对于某个时刻t0,其定义如下:
| $ {C_{\rm{d}}}({t_0}) = \frac{{{F_{\rm{d}}}({t_0})}}{{2\rho {v^2}{S_{{\rm{fin}}}}}} $ | (3) |
式中:ρ为流体密度,v为来流速度,Sfin为鱼鳍有效迎水面积,Fd为阻力大小.则无量纲阻力系数的时间平均值可统一用式(4) 计算:
| $ {{\bar C}_{\rm{d}}} = \frac{{\int\limits_{mt}^{\left( {m + j} \right)t} {\frac{{{F_{\rm{d}}}\left( t \right)}}{{2\rho {v^2}{S_{{\rm{fin}}}}}}{\rm{d}}t} }}{{jt}} $ | (4) |
式中:m和j取0,1,2,…,n等自然数,n为采样点个数,t为时间.
3.3 涡量场计算本文仅讨论沿鳍面长度方向截面(即xoy平面) 上二维涡量ω分布情况,其计算公式如式(5) 所示:
| $ \omega = \frac{{\partial v}}{{\partial x}}-\frac{{\partial u}}{{\partial y}} $ | (5) |
式中u和v分别是沿x轴和y轴的速度分量.
4 计算条件设置 4.1 控制方程控制方案采用黏性不可压缩流体的无量纲Navier-Stokes方程,如式(6) 和式(7):
| $ \frac{{\partial v}}{{\partial t}} + (v \bullet \nabla )v =-\nabla p + \frac{1}{{{\mathop{\rm Re}\nolimits} }}{\nabla ^2}v + F $ | (6) |
| $ \nabla \bullet v = 0 $ | (7) |
式中:p代表压强,雷诺数Re=vL/ν,v为来流速度,L为模型的特征长度尺寸,ν为流体的动黏性系数,F为作用于网格点上的附加虚力.
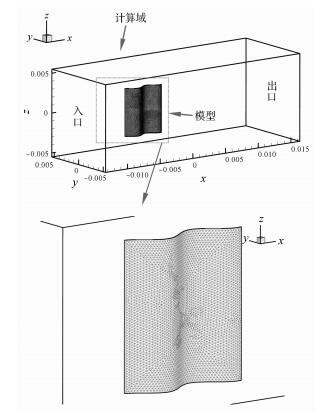
4.2 计算区域离散坐标原点位于模型前端面;定义x轴正向为来流方向,入口边界距离鱼鳍模型前端1个模型长度,出口边界距离模型末端3个模型长度;y轴为鳍条摆动方向,上下边界距离模型10个摆幅;z轴正向为鳍面延展方向,距离模型边界1个模型宽度,如图 5所示.由于涉及动网格,故采用四面体非结构网格对计算区域进行离散,并对模型周边及尾迹区域进行局部网格加密.动网格法是根据当前时刻的边界位置和速度以及时间增量,确定下一时刻的边界位置,对超出网格偏斜度或尺寸标准的网格进行局部网格重构.此方法在处理移动边界问题上非常有效[32-34].
|
| 图 5 计算域及计算网格划分 Fig.5 Calculation domain and mesh generation |
入口边界条件为速度入口(velocity inlet),来流速度v=0.01 m/s;出口边界条件为压力出口(pressure outlet);模型上下表面为无滑移及无穿透壁面边界,其他边界使用无滑移壁面边界条件.如式(8) 所示[30]:
| $ v = {v_\infty }, \frac{{\partial v}}{{\partial \mathit{\boldsymbol{n}}}} = 0, p = {p_\infty }, \frac{{\partial p}}{{\partial \mathit{\boldsymbol{n}}}} = 0 $ | (8) |
式中n为法向矢量.
4.3.2 计算方法计算方法采用有限体积法(FVM),其核心思想是把计算区域离散成很多小的控制体,然后将各个变量在每个控制体内进行积分.模型的运动方程由用户自定义函数(UDF) 控制.
4.3.3 参数设置在低雷诺数下,采用层流模型.用一阶隐式格式(first order implicit) 的时间离散,黏性项采用标准模态离散,压力-速度耦合项用SIMPLE算法,而对流项则用二阶迎风格式(second order upwind) 离散,不考虑重力的影响,其他参数的取值如表 1所示.
| 参数 | 量值 |
| 弹簧常数因子 | 1 |
| 边界节点松弛因子 | 1 |
| 收敛公差 | 0.001 |
| 迭代次数 | 30 |
| 最小长度尺寸 | 0.000 04 m |
| 最大长度尺寸 | 0.000 9 m |
| 最大单元畸变 | 0.6 |
| 时间步长 | 0.005 s |
| 时间步数 | 1 000 |
| 每时间步最大迭代次数 | 40 |
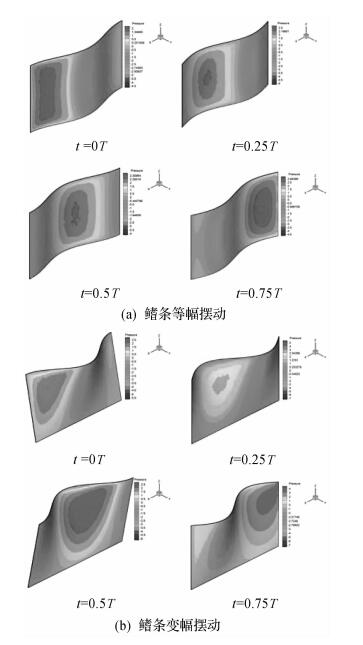
鳍条的2种运动模式下所形成的鳍面压力在一个波动周期内的变化如图 6所示.2种运动模式下鳍面上高压区和低压区均呈现交替分布,且随着鳍面运动由前往后传递.高压区和低压区交替分布使得鳍面两侧形成一定的压力差,为游动提供了主要推力和升力,其数值大小Fp可由式(9) 计算[35-36]:
|
| 图 6 1个波动周期内鳍面压力变化 Fig.6 Pressure change of fin surface during one undulating cycle |
| $ {F_{\rm{p}}} = \frac{1}{2}\rho {v^2}{C_{\rm{p}}}{S_{{\rm{fin}}}} $ | (9) |
式中
鳍条运动模式的差异,导致鳍面上压力分布形式存在差别.对于鳍条等幅摆动而言,压力呈现以中间向两侧对称递减的规律,鳍面中间压力最大;对于鳍条变幅摆动模式,随着鳍条摆幅从根部至端部逐渐增大,鳍面上压力呈现相似的渐增变化规律,根部压力较小,靠近端部附近压力值最大.
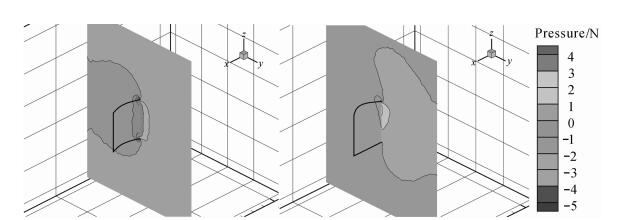
5.2 沿鳍条方向切面的速度场和压力场进一步给出沿鳍条方向切面x=5 mm (选取中间位置) 上压力场和速度矢量场情况,如图 7和图 8所示.
|
| 图 7 x=5 mm截面处压力分布 Fig.7 The pressure distribution at x=5 mm |
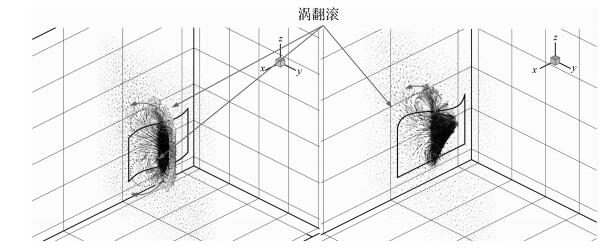
|
| 图 8 x=5 mm截面处速度矢量场 Fig.8 The velocity vector field at x=5 mm |
图 7为x=5 mm平面上压力分布,从图中可以看出越靠近鳍面处压力数值越大,随着离鱼鳍表面距离增大,压力逐渐减小,说明鱼鳍对流体的扰动减小.压力沿鳍条方向的分布规律与图 6相似.此外,鳍面一侧若出现高压区,则与之相对应的背面则出现低压区.图 8为x=5 mm平面上速度矢量场,箭头长短代表该处速度的大小,箭头方向代表该处当前时刻流体颗粒移动方向.类似地,对于等幅摆动,鳍面中部流体加速程度较两侧大,两侧边缘有部分流体翻过鳍面进入背面流体区域,即存在涡翻滚现象;对于变幅摆动,鳍面流体加速程度从根部往端部逐渐加大,在端部同样存在明显的涡翻滚现象.流体越过鳍正面进入背面过程导致正面局部压力损失,这很好地解释了图 6等幅摆动中压力在两侧下降以及变幅摆动中端部压力不升反降的现象.
5.3 无量纲阻力系数比较研究了不同运动学参数下鳍条的2种运动模式产生的推进力情况.运动学参数为频率、摆幅和波长.
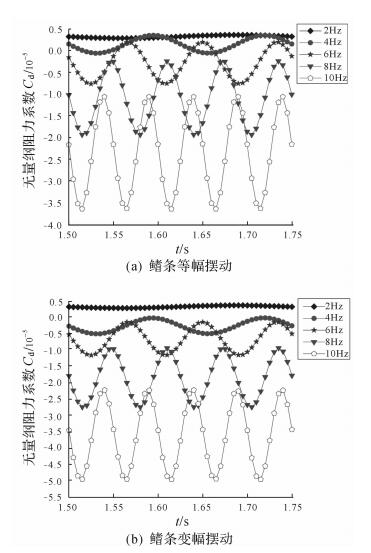
5.3.1 频率的影响图 9给出了摆幅A=0.6 mm,波长λ=10.0 mm时不同频率下无量纲阻力系数随时间的变化情况,横坐标为时间,纵坐标为无量纲阻力系数Cd.无量纲阻力系数Cd定义如式(3) 所示,此处,Cd为负数说明鱼鳍波动产生正向推进力,而负数的绝对值越大表示产生的推进力越大.可以看出,不管对于何种鳍条运动模式,无量纲阻力系数随时间的变化呈现周期性的波动,变化频率为鱼鳍波动频率的2倍.另外,随着频率的增加,Cd曲线的震荡剧烈程度随之提高,表明鱼鳍运动对周边流体的扰动程度也在提高.同时,Cd曲线随着频率的增加整体下移,说明推进力随着频率增加而变大.
|
| 图 9 不同频率下无量纲阻力系数随时间的变化情况(A=0.6 mm,λ=10.0 mm) Fig.9 The change of non-dimensional drag coefficient with time at different frequency (A=0.6 mm, λ=10.0 mm) |
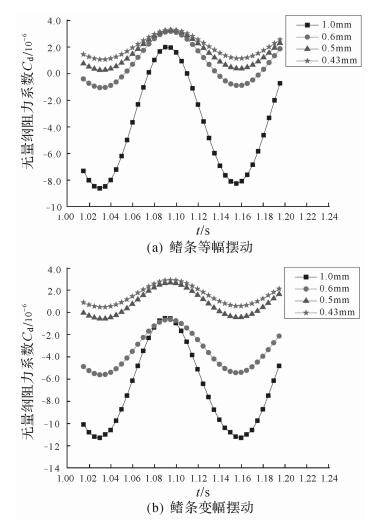
无量纲阻力系数随摆幅变化的规律与随频率变化类似,如图 10所示为频率f=4 Hz,波长λ=10.0 mm时,不同摆幅下无量纲阻力系数随时间的变化情况.不同摆幅下无量纲阻力系数Cd以相同的周期波动,且为鱼鳍波动频率的2倍,说明控制Cd曲线周期的参数为鱼鳍的运动频率.随着摆幅的增加,Cd曲线的震荡剧烈程度同样随之提高,曲线整体沿纵坐标下移,推进力增大.
|
| 图 10 不同摆幅下无量纲阻力系数随时间的变化情况(f=4 Hz, λ=10.0 mm) Fig.10 The change of non-dimensional drag coefficient with time at different amplitude (f=4 Hz, λ=10.0 mm) |
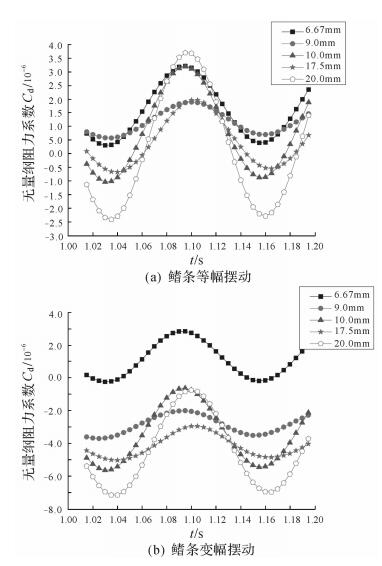
波长的变化直接影响鳍面波形,较短的波长使鳍面上呈现较多完整的波.图 11所示为频率f=4 Hz, 摆幅A=0.6 mm时,不同波长下无量纲阻力系数随时间的变化情况.同样,波长的增加使得推进力增大,对流体的扰动程度也提高.与随频率或摆幅变化不同的是,无量纲阻力系数曲线分布随波长的变化存在明显的相互交织现象,曲线沿纵坐标下移并不十分明显.在计算范围内,波长从6.67 mm至9.0 mm的变化过程中,仅鳍条变幅摆动曲线下降幅度比较大.
|
| 图 11 不同波长下无量纲阻力系数随时间的变化情况(f=4 Hz, A=0.6 mm) Fig.11 The change of non-dimensional drag coefficient with time at different wavelength (f=4 Hz, A=0.6 mm) |
对计算结果进行讨论,尤其是比较分析鳍条的2种运动模式下平均无量纲阻力系数(见式(4)) 随不同运动学参数的变化趋势,并从涡动力学角度分析运动学参数对推进力影响的本质.
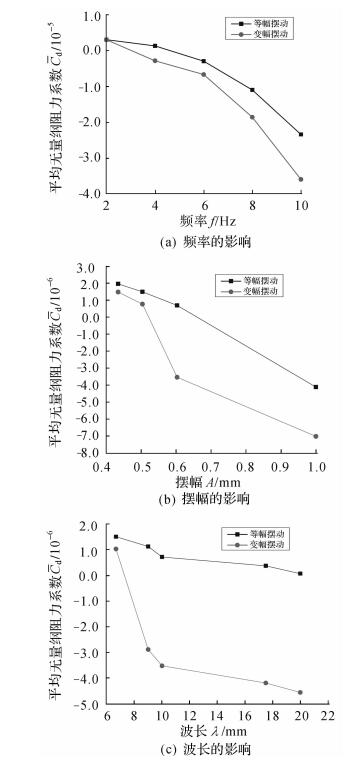
6.1 运动学参数的影响图 12为鳍条2种运动模式下不同运动学参数对平均无量纲阻力系数影响的对比.由结果可知,鳍条2种运动模式下产生的平均推进力均随频率、摆幅和波长的增加而增大.在相同运动学参数下,鳍条变幅摆动产生的推进力始终大于等幅摆动产生的推进力.在自然界中,无论是依靠胸鳍、腹鳍、背鳍还是臀鳍波动推进的鱼类都有一个共同点,采用即均变幅摆动.本文的数值研究在一定程度上解释了长期自然进化使鱼类形成最适应自身生存环境的运动方式.同时,平均无量纲阻力系数随频率和摆幅变化的程度相对波长而言要高,其原因有待进一步深入研究.
|
| 图 12 运动学参数对平均无量纲阻力系数的影响 Fig.12 The influence of kinematic parameters on averaged non-dimensional drag coefficient |
从沿鳍面长度方向z=3 mm截面上二维涡街分布情况看,鳍条2种运动模式下形成的涡街结构和分布形态非常类似,故以等幅摆动为例,分析运动学参数变化对鱼鳍波动形成周边及尾涡流场的影响,解释推进力随运动学参数变化而改变的原因.
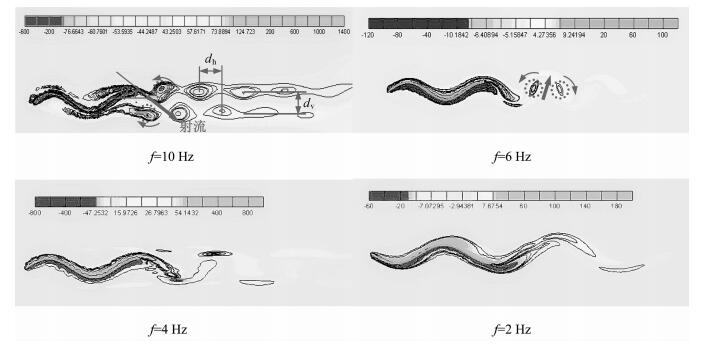
6.2.1 不同频率下的涡量图图 13给出4种不同频率(2,4,6,10 Hz) 时z=3 mm截面上的涡街云图.
|
| 图 13 4种不同频率下沿鳍条长度方向z=3 mm截面上涡街分布 Fig.13 Vortex distribution at four different frequencies at z=3 mm along the fin ray direction |
在频率为10 Hz时,可以在鱼鳍尾迹区域看到明显的反卡门涡街,其中位于上方的为逆时针旋转的涡,位于下方的为顺时针旋转的涡.相邻一对顺时针和逆时针旋涡之间形成一股射流,该射流的大小和鱼前行方向的夹角α是决定流体反作用于鱼鳍并使其产生推进力的重要原因之一.射流大小由涡对强度决定,而射流方向则由涡对位置控制.图 13中,涡对位置随着dh和dv的变化而改变,dh为相邻涡对横向间距(流体流向),dv为上下涡列间距(垂直流体流向).随着摆动频率的降低,dh和dv均发生变化,dh逐渐变大,dv先变小后增大,且上下涡列发生移动,上一涡列由逆时针旋转变为顺时针旋转,下一涡列则刚好与之相反,同时涡街强度也逐渐变弱.这一变化使得涡对间射流强度以及作用于鱼鳍前行方向的分力减小,从而使产生的推进力变小.尤其是当频率减小到一定程度后,尾迹反卡门涡街逐渐消失.
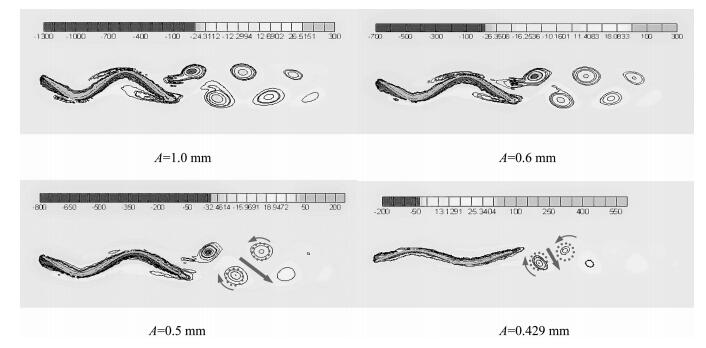
6.2.2 不同摆幅下的涡量图图 14给出4种不同摆幅(0.429,0.5,0.6,1.0 mm) 时z=3 mm截面上的涡街云图.与频率变化对涡街影响所不同的是,随着摆幅的增大,涡街的强度和dv随之增大,dh几乎不变,使得涡对间射流的强度增大,射流与前行方向的夹角α减小,推进力增大.综上发现:摆幅是决定dv大小的因素之一,频率是决定dh大小的因素之一.
|
| 图 14 4种不同摆幅下沿鳍条长度方向z=3 mm截面上涡街分布 Fig.14 Vortex distribution at four different amplitudes at z=3 mm along the fin ray direction |
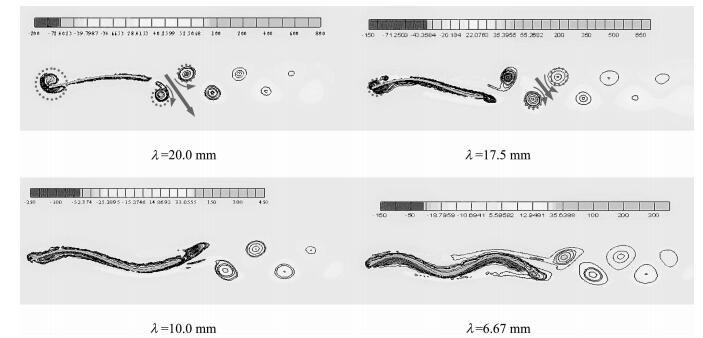
图 15给出4种不同波长(6.67,10.0,17.5,20.0 mm) 时z=3 mm截面上的涡街云图.波长的改变对dv和dh的影响不大,因此射流与前行方向的夹角α随波长的减小几乎未发生变化,而射流强度逐渐变弱,故产生的推进力随波长的减小而变小.在波长较大时(λ=20.0 mm),鱼鳍前端面出现非常明显的涡,并随鳍面波动由前往后进入尾迹,使尾涡强度加强,从计算结果看,前缘涡的存在有益于推进力的加强.当波长减小时,前缘涡逐渐消失,尾涡强度则渐弱.
|
| 图 15 4种不同波长下沿鳍条长度方向z=3 mm截面上涡街分布 Fig.15 Vortex distribution at four different wavelengths at z=3 mm along the fin ray direction |
建立了鳍条的2种运动模式下的运动学方程,通过求解黏性不可压缩流体Navier-Stores方程,比较不同运动学参数下鳍条2种运动模式所产生推进力的大小及其变化规律,最后通过截面二维涡量图解释这种变化形成的本质原因,得出如下几点结论:
1) 2种运动模式产生的平均推进力均随着频率、摆幅和波长的增大而增加,但鳍条等幅摆动产生的平均推进力始终小于变幅摆动产生的推进力;
2) 2种运动模式下模型中部切面的速度场和压力场存在明显的差异,而尾迹二维涡量场结构和分布形态十分相似,这在一定程度上说明影响2种运动模式游动效果的主要原因之一来自于沿鳍条方向的差异;
3) 尾涡的结构和分布形态随运动学参数的变化发生较大的改变,这种改变主要体现在涡街强度以及涡对间射流大小和方向上,从而导致推进力的变化;
4) 从游动产生的推进力角度考虑,仿波动鳍推进器宜采用鳍条变幅摆动推进模式的游动方式.
同时我们发现平均无量纲阻力系数大小随频率和摆幅变化的程度相对波长的变化要高,其原因有待进一步深入研究.另外,鳍条2种运动模式下产生的截面上二维涡量场结构和形态的差异并不明显,今后将进一步深入研究三维涡量场分布的细节.
| [1] | BREDER C M. The locomotion of fishes[J]. Zoologica, 1926, 4(5): 159–297. |
| [2] | MADIS L, GEORG M, DEIVID P, et al. Design of a semiautonomous biomimetic underwater vehicle for environmental monitoring[C]//Proceedings of the 2005 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Espoo, Finland, Jun.27-30, 2005:9-14. |
| [3] | SFAKIOTAKIS M, LANE D M, DAVIES B C. An experimental undulating-fin device using the parallel bellows actuator[C]//Proceedings of the IEEE International Conference on Robotics & Automation. Seoul, Korea, May.21-26, 2001:2356-2362. |
| [4] | BOILEAU R, FAN L, MOORE T. Mechanization of rajiform swimming motion:the making of robot-ray[R]. Vancouver:University of British Columbia, 2002. |
| [5] | EPSTEIN M, COLGATE J E, MACIVER M A. A biologically inspired robotic ribbon fin[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, Workshop on Morphology, Control, and Passive Dynamics, Edmonton, Alberta, Canada, Aug.2-6, 2005:2412-2417. |
| [6] | CHRISTENSEN B. Squid robot underwater inspector has unique propulsion[EB/OL]. (2011-08-01)[2013-02-16]. http://www.technovelgy.com/ct/Science-Fiction-News.asp?NewsNum=815. |
| [7] | TAKAGI K. Development of a rajiform swimming robot using ionic polymer artificial muscles[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. San Diego, California, USA, Oct. 9-15, 2006:1861-1866. |
| [8] | LOW K H. Modelling and parametric study of modular undulating fin rays for fish robots[J]. Mechanism and Machine Theory, 2009, 44(3): 615–632. DOI:10.1016/j.mechmachtheory.2008.11.009 |
| [9] | ALVARADO P V, CHIN S, LARSON W, et al. A soft body under-actuated approach to multi degree of freedom biomimetic robots:a stingray example[C]//3rd IEEE RAS and EMBS International Conference, Tokyo, Sep.25-29, 2010:473-478. |
| [10] | HU Tian-jiang, SHEN Lin-cheng, LIN Long-xin, et al. Biological inspirations, kinematics modeling, mechanism design and experiments on an undulating robotic fin inspired by Gymnarchus niloticus[J]. Mechanism and Machine Theory, 2009, 44(3): 633–645. DOI:10.1016/j.mechmachtheory.2008.08.013 |
| [11] | LIU Fang-fang, LEE K M, YANG Can-jun. Hydrodynamics of an undulating fin for a wave-like locomotion system design[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(3): 554–562. DOI:10.1109/TMECH.2011.2107747 |
| [12] | KALUMUCK K M, BRANDT A, ARMAND M. Biomimetic undulating fin propulsion for maneuvering underwater vehicles[J]. Johns Hopkins APL Technical Digest, 2010, 28(3): 222–223. |
| [13] | CURET O M, PATANKAR N A, LAUDER G V, et al. Mechanical properties of a bio-inspired robotic knifefish with an undulatory propulsor[J]. Bioinspiration & Biomimetics, 2011, 6(2): 026004. |
| [14] | ZHOU Chun-lin, LOW K H. Kinematic modeling framework for biomimetic undulatory fin motion based on coupled nonlinear oscillators[C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, Oct.18-22, 2010:934-939. |
| [15] | PUNNING A, ANTON M, KRUUSMAA M, et al. A biologically inspired ray-like underwater robot with electroactive polymer pectoral fins[C]//International IEEE Conference on Mechatronics and Robotics (MechRob'04), Aachen, Germany, Jun.3-5, 2004:241-245. |
| [16] | RATNAWEERA P B, FISCHER R, PRADALIER W, et al. Design and evaluation of a fin-based underwater propulsion system[C]//2010 IEEE International Conference on Robotics and Automation Anchorage Convention District Anchorage, Alaska, USA, May 3-8, 2010:3751-3756. |
| [17] | LAMAS M I, RODRIGUES J D, RODRIGUEZ C G. CFD analysis of biologically-inspired marine propulsors[J]. Brodogradnja, 2012, 63(2): 125–133. |
| [18] | LAMAS M I, RODRIGUES J D, RODRIGUEZ C G, et al. Three-dimensional CFD analysis to study the thrust and efficiency of a biologically inspired marine propulsor[J]. Polish Maritime Research, 2011, 18(1): 10–16. |
| [19] | SCHULTZ W W, ZHOU Q N, WEBB P W. A two-dimensional model of fish swimming[C]//Mechanics and Physiology of Animal Swimming Meeting, Marine Biological Association, Plymouth, U.K, Apr.15-18, 1991. |
| [20] | LIU Hui, KAWACHI K. A numerical study of undulatory swimming[J]. Journal of Computational Physics, 1999, 155(2): 223–247. DOI:10.1006/jcph.1999.6341 |
| [21] | LIU Hui, KAWACHI K. The three-dimensional hydrodynamics of tadpole locomotion[J]. The Journal of Experimental Biology, 1997, 200(4): 2807–2819. |
| [22] | DONG Gen-jin, LU Xi-yun. Numerical analysis on the propulsive performance and vortex shedding of fish-like travelling wavy plate[J]. International Journal for Numerical Methods in Fluids, 2005, 48(12): 1351–1373. DOI:10.1002/(ISSN)1097-0363 |
| [23] | RAMAMURTI R, WILLIAM C S, RAINALD L, et al. Fluid dynamics of flapping aquatic flight in the bird wrasse:three-dimensional unsteady computations with fin deformation[J]. Journal of Experimental Biology, 2002, 205(19): 2997–3008. |
| [24] | SUZUKI H, KATO N. A numerical study on unsteady flow around a mechanical pectoral fin[J]. International Journal of Offshore and Polar Engineering, 2005, 15(3): 161–167. |
| [25] | SINGH S N, SIMHA A, MITTAL R. Biorobotic AUV maneuvering by pectoral fins:inverse control design based on CFD parameterization[J]. IEEE Journal of Oceanic Engineering, 2004, 29(3): 777–785. DOI:10.1109/JOE.2004.833117 |
| [26] | SARKAR S, VENKATRAMAN K. Numerical simulation of thrust generating flow past a pitching airfoil[J]. Computers & Fluids, 2005, 35(1): 16–42. |
| [27] | LEWIN G C, HAJHARIRI H. Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow[J]. Journal of Fluid Mechanics, 2003, 492(492): 339–362. |
| [28] | BOZKURTTAS M, DONG H, MITTAL R, et al. Hydrodynamic performance of deformable fish fins and flapping foils[C]//44rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, Jan.10-13, 2006:1392-1403. |
| [29] | HE Jian-hui, ZHANG Yong-hua. Development and motion testing of a robotic ray[J]. Journal of Robotics, 2015, 2015(24): 1–13. |
| [30] | ZHANG Yong-hua, HE Jian-hui, YANG Jie. Computational research on modular undulating fin for biorobotic underwater propulsor[J]. Journal of Bionic Engineering, 2007, 4(1): 25–32. DOI:10.1016/S1672-6529(07)60009-2 |
| [31] |
章永华, 何建慧, 颜钦.
仿生机器鲫鱼的设计及运动学实验研究[J]. 工程设计学报, 2011, 18(3): 167–173.
ZHANG Yong-hua, HE Jian-hui, YAN Qin. Design and kinematics parametric investigation of biomimetic robotic crucian[J]. Chinese Journal of Engineering Design, 2011, 18(3): 167–173. |
| [32] |
杨建明, 吴建华.
动网格技术数值模拟挑流冲刷过程[J]. 水动力学研究与进展, 2001, 16(2): 156–161.
YANG Jian-ming, WU Jian-hua. Numerical modeling of the scouring process of free jet using moving grids[J]. Journal of hydrodynamics, 2001, 16(2): 156–161. |
| [33] |
夏全新, 鲁传敬, 吴磊.
鱼类波状摆动推进的数值模拟[J]. 水动力学研究与进展, 2005, 19(S1): 921–928.
XIA Quan-xin, LU Chuan-jing, WU Lei. Numerical simulation about fish undulating advancing[J]. Journal of hydrodynamics, 2005, 19(S1): 921–928. |
| [34] | HE Jian-hui, ZHANG Yong-hua, LOW K H. Comparative study of effect of fin arrangement on propulsion performance of bio-inspired underwater vehicles with multiple SMA fins[J]. International Journal of Advanced Robotic System, 2015, 12(9): 1–15. |
| [35] | BATCHELOR G K. An introduction to fluid dynamics[M]. Cambridge: Cambridge University Press, 1967. |
| [36] | MCHENRY M J, AZIZI E, STROTHER J A. The hydrodynamics of locomotion at intermediate Reynolds numbers:undulatory swimming in ascidian larvae[J]. Journal of Experimental Biology, 2003, 206(3): 27–43. |


