过盈联接在机械工程领域有着广泛的应用,机械传动系统利用过盈联接传递扭矩和轴向力,典型的应用实例有锁紧盘等[1];大中型设备和零件应用过盈联接可以保护主部件和节约材料,比如油膜轴承弹性结合锥套[2];化工机械应用过盈联接以增强高压容器承载能力并节约材料,比如热套压力容器[3].
目前,过盈联接研究主要集中在单层过盈联接,比如:许定奇等[4]基于厚壁圆筒理论推导了圆柱、圆锥过盈联接的设计计算方法;Boutoutaou和Hamid等[5-6]基于有限元方法分析了表面粗糙度对圆柱过盈联接的影响;Lucjan等[7]研究了激光强化处理对圆锥过盈联接承载性能的影响;Irappa等[8]研究了不同冷处理装配及不同冷却时间对过盈联接承载性能的影响;贾国海和Frederic等[9-10]研究了微动磨损和微动疲劳对圆柱过盈联接的影响;Giorgio等[11]探讨了在圆柱过盈接触面间添加黏结剂对其承载能力的影响;马平和张国军等[12-13]分析了转速大小对过盈配合的影响;Marshall等[14]通过超声波仪器间接测量得到了圆柱过盈联接结合压力值.通过查阅文献发现有关多层过盈联接的研究较少,并且大多集中在3层以内的过盈联接[15-18].
本文依据厚壁圆筒理论和过盈联接中各圆筒的几何关系,推导了N层过盈联接结合压力与过盈量关系的通用算法.利用所得解析法和Abaqus数值法对不同过盈层数模型各结合面的结合压力分别进行求解,对比分析了2种方法所得的过盈联接结合压力.同时,对各层结合压力和应力集中进行了分析.
1 理论算法推导依据厚壁圆筒理论,基于Lame方程得到厚壁圆筒受内外压时,筒内任意一点的径向位移[19]为:
| $ u = \frac{{1-\upsilon }}{E}\cdot\frac{{{a^2}{p_1}-{b^2}{p_2}}}{{{b^2}-{a^2}}}\cdot\rho - \frac{{1 + v}}{E}\cdot\frac{{{a^2}{b^2}({p_1} - {p_2})}}{{{b^2} - {a^2}}}\cdot\frac{1}{\rho } $ | (1) |
式中:E为材料的弹性模量;υ为材料的泊松比;p1为圆筒所受内压;p2为圆筒所受外压;a为圆筒的内径;b为圆筒的外径;ρ为圆筒内任意一点的半径.
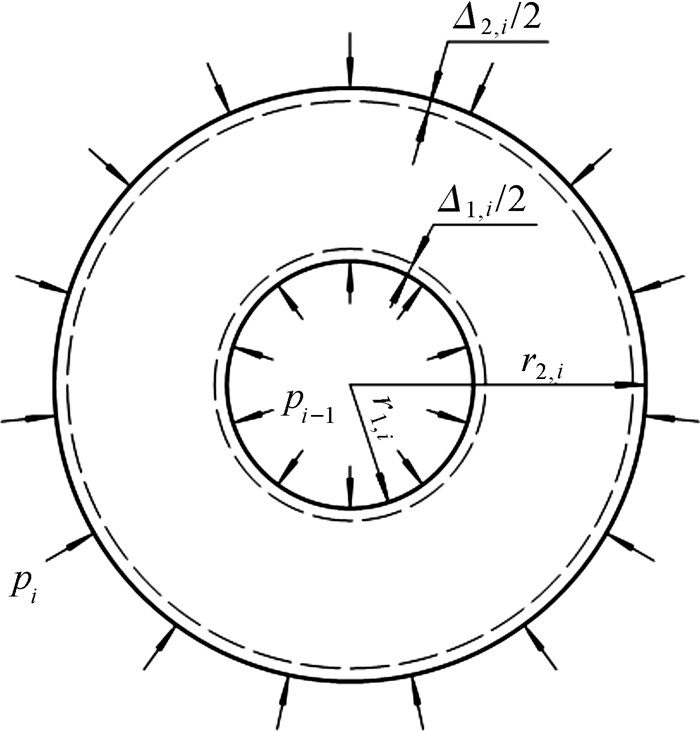
图 1为N层圆筒过盈联接中圆筒Ci的受力及变形图.定义pi-1为圆筒Ci-1和Ci过盈联接的结合压力;pi为圆筒Ci和Ci+1过盈联接的结合压力;Δ1,i为圆筒Ci受压后内表面的径向位移;Δ2,i为圆筒Ci受压后外表面的径向位移,由公式(1) 可得:
|
| 图 1 N层圆筒过盈联接中圆筒Ci的受力及变形 Fig.1 The stress and deformation of cylinder Ci in N-layer interference fit |
1) 圆筒Ci内表面的径向位移:
| $ \begin{array}{l} {\Delta _{1, i}} = \frac{{1-{\upsilon _i}}}{{{E_i}}}\cdot\frac{{{d^2}_{1, i}{p_{i-1}}-{d^2}_{2, i}{p_i}}}{{{d^2}_{2, i} - {d^2}_{1, i}}}\cdot{d_{1, i}} + \frac{{1 + {\upsilon _i}}}{{{E_i}}}\cdot\frac{{{d^2}_{1, i}{d^2}_{2, i}({p_{i - 1}} - {p_i})}}{{{d^2}_{2, i} - {d^2}_{1, i}}}\cdot\frac{1}{{{d_{1, i}}}}\\ = {K_{1, i}}{p_{i - 1}} - {K_{2, i}}{p_i} \end{array} $ | (2) |
式中: Ei为圆筒Ci的弹性模量;υi为圆筒Ci的泊松比;d1,i为圆筒Ci的内径, d2,i为圆筒Ci的外径,
2) 圆筒Ci外表面的径向位移:
| $ \begin{array}{l} {\Delta _{2, i}} = \frac{{1-{\upsilon _i}}}{{{E_i}}}\cdot\frac{{{d^2}_{1, i}{p_{i-1}}-{d^2}_{2, i}{p_i}}}{{{d^2}_{2, i} - {d^2}_{1, i}\cdot}}{d_{2, i}} + \frac{{1 + {\upsilon _i}}}{{{E_i}}}\cdot\frac{{{d^2}_{1, i}{d^2}_{2, i}({p_{i - 1}} - {p_i})}}{{{d^2}_{2, i} - {d^2}_{1, i}}}\cdot\frac{1}{{{d_{2, i}}}} = \\ {K_{3, i}}{p_{i - 1}} - {K_{4, i}}{p_i} \end{array} $ | (3) |
式中:
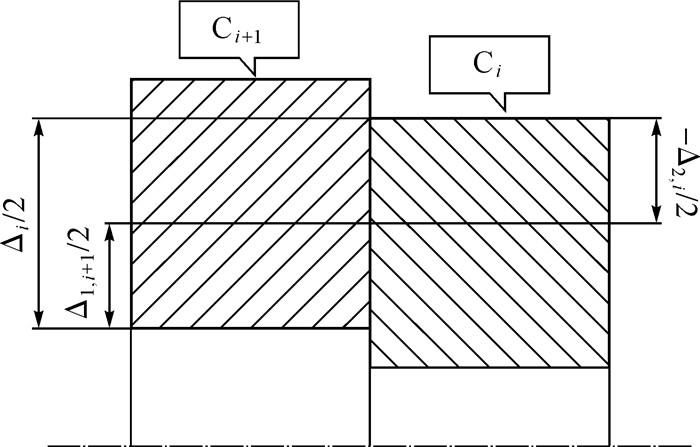
由图 2可得,N层过盈联接中,圆筒Ci和Ci+1过盈联接的过盈量与圆筒内、外径位移变化的关系为:
|
| 图 2 圆筒Ci与Ci+1过盈联接 Fig.2 The interference fit of Ci and Ci+1 |
| $ {\delta _i} = {\Delta _{1, i + 1}}-{\Delta _{2, i}} =-{K_{3, i}}{p_{i-1}} + ({K_{1, i + 1}} + {K_{4, i}}){p_i} - {K_{2, i + 1}}{p_{i + 1}} $ | (4) |
式中δi为第i层过盈联接层过盈量,i=1,2,…,n.
由公式(4) 得到,N层过盈联接结合压力与过盈量之间的矩阵表达式为:
| $ \mathit{\boldsymbol{KP = \delta }} $ | (5) |
式中:δ=[δ1,δ2,…,δnT
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = {[{p_1}, {p_2}, \cdots, {p_n}]^{\rm{T}}}\\ \mathit{\boldsymbol{K}} = \left[{\begin{array}{*{20}{c}} {{K_{1, 2}} + {K_{4, 1}}}&{-{K_{2, 2}}}& \cdots &0&0\\ 0&0& \cdots &0&0\\ \vdots & \vdots &{}& \vdots & \vdots \\ 0&0& \cdots &{-{K_{3, n}}}&{({K_{1, n + 1}} + {K_{4, n}})} \end{array}} \right] \end{array} $ |
文中共设计了4种模型,分别由不同数量的圆筒组成,其中不同模型所涉及的圆筒编号为C1,C2,C3,C4和C5,模型依次编号为Ma(C1,C2),Mb(C1,C2,C3),Mc(C1,C2,C3,C4) 和Md(C1,C2,C3,C4,C5),圆筒基本尺寸见表 1.
| 圆筒序号 | C1 | C2 | C3 | C4 | C5 |
| 内径/mm | 100 | 200 | 300 | 400 | 500 |
| 外径/mm | 200 | 300 | 400 | 500 | 600 |
| 长度/mm | 100 |
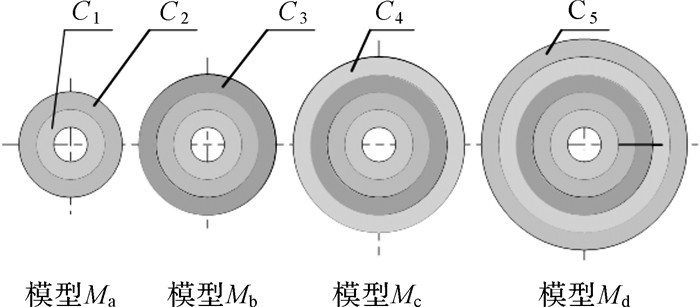
各模型组成分别为:Ma由圆筒C1和C2组成单层过盈联接;Mb由圆筒C1,C2和C3组成2层过盈联接;Mc由圆筒C1,C2,C3和C4组成3层过盈联接;Md由圆筒C1,C2,C3,C4和C5组成4层过盈联接,具体详见示意图 3.参考国家标准GB/T1801-2009,模型中均采用H7/t6最大极限过盈配合.
|
| 图 3 各模型示意图 Fig.3 The sketch of each model |
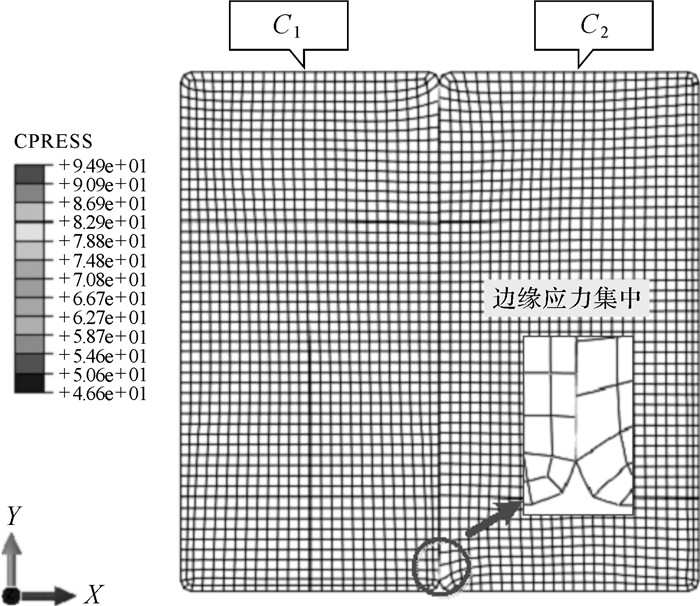
利用有限元软件Abaqus对模型Ma,Mb,Mc,Md结合压力进行模拟计算.选择单元类型为二维轴对称减缩积分单元CAX4R.材料的弹性模量为210 GMPa,泊松比为0.3,密度为7 800 kg/m3.网格选择Quad单元,网格尺寸均为2 mm;各接触面采用Penalty (罚函数) 摩擦公式,摩擦系数设定为0.15;分析步类型设置为Static,General.图 4为模型Ma结合压力的数值法计算结果.
|
| 图 4 模型Ma中圆筒C1和C2的结合压力 Fig.4 The coupling pressure between C1 and C2 in model Ma |
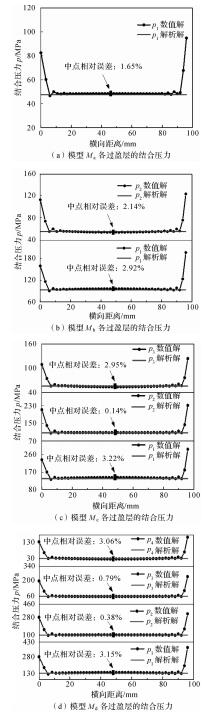
设定结合压力随结合直径由内到外依次定义为p1,p2,p3,p4.为了减少数值计算中应力集中的影响,采用轴向距离中点的相对误差作为2种方法的比较基准(图中简称为“中点相对误差”).图 5所示为模型Ma,Mb,Mc和Md结合压力值随轴向距离的变化.
|
| 图 5 各模型过盈联接结合压力 Fig.5 The coupling pressure of interference fit of each model |
通过对比解析法和数值法计算结果可知,结合压力在圆筒两端相差较大,其余部分相差较小.圆筒过盈联接时,其结合面两端存在应力集中[20],由于厚壁圆筒理论假设包容件和被包容件在结合长度上的结合压力为常数,故解析法反映不出接触边缘处的应力集中.
比较各模型不同结合面的结合压力可知,结合压力随着结合直径的增加而减小,即pi>pi+1.由公式(4) 得到单层过盈联接结合压力与过盈量关系式:
| $ p = \frac{\delta }{{d\left[{\frac{1}{{{E_2}}}\left( {\frac{{{n^2}_2 + 1}}{{{n^2}_2-1}}-{\nu _2}} \right) + \frac{1}{{{E_1}}}\left( {\frac{{{n^2}_1 + 1}}{{{n^2}_1-1}} + {\nu _1}} \right)} \right]}} $ | (6) |
由公式(6) 可以看出,单层过盈联接中,结合直径d对结合压力影响较大,结合直径越大,结合压力越小.分析N层过盈联接结合压力pi时,把圆筒C1至Ci看成一个整体,圆筒Ci+1至Cn看成另一个整体,那么结合压力与结合直径成反比,即结合压力随着结合直径的增加而减小.
比较各模型结合压力p1的变化可知,结合压力p1随过盈层数N的增加而增大.如果把圆筒C2至Cn视为一个整体Cx,N层过盈联接可以视为是圆筒C1与圆筒Cx的单层过盈联接.由公式(6) 可知,组成Cx的圆筒个数越多,公式(6) 中直径比n2越大,结合压力增大,所以p1随过盈层数的增加而增大.
对比解析法和数值法误差,表明2种方法求解相对误差均小于4%,吻合度较好,各模型中最内层结合压力的相对误差比其他各过盈层要大.
4.2 应力集中分析在材料弹性范围内,应力集中通过理论应力集中系数kti反映,kti=σmax/σn,其中σmax为局部最大应力,σn为名义应力.文中名义应力σn为数值解轴向距离中点位置的应力,局部最大应力σmax为数值解轴向最大应力.表 2给出了各模型每层过盈联接面的理论应力集中系数.
| kti | Ma | Mb | Mc | Md |
| 第1层kt1 | 1.96 | 2.04 | 2.03 | 2.04 |
| 第2层kt2 | - | 2.27 | 2.15 | 2.12 |
| 第3层kt3 | - | - | 2.30 | 2.17 |
| 第4层kt4 | - | - | - | 2.29 |
各模型中由圆筒C1和C2组成的最内层过盈联接的过盈量和结合直径相同.不同模型中圆筒C2所受外压力不同.由图 5可知,圆筒C2所受外压力在模型Ma,Mb,Mc,Md中依次增大;由表 2可知,最内层过盈联接的理论应力集中系数kt1相对最小,波动区间(1.96,2.04) 较小,说明理论应力集中系数受组合圆筒外压力的影响较小;各模型理论应力集中系数kti都随着过盈层数的增加逐渐增大,即:kt (i+1)>kti,且最外层过盈联接的理论应力集中系数相对最大.
5 结论1) 以厚壁圆筒理论为基础,根据过盈联接中过盈量与圆筒内、外径位移的变化关系,得到了N层过盈联接结合压力与过盈量的矩阵表达式.
2) 通过对比数值法与解析法的计算结果,发现2种方法在过盈结合面轴向中间区域吻合度较好,相对误差均小于4%,在两端重合度误差稍大,表明解析法可以为N层过盈联接设计提供可靠的理论指导.
3) N层过盈联接中结合压力由内到外依次减小,即:结合直径越大,结合压力越小;最内层过盈的结合压力随着过盈层数的增加而增加.
4) 数值法表明过盈结合面两端存在应力集中现象,不同模型最内层过盈联接的理论应力集中系数kt1相对最小,波动区间较小;各模型中kti随过盈层数的增加逐渐增大.
| [1] |
王建梅, 唐亮.
锁紧盘设计理论与方法研究[M]. 北京: 冶金工业出版社, 2014: 1-3.
WANG Jian-mei, TANG Liang. Research on design theory and method of shrink[M]. Beijing: Metallurgical Industry Press, 2014: 1-3. |
| [2] |
黄庆学, 王建梅, 静大海, 等.
油膜轴承锥套过盈装配过程中的压力分布及损伤[J]. 机械工程学报, 2006, 42(10): 102–108.
HUANG Qing-xue, WANG Jian-mei, JING Da-hai, et al. Pressure distribution and damages of oil-film bearing sleeve during the process of interference fit[J]. Journal of Mechanical Engineering, 2006, 42(10): 102–108. DOI:10.3901/JME.2006.10.102 |
| [3] | YUAN Ge-xia, LIU Hong-zhao. Optimum design for shrink-fit multi-layer vessels under ultrahigh pressure using different materials[J]. Chinese Journal of Mechanical Engineering, 2010, 23(5): 582–589. DOI:10.3901/CJME.2010.05.582 |
| [4] |
许定奇, 孙荣文.
过盈联结的设计、计算与装拆[M]. 北京: 中国计量出版社, 1992: 113-127.
XU Ding-qi, SUN Rong-wen. The design, calculation and installation of interference coupling[M]. Beijing: China Metrology Press, 1992: 113-127. |
| [5] | BOUTOUTAOU H, BOUAZIZ M, FONTAIN J F. Modeling of interference fits taking form defects of the surfaces in contact into account[J]. Materials and Design, 2011, 32(7): 3692–3701. DOI:10.1016/j.matdes.2011.03.059 |
| [6] | HAMID B, MOHAMED B, JEAN-FRANCOIS F. Modeling of interference fits with taking into account surfaces roughness with homogenizeation technique[J]. International Journal of Mechanical Sciences, 2013, 69(4): 21–31. |
| [7] | LUCJAN S, JOLANTA Z, ANDRZEJ Z. The carrying capacity of conical interference-fit joints with laser reinforcement zones[J]. Journal of Materials Processing Technology, 2010, 210(6/7): 914–925. |
| [8] | SOGALAD I, UDUPA N G S. Influence of cryogenic treatment on load bearing ability of interference fitted assemblies[J]. Materials and Design, 2010, 31(1): 564–569. DOI:10.1016/j.matdes.2009.07.007 |
| [9] |
贾国海, 龚金科, 鄂加强, 等.
齿轮轴过盈配合对轴肩微动磨损的影响研究[J]. 湖南大学学报(自然科学版), 2013, 40(5): 31–36.
JIA Guo-hai, GONG Jin-ke, E Jia-qiang, et al. Effect of interference fit on fretting ware of gear shaft shoulder[J]. Journal of Hunan University (Natural Sciences), 2013, 40(5): 31–36. |
| [10] | FREDERIC L, AURELIAN V, BERNAED S. Fretting fatigue strength reduction factor for interference fits[J]. Simulation Modeling Practice and Theory, 2011, 19(9): 1811–1823. DOI:10.1016/j.simpat.2011.05.004 |
| [11] | GIORGIO G, MARIANGELA L, DAVIDE R, et al. Influence of the mechanical behavior of different adhesives on an interference-fit cylindrical joint[J]. International Journal of Adhesion & Adhesives, 2013, 47: 63–68. |
| [12] |
马平, 莫德云, 吴广荣.
电主轴阶梯动态过盈量对主轴扭矩传递能力的影响[J]. 中国机械工程, 2013, 24(21): 2933–2938.
MA Ping, MO De-yun, WU Guang-rong. Effects of step dynamic interference fit on transmitting torque capacity of motorized spindle[J]. China Mechanical Engineering, 2013, 24(21): 2933–2938. |
| [13] |
张国军, 臧运峰, 吕枫, 等.
数控机床HSK刀柄和主轴在高速旋转下的连接性能分析[J]. 中国机械工程, 2012, 23(6): 631–636.
ZHANG Guo-jun, ZANG Yun-feng, LV Feng, et al. Anslysis on HSK tool holder-spindle interface at high rotational speed for CNC machine tools[J]. China Mechanical Engineering, 2012, 23(6): 631–636. |
| [14] | LEWIS R, MARSHALL M B, DWYER-JOYCE R S. Measurement of interface pressure in interference fits[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2005, 219(2): 127–139. DOI:10.1243/095440605X8432 |
| [15] |
王建梅, 陶德峰, 黄庆学.
多层圆筒过盈配合的接触压力与过盈量算法研究[J]. 工程力学, 2013, 30(9): 270–275.
WANG Jian-mei, TAO De-feng, HUANG Qing-xue. Algorithm research on contact pressure and magnitude of interference for multi-layer cylinder's interference fit[J]. Engineering Mechanics, 2013, 30(9): 270–275. |
| [16] |
王建梅, 康建峰, 陶德峰.
多层过盈联接的设计方法[J]. 四川大学学报(工程科学版), 2013, 45(4): 84–89.
WANG Jian-mei, KANG Jian-feng, TAO De-feng. Design method for multi-layer interference fit[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(4): 84–89. |
| [17] |
赵永翔, 蔡慧, 敬霖.
HXD2机车动力轮对的集成有限元模型[J]. 机械工程学报, 2014, 50(14): 21–26.
ZHAO Yong-xiang, CAI Hui, JING Lin. Integral finite modeling for the powered wheelset of HXD2 locomotive[J]. Journal of Mechanical Engineering, 2014, 50(14): 21–26. DOI:10.3901/JME.2014.14.021 |
| [18] | WANG Jian-mei, KANG Jian-feng, TANG Liang. Theoretical and experimental studies for wind turbine's shrink disk[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science February, 2015, 229(2): 325–334. DOI:10.1177/0954406214533529 |
| [19] |
刘鸿文.
材料力学[M]. 北京: 高等教育出版社, 2004: 230-234.
LIU Hong-wen. Mechanics of materials[M]. Beijing: Higher Education Press, 2004: 230-234. |
| [20] |
滕瑞静, 张余斌, 周晓军.
圆柱面过盈连接的力学特性及设计方法[J]. 机械工程学报, 2012, 48(13): 160–166.
TENG Rui-jing, ZHANG Yu-bin, ZHOU Xiao-jun. Mechanical properties and design method of cylindrical interference fit[J]. Journal of Mechanical Engineering, 2012, 48(13): 160–166. DOI:10.3901/JME.2012.13.160 |



