位于盾构机前端的刀盘在盾构掘进过程中与土体直接接触,主要有开挖地层、稳定掌子面、搅拌排土三大功能,是盾构机的核心部件,其性能的优劣直接影响盾构的掘进效率[1-2].因此对刀盘结构强度、刚度的分析对提高盾构机性能具有重要的实际意义.
文献[3-5]对某种刀盘在不同工况下的受力特性进行分析,得到了各工况下应力应变分布规律,为刀盘结构设计提供了基础数据.文献[6-7]完成了有限元建模系统的开发,实现了刀盘自动建模和有限元分析,一定程度上缩短了刀盘设计时间.文献[8-10]运用有限元分析软件对盾构刀盘在不同工况下的受力进行了模拟,并对结构作了相应的优化.以上各文献的研究均是针对单一模式的盾构,而对于复合地层条件下双模式盾构的刀盘结构分析尚属空白.
本文根据新街煤矿斜井的地层参数,采用ANSYS有限元软件对斜井双模式盾构在开、闭两种模式下的刀盘模型分别进行分析,得出了刀盘的应力应变规律,验证了新街煤矿斜井刀盘设计的合理性,并针对应力集中的薄弱位置给出了优化方案,这对我国自主研发双模式盾构具有重要意义,也为同类工程刀盘结构设计提供一定的理论支撑.
1 2种模式下多工况刀盘载荷计算公式根据本工程施工特点,盾构掘进过程中可能会出现3种工况:正常掘进工况、静扭脱困工况、偏载堵转工况[11].对各工况的刀盘载荷组成进行分析,分别建立了EPB模式和TBM模式下正常掘进、静扭脱困和偏载堵转这3种工况的载荷计算公式.
1.1 正常掘进工况对于EPB模式,正常掘进时,主要存在刀盘掘进前方工作面的正面水土压力和刀具切削土体产生的推进阻力.刀盘在旋转开挖过程中所受到的阻力矩包括刀具切削土体时产生的切削阻力矩、刀盘和土体接触产生的摩擦阻力矩、搅拌土体产生的搅拌阻力矩.其载荷计算公式为:
| $ \left\{ \begin{array}{l} {F_{{\rm{n}}1}} = {F_1} + {F_2} + {F_3}\\ {T_{{\rm{n1}}}} = \sum\limits_{i = 1}^6 {{T_i}} \end{array} \right. $ | (1) |
对于围岩自稳性较好的硬岩地层,主机在TBM模式下工作,此时刀盘正面只有滚刀与掌子面接触进行破岩,刀盘转动时克服的阻力矩主要是滚刀破岩的滚动阻力矩.正常掘进工况下,其载荷计算公式表示为:
| $ \left\{ \begin{array}{l} F{\prime _{{\rm{n}}1}} = F{\prime _3}\\ T{\prime _{{\rm{n}}1}} = T{\prime _5} \end{array} \right. $ | (2) |
式中:Fn, Fn′分别是EPB模式、TBM模式推进时各工况刀盘上作用的推进阻力;Tn, Tn′分别是EPB模式、TBM模式推进时各工况刀盘上作用的阻力矩;F1是刀盘正前方水土压力;F2是切刀切削土体产生的推进阻力;F3, F′3分别是2种模式下滚刀破岩产生的推进阻力;T1是刀盘正面与土体之间的摩擦阻力矩;T2是刀盘侧面与土层的摩擦阻力矩;T3是刀盘背面摩擦阻力矩;T4是刀盘开口内土柱的剪切摩擦阻力矩;T5, T′5分别是2种模式下刀具产生的切削阻力矩;T6是刀盘土仓内的搅拌阻力矩.
1.2 静扭脱困工况在刀盘启动或者是在掘进过程中遇到刀盘卡壳现象时,盾构需要加大力矩来脱困,此时刀盘转动阻力最大,为刀盘设计脱困力矩.这种工况称为静扭脱困工况,在静摩擦力的作用下,刀盘的摩擦转动阻力相对于正常掘进时要高.盾构机不再掘进,因此EPB模式下F2, F3可按零计算,TBM模式下F′3可按零计算,此时2种模式下静扭脱困工况的载荷计算公式为:
| $ \left\{ \begin{array}{l} {F_{{\rm{n}}2}} = {F_1}\\ {T_{{\rm{n2}}}} = {T_{\rm{k}}}-{T_{\rm{m}}} \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} F{\prime _{{\rm{n}}2}} = 0\\ T{\prime _{{\rm{n2}}}} = {T_{\rm{k}}}-T{\prime _{\rm{m}}} \end{array} \right. $ | (4) |
式中:Tk是刀盘设计脱困力矩,取10 000 kN;Tm, T′m分别是2种模式下掘进过程中刀盘轴承密封装置的摩擦阻力矩T7、主轴承的摩擦阻力矩T8、减速装置的摩擦损耗力矩T9的总和.
1.3 偏载堵转工况EPB模式软岩掘进时,由于盾构掘进较快或者工作面塌陷以及遭遇孤石等状况时,将使刀盘产生偏载,当工作面上的土体堆积高度达到1 m左右时刀盘将停转,这种软土偏载工况称为软土1 m处堵转, 如图 1所示.
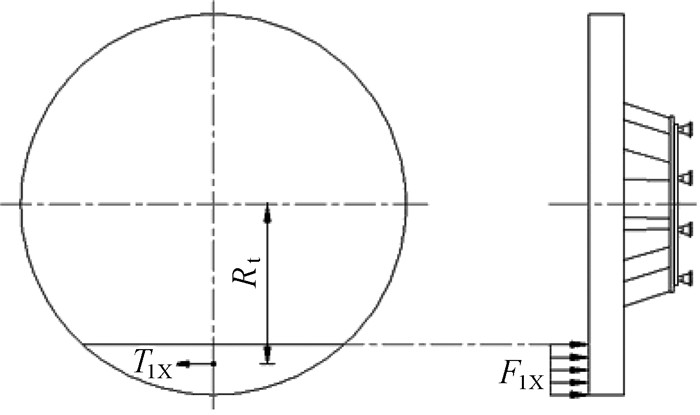
|
| 图 1 软土1 m处堵转示意图 Fig.1 Schematic digram of plug and turn at 1 m of soft soil |
得到载荷计算公式为:
| $ \left\{ \begin{array}{l} {T_{{\rm{1x}}}} = {T_{\rm{k}}}-\sum\limits_{i = 2}^9 {{T_i}} \\ {F_{1{\rm{x}}}} = \frac{{{T_{{\rm{1x}}}}}}{{{R_{\rm{t}}}\cdot{\mu _0}}} \end{array} \right. \to \left\{ \begin{array}{l} {F_{{\rm{n}}3}} = {F_{{\rm{1x}}}}\\ {T_{{\rm{n3}}}} = {T_{\rm{k}}}-{T_{\rm{m}}} \end{array} \right. $ | (5) |
TBM模式硬岩掘进时,一般在土体堆积高度达到刀盘半径三分之一左右时,刀盘将停转,称这种硬岩偏载堵转工况为三分之一半径堵转.其载荷计算公式为:
| $ \left\{ \begin{array}{l} F{\prime _{{\rm{n3}}}} = \frac{{{T_{\rm{k}}}-T{\prime _{\rm{m}}}}}{{R{\prime _{\rm{t}}}\cdot{\mu _0}}}\\ T{\prime _{{\rm{n3}}}} = {T_{\rm{k}}}-T{\prime _{\rm{m}}} \end{array} \right. $ | (6) |
式中:T1x,F1x是T1,F1的修正值;Rt,R′t是2种模式接触面几何中心到刀盘中心的距离;μ0是渣土和金属接触的摩擦系数.
式(1) 至式(6) 中出现的各载荷模型分量F1,…,F′3及T1,…,T9的具体计算公式均可以参照文献[12-13],此处不再解释详细计算过程,各工况载荷值可根据新街工程具体参数计算得到.
1.4 双模式盾构各工况载荷计算结果根据新街煤矿斜井双模式盾构工程地质和刀盘的主要参数(见表 1),分别计算出2种模式下刀盘各工况的载荷.计算结果如表 2、表 3所示.
| 参数 | 数值 |
| 土与土之间的摩擦 系数μ1 |
0.4 |
| 盾构刀盘直径Dc/m | 7.62 |
| 刀盘宽度tc/m | 0.31 |
| 隧道轴线与水平 夹角α/(°) |
6 |
| 土体重力密度γ/ (kN/m3) |
20 |
| 水平侧向土压力 系数Kh |
0.27 |
| EPB模式下刀盘 开口率η |
35% |
| 滚刀数量n1 | 47 |
| 切刀数量n2 | 66 |
| 刮刀数量n3 | 12 |
| 切刀切削角β/(°) | 80 |
| 切刀后角δ/(°) | 11 |
| 土体与金属的摩擦 系数μ0 |
0.15 |
| 切刀宽度b/m | 0.16 |
| 围岩黏聚力c/kPa | 30 |
| 土体内摩擦角φ/(°) | 35 |
| 滚刀直径Rg/m | 0.432 |
| 贯入度p/m | 0.015 |
| 刀间距S/m | 0.1 |
| 岩土抗压强度σc/kPa | 1×105 |
| 岩土抗剪强度τ/kPa | 1×104 |
| 盘形滚刀刀刃角γ/(°) | 10 |
| 搅拌棒数目n | 4 |
| 搅拌棒安装半径 Rb/m |
0.8 |
| 搅拌棒直径Db/m | 0.19 |
| 搅拌棒长度Lb/m | 0.45 |
| 工况 | Fn/kN | Tn/kN·m |
| 正常掘进 | 3 285.6 | 7 282.0 |
| 静扭脱困 | 3 271.4 | 8 000.0 |
| 软土1 m处偏转 | 2 482.8 | 8 000.0 |
| 工况 | F′n/kN | T′n/kN·m |
| 正常掘进 | 8 758.8 | 2 543.2 |
| 静扭脱困 | 0 | 8 000.0 |
| 三分之一半径堵转 | 4 924.6 | 8 000.0 |
斜井双模式盾构刀盘采用碳素结构钢Q345C,其弹性模量为206 GPa,泊松比为0.3,密度为7.9×103 kg/m3.
图 2中(a)、(b) 为2种模式下的刀盘结构图.为提高网格划分精度和减少计算时间,在导入ANSYS软件前,采用Solidwoks软件建立模型时对结构进行简化,删除刀盘中所有圆角、倒角、螺栓孔等特征,虽然局部结构改变,但对于总体应力的分布影响不大[10].
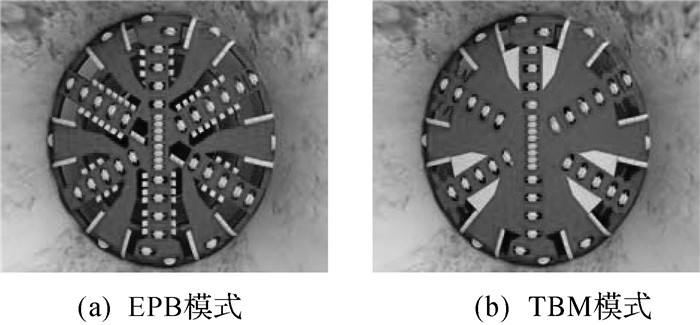
|
| 图 2 2种模式下刀盘结构图 Fig.2 Cutter head structure of two modes |
根据盾构刀盘的特点,确定采用六面体八节点的Solid45单元对其进行网格划分,网格单元长度为0.01 m,对分析的重点(辐条、辐板及牛腿) 控制单元进行局部网格加密.EPB模式有限元模型有225 840个单元、164 774个节点,网格划分如图 3(a)所示.TBM模式有限元模型有247 172个单元、170 643个节点,网格划分如图 3(b)所示.
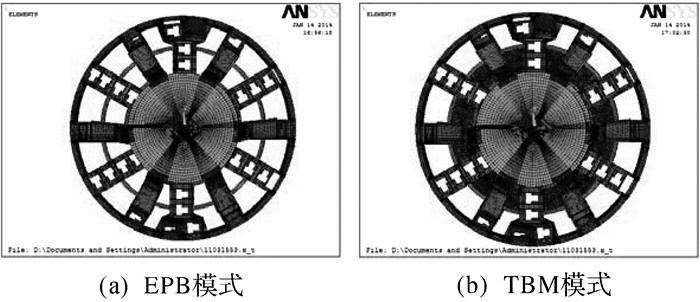
|
| 图 3 2种模式下刀盘的网格划分模型 Fig.3 Meshing models of cutter head in two modes |
由于在盾构掘进切削过程中,刀盘推进速度和刀盘转速都比较小,因此采用静力分析模式进行分析[4].
EPB模式下刀盘载荷的加载位置如图 4所示.F1加载在刀盘正面,F2加载在切刀安装架上,F3加载在滚刀安装架上;T1加载到刀盘正面面板,T2加载到刀盘侧面,T3加载到刀盘背面,T4和T5加载到刀盘开口处顺时针侧面(假设刀盘逆时针旋转),T6加载到刀盘牛腿的迎土面;对法兰盘端面施加位移全约束.
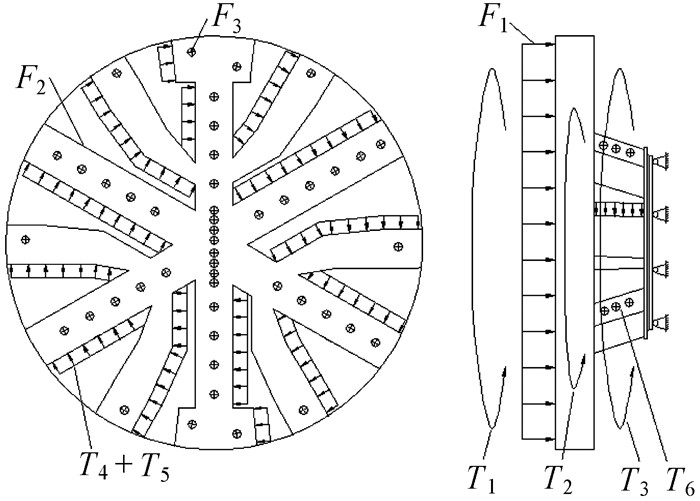
|
| 图 4 EPB模式下刀盘载荷加载位置 Fig.4 Loading position on cutter head in EPB mode |
TBM模式下,正常掘进工况,刀盘推进阻力与转动阻力均以均布载荷形式加载到各个滚刀安装座上;静扭脱困工况,将转动扭矩加载到刀盘侧面,与EPB模式下的T2相同;偏载堵转工况,推进阻力以均布载荷形式加载在刀盘1/3高度的面板上,转动扭矩加载到刀盘侧面,约束方式和EPB模式一样.
2种模式在偏载堵转工况时,不同的偏载角度得到的刀盘应力、应变不同,此处EPB模式选择偏载0°工况分析,TBM模式选择偏载30°工况分析.
2.3 有限元结果分析

|
| 图 5 EPB模式多工况下刀盘的应力和应变 Fig.5 Stress and strain of cutter head in EPB mode under multiple conditions |

|
| 图 6 TBM模式多工况下刀盘的应力和应变 Fig.6 Stress and strain of cutter head in TBM mode under multiple conditions |
表 4为2种模式多工况下刀盘应力、应变统计结果,其中最大位移、最大应力、最大应力位置可以从图 5、图 6得到,变形率为各个工况下最大位移与盾构直径的比值,其计算公式为:
| 工况 | 最大位移xmax/mm | 变形率ε/% | 最大应力σmax/MPa | 最大应力出现位置 |
| EPB模式正常掘进 | 1.859 | 0.024 | 146 | 牛腿与法兰盘连接处牛腿上 |
| EPB模式静扭脱困 | 2.524 | 0.033 | 193 | 牛腿与法兰盘连接处牛腿上 |
| EPB模式偏载堵转 | 3.821 | 0.050 | 270 | 牛腿与刀盘连接处牛腿上 |
| TBM模式正常掘进 | 1.109 | 0.015 | 95.9 | 牛腿与刀盘连接处牛腿上 |
| TBM模式静扭脱困 | 1.921 | 0.025 | 96 | 牛腿与法兰盘连接处牛腿上 |
| TBM模式偏载堵转 | 3.446 | 0.045 | 284 | 牛腿与刀盘连接处牛腿上 |
| $ \varepsilon = \frac{{{x_{{\rm{max}}}}}}{{{D_{\rm{c}}}}} $ | (7) |
由表 4分析可得,在应力方面,各工况下最大应力均出现在牛腿与法兰盘或是牛腿与刀盘连接处的牛腿上,最大变形出现在EPB模式偏载堵转工况中,为3.821 mm,最小变形出现在TBM模式正常掘进工况中,为1.109 mm,6种情况下变形率均小于0.1%,表明应变较小.EPB模式正常掘进工况最大应力为146 MPa,静扭脱困最大应力为193 MPa,偏载堵转工况最大应力为270 MPa.TBM模式正常掘进工况最大应力为95.9 MPa,静扭脱困工况最大应力为96 MPa,偏载堵转工况最大应力为284 MPa.
其中在EPB模式静扭脱困工况、偏载堵转工况和TBM模式偏载堵转工况下刀盘应力最大值大于Q345C材料的许用应力173 MPa,但仍小于其屈服应力295 MPa (板厚为60 mm),而且由于盾构施工时不会在这几种工况下长期运行,所以工程上还是允许的.并且3种工况的最大工作应力是位于牛腿上的小范围应力集中,实际上刀盘牛腿是焊接结构,交界处采取了圆弧处理,实际应力值要小于仿真结果.综上所述,双模式盾构刀盘设计满足强度、刚度要求,但是仍然要对应力集中和应力值较大的薄弱部位进行局部结构优化,增大其强度和刚度.此处提出以下2点建议[14, 15].
1) 改变牛腿形状,将方形牛腿改为圆柱形牛腿,因为圆形界面抗扭性能较好,因此采用空心圆柱结构可改善牛腿的受力.
2) 增加板厚,将牛腿与刀盘面板连接处的刀盘面板、牛腿与法兰盘连接处的法兰盘以及筋板与辐板连接处辐板的厚度加大5 mm.
3 结论本文结合新街煤矿斜井工程,对煤矿斜井双模式盾构刀盘结构强度、刚度进行了有限元分析,得到的研究结果可为同类刀盘结构设计和工程施工提供一定的理论支撑.
1) 针对新街煤矿斜井工程的特点,给出了双模式盾构不同模式时在多种工况下载荷的计算方法和公式,为有限元分析作准备.
2) 对盾构刀盘进行三维建模,通过有限元分析结果发现,最大变形出现在EPB模式偏载堵转工况中,为3.821 mm,最大应力出现在TBM模式载堵转工况中,为284 MPa,多种工况最大应力值出现位置均位于牛腿与法兰盘连接处或牛腿与刀盘连接处.
3) 根据有限元分析可知新街煤矿斜井双模式盾构刀盘设计满足强度、刚度要求,但是仍然可以对应力集中和应力值较大的薄弱部位进行局部结构优化.
对于隧道贯穿的工程,当隧道即将贯穿时,会出现盾构刀盘停转,用最大推力把残余岩体推倒的最大推力工况.本工程在双模式盾构掘进到终点时并不需要把隧道掘穿,因此没有考虑最大推力工况.
| [1] |
何其平.
土压平衡盾构刀盘结构探讨[J]. 工程机械, 2003, 36(11): 10–16.
HE Qi-ping. Investigation in the structure of soil pressure balancing shield[J]. Construction Machinery and Equipment, 2003, 36(11): 10–16. |
| [2] |
BURGERW, 卓永军.
盾构刀盘设计综述[J]. 建筑机械, 2006(21): 67–71.
BURGER W, ZHUO Yong-jun. Summary of cutter head of shield-drivenmachine[J]. Construction Machinery, 2006(21): 67–71. |
| [3] |
夏毅敏, 罗德志, 欧阳涛.
小型盾构刀盘有限元建模与分析[J]. 制造业自动化, 2010, 32(2): 15–17.
XIA Yi-min, LUO De-zhi, OUYANG Tao. Finite element modeling and analysis for a small shield cutterhead[J]. Manufacturing Automation, 2010, 32(2): 15–17. |
| [4] |
关天民, 刘春花, 武力, 等.
砂卵石地层盾构刀盘有限元分析[J]. 大连交通大学学报, 2015, 36(1): 43–46.
GUAN Tian-min, LIU Chun-hua, WU Li, et al. Finite element analysis of shield cutterhead in sandy cobble stratum[J]. Journal of Dalian Jiaotong University, 2015, 36(1): 43–46. |
| [5] |
刘守法.
新型盾构机刀盘设计与有限元分析[J]. 机械设计与制造, 2010(3): 59–60.
LIU Shou-fa. Design and finite element analysis of a new type cutterhead for shield machine[J]. Machinery Design & Manufacture, 2010(3): 59–60. |
| [6] |
陈馈, 苏翠侠, 王燕群.
盾构刀盘的有限元参数化建模及其分析[J]. 隧道建设, 2011, 31(1): 37–41.
CHEN Kui, SU Cui-xia, WANG Yan-qun. Finite element parameterized modeling and analysis on cutter head of shield machine[J]. Tunnel Construction, 2011, 31(1): 37–41. |
| [7] |
韩伟锋, 李凤远, 王助锋.
盾构刀盘参数化建模系统开发[J]. 隧道建设, 2012, 32(2): 142–145.
HAN Wei-feng, LI Feng-yuan, WANG Zhu-feng. Development of parameterized modeling system of cutter heads of shield machine[J]. Tunnel Construction, 2012, 32(2): 142–145. |
| [8] |
吴玉厚, 王超, 孙红, 等.
基于ANSYS的岩石掘进机刀盘有限元分析[J]. 中国工程机械学报, 2012, 10(2): 171–176.
WU Yu-hou, WANG Chao, SUN Hong, et al. ANSYS-based finite element analysis on cutter-plate of rock excavators[J]. Chinese Journal of Construction Machinery, 2012, 10(2): 171–176. |
| [9] |
陈长冰, 梁醒培, 王豪.
大直径盾构刀盘结构整体强度分析[J]. 机械设计, 2012, 29(1): 29–31.
CHEN Chang-bing, LIANG Xing-pei, WANG Hao. Intergral intensity analysis of large diameter shield cutter-head structure[J]. Journal of Machine Design, 2012, 29(1): 29–31. |
| [10] |
王玮, 李自贵, 赵海峰, 等.
全断面掘进机综合试验机刀盘有限元分析[J]. 机械设计与制造, 2013(6): 137–140.
WANG Wei, LI Zi-gui, ZHAO Hai-feng, et al. Finite element analysis on the comprehensive testing machine of tunnel boring machine cutter head[J]. Machinery Design & Manufacture, 2013(6): 137–140. |
| [11] |
韩勇.盾构刀盘轻量化优化设计研究[D].成都:西南交通大学机械工程学院, 2013:35-37.
HAN Yong. Study on weight lightening optimization design of cutter head[D]. Chengdu:Southwest Jiaotong University, College of Mechanical Engineer, 2013:35-37. |
| [12] |
管会生.土压平衡盾构机关键参数与力学行为的计算模型研究[D].成都:西南交通大学土木工程学院, 2007:49-66, 76-89.
GUAN Hui-sheng. Study on the calculating model of the EPBS key parameter and mechanical behavior[D]. Chengdu:Southwest Jiaotong University, College of Civil Engineering, 2007:49-66, 76-89. |
| [13] |
管会生, 高波.
盾构刀盘扭矩估算的理论模型[J]. 西南交通大学学报, 2008, 43(2): 213–226.
GUAN Hui-sheng, GAO Bo. Theoretical model for estimation of cutter head torque in shield tunneling[J]. Journal of Southwest Jiaotong University, 2008, 43(2): 213–226. |
| [14] |
仝哲.盾构刀盘的受力分析及结构优化[D].河南:郑州大学机械工程学院, 2012:46-47.
TONG Zhe.The analysis structural optimization of shield cutter[D].Henan:Zhengzhou University, College of Mechanical Engineer, 2012:46-47. |
| [15] |
任龙, 吴恩启, 闵瑞, 等.
土压平衡盾构机刀盘牛腿的有限元分析[J]. 机械工程与自动化, 2015(1): 72–74.
REN Long, WU En-qi, MIN Rui, et al. Stiffness analysis of deep hole processing drill pipe by finite element method[J]. Mechanical Engineering & Automation, 2015(1): 72–74. |


