2. 西南交通大学 机械工程学院, 四川 成都 610031
2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
随着定向井、水平井、超深井等新型油气井钻井技术的发展,钻井过程中遇到的地层结构日益复杂.其中,研磨性地层可钻性差、钻井成本高、钻井周期长等问题日益凸显,如何有效提高研磨性地层钻进效率、控制钻井成本一直以来都是钻井工程亟待解决的关键问题.而聚晶金刚石复合片作为PDC钻头最重要的切削单元,其性能的优劣在很大程度上影响着PDC钻头的整体性能[1-5].同时,PDC钻头破岩效率和钻进性能的提高,更多地依赖于对复合片结构的优化及其对磨损规律的认识[6-9].
在研磨性、不均质等复杂难钻地层,常出现复合片大块脱落、崩刃等非正常磨损现象,造成PDC钻头使用寿命大大缩短.通常,聚晶金刚石层由金刚石粉和黏接剂钴在高温高压下合成,由于黏接剂钴的热膨胀系数比金刚石大,因此其热膨胀速度远大于金刚石粉.在PDC钻头实际钻进的过程中,复合片与岩石的作用面会产生大量的摩擦热,而不同的热膨胀速率使聚晶金刚石层内部产生大量的晶间裂缝,迅速降低其结构强度[10-15].虽然聚晶金刚石层在硬质合金支撑体的作用下,其抗冲击性能有所提高,但其内部较大的残余应力使复合片受到较大冲击载荷后仍易大块剥损脱落,导致切削齿快速钝化,进而丧失切削能力[16-20].
根据传统一体式金刚石复合片的不足,本文提出了一种新型环嵌式金刚石复合片.基于几何研究方法,采用嵌入式设计原理,分析了均布式组合规律对其磨损特性的影响.同时,结合PDC钻头磨损机理,提出了环嵌式金刚石复合片有效切削刃长的概念,并分析了PDC钻头在钻进初期、中期以及末期三个阶段环嵌式PDC有效切削刃长的变化规律.同时试制出环嵌式复合片的实物,将其镶嵌在PDC钻头的肩部,并在相同层位与普通PDC钻头开展了对比钻进试验,并分析了环嵌式复合片相比于一体式复合片的优点.
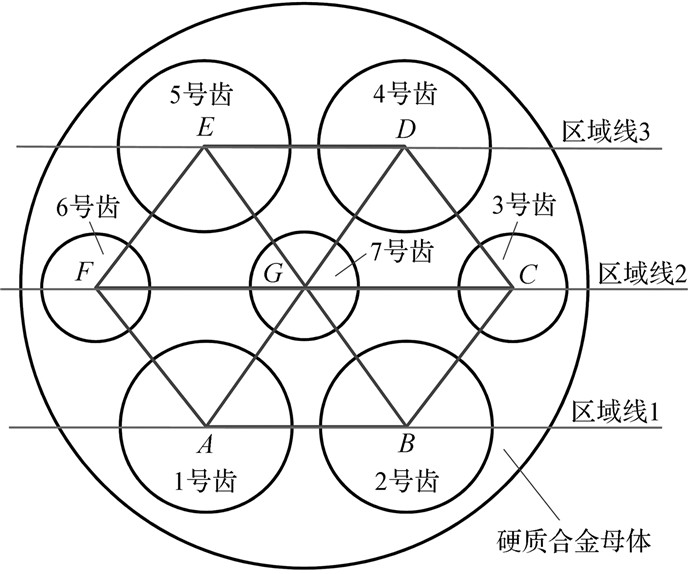
1 环嵌式PDC设计 1.1 几何特性基于均布式的设计理念,采用线型组合规律,并结合几何分析方法,研究嵌入聚晶金刚石层的排列方式对复合片聚晶金刚石层出露量以及有效切削刃长的影响.现采用六齿环绕中心齿的布置方式构成如图 1所示的环嵌式PDC,其中复合片硬质合金母体直径为16 mm,嵌入齿A,B,D,E的直径为5 mm,嵌入齿F,G,C的直径为3 mm.
|
| 图 1 环嵌式PDC端面 Fig.1 The end face of ring-embedded PDC |
为保证各嵌入齿内部之间的稳定性,将环嵌齿A,B,C,D,E,F圆心之间的连线构成正六边形.同时连接CF交BE于G,从而确定7号嵌入齿的圆心.如图 1所示,两两相邻的环嵌齿与7号嵌入齿均组成了正三角形的几何结构.由于正三角形的稳定性较普通三角形高,因此各嵌入齿之间的几何约束关系能保证其在破岩过程中的相对稳定性,能有效避免嵌入齿在承受较大交变载荷时过早脱落.其中,聚晶金刚石层A,B,C,G,F组成倒梯形,1号和2号嵌入齿的圆心分别位于ΔFGA和ΔCGB的顶点,有效保证主切削齿在钻进初期较强的地层吃入能力及切削稳定性,并将复合片磨损至区域线1和区域线2之间(钻进中期) 的状态称为倒梯形磨损.该设计方案采用碎片化的布齿机理并结合均布式设计理念,将传统一体式切削齿的磨损量分布在不同的嵌入齿上,有效提高复合片的地层吃入能力及抗磨损强度.
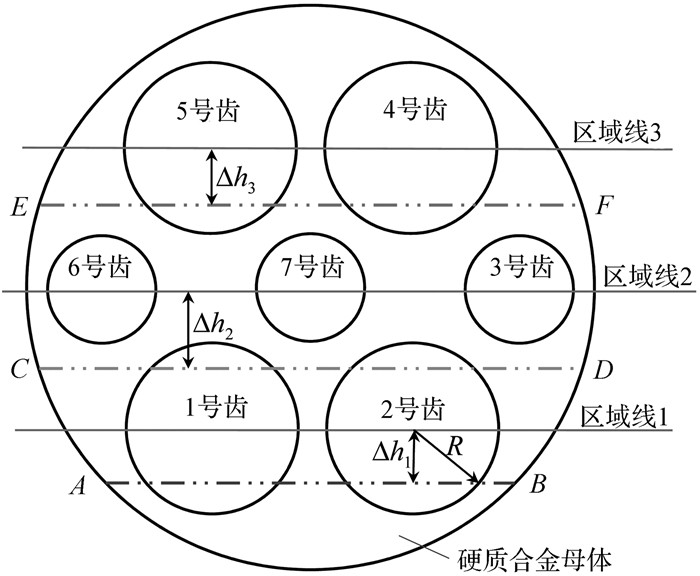
1.2 有效切削刃长分布规律根据环嵌式PDC的磨损规律,提出聚晶金刚石层有效切削刃长的概念,并建立其有效切削刃长的分析模型,如图 2所示.其中:区域线1经过1号和2号嵌入齿的圆心;区域线2经过6号、7号以及3号嵌入齿的圆心;区域线3经过5号和4号嵌入齿的圆心;1号、2号、4号以及5号嵌入齿的半径均为R;6号、7号以及3号嵌入齿的半径均为r;区域线1和区域线2之间的垂直距离以及区域线2和区域线3之间的垂直距离均为(r+R).假设斜镶于钻头胎体上的环嵌式PDC与井底岩石接触均匀,且压力均匀分布在碳化钨层和金刚石层.根据复合片磨损的不同阶段,推导出环嵌式PDC在钻进初期、钻进中期以及钻进末期三个阶段的聚晶金刚石层有效切削刃长.
|
| 图 2 环嵌式PDC磨损规律 Fig.2 The wear law of ring-embedded PDC |
1) 钻进初期(区域线1以下部分).
设切削端面磨损至图 2中点划线AB处(即LAB处);Δh1表示以区域线1为基准,磨损线LAB与区域线1之间的垂直距离;则钻进初期聚晶金刚石层的有效切削刃长L1的计算公式如下:
| $ {L_1} = \left\{ \begin{array}{l} 0(\Delta {h_1} > R)\\ 4\sqrt {{R^2}-\Delta h_1^2} (0 < \Delta {h_1} \le R) \end{array} \right. $ |
2) 钻进中期(区域线1和区域线2之间).
设切削端面磨损至图 2中点划线CD处(即LCD处);Δh2表示以区域线2为基准,磨损线LCD与区域线2之间的垂直距离;则钻进中期聚晶金刚石层的有效切削刃长L2的计算公式如下:
| $ {L_2} = \left\{ \begin{array}{l} 6\sqrt {{r^2}-\Delta h_2^2} (0 < \Delta {h_2} \le r)\\ 4\sqrt {{R^2}-{{(R + r-\Delta {h_2})}^2}} (r < \Delta {h_2} \le r + R) \end{array} \right. $ |
3) 钻进末期(区域线2和区域线3之间).
设切削端面磨损至图 2中点划线EF处(即LEF处);Δh3表示以区域线3为基准,磨损线LEF与区域线3之间的垂直距离;则钻进末期聚晶金刚石层的有效切削刃长L3的计算公式如下:
| $ {L_3} = \left\{ \begin{array}{l} 4\sqrt {{R^2}-\Delta h_3^2} (0 < \Delta {h_3} \le R)\\ 6\sqrt {{r^2}-{{(R + r-\Delta {h_3})}^2}} (R < \Delta {h_3} \le r + R) \end{array} \right. $ |
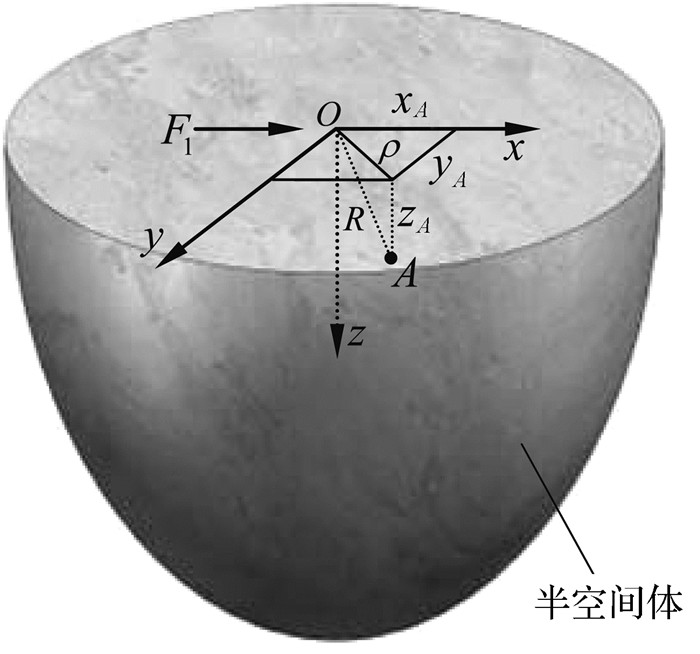
为分析环嵌式PDC在破岩过程中的三维切削效果,现建立其斜向压入岩石的力学模型,如图 3所示.在真实的三维切削破岩过程中,环嵌式PDC对岩石的作用效果包括竖直方向的挤压和水平方向的剪切.由于岩石的抗压强度比抗剪强度大得多,因此环嵌式PDC的破岩更多是依靠钻头施加给复合片的剪切力.对于整个地层而言,环嵌式PDC施加给岩石的剪切受力模型可看作半空间体(整个地层岩石) 在边界上受切向集中力的作用,使岩石局部产生较大的“分裂应力”,破坏岩石内部固有的稳定性,从而达到破碎岩石的目的.为求解剪切力作用下岩石受力点局部的位移和应力,现绘出在剪切力作用下的岩石半空间体受力分析模型,如图 4所示.
|
| 图 3 环嵌式PDC斜向压入岩石的力学模型 Fig.3 Mechanical model of ring-embedded PDC intruding into rock obliquely |
|
| 图 4 剪切力作用下的岩石半空间体受力分析模型 Fig.4 The force analysis model of rock half-space under the action of shear stress |
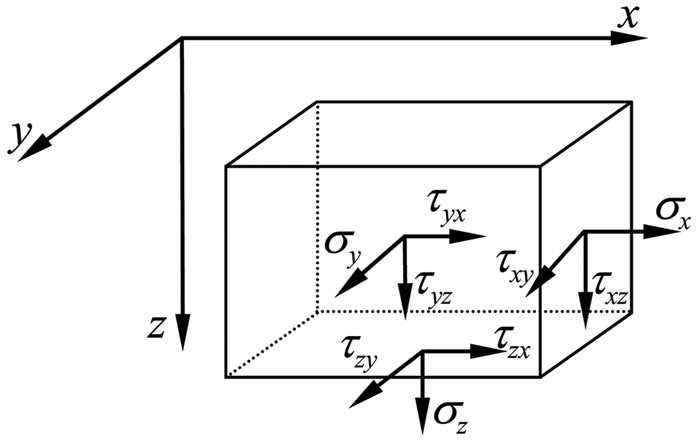
图 4中:F1为聚晶金刚石层给予岩石表面的剪切作用力;O为岩石表面的剪切受力点;A为受力点O局部的任意一点;xA,yA,zA为A点在三维坐标系O-xyz下的坐标值;ρ为A点在xOy面的极径;R为A点离坐标原点O的距离.
为清晰表示三维坐标下各应力的分布方向,绘出三维空间下岩体的应力方向示意图,如图 5所示.
|
| 图 5 三维空间下岩体的应力方向 Fig.5 Rock stress direction under the three dimensional space |
根据弹性力学理论,岩体的应力边界满足:
| $ {({\sigma _z}, {\tau _{zx}}, {\tau _{zy}})_{z = 0, \rho \ne 0}} = 0 $ |
由岩体内部受力平衡可得:
| $ \left\{ \begin{array}{l} \sum {F_x} = 0, \int_{-\infty }^\infty {\int_{-\infty }^\infty {{\tau _{zx}}{d_x}{d_y} + {F_1} = 0} } \\ \sum {F_y} = 0, \int_{-\infty }^\infty {\int_{ - \infty }^\infty {{\tau _{zy}}{d_x}{d_y} = 0} } \\ \sum {F_z} = 0, \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{\sigma _z}{d_x}{d_y} = 0} } \end{array} \right. $ |
由岩体内部力矩平衡可得:
| $ \left\{ \begin{array}{l} \sum {M_x} = 0, \int_{-\infty }^\infty {\int_{-\infty }^\infty {({y_{\rm{A}}}{\sigma _z}-{z_{\rm{A}}}{\tau _{zy}}){d_x}{d_y} = 0} } \\ \sum {M_y} = 0, \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {({x_{\rm{A}}}{\sigma _z} - {z_{\rm{A}}}{\tau _{zx}}){d_x}{d_y} = 0} } \\ \sum {M_z} = 0, \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {({y_{\rm{A}}}{\tau _{zx}} - {x_{\rm{A}}}{\tau _{zy}}){\sigma _z}{d_x}{d_y} = 0} } \end{array} \right. $ |
由乐甫位移函数以及伽辽金位移函数求得A点的位移和应力为:
| $ \left\{ \begin{array}{l} u = \frac{{(1 + \mu ){F_1}}}{{2\pi ER}}\left[{(1-2\mu )(\frac{R}{{R + {z_{\rm{A}}}}}-\frac{{x_{\rm{A}}^2}}{{{{(R + {z_{\rm{A}}})}^2}}} + 1 + \frac{{x_{\rm{A}}^2}}{{{R^2}}}} \right]\\ v = \frac{{(1 + \mu ){F_1}}}{{2\pi ER}}\left[{\frac{{{x_{\rm{A}}}{y_{\rm{A}}}}}{{{R^2}}}-\frac{{(1-2\mu ){x_{\rm{A}}}{y_{\rm{A}}}}}{{{{(R + {z_{\rm{A}}})}^2}}}} \right]\\ w = \frac{{(1 + \mu ){F_1}}}{{2\pi ER}}\left[{\frac{{(1-2\mu ){x_{\rm{A}}}}}{{R + {z_{\rm{A}}}}} + \frac{{{x_{\rm{A}}}{z_{\rm{A}}}}}{{{R^2}}}} \right] \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {\sigma _x} = \frac{{{x_{\rm{A}}}{F_1}}}{{2\pi {R^3}}}\left[{\frac{{1-2\mu }}{{{{(R + {z_{\rm{A}}})}^2}}}({R^2}-y_{\rm{A}}^2-\frac{{2Ry_{\rm{A}}^2}}{{R + {z_{\rm{A}}}}}) - \frac{{3x_{\rm{A}}^2}}{{{R^2}}}} \right]\\ {\sigma _y} = \frac{{{x_{\rm{A}}}{F_1}}}{{2\pi {R^3}}}\left[{\frac{{1-2\mu }}{{{{(R + {z_{\rm{A}}})}^2}}}(3{R^2}-x_{\rm{A}}^2-\frac{{2Rx_{\rm{A}}^2}}{{R + {z_{\rm{A}}}}}) - \frac{{3y_{\rm{A}}^2}}{{{R^2}}}} \right]\\ {\sigma _z} = - \frac{{3{F_1}{x_{\rm{A}}}z_{\rm{A}}^2}}{{2\pi {R^5}}}\\ {\tau _{yz}} = - \frac{{3{F_1}{x_{\rm{A}}}{y_{\rm{A}}}{z_{\rm{A}}}}}{{2\pi {R^5}}}\\ {\tau _{zx}} = - \frac{{3{F_1}zx_{\rm{A}}^2}}{{2\pi {R^5}}}\\ {\tau _{xy}} = \frac{{{F_1}{y_{\rm{A}}}}}{{2\pi {R^3}}}\left[{\frac{{1-2\mu }}{{{{(R + {z_{\rm{A}}})}^2}}}(x_{\rm{A}}^2 + \frac{{2Rx_{\rm{A}}^2}}{{R + {z_{\rm{A}}}}}-{R^2})-\frac{{3x_{\rm{A}}^2}}{{{R^2}}}} \right] \end{array} \right. $ |
其中:μ表示岩体的泊松比;E表示岩体的弹性模量;u表示A点在剪切力F1作用下沿x轴方向的位移;v表示A点在剪切力F1作用下沿y轴方向的位移;w表示A点在剪切力F1作用下沿z轴方向的位移.
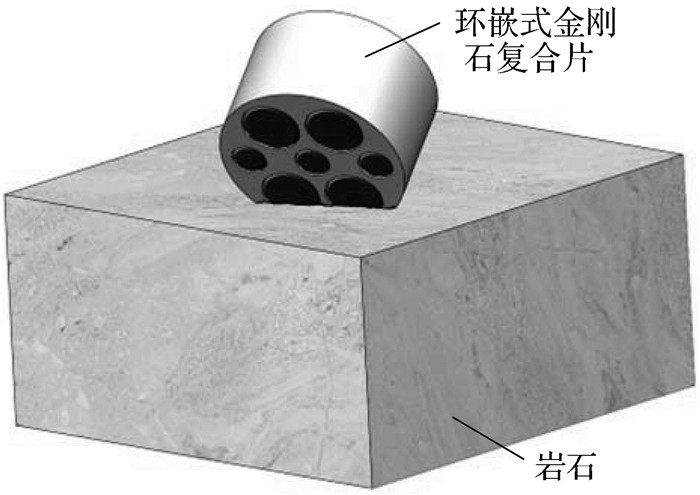
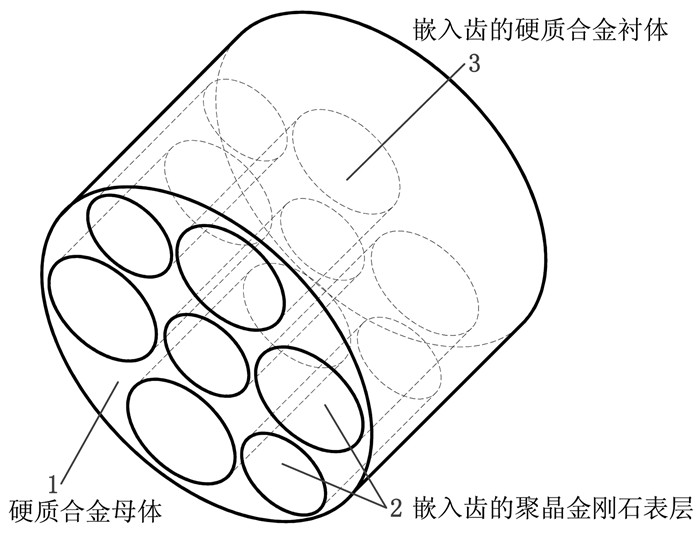
3 实验与分析环嵌式PDC三维轮廓如图 6所示.其中嵌入齿的加工方式和常规PDC相同,均是采用中间过渡层技术,将聚晶金刚石层黏附于硬质合金衬体表面.为测试环嵌式PDC的切削性能,现将其镶嵌于PDC钻头刀翼的肩部(载荷最大部位),并且每个刀翼肩部均镶嵌5个新型的复合片.环嵌式PDC加工成品如图 7所示,其中黑色部分为嵌入齿的聚晶金刚石层.
|
| 图 6 环嵌式PDC线型轮廓 Fig.6 The linear contour of ring-embedded PDC |

|
| 图 7 肩部镶嵌有环嵌式复合片的新型PDC钻头 Fig.7 The new PDC drill bit inlaid with ring-embedded compact on shoulder |
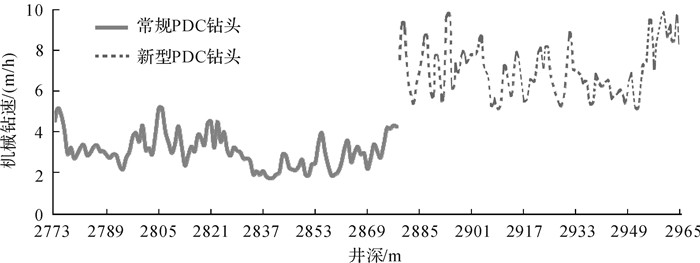
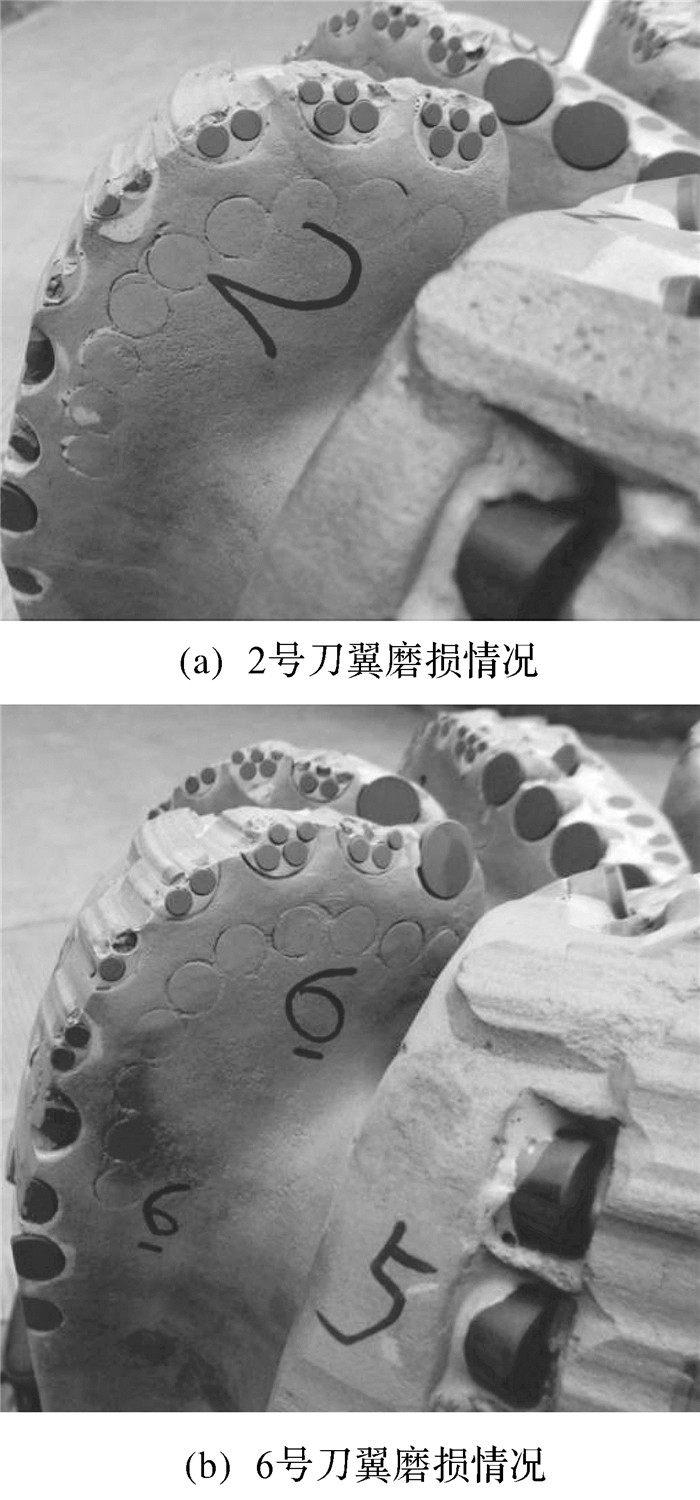
为测试环嵌式PDC的切削性能,在龙岗47#井完成新钻头与常规PDC钻头的对比测试.在对比测试过程中,该新型钻头与常规PDC钻头的试验参数保持相同,且2种钻头测试井段的地层属性基本一致,均为中硬地层.根据现场井下试验,整理出钻井数据如表 1所示,新型PDC钻头与常规PDC钻头的机械钻速对比如图 8所示,新型PDC钻头钻进后的磨损情况如图 9所示,常规PDC钻头钻进后的磨损情况如图 10所示.
| 钻头类型 | 钻压/kN | 钻井参数 | 钻进距离/m | 平均机械钻速/(m/h) | |
| 测试井段/m | 转速/(r/min) | ||||
| 常规PDC钻头 | 60~130 | 2 773~2 878 | 55~70 | 105 | 3.46 |
| 新型PDC钻头 | 60~130 | 2 879~2 965 | 55~70 | 86 | 6.83 |
|
| 图 8 新型PDC钻头与常规PDC钻头的机械钻速对比 Fig.8 The ROP contrast between new PDC drill bit and general PDC drill bit |
|
| 图 9 新型PDC钻头钻进后的磨损情况 Fig.9 The wear condition of new PDC drill bit after drilling |

|
| 图 10 常规PDC钻头钻进后的磨损情况 Fig.10 The wear condition of general PDC drill bit after drilling |
从表 1、图 8、图 9及图 10中可看出:在该测试井段,新型PDC钻头的平均机械钻速几乎是常规PDC钻头的2倍;起钻后,镶嵌在PDC钻头刀翼肩部的环嵌式复合片虽然磨损严重,但在实验参数一致的前提下,其在中硬地层表现出较快的机械钻速;对比新钻头和常规钻头复合片的磨损情况,可看出常规PDC钻头复合片钝化严重且其利用率较低,而环嵌式复合片利用硬质合金衬体与聚晶金刚石层不同的磨损速率,使其各磨损阶段均有不同的聚晶金刚石层参与破岩,提高复合片的自锐能力,增强其地层吃入能力,并有效抑制了复合片承受较大交变载荷时的应力集中现象.
4 结论1) 根据复合片的结构特征,采用线型组合规律,并结合几何分析方法,提出了环嵌式嵌入设计方案,并设计和分析了嵌入聚晶金刚石层的数量、大小、位置及组合方式对嵌入式PDC切削性能的影响.
2) 基于环嵌式PDC的磨损分析模型以及聚晶金刚石层有效切削刃长的理论研究,完成环嵌式复合片的加工,并将其镶嵌于PDC钻头刀翼的肩部.现场钻进试验表明:肩部镶嵌有环嵌式复合片的PDC钻头的机械钻速几乎是常规PDC钻头的2倍,同时在钻头参数及实验参数一致的前提下,其在中硬地层表现出了较快的机械钻速,因此嵌入式的设计方案使得该新型复合片具有较强的地层吃入能力,其对提高PDC钻头在研磨性地层的钻进性能有较大的促进作用.
| [1] | TIAN J, YUAN C, YANG L, et al. Rock-breaking analysis model of new drill bit with tor-nado-like bottomhole model[J]. Journal of Mechanical Science and Technology, 2015, 29(4): 1745–1752. DOI:10.1007/s12206-015-0348-y |
| [2] |
张绍和, 谢晓红, 方海江, 等.
PDC钻头出露量和线速度对复合片磨损规律的影响[J]. 中南大学学报(自然科学版), 2010, 41(6): 2173–2177.
ZHANG Shao-he, XIE Xiao-hong, FANG Hai-jiang, et al. PDC abrasion rule affected by height of protrusion and linear velocity[J]. Journal of Central South University (Science and Technology), 2010, 41(6): 2173–2177. |
| [3] | TIAN J, YANG Z, LI Y, et al. Vibration analysis of new drill string system with hydro oscillator in horizontal well[J]. Journal of Mechanical Science & Technology, 2016, 30(6): 2443–2451. |
| [4] | TIAN J, WU C, YANG L, et al. Mathematical modeling and analysis of drill string longitudinal vibration with lateral inertia effect[J]. Shock & Vibration, 2016, 2016(2): 1–8. |
| [5] | LING T D, LIU P, XIONG S, et al. Surface texturing of drill bits for adhesion reduction and tool life enhancement[J]. Tribology Letters, 2013, 52(1): 113–122. DOI:10.1007/s11249-013-0198-7 |
| [6] | TIAN J, WU C, YANG L, et al. Bottom hole model and rock-breaking features study of new drill bit with swirling-cutting motion[J]. Journal of the Chinese Society of Mechanical Engineers, 2016, 37(3): 221–229. |
| [7] |
蔡灿, 伍开松, 廉栋, 等.
单齿冲击作用下破岩机制分析[J]. 岩土力学, 2015, 36(6): 1599–1666.
CAI Can, WU Kai-song, LIAN Dong, et al. Study of rock-breaking mechanism under single-tooth impact[J]. Rock and Soil Mechanics, 2015, 36(6): 1599–1666. |
| [8] | BESTE U, JACOBSON S, HOGMARK S. Rock penetration into cemented carbide drill buttons during rock drilling[J]. Wear, 2008, 264(11): 1142–1151. |
| [9] | LIU S, LIU Z, CUI X, et al. Rock breaking of conical cutter with assistance of front and rear water jet[J]. Tunnelling & Underground Space Technology, 2014, 42(5): 78–86. |
| [10] |
梁尔国, 李子丰, 邹德永.
PDC钻头综合受力模型的试验研究[J]. 岩土力学, 2009, 30(4): 938–942.
LIANG Er-guo, LI Zi-feng, ZOU De-yong. Experimental research on integrated mechanical model of PDC bit[J]. Rock and Soil Mechanics, 2009, 30(4): 938–942. |
| [11] |
徐国平, 陈启武, 尹志民, 等.
金刚石层厚度对复合片(PDC) 残余应力的影响[J]. 高压物理学报, 2009, 23(1): 24–30.
XU Guo-ping, CHEN Qi-wu, YIN Zhi-min, et al. The effect of thickness of diamond layer on residual stresses in polycrystalline diamond compact[J]. Chinese Journal of High Pressure Physics, 2009, 23(1): 24–30. |
| [12] |
蓝红.含金刚石复合石油钻齿的性能研究[D].成都:西南石油大学机电工程学院, 2014:2-7.
LAN Hong. The properties of composite oil drilling teeth containing diamond[D].Chengdu:Southwest Petroleum University, School of Mechanical Engineering, 2014:2-7. |
| [13] |
曲冠政, 曲大伟, 郭瑞, 等.
PDC钻头复合片磨损速度模型研究[J]. 复杂油气藏, 2013, 6(1): 62–64.
QU Guan-zheng, QU Da-wei, GUO Rui, et al. Study on a swear rate model of PDC composite cutters[J]. Complex Hydrocarbon Reservoirs, 2013, 6(1): 62–64. |
| [14] | LU Y, TANG J, GE Z, et al. Hard rock drilling technique with abrasive water jet assistance[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(2): 47–56. |
| [15] | LI X B, SUMMERS D A, RUPERT G, et al. Experimental investigation on the breakage of hard rock by the PDC cutters with combined action modes[J]. Tunnelling and Underground Space Technology, 2001, 16(2): 107–114. DOI:10.1016/S0886-7798(01)00036-0 |
| [16] | JU P, WANG Z, ZHAI Y, et al. Numerical simulation study on the optimization design of the crown shape of PDC drill bit[J]. Journal of Petroleum Exploration & Production Technology, 2014, 4(4): 343–350. |
| [17] |
陈超, 林峰, 盘玉英, 等.
金刚石复合片耐磨性研究[J]. 超硬材料工程, 2013, 25(5): 11–15.
CHEN Chao, LIN Feng, PAN Yu-ying, et al. Study on abrasion ratio of polycrystalline diamond compact[J]. Super-hard Material Engineering, 2013, 25(5): 11–15. |
| [18] |
王家骏, 邹德永, 杨光, 等.
PDC切削齿与岩石相互作用模型[J]. 中国石油大学学报(自然科学版), 2014, 38(4): 104–109.
WANG Jia-jun, ZOU De-yong, YANG Guang, et al. Interaction model of PDC cutter and rock[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014, 38(4): 104–109. |
| [19] | ZHANG Z H, SUN F. The three-dimension model for the rock-breaking mechanism of disc cutter and analysis of rock-breaking forces[J]. Acta Mechanica Sinica, 2012, 28(3): 675–682. DOI:10.1007/s10409-012-0076-9 |
| [20] | PESSIER R, DAMSCHEN M. Hybrid bits offer distinct advantages in selected roller-cone and PDC bit applications[J]. SPE Drilling & Completion, 2011, 26(1): 96–103. |


