汽车Anti-lock Braking System (ABS) 多数采用逻辑门限、bang-bang控制、模糊控制、滑模变结构、滑模极限值搜索等控制方法。逻辑门限法控制简单可行,效果能满足要求,但依赖于经验确定阈值。由于不同的车和路面工况会出现不同的阈值,该方法需要大量的实验[1-2]。将自适应控制,模糊控制用于防抱制动系统,可以增强防抱制动系统对各种路况的自适应能力,进一步缩短制动距离[3],但缺少一定的理论基础,比如控制系统的稳定性研究等。滑模变结构控制具有响应速度快、对参数及外加干扰不灵敏、无需系统在线辨识、物理实现简单等许多本质上的优点,在汽车ABS闭环控制中被证明具有无与伦比的抗扰动性,但滑移率存在的抖动比较大[4-6]。
针对上述问题,结合灰色预测和滑模变结构方法,提出一种新的汽车ABS灰色滑模综合控制方法,使ABS系统趋于最佳滑移率的时间进一步缩短,提高ABS系统的动态响应和鲁棒性,缓解由于滑模控制算法自身所带来的抖动缺陷,且使汽车ABS系统运行更加稳定。
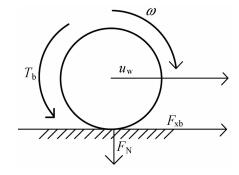
1 汽车单轮车轮模型简化分析研究的问题,建立单轮车辆系统模型[7, 8],如图 1所示。
|
| 图 1 汽车ABS车轮分析图 Fig.1 Automobile ABS wheel analysis diagram |
滑移率定义:
| $ s = \frac{{{u_{\rm{w}}}-r{\omega _{\rm{r}}}}}{{{u_{\rm{w}}}}} $ | (1) |
车轮运动方程:
| $ I\dot \omega = {F_{{\rm{xb}}}}r-{T_{\rm{b}}} $ | (2) |
车轮纵向摩擦力:
| $ {F_{{\rm{xb}}}} = {F_{\rm{N}}} \times \mu $ | (3) |
式中,S为滑移率;uw为车轮中心速度(m/s);r为车轮滚动半径(m);ωr为车轮旋转角速度(rad/s);I为车轮的转动惯量(Kg·m2);Fxb地面的制动力(N);Tb车轮的制动力扭矩(N·m)。
由简化的Dugoff模型,汽车附着系数φ与汽车滑移率s的函数关系,其具体表达式为:
| $ \varphi = \left\{ \begin{array}{l} \frac{{{\varphi _{\rm{h}}}}}{{{s_0}}}s\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s \le {s_0}\\ \frac{{{\varphi _{\rm{h}}}-{\varphi _{\rm{g}}}s}}{{1-{s_0}}}-\frac{{{\varphi _{\rm{h}}} - {\varphi _{\rm{g}}}}}{{1 - {s_0}}}s\;\;\;s > {s_0} \end{array} \right. $ | (4) |
本文将查表形式用于仿真程序,其轮胎特性曲线关系波形如下图 2所示:

|
| 图 2 轮胎特性曲线图 Fig.2 Tire characteristics |
ABS灰色预测与滑模变结构综合控制
2.1 灰色预测GM (1,1) 模型灰色预测模型是通过对反映数曲线进行模拟,最后利用最小二乘准则求解模型参数的指数拟合模型[9-11]。ABS灰色预测GM (1,1) 模型是将原始数据处理成1-AGO序列以改善预测模型的精度。本文原始数据为汽车车轮的角速度ω和汽车车速Vs两部分。其GM (1,1) 模型理论流程如下:
设原始数据ω或Vs序列为:
| $ {X^{(0)}} = ({x^{(0)}}(1), {x^{(0)}}(2), {x^{(0)}}(3), \cdots, {x^{(0)}}(n)) $ | (5) |
考虑到滑模变结构与汽车ABS实际的运行,将原始数据序列进行一阶缓冲计算,消除由于滑模变结构抖动现象带来的灰色预测精度降低的现象,实际仿真结果表明一阶缓冲算子的存在,有利于系统鲁棒性的提高。
设D为其一阶缓冲算子,则序列表达式为:
| $ {X^{(0)}}D = ({x^{(0)}}\left( 1 \right)d, {x^{(0)}}\left( 2 \right)d, {x^{(0)}}\left( 3 \right)d, \cdots, {x^{(0)}}\left( n \right)d) $ | (6) |
式中:
| $ \begin{array}{l} {x^{(0)}}\left( k \right)d = \frac{1}{{n- k + 1}}[{x^{(0)}}\left( k \right) + {x^{(0)}}\left( {k + 1} \right) + \cdots + \\ {x^{(0)}}\left( n \right)], k = 1, 2, 3, \cdots, n \end{array} $ | (7) |
为方便计算,取n=5,将经一阶缓冲算子处理的原始数据进行计算得到1-AGO序列.
| $ {X^{(1)}} = ({x^{(1)}}\left( 1 \right), {x^{(1)}}\left( 2 \right), {x^{(1)}}\left( 3 \right), \cdots, {x^{(1)}}\left( n \right)) $ | (8) |
式中:
| $ {x^{(1)}}\left( i \right) = \sum\limits_{k = 1}^i {{x^{(1)}}\left( i \right), i = 1, 2, 3, \cdots, n} $ | (9) |
1-AGO序列生成紧邻序列:
| $ {Z^{(1)}} = ({z^{(1)}}\left( 2 \right), {z^{(1)}}\left( 3 \right), {z^{(1)}}\left( 4 \right), \cdots, {z^{(1)}}\left( n \right)) $ | (10) |
式中:
| $ {z^{(1)}}\left( i \right) = \mu {x^{(1)}}\left( i \right) + \left( {1- \mu } \right){x^{(1)}}\left( {i- 1} \right), \mu \in [0.1, 0.9] $ | (11) |
μ由迭代计算得,本文取迭代数为10次,并保证平均相对误差最小.由一阶缓冲序列与紧邻序列求得灰色微分方程为:
| $ {x^{(0)}}\left( i \right) + a{z^{(1)}}\left( i \right) = b $ | (12) |
由1-AGO序列求其白化方程:
| $ \frac{{{\rm{d}}{x^{(1)}}}}{{{\rm{d}}t}} + a{X^{(1)}} = b $ | (13) |
由灰色微分方程(12) 求出参数序列
| $ \mathit{\boldsymbol{Y = }}\left[{\begin{array}{*{20}{c}} {{x^{(0)}}(2)}\\ {{x^{(0)}}(3)}\\ \vdots \\ {{x^{(0)}}(n)} \end{array}} \right], \mathit{\boldsymbol{B = }}\left[{\begin{array}{*{20}{c}} {-{z^{(1)}}(2)}&1\\ {-{z^{(1)}}(3)}&1\\ \vdots & \vdots \\ {-{z^{(1)}}(n)}&1 \end{array}} \right] $ |
由最小二乘法可求得参数序列:
| $ \mathit{\boldsymbol{\hat a}} = {\left( {a, b} \right)^{\rm{T}}} = {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})^{-1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $ | (14) |
由此,原始序列的预测序列为:
| $ {{\hat x}^{(0)}}\left( {i + 1} \right) = (1- {{\rm{e}}^a})[{x^{(0)}}\left( 1 \right)-\frac{b}{a}] \times {{\rm{e}}^{ -ai}}, i = 1, 2, 3, \cdots, n $ | (15) |
误差检验,残差序列:
| $ {\varepsilon ^{(0)}} = ({\varepsilon ^{(0)}}\left( 1 \right), {\varepsilon ^{(0)}}\left( 2 \right), {\varepsilon ^{(0)}}\left( 3 \right), \cdots, {\varepsilon ^{(0)}}\left( n \right)) $ | (16) |
式中:
| $ {\varepsilon ^{(0)}}\left( i \right) = {x^{(0)}}\left( i \right){-^{(0)}}\left( i \right), i = 1, 2, 3, \cdots, n $ | (17) |
相对误差序列表达式:
| $ \Delta = \left( {\left| {\frac{{{\varepsilon ^{(0)}}(1)}}{{{x^{(0)}}(1)}}} \right|, \left| {\frac{{{\varepsilon ^{(0)}}(2)}}{{{x^{(0)}}(2)}}} \right|, \left| {\frac{{{\varepsilon ^{(0)}}(3)}}{{{x^{(0)}}(3)}}} \right|, \cdots, \left| {\frac{{{\varepsilon ^{(0)}}(n)}}{{{x^{(0)}}(n)}}} \right|} \right) = \left\{ {{\Delta _i}} \right\}_1^n $ | (18) |
平均相对误差:
| $ \bar \Delta = \frac{1}{n}\sum\limits_{i = 1}^n {{\Delta _i}} $ | (19) |
滑模控制是根据系统状态偏离滑模面的程度来改变控制器结构,使系统按照滑模面所规定的规律运行[12].而且,滑动模态可自行设计,与被控对象系统参数及外部扰动无关,具有较强的鲁棒性和较高的控制精度[13-14].
1) 滑模控制输出函数.
为实现汽车ABS滑移率的控制目标要求,定义滑移率的跟踪误差:
| $ e(t) = \mathop \lambda \nolimits_{\rm{ref}}-\lambda $ | (20) |
式中:λref为滑移率参考值;λ为滑移率的实际测量值.
积分滑模面具有平滑转矩的作用,可以很好地削弱抖动的影响,因此,在切换函数中引入积分项,构造积分型滑模面[15-18]:
| $ S = e(t) + \mathop c\nolimits_{_1} \int_0^t {e(t){\rm{d}}t} $ | (21) |
式中:c1为常数且大于0,最终根据趋近滑模面的速度与振动情况选取;t为时间,s.
求导可得:
| $ \dot S =-\dot \lambda + {c_1}({\lambda _{{\rm{ref}}}}-\lambda ) $ | (22) |
由式(1) 得:
| $ \dot \lambda = \frac{{\left( {1-\lambda } \right){{\dot u}_{\rm{w}}}-r\dot \omega }}{{{u_{\rm{w}}}}} $ | (23) |
由式(2) 得:
| $ \dot \omega = \frac{{Fr-{T_{\rm{b}}}}}{I} $ | (24) |
当系统进入滑模面运动时存在如下形式:
| $ \frac{{{\rm{d}}S}}{{{\rm{d}}t}} = 0 $ | (25) |
式(20) 变形得:
| $ \lambda = {\lambda _{{\rm{ref}}}}-e\left( t \right) $ | (26) |
将公式(23)、(24)、(26) 代入(22),得:
| $ \dot S =-\frac{{\left( {1-{\lambda _{{\rm{ref}}}} + e(t)} \right)\dot v-\frac{r}{I}({F_{{\rm{xb}}}} - {T_{\rm{b}}})}}{v} + {c_1}e(t) $ | (27) |
为提高系统的动态响应,滑模控制器采用指数趋近规律:
| $ \dot s =-\xi {\mathop{\rm sgn}} (s)-Ks $ | (28) |
式中:ξ>0,K>0,sgn (S) 为符号函数,S为滑模面.一般取ξ值较大,K值较小,从而保证趋近速率在远离切换面时较大,而在切换面附近较小,有利于控制抖振的幅度.
故,滑模控制器的输出函数为:
| $ {T_{\rm{b}}} = {F_{{\rm{xb}}}}r- \frac{{{u_w}I}}{r}[-\varepsilon {\mathop{\rm sgn}} (S)-kS + \frac{{{{\dot u}_{\rm{w}}}}}{{{u_{\rm{w}}}}}(1-{\lambda _{{\rm{ref}}}}) + (\frac{{{{\dot u}_{\rm{w}}}}}{{{u_w}}} - {c_1})e(t)] $ | (29) |
滑模控制器输出函数受外在转矩和参考转速的影响,因此,此设计可以接受2个变量变化的影响,能够在不同的负载情况下实现转速的目标要求.
2) 滑模控制系统的存在性、可达性与稳定性判断.
汽车动力源控制系统的滑模存在性及其可达性的证明如下:
| $ S\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = S(-\xi {\rm{sgn}}\left( S \right)-kS) $ | (30) |
| $ S\frac{{{\rm{d}}S}}{{{\rm{d}}t}} =-\xi \frac{{{S^2}}}{{|S|}}-k{S^2} $ | (31) |
可得SṠ < 0,故满足可达性条件.
选取李雅普诺夫函数评价滑模控制的稳定性:
| $ V\left( S \right) = \frac{1}{2}{S^2} $ | (32) |
由上面滑模可达性条件:SṠ < 0,得知:V(Ṡ) < 0.因此,系统是稳定的.
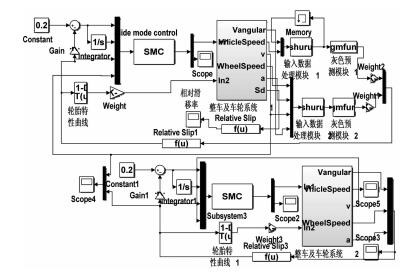
3 仿真分析 3.1 汽车ABS建模将灰色预测与滑模变结构综合运用于汽车ABS,建立Simulink仿真模型,如图 3所示,表 1为汽车ABS动力学参数.
|
| 图 3 基于灰色预测与滑模变结构的ABS仿真模型 Fig.3 ABS simulation model based on grey prediction and sliding mode variable structure |
| 参数 | 车轮质量 m/kg |
车轮滚动 半径r/m |
转动惯量 I/kg·m2 |
初始车速 v/(km/h) |
| 数值 | 402.25 | 0.253 | 5 | 64.12 |
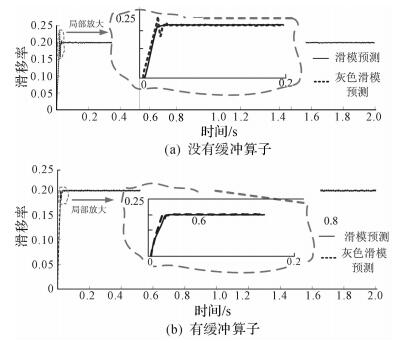
要实现灰色预测与滑模变结构综合控制,首先要对一部分数据进行处理,使数据序列更加有规律可循,但可能由于算法的原始数据存在较大的波动,会带来意想不到的结果.因此,缓冲算子的存在是非常必要的.如图 4所示,对比分析缓冲算子存在与否的2种情况.显然,没有缓冲算子时,在0-0.05 s内存在比较严重的抖动现象,抖动范围为0.15~0.25,而有缓冲算子时的整体比较平缓,仿真结果如图 4(b),在0.05 s时,很平缓,几乎没有波动.
|
| 图 4 缓冲算子存在与否滑移率对比 Fig.4 Comparison of slip ratio between buffer operator presence and absence |
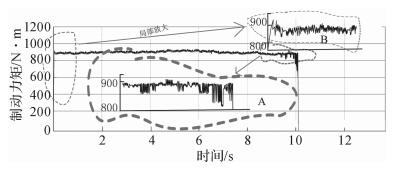
由汽车ABS制动力矩输出(图 5) 可知灰色滑模变结构控制输出的制动力矩在900 N·m处波动.由图 5的A部分可以看出在约10.21 s处制动力矩输出为零,即处于停车状态;由B部分可以看出制动力矩输出比较迅速,即实时性较强.
|
| 图 5 ABS制动力矩输出 Fig.5 Braking torque output of ABS |
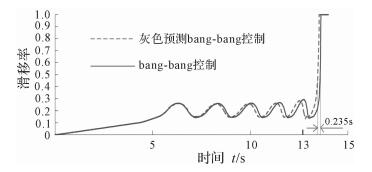
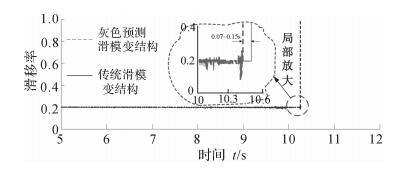
为凸显灰色预测在ABS算法中能起到超前的作用,选取bang-gang和灰色预测滑模两种实时性不同的控制方法.首先对比分析灰色预测bang-bang控制和传统bang-bang控制下的滑移率,灰色预测的bang-bang控制比一般bang-bang控制约提前0.235 s达到期望滑移率,如图 6所示.其次,对比分析灰色预测滑模变结构控制和传统滑模变结构控制,前者超前约0.07~0.1 s达到期望滑移率,如图 7所示.
|
| 图 6 灰色预测bang-bang与传统bang-bang控制下的滑移率 Fig.6 Slip ratio controlled by grey prediction bang-bang and traditional bang-bang |
|
| 图 7 传统滑模变结构与灰色预测滑模变结构控制下的滑移率 Fig.7 Slip ratio controlled by grey prediction sliding mode variable structure and traditional sliding mode variable structure |
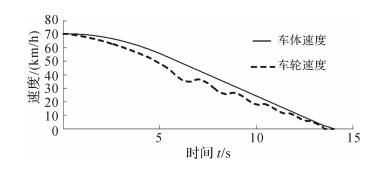
对比分析灰色预测滑模变结构控制和传统bang-bang控制下的车轮速度和车速,如图 8和图 9所示.可以看出,汽车制动到停车所用时间缩短了近4 s,车速变化平稳,鲁棒性强,有利于汽车舒适性的提高,且制动车轮的速度随车速的降低而均匀减小,没有抱死现象发生,进一步说明汽车具有良好的方向操纵性和制动效能.

|
| 图 8 基于灰色预测滑模控制的车轮速度与车速 Fig.8 Wheel velocity and autombile speed based on grey prediction sliding mode control |
|
| 图 9 基于Bang-bang控制的车轮速度与车速 Fig.9 Wheel velocity and automobile speed based on bang-bang control |
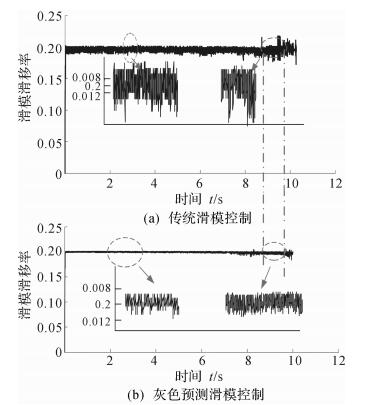
对比分析灰色预测滑模变结构和传统滑模变结构控制下的自带抖动现象,如图 10所示.可以看出,灰色预测与滑模控制的结合有利于缓解滑模自身带来的抖动现象,有利于滑模变结构在汽车ABS上更加稳定的运行.
|
| 图 10 灰色预测滑模控制与传统滑模控制下的抖动现象 Fig.10 Shaking phenomenon controlled by grey prediction sliding mode and traditional sliding mode |
针对汽车ABS的控制,结合灰色预测与滑模变结构控制,提出了汽车ABS灰色预测与滑模变结构综合控制方法,并建立ABS仿真模型,对比分析了灰色预测滑模控制、传统滑模控制、灰色预测与bang-bang控制以及传统的bang-bang控制下的滑移率变化.
1) 缓冲算子在灰色预测与滑模变结构综合控制的ABS控制中是不可或缺的,有利于汽车ABS稳定性的提高.
2) 灰色预测与滑模变结构控制、灰色预测与bang-bang控制和bang-bang控制对比,结果显示分别比原来的控制方法超前约0.09 s和0.235 s;灰色预测的引入起到了超前的作用,有助于减小趋于最佳目标滑移率的时间.
3) 灰色滑模控制与bang-bang控制的对比发现,采用灰色滑模变结构算法有助于汽车ABS缩短制动时间,约3 s.
4) 灰色预测与滑模变结构结合控制有利于减缓滑模固有的抖动缺陷,有助于滑模变结构在汽车ABS上稳定运行.
| [1] |
李果.
车辆防抱死制动理论与应用[M]. 北京: 国防工业出版社, 2009: 46-202.
LI Guo. Vehicle anti-lock braking theory and application[M]. Beijing: National Defense Industry Press, 2009: 46-202. |
| [2] |
王伟达, 丁能根.
ABS逻辑门限值自调整控制方法研究与试验验证[J]. 机械工程学报, 2010, 46(22): 90–95.
WANG Wei-da, DING Neng-gen. ABS logic threshold self-tuning control method research and test[J]. Journal of Mechanical Engineering, 2010, 46(22): 90–95. DOI:10.3901/JME.2010.22.090 |
| [3] |
晏蔚光, 余达太, 李果, 等.
汽车防抱制动系统自适应模糊控制算法[J]. 北京信息科技大学学报, 2004, 26(2): 188–191.
YAN Wei-guang, YU Da-tai, LI Guo, et al. Car against holding brake system adaptive fuzzy control Algorithm[J]. Journal of Beijing University of Information Science and Technology, 2004, 26(2): 188–191. |
| [4] | TORRES J D S, GALICIA M, LOUKIANOV A G, et al. A sliding mode regulator for antilock brake system[C]. 18th World Congress of the International Federation of Automatic Control. Milano, August 28-September 2, 2011:134-142. |
| [5] | DOUGLAS A R. An overview of automatic speaker recognition technology[J]. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, 2002, 4(1): 4072–4075. |
| [6] |
周兵, 徐蒙.
基于滑模极值搜索算法的车辆驱动防滑控制策略[J]. 农业机械学报, 2015, 46(2): 307–311.
ZHOU Bing, XU Meng. Based on sliding mode extremum search algorithm of vehicle drive torque control Strategy[J]. Journal of Agricultural Machinery, 2015, 46(2): 307–311. |
| [7] |
崔杰, 耀国, 刘思峰.
一种新的灰色预测模型及其建模机理[J]. 控制与决策, 2009, 24(11): 1702–1706.
CUI Jie, YAO Guo, LIU Si-feng. A new grey forecasting model and its modeling mechanism[J]. Control and Decision Making, 2009, 24(11): 1702–1706. |
| [8] | LUO Ding-sheng, CHEN Ke. Refine decision boundaries of a statistical ensemble by active learning[J]. Proceedings of the International Joint Conference on Neural Networks, 2003, 2(1): 1523–1528. |
| [9] | KYUNG Y J, LEE H S. Bootstrap and aggregating VQ classifier for speaker recognition[J]. Electronics Letters, 1999, 35(12): 973–974. DOI:10.1049/el:19990706 |
| [10] |
李艳鸽, 李粮纲, 张乾.
基于优化GM (1, 1) 模型的可视化沉降预测数据的精度研究[J]. 工程设计学报, 2009, 16(2): 145–148.
LI Yan-ge, LI Liang-gang, ZHANG Qian. Research on accuracy of visualized settlement prediction based on optimized GM (1, 1)[J]. Chinese Journal of Engineering Design, 2009, 16(2): 145–148. |
| [11] |
谢乃明, 刘思峰.
离散GM (1, 1) 模型与灰色预测模型建模机理[J]. 系统工程理论与实践, 2005(1): 93–98.
XIE Nai-ming, LIU Si-feng. Discrete GM (1, 1) model and the modeling mechanism of gray prediction model[J]. Systems Engineering:Theory & Practice, 2005(1): 93–98. |
| [12] |
刘波, 张玘.
汽车防抱制动系统自适应滑模控制算法的研究和半实物仿真[J]. 国防科技大学学报, 2008, 30(5): 125–130.
LIU Bo, ZHANG Qi. Car against holding brake system adaptive sliding mode control algorithm research and hardware-in-the-loop simulation[J]. Journal of National University of Defense Technology, 2008, 30(5): 125–130. |
| [13] | REN H P, LIU D. Nonlinear feedback control of chaos in permanent magnet synchronous motor[J]. IEEE Transactions on Circuits and Systems Ⅱ, 2006, 53(1): 45–50. DOI:10.1109/TCSII.2005.854592 |
| [14] |
唐国元, 宾鸿赞.
ABS的模糊滑模变结构控制方法及仿真研究[J]. 中国机械工程, 2007, 18(13): 1629–1632.
TANG Guo-yuan, BIN Hong-zan. ABS fuzzy sliding mode variable structure control method and simulation study[J]. China Mechanical Engineering, 2007, 18(13): 1629–1632. |
| [15] |
林程, 彭春雷, 曹万科.
独立驱动电动汽车稳定性的滑模变结构控制[J]. 汽车工程, 2015, 37(2): 132–138.
LIN Cheng, PENG Chun-lei, CAO Wan-ke. Sliding mode variable structure control for the stability of independent drive electric vehicle[J]. Automotive Engineering, 2015, 37(2): 132–138. |
| [16] |
张兵, 唐猛, 廖海洲.
基于负载观测的PMSM滑模抗扰动自适应控制[J]. 工程设计学报, 2013, 20(5): 427–433.
ZHANG Bing, TANG Meng, LIAO Hai-zhou. Anti-disturbance adaptive sliding mode control of PMSM based on load torque observer[J]. Chinese Journal of Engineering Design, 2013, 20(5): 427–433. |
| [17] | WEI D Q, LUO X S, WANG B H, et al. Robust adaptive dynamic surface control of chaos in permanent magnet synchronous motor[J]. Physics Letters A, 2007, 363(1/2): 71–77. |
| [18] | ŠIMÁNEK J, NOVÁK J, DOLEEK R. Control algorithms for permanent magnet synchronous traction motor[C]. The International Conference on Computer as a Tool in Eurocon, Warsaw, Sep.9-12, 2007. |


