2. 许继(厦门) 智能电力设备股份有限公司, 福建 厦门 361000
2. XuJi (Xiamen) Intelligent Switchgear Manufacturing Co., Ltd., Xiamen 361000, China
配电网直接面向终端电能用户,如何保证配电网供电质量安全可靠,并提高运行效率一直以来都是研究的重点[1].随着分布式电源在配电网中的渗透率逐渐增大,各类新型负荷(如电动汽车) 不断接入,配电网的运行状态具有更大的不可控性和不确定性,如何在新形势下保证配电网的安全可靠运行是一个亟待研究和解决的问题[2].
最大供电能力是衡量配电网运行状态的安全性指标[3].学者们已针对该指标进行了一定研究.文献[4-5]对供电能力进行了精确计算和建模研究;文献[6]提出了提升最大供电能力的配电网规划方法,充分利用网络结构和运行方式的变化,实现对新增负荷的消纳,避免了新增变电容量;文献[7]建立了计及用户互动的最大供电能力模型,讨论了可中断负荷对最大供电能力的影响,验证了最大供电能力将随用户负荷削减量的增大而增大;文献[8-9]研究了馈线联络和网络重构对配电网最大供电能力的作用,通过灵活的网络拓扑变换,实现负荷转供,达到提升最大供电能力的目的.文献[10]考虑了配电网中分布式电源出力的波动性和间歇性,建立了储能功率优化模型,能够有效提升配电网的供电能力.以上研究成果对配电网最大供电能力的提升具有指导意义,但均没有考虑多种影响因素联合作用的结果.
本文从尽可能避免网络拓扑频繁变动的角度出发,基于最大供电能力指标,利用储能系统(energy storage system,ESS) 双向负荷的特性和备用作用,建立了考虑储能的配电网预防重构的多级目标模型,制定了储能充放电和预防重构策略.通过在各个时段保证储能对最大供电能力指标的最大调整能力和优先利用储能进行调整的策略,减少发生网络重构的次数.在负荷过重时,联合利用储能和网络重构对安全指标的提升作用,使安全指标达到设定警戒值之上,有效避免了采取切负荷等其他方式保证配电网安全运行的情况出现.
1 储能模型和安全性指标 1.1 ESS充放电模型ESS是一类比较稳定的分布式电源,其充放电功率可以根据需求进行适当控制.对于考虑一段时间内的储能充放电情况,储能在某一时刻的容量将决定该时刻的最大输出功率,且影响到下一时刻的储能容量.设网络中第m个储能的额定容量为Emax(m),其额定充、放电功率为Pc(m) 和Pd(m),充、放电效率为ηc(m) 和ηd(m),在t时刻的荷电状态(state of charge,SOC) 为λ(m,t),ESS稳定运行时允许的SOC上、下限分别为λmax(m) 和λmin(m).t为任意时间段[T1,T2]中的某一时刻,则ESS的有功出力PGc(m,t) 和有功负荷PGd(m,t) 需要满足约束条件:
| $0 \le {P_{G{\rm{c}}}}(m, t) \le {P_{\rm{c}}}(m)$ | (1) |
| $0 \le {P_{G{\rm{d}}}}(m, t) \le {P_{\rm{d}}}(m)$ | (2) |
| $\lambda (m, t) = {\lambda _{{T_1}}}(m) + {({E_{\max }}(m))^{ - 1}}\int\limits_{{T_1}}^t {({\eta _{\rm{c}}}} {P_{G{\rm{c}}}}(m, \sigma ) - \eta _{\rm{d}}^{ - 1}{P_{G{\rm{d}}}}(m, \sigma )){\rm{d}}\sigma $ | (3) |
| ${\lambda _{\min }}(m) \le \lambda (m, t) \le {\lambda _{\max }}(m)$ | (4) |
| ${P_{G{\rm{c}}}}(m, t){P_{G{\rm{d}}}}(m, t) = 0$ | (5) |
式中:λ(m,t) 为第m个ESS在t时刻的SOC值.式(5) 表示储能不能同时处于充放电两种状态下,可以通过引入整数变量将其化为线性约束[11].
1.2 安全性指标本文将配电网的供电能力作为系统的安全性指标.与输电系统供电能力主要受热极限、稳定极限、电压降极限影响不同[12],配电网的供电能力是指在满足支路功率约束和节点电压约束的条件下,系统所能供给的最大负荷,主要取决于网络的拓扑结构、负荷水平和负荷增长方式[9].配电网的最大供电能力数学模型如下:
| ${\rm{PSCI = }}\max S = \sum\limits_{i = 1}^N {{S_{0i}}} + \sum\limits_{i \in C} {k{S_{di}}} $ | (6) |
式中:S为评估区域所能供给的最大负荷;S0i为节点i的实际负荷;N为负荷节点数,因此等式右边的第1项即为所有节点负荷之和,即实际系统负荷;Sdi为评估区域中节点i的负荷增长基数,本文取S0i=Sdi;k为负荷增长倍数;C为供电能力评估区域,本文是对整个配电网的供电能力进行评估,因此C即为整个配电网络.采用变步长潮流算法计算最大供电能力[13].定义最大供电能力倍数K=k+1,可设定其限值Kset以确保系统运行的安全性.
2 预防重构数学模型储能具有一定的备用作用,通过适当的充放电控制策略,可以提升配电网最大供电负荷,提高运行的安全性[10].本文综合考虑了储能和网络重构对安全性指标的影响.以整个调度周期内重构次数最少为一级目标,根据不同时段网络状态制定储能和重构相关的二级目标,其数学模型介绍如下.
2.1 目标函数 2.1.1 一级目标函数一级目标函数为min ∂,其中∂为调度周期内发生重构的次数.
2.1.2 二级目标函数1) 储能在t时刻充放电目标函数为
2) 网络重构目标函数为max K,其中K为最大供电能力倍数,即安全性指标.确保在重构以后K能有较大值,重构时以获得最大K为目标函数.
2.2 约束条件在确定储能充放电状态和网络重构方案选取时,有以下约束条件:
1) 储能充放电需要满足式(1) 至式(5).
2) 网络潮流约束:
| $ \begin{array}{l} V_i^{\min } \le {V_i} \le V_i^{\max }, i \in B\\ {I_j} \le I_j^{\max }, j \in L \end{array} $ |
式中:B是所有节点集合;Vi为第i个节点的实际电压,Vi,max,Vi,min为第i个节点的电压上、下限值;L为所有支路集合;Ij为第j条支路的实际电流,Ij,max为第j条支路的电流上限.
3) 网络辐射状约束.
此外,在进行网络重构时,还需满足:
| $ H = G + 1 $ |
式中:H为网络节点数,G为网络支路数.
4) 网络连通性约束.
对于网络中任意节点i,有:
| $ {a_j} = 1, \exists {l_{i, 0}}, \forall j \in {l_{i, 0}} $ |
式中:aj=1表示第j条支路闭合;li,0为第i个节点到网络源节点路径所含支路集合.即对任意节点i,存在一条到源节点的闭合路径.
在进行储能充放电计算时,需要将设定的供电能力倍数限值Kset加入约束条件中.此时是一个大规模非线性优化问题,可以采用广义简约梯度法进行求解[14].
3 考虑储能的网络预防重构求解策略 3.1 网络重构求解为了获得较高的重构求解效率,本文采用了文献[15]提出的混合粒子群算法对网络重构进行求解计算.
网络重构目标函数max K的求解步骤如下:
1) 网络化简.
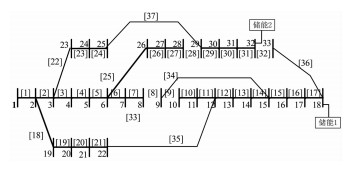
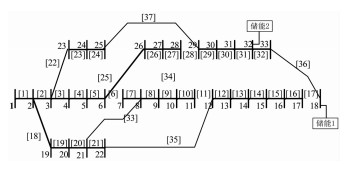
①不在环路上的支路,如图 1中支路1,编码时不需要考虑,仅将回路上的支路开合状态作为变量;
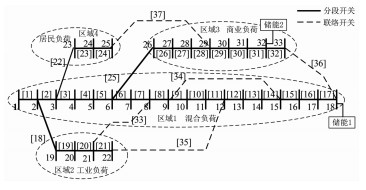
|
| 图 1 含储能的33节点配电系统 Fig.1 33-bus distribution system with energy storage |
②将解环效果一样的支路合并为一个支路组,如图 1中支路3,4,5可合并为一个支路组{3,4,5}.
2) 编码.粒子的每一维代表一个支路组,其值为x.x=0表示该支路组中没有支路断开,x为非0表示该支路组中第x条支路断开.显然x不大于支路组中所含支路数.采用该编码方式,图 1所示系统对应粒子的维数为13.第1维粒子对应支路组为{2},第2维的为{3,4,5},第3维的为{6,7},其他依此类推.
3) 利用改进二进制粒子群算法确定断开的支路组.根据迭代公式计算每一维的速度vid和对应的sigmod函数值.考虑到网络辐射状约束和连通性约束,重构时断开的支路数应该等于环路数,断开的支路应该属于不同的支路组.直接利用二进制粒子群算法效率较低.采用轮盘赌规则,根据各维置1概率的大小(sigmod值),随机选取n维置1,判断网络是否连通,连通则优化结束,不连通则再次利用轮盘赌将n维置1,直到满足连通约束.
4) 支路组内部支路选择优化.确定支路组内部断开支路时,变量非零状态取值为若干整数,利用离散粒子群算法对其进行求解,得到该次迭代产生的粒子群.
5) 更新迭代,直到达到最大迭代次数.计算出粒子的当前适应值,更新粒子个体极值Pbest和位置Pxbest;更新全局历史最优极值Gbest和位置Gxbest.判断是否达到最大迭代次数,未达到则返回步骤3) 进行下一次进化迭代,达到则停止,输出重构结果.
网络重构求解的流程如图 2所示.
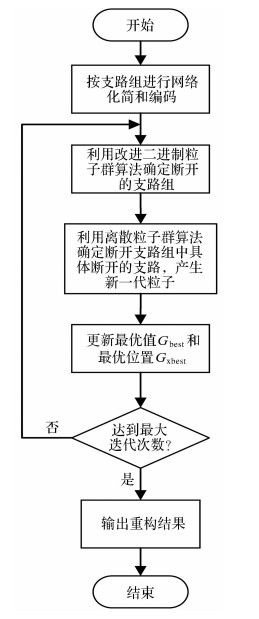
|
| 图 2 网络重构求解流程 Fig.2 Flow of network reconfiguration solving |
在含有储能的配电网中,储能有充放电两种状态,具有一定的供电备用能力.控制储能的充放电功率大小可调节配电网的最大供电能力.考虑到储能和网络重构对网络最大供电能力的调节作用,需要对储能的充放电状态和网络重构制定适当的控制策略,以最大限度地发挥储能在预防控制中的备用能力,避免网络拓扑频繁发生变化.具体策略如下:
1) 计算t时刻配电网的最大供电能力K,若K≥Kset,则将Kset作为约束条件,以
2) 以储能当前最大放电功率进行计算,计算配电网的最大供电能力K.若K≥Kset,则将Kset作为约束条件,以
3) 若此时储能出力能力无法将K调节到Kset以上,需进行网络重构.先不计及储能出力,以max K为目标函数,考虑潮流约束、网络辐射状约束和网络连通性约束,进行网络重构.若最终目标函数值不小于Kset,则按重构结果调整网络拓扑,再将Kset作为约束条件,以
4) 若此时单一重构无法将K值调节到Kset以上,需要储能联合调整.先以储能当前最大放电功率进行计算,以max K为目标函数,考虑潮流约束、网络辐射状约束和网络连通性约束,进行网络重构.若最终目标函数值不小于Kset,按重构结果调整网络拓扑,再将Kset作为约束条件,以
5) 利用切负荷或其他方式,调节配电网最大供电能力不小于设定值Kset.此内容非本文重点,不作详细说明.
6) t=t+1,进入下一时刻状态.
考虑储能的预防重构模型求解策略流程如图 3.
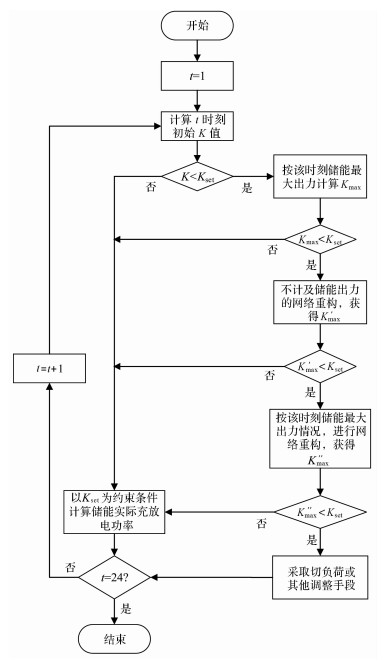
|
| 图 3 预防重构求解策略流程 Fig.3 Flow of preventive reconfiguration solving strategy |
如图 1所示,以IEEE-33节点系统为例对所提出的预防重构模型和方法进行验证和说明,相关参数参照文献[16],系统基准电压为12.66 kV.将系统分为4个不同区域:区域1电流上限取595 A,区域2电流上限取160 A,区域3电流上限取460 A,区域4电流上限取325 A;系统电压下限取0.9,上限取1.1[17].在节点18和32处安装储能装置,额定容量为1 800 kWh,最小容量为300 kWh,额定输出功率为450 kW,充放电效率分别为0.9和0.8,假设在开始计算时2个储能的容量水平均为0.5.取系统的最大供电能力设定值Kset=2[9].
为了使算例更符合实际,本文基于一个典型的全天负荷分区增长曲线对所提方法进行验证,将配电系统分为工业区、商业区、居民区以及混合区,如图 1所示.不同区域的负荷采用不同的负荷日增长曲线,具体负荷日增长曲线见文献[18].考虑储能的配电网预防重构仿真结果如下.
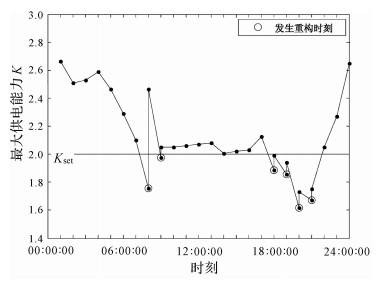
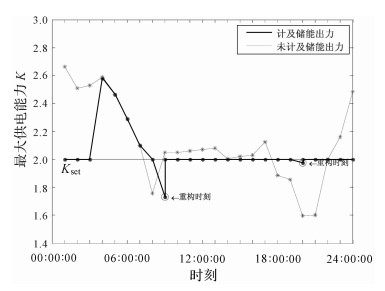
图 4是配电网最大供电能力K值日变化情况,其中实线为计及储能出力后计算出的K值,点划线为未计及储能出力时的K值.由于储能充放电作用,实线各个时刻的K值分布较之点划线会更贴近设定值Kset.
|
| 图 4 最大供电能力K值变化情况 Fig.4 The change of maximum supply energy capability K |
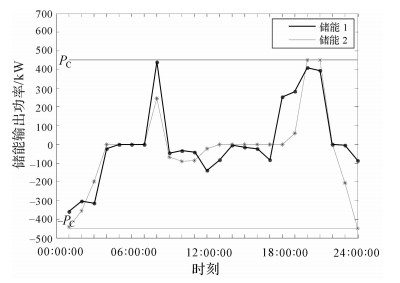
图 5为储能出力的日变化情况,出力值为正表示储能处于放电状态,为负表示处于充电状态.实线为储能1的输出功率曲线,点划线为储能2的输出功率曲线,PC为储能额定输出功率.
|
| 图 5 储能出力变化情况 Fig.5 The change of energy storage output power |
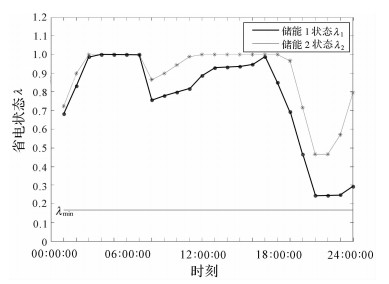
图 6为荷电状态日变化曲线,曲线标记点值为在t时刻结束时的荷电状态,图中λmin=ESSmin/ESSmax,ESSmax和ESSmin分别为储能额定和最小容量.本文暂不考虑储能过充情况,取λmax=1.
|
| 图 6 荷电状态变化情况 Fig.6 The change of state of charge |
结合图 4至图 6可以看出,在04:00:00之前,储能装置均处在充电状态,储能作为负荷接入配电网,使得K值稳定在设定值Kset=2上.在04:00:00-08:00:00时间段内,系统负荷较小,K值大于设定值,储能均达到最大容量水平值1,此时储能装置输出功率为0.在08:00:00时,由图 4中的点划线曲线可以看出,出现了K值小于设定值的情况.此时,储能装置将处在放电状态,作为电源接入系统,将K值调整至设定值Kset,如图 4实线在08:00:00时所示.在09:00:00时,网络负荷进一步加重,储能无法将K值调节至Kset以上,则进行网络重构.重构结果如图 7所示,开关8,9,28,32,33断开.重构后,系统K值位于Kset之上,储能再次进入充电状态,直到17:00:00时结束.在18:00:00和19:00:00两个时刻,出现K值低于设定值的情况,均可以通过储能调节到设定值.在20:00:00时,第2次出现了需要重构的情况.从图 5可以看出,与09:00:00发生重构后的储能的状态不同,20:00:00时刻储能处在放电状态.原因在于该时刻系统负荷过重,无法通过单一的网络重构将K值调整到设定值之上,必须结合储能协调控制,才能完成K值的调整.网络重构的结果如图 8所示,开关6,11,17,28,34断开.以后时段的状态分析与前所述相同,不再作分析说明.
|
| 图 7 09:00:00时的重构结果 Fig.7 Reconfiguration result at 09:00:00 |
|
| 图 8 20:00:00时的重构结果 Fig.8 Reconfiguration result at 20:00:00 |
利用文献[9]的方法,只考虑重构对最大供电能力的作用,计算出的K值日变化曲线如图 9所示.
从图 9中可以看出,在没有储能装置时,在08:00:00和09:00:00时刻均发生了重构.在负荷较重的18:00:00-21:00:00时段内,出现K值连续低于设定值的情况,此时由于网络负荷过重,已无法通过单一的网络重构将K值调整到设定值以上,需要采取切负荷或其他措施提高K值,才能保障系统在一定安全裕度下运行.
对比图 4与图 9所示结果可知,本文所述方法能够充分发挥储能在系统中的备用调节作用,可以有效减少网络的重构次数.
与之前的研究相比,本文的创新点主要体现在以下两方面:
1) 在预防重构中,考虑了储能在系统中的备用作用.预防重构是以某一安全裕度指标为目标,通过控制开关的状态进行的网络拓扑变换.由于储能双向负荷的作用,势必会影响到系统的安全裕度指标,研究其影响效果有必要性.
2) 制定了储能充放电和网络重构的协调控制策略.基于该控制策略,可充分保证储能在下一时刻具有最大的安全指标调整能力;在负荷过重,单一的储能作用和网络重构都无法将安全指标调整到设定值之上时,通过储能和重构的协同作用,可完成目标的调整.
5 结论本文考虑了储能的备用作用对供电能力指标的影响,建立了考虑储能充放电的预防重构模型,制定了储能充放电和网络重构的控制策略,利用广义简约梯度算法和混合粒子群算法对模型进行了求解,对比了不考虑储能作用的预防重构情况.基于典型日负荷曲线的算例,表明储能对于供电能力指标有一定的调节作用,且在负荷较重时,可以与网络重构协同作用,更大限度地对供电能力进行调整.算例的计算与分析结果验证了本文模型方法的有效性和优越性.
| [1] | NAGATA T, SASAKI H, YOKOYAMA R. Power system restoration by joint usage of expert system and mathematical programming approach[J]. IEEE Transactions on Power Systems, 1995, 10(3): 1473–1479. DOI:10.1109/59.466501 |
| [2] | MU Yun-fei, WU Jian-zhong, EKANAYAKE J, et al. Primary frequency response from electric vehicles in the great Britain power system[J]. IEEE Transactions on Smart Grid, 2013, 4(2): 1142–1150. DOI:10.1109/TSG.2012.2220867 |
| [3] |
李振坤, 陈星莺, 刘皓明, 等.
配电网供电能力的实时评估分析[J]. 电力系统自动化, 2009, 33(6): 36–39.
LI Zhen-kun, CHEN Xing-ying, LIU Hao-ming, et al. Online assessment of distribution network loading capability[J]. Automation of Electric Power Systems, 2009, 33(6): 36–39. |
| [4] | LUO Feng-zhang, WANG Cheng-shan, XIAO Jun, et al. Rapid evaluation method for power supply capability of urban distribution system based on N-1 contingency analysis of main-transformers[J]. International Journal of Electrical Power & Energy Systems, 2010, 32(10): 1063–1068. |
| [5] |
肖峻, 谷文卓, 郭晓丹.
配电系统供电能力模型[J]. 电力系统自动化, 2011, 35(24): 47–52.
XIAO Jun, GU Wen-zhuo, GUO Xiao-dan. Total supply capability model for distribution systems[J]. Automation of Electric Power Systems, 2011, 35(24): 47–52. |
| [6] |
肖峻, 张婷, 张跃, 等.
基于最大供电能力的配电网规划理念和方法[J]. 中国电机工程学报, 2013, 33(10): 106–113.
XIAO Jun, ZHANG Ting, ZHANG Yue, et al. TSC-based planning idea and method for distribution networks[J]. Proceedings of the CSEE, 2013, 33(10): 106–113. |
| [7] |
肖峻, 李思岑, 王丹.
计及用户分级与互动的配电网最大供电能力模型[J]. 电力系统自动化, 2015, 39(7): 19–25.
XIAO Jun, LI Si-cen, WANG Dan. Model of total supply capability for distribution network considering customer classification and interaction[J]. Automation of Electric Power Systems, 2015, 39(7): 19–25. |
| [8] |
肖峻, 祖国强, 贺琪博, 等.
馈线联络对配电网最大供电能力的作用机理[J]. 电力系统自动化, 2015, 39(8): 38–44.
XIAO Jun, ZU Guo-qiang, HE Qi-bo, et al. Mechanism of feeder links on total supply capability for distribution networks[J]. Automation of Electric Power Systems, 2015, 39(8): 38–44. |
| [9] |
靳小龙, 穆云飞, 贾宏杰, 等.
面向最大供电能力提升的配电网主动重构策略[J]. 电工技术学报, 2014, 29(12): 137–147.
JIN Xiao-long, MU Yun-fei, JIA Hong-jie, et al. An active reconfiguration strategy for distribution network based on maximum power supply capability[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 137–147. |
| [10] |
国宗, 韦钢, 郭运城, 等.
面向供电能力提升的配电网储能功率动态优化[J]. 电力系统保护与控制, 2015, 49(19): 1–8.
GUO Zong, WEI Gang, GUO Yun-cheng, et al. Dynamic optimization of energy storage power in distribution network based on power supply capacity[J]. Power System Protection and Control, 2015, 49(19): 1–8. |
| [11] |
刘伟佳, 吴秋伟, 文福拴, 等.
电动汽车和可控负荷参与配电系统阻塞管理的市场机制[J]. 电力系统自动化, 2014, 38(24): 26–33.
LIU Wei-jia, WU Qiu-wei, WEN Fu-shuang, et al. A market mechanism for participation of electric vehicles and dispatchable load in distribution system congestion management[J]. Automation of Electric Power Systems, 2014, 38(24): 26–33. |
| [12] | DUNLOP R D, GUTMAN R, MARCHENKO P P. Analytical development of load ability characteristics for EHV and UHV transmission line[J]. IEEE Trans on Power Apparatus and Systems, 1979, 98(2): 606–613. |
| [13] | OU Yan, SINGH C. Assessment of available transfer capability and margins[J]. IEEE Transactions on Power Systems, 2002, 17(2): 463–468. DOI:10.1109/TPWRS.2002.1007919 |
| [14] | GABASH A, LI P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage[J]. IEEE Trans on Power Systems, 2012, 27(4): 2026–2035. DOI:10.1109/TPWRS.2012.2187315 |
| [15] |
李振坤, 陈星莺, 余坤, 等.
配电网重构的混合粒子群算法[J]. 中国电机工程学报, 2008, 28(31): 35–41.
LI Zhen-kun, CHEN Xing-ying, YU Kun, et al. Hybrid particle swarm optimization for distribution network reconfiguration[J]. Proceedings of the CSEE, 2008, 28(31): 35–41. |
| [16] |
唐贤伦, 程祥, 汪斌全.
采用多agent混沌粒子群算法的配电网重构[J]. 电力系统及其自动化学报, 2015, 27(3): 17–23.
TANG Xian-lun, CHENG Xiang, WANG Bin-quan. Distribution network reconfiguration adopting chaos particle algorithm of multi-agent system[J]. Proceeding of the CSU-EPSA, 2015, 27(3): 17–23. |
| [17] | European Committee for Electrotechnical Standardization. Voltage characteristics of electricity supplied by public distribution systems:EN 50160[S]. Brussels, 2007:1-24. |
| [18] | MU Yun-fei, WU Jian-zhon, JENKINS N, et al. A spatial-temporal model for grid impact analysis of plug-in electric vehicles[J]. Applied Energy, 2014, 114(2): 456–465. |