随着经济全球化的不断深入,客户可以在更为广泛的范围内选择所需产品和服务,从而增强了对产品和服务的个性化定制需求,使得大批量定制(mass customization,MC) 生产成为当前先进制造的研究前沿和发展趋势.大批量定制生产是一种从市场需求和预测出发,以大批量生产的效率与效益,即以低成本、快速度和高质量,按照每个客户的特殊需求生产定制产品的新型生产模式[1].客户需求是实现大批量定制生产的基础和前提,通过客户需求(customer needs,CNs)、功能需求(functional requirements,FRs)、设计参数(design parameters,DPs) 的映射过程,将客户需求进行量化并转化为表征产品功能属性的技术指标和参数,对技术指标和参数进行分析以实现产品族的构建.产品族规划是实现大批量定制规模经济、范围经济及经验经济效应的一种有效方式,在某种程度上,产品族的构建直接影响到大批量定制的成败.因此,研究产品族客户需求模型是很有必要的.
各国学者对大批量定制下的客户需求模型进行了研究.Wang等[2]采用一种线性目标规划方法,得到客户需求的相对重要性权重.Maldonado等[3]提出通过构建相关矩阵同时识别客户的需求偏好和最相关属性.Yu等[4]通过运用质量功能配置技术,了解客户需求,并运用模糊聚类实现产品族的构建.Jiao等[5]对客户需求模型进行分析,建立了一个产品族框架,使企业在满足客户个性化需求的前提下更加迅速地设计出合理的产品.Wang等[6]提出了在产品的开发过程中加入客户偏好属性,将客户需求和功能要求进行可视化识别,最后对需求模型进行评估.经有国等[7]针对半结构化客户需求信息的模糊性、不易处理性等特点,提出了一种客户需求信息的数学描述方法,并建立了客户需求信息转换体系结构.黄辉等[8]建立了基于顾客需求-功能-原理-结构的大批量定制产品族扩展模型.周春景等[9]提出一种以顾客需求为导向的产品配置优化方法,建立了以成本可行为约束条件的产品优化配置的数学模型.但斌等[10]通过本体中概念之间的相似度的计算,提出了一种面向模糊客户需求的产品配置方法.
在前人研究的基础上,本文构建了面向大批量定制的产品族客户需求模型,并从客户喜好程度出发,运用联合分析法对客户需求信息进行量化得到客户需求倾向,从而实现客户需求到功能需求的转换.运用模糊聚类分析对产品设计关联矩阵进行解耦,最终获得解耦设计关联矩阵,为产品族的构建提供理论依据.
1 大批量定制客户需求模型构建客户需求分析的主要目的是将具有相似消费特征的消费群体的需求经过工程技术特征转化,形成面向产品开发和设计的需求[11].
1.1 客户需求-功能需求-设计参数的分析与映射对客户需求信息进行有效获取,并在产品设计中准确表达,是产品设计与开发中至关重要的一步,同时客户需求的提取也是需求分析中的关键步骤.通过需求与功能的联合分析,可以建立客户需求与功能需求之间的映射关系,采用模糊聚类分析,可以建立功能属性与设计参数的映射关系,如图 1所示.
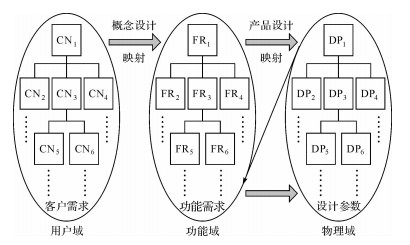
|
| 图 1 CNs,FRs和DPs的映射关系 Fig.1 Mapping relationship between CNs, FRs and DPs |
利用设计方程表达域之间的映射过程.以功能需求作为设计目标,构成功能需求集FRs.选择物理域中满足功能需求的设计参数,构成设计参数集DPs.功能需求与设计参数之间的关系可用函数描述如下:
| $ \left| {\begin{array}{*{20}{c}} {F{R_1}}\\ {F{R_2}}\\ { \cdot \cdot \cdot }\\ {F{R_n}} \end{array}} \right| = \boldsymbol{A}\left| {\begin{array}{*{20}{c}} {D{P_1}}\\ {D{P_2}}\\ { \cdot \cdot \cdot }\\ {D{P_n}} \end{array}} \right| $ | (1) |
式中
FRs-DPs的设计矩阵通常有3种:无耦合设计、解耦设计和耦合设计.事实上,多数情况下设计矩阵是耦合的,进而造成功能耦合.因此,通过需求模型的构建进行需求分析,将设计参数中各功能耦合的单元进行聚类形成模块,使模块内部具有较强的耦合关系,模块之间没有或者耦合关系较弱,从而确保模块之间的相对独立性.
1.2 大批量定制客户需求模型假设某一定制产品具有M个功能属性,其中每个功能属性具有N个离散水平,所有功能属性离散水平的集合θ为:
| $ \theta = \left\{ {{\theta _{11}}, {\theta _{12}}, \cdot \cdot \cdot, {\theta _{1{N_1}}}, \cdot \cdot \cdot, {\theta _{ij}}, \cdot \cdot \cdot, {\theta _{M{N_M}}}} \right\} $ | (2) |
式中θij为产品属性i的第j个离散水平.
假设市场调查客户需求数据为D,通过联合分析所得产品属性效用值的集合V为:
| $ V = \left\{ {{u_{11}}, {u_{12}}, \cdot \cdot \cdot, {u_{1{N_1}}}, \cdot \cdot \cdot, {u_{ij}}, \cdot \cdot \cdot, {u_{M{N_M}}}} \right\} $ | (3) |
式中uij为产品属性i的第j个水平的效用值.
利用效用值计算属性i的重要程度Wi为:
| $ {W_i} = \{ {w_{i1}}, {w_{i2}}, {w_i}_3, \cdot \cdot \cdot, {w_{in}}\} $ | (4) |
假设功能需求与设计参数的设计矩阵为A,客户需求与功能需求的设计矩阵为B,以设计参数之间的关联程度为参照,将公理设计矩阵转化为设计关联矩阵,得到DPs-DPs的设计关联矩阵为:
| $ \boldsymbol{C} = \left| {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{..., }&{{c_{1j}}}\\ {{c_{21}}}&{{c_{22}}}&{..., }&{{c_{2j}}}\\ {..., }&{..., }&{..., }&{...}\\ {{c_{i1}}}&{{c_{i2}}}&{..., }&{{c_{ij}}} \end{array}} \right| $ |
客户需求模型建模流程如图 2所示.

|
| 图 2 客户需求模型建模流程 Fig.2 Modeling process of customer requirement model |
通过市场调研和联合分析得到需求模型数据集合,实现需求模型的量化,是进行需求分析的基础.联合分析(conjoint analysis,CA) 为分析客户选择多属性产品并作出决策的一种重要方法.首先运用正交试验设计方法产生一系列的概念产品组合,通过调查分析得到客户对概念产品的偏好程度,采用联合分析法获得产品属性的水平效用值和属性间的相对重要程度,从而实现对抽象客户需求信息的量化处理.
2.1 联合分析的水平效用模型属性的水平效用表示客户对产品属性水平的偏好程度,水平效用值越大表示客户对该产品属性越偏爱.通常根据客户对概念产品的偏好程度,将客户需求信息分解成所有功能属性的水平效用值.假设概念产品有M个属性,每个属性包含N个水平,那么联合分析效用模型可以表示为:
| $ U = {\beta _0} + \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{u_{ij}}{x_{ij}} + \varepsilon } } $ | (5) |
式中:U为客户对概念产品的评价得分;β0为截距;uij为属性i的第j个水平的效用值;xij为属性i的第j个水平的哑变量,即如果该水平出现,则xij=1,反之,xij=0;ε为回归误差.
2.2 基于最小二乘法的属性效用求解采用虚拟变量的最小二乘法对属性水平效用进行求解.根据式(5) 可将效用模型总体回归方程简化表示为:
| $ {U_i} = {\beta _0} + {\beta _1}{x_{i1}} + {\beta _2}{x_{i2}} + \cdot \cdot \cdot + {\beta _i}{x_{ij}} $ | (6) |
最小二乘法是将每一条记录的观测值Ui与预测值Ȗi的离差平方和进行累加,累加值最小的β0,β1,…,βi即为该模型参数的最小二乘估计.假设
| $ \begin{array}{l} Q({{\hat \beta }_0}, {{\hat \beta }_1}, \cdot \cdot \cdot, {{\hat \beta }_i}) = \mathop {\min }\limits_{{\beta _0}, {\beta _1}, \cdot \cdot \cdot {\beta _i}} Q\left( {{\beta _0}, {\beta _1} \cdot \cdot \cdot, {\beta _i}} \right)\\ = \sum\limits_{i = 1}^n {{{[{U_i}-({{\hat \beta }_0} + {{\hat \beta }_1}{x_{i1}} + {{\hat \beta }_2}{x_{i2}} + \cdot \cdot \cdot + {{\hat \beta }_i}{x_{ij}})]}^2}} \end{array} $ | (7) |
对式(7) 分别关于β0,β1,…,βi求偏导并令偏导数为0,求解方程组如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial Q}}{{\partial {\beta _0}}}} \right|}_{{\beta _0} = {{\hat \beta }_0}}} =-2\sum\limits_{i = 1}^n {({U_i}-{{\hat \beta }_0}-{{\hat \beta }_1}{x_{i1}} - \cdot \cdot \cdot - {{\hat \beta }_i}{x_{ij}}) = 0} }\\ {{{\left. {\frac{{\partial Q}}{{\partial {\beta _1}}}} \right|}_{{\beta _1} = {{\hat \beta }_1}}} = - 2{x_{i1}}\sum\limits_{i = 1}^n {({U_i} - {{\hat \beta }_0} - {{\hat \beta }_1}{x_{i1}} - \cdot \cdot \cdot - {{\hat \beta }_i}{x_{ij}}) = 0} }\\ { \cdot \cdot \cdot }\\ { \cdot \cdot \cdot }\\ {{{\left. {\frac{{\partial Q}}{{\partial {\beta _i}}}} \right|}_{{\beta _i} = {{\hat \beta }_i}}} = - 2{x_{ij}}\sum\limits_{i = 1}^n {({U_i} - {{\hat \beta }_0} - {{\hat \beta }_1}{x_{i1}} - \cdot \cdot \cdot - {{\hat \beta }_i}{x_{ij}})} = 0} \end{array}} \right. $ | (8) |
整理可得回归参数最小二乘估计为:
| $ \hat \beta = {({\boldsymbol{X}^{\rm{T}}}\boldsymbol{X})^{-1}}{\boldsymbol{X}^{\rm{T}}}\boldsymbol{\bar U} $ | (9) |
式中:U为客户评分向量;X为哑变量矩阵;XT为哑变量矩阵的转置矩阵.求解获得的
属性的相对重要度反映了客户对产品属性的重视程度,重要度越大表示对这种属性越偏爱,表明该属性对客户更具吸引力.通常用属性水平效用值的差值来反映属性的相对重要度,差值越大表示该属性重要性越高.属性相对重要度描述为:
| $ {W_i} = \frac{{{R_i}}}{{\sum\limits_i {{R_i}} }}{\rm{, }}{R_i} = \mathop {\max }\limits_j ({u_{ij}})-\mathop {\min }\limits_j ({u_{ij}}) $ | (10) |
式中:Wi为产品第i个属性重要度;
运用联合分析对需求模型进行量化后,获得了产品各属性的重要度.以属性的重要度为依据,计算属性与属性间的相关系数,从而构建模糊相似矩阵.对属性之间进行聚类分析找到属性之间共性的一面,通过构造类间偏差和类内偏差来确定聚类的最佳阈值.
3.1 模糊相似矩阵的构建模糊相似矩阵的构建是聚类分析的前提条件.目前用于研究属性之间的相似性度的方法通常有2种.一种是相似系数法,性质越接近的属性,它们的相似系数的绝对值越接近1;反之,彼此无关的属性,它们的相似系数的绝对值越接近0.另一种是将属性看作空间中的一点,通过定义空间中点与点之间的距离,来表示属性间的相似性[12].本节根据式(10) 所得属性的重要度,计算属性间的皮尔逊相关系数,用相关系数描述属性间的相互关系.属性i与属性s之间的相关系数可定义为:
| $ {r_{ij}} = \left\{ {\begin{array}{*{20}{l}} 1&{i = s}\\ {\frac{{\sum\limits_{a = 1}^p {({w_{ia}}-{{\bar w}_i})({w_{ia}}-{{\bar w}_j})} }}{{\sqrt {\sum\limits_{a = 1}^p {{{({w_{ia}}-{{\bar w}_i})}^2} \cdot \sum\limits_{a = o}^p {{{({w_{ja}} - {{\bar w}_j})}^2}} } } }}}&{i \ne s} \end{array}} \right.{\rm{ }} $ | (11) |
式中:
聚类分析是通过衡量聚类对象之间的相似度来确定它们的亲疏关系,常用的模糊聚类算法有系统聚类法、k-mean聚类法、最大树聚类法和传递闭包法等.本文采用以模糊相似矩阵为基础的模糊最大树聚类算法来完成聚类过程,具体步骤如下.
步骤1:将ris(1 < i,s < n) 按从大到小进行排序:a1 < a2 < … < aγ < … < an,其中aγ(γ=1,2,…,n) 表示排序在γ位置上的相关系数.
步骤2:将相似系数为a1的对象用线连接.所有连接都以不形成闭合回路为准则,并在相应位置标明权重,权值为a1.
步骤3:对a2,a3,…, an依次进行相似操作.如果某一连接出现闭环,就将这条连接舍弃,当所有对象都连接完成后,最终就得到一棵最大树.
步骤4:选取最佳截断阈值对最大树进行截断,所有低于该阈值的连接都被截断,这样就能形成若干子树,这些子树集合即为聚类的结果簇.
3.3 基于样本几何结构的最佳阈值选择选择全局最优阈值,得到最佳聚类,是构建非耦合设计矩阵的关键.基于数据集样本几何结构,确定一个合适的聚类有效性指标,通过评估不同阈值下聚类结果的质量,最终获得对产品族设计具有指导意义的最佳聚类.
聚类有效性指标用于评估同一聚类算法在不同阈值条件下聚类结果的优良程度.好的聚类结果应有较好的类内紧密度和类间分离度.本文选取Krzanowski-Lai指标[13]作为衡量聚类质量的有效性指标.用KL指标对利用不同阈值获得的不同聚类结果的统计特征进行评估,不依赖外部的参考标准,依据数据集样本本身获得最佳聚类数.假设φ={λ1,λ2,…,λn}表示聚类阈值集合,k(k=2,…,n) 为聚类数.W(k) 为类内离差矩阵的迹,p表示数据集样本变量数,DIFF (k) 为样本类内离差矩阵测度,其数学模型表达式为:
| $ {\rm{DIFF}}(k) = {(k - 1)^{2/p}}W(k - 1) - {k^2}W(k) $ | (12) |
KL指数表示全部样本的类内离差矩阵的测度,将KL指标定义为:
| $ {\rm{KL}}(k) = \left| {\frac{{{\rm{DIFF}}(k)}}{{{\rm{DIFF}}(k + 1)}}} \right| $ | (13) |
基于样本几何结构的阈值最优化原则就是通过定义类内相似度和类间非相似度来衡量聚类结果质量.KL指标是以类内离差为主要评估依据,因此,KL (k) 值达到最大的聚类即为最优聚类,最优聚类对应的阈值为最佳阈值.聚类质量评价目标函数如下:
| $ {\rm{KL}}({k_0}) = \mathop {\max }\limits_{k = 2, \cdot \cdot \cdot, n} \left\{ {{\rm{KL}}(k)} \right\} $ | (14) |
式中k0为最优聚类数.
4 实例分析减速器是连接原动机和工作机的独立的闭式机械传动装置,其主要功能是降低转速和增大转矩,以满足工作机的转速和转矩需求,广泛应用于矿产、建筑、纺织、化工等行业.随着客户个性化需求的不断提升,减速器制造商为了降低设计和制造成本,开始逐步向大批量定制化转变.以圆柱齿轮减速器为例,对其客户需求模型进行分析,以初始化产品族规划为目标,验证所提方法的有效性和可行性.图 3为单级圆柱齿轮减速器零件分解图.
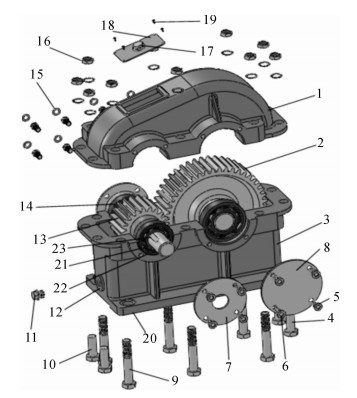
|
| 1-箱盖; 2-大齿轮; 3-油标尺; 4-起盖螺钉; 5,9-螺栓; 6-调整垫片; 7,8-轴承盖; 11-螺塞; 12-封油圈; 13-小齿轮; 14-齿轮轴; 15-弹簧垫圈; 16-螺母; 17-通气器; 18-检查孔盖; 19-螺钉; 20-箱座; 21-轴承; 22-毡圈; 23-键 图 3 单级圆柱齿轮减速器零件分解图 Fig.3 Exploded view of ingle stage cylindrical gear reducer |
为了能将尽量多的减速器产品规划到产品族中,而又不致使分析过程过于复杂,以减速器功能分解图为依据,选取产品的主要特征属性进行分析并构建产品族模型,图 4为齿轮减速器功能分解图.由于减速器的高速轴和低速轴主要由电动机型号、传动比和电机转速等共同决定,因此将其归为传动模块,不再分开考虑.同样将上箱盖和下箱体归为箱体模块.齿轮减速器产品的主要特征属性包括传动轴组DP0、箱体DP3、检查孔盖DP41、螺塞DP42、油标尺DP43、通气孔DP44、定位销DP45、起盖螺钉DP46、起吊装置DP47和轴承盖DP48.选取产品10个属性的3个特征水平进行分析.产品属性及其特征水平如表 1所示.
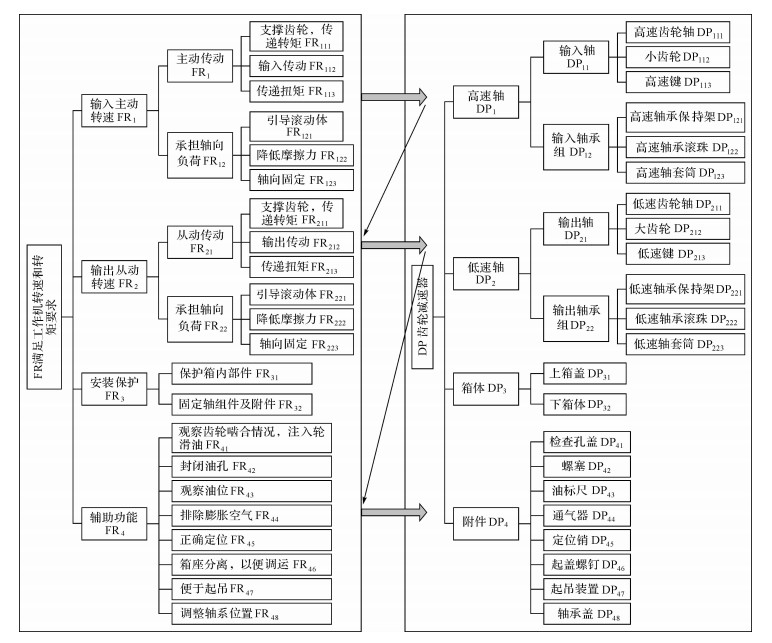
|
| 图 4 圆柱齿轮减速器功能分解图 Fig.4 Functional decomposition diagram of cylindrical gear reducer |
| 轴组 | 箱体 | 检查孔盖 | 螺塞 | 油标尺 | 通气器 | 定位销 | 起盖螺钉 | 起吊装置 | 嵌入式轴承盖(O形截面直径) |
| Y160M1-2 | 铸铁HT200 | 90 mm×70 mm | M14×1.5 | M12 | M12×1.25 | M6 | M8×25 | 箱座吊耳+吊环螺钉M10 | 2.65 mm |
| Y160M2-2 | 铸铁HT250 | 130 mm×90 mm | M16×1.5 | M16 | M14×1. 5 | M8 | M10×35 | 箱座吊耳+吊环螺钉M12 | 3.55 mm |
| Y160L-2 | 铸钢 | 180 mm×130 mm | M20×1.5 | M20 | M20×1.5 | M10 | M12×40 | 箱座吊耳+吊环螺钉M14 | 5.3 mm |
根据减速器产品属性及其特征水平可以组合成310种减速器产品.若客户对所有减速器产品逐一进行评分,那将难以实现.因此,综合考虑产品属性的均衡分散性和评分结果的整齐可比性,采用正交试验设计筛选概念产品,从而减少被访者对概念产品的评分个数.本例中所有产品属性均包含3个特征水平,故适用同位级正交表中的三位级正交表L27(313),根据正交表一一对应筛选获得27个概念产品.对运用正交试验设计方法筛选得到的概念产品进行结构设计检验,通过校核计算表明所有概念产品均满足设计要求.对50个客户进行市场调查,运用9分法评价,其中1表示客户对概念产品完全不偏爱,9表示极度偏爱.通过调查可以得到27个概念产品的客户评分.限于篇幅,这里只列出10个概念产品和客户1的评分,正交设计的概念产品及客户评分如表 2所示.
| 产品号 | 轴组 | 箱体 | 检查孔盖 | 螺塞 | 油标尺 | 通气器 | 定位销 | 起盖螺钉 | 起吊装置 | 嵌入式轴承盖(O形截面直径/mm) | 评分1 |
| 1 | Y160M1-2 | 铸铁HT250 | 90 mm×70 mm | M20×1.5 | M16 | M14×1. 5 | M6 | M8×25 | 箱座吊耳+吊环螺钉M12 | 5.3 | 3 |
| 2 | Y160L-2 | 铸铁HT250 | 130 mm×90 mm | M20×1.5 | M20 | M12×1.25 | M8 | M8×25 | 箱座吊耳+吊环螺钉M14 | 2.65 | 5 |
| 3 | Y160M2-2 | 铸钢 | 130 mm×90 mm | M20×1.5 | M12 | M12×1.25 | M6 | M10×35 | 箱座吊耳+吊环螺钉M12 | 3.55 | 4 |
| 4 | Y160M2-2 | 铸铁HT200 | 130 mm×90 mm | M16×1.5 | M16 | M14×1. 5 | M6 | M10×35 | 箱座吊耳+吊环螺钉M14 | 2.65 | 4 |
| 5 | Y160L-2 | 铸铁HT200 | 90 mm×70 mm | M16×1.5 | M12 | M20×1.5 | M10 | M10×35 | 箱座吊耳+吊环螺钉M12 | 5.3 | 4 |
| 6 | Y160M2-2 | 铸钢 | 180 mm×130 mm | M16×1.5 | M16 | M12×1.25 | M10 | M8×25 | 箱座吊耳+吊环螺钉M12 | 2.65 | 9 |
| 7 | Y160M1-2 | 铸铁HT200 | 180 mm×130 mm | M16×1.5 | M20 | M12×1.25 | M8 | M10×35 | 箱座吊耳+吊环螺钉M10 | 3.55 | 5 |
| 8 | Y160M2-2 | 铸铁HT250 | 90 mm×70 mm | M16×1.5 | M16 | M20×1.5 | M8 | M12×40 | 箱座吊耳+吊环螺钉M10 | 2.65 | 4 |
| 9 | Y160L-2 | 铸钢 | 130 mm×90 mm | M16×1.5 | M12 | M14×1. 5 | M8 | M8×25 | 箱座吊耳+吊环螺钉M10 | 5.3 | 6 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 27 | Y160M2-2 | 铸铁HT250 | 130 mm×90 mm | M14×1.5 | M20 | M20×1.5 | M6 | M10×35 | 箱座吊耳+吊环螺钉M10 | 5.3 | 1 |
获得概念产品和客户评分数据后,根据式(5) 至式(10) 求解出产品属性的水平效用和属性相对重要度.由于数据量较大,运用最小二乘法求解时可以借助数据统计分析软件SAS中的conjoint analysis模块进行求解.表 3所示为根据客户1评分所得的产品属性的水平效用和重要程度.对客户打分进行方差分析,选取10个有效打分.分析结果碍于篇幅不详细列出,给出重要度汇总表,如表 4所示.
| 属性 | 属性水平 | 水平效用 | 重要度/% | 属性 | 属性水平 | 水平效用 | 重要度/% |
| 轴组 | Y160M1-2 Y160M2-2 Y160L-2 |
0.518 52 -0.481 48 -0.037 04 |
7.894 7 | 箱体 | 铸铁HT200 铸铁HT250 铸钢 |
-0.370 37 -0.703 70 1.074 07 |
14.035 1 |
| 检查孔盖 | 90 mm×70 mm 130 mm×90 mm 180 mm×130 mm |
-0.259 26 -0.037 04 0.296 30 |
4.386 0 | 螺塞 | M14×1.5 M16×1.5 M20×1.5 |
-0.814 81 0.185 19 0.629 63 |
11.912 3 |
| 油标尺 | M12 M16 M20 |
-0.037 04 0.962 96 -0.925 93 |
14.912 3 | 通气器 | M12×1.25 M14×1.5 M20×1.5 |
0.851 85 -0.370 37 -0.481 48 |
10.526 3 |
| 定位销 | M6 M8 M10 |
-1.370 37 0.629 63 0.740 74 |
16.666 7 | 起盖螺钉 | M8×25 M10×35 M12×40 |
-0.370 37 0.407 41 -0.037 04 |
6.140 4 |
| 起吊装置 | 箱座吊耳+吊环螺钉M10 箱座吊耳+吊环螺钉M12 箱座吊耳+吊环螺钉M14 |
-0.148 15 -0.259 26 0.407 41 |
5.263 2 | 嵌入式轴承盖 | 2.65 3.55 5.3 |
0.518 52 -0.592 59 0.074 07 |
8.771 9 |
| 客户 | 属性重要度/% | |||||||||
| 轴组 | 箱体 | 检查孔盖 | 螺塞 | 油标尺 | 通气器 | 定位销 | 起盖螺钉 | 起吊装置 | 嵌入式轴承盖 | |
| 1 | 7.894 7 | 14.035 1 | 4.386 0 | 11.912 3 | 14.912 3 | 10.526 3 | 16.666 7 | 6.140 4 | 5.263 2 | 8.771 9 |
| 2 | 5.932 2 | 29.661 0 | 4.322 0 | 3.779 7 | 6.254 2 | 10.474 6 | 3.542 4 | 12.542 4 | 14.169 5 | 9.322 0 |
| 3 | 13.333 3 | 28.571 4 | 7.523 8 | 6.619 0 | 4.619 0 | 4.761 9 | 5.714 3 | 13.476 2 | 7.761 9 | 7.619 0 |
| 4 | 4.761 9 | 9.523 8 | 5.936 5 | 6.904 8 | 8.317 5 | 9.381 0 | 8.730 2 | 11.523 8 | 16.666 7 | 18.254 0 |
| 5 | 3.305 8 | 9.917 4 | 10.223 1 | 9.223 1 | 8.438 0 | 7.396 7 | 13.223 1 | 14.090 9 | 9.305 8 | 14.876 0 |
| 6 | 9.302 3 | 18.604 7 | 6.876 0 | 5.527 1 | 6.201 6 | 8.302 3 | 15.503 9 | 12.627 9 | 9.302 3 | 7.751 9 |
| 7 | 6.521 7 | 17.391 3 | 7.420 3 | 6.347 8 | 11.666 7 | 9.666 7 | 7.246 4 | 10.072 5 | 13.521 7 | 10.144 9 |
| 8 | 16.778 5 | 10.738 3 | 7.053 7 | 8.409 4 | 9.409 4 | 6.711 4 | 13.422 8 | 5.355 7 | 8.026 8 | 14.094 0 |
| 9 | 13.084 1 | 19.626 2 | 3.607 5 | 4.803 7 | 6.887 9 | 10.476 6 | 13.084 1 | 10.345 8 | 10.607 5 | 7.476 6 |
| 10 | 8.800 0 | 15.200 0 | 6.600 0 | 6.200 0 | 7.600 0 | 10.000 0 | 6.400 0 | 10.400 0 | 16.800 0 | 12.000 0 |
以重要度为依据,根据式(11) 计算得到属性间的皮尔逊相关系数.用皮尔逊相关系数来描述属性间的相似程度,构造模糊相似矩阵,也称设计关联矩阵,如表 5所示.
| DP0 | DP3 | DP41 | DP42 | DP43 | DP44 | DP45 | DP46 | DP47 | DP48 | ||||||
| DP11 | DP12 | DP21 | DP22 | DP31 | DP32 | ||||||||||
| DP0 | DP11 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.202 | 0.065 | 0.207 | 0.416 | 0.168 | 0.466 | 0.426 | 0.350 |
| DP12 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.202 | 0.065 | 0.207 | 0.416 | 0.168 | 0.466 | 0.426 | 0.350 | |
| DP21 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.202 | 0.065 | 0.207 | 0.416 | 0.168 | 0.466 | 0.426 | 0.350 | |
| DP22 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.202 | 0.065 | 0.207 | 0.416 | 0.168 | 0.466 | 0.426 | 0.350 | |
| DP3 | DP31 | 0.177 | 0.177 | 0.177 | 0.177 | 1 | 1 | 0.332 | 0.618 | 0.524 | 0.081 | 0.561 | 0.398 | 0.023 | 0.727 |
| DP32 | 0.177 | 0.177 | 0.177 | 0.177 | 1 | 1 | 0.332 | 0.618 | 0.524 | 0.081 | 0.561 | 0.398 | 0.023 | 0.727 | |
| DP41 | 0.202 | 0.202 | 0.202 | 0.202 | 0.332 | 0.332 | 1 | 0.294 | 0.109 | 0.656 | 0.010 | 0.367 | 0.082 | 0.394 | |
| DP42 | 0.065 | 0.065 | 0.065 | 0.065 | 0.618 | 0.618 | 0.294 | 1 | 0.725 | 0.176 | 0.589 | 0.487 | 0.575 | 0.291 | |
| DP43 | 0.207 | 0.207 | 0.207 | 0.207 | 0.524 | 0.524 | 0.109 | 0.725 | 1 | 0.404 | 0.440 | 0.697 | 0.259 | 0.136 | |
| DP44 | 0.416 | 0.416 | 0.416 | 0.416 | 0.081 | 0.081 | 0.656 | 0.176 | 0.404 | 1 | 0.018 | 0.226 | 0.431 | 0.070 | |
| DP45 | 0.168 | 0.168 | 0.168 | 0.168 | 0.561 | 0.561 | 0.010 | 0.589 | 0.440 | 0.018 | 1 | 0.418 | 0.658 | 0.038 | |
| DP46 | 0.466 | 0.466 | 0.466 | 0.466 | 0.398 | 0.398 | 0.367 | 0.487 | 0.697 | 0.226 | 0.418 | 1 | 0.303 | 0.047 | |
| DP47 | 0.426 | 0.426 | 0.426 | 0.426 | 0.023 | 0.023 | 0.082 | 0.575 | 0.259 | 0.431 | 0.658 | 0.303 | 1 | 0.416 | |
| DP48 | 0.350 | 0.350 | 0.350 | 0.350 | 0.727 | 0.727 | 0.394 | 0.291 | 0.136 | 0.070 | 0.038 | 0.047 | 0.416 | 1 | |
根据设计关联矩阵,运用模糊最大树聚类算法,画出关联矩阵最大树,如图 5所示.
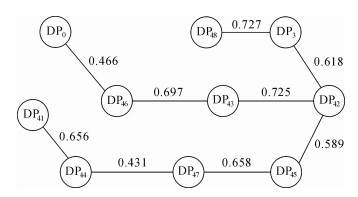
|
| 图 5 关联矩阵最大树 Fig.5 The maximal tree of association matrix |
由图 5可知阈值的取值集合为{0.727,0.725,0.697,0.658,0.656,0.618,0.589,0.466,0.431},取不同的阈值可以得到不同的聚类结果:
1) 取λ1=1,将设计参数分为10类,即{DP0},{DP3},{DP41},{DP42},{DP43},{DP44},{DP45},{DP46},{DP47},{DP48};
2) 取λ2=0.727,将设计参数分为9类,即{DP3,DP48},{DP0},{DP41},{DP42},{DP43},{DP44},{DP45},{DP46},{DP47};
……
9) 取λ9=0.466,将设计参数分为2类,即{DP3,DP48,DP41,DP42,DP43,DP44,DP45,DP46,DP47}和{DP0}.
阈值的选择直接影响聚类质量,运用基于样本几何结构的KL指标评估聚类结果,得到最佳聚类数.构建类内离差矩阵测度数学模型(式(12)),建立其目标函数数学模型式(14).通过MATLAB编程计算可得各聚类数的KL指标值,如表 6所示.图 6为在MATLAB中运行求解KL指标随聚类数变化折线图.
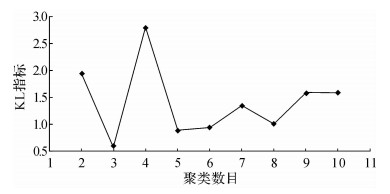
|
| 图 6 KL指标变化折线图 Fig.6 Change line chart of KL index |
| 聚类数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| KL (k) | 1.941 2 | 0.592 9 | 2.795 6 | 0.881 8 | 0.942 9 | 1.347 9 | 1.010 4 | 1.586 3 | 1.586 3 |
通过计算可知,最佳聚类数为4.由此,可以得到4个基本模块{DP0},{DP3,DP42,DP43,DP46,DP48},{DP41,DP44}和{DP45,DP47}.根据聚类结果对设计关联矩阵进行解耦,得到非耦合关联矩阵如表 7所示.以非耦合关联矩阵为依据,继而确定系列化的参数化产品族.
| DP0 | DP3 | DP42 | DP43 | DP46 | DP48 | DP41 | DP44 | DP45 | DP47 | ||||||
| DP11 | DP12 | DP21 | DP22 | DP31 | DP32 | ||||||||||
| DP0 | DP11 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.065 | 0.207 | 0.466 | 0.350 | 0.202 | 0.416 | 0.168 | 0.426 |
| DP12 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.065 | 0.207 | 0.466 | 0.350 | 0.202 | 0.416 | 0.168 | 0.426 | |
| DP21 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.065 | 0.207 | 0.466 | 0.350 | 0.202 | 0.416 | 0.168 | 0.426 | |
| DP22 | 1 | 1 | 1 | 1 | 0.177 | 0.177 | 0.065 | 0.207 | 0.466 | 0.350 | 0.202 | 0.416 | 0.168 | 0.426 | |
| DP3 | DP31 | 0.177 | 0.177 | 0.177 | 0.177 | 1 | 1 | 0.618 | 0.524 | 0.398 | 0.727 | 0.332 | 0.081 | 0.561 | 0.023 |
| DP32 | 0.177 | 0.177 | 0.177 | 0.177 | 1 | 1 | 0.618 | 0.524 | 0.398 | 0.727 | 0.332 | 0.081 | 0.561 | 0.023 | |
| DP42 | 0.065 | 0.065 | 0.065 | 0.065 | 0.618 | 0.618 | 1 | 0.725 | 0.487 | 0.291 | 0.294 | 0.176 | 0.587 | 0.575 | |
| DP43 | 0.207 | 0.207 | 0.207 | 0.207 | 0.524 | 0.524 | 0.725 | 1 | 0.697 | 0.136 | 0.109 | 0.404 | 0.440 | 0.259 | |
| DP46 | 0.466 | 0.466 | 0.466 | 0.466 | 0.398 | 0.398 | 0.487 | 0.697 | 1 | 0.047 | 0.367 | 0.226 | 0.418 | 0.303 | |
| DP48 | 0.350 | 0.350 | 0.350 | 0.350 | 0.727 | 0.727 | 0.291 | 0.136 | 0.047 | 1 | 0.394 | 0.070 | 0.038 | 0.416 | |
| DP41 | 0.202 | 0.202 | 0.202 | 0.202 | 0.332 | 0.332 | 0.294 | 0.109 | 0.367 | 0.394 | 1 | 0.656 | 0.010 | 0.082 | |
| DP44 | 0.416 | 0.416 | 0.416 | 0.416 | 0.081 | 0.081 | 0.176 | 0.404 | 0.226 | 0.070 | 0.656 | 1 | 0.018 | 0.431 | |
| DP45 | 0.168 | 0.168 | 0.168 | 0.168 | 0.561 | 0.561 | 0.587 | 0.440 | 0.418 | 0.038 | 0.010 | 0.018 | 1 | 0.658 | |
| DP47 | 0.426 | 0.426 | 0.426 | 0.426 | 0.023 | 0.023 | 0.575 | 0.259 | 0.303 | 0.416 | 0.082 | 0.431 | 0.658 | 1 | |
产品族规划是实现大批量定制生产的有效方式,客户需求模型是产品族规划的重要内容.本文以公理设计为指导,针对需求信息具有的抽象性、模糊性等特点,采用联合分析法对客户需求信息进行量化处理,将客户需求信息分解成所有功能属性的水平效用值,并计算属性间的相对重要度;建立了以皮尔逊相关系数为度量的设计关联矩阵,运用最大树模糊聚类法对设计关联矩阵进行聚类分析,并结合基于样本几何结构的最优阈值选择,得到最优聚类结果.以最优聚类结果为依据,对设计关联矩阵进行解耦,从而为产品族规划提供了理论依据.通过对客户需求模型进行研究得到的产品族能够使企业更好地响应客户的多样化需求,提高产品的市场竞争力,同时也为产品族规划提供一个新的研究思路.最后通过一个实例描述了基于联合分析和模糊聚类的产品族客户需求模型的分析过程,验证了该方法的有效性和可行性.
| [1] |
祁国宁, 顾新建, 谭建荣.
大批量定制技术及其应用[M]. 北京: 机械工业出版社, 2003: 40-46.
QI Guo-ning, GU Xin-jian, TAN Jian-rong. Technologies and applications of mass customization[M]. Beijing: China Machine Press, 2003: 40-46. |
| [2] | WANG Y M, CHIN K S. A linear goal programming approach to determining the relative importance weights of customer requirements in quality function deployment[J]. Information Sciences, 2011, 181(24): 5523–5533. DOI:10.1016/j.ins.2011.08.016 |
| [3] | MALADONADO S, MONTOYA R, WEBER R. Advanced conjoint analysis using feature selection via support vector machines[J]. European Journal of Operational Research, 2015, 241(2): 564–574. DOI:10.1016/j.ejor.2014.09.051 |
| [4] | YU S, YANG Q, TAO J, et al. Incorporating quality function deployment with modularity for the end-of-life of a product family[J]. Journal of Cleaner Production, 2015, 87(1): 423–430. |
| [5] | JIAO J, TSENG M M. Methodology of developing product family architecture for mass customization[J]. Journal of Intelligent Manufacturing, 1999, 10(1): 3–20. DOI:10.1023/A:1008926428533 |
| [6] | WANG C H, SHIH C W. Integrating conjoint analysis with quality function deployment to carry out customer-driven concept development for ultrabooks[J]. Computer Standards & Interfaces, 2013, 36(1): 89–96. |
| [7] |
经有国, 但斌, 张旭梅, 等.
MC半结构化客户需求信息表达与处理方法[J]. 管理科学学报, 2011, 14(1): 78–85.
JING You-guo, DAN Bin, ZHANG Xu-mei, et al. Expressing and processing approach for semi-structured customer needs under mass customization[J]. Journal of Management Sciences in China, 2011, 14(1): 78–85. |
| [8] |
黄辉, 梁工谦, 隋海燕.
大规模定制产品族设计中的原理聚类研究[J]. 管理工程学报, 2008, 22(3): 110–114.
HUANG Hui, LIANG Gong-qian, SUI Hai-yan. Principle clustering of product families for mass customization design[J]. Journal of Industrial Engineering and Engineering Management, 2008, 22(3): 110–114. |
| [9] |
周春景, 林志航, 刘春涛.
顾客需求驱动的产品配置优化[J]. 西安交通大学学报, 2007, 41(3): 339–343.
ZHOU Chun-jing, LIN Zhi-hang, LIU Chun-tao. Customer requirements driven product configuration optimization[J]. Journal of Xi'an Jiaotong University, 2007, 41(3): 339–343. |
| [10] |
但斌, 姚玲, 经有国, 等.
基于本体映射面向模糊客户需求的产品配置研究[J]. 计算机集成制造系统, 2010, 16(2): 225–232.
DAN Bin, YAO Ling, JING You-gou, et al. Product configuration oriented to fuzzy customer requirement based on ontology mapping[J]. Computer Integrated Manufacturing Systems, 2010, 16(2): 225–232. |
| [11] |
蒋建东, 张立彬, 胥芳, 等.
面向大批量定制生产的小型农业作业机客户需求模型的构建研究[J]. 农业工程学报, 2005, 21(9): 98–102.
JIANG Jian-dong, ZHANG Li-bin, XU Fang, et al. Model for customer requirements of small agricultural machinery product under mass customization[J]. Transaction of the Chinese Society of Agricultural Engineering, 2005, 21(9): 98–102. |
| [12] |
李卫东.
应用多元统计分析[M]. 北京: 北京大学出版社, 2008: 291-295.
LI Wei-dong. Applied multivariate statistical analysis[M]. Beijing: Peking University Press, 2008: 291-295. |
| [13] | KRZANOWSKI W J, LAI Y T. A criterion for determining the number of groups in a data set using sum-of-squares clustering[J]. Biometrics, 1988, 44(1): 23–34. DOI:10.2307/2531893 |
| [14] |
肖人彬, 程贤福, 陈诚, 等.
基于公理设计和设计关联矩阵的产品平台设计新方法[J]. 机械工程学报, 2012, 48(11): 94–103.
XIAO Ren-bin, CHENG Xian-fu, CHEN Cheng, et al. New approach to product platform design based on axiomatic design and design relationship matrix[J]. Journal of Mechanical Engineering, 2012, 48(11): 94–103. DOI:10.3901/JME.2012.11.094 |
| [15] |
邵云飞, 杜欣, 唐小我.
基于6σ/QFD/TRIZ集成的产品创新设计方法[J]. 系统工程, 2011(4): 77–83.
SHAO Yun-fei, DU Xin, TANG Xiao-wo. Innovative design method of products based on the integration of Six Sigma, QFD and TRIZ Model[J]. Systems Engineering, 2011(4): 77–83. |
| [16] |
杨沁, 唐伟.
面向产品族的客户需求最佳聚类确定方法[J]. 工程设计学报, 2013, 20(2): 97–101.
YANG Qin, TANG Wei. The determination of the optimal clustering of customer demands for product family[J]. Chinese Journal of Engineering Design, 2013, 20(2): 97–101. |
| [17] | CHENG X, LAN G, ZHU Q. Scalable product platform design based on design structure matrix and axiomatic design[J]. International Journal of Product Development, 2015, 20(2): 91–106. DOI:10.1504/IJPD.2015.068962 |
| [18] |
李柏姝, 唐加福, 雒兴刚.
面向细分市场的产品族规划方法及应用[J]. 计算机集成制造系统, 2009, 15(6): 1055–1061.
LI Bai-shu, TANG Jia-fu, LUO Xing-gang. Method and application of product family design for market niche[J]. Computer Integrated Manufacturing Systems, 2009, 15(6): 1055–1061. |
| [19] |
唐中君, 龙玉玲.
基于Kano模型的个性化需求获取方法研究[J]. 软科学, 2012, 26(2): 127–131.
TANG Zhong-jun, LONG Yu-ling. Research on method of acquiring individual demand based on kano model[J]. Soft Science, 2012, 26(2): 127–131. |
| [20] |
周世兵, 徐振源, 唐旭清.
基于近邻传播算法的最佳聚类数确定方法比较研究[J]. 计算机科学, 2011, 38(2): 225–228.
ZHOU Shi-bing, XU Zhen-yuan, TANG Xu-qing. Comparative study on method for determining optimal number of clusters based on affinity propagation clustering[J]. Computer Science, 2011, 38(2): 225–228. |


