全向轮式移动机器人因比腿式移动机器人更易于加工制造, 承载能力和效率更高, 运动灵活以及能在狭窄和拥挤的环境中运行, 而得到了越来越广泛的应用^[1].目前轮式移动机器人常采用的轮子有3种:普通轮、全向轮以及球形轮^[2].普通轮就是日常所见的在各类车辆上使用的轮子；全向轮是在普通轮的圆周上再安装上一定数量的滚子, 又被称为麦克纳母轮；球形轮是一种形状为球形的滚轮^[3].三者之中普通轮结构最简单, 但是其不能提供全向移动功能.麦克纳母轮的设计以及控制较为繁琐, 由于轮子的圆周上均匀分布着许多小的滚子, 在运动时不可避免地产生振动和打滑, 而球形轮的运动控制又较为困难^[4].基于上述原因, 在设计全向移动机器人时考虑采用另外一种形式的轮子, 即:万向轮作为移动机器人的移动基础部件^[5].因其具有2个运动自由度, 运动过程又可保持连续, 所以它可提供完全的机动性与灵活性并且能实现全向移动功能.

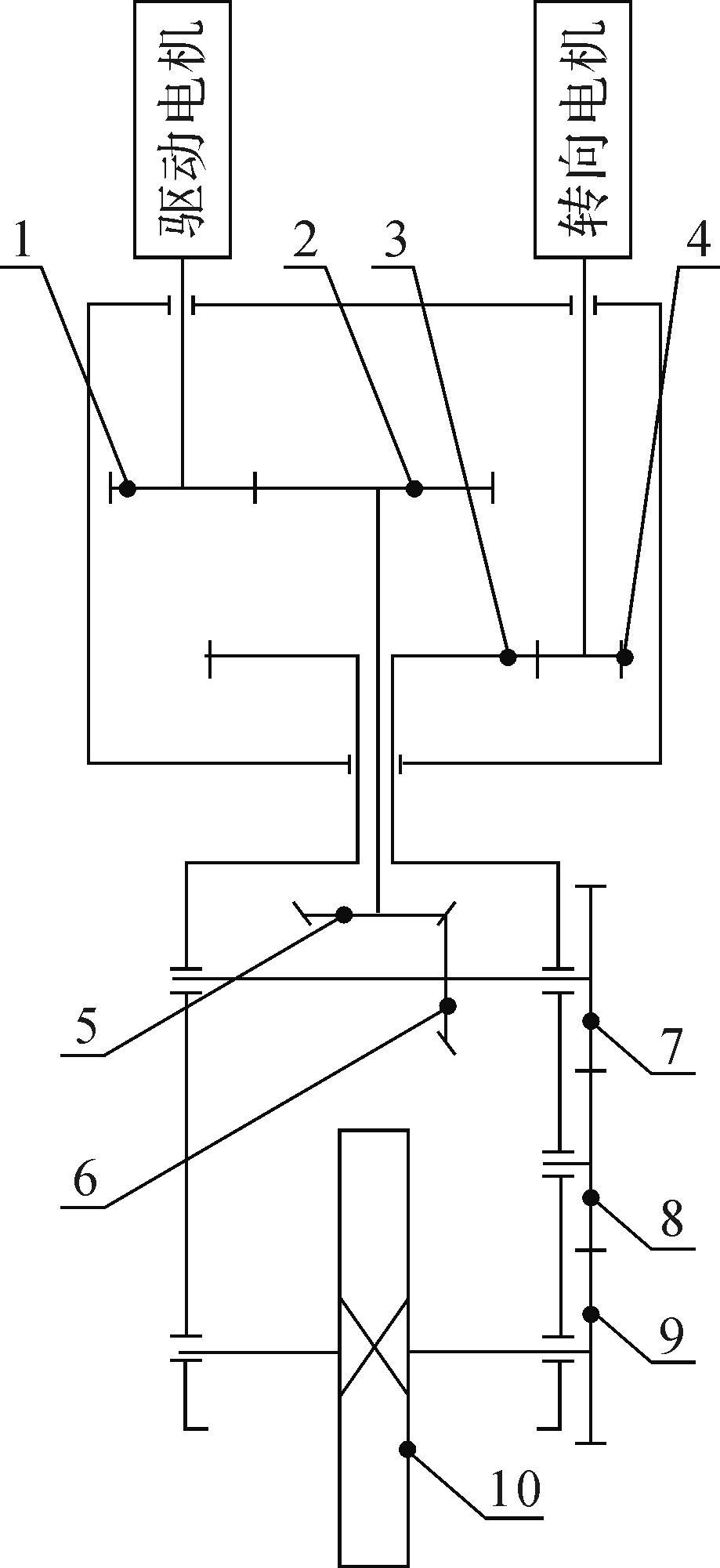
1 驱动万向轮结构设计

所要设计的驱动万向轮^[6-8]具有绕水平轮轴滚动和绕垂直轴转动的自由度, 通过2个电机分别给这2个方向的运动自由度提供动力, 只要控制这2个电机就可以实现对该万向轮的控制^[9-12].基本设计思路是:一个电机(称为驱动电机)通过传动系统把运动传递给滚轮, 使它滚动；另一个电机(称为转向电机)通过传动系统把运动传递给支撑框架, 使它带动滚轮实现转向运动^[13-15].其具体原理如图 1所示, 图中数字表示万向轮上各个齿轮和滚轮的标号.

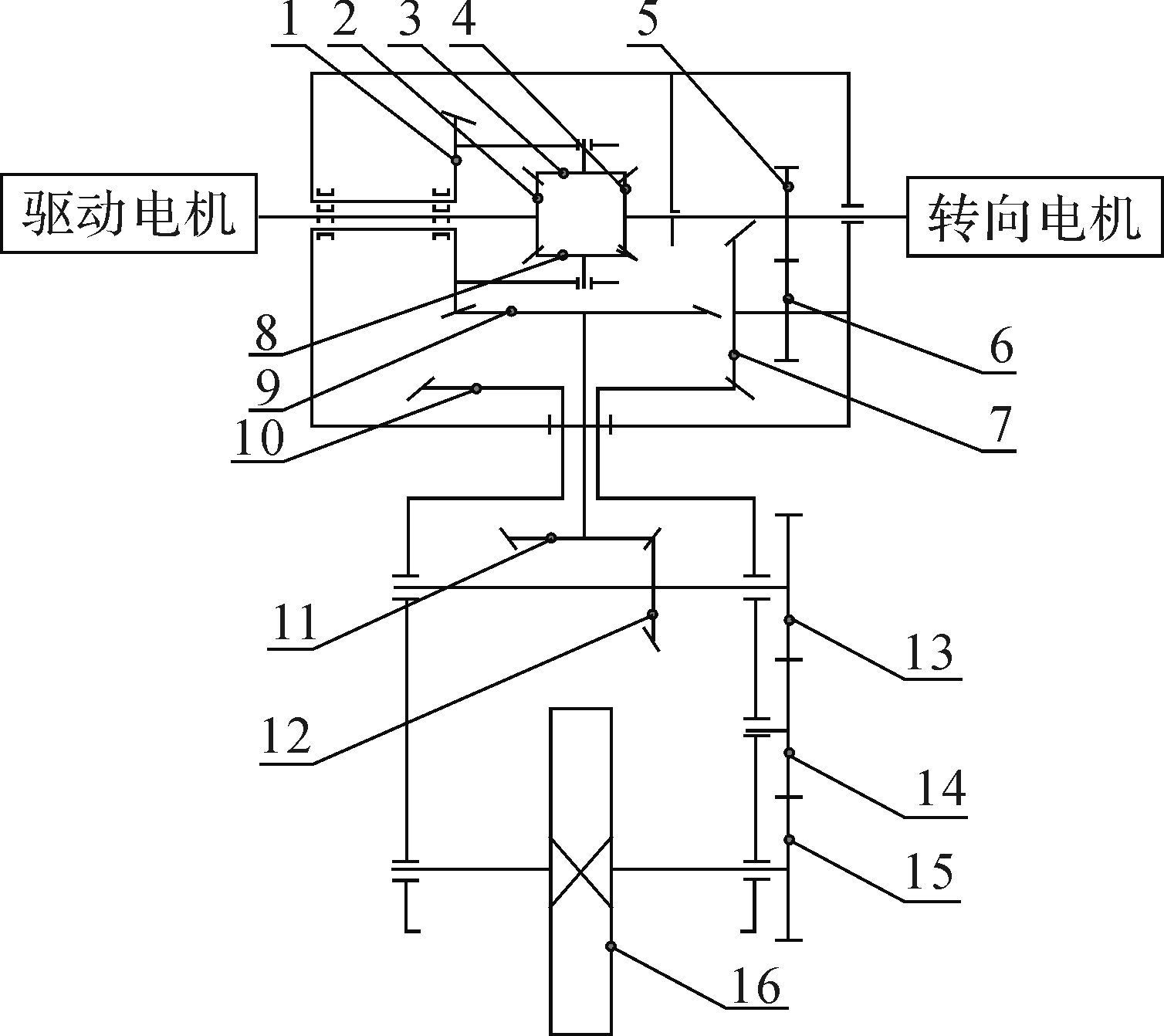
但此时会出现一个问题, 从图 1中可以看出齿轮6通过支撑轴安装在转向框架上, 转向电机通过传动齿轮带动滚轮绕垂直轴线转向时会使齿轮6在绕齿轮5转动的同时绕自身支撑轴旋转, 这样会使滚轮在转向时产生额外的滚动输出, 形成转向运动与滚动输出的运动耦合.这部分额外的滚轮运动将会造成驱动万向轮的运动不稳定, 并且将增加控制算法的复杂性, 使得整体协调控制难度加大.为了解决上述问题, 必须设法从结构设计上消除这部分额外的滚动输出.为此, 考虑在驱动传动系统和转向传动系统之间加入一个差速行星齿轮组, 利用该差速行星齿轮组具有的1个输入可以产生2个输出的特性, 使转向电机的运动分为2个部分:一部分通过传动系统带动滚轮转向, 另一部分通过传动系统带动滚轮转动, 这样只要这2个运动获得一定的匹配就可以把额外的滚动输出消除, 使得额外的滚动输出运动从转向运动中得到解耦.具体原理如图 2所示, 数字表示各个齿轮标号.

下面对驱动万向轮的运动解耦原理进行分析.此处设驱动电机的输入转速为n_d, 转向电机输入转速为n_s, 驱动电机通过传动系统传递给轮子的输出转速为n_dr, 转向电机通过传动系统传递给框架转向时的转速为n_sk, 由转向所引起的轮子额外转速为n_sr, 轮子最终的滚动转速为n_r.

其中各组齿轮传动比表示如下:

1) ${{i}_{19}}=\frac{{{z}_{9}}}{{{z}_{1}}},~{{z}_{9}}$表示齿轮9的齿数, z₁表示齿轮1的齿数;

2) ${{i}_{56}}=\frac{{{z}_{6}}}{{{z}_{5}}},~{{z}_{5}}$表示齿轮5的齿数, z₆表示齿轮6的齿数;

3) ${{i}_{710}}=\frac{{{z}_{10}}}{{{z}_{7}}},~{{z}_{7}}$表示齿轮7的齿数, z₁₀表示齿轮10的齿数;

4) ${{i}_{1112}}=\frac{{{z}_{12}}}{{{z}_{11}}},~{{z}_{11}}$表示齿轮11的齿数, z₁₂表示齿轮12的齿数;

5) ${{i}_{1315}}=\frac{{{z}_{15}}}{{{z}_{13}}},~{{z}_{13}}$表示齿轮13的齿数, z₁₅表示齿轮15的齿数;

6) ${{i}_{x}}=1+\frac{{{z}_{4}}}{{{z}_{2}}},~{{z}_{2}}$表示齿轮2的齿数, z₄表示齿轮4的齿数, i_x为差速行星齿轮组的传动比.

由此可得各转速如下:

${{n}_{r}}={{n}_{dr}}+{{n}_{sr}},$

(1)

${{n}_{sk}}=\frac{{{n}_{s}}}{{{i}_{56}}{{i}_{710}}},$

(2)

${{n}_{sr}}=-\frac{{{n}_{s}}}{{{i}_{1112}}{{i}_{1315}}{{i}_{56}}{{i}_{710}}}+\frac{{{n}_{s}}}{{{i}_{x}}{{i}_{19}}{{i}_{1112}}{{i}_{1315}}},$

(3)

${{n}_{dr}}=\frac{{{n}_{d}}}{{{i}_{x}}{{i}_{19}}{{i}_{1112}}{{i}_{1315}}},$

(4)

${{n}_{r}}=\frac{{{n}_{d}}}{{{i}_{x}}{{i}_{19}}{{i}_{1112}}{{i}_{1315}}}+(\frac{1}{{{i}_{x}}{{i}_{19}}{{i}_{1112}}{{i}_{1315}}}-\frac{1}{{{i}_{1112}}{{i}_{1315}}{{i}_{56}}{{i}_{710}}}){{n}_{s}}.$

(5)

由以上关系式可见, 只要合理设置各个齿轮的齿数使得关系式(6) 得到满足, 就可以消除转向电机对于轮子滚动输出的影响, 达到运动解耦的目的.

$\frac{1}{{{i}_{x}}{{i}_{19}}{{i}_{1112}}{{i}_{1315}}}-\frac{1}{{{i}_{1112}}{{i}_{1315}}{{i}_{56}}{{i}_{710}}}=0.$

(6)

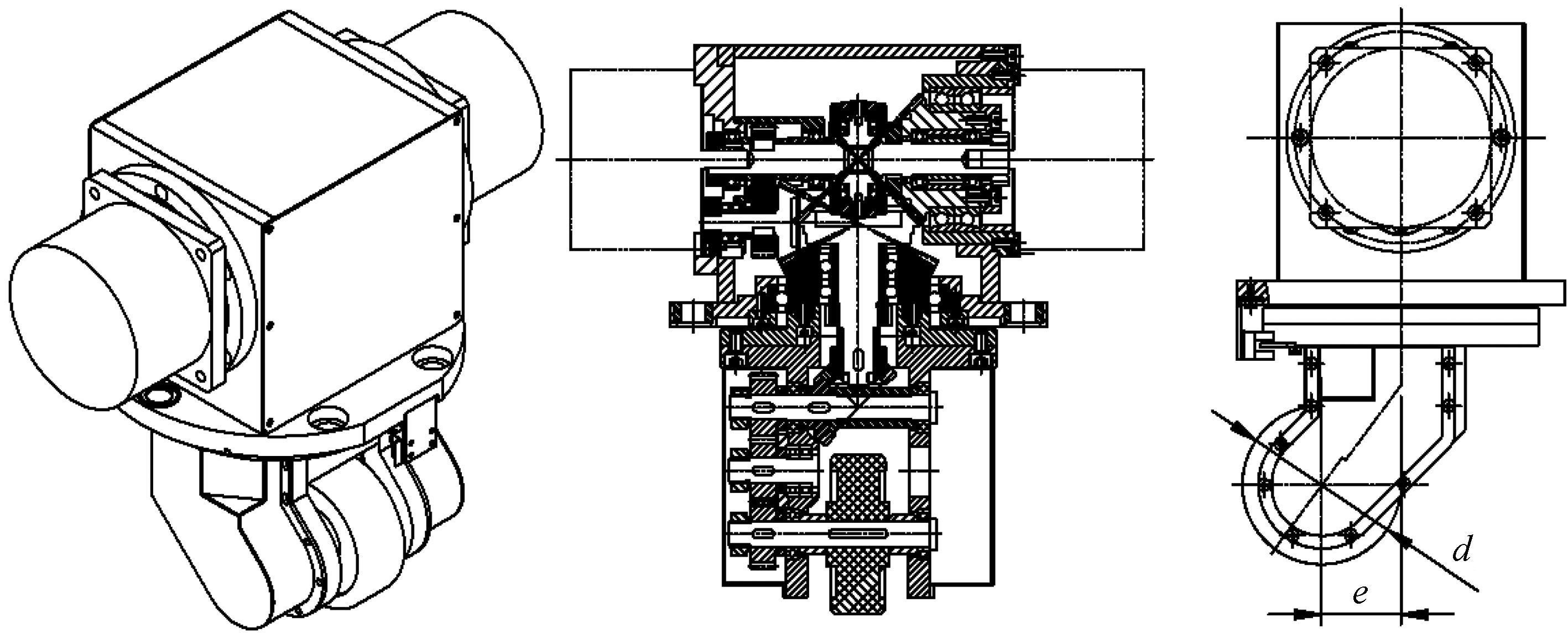
基于上述分析计算, 最终设计的驱动万向轮结构如图 3所示.这里所使用的滚轮直径为d, 材料为橡胶.为了增强万向轮的运动稳定性, 设置滚轮水平中心轴线与垂直轴线的偏置距离e=d/2.各齿轮的齿数分别设计如下:齿轮1为40齿, 齿轮2为13齿, 齿轮3为13齿, 齿轮4为13齿, 齿轮5为20齿, 齿轮6为20齿, 齿轮7为25齿, 齿轮8为13齿, 齿轮9为40齿, 齿轮10为50齿, 齿轮11为17齿, 齿轮12为17齿, 齿轮13为20齿, 齿轮15为20齿.将它们分别代入各传动比表达式以及式(6) 后可以得到$\frac{1}{2\times 1\times 1\times 1}-\frac{1}{1\times 1\times 1\times 2}=0$, 使得式(6) 的解耦条件得到满足.

2 全向移动机器人结构设计

在移动机器人本体上将驱动万向轮进行合理布局, 这里采用2个驱动万向轮和2个随动辅助万向轮的组合形式, 对角线对称布置, 最后设计形成的移动机器人的外形结构如图 4所示.

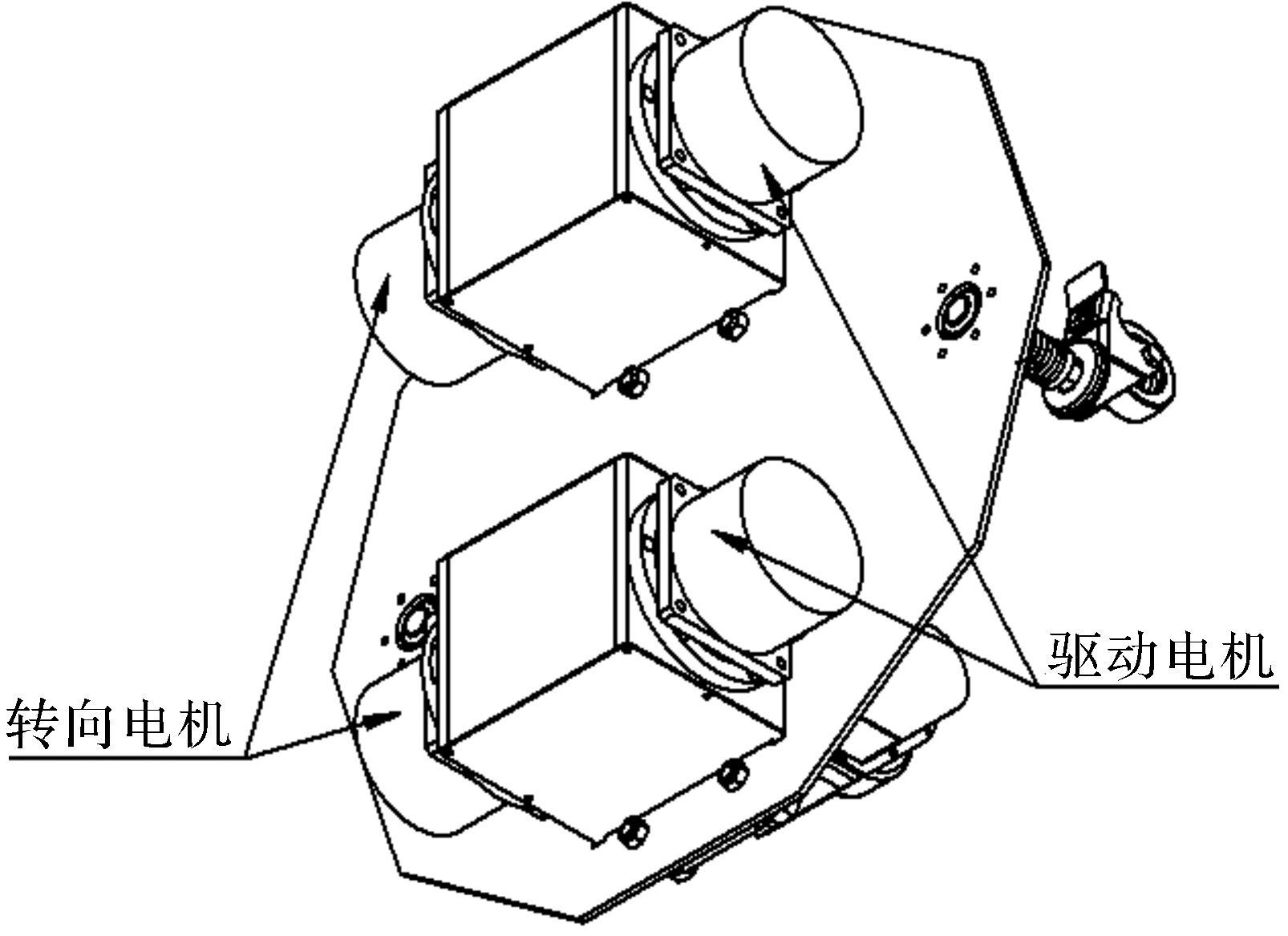
该全向移动机器人主要由本体、2个驱动万向轮、2个随动辅助万向轮以及连接本体和各个万向轮的悬架结构所组成.4个万向轮安装在本体底部并呈对角线对称布置, 保证整个机器人在执行直行、侧行、斜行、原地旋转等运动时的平稳性和可靠性.因底部采用了四轮布局方式, 所以本体与各个万向轮需要通过悬架连接在一起, 这样能保证机器人在凹凸不平的路面上平稳行走以及四轮同时着地, 通过悬架结构中的弹簧能有效减少和降低机器人在运行过程中的振动与噪音, 并能根据实时路况做到相应的自适应调节.其中驱动万向轮与本体的连接采用四点支撑、两点导向悬架, 随动辅助万向轮与本体连接采用单点支撑、单点导向悬架.整个机器人的运动由2个驱动万向轮的驱动电机(如图 5所示)通过传动系统来实现, 机器人的运行方向变换由安装在2个驱动万向轮上的转向电机(如图 5所示)通过传动系统来实现.因此, 我们可以对驱动万向轮上的各个电机作运动控制, 通过各电机的联动就可以实现整个机器人在不改变运动姿势的前提下实现直行、侧行、斜行、原地旋转等各种运动, 这样就实现了所要求的全向移动.

3 全向移动机器人运动学分析

如图 6所示, 建立移动机器人在平面内的位姿坐标系, 其中全局坐标为XOY, 固定在机器人上的局部坐标为X_ROY_R, P点为移动机器人的质心, θ为机器人的转动角度.因此, 该机器人在平面上的位姿可以表示为ξ=[x y θ]^T.假设机器人本体以及轮子是刚体, 所设计的全向移动机器人应用于室内环境, 通过上述结构设计使得每个轮子都与地面垂直, 每个轮子与地面只有1个接触点.因此, 当满足轮子与地面纯滚动和无相对滑动的条件时, 轮子与地面接触点处的速度为0, 即:该点在垂直于轮子平面方向的速度和沿着运动方向上的速度为0.由此得到轮子在纯滚动和无相对滑动的条件为^[16]:

$\left[ sin\text{ }\left( \alpha +\beta \right)\text{ }-cos\text{ }\left( \alpha +\beta \right)\text{ }-lcos\text{ }\beta \right]R\left( \theta \right)-r\dot{\rho }=0,$

(7)

$\left[ cos\text{ }\left( \alpha +\beta \right)\text{ }sin\text{ }\left( \alpha +\beta \right)\text{ }d+lsin\text{ }\beta \right]R\left( \theta \right)+e\dot{\beta }=0,$

(8)

$R\left( \theta \right)=\left[ \begin{matrix} cos\text{ }\theta & sin\text{ }\theta & 0 \\ -sin\text{ }\theta & cos\text{ }\theta & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$

(9)

式中:R(θ)为全局坐标系转化为机器人局部坐标系的变换矩阵；[l α]为各轮子在机器人本体上的支撑点在机器人坐标系中的极坐标位置；β为每个轮子相对于机器人本体的转向角度；e为万向轮水平轴线相对于垂直轴线的偏置距离； r为轮子半径；ρ为轮子滚动转过的角度；为机器人的运动速度,$\xi ={{\left[ \begin{matrix} {\dot{x}} & {\dot{y}} & {\dot{\theta }} \\ \end{matrix} \right]}^{T}}$为轮子转向角速度；${\dot{\rho }}$为轮子滚动的角速度.

所设计的全向移动机器人由4个万向轮组成, 它们的布局位置为对角线对称布置.由式(7) 和式(8) 可以得到移动机器人的运动学方程如下:

$\left[ \begin{array}{*{35}{l}} {{{\dot{\rho }}}_{1}} \\ {{{\dot{\rho }}}_{2}} \\ {{{\dot{\rho }}}_{3}} \\ {{{\dot{\rho }}}_{4}} \\ {{{\dot{\beta }}}_{1}} \\ \begin{align} & {{{\dot{\beta }}}_{2}} \\ & {{{\dot{\beta }}}_{3}} \\ \end{align} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} -sin\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/r & cos\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/r & l/rcos\text{ }{{\beta }_{1}} \\ -sin\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/r & cos\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/r & l/rcos\text{ }{{\beta }_{2}} \\ -sin\text{ }({{\alpha }_{3}}+{{\beta }_{3}}+\theta )/r & cos\text{ }({{\alpha }_{3}}+{{\beta }_{3}}+\theta )/r & l/rcos\text{ }{{\beta }_{3}} \\ -sin\text{ }({{\alpha }_{4}}+{{\beta }_{4}}+\theta )/r & cos\text{ }({{\alpha }_{4}}+{{\beta }_{4}}+\theta )/r & l/rcos\text{ }{{\beta }_{4}} \\ cos\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/e & sin\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/e & 1+l/esin\text{ }{{\beta }_{1}} \\ cos\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/e & sin\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/e & 1+l/esin\text{ }{{\beta }_{2}} \\ cos\text{ }({{\alpha }_{3}}+{{\beta }_{3}}+\theta )/e & sin\text{ }({{\alpha }_{3}}+{{\beta }_{3}}+\theta )/e & 1+l/esin\text{ }{{\beta }_{3}} \\ cos\text{ }({{\alpha }_{4}}+{{\beta }_{4}}+\theta )/e & sin\text{ }({{\alpha }_{4}}+{{\beta }_{4}}+\theta )/e & 1+l/esin\text{ }{{\beta }_{4}} \\ \end{array} \right]\left[ \begin{matrix} {\dot{x}} \\ {\dot{y}} \\ {\dot{\theta }} \\ \end{matrix} \right].$

(10)

由以上关系式可见, 该移动机器人有3个运动自由度, 每个万向轮具有2个驱动关节, 通过选择一组驱动轮控制关节的组合, 控制4个或4个以上的运动自由度就可以使得雅克比矩阵^[17-18]的行列式不为零, 避免机器人奇异位姿的产生.这里选取2个驱动万向轮和2个随动辅助万向轮的形式, 分别控制ρ₁,ρ₂,β₁, β₂.通过把驱动万向轮的驱动电机输入转速和转向电机的输入转速代入关系式(10) , 可得电机输入转速[n_s n_d]和机器人运动速度$\xi ={{\left[ \begin{matrix} {\dot{x}} & {\dot{y}} & {\dot{\theta }} \\ \end{matrix} \right]}^{T}}$的关系式, 如式(11) 所示.

$\left[ \begin{array}{*{35}{l}} {{n}_{d1}} \\ {{n}_{s1}} \\ {{n}_{d2}} \\ {{n}_{s2}} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} -{{i}_{d}}sin\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/r & {{i}_{d}}cos\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/r & {{i}_{d}}l/rcos\text{ }{{\beta }_{1}} \\ -{{i}_{s}}cos\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/e & {{i}_{s}}sin\text{ }({{\alpha }_{1}}+{{\beta }_{1}}+\theta )/e & {{i}_{s}}+{{i}_{s}}l/esin\text{ }{{\beta }_{1}} \\ -{{i}_{d}}sin\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/r & {{i}_{d}}cos\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/r & {{i}_{d}}l/rcos\text{ }{{\beta }_{2}} \\ -{{i}_{s}}cos\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/e & {{i}_{s}}sin\text{ }({{\alpha }_{2}}+{{\beta }_{2}}+\theta )/e & {{i}_{s}}+{{i}_{s}}l/esin\text{ }{{\beta }_{2}} \\ \end{array} \right]\left[ \begin{matrix} {\dot{x}} \\ {\dot{y}} \\ {\dot{\theta }} \\ \end{matrix} \right].$

(11)

式中i_s,i_d为驱动万向轮内部转向和驱动传动系统传动比.

由式(11) 可见, 对于要求的移动机器人的任意运动速度$\xi ={{\left[ \begin{matrix} {\dot{x}} & {\dot{y}} & {\dot{\theta }} \\ \end{matrix} \right]}^{T}}$都可以通过控制驱动万向轮的驱动电机转速和转向电机转速来实现, 为移动机器人的运动控制提供了依据.

4 结论

基于驱动万向轮设计了一种全新的全向移动机器人.其中所设计的驱动万向轮可以提供连续顺滑的运动, 使得机器人在不改变自身姿态的情况下可以沿平面内任意方向运动, 真正实现了全向移动.同时利用差速行星齿轮机构对驱动万向轮在转向时所引起的轮子额外滚动运动进行解耦, 使得驱动万向轮在转向时无额外的轮子滚动输出, 这样保证了控制精度, 提高了机器人运动稳定性.最后, 通过建立移动机器人的运动学模型, 分析得到了控制电机输入转速与机器人运动速度之间的关系, 验证了机器人所具备的全向移动功能以及驱动轮的正确设置方式, 并为机器人运动控制提供了依据.