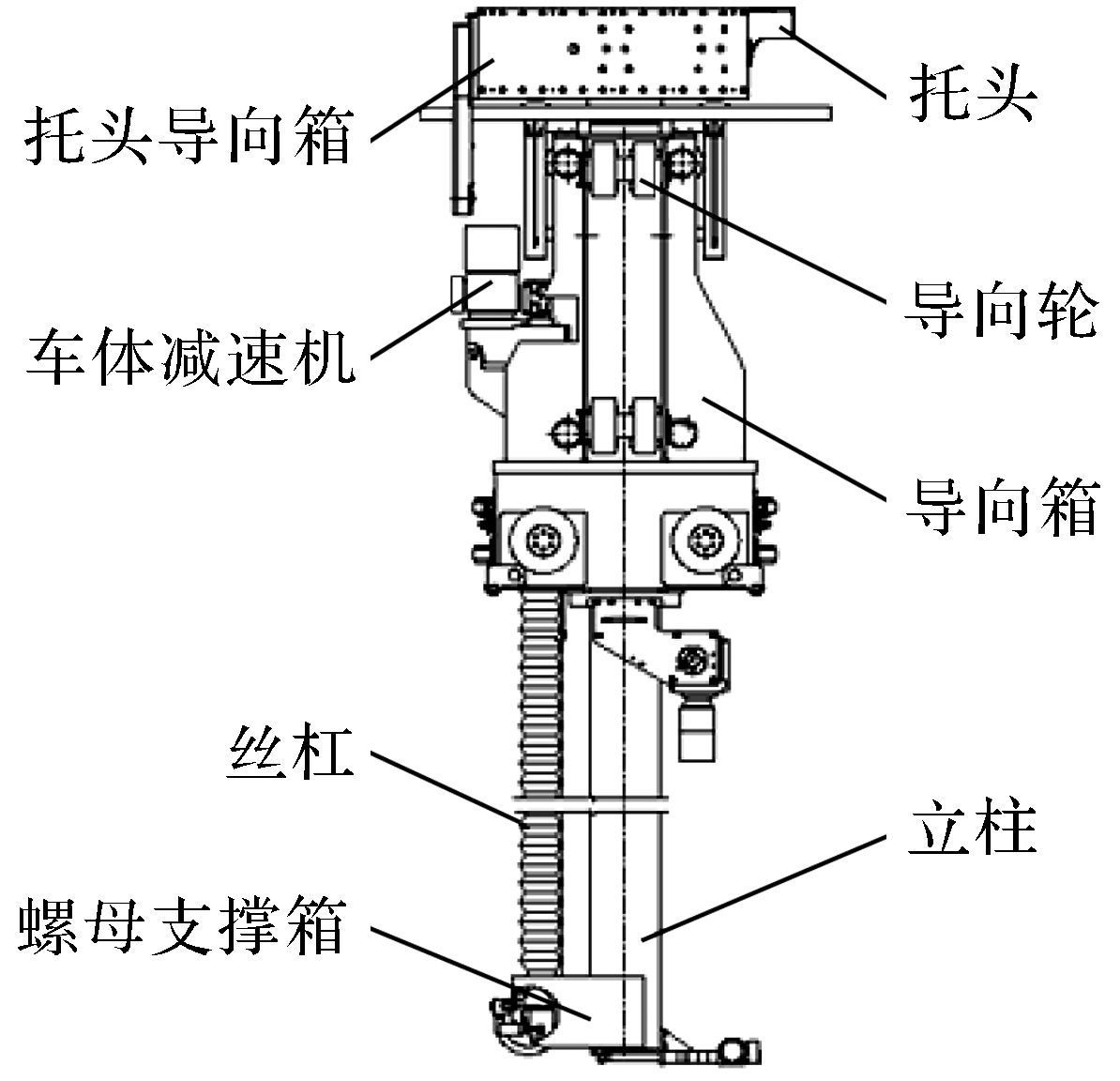
地坑式架车机作为动车组三级修程中必备的大型关键设备之一, 主要用于举升动车组、更换转向架和对底部进行维修[1-4].图 1为车体举升单元结构示意图, 其工作原理为:立柱底部与螺母支撑箱连接, 通过电机带动丝杠, 利用丝杠和螺母的螺旋传动带动立柱垂直运动从而举升车体.
作为大型检修设备, 地坑式架车机整体结构非常复杂, 整个16编组地坑式架车机总重达1 000 t[5].当前, 国内厂家对架车机结构件的设计依赖于经验, 且没有统一的设计规范, 校核计算主要参考《起重机设计规范》.为安全起见, 结构强度等性能参数所留余量较大, 因此有必要对各结构件进行优化.
|
| 图 1 车体举升单元结构示意图 Fig.1 The structure diagram of lifting unit |
由于结构复杂, 传统有限元优化设计计算成本太大, 本文采用多学科设计优化软件ISIGHT, 对参数进行灵敏度分析, 并将近似模型技术应用于优化设计中, 探究出适用于地坑式架车机的结构优化方法.
1 整机优化模型的建立 1.1 设计变量以某研究所研制的地坑式架车机为例, 对图 1中的立柱、螺母支撑箱及导向箱等主要结构进行优化设计.该架车机最大举升高度为2.7 m, 额定举升重量Q=1.7×105 N[6], 考虑偏载等情况, 取载荷放大系数ψ=1.4, 故计算载荷F=1.4×1.7×105 N=2.38×105 N.各部件材料均为Q345, 材料许用应力[σ]=275 MPa[7].为保证机构各零部件与结构件的连接位置不变, 只对各结构件的板厚进行优化,具体设计变量如表 1所示.
| 设计变量 | 变量含义 | 变量范围/mm |
| x1 | 立柱上半截板厚 | 30≤x1≤50 |
| x2 | 立柱下半截板厚 | 6≤x2≤26 |
| x3 | 立柱底部板厚 | 5≤x3≤25 |
| x4 | 立柱中部横隔板厚度 | 10≤x4≤30 |
| x5 | 立柱与螺母支撑箱连接处板厚 | 26≤x5≤46 |
| x6 | 螺母支撑箱板厚 | 10≤x6≤30 |
| x7 | 导向箱顶部板厚 | 5≤x7≤25 |
| x8 | 导向箱中部板厚 | 5≤x8≤25 |
| x9 | 导向箱下部前侧板厚 | 5≤x9≤25 |
| x10 | 导向箱下部后侧板厚 | 10≤x10≤30 |
| x11 | 导向箱中部肋板厚 | 5≤x11≤25 |
为减轻结构自重, 达到轻量化设计的目的, 以地坑式架车机结构系统的质量为优化设计目标, 即
| $\text{min }F\left( x \right)=T\_\text{MASS},$ | (1) |
式中T_MASS为架车机结构自重.
1.3 约束条件1) 静强度约束为
| ${{g}_{1}}\left( x \right)=SG\le \left[ \sigma \right],\text{ }$ | (2) |
式中:SG为架车机在工作状态下的最大等效应力, [σ]=275 MPa.
2) 静刚度约束为
| ${{g}_{2}}\left( x \right)=DG\le 10\text{ mm},$ | (3) |
式中DG为架车机工作状态下最大垂直静挠度, 根据设计要求, 最大值不超过10 mm.
3) 设计变量上下限约束为
| ${{x}^{l}}\le {{x}_{i}}\le {{x}^{u}},\text{ }i=1,\text{ }2,\text{ }\ldots .$ | (4) |
式中xu, xl为设计变量上、下限, 具体见表 1.
1.4 有限元模型对架车机结构进行部分简化, 利用ANSYS中的APDL语言建立整机的有限元参数化模型, 如图 2所示.其中, 托头、滑块、滑轨等构件以及较厚板采用SOLID45单元模拟, 其余板结构用SHELL63单元模拟, 弹性模量 Ex=2.1×1011 N/m2, 泊松比μ=0.3, 材料密度ρ=7 850 kg/m3.

|
| 图 2 地坑式架车机有限元模型 Fig.2 The finite element model of underfloor lifting system |
ISIGHT软件是一款先进的基于参数的多学科设计优化软件[8-9], 其主要优势是将优化方法、数值计算等技术有机结合, 使设计流程集成化、自动化、最优化, 从而大大提高优化设计效率.
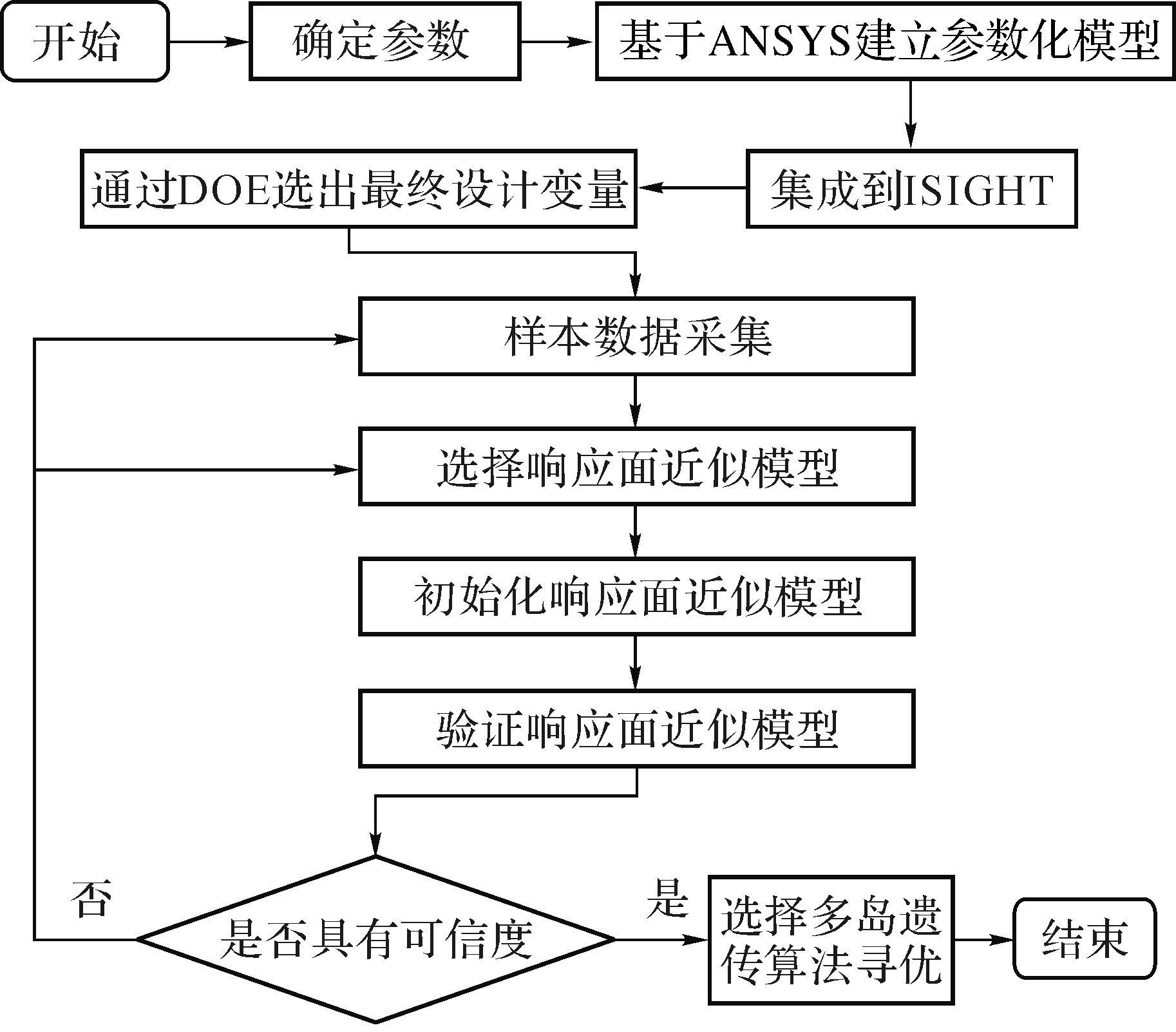
通过将基于ANSYS建立的参数化模型集成到ISIGHT中, 利用试验设计方法(design of experiments, DOE)选出对约束条件和目标函数影响较大的设计变量, 并建立响应面模型, 以结构自重为目标函数建立优化模型, 并利用多岛遗传算法(multi-is land genetic algorithm, MIGA)对模型进行优化.架车机轻量化设计的具体流程如图 3所示.
|
| 图 3 架车机轻量化设计流程图 Fig.3 The flow chart of lightweight design for underfloor lifting system |
由于设计变量较多, 为了减少部分次要变量以提高优化效率, 采用ISIGHT软件中的DOE模块分析各设计变量对约束条件和目标函数的灵敏度, 然后利用最优拉丁超立方试验设计方法来获得最终设计变量.最优拉丁超立方设计通过改进随机拉丁超立方设计的均匀性, 使因子和响应的拟合更加精确真实.最优拉丁超立方设计使试验点尽可能均匀地分布于设计空间, 具有很好的空间填充性与均衡性.
最优拉丁超立方试验设计法是在[0,1] 之间选取样本点, 所以必须根据设计变量的取值范围来确定样本点的实际值, 其转换关系如下:
| ${{P}_{i}}={{P}_{\text{max}}}-{{P}_{\text{min}}}{{R}_{i}}+{{P}_{\text{min}}},$ | (5) |
式中:Pi为设计变量的实际样本点;Pmax和Pmin分别为取值范围的最大值与最小值;Ri为最优拉丁超立方采样法选取的样本点[10].
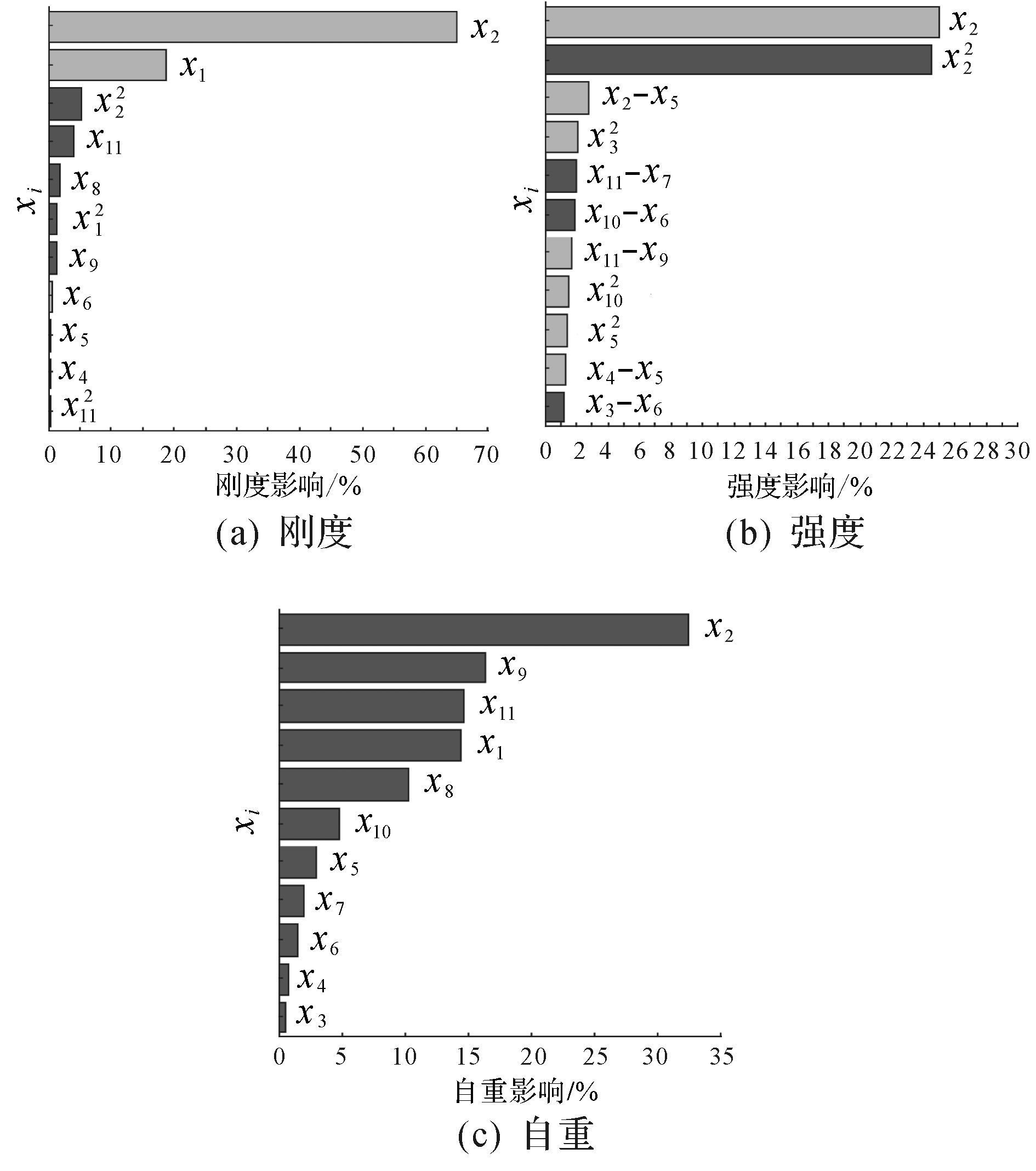
选择最优拉丁超立方设计法, 选取150个样本点进行计算, DOE试验结果如图 4所示.
|
| 图 4 设计变量对结构刚度、强度、自重的Pareto图 Fig.4 The Pareto diagram of design variables for the structural stiffness, strength and weight |
图 4中x12, x22, x32, x102, x112分别为x1, x2, x3, x10, x11的二次项;x1-x5, x11-x7, x10-x6, x11-x9, x4-x5, x3-x6为交叉项.从图 4可以看出, 设计变量x1, x2对刚度影响较大, 设计变量x2对强度影响最大, 设计变量x1, x2, x5, x8, x9,x10,x11对质量影响较大.综合考虑, 选取x1, x2, x5, x8,x9,x10,x11为设计变量, 从而减小设计变量空间, 提高优化效率.
2.2 响应面近似模型构造近似模型技术是利用数学模型的方法逼近一组输入变量与输出变量的方法.通过近似模型方法, 能极大地提高优化算法的寻优速度.由于响应面法能利用较少的试验获得比较精确的逼近函数关系, 计算简单, 并且拥有很好的鲁棒性, 本文将采用响应面模型来构造地坑式架车机的近似模型.
响应面法主要利用多项式函数对设计空间进行拟合, 可表示为模拟响应变量(x)与输入变量xi之间的近似函数关系[11].对于工程计算, 二阶多项式响应面函数即可满足精度要求[12-13], 其表达式为
| $\tilde{y}\left( x \right)={{a}_{0}}+\sum\limits_{i=1}^{N}{{{b}_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{N}{{{c}_{ii}}{{x}_{i}}^{2}}+\sum\limits_{ij(i <j)}^{N}{{{c}_{ij}}{{x}_{i}}{{x}_{j}}},$ | (6) |
式中:N为模型的输入变量个数;xi为输入变量;a, b, c为响应面多项式的待定系数.
对于待定系数的计算, 是通过将待定系数组成一个列矩阵β, 并通过最小二乘法得到系数矩阵[14-15]:
| $\beta ={{({{X}^{T}}X)}^{-1}}({{X}^{T}}Y),\text{ }$ | (7) |
式中, X为响应面样本点矢量, Y为样本点对应的响应矢量, 具体可表示为如下:
| $X=\left[ \begin{array}{*{35}{l}} 1 & {{X}_{1,\text{ }1}} & {{X}_{1,\text{ }2}} & \ldots & {{X}_{1,\text{ }N}} \\ 1 & {{X}_{2,\text{ }1}} & {{X}_{2,\text{ }2}} & \ldots & {{X}_{2,\text{ }N}} \\ \vdots & \vdots & \vdots & {} & \vdots \\ 1 & {{X}_{M,\text{ }1}} & {{X}_{M,\text{ }2}} & \ldots & {{X}_{M,\text{ }N}} \\ \end{array} \right],Y=\left[ \begin{array}{*{35}{l}} {{Y}_{1}} \\ {{Y}_{2}} \\ \vdots \\ {{Y}_{M}} \\ \end{array} \right].$ | (8) |
将式(8) 代入式(7) 中即可求出响应面函数的系数矩阵β, 从而得到具体的响应面函数表达式.
选择DG, SG和T_MASS为输出响应, 通过选取150个模型样本点和20个误差分析样本点, 利用ISIGHT软件中的误差分析模块对建立的响应面模型进行误差分析, 其结果如表 2所示, 各项误差指标均在允许范围内, 表明该近似模型可信度较高, 可以代替仿真程序进行优化设计.
| 输出响应 | R2误差(>0.9) | 均方根值(<0.2) | 平均误差(<0.2) | 最大误差(<0.3) |
| DG | 1 | 2.08×10-8 | 1.86×10-8 | 3.37×10-8 |
| SG | 0.999 5 | 0.002 72 | 0.002 27 | 0.005 23 |
| T_MASS | 0.999 6 | 0.002 01 | 0.001 62 | 0.003 76 |
传统优化算法经常收敛于局部最优解, 导致寻优不彻底, 而ISIGHT软件提供了全局优化算法——多岛遗传算法(MIGA).该算法改进了传统遗传算法进行优化设计时容易陷入早熟的缺陷.MIGA将进化种群划分成若干个子种群, 在子种群中独立地进行遗传算法的选择、交叉、变异等操作, 从而有效抑制早熟现象[16-17].作为一种伪并行遗传算法, MIGA能够更好地在优化域中寻找全局最优解, 使优化过程更高效和精确.因此, 本文采用MIGA进行全局寻优.
在实际生产中, 由于钢材厚度为离散整数, 因此, 在优化过程中对涉及板厚的设计参数进行离散化处理[18].
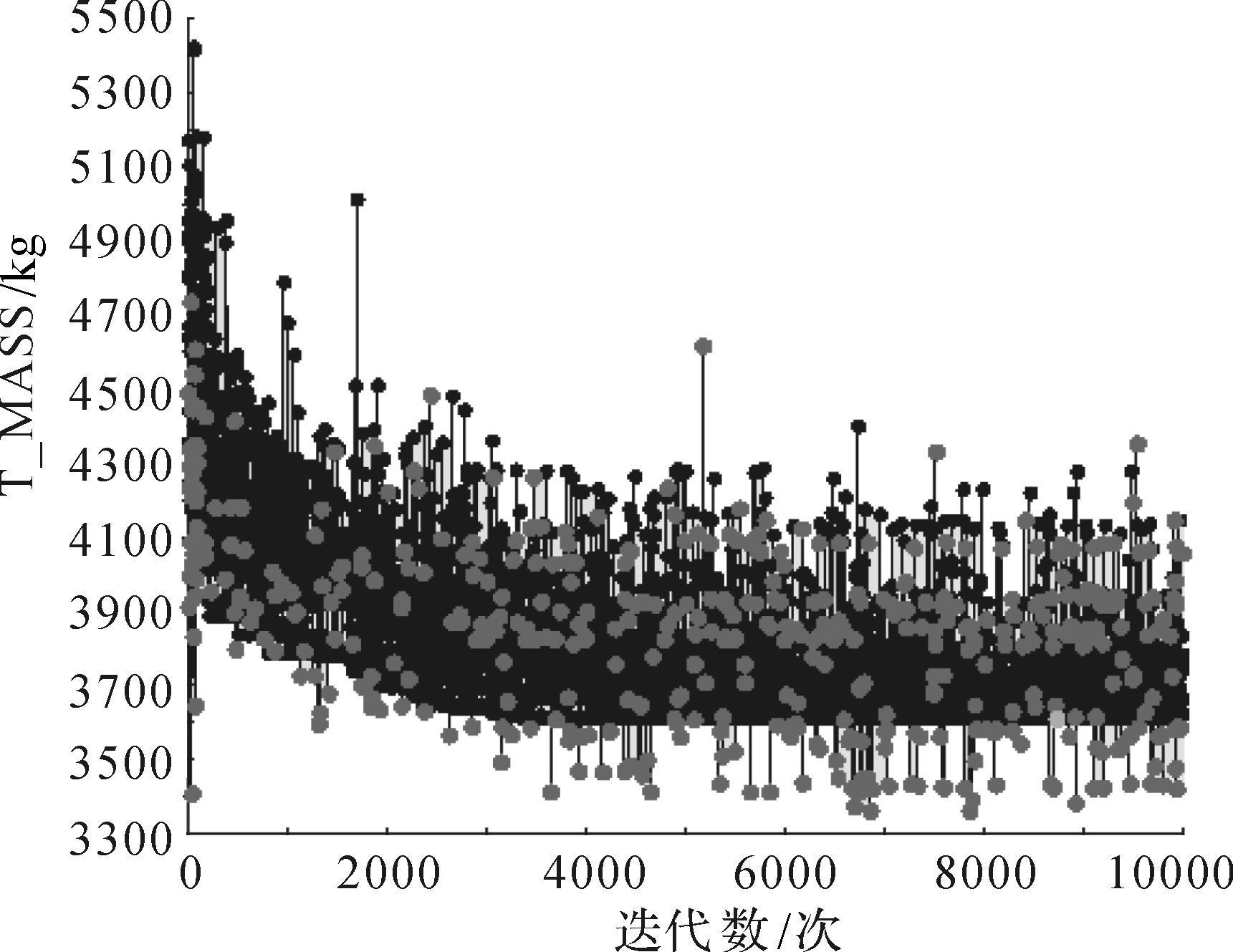
在本文的优化设计中, 子群规模设定为10, 子群数为10, 总进化代数为100, 交叉概率Pc=0.8, 变异概率Pm=0.08.目标函数的迭代寻优历程如图 5所示, 各设计变量、状态变量及目标函数优化前后对比如表 3所示.
|
| 图 5 目标函数寻优历程 Fig.5 Objective function optimization process |
| 参数 | 初始值 | 优化值 |
| x1/mm | 40 | 30 |
| x2/mm | 16 | 13 |
| x5/mm | 36 | 26 |
| x8/mm | 15 | 5 |
| x9/mm | 15 | 5 |
| x10/mm | 20 | 10 |
| x11/mm | 15 | 5 |
| DG/mm | 4.45 | 4.99 |
| SG/MPa | 212.51 | 244.32 |
| T_MASS/kg | 4 534.29 | 3 598.19 |
从优化结果可以看出, 各个设计变量的值均有所减小, 而应力和位移有所增大, 但在允许范围内, 结构自重明显降低.
为验证基于响应面近似模型的优化设计结果的准确性, 将优化后各设计变量的值代入有限元模型, 利用ANSYS对其进行有限元分析.仿真结果如图 6和图 7所示.

|
| 图 6 优化后架车机等效应力图 Fig.6 The Von Mises stress diagram of lifting system after optimization |
|
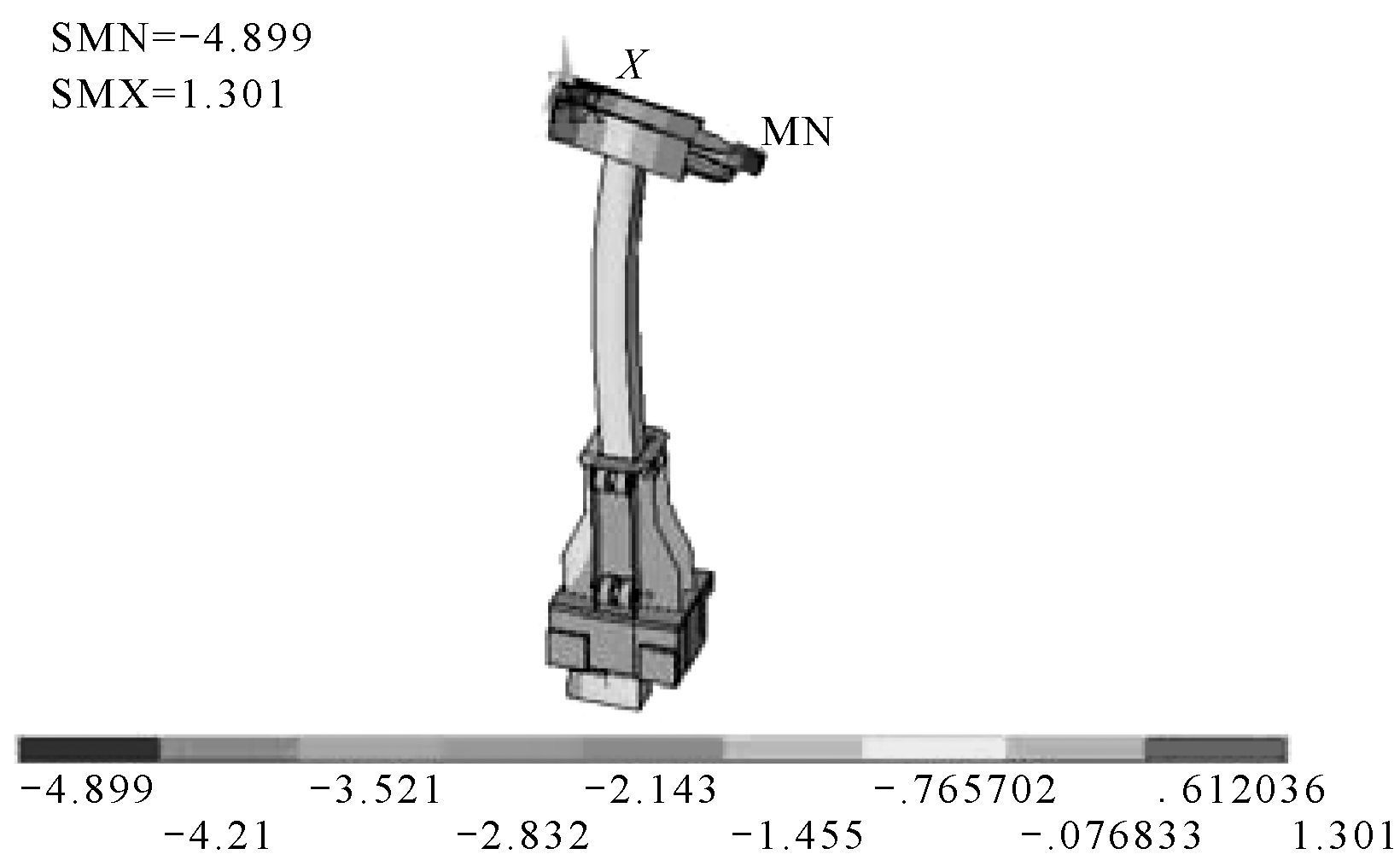
| 图 7 优化后架车机位移等值线图 Fig.7 The displacement contour diagram of lifting system after optimization |
结果表明, 优化后架车机最大等效应力为256.48 MPa, 垂直方向最大位移为4.899 mm, 均小于许用值, 与响应面近似模型优化结果(表 3) 相比, 误差分别为4.7%, 1.8%.优化后架车机结构自重为3 598.19 kg, 相较于原自重减少了20.64%, 优化效果显著.
3 结论1) 利用最优拉丁超立方设计法对设计变量进行灵敏度分析, 通过减少设计变量的数量, 有效提高优化效率.
2) 将响应面近似模型法引入地坑式架车机结构轻量化设计中, 大大缩减计算时间, 显著提高优化设计效率.
3) 通过多学科优化软件ISIGHT和ANSYS的集成, 利用多岛遗传算法对地坑式架车机进行优化, 使结构自重减少20.64%, 验证了此方法的可行性, 为地坑式架车机的结构设计和改进提供参考依据, 具有较强的理论与实际意义.
| [1] |
丁辉, 王明海.
CHR动车组地坑式架车机的研究与设计[J]. 电力机车与城轨车辆 , 2011, 34 (2) : 19–21.
DING Hui, WANG Ming-hai. Research and design of CRH EMU underfloor lifting system[J]. Electric Locomotives and Urban Rail Vehicle , 2011, 34 (2) : 19–21. |
| [2] |
喻贵忠, 刘广丹, 吕安庶, 等.
国产动车组新颖架车机[J]. 机车电传动 , 2010 (3) : 37–41.
YU Gui-zhong, LIU Guang-dan, LÜ An-shu, et al. Domestic EMU new lifting system[J]. Electric Drive for Locomotives , 2010 (3) : 37–41. |
| [3] |
缪东.
固定式架车机在地铁车辆段中应用实践[J]. 铁道工程学报 , 2008 (10) : 92–96.
MIAO Dong. The application and practice of stationary frame machine in metro car depot[J]. Journal of Railway Engineering Society , 2008 (10) : 92–96. |
| [4] |
黎英豪, 刘广丹, 喻贵忠.
高速动车组的新颖地坑式架车机[J]. 铁道机车车辆 , 2010, 30 (4) : 72–76.
LI Ying-hao, LIU Guang-dan, YU Gui-zhong. High speed CRH novel pit cars transferring machine[J]. Railway Locomotive & Car , 2010, 30 (4) : 72–76. |
| [5] |
张树申, 刘广丹, 喻贵忠, 等.
轨道交通车组检修用新颖地坑式架车机[J]. 现代城市轨道交通 , 2010 (5) : 5–8.
ZHANG Shu-shen, LIU Guang-dan, YU Gui-zhong, et al. Novel underfloor lifting system for rail traffic vehicle maintenance[J]. Modern Urban Transit , 2010 (5) : 5–8. |
| [6] |
丁辉, 邢晓东.
整列地坑式架车机在我国高速列车检修中的运用[J]. 机车电传动 , 2011 (2) : 31–33.
DING Hui, XING Xiao-dong. The entire column underfloor lifting system in the maintenance of high-speed trains in China[J]. Electric Drive for Locomotives , 2011 (2) : 31–33. |
| [7] |
王金诺, 于兰峰.
起重运输机械金属结构[M]. 北京: 中国铁道出版社 ,2002 : 43 -47.
WANG Jin-nuo, YU Lan-feng. Hoisting and conveying machinery metal structure[M]. Beijing: China Railway Press , 2002 : 43 -47. |
| [8] |
赖宇阳.
Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社 ,2012 : 3 -7.
LAI Yu-yang. Parameter optimization theory and examples of Isight[M]. Beijing: Beihang University Press , 2012 : 3 -7. |
| [9] |
聂勇军, 廖启征.
基于ISIGHT的桁架结构优化设计[J]. 煤矿机械 , 2011, 32 (2) : 32–34.
NIE Yong-jun, LIAO Qi-zheng. Optimization design of truss structure based on ISIGHT[J]. Coal Mine Machinery , 2011, 32 (2) : 32–34. |
| [10] |
文桂林, 崔中, 彭克立.
基于近似模型的高速磨床零部件结构优化设计研究[J]. 中国机械工程 , 2009, 20 (8) : 906–910.
WEN Gui-lin, CUI Zhong, PENG Ke-li. Research on structure optimization of high speed grinding machine based on approximate model[J]. China Mechanical Engineering , 2009, 20 (8) : 906–910. |
| [11] |
王志龙. 桁架式桥梁检测车臂架系统结构分析及优化设计[D]. 成都:西南交通大学机械工程学院,2011:53-54.
WANG Zhi-long. Structural analysis and optimum design of truss structure bridge inspecting vehicle[D]. Chengdu:Southwest Jiaotong University, College of Mechanical Engineering, 2011:53-54. |
| [12] |
里超. 连续卸船机结构系统可靠性分析及优化设计[D]. 成都:西南交通大学机械工程学院,2011:12-13.
LI Chao. Reliability analysis and optimum design of continuous ship unloading machine[D].Chengdu:Southwest Jiaotong University, College of Mechanical Engineering,2011:12-13. |
| [13] |
唐辉, 于兰峰, 严飞, 等.
L型门式起重机主梁非概率可靠性分析[J]. 矿山机械 , 2015, 43 (11) : 59–62.
TANG Hui, YU Lan-feng, YAN Fei, et al. Non-probability reliability analysis on girder of L-typed gantry crane[J]. Mining & Processing Equipment , 2015, 43 (11) : 59–62. |
| [14] |
吕辉, 于德介, 谢展, 等.
基于响应面法的汽车盘式制动器稳定性优化设计[J]. 机械工程学报 , 2013, 49 (9) : 55–60.
LÜ Hui, YU De-jie, XIE Zhan, et al. Optimization design of vehicle disc brake stability based on response surface methodology[J]. Journal of Mechanical Engineering , 2013, 49 (9) : 55–60. DOI:10.3901/JME.2013.09.055 |
| [15] |
廖兴涛, 张维刚, 李青, 等.
响应表面法在薄壁构件耐撞性优化设计中的应用研究[J]. 工程设计学报 , 2006, 13 (5) : 298–302.
LIAO Xing-tao, ZHANG Wei-gang, LI Qing, et al. Application of response surface method in optimization design of thin-walled component[J]. Chinese Journal of Engineering Design , 2006, 13 (5) : 298–302. |
| [16] |
张俊红, 朱传峰, 毕凤荣, 等.
基于DOE和MIGA的消声器优化设计[J]. 机械科学与技术 , 2016, 35 (2) : 296–302.
ZHANG Jun-hong, ZHU Chuan-feng, BI Feng-rong, et al. Optimization design of muffler based on DOE and MIGA[J]. Mechanical Science and Technology for Aerospace Engineering , 2016, 35 (2) : 296–302. |
| [17] |
赵志国, 司传胜.
基于多岛遗传算法的铰接车轮边减速器优化设计[J]. 机械设计与制造 , 2010 (12) : 213–215.
ZHAO Zhi-guo, SI Chuan-sheng. Optimization design of articulated wheel side reducer based on multi Island genetic algorithm[J]. Mechanical Design and Manufacturing , 2010 (12) : 213–215. |
| [18] |
朱小龙, 于兰峰, 郭俊才, 等.
基于ANSYS和ISIGHT的桥式起重机主梁结构轻量化设计[J]. 矿山机械 , 2012, 40 (7) : 52–55.
ZHU Xiao-long, YU Lan-feng, GUO Jun-cai, et al. Lightweight design on girder of bridge crane based on ANSYS and ISIGHT[J]. Mining & Processing Equipment , 2012, 40 (7) : 52–55. |



