汽车轻量化对汽车节油、降低排放、改善性能及促进汽车产业健康发展都具有重要意义, 是当今汽车研究领域的一项重要内容.汽车轻量化是在保证汽车强度和安全性能的前提下, 尽可能地降低汽车的整备质量.目前结构的轻量化大多是通过采用一些轻质合金材料、高强钢或者新型复合材料替代当下常用的钢铁材料来实现.在这些材料中, 由于碳纤维增强复合材料(CFRP)具有高强度、高刚度以及高阻尼等特性, 越来越多地被应用于结构的轻量化设计中[1].当前CFRP多用于承载不大的内外饰部件, 例如底护板、车顶盖、后背门等[2], 而用于关键承载部件的设计则处于探索阶段, 与此相关的结构设计方法有待进一步发展.
悬架控制臂作为连接车轮与车身的主要部件, 直接影响到悬架系统的性能以及整车平顺性和操纵稳定性[3].悬架控制臂的刚度对车轮的外倾和前束等参数的稳定有很大影响, 因而控制臂的刚度成为考核控制臂设计优劣的关键参数之一[4].同时, 悬架控制臂在车辆行驶过程中承受着各种激励, 其固有频率对于悬架控制臂结构的动态特性至关重要, 是评价结构动态性能的主要参数.因此, 在对悬架控制臂进行轻量化设计的过程中, 保证悬架控制臂结构性能尤为重要[5].本文在采用CFRP对控制臂结构进行轻量化设计的同时, 系统探讨了基于铺层设计特征的复合材料结构设计方法和流程.
复合材料结构设计并不是简单地直接替换传统金属材料, 它的铺层结构设计尤为重要, 存在着相关结构设计、铺层设计以及工艺设计等一系列难题[6-7].鉴于碳纤维增强复合材料的铺层厚度与铺层角度对复合材料结构的性能有着很大的影响, 同时铺层设计工艺对于复合材料结构设计也存在着制约, 因而, 综合考虑这些影响因素来开展复合材料结构优化设计研究有望为该领域提供新的研究思路.
本文提出一种综合考虑几何结构与复合材料铺层设计各环节序列关系的结构优化设计方法.在传统钢质悬架控制臂的基础上, 采用碳纤维增强复合材料对控制臂进行结构轻量化设计, 以控制臂刚度和振动固有频率为目标, 从结构设计、铺层设计、铺层优化以及工艺可行性等方面进行了系统探讨.
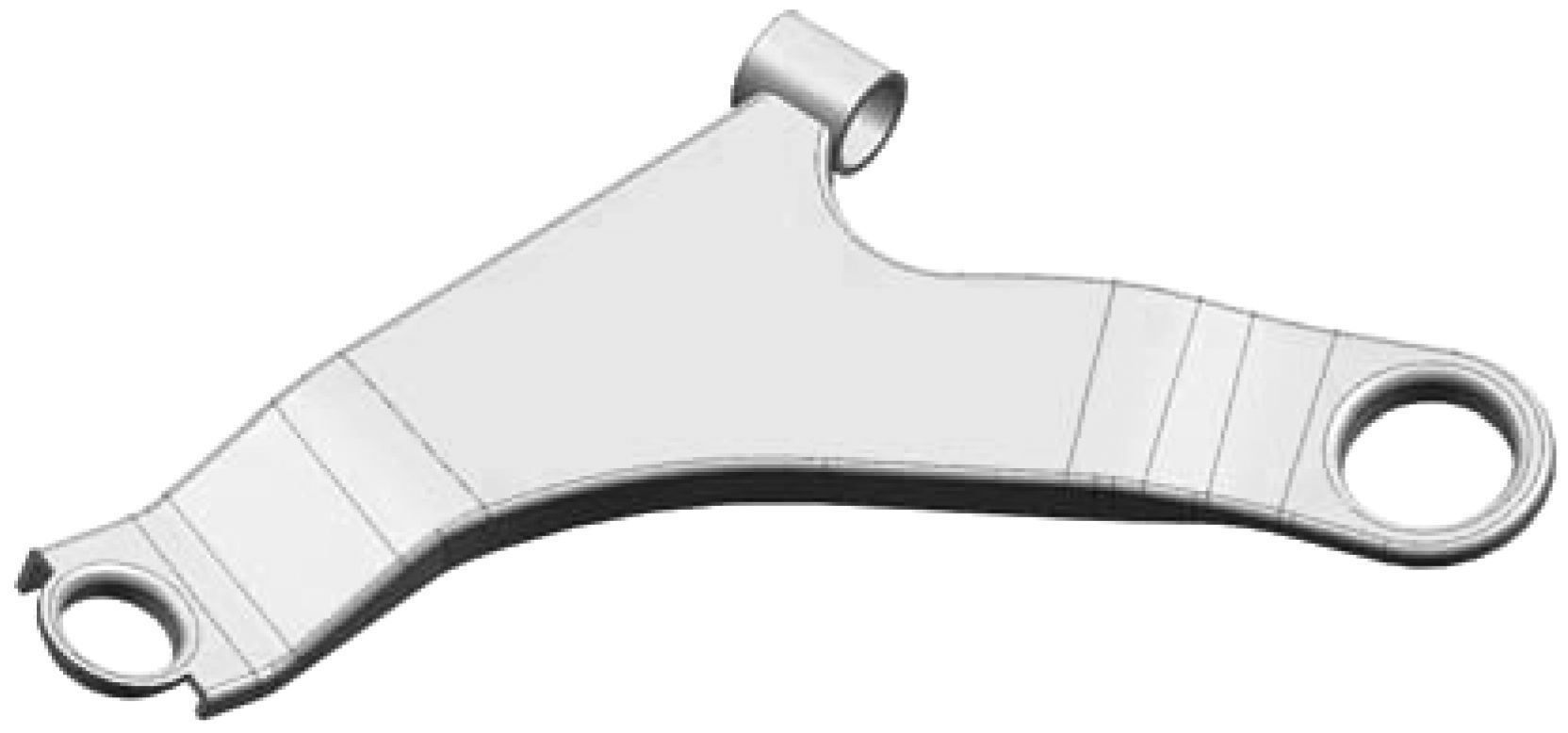
1 结构优化设计模型建立 1.1 几何设计空间建立图 1 (a)为本文所设计参照的钢质悬架控制臂, 它分别通过球绞和衬套把车轮和车身弹性地连接在一起.控制臂的几何结构模型如图 1 (b)所示, 可以看出钢质控制臂结构的几何特征比较复杂, 尤其是其主体上用于减重的孔洞结构并不符合复合材料铺层设计的要求, 所以需对其几何特征进行处理, 建立适合复合材料铺层的几何结构[8].对结构几何特征的处理原则如下:
1) 保证控制臂的基本导向功能不变, 即悬架结构的硬点数据(球绞和衬套安装点)不变.
2) 尽量维持结构的主要几何框架不变, 以保证不与悬架其他部件发生干涉.
3) 考虑到在同样性能指标的要求下复合材料结构的厚度大于钢质材料, 因而进行复合材料铺层时, 要保证厚度的增加不会导致几何结构自我干涉.

|
| 图 1 传统钢质悬架控制臂 Fig.1 The conventional steel control arm |
基于钢质控制臂模型, 简化后得到复合材料控制臂的模型如图 2所示.
|
| 图 2 复合材料控制臂模型 Fig.2 Composite control arm model |
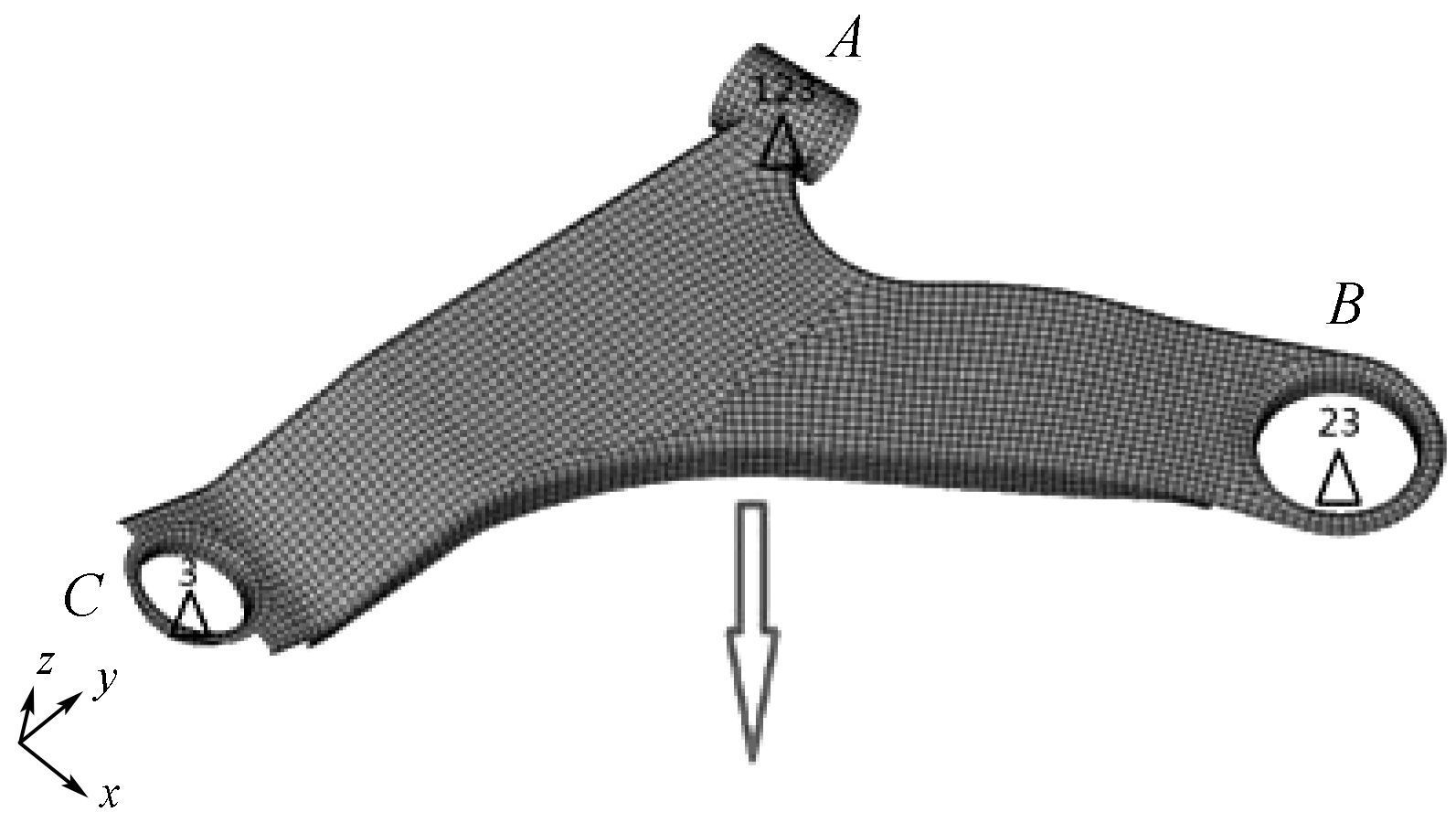
建立有限元分析模型, 如图 3所示.模型的复合材料铺层堆叠方向如图 3中箭头所示, 同时调整模型的材料方向, 保证复合材料铺层角度基准的连续性.
对于控制臂的刚度分析, 需要根据控制臂实际工作状态对其进行合理的约束并施加载荷[9].本文采用汽车坐标系, 约束控制臂前点(图 3中A点)x, y和z三个方向的平动自由度, 约束控制臂后点(图 3中B点)y和z方向的平动自由度, 约束控制臂外点(图 3中C点)z方向的平动自由度, 约束情况如图 3所示.控制臂与橡胶衬套之间的连接关系采用刚性单元来模拟.
|
| 图 3 控制臂的有限元模型 Fig.3 Finite element model of control arm |
麦弗逊悬架控制臂结构在汽车加速、制动和过坎时主要承受纵向力, 在转向时主要承受侧向力.对于垂向力, 控制臂只抵消前后橡胶衬套被扭转变形时的一些结构反力, 垂向力主要由滑柱弹簧承受, 作用在控制臂上的垂向力在数量级上远小于纵向力和侧向力, 因而在校核控制臂时通常不考虑[4].根据已有的整车参数, 建立相应的悬架动力学模型, 分析在制动与转向工况下悬架控制臂外点受力情况, 得到2种工况下的极限载荷, 如表 1所示.
| 工况 | Fx/N | Fy/N | Fz/N |
| 制动 | 2 370 | 895 | 107 |
| 转向 | 1 170 | 2 785 | 117 |
依据上述制动和转向工况下的载荷以及模型约束情况, 对钢质控制臂进行有限元分析, 得到钢质悬架结构的刚度以及1阶固有频率性能指标, 如表 2所示, 将其作为之后复合材料悬架结构性能的设计对标值.
| 质量/kg | 控制臂外点位移/mm | 1阶振动固有频率/Hz | |
| 制动 | 转向 | ||
| 1.94 | 0.69 | 0.10 | 347.7 |
在复合材料结构铺层设计中, 主要包含铺层厚度、铺层角度、工艺约束等.它们之间存在设计序列关系, 其中首要考虑的是如何对复合材料铺层厚度进行设计, 以保证结构的基本性能.进而是如何对复合材料铺层角度进行优化来提升结构的性能, 同时在这个过程中确保复合材料设计的工艺约束.本文将按照复合材料铺层设计环节中的序列关系对复合材料控制臂展开设计.
文中复合材料控制臂所使用的材料为韩国SK公司所生产的USN150规格的单向碳纤维预浸布, 其材料参数如表 3所示.
| 性能 | 量值 |
| 纵向拉伸模量E1 | 131.6 GPa |
| 横向拉伸模量E2 | 10.8 GPa |
| 剪切模量G12 | 5.65 GPa |
| 剪切模量G23 | 3.38 GPa |
| 泊松比ν12 | 0.28 |
| 密度ρ | 1 540 kg/m3 |
| 纵向拉伸强度Xt | 2 000 MPa |
| 纵向压缩强度Xc | 1 400 MPa |
| 横向拉伸强度Yt | 61.0 MPa |
| 横向压缩强度Yc | 130 MPa |
| 面内剪切强度S | 70 MPa |
| 单层厚度 | 0.146 mm |
对于复合材料结构的铺层设计, 由于复合材料各向异性的材料力学特性, 难以确定所需复合材料的铺层厚度.因此, 采用能显著降低复合材料各向异性的准各向同性铺层[±45°/90°/0°]s[10], 以钢质控制臂性能指标为约束来确定控制臂复合材料的铺层厚度, 之后再对其铺层角度进行优化设计.
建立包含复合材料铺层参数的控制臂有限元模型, 赋予准各向同性的铺层角度, 对其采取与钢质控制臂同样的分析方法, 通过初步计算, 可以得到当准各向同性铺层的复合材料铺层数为80层时, 其结构性能指标基本满足钢质控制臂的要求, 其控制臂外点的位移在制动工况下为0.55 mm, 在转向工况下为0.11 mm, 其1阶振动固有频率为613.0 Hz.
对比准各向同性铺层复合材料控制臂与钢质控制臂的性能指标如表 4所示, 可以看出, 除了转向工况下的位移情况略差于钢质控制臂以外, 复合材料控制臂的其他指标均满足要求, 其中质量减少了47.9%, 轻量化效果明显.
| 对比项 | 质量/kg | 控制臂外点位移/mm | 1阶振动固有频率/Hz | |
| 制动 | 转向 | |||
| 准各项同性铺层复合材料控制臂 | 1.01 | 0.55 | 0.11 | 613.0 |
| 钢质控制臂 | 1.94 | 0.69 | 0.10 | 347.7 |
采取准各向同性铺层设计的复合材料控制臂, 虽然减重效果明显, 但其性能指标并没有很大的提升, 其中转向工况下的变形情况还略差于钢质控制臂.考虑到复合材料铺层角度对于复合材料结构性能有着较大的影响, 在此对有限元模型中的铺层角度参数进行多目标优化设计, 以进一步改善其结构性能, 得到最大化刚度和1阶振动固有频率的铺层结果.
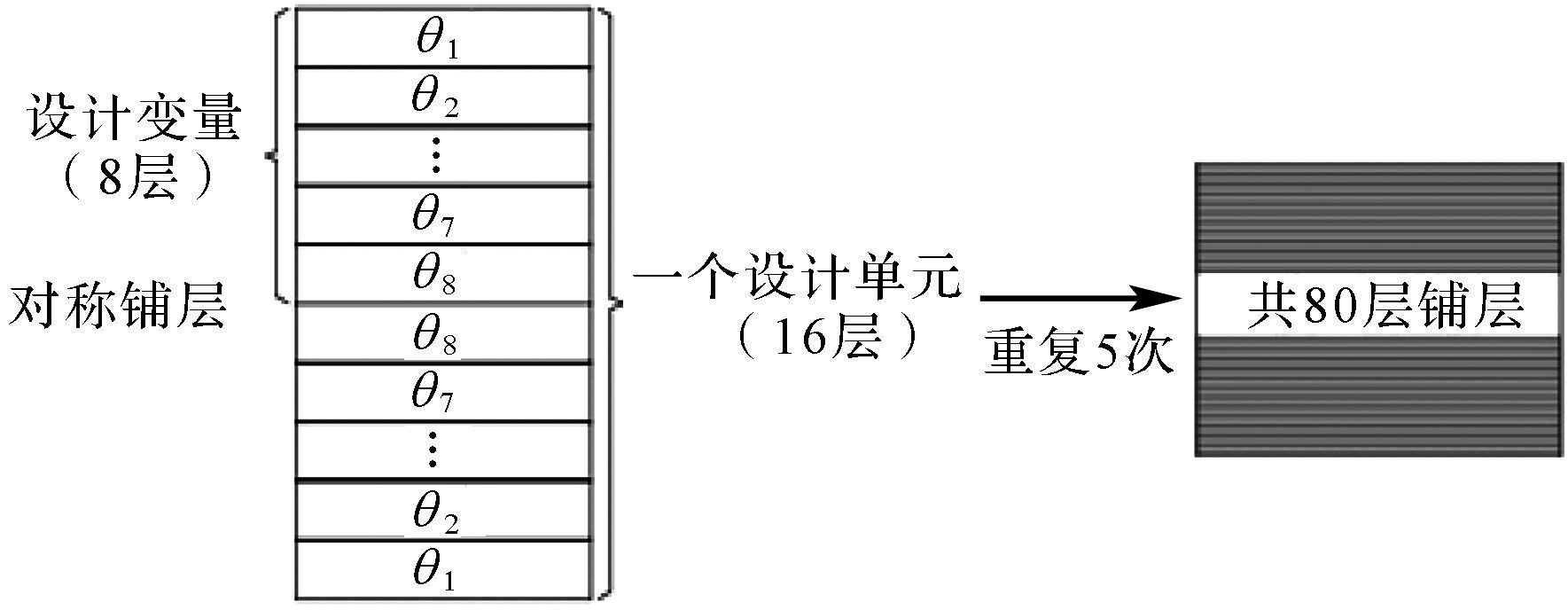
3.2 设计变量碳纤维复合材料的铺层共有80层, 参考铺层设计原则, 选取对称的16层铺层作为一个设计单元, 将这个设计单元重复5次, 构成总共80层的铺层.设计变量为一个设计单元中的8个铺层角度(θ1, θ2, …, θ8), 如图 4所示.每个铺层角度θ从-60°, -45°, -30°, 0°, 30°, 45°, 90°这些离散的值中选取, θ∈[-60°, -45°, -30°, 0°, 30°, 45°, 90°].
|
| 图 4 复合材料结构的设计变量 Fig.4 Design variables for the composite structure |
对复合材料铺层角度进行多目标优化, 目的是在铺层厚度一定的情况下, 尽可能地同时提高控制臂的刚度和低阶振动频率, 即控制臂外点在2种工况下的位移最小, 以及1阶振动固有频率最大.为了方便, 对位移取倒数为D, 位移最小即使D最大.
目标函数为
| $\left\{ \begin{array}{*{35}{l}} \text{max}{{f}_{1}}={{D}_{1}}, \\ \text{max}{{f}_{2}}={{D}_{2}}, \\ \text{max}{{f}_{3}}=f. \\ \end{array} \right.$ |
式中:D1为制动工况下控制臂外点位移的倒数, D2为转向工况下控制臂外点位移的倒数, f为控制臂1阶振动固有频率.
3.4 约束条件依据前文分析内容, 选取准各向同性铺层控制臂外点在制动工况下的位移0.55 mm, 即D1=1.82 mm-1.钢质控制臂外点在转向工况下的位移0.10 mm, 即D2=9.69 mm-1, 以及准各向同性铺层控制臂的1阶振动固有频率f=613.0 Hz作为约束.
约束条件为
| $\left\{ \begin{array}{*{35}{l}} {{D}_{1}}\ge 1.82\text{ m}{{\text{m}}^{-1}}, \\ {{D}_{2}}\ge 9.69\text{ m}{{\text{m}}^{-1}}, \\ f\ge 613.0\text{ Hz}. \\ \end{array} \right.$ |
综合上述设计变量、目标函数以及约束条件, 可知此问题属于离散变量的多目标设计优化问题, 它的数学模型表达如下:
| $\begin{array}{*{35}{l}} \text{max }\left[ {{f}_{1}},\text{ }{{f}_{2}},\text{ }{{f}_{3}} \right], \\ s.t.\text{ }\theta \in \left[ -60{}^\circ ,\text{ }-45{}^\circ ,\text{ }-30{}^\circ ,\text{ }0{}^\circ ,\text{ }30{}^\circ ,\text{ }45{}^\circ ,\text{ }90{}^\circ \right], \\ {{D}_{1}}\ge 1.82\text{ m}{{\text{m}}^{-1}}, \\ {{D}_{2}}\ge 9.69\text{ m}{{\text{m}}^{-1}}, \\ f\ge 613.0\text{ Hz}. \\ \end{array}$ |
本文采用非支配排序遗传算法(NSGA-Ⅱ)来对其进行求解, NSGA-Ⅱ适用于离散变量问题, 它降低了非劣排序遗传算法的复杂性, 计算效率高, 解集的收敛性好, 在多目标优化领域得到了广泛应用[11].利用NSGA-Ⅱ对上述优化设计模型进行求解, 可以得到75组Pareto解, Pareto最优解集如图 5所示.

|
| 图 5 Pareto最优解 Fig.5 Pareto optimal solution |
在复合材料层压板工艺设计中应考虑层压板铺层设计的主要原则[12-13], 避免固化中由于弯曲、拉伸、扭转等耦合效应引起的翘曲变形、树脂裂纹、分层等[14-15].因此基于工艺可行性的考虑, 此多目标问题的Pareto最优解集筛选的原则如下:
1) 避免使用同一方向的铺层组, 如果使用, 不得多于4层.
2) 确保每一种铺层角度所占比例的最小值, 最小为10%.
3) ±45°的铺层应成对出现.
4) 应把±45°铺层尽量铺设在远离结构中性层的位置上, 即两侧表面上.
5) 从提高结构稳定性、减少泊松比和热应力及避免树脂直接受载考虑, 建议应同时包含4种铺层.
对75组Pareto解, 依据上述原则筛选, 并综合考虑性能指标, 选取的最终铺层角度为[-45°/45°/-30°/30°/0°/90°/0°/0°]s.
对其进行分析, 得到其控制臂外点的位移在制动工况下为0.49 mm, 在转向工况下为0.09 mm, 其1阶振动固有频率为631.3 Hz.控制臂性能指标对比如表 5所示, 可以看出通过对复合材料铺层角度的优化, 控制臂在2种工况下的刚度以及1阶振动固有频率均有提升.同时, 重量减轻47.9%, 实现了结构的轻量化设计.
| 对比项 | 质量/kg | 控制臂外点位移/mm | 1阶振动固有频率/Hz | |
| 制动 | 转向 | |||
| 优化铺层角度的复合材料控制臂 | 1.01 | 0.49 | 0.09 | 631.3 |
| 准各项同性铺层复合材料控制臂 | 1.01 | 0.55 | 0.11 | 613.0 |
| 钢质控制臂 | 1.94 | 0.69 | 0.10 | 347.7 |
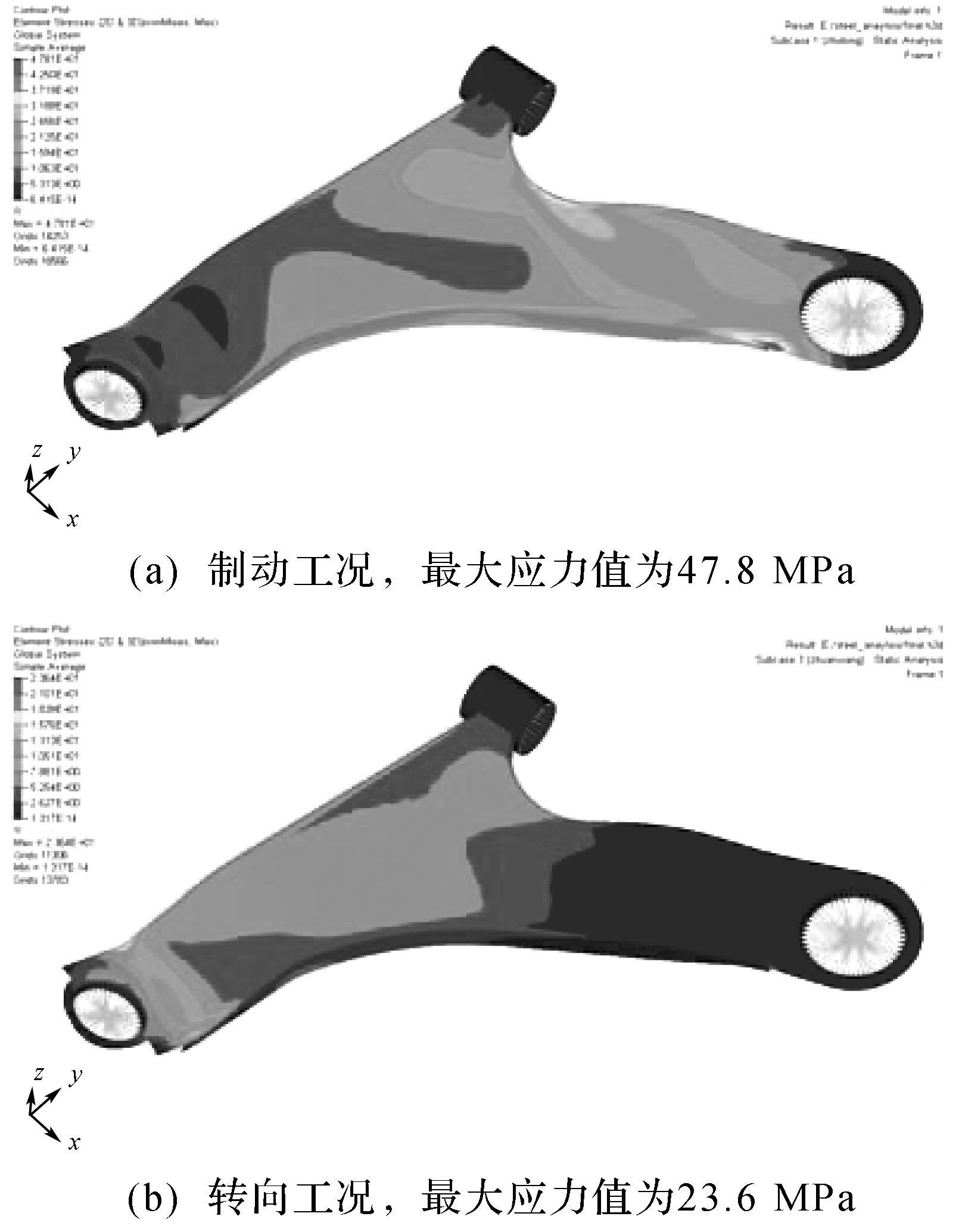
为了检验所设计复合材料控制臂的强度情况, 对优化后的控制臂结构进行分析, 得到制动和转向工况下悬架控制臂的应力云图如图 6所示, 结构的应力情况满足强度要求.同时采用Tsai-Wu强度准则[16], 对最终复合材料控制臂结构的失效情况进行仿真分析, 得到在2种工况下复合材料控制臂的最大失效指数均小于1, 表明最终所设计的复合材料控制臂结构满足强度要求.
|
| 图 6 悬架控制臂应力云图 Fig.6 Stress nephogram of the suspension control arm |
与金属材料相比, 复合材料具有更好的抗疲劳特性, 但是由于其疲劳寿命问题的复杂性以及重要性, 复合材料结构的疲劳损伤机理以及寿命预测也是目前一项重要的研究内容[17].而本文的研究重点在于结构的刚度、固有频率等基本性能指标, 复合材料结构的疲劳寿命将作为下一步的研究内容.
4 结论在传统钢质悬架控制臂的基础上, 从几何结构设计、铺层厚度、铺层角度以及工艺可行性等方面, 使用碳纤维复合材料对控制臂结构进行优化设计, 在满足强度要求的前提下, 使控制臂的刚度和固有频率性能指标得到较大提升, 同时与钢质控制臂相比其质量减少了47.9%, 轻量化效果明显.文中所提出的基于铺层设计特征的复合材料结构设计方法和流程, 考虑了复合材料结构设计环节中序列关系, 兼顾了结构特征和复合材料的设计要求, 为结构材料结构设计提供了有益参考.
| [1] | JEONG P Y. A Development of composite material suspension arm[J]. SAE Fechnical Paper , 2012 : 2012–01. |
| [2] | BOTKIN M E. Modelling and optimal design of a carbon fiber reinforced composite automotive roof[J]. Engineering with Computers , 2000, 16 (1) : 16–23. DOI:10.1007/s003660050033 |
| [3] | KIM J, LEI L P, HWANG S M, et al. Manufacture of an automobile lower arm by hydroforming[J]. International Journal of Machine Tools and Manufacture , 2002, 42 (1) : 69–78. DOI:10.1016/S0890-6955(01)00087-6 |
| [4] |
李成.
基于OptiStruct的麦弗逊悬架下控制臂优化[J]. 计算机辅助工程 , 2012, 21 (5) : 49–52.
LI Cheng. Optimization on lower control arm of McPherson suspension based on OptiStruct[J]. Computer Aided Engineering , 2012, 21 (5) : 49–52. |
| [5] |
乐天聪. 某轿车悬架控制臂有限元分析与结构优化[D]. 长春:吉林大学汽车工程学院,2009:1-6.
LE Tian-cong. The finite element analysis and structure optimization of sedan car suspension control arm[D]. Changchun:Jilin University, College of Automotive Engineering, 2009:1-6. |
| [6] |
高希. 复合材料悬架横臂的优化设计[D]. 太原:中北大学机械与动力工程学院,2014:14-21.
GAO Xi. Design optimization of composite control arm[D]. Taiyuan:North University of China, School of Mechanical and Power Engineering, 2014:14-21. |
| [7] | ÇOBI A C. Design of a carbon fiber suspension system for FSAE applications[D]. Cambridge:Massachusetts Institute of Technology, Department of Mechanical Engineering, 2012:21-28. |
| [8] | KIM D H, CHOI D H, KIM H S. Design optimization of a carbon fiber reinforced composite automotive lower arm[J]. Composites Part B:Engineering , 2014, 58 : 400–407. DOI:10.1016/j.compositesb.2013.10.067 |
| [9] |
黄亚威. 轿车悬架控制臂性能分析与参数化轻量化优化设计[D]. 长春:吉林大学汽车工程学院,2014:38-40.
HUANG Ya-wei. Performance analysis and parameterization lightweight optimization design for car suspension control arm[D]. Changchun:Jilin University, College of Automotive Engineering, 2014:38-40. |
| [10] | SMITH P A, PASCOE K J. The effect of stacking sequence on the bearing strengths of quasi-isotropic composite laminates[J]. Composite Structures , 1986, 6 (1) : 1–20. |
| [11] |
王茜, 张粒子.
采用NSGA-Ⅱ混合智能算法的风电场多目标电网规划[J]. 中国电机工程学报 , 2011, 31 (19) : 17–24.
WANG Qian, ZHANG Li-zi. Multi-objective transmission planning associated with wind farms applying NSGA-II hybrid intelligent algorithm[J]. Proceedings of the CSEE , 2011, 31 (19) : 17–24. |
| [12] | TOROPOV V V, JONES R, WILLMENT T, et al. Weight and manufacturability optimization of composite aircraft components based on a genetic algorithm[C]. 6th World Congresses of Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazil, May. 30-Jun. 03, 2005. |
| [13] | NEVEY S, ALVAREZ L. Optimize the optimized:weight reduction of an F1 composite wing[J/OL].[2016-06-01]. http://www.luis-alvarez.es/includes/jaguar_racing.pdf. |
| [14] |
沈真, 章怡宁, 黎观生.
复合材料结构设计手册[M]. 北京: 航空工业出版社 ,2001 : 80 -87.
SHEN Zhen, ZHANG Yi-ning, LI Guan-sheng. Composite structure design manual[M]. Beijing: Aviation Industry Press , 2001 : 80 -87. |
| [15] |
冯消冰, 黄海, 王伟.
大型风机复合材料叶片铺层优化设计[J]. 玻璃钢/复合材料 , 2013, 1 (3) : 3–7.
FENG Xiao-bing, HUANG Hai, WANG Wei. Composite laminate optimization design of large wind turbine blades[J]. Fiber Reinforced Plastics/Composites , 2013, 1 (3) : 3–7. |
| [16] | RASTOGI N. Stress analysis and lay-up optimization of an all-composite pick-up truck chassis structure[J]. SAE Transactions , 2004, 113 (5) : 660–671. |
| [17] |
张文姣. 纤维增强复合材料的疲劳损伤模型及分析方法[D]. 哈尔滨:哈尔滨工业大学航天学院,2015:14-34.
ZHANG Wen-Jiao. Fatigue damage modelling and analysis for fiber reinforced composite materials[D]. Harbin:Harbin Institute of Technology, School of Astronautics, 2015:14-34. |



