2. 徐州奥博机械科技有限公司, 江苏 徐州 221100;
3. 合肥恒力电子装备公司, 安徽 合肥 230088
2. Xuzhou Aobo Mechanical Technology Co., Ltd., Xuzhou 221100, China ;
3. Hengli Eletek Co., Ltd., Hefei 230088, China
斜盘作为轴向柱塞泵中的重要部件之一[1-2], 承受较大的周期性力和力矩.斜盘力矩经柱塞滑靴组件作用于斜盘并使其具有转动的趋势[3], 表现为频率较高的交变力矩, 对缸体受力、整泵的振动和噪声均有直接影响[4-5].丛凤杰等[6]分析了旋转斜盘型变量柱塞泵的受力情况, 建立其转矩、泵瞬时流量公式, 并与普通轴向柱塞泵进行了对比分析.石金艳等[7]分析了斜盘倾角对柱塞相对缸体运动的位移、速度、加速度的影响, 指出斜盘支承反力过大将加剧柱塞与滑靴之间、配流盘与缸体之间的摩擦.刘健等[8]分析计算了轴向柱塞泵斜盘支承反力, 为轴向柱塞泵斜盘结构及参数的设计提供理论依据.朱钰[9]建立了轴向柱塞变量泵斜盘力矩的仿真模型, 分析了配油盘结构对斜盘力矩的影响.徐兵等[10]研究并优化了一种柱塞泵斜盘交错角新型降噪结构, 分析了其旋转角度大小对柱塞泵出口流量脉动的影响, 同时给出某典型工况下推荐的交错角大小;并分析了不同工况下交错角的降噪效果.Zeiger等[11]推导了斜盘力矩的数学模型, 并通过实验验证了其正确性.以上研究有效地减少了轴向柱塞泵的振动和降低了噪声, 并优化其流量调节能力.
平衡式两排轴向柱塞泵[12-13]是一种新型轴向柱塞泵, 其斜盘结构与普通轴向柱塞泵存在较大差异, 如图 1所示, 斜盘为2个不同倾角的斜面, 同时承受内、外两排柱塞的周期性作用力和力矩, 引发振动与噪声, 降低斜盘与缸体连接螺栓的寿命, 同时周期性作用力和力矩对其变量特性有直接影响, 斜盘内、外排力矩的相互作用规律有待完善.基于上述问题, 建立了平衡式两排轴向柱塞泵的仿真模型和斜盘受力特性模型, 分析其内、外排柱塞直径, 内、外排柱塞分布圆半径及斜盘倾角对斜盘力矩的影响.
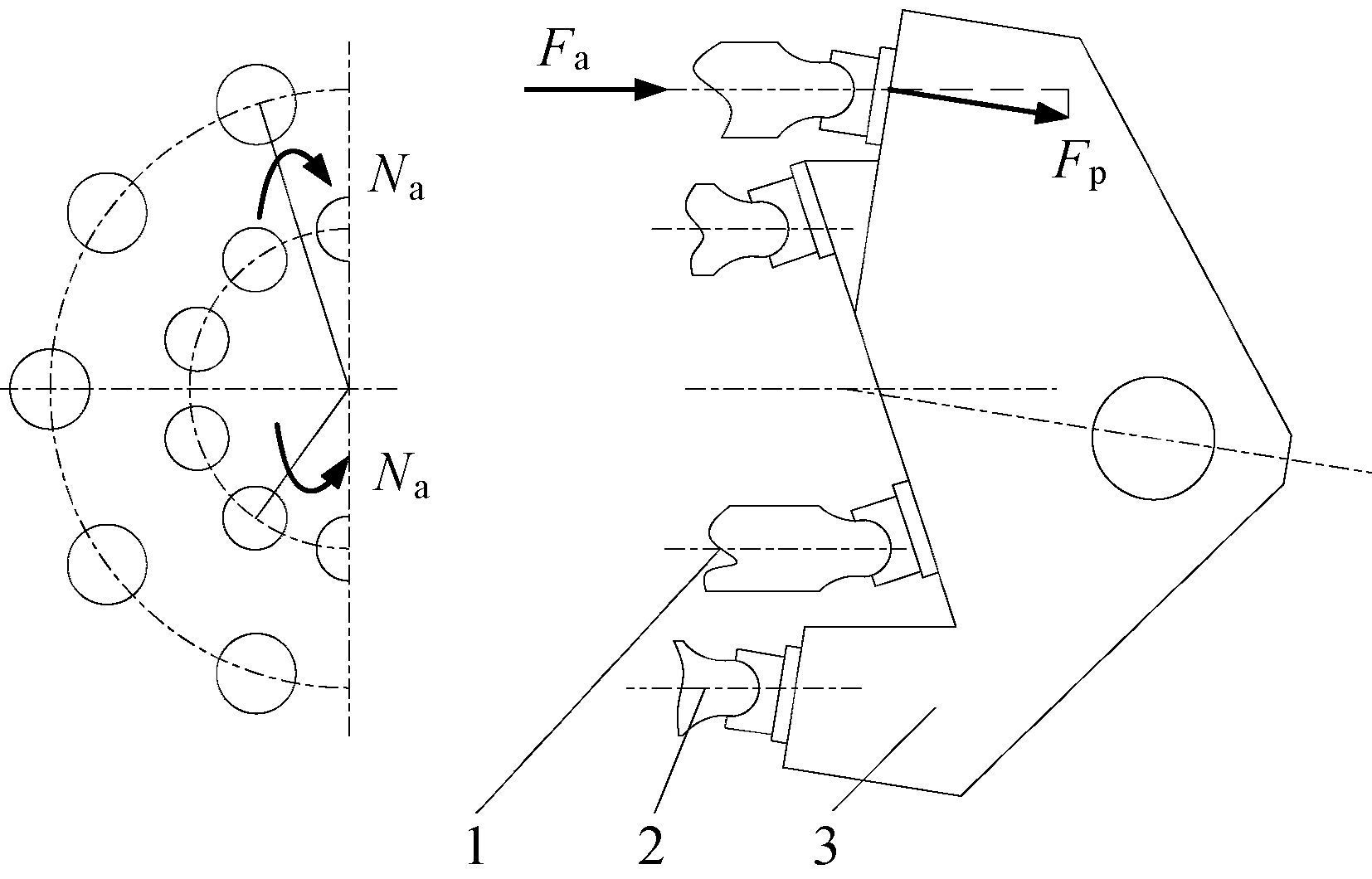
|
| 1—内排柱塞与滑靴组件;2—外排柱塞与滑靴组件;3—斜盘. 图 1 平衡式两排轴向柱塞泵斜盘受力分析 Fig.1 The swash plates force analysis of balanced two-ring axial piston pump |
作为支撑滑靴运动的斜盘, 其受力与滑靴组件紧密相关.其所受力矩主要包括2个部分:一部分是作用于斜盘轴向引起斜盘轴向转动, 主要来自于滑靴副的轴向分力、惯性力等;另外一部分引起斜盘周向运动, 这部分力主要由定位销或键承受.由于普通轴向柱塞泵采用改变斜盘倾角方式实现变量[14], 故应主要考虑第一部分力和力矩.不计斜盘摩擦力和重力导致的斜盘偏转, 由滑靴副和惯性力引起的力和力矩[15-16]的表达式如下:
| ${{F}_{p}}=\frac{1}{4}\pi {{d}^{2}}{{p}_{h}}/c\text{os }\gamma ,$ | (1) |
| ${{N}_{x}}=\left\{ \begin{array}{*{35}{l}} {{F}_{p}}R\frac{sin\text{ }\left( \pi /2z-\varphi \right)}{2sin\text{ }\left( \pi /2z \right)cos\text{ }\gamma },\text{ }0<\varphi <\pi z, \\ {{F}_{p}}R\frac{sin\text{ }\left( 3\pi /2z-\varphi \right)}{2sin\text{ }\left( \pi /2z \right)cos\text{ }\gamma },\text{ }\pi z<\varphi <2\pi z. \\ \end{array} \right.$ | (2) |
| ${{F}_{a}}=-\sum\limits_{i=1}^{z}{{{m}_{z}}}{{a}_{i}},$ | (3) |
| ${{N}_{a}}=-\frac{z{{m}_{z}}{{R}^{2}}{{\omega }^{2}}tan\text{ }\gamma }{2\text{co}{{\text{s}}^{2}}\gamma },\text{ }$ | (4) |
式中:Fp——斜盘反力, N;
γ——斜盘倾角, rad;
ph——液压泵高压腔压力, MPa;
Nx——滑靴副引起的力矩, N·m;
R——柱塞分度圆半径, mm;
z——柱塞数目, 个;
mz——单个柱塞质量, kg;
Fa——惯性力, N;
Na——惯性力矩, N·m;
ai——第i个柱塞的轴向加速度, m/s2;
ω——缸体的转动角速度, rad/s.
由式(1) 至式(4) 可知, 影响斜盘力矩的因素主要有柱塞数目、斜盘倾角、柱塞直径、柱塞分布圆半径、高压腔压力和角速度等.不同于普通轴向柱塞泵, 平衡式两排轴向柱塞泵还需考虑内外柱塞数量、斜盘斜面倾角的匹配等问题.
2 平衡式两排轴向柱塞泵仿真模型如图 2所示, 建立基于AMESim的平衡式两排轴向柱塞泵仿真模型, 由配流盘超级元件、斜盘柱塞连接器元件等结构元件构成.利用AMEsim中的Post processing进一步完成平衡式两排轴向柱塞泵斜盘的受力分析.
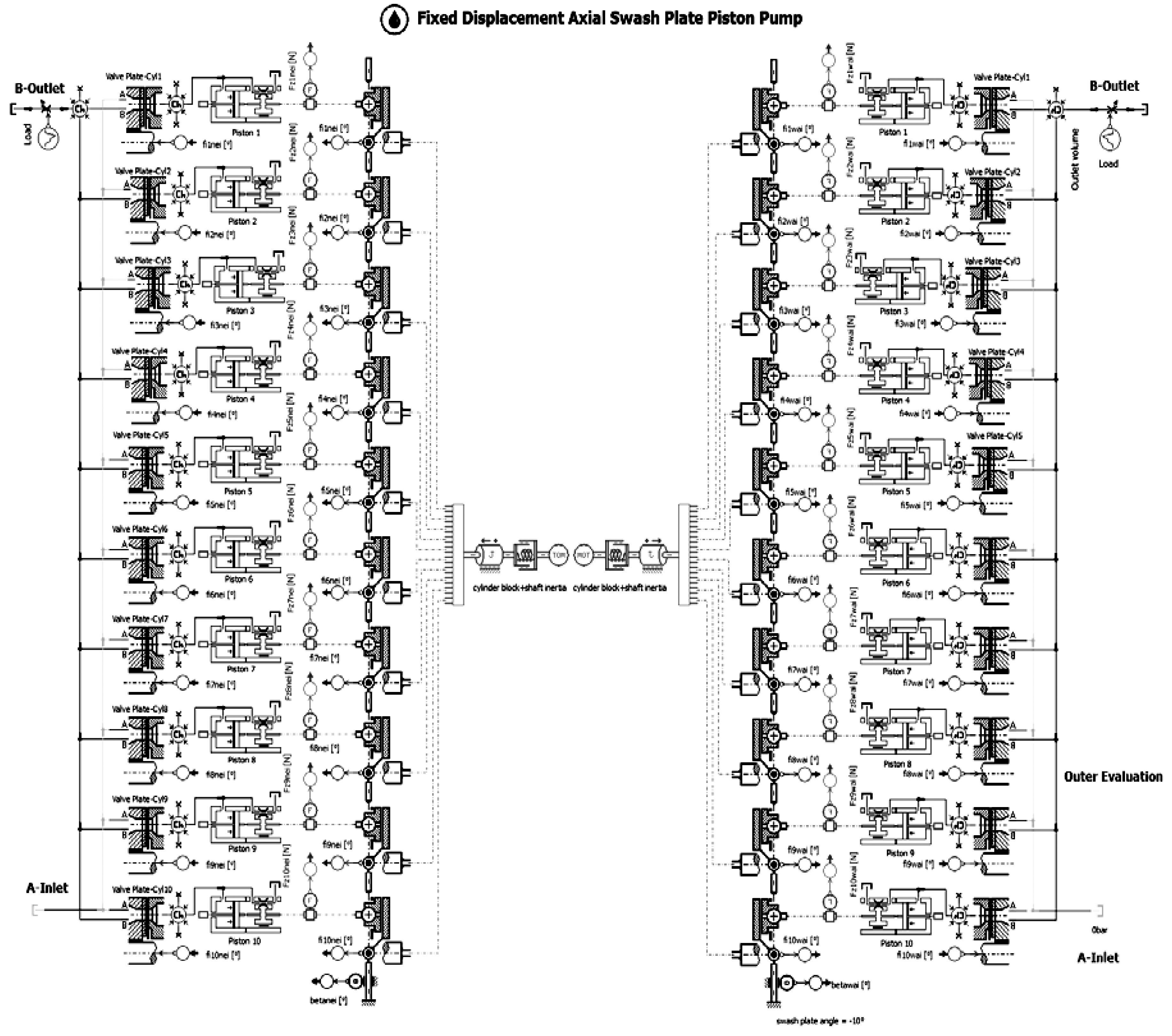
|
| 图 2 平衡式两排轴向柱塞泵模型 Fig.2 Model of balanced two-ring axial piston pump |
依照所设计的平衡式两排轴向柱塞泵(已加工样机)的尺寸, 将上述模型的参数设置为:内排柱塞分布圆半径为0.030 m, 外排柱塞分布圆半径为0.055 m, 内、外排柱塞数均为10个, 内排柱塞直径为13 mm, 外排柱塞直径为15 mm, 内排斜盘倾角为17°, 外排斜盘倾角为10°, 柱塞直径间隙为0.005 mm, 交错角为9°[13].电机转速为1 000 r/min, 扭矩模型中的弹簧刚度为1 000 N·m/(°), 出油口流量阀最大开度为2.5 mm.
考虑平衡式两排轴向柱塞泵结构, 其内、外排柱塞分布圆直径, 柱塞直径, 斜盘斜面倾角及其相互匹配关系对斜盘受力和力矩影响较大, 同时, 合力轨迹反映了斜盘受力的稳定性, 故对其主要影响因素进行分析.
3 仿真及结果分析 3.1 柱塞分布圆半径对斜盘力矩的影响上述其他参数不变, 内排柱塞分布圆半径R1分别取45, 40, 30, 20, 15 mm, 可得不同内排柱塞分布圆半径R1下斜盘所受合力矩的变化情况, 如图 3所示.
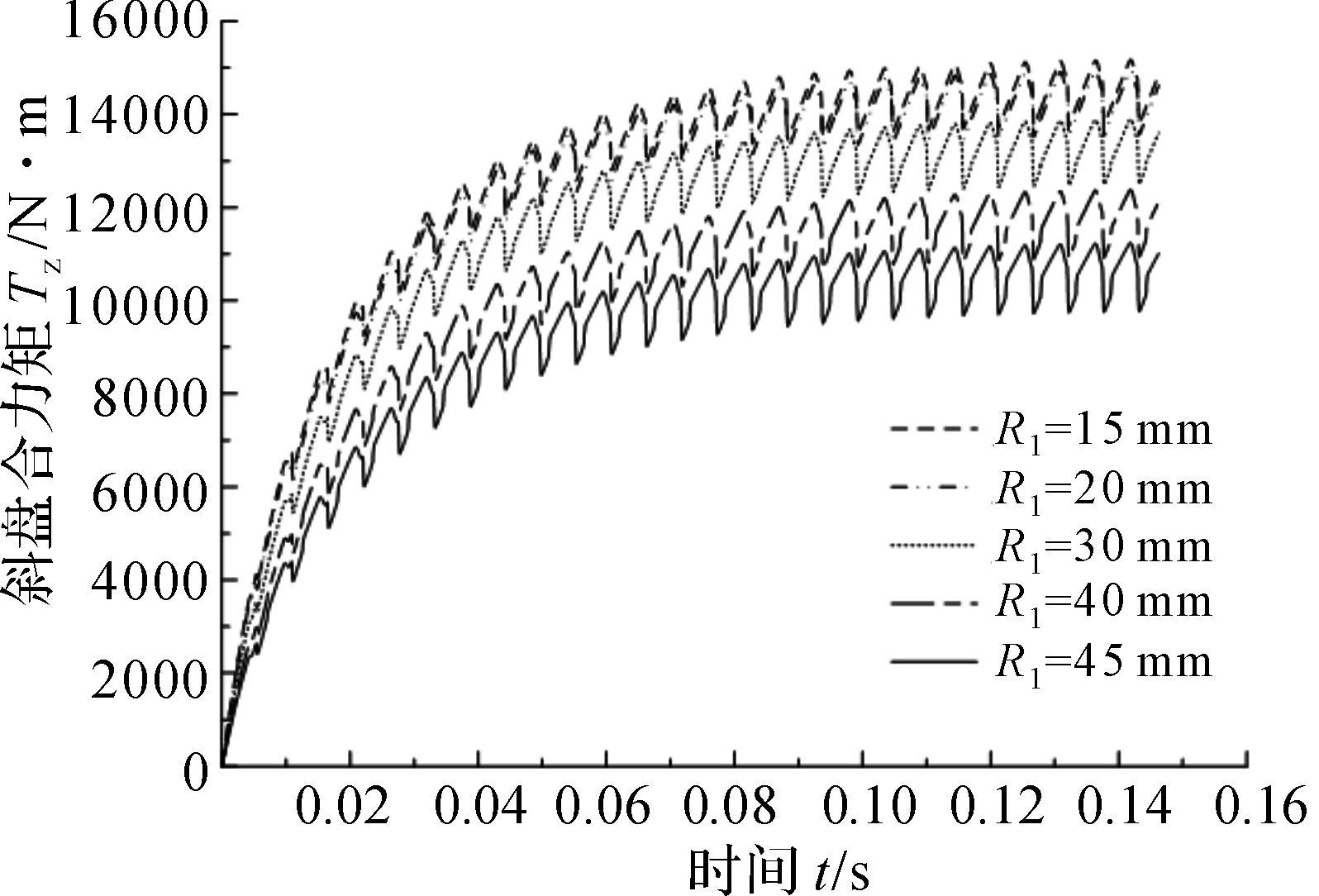
|
| 图 3 不同内排柱塞分布圆半径下的斜盘合力矩 Fig.3 Swash plate total moment under different inner piston distribution circle radius |
对图 3不同内排柱塞分布圆半径下的斜盘力矩数据进行处理, 如表 1所示.
当R1=45 mm时, Tz=10 458.75 N·m;R1=15 mm时,
| 内排柱塞分布圆半径R1/mm | 斜盘合力矩Tz/N·m | ||
| 峰值Tzmax | 谷值Tzmin | 平均值Tz | |
| 45 | 11 190.98 | 9 726.17 | 10 458.75 |
| 40 | 12 328.03 | 10 894.81 | 11 611.42 |
| 30 | 13 848.58 | 12 454.51 | 13 151.55 |
| 20 | 14 887.16 | 13 512.39 | 14 199.78 |
| 15 | 15 120.62 | 13 746.42 | 14 433.52 |
采用上述同样方法, 外排柱塞分布圆半径R2分别取65,60,55,50,45 mm, 分析斜盘所受合力矩的变化情况, 如图 4所示.
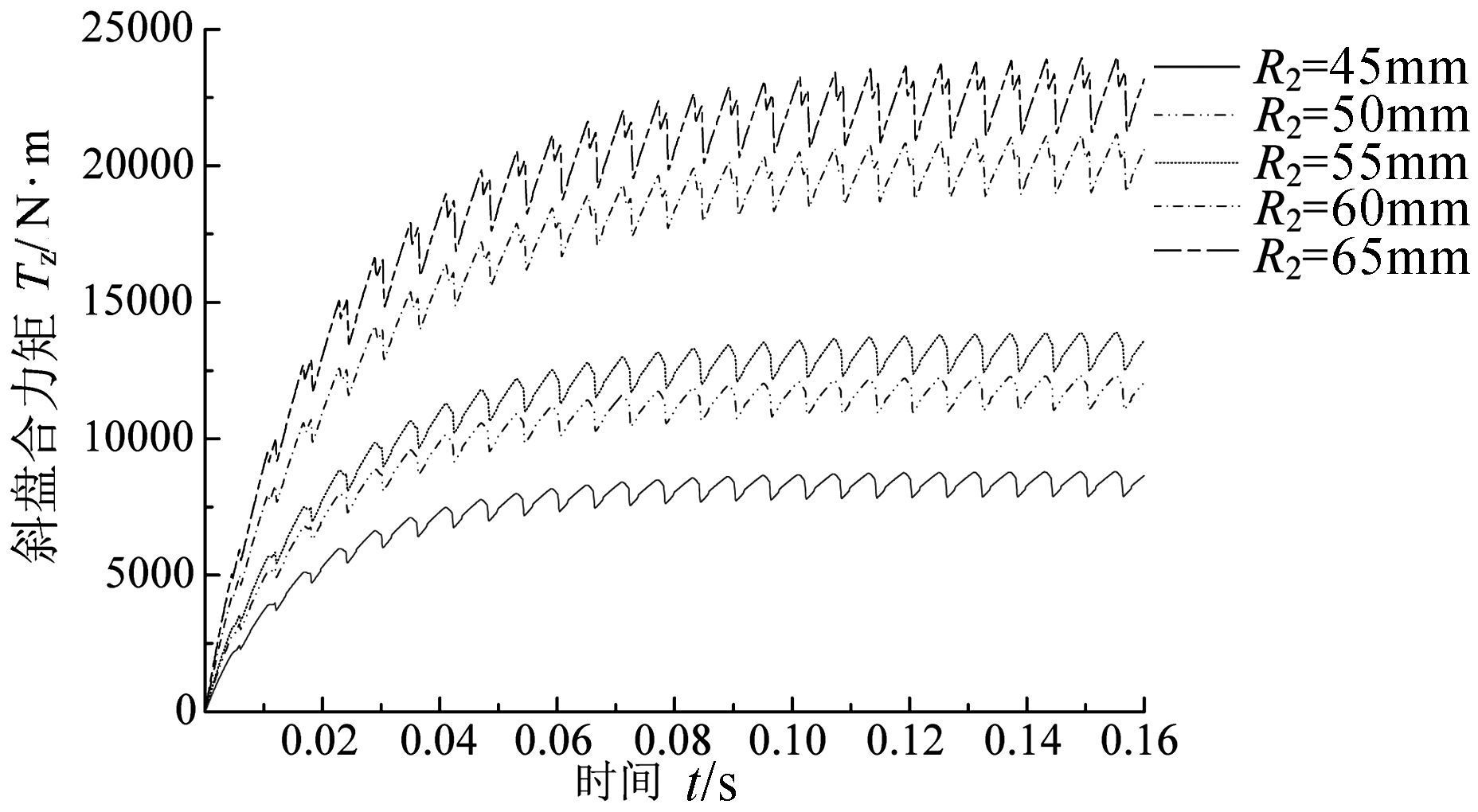
|
| 图 4 不同外排柱塞分布圆半径下的斜盘合力矩 Fig.4 Swash plate total moment under different outer piston distribution circle radius |
对图 4不同分布圆半径下的斜盘力矩数据进行处理, 如表 2所示.
| 内排柱塞分布圆半径R1/mm | 斜盘合力矩Tz/N·m | ||
| 峰值Tzmax | 谷值Tzmin | 平均值Tz | |
| 65 | 23 618.91 | 20 991.28 | 22 305.10 |
| 60 | 20 831.60 | 18 806.25 | 19 818.93 |
| 55 | 13 794.36 | 12 405.83 | 13 100.10 |
| 50 | 12 237.70 | 10 995.45 | 11 616.58 |
| 45 | 8 760.16 | 7 850.85 | 8 305.51 |
当R2=65 mm时, Tz=22 305.10 N·m;R2=45 mm时, Tz=8 305.51 N·m.从图 4和表 2中可见, 随着外排柱塞分布圆半径的增大, 斜盘所受合力矩增大.外排柱塞分布圆半径增大44%, 斜盘所受平均合力矩增大168.57%.可见, 较小的外排柱塞分布圆半径, 有利于降低斜盘合力矩.对比图 3可知, 内排柱塞分布圆尺寸增大, 有利于合力矩的减小, 与外排柱塞分布圆尺寸增大对合力矩的影响相反.在内、外排柱塞分布圆半径增长率相同的情况下, 外排柱塞分布圆半径增长后合力矩的增大率约为内排柱塞分布圆半径增长后合力矩减小率的27.82倍, 表明外排分布圆半径对合力矩的影响远大于内排对其影响.
图 5为将内、外排柱塞分布圆半径R1 , R2作为双因素影响变量, 斜盘合力矩Tz作为输出参数.从图 5中可见:随着内排柱塞分布圆半径R1的增大, 斜盘合力矩Tz减小;随着外排柱塞分布圆半径R2的增大, 斜盘合力矩Tz显著增大;外排柱塞分布圆半径R2对斜盘合力矩Tz影响较大.结果同图 3、图 4反映规律一致.
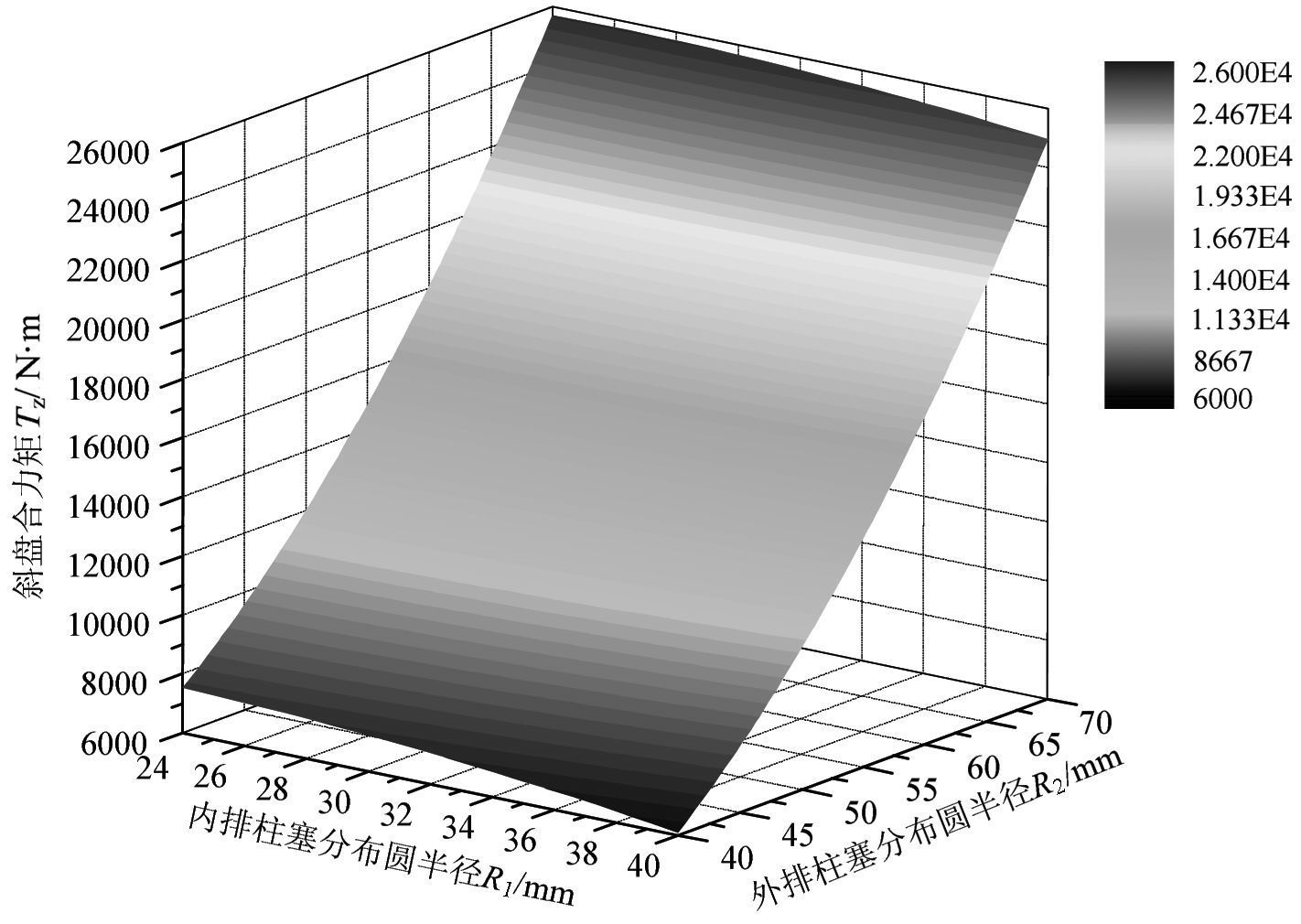
|
| 图 5 内、外排柱塞分布圆半径与斜盘合力矩三维图 Fig.5 3D diagram of inner and outer piston distribution circle radius with swash plate total moment |
保持其他参数不变, 内排柱塞直径d1分别取17, 15, 13, 11, 9 mm, 分析不同内排柱塞直径对斜盘所受合力矩的影响, 如图 6所示.
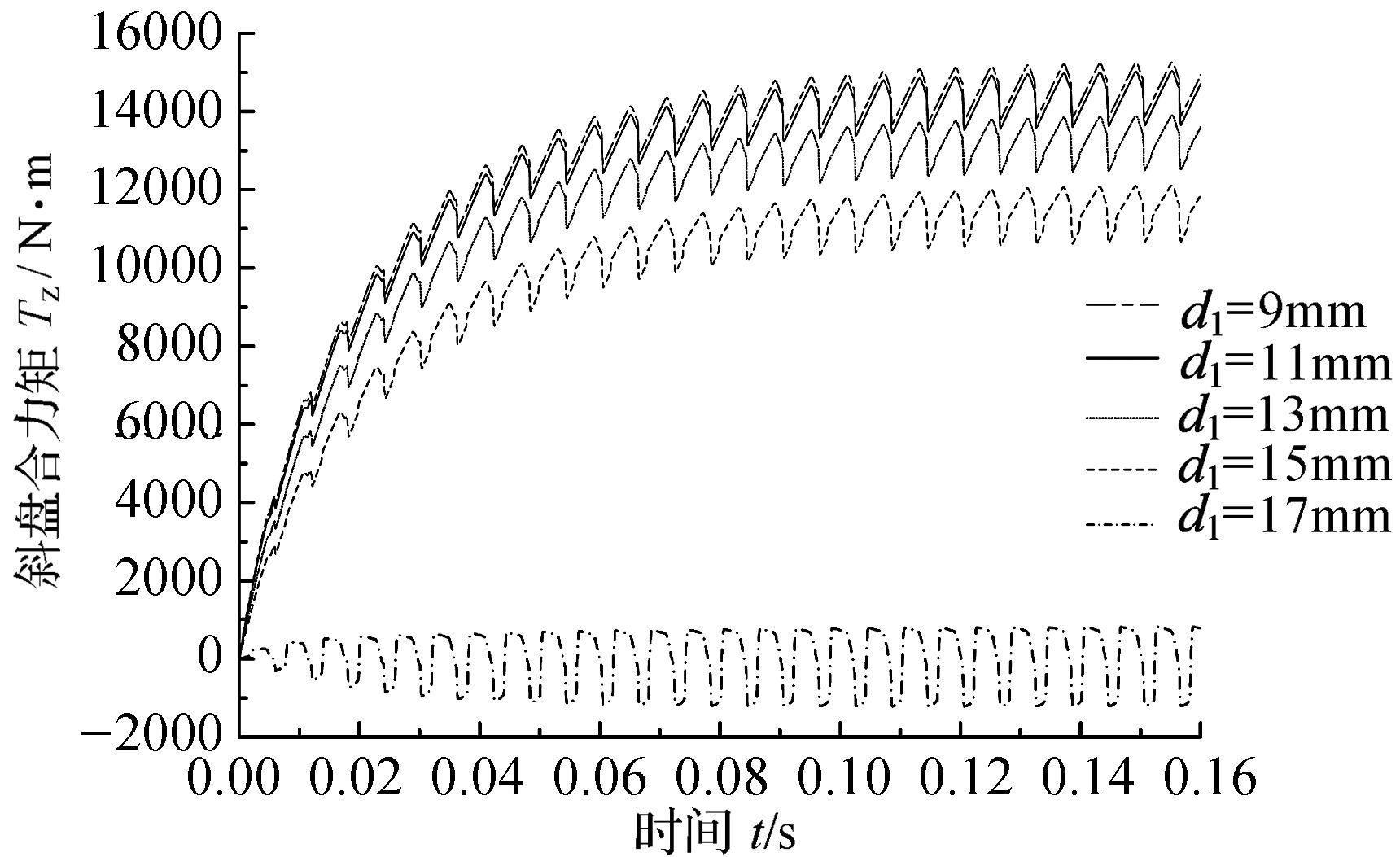
|
| 图 6 不同内排柱塞直径下的斜盘合力矩 Fig.6 Swash plate total moment under different inner piston diameters |
从图 6可以看出, 随着内排柱塞直径增大, 斜盘合力矩依次减小, 当d1=17 mm时, 斜盘所受合力矩最小, 且从图中可知当d1=17 mm时斜盘所受合力矩为交变合力矩, 易产生机械振动, 所以在上述参数下, 内排柱塞直径不应超过此数值.
采用上述方法, 外排柱塞直径d2分别取19, 17, 15, 13, 11 mm, 分析不同d2取值对斜盘所受合力矩的影响, 如图 7所示.

|
| 图 7 不同外排柱塞直径下斜盘合力矩 Fig.7 Swash plate total moment under different outer piston diameters |
从图 7可以看出, 随着外排柱塞直径增大, 斜盘所受合力矩依次增大, 当d2=11 mm时, 斜盘所受合力矩最小, 此时斜盘合力矩的脉动情况优于其他d2时的受力情况.因此设计时, 可考虑适当减小外排柱塞直径以减小斜盘合力矩的脉动情况.
图 8为将内、外排柱塞直径d1, d2作为双因素影响变量, 斜盘合力矩Tz作为输出参数. 从图 8中可以看出:随着内排柱塞直径d1增大;斜盘合力矩Tz减小;随着外排柱塞直径d2增大, 斜盘合力矩Tz显著增大;外排柱塞直径d2对斜盘合力矩Tz影响较大.结果同图 6、图 7规律一致.
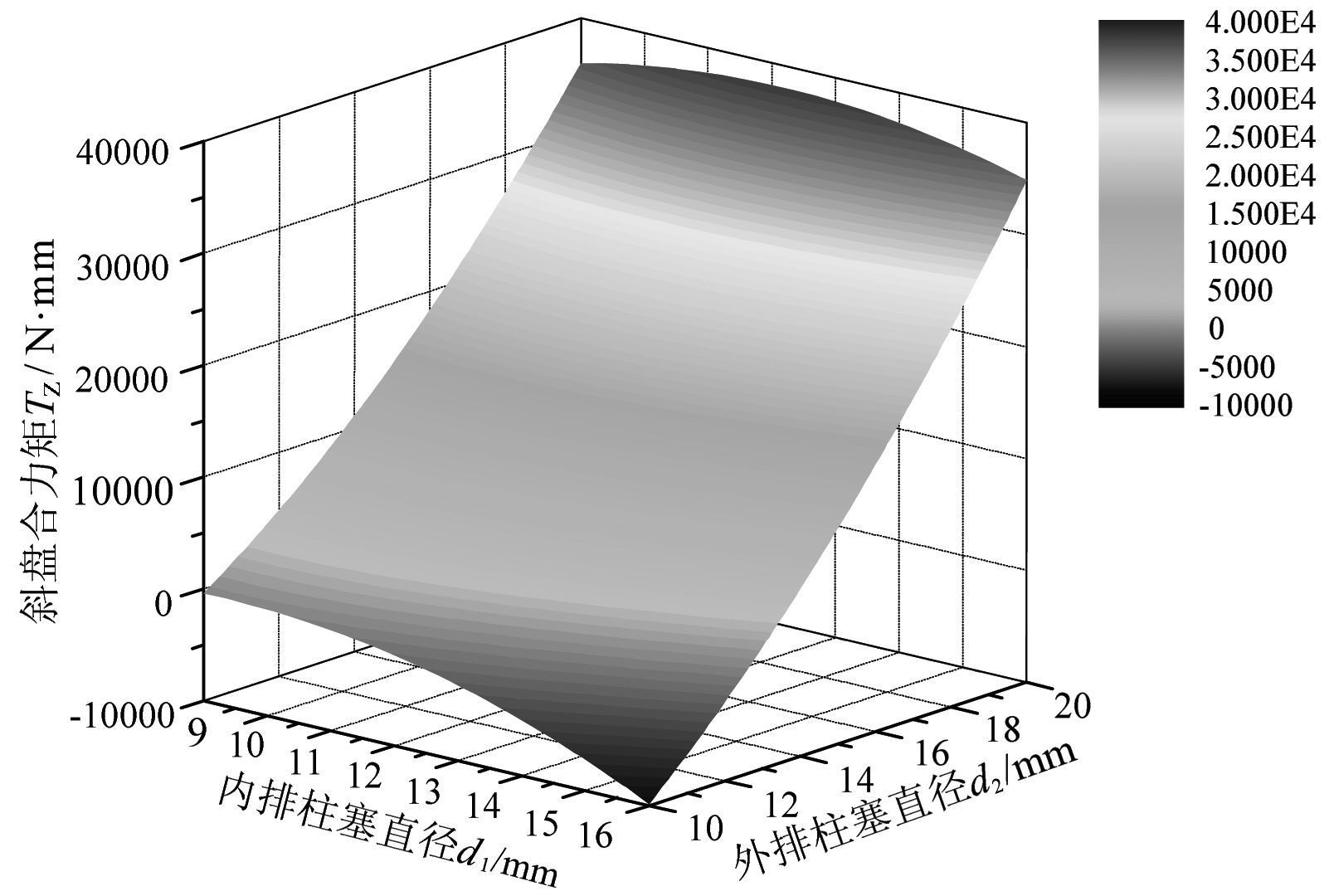
|
| 图 8 内外排柱塞直径与斜盘合力矩三维图 Fig.8 3D diagram of inner and outer piston diameter with swash plate total moment |
为讨论斜盘倾角对内外排斜盘力矩的影响, 将缸体的结构参数以及内外排斜盘的倾角参数添加到AMEsim输出模块Export Parameters Setup中, 将其作为输入参数, 且以内外排斜盘的合力矩为输出参数.建立内外排斜盘的力学模型, 如图 9所示.
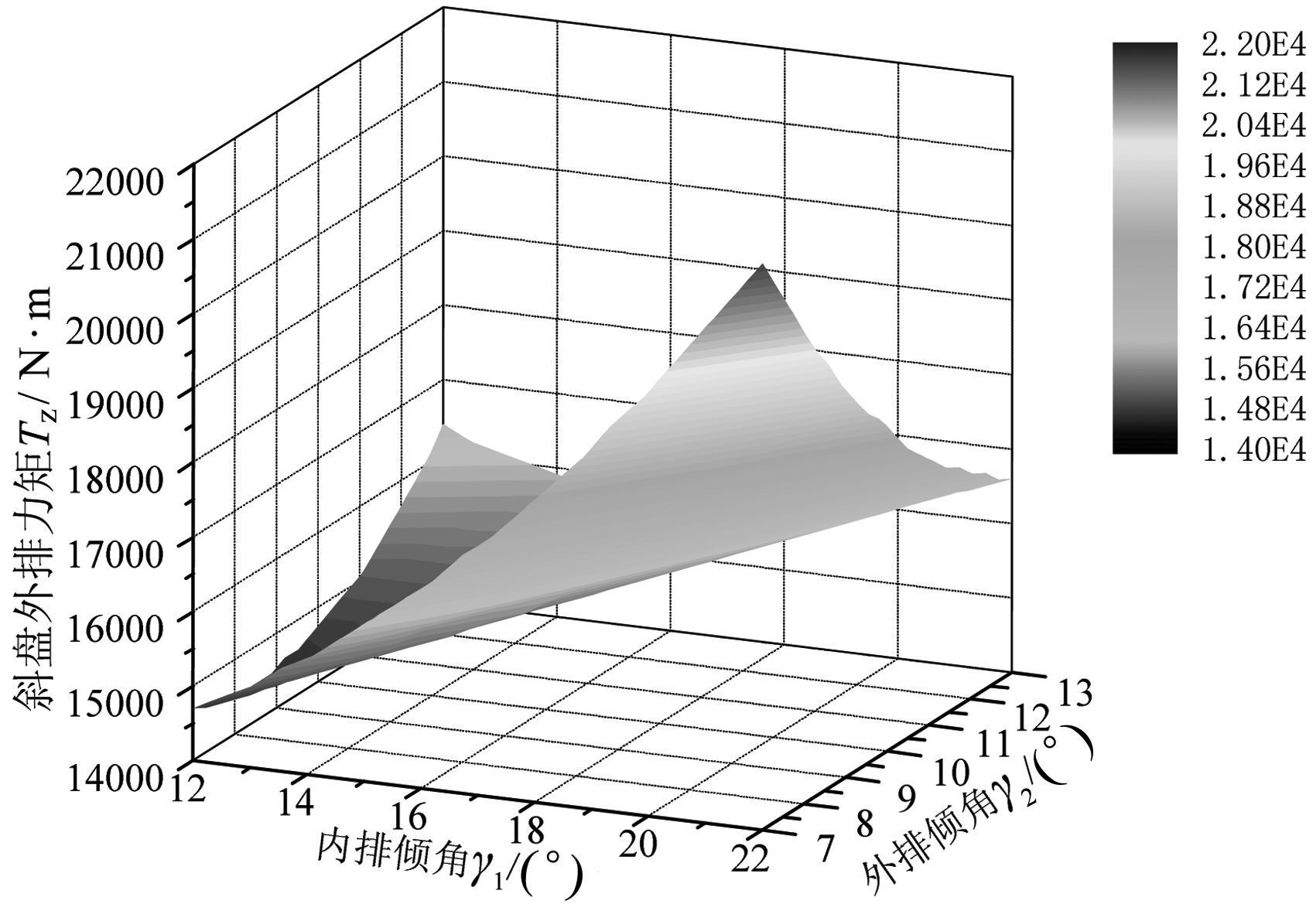
利用蒙特卡罗方法进行仿真, 得到内外排斜盘倾角与内外排斜盘受力的响应面关系图, 如图 10和图 11所示.
图 10、图 11的横坐标分别为内、外排斜盘斜面倾角, 纵坐标为斜盘力矩.从图 10中可以看出, 当γ1=12°时, T内恒取得最小值;从图 11中亦可以看出, 当γ1=12°, γ2在7°~10°变化范围内, T外取得最小值.考虑到较小的斜盘力矩具有有益的受力及工况, 因此, 取γ1=12°.对于外排斜盘倾角, 由上可知, γ2在7°~10°变化时, 对应斜盘外排力矩较小, 与内排力矩可最大程度相互抵消, 使斜盘具有良好的受力效果.因外排斜盘的分布圆直径较大, 故其力臂较大, 同时, 外排配流盘对应的高压配油窗口半径同样较大, 为实现平衡式两排轴向柱塞泵关键零部件的受力均衡, 在内排力臂较小的情况下, 需通过增大对应力臂垂直方向上的力, 以提高其力矩, 达到内外排力矩趋于接近甚至相等.
显然, 在合力一定的前提下, 增大内排斜盘倾角, 可增大其相应分力.为此, 取内排斜盘倾角大于外排斜盘倾角, 即:γ1=12°, γ2<12°, 设置参数如表 3所示, 进一步分析内、外排斜盘倾角的匹配程度.
|
| 图 9 斜盘力学模型 Fig.9 Swash plate mechanics model |

|
| 图 10 不同内外排斜盘斜面倾角下的内排斜盘力矩 Fig.10 Inner swash plate moment under different inner and outer swash plate angles |
|
| 图 11 不同内外排斜盘斜面倾角下的外排斜盘力矩 Fig.11 Outer swash plate moment under different inner and outer swash plate angles |
| (°) | ||||||
| γ1 | 12 | 12 | 12 | 12 | 12 | 12 |
| γ2 | 11 | 10 | 9 | 8 | 7 | 6 |
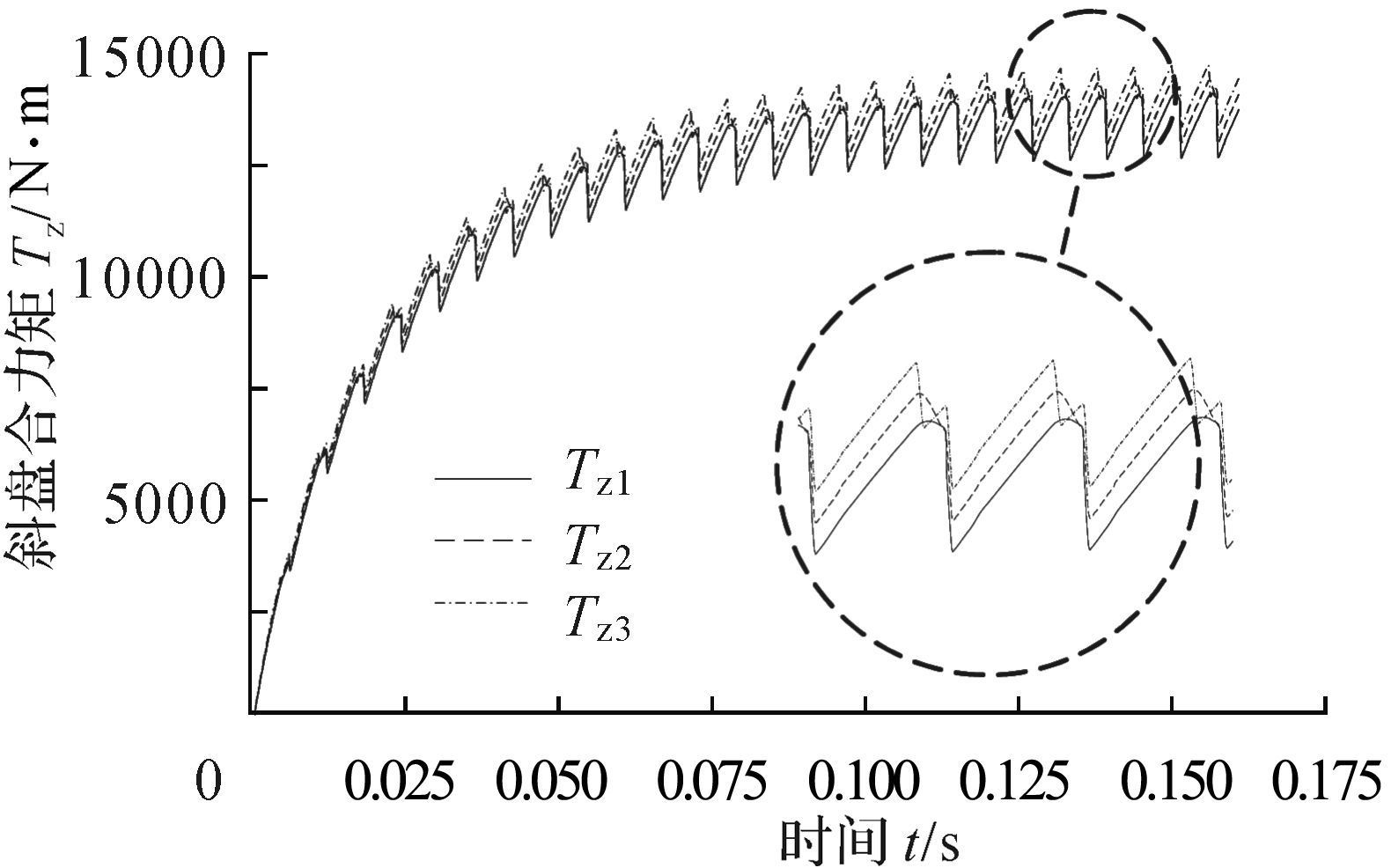
图 12为前三组数据仿真曲线.从图中依次可测得其峰值之差ΔTz1=1 417.92 N·m, ΔTz2=1 379.73 N·m, ΔTz3=1 361.7 N·m, 可见第3组数据仿真下的斜盘合力矩具有更小的脉动, 优于前两组数据.
|
| 图 12 前三组斜盘倾角系列下的合力矩曲线 Fig.12 Swash plate moment curve of first three sets of oblique angle series |
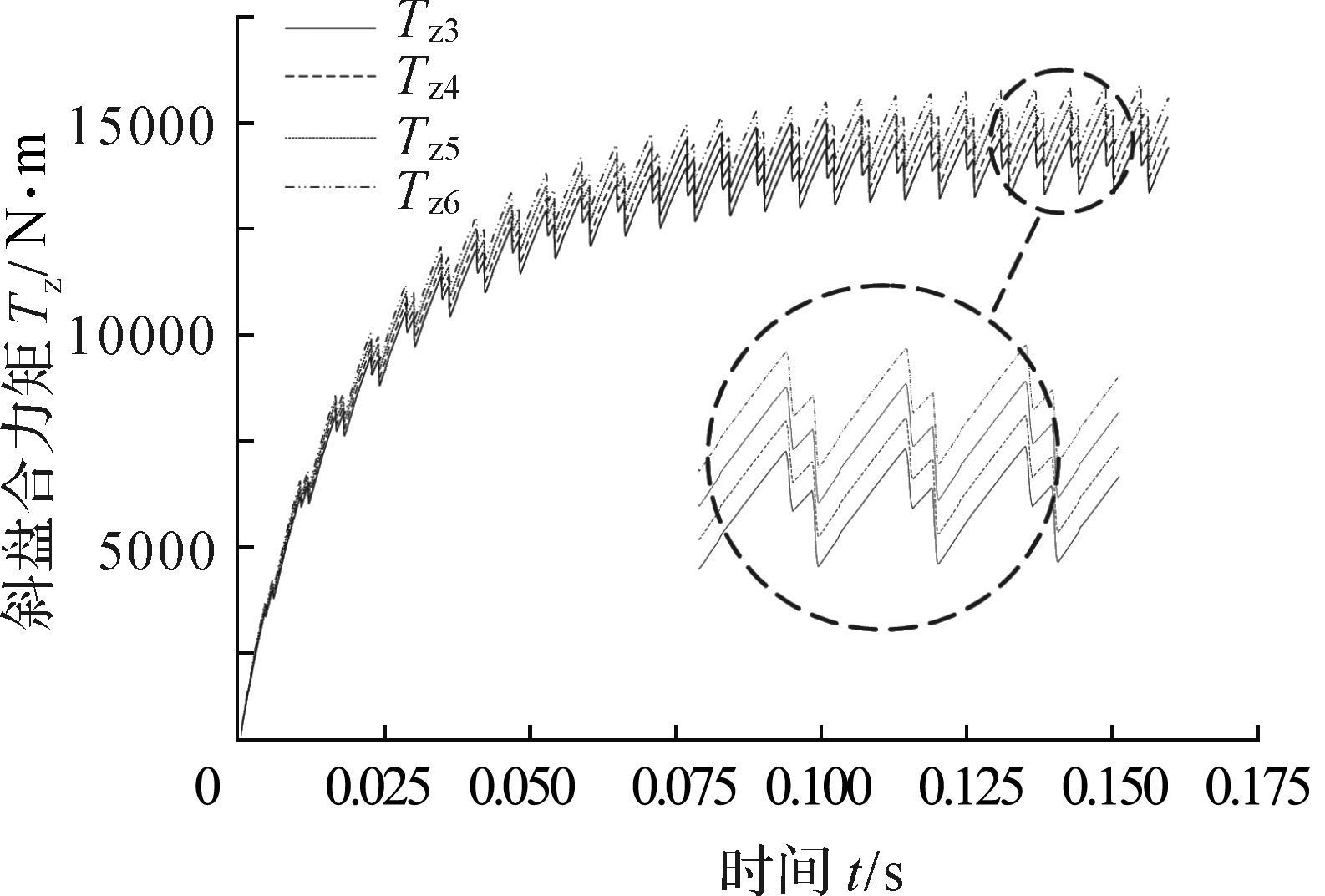
从图 13中可以看出, 后四组数据Tz3,Tz4,Tz5,Tz6在斜盘合力矩方面曲线走势完全一样, 由前述可知, 内排斜盘倾角应尽量大, 同时从图 11可以看出γ2<8°时, 所对应T外的极值已超出图形范围, 并有微微上扬的趋势, 因此取γ2=9°.
|
| 图 13 后四组斜盘倾角系列下的合力矩曲线 Fig.13 Swash plate moment curve of after four sets of oblique angle series |
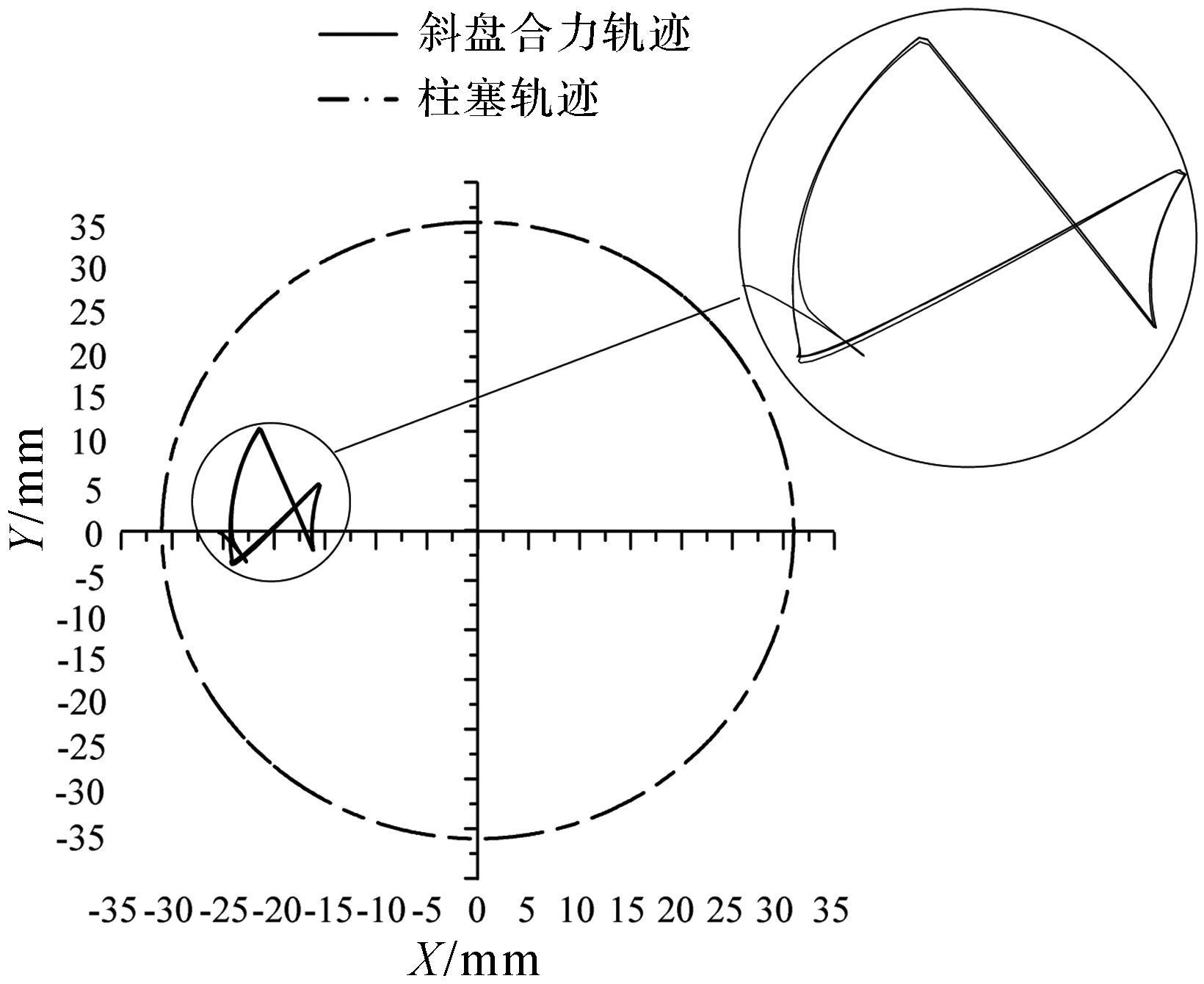
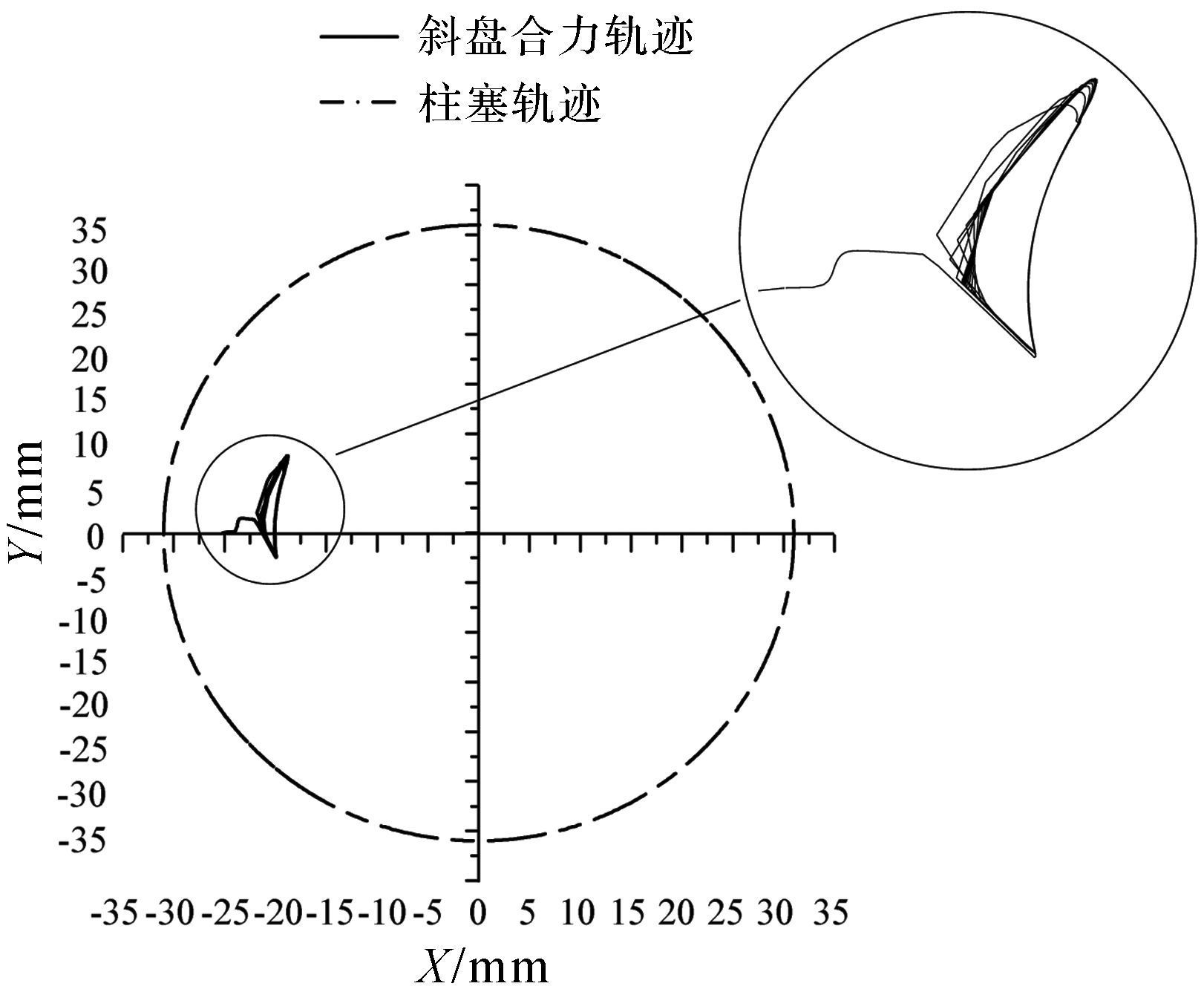
斜盘合力轨迹范围反映斜盘受力稳定性, 合力轨迹范围越小, 斜盘受力越稳定。
通过AMEsim中的Post processing及Plot manager, 可得斜盘所受合力轨迹与柱塞轨迹关系, 如图 14和图 15所示.
|
| 图 14 普通轴向柱塞泵斜盘合力轨迹 Fig.14 Ordinary axial piston pump resultant trace |
|
| 图 15 平衡式两排轴向柱塞泵斜盘合力轨迹 Fig.15 Balanced two-ring axial piston pump resultant trace |
从图 14和图 15中可以看出, 平衡式两排轴向柱塞泵和普通轴向柱塞泵斜盘合力轨迹均存在正负交替变化的现象, 不同的是平衡式两排轴向柱塞泵的合力轨迹呈类“三角形”, 其处于负值处的轨迹较普通轴向柱塞泵的类“蝴蝶型”合力轨迹处于负值处的轨迹要少.据此可知, 其因合力正负交变引起的机械振动小, 因此产生的机械噪声小.而且从其合力轨迹可以看出平衡式两排轴向柱塞泵的合力轨迹转折点少, 方向突变性低, 合力变化平缓, 说明类“三角形”轨迹较类“蝴蝶型”轨迹而言, 前者条件下斜盘受力良好, 运行更平稳, 振动更小.
4 结论在对平衡式两排轴向柱塞泵斜盘力学特性分析的基础上, 建立其仿真模型, 分析了柱塞分布圆半径、柱塞直径、斜盘倾角对斜盘合力矩的影响, 得出如下结论:
1) 随着内排柱塞分布圆半径的增大, 斜盘所受合力矩减小;随着外排柱塞分布圆半径的增大, 斜盘所受合力矩增大, 且外排分布圆半径对合力矩的影响远大于内排对其影响.为降低斜盘合力矩, 应在平衡式两排轴向柱塞泵结构允许的条件下, 尽可能减小内外排柱塞分布圆半径差.
2) 随着内排柱塞直径的增大, 斜盘所受合力矩减小;随着外排柱塞直径的增大, 斜盘所受合力矩增大, 且其影响超过内排直径的影响.为降低斜盘合力矩, 应使内排柱塞直径尽可能接近外排柱塞直径, 这同时也为达到降低平衡式两排轴向柱塞泵流量脉动的要求.
3) 平衡式两排轴向柱塞泵和普通轴向柱塞泵均存在合力矩正负交替情况, 其中平衡式两排轴向柱塞泵的类“三角形”轨迹较普通轴向柱塞泵的类“蝴蝶型”轨迹有较明显优势, 合力轨迹转折点少, 方向突变性低, 合力变化平缓, 使得平衡式两排轴向柱塞泵斜盘受力良好, 运行更平稳, 振动更小.
| [1] | KIM J H, JEON C S, HONG Y S. Constant pressure control of a swash plate type axial piston pump by varying both volumetric displacement and shaft speed[J]. International Journal of Precision Engineering & Manufacturing , 2015, 16 (11) : 2395–2401. |
| [2] |
杨华勇, 宋月超, 徐兵.
复杂工况下柱塞泵流量脉动并行仿真与试验研究[J]. 中国科学(技术科学) , 2012, 42 (12) : 1463–1471.
YANG Hua-yong, SONG Yue-chao, XU Bing. Parallel simulation and experimental research on flow ripple of axial piston pump under complicated conditions[J]. Scientia Sinica (Technologica) , 2012, 42 (12) : 1463–1471. |
| [3] | OUYANG Xiao-ping, FANG Xu, YANG Hua-yong. An investigation into the swash plate vibration and pressure pulsation of piston pumps based on full fluid-structure interactions[J]. Journal of Zhejiang University-Science A(Applied Physics & Engineering) , 2016, 17 (3) : 202–214. |
| [4] |
胡敏, 徐兵, 周万仁, 等.
轴向柱塞泵柱塞滑靴组件动力学特性建模与分析[J]. 农业机械学报 , 2016, 47 (3) : 373–341.
HU Min, XU Bing, ZHOU Wan-ren, et al. Modeling and analysis of dynamics characteristics of piston-slipper group of axial piston pump[J]. Transactions of the Chinese Society for Agricultural Machinery , 2016, 47 (3) : 373–341. |
| [5] |
那成烈, 李书泽, 那焱青.
轴向柱塞泵配流盘对缸体液压作用力矩的稳定性分析[J]. 甘肃工业大学学报 , 2001, 27 (3) : 41–43.
NA Cheng-lie, LI Shu-ze, NA Yan-qing. Stability analysis of hydraulic moment on cylinder of axial piston pump caused by valve plate[J]. Journal of Gansu University of Technology , 2001, 27 (3) : 41–43. |
| [6] |
丛凤杰, 仲梁维.
旋转斜盘实现变量的轴向柱塞泵研究[J]. 包装工程 , 2014, 35 (19) : 82–87.
CONG Feng-jie, ZHONG Liang-wei. Variable displacement of axial piston pump by rotating its swash-plate[J]. Packaging Engineering , 2014, 35 (19) : 82–87. |
| [7] |
石金艳, 谢永超.
斜盘倾角对柱塞运动影响的研究与分析[J]. 流体传动与控制 , 2010, 42 (5) : 30–32.
SHI Jin-yan, XIE Yong-chao. Study on the influence of the angle of slanting plate on piston movement[J]. Fluid Power Transmission & Control , 2010, 42 (5) : 30–32. |
| [8] |
刘健, 罗斌, 姜伟.
斜盘支承反力对轴向柱塞泵结构及参数的影响[J]. 科技通报 , 2006, 22 (2) : 206–207.
LIU Jian, LUO Bin, JIANG Wei. Effects of slanting plate force on the structural parameters of axial piston pump[J]. Bulletin of Science & Technology , 2006, 22 (2) : 206–207. |
| [9] |
朱钰.
轴向变量柱塞泵斜盘力矩的研究[J]. 船海工程 , 2008, 37 (6) : 74–76.
ZHU Yu. Research on the swash plate torque of axial variable piston pump[J]. Ship & Ocean Engineering , 2008, 37 (6) : 74–76. |
| [10] |
徐兵, 宋月超, 杨华勇.
柱塞泵斜盘交错角降噪结构优化[J]. 浙江大学学报(工学版) , 2013, 47 (6) : 1043–1050.
XU Bing, SONG Yue-chao, YANG Hua-yong. Optimization of swash-plate cross angle noise-reduction structure for swash-plate-type axial piston pump[J]. Journal of Zhejiang University (Engineering Science) , 2013, 47 (6) : 1043–1050. |
| [11] | ZEIGER G, AKERS A. Torque on the swash plate of an axial piston pump[J]. Journal of Dynamic Systems Measurement & Control , 1985, 107 (3) : 220–226. |
| [12] |
邓海顺, 王传礼, 张立祥.
平衡式两排轴向柱塞泵流量脉动的研究[J]. 农业机械学报 , 2014, 45 (5) : 305–309.
DENG Hai-shun, WANG Chuan-li, ZHANG Li-xiang. Study on flow ripple of balanced two-ring axial piston pump[J]. Transactions of the Chinese Society for Agricultural Machinery , 2014, 45 (5) : 305–309. |
| [13] |
邓海顺, 黄坤, 王传礼, 等.
平衡式两排轴向柱塞泵缸体倾覆力矩[J]. 吉林大学学报(工学版) , 2015, 61 (2) : 723–737.
DENG Hai-shun, HUANG Kun, WANG Chuan-li, et al. Overturning moment of cylinder of balanced two-ring axial piston pump[J]. Journal of Jilin University(Engineering and Technology Edition) , 2015, 61 (2) : 723–737. |
| [14] | MANRING N D. The control and containment forces on the swash plate of an axial piston pump utilizing a secondary swash-plate angle[C]//Proceedings of the 2002 American Control Conference. Anchorage:IEEE, 2002:4837-4842. |
| [15] |
李壮云. 液压元件与系统[M]. 3版. 北京:机械工业出版社,2011:82-84.
LI Zhuang-yun. Hydraulic components and systems[M]. 3th ed. Beijing:Mechanical Industry Press, 2011:82-84. |
| [16] | ZHANG X, CHO J, NAIR S S, et al. Damping on the swash plate of an axial-piston pump[C]//Proceedings of the 2000 American Control Conference. Chicago:IEEE, 2000:3590-3594. |



