2. 哈尔滨工业大学 机器人技术与系统国家重点实验室, 黑龙江 哈尔滨 150080;
3. 江南大学 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China ;
3. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Jiangnan University, Wuxi 214122, China
柔顺机构是一种利用柔性部件的变形来实现运动和力转换及传递的新型机构[1].柔顺机构在结构上用柔性铰链代替了刚性运动关节, 因此其构件数目要远少于传统机构, 最明显的效果就是避免了机构中的摩擦、间隙及润滑等方面的问题[2], 故而其在精密工程、仿生机器人、智能结构三大领域得到了广泛应用[3].平面折展机构(lamina emergent mechanisms, LEMs)是一种从平面中制造并且能够“浮出”制造平面的新型柔顺机构[4].LEMs在拥有其他柔顺机构优点的同时还具有以下无可比拟的优势:1) LEMs在平面状态下体积小, 能减少运输和储藏空间;2) 加工工艺简单, 制造成本低;3) 能以简单的拓扑结构实现较为复杂的机械动作.Wilding等在球面机构基础上利用LEMs简洁紧凑的特性, 获得了21种球面LEMs四杆机构[5].Gollnick等通过观察研究, 率先提出了多层LEMs的概念[6].楚红岩采用刚体代替法设计了多层LEMs水杯固定器[7].邱丽芳等基于微型升降机构的原理, 设计了一种LEMs柔顺升降机构[8].
目前, 对LEMs的研究主要集中于柔性铰链的设计及分析.Jacobsen等[9]提出了LEMs柔性铰链的基本设计准则, 并用实例加以验证.之后, Jacobsen等[10]率先提出了符合平面特性的内LET柔性铰链和外LET柔性铰链, 并推导了其等效弹簧刚度模型.韦志鸿[11]以外LET柔性铰链的结构参数为设计变量, 采用模拟退火法实现了LET柔性铰链的参数优化.Magleby等[12]提出了LEMs柔性铰链的新设计标准, 并以此为基础设计了可应用于钣金材料的RUFF(revolute U-form flexure)铰链及TUFF (torsional U-form flexure)铰链.Wilding等[13]对外LET柔性铰链进行优化, 提出了可以承受轴向拉力和压力作用的外LET铰链.邱丽芳等[14-16]设计了具有较大转动角度的S型柔性铰链和梳齿型柔性铰链, 并结合S型铰链和外LET铰链的优点, 得到了一种S-LET复合型柔性铰链.综上所述, 国内外学者已在柔性铰链这一研究领域取得了丰硕成果, 但是对于内LET柔性铰链, 其仍存在轴向刚度低, 压缩载荷作用下易产生寄生运动, 从而影响机构工作精度的问题.
针对上述问题, 本文基于倒置原则[17]提出了一种抗压内LET柔性铰链, 推导了该铰链的弯曲等效刚度和抗压等效刚度, 并用有限元分析实例验证了其正确性;最后将抗压内LET柔性铰链与内LET柔性铰链的性能进行比较, 证明了其优越性.
1 抗压内LET柔性铰链设计目前, 在LEMs中最常用的内LET柔性铰链如图 1所示, 其能实现单自由度转动, 但当内LET柔性铰链受轴向压力载荷作用时, 柔顺片段会产生连带运动, 从而影响机构的动作精度.由于柔顺片段的抗拉强度远大于抗压强度, 故为了提高内LET铰链的抗压性能, 本文基于倒置原则设计了如图 2所示的抗压内LET柔性铰链.

|
| 图 1 内LET柔性铰链 Fig.1 Inside LET flexure hinge |

|
| 图 2 抗压内LET柔性铰链 Fig.2 Compressive inside LET flexure hinge |
如图 2所示, 抗压内LET柔性铰链关于y轴对称, 其由柔顺片段A, B, C, D, E, F, G连接组成.抗压内LET柔性铰链的工作情况主要分为2种:1) 抗压内LET柔性铰链两端受转矩作用, 柔顺片段可根据各部分所起的作用分为弯曲片段和扭转片段, 其中柔顺片段A, B, C, D, E为弯曲片段, 柔顺片段F, G为扭转片段;2) 抗压内LET柔性铰链两端受压力作用, 此时柔顺片段可分为拉伸片段、压缩片段和弯曲片段, 其中柔顺片段C为拉伸片段, 柔顺片段A, B, D, E为压缩片段, 柔顺片段F, G为弯曲片段.当铰链所受载荷为压力时, 刚度较小的柔顺片段C承受拉力作用, 大幅减少了铰链的连带运动, 提高了抗压刚度.
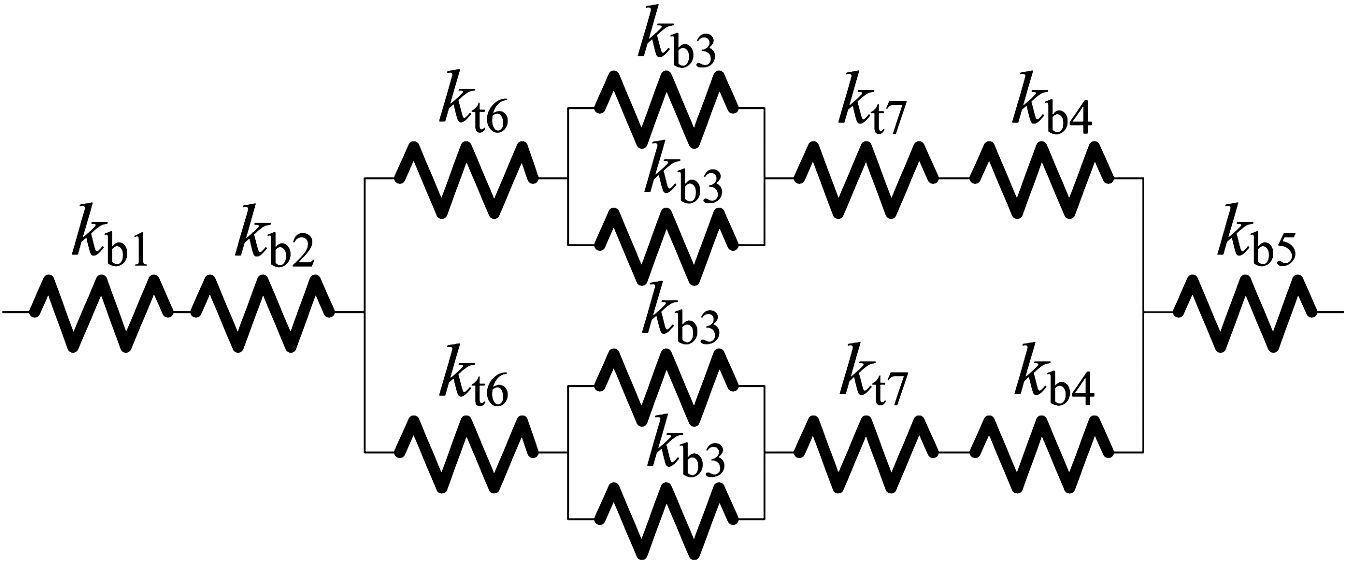
2 抗压内LET柔性铰链弯曲等效刚度分析 2.1 抗压内LET柔性铰链弯曲等效刚度当抗压内LET柔性铰链受如图 2所示的转矩T作用时, 根据Jacobsen等提出的等效法[10], 首先将弯曲片段和扭转片段分别等效为与之对应的弯曲弹簧及扭转弹簧, 其次利用弹簧串并联原理, 推导整个铰链的弯曲等效刚度keq, bend.各个柔顺片段的尺寸变量定义如图 3所示, 抗压内LET铰链对应的弯曲等效弹簧刚度模型如图 4所示.

|
| 图 3 抗压内LET柔性铰链各柔顺片段尺寸示意图 Fig.3 Dimension parameter diagram of compliant segments of the compressive inside LET flexure hinge |
|
| 图 4 弯曲等效弹簧刚度模型 Fig.4 Bending equivalent spring stiffness model |
基于图 4所示的弹簧模型, 利用弹簧串并联原理可得到抗压内LET铰链弯曲等效刚度:
| ${{k}_{eq,\text{ }bend}}=\frac{{{k}_{b1}}{{k}_{b2}}{{k}_{s1}}{{k}_{b5}}}{{{k}_{b2}}{{k}_{s1}}{{k}_{b5}}+{{k}_{b1}}{{k}_{s1}}{{k}_{b5}}+{{k}_{b1}}{{k}_{b2}}{{k}_{b5}}+{{k}_{b1}}{{k}_{b2}}{{k}_{s1}}},$ | (1) |
其中
| ${{k}_{s1}}=\frac{4{{k}_{t6}}{{k}_{b3}}{{k}_{t7}}{{k}_{b4}}}{2{{k}_{b3}}{{k}_{t7}}{{k}_{b4}}+{{k}_{t6}}{{k}_{t7}}{{k}_{b4}}+2{{k}_{t6}}{{k}_{b3}}{{k}_{b4}}+2{{k}_{t6}}{{k}_{b3}}{{k}_{t7}}},$ | (2) |
式中:kbi(i=1, 2, 3, 4, 5) 为柔顺片段A, B, C, D, E的弯曲等效弹簧刚度, kti(i=6, 7) 为柔顺片段F, G的扭转等效弹簧刚度.
kbi可由下式求得:
| ${{k}_{bi}}=\frac{E{{w}_{i}}{{t}^{3}}}{12{{L}_{i}}},$ | (3) |
式中:E为材料的弹性模量, wi(i=1, 2, 3, 4, 5) 为弯曲片段宽度, t为抗压内LET铰链厚度, Li(i=1, 2, 3, 4, 5) 为弯曲片段长度.
kti可表示为[18]
| ${{k}_{ti}}=\frac{Gt{{w}_{i}}^{3}}{{{L}_{i}}(3.5+3.5{{w}_{i}}^{2}/{{t}^{2}})},$ | (4) |
式中:G为材料的剪切模量, Li(i=6, 7) 为扭转片段长度, wi(i=6, 7) 为扭转片段宽度.
2.2 弯曲刚度的有限元仿真与验证对于后续分析所需的实例, 选择强度与弹性模量之比较高的ABS工程塑料作为抗压内LET柔性铰链的材料, 其弹性模量E=220 0 MPa, 泊松比v=0.34, 该铰链的各个尺寸值如表 1所示.
| 尺寸 | 量值/mm |
| L1 | 22.2 |
| w1 | 5.0 |
| L2 | 16.0 |
| w2 | 5.0 |
| L3 | 10.0 |
| w3 | 0.8 |
| L4 | 14.5 |
| w4 | 5.0 |
| L5 | 22.2 |
| w5 | 5.0 |
| L6 | 5.6 |
| L7 | 8.1 |
| w6 | 3.5 |
| w7 | 5.0 |
| t | 0.5 |
抗压内LET柔性铰链所受x轴方向转矩T与铰链转角φ之间的关系可以表示为
| $T={{k}_{eq,\text{ }bend}}\varphi ,$ | (5) |
其中弯曲等效弹簧刚度keq, bend可以通过将表 1中的数据代入式(1) 求得, 其值为2.439 6 N·mm/rad.根据式(3) 、(4) 、(5) , 即可得到不同转矩作用下铰链转角的理论值和铰链弯曲、扭转所占的变形比例, 结果如表 2所示.
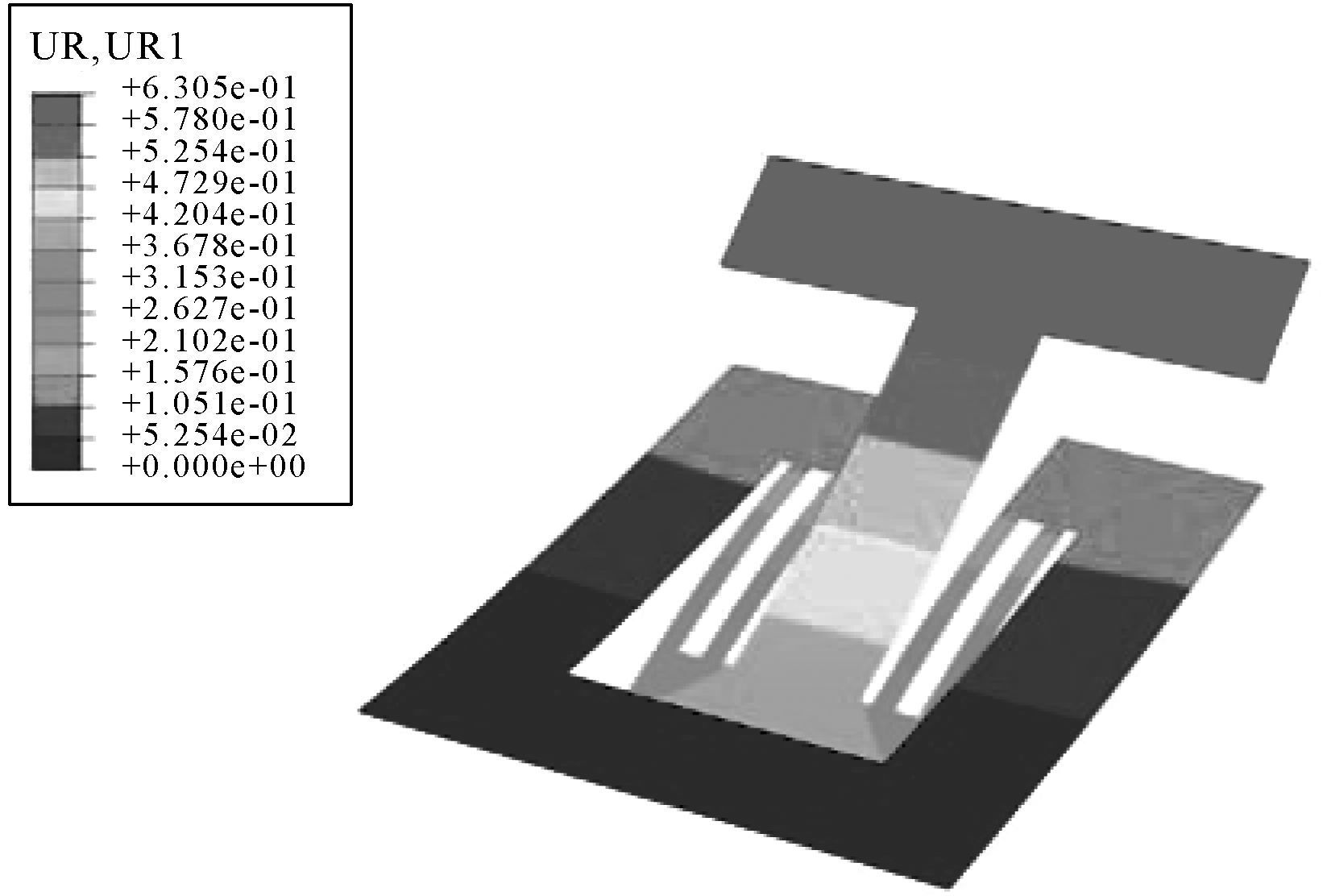
为验证所推导的弯曲等效弹簧刚度模型的正确性, 根据表 1中的尺寸数据, 利用CAE有限元仿真软件建立抗压内LET铰链的三维模型, 并对其施加约束及载荷.如图 5所示, 当转矩T=1.5 N/mm时, 铰链的转角为0.630 5 rad.输入不同的转矩, 可以得到对应的转角仿真值, 如表 2所示.
| 转矩/N·mm | 转角理论值/rad | 扭转所占变形比例/% | 弯曲所占变形比例/% | 转角仿真值/rad | 相对误差/% |
| 0.3 | 0.123 0 | 12.44 | 87.56 | 0.126 2 | -2.54 |
| 0.6 | 0.245 9 | 12.44 | 87.56 | 0.252 4 | -2.58 |
| 0.9 | 0.368 9 | 12.44 | 87.56 | 0.378 5 | -2.54 |
| 1.2 | 0.491 9 | 12.44 | 87.56 | 0.504 6 | -2.52 |
| 1.5 | 0.614 9 | 12.44 | 87.56 | 0.630 5 | -2.47 |
| 1.8 | 0.737 8 | 12.44 | 87.56 | 0.756 4 | -2.46 |
| 2.1 | 0.860 8 | 12.44 | 87.56 | 0.882 2 | -2.43 |
| 2.4 | 0.983 8 | 12.44 | 87.56 | 1.008 0 | -2.40 |
| 2.7 | 1.107 0 | 12.44 | 87.56 | 1.133 0 | -2.29 |
| 3.0 | 1.230 0 | 12.44 | 87.56 | 1.259 0 | -2.30 |
|
| 图 5 载荷为转矩时的抗压内LET柔性铰链角位移云图 Fig.5 Angular displacement nephogram of compressive inside LET flexure hinge under the effect of torque |
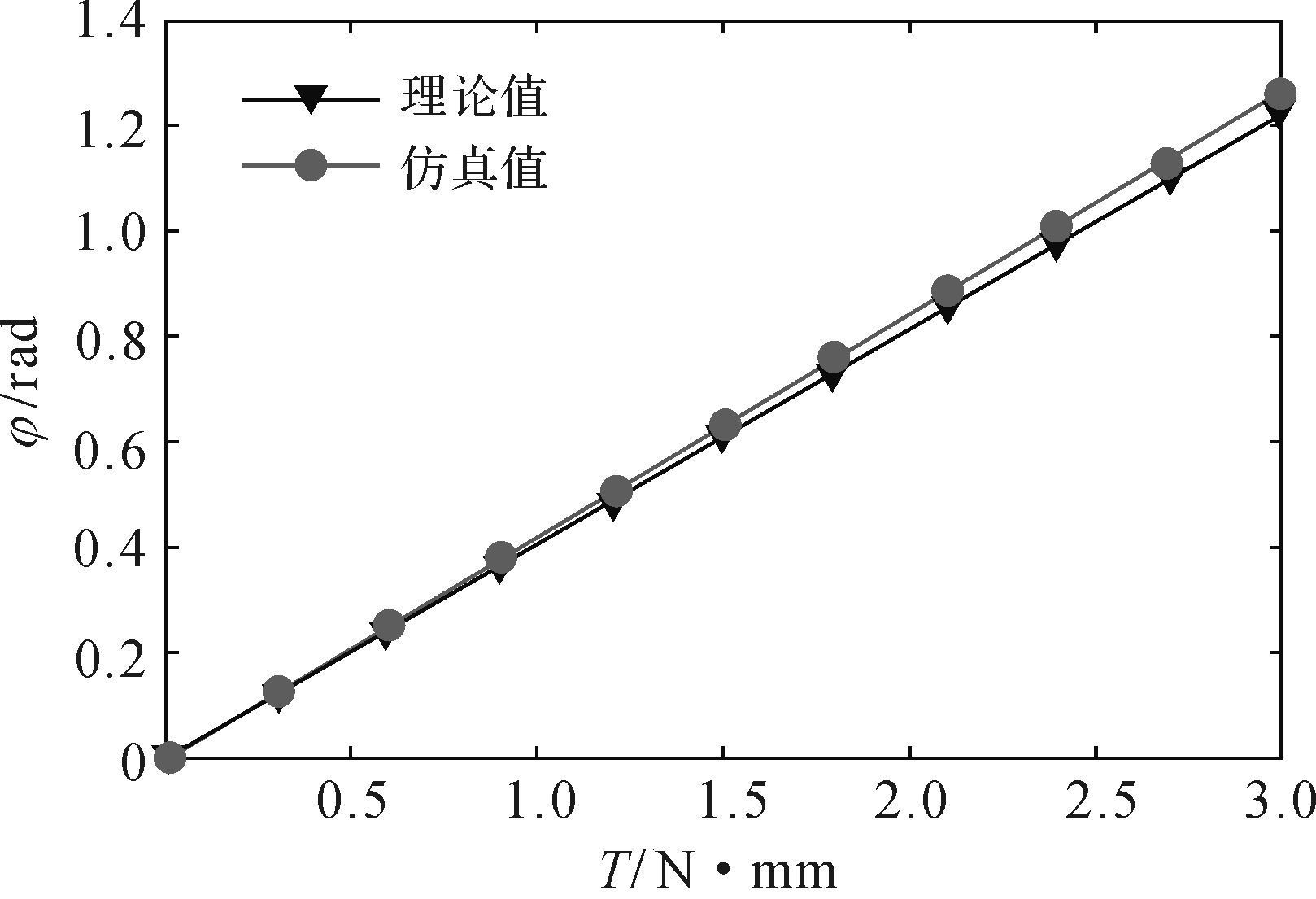
为了更加直观地表达转矩相同时转角理论计算值与转角仿真值之间的关系, 按照表 2中的数值, 绘制得到如图 6所示的抗压内LET柔性铰链转矩与转角之间的关系图.由图 6发现:相同转矩作用下, 铰链的转角理论计算值与仿真值高度吻合, 最大误差不超过2.58%;且转矩与转角间保持良好的线性关系, 即铰链的弯曲刚度较为稳定.上述分析证明了所推得弯曲等效刚度的正确性.
|
| 图 6 抗压内LET柔性铰链扭矩与转角关系 Fig.6 Relationship of torque and torsion angle of compressive inside LET flexure hinge |
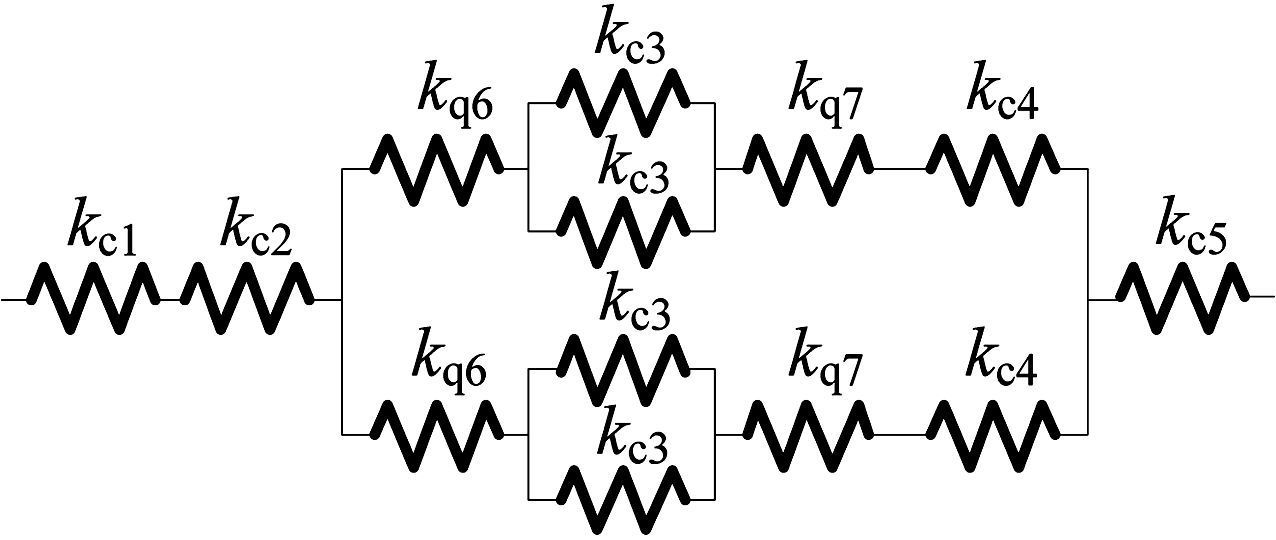
当抗压内LET柔性铰链受如图 2所示的压力载荷p作用时, 基于等效法可以将铰链的拉伸片段及压缩片段等效为拉压弹簧, 将弯曲片段等效为弯曲弹簧, 根据弹簧串并联原理可推导铰链的抗压等效刚度keq, comp.抗压内LET铰链对应的抗压等效弹簧刚度模型如图 7所示.
|
| 图 7 抗压等效弹簧刚度模型 Fig.7 Compressive equivalent spring stiffness model |
根据图 7所示的弹簧模型, 利用弹簧串并联原理可以得到抗压内LET铰链的抗压等效刚度:
| ${{k}_{eq,\text{ }comp}}=\frac{{{k}_{c1}}{{k}_{c2}}{{k}_{s2}}{{k}_{c5}}}{{{k}_{c2}}{{k}_{s2}}{{k}_{c5}}+{{k}_{c1}}{{k}_{s2}}{{k}_{c5}}+{{k}_{c1}}{{k}_{c2}}{{k}_{c5}}+{{k}_{c1}}{{k}_{c2}}{{k}_{s2}}},$ | (6) |
其中
| ${{k}_{s2}}=\frac{4{{k}_{q6}}{{k}_{c3}}{{k}_{q7}}{{k}_{c4}}}{2{{k}_{c3}}{{k}_{q7}}{{k}_{c4}}+{{k}_{q6}}{{k}_{q7}}{{k}_{c4}}+2{{k}_{q6}}{{k}_{c3}}{{k}_{c4}}+2{{k}_{q6}}{{k}_{c3}}{{k}_{q7}}},$ | (7) |
式中:kci(i=1, 2, 3, 4, 5) 为柔顺片段A, B, C, D, E的抗压等效弹簧刚度, kqi(i=6, 7) 为柔顺片段F, G的弯曲等效弹簧刚度.
kci可由下式求得:
| ${{k}_{ci}}=\frac{E{{w}_{i}}t}{{{L}_{i}}}.$ | (8) |
弯曲片段的刚度可利用伪刚体模型求得, 即:将压力载荷作用下产生弯曲变形的柔顺片段视为如图 8所示的刚体.

|
| 图 8 悬臂梁的伪刚体模型 Fig.8 Pseudo-rigid-body model of cantilever beam |
如图 8所示的伪刚体模型中的扭簧刚度系数Kfg可表示为
| ${{K}_{fg}}=\frac{\gamma {{K}_{\theta }}EI}{L},$ | (9) |
式中:γ为伪刚体模型的特征半径系数, Kθ为扭簧系数, 通常分别取γ=0.85, Kθ=2.65;I为梁的惯性矩;L为梁的长度.
在垂直力F作用下梁的挠度即弯曲片段的变形量d1可表示为
| ${{d}_{1}}=\gamma L\text{sin }\theta ,$ | (10) |
式中θ可以根据扭簧的受力关系求解.
| $FL\gamma \text{cos }\theta ={{K}_{fg}}\theta .$ | (11) |
联立式(10) 和式(11) , 得
| $\frac{F}{{{d}_{1}}}=\frac{{{K}_{\theta }}EI}{\gamma {{L}^{3}}},\text{ }$ | (12) |
即柔顺片段F, G的弯曲等效弹簧刚度kqi可表示为
| ${{k}_{qi}}=\frac{F}{{{d}_{1}}}=\frac{{{K}_{\theta }}E{{I}_{i}}}{\gamma {{L}_{i}}^{3}},$ | (13) |
式中:Ii(i=6, 7) 为弯曲片段截面的惯性矩;Li(i=6, 7) 为弯曲片段的长度.
3.2 抗压刚度的有限元仿真与验证抗压内LET柔性铰链所受y轴方向的压力载荷p与轴向变形量d之间的关系可表示为
| $p={{k}_{eq,\text{ }comp}}d,$ | (14) |
式中:抗压等效弹簧刚度keq, comp可由将2.2节的设计实例数值代入式(6) 求得, 其值为45.285 2 N/mm.基于式(8) 、(13) 、(14) , 即可得到不同压力作用下铰链的轴向变形量和铰链压缩、弯曲所占的变形比例, 如表 3所示.
| 压力/N | 变形理论值/mm | 压缩所占变形比例/% | 弯曲所占变形比例/% | 变形仿真值/mm | 相对误差/% |
| -0.2 | -0.004 416 | 33.86 | 66.14 | -0.004 655 | -5.13 |
| -0.4 | -0.008 833 | 33.86 | 66.14 | -0.009 311 | -5.13 |
| -0.6 | -0.013 250 | 33.86 | 66.14 | -0.013 970 | -5.15 |
| -0.8 | -0.017 670 | 33.86 | 66.14 | -0.018 620 | -5.10 |
| -1.0 | -0.022 080 | 33.86 | 66.14 | -0.023 280 | -5.15 |
| -1.2 | -0.026 500 | 33.86 | 66.14 | -0.027 930 | -5.12 |
| -1.4 | -0.030 920 | 33.86 | 66.14 | -0.032 580 | -5.10 |
| -1.6 | -0.035 330 | 33.86 | 66.14 | -0.037 240 | -5.13 |
| -1.8 | -0.039 740 | 33.86 | 66.14 | -0.041 890 | -5.13 |
| -2.0 | -0.044 160 | 33.86 | 66.14 | -0.046 550 | -5.13 |
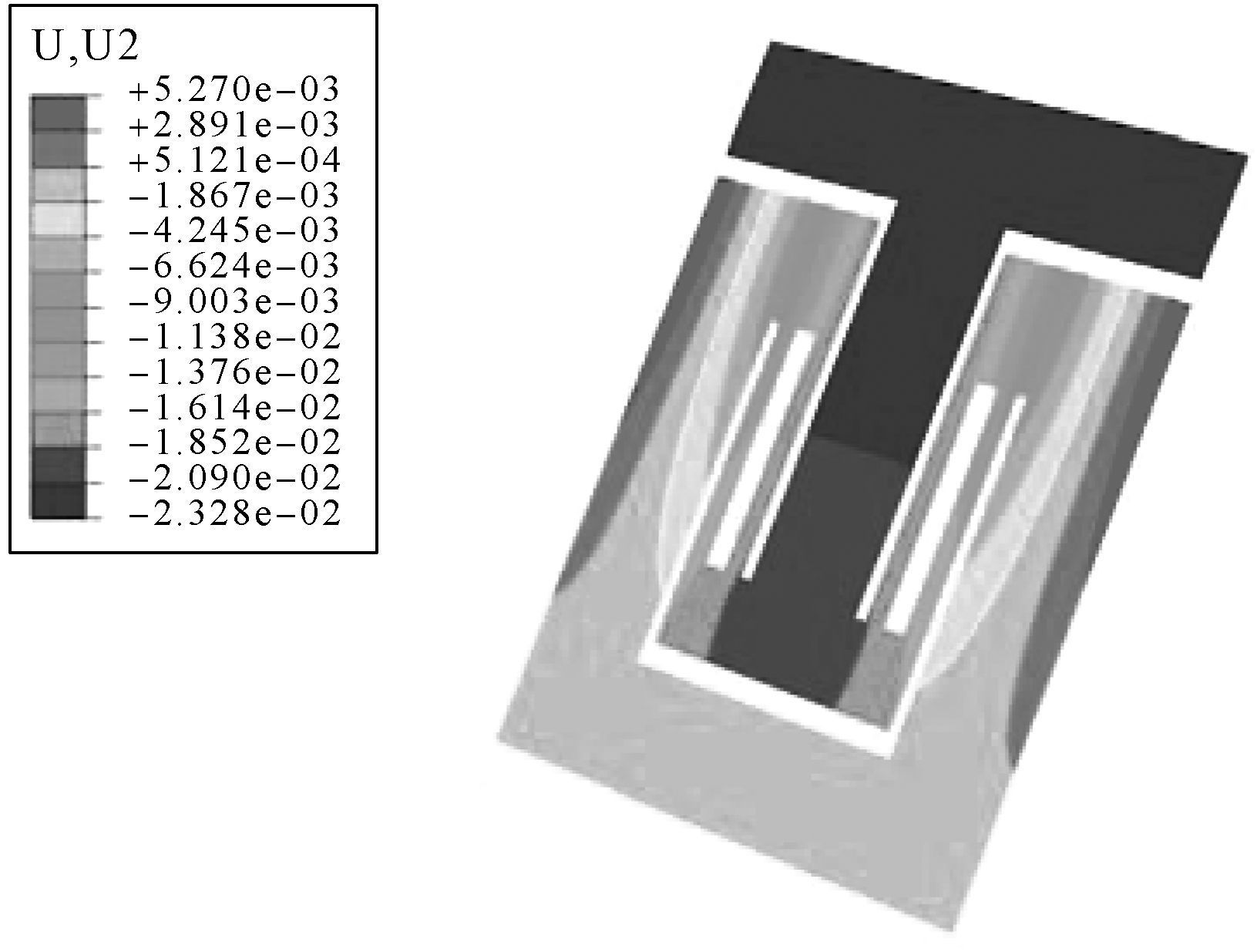
在仿真验证时, 对抗压内LET柔性铰链施加压力及约束.如图 9所示, 当压力p=-1.0 N时, 铰链的轴向变形量d=-0.023 28 mm.输入大小不同的压力, 即可得到如表 3所示的仿真值.
|
| 图 9 载荷为压力时的抗压内LET柔性铰链Y轴方向位移云图 Fig.9 Y axial direction displacement nephogram of compressive inside LET flexure hinge under the effect of pressure |
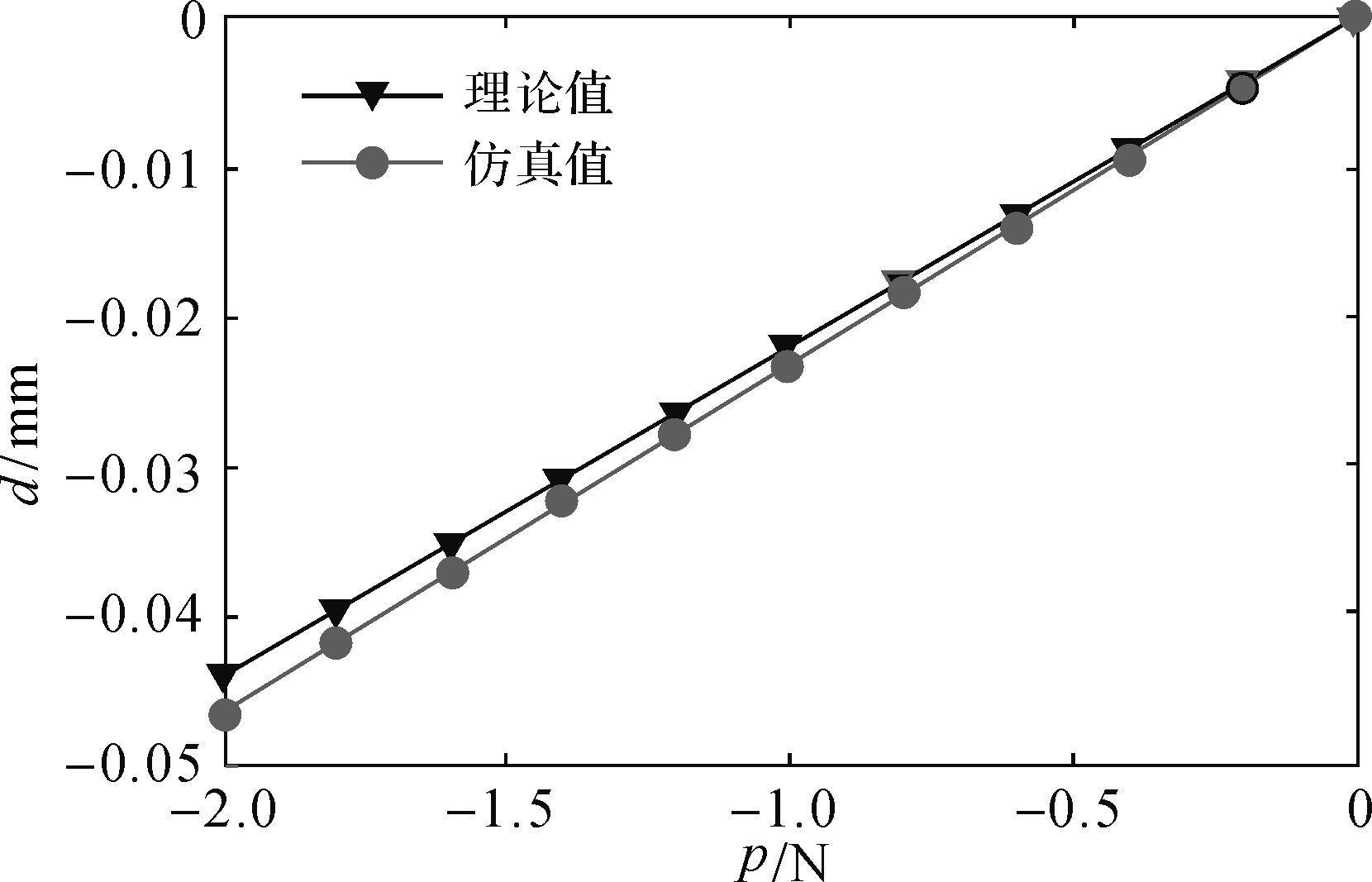
按照表 3中的数据, 绘制得到如图 10所示的抗压内LET铰链所受压力与轴向位移之间的关系图.分析可知, 轴向位移理论计算值与仿真值较为接近, 误差不超过5.15%, 且各自都具有较优的线性关系.证明了上述抗压等效弹簧刚度模型的正确性.
|
| 图 10 抗压内LET柔性铰链力与位移关系 Fig.10 Relationship of force and deformation of compressive inside LET flexure hinge |
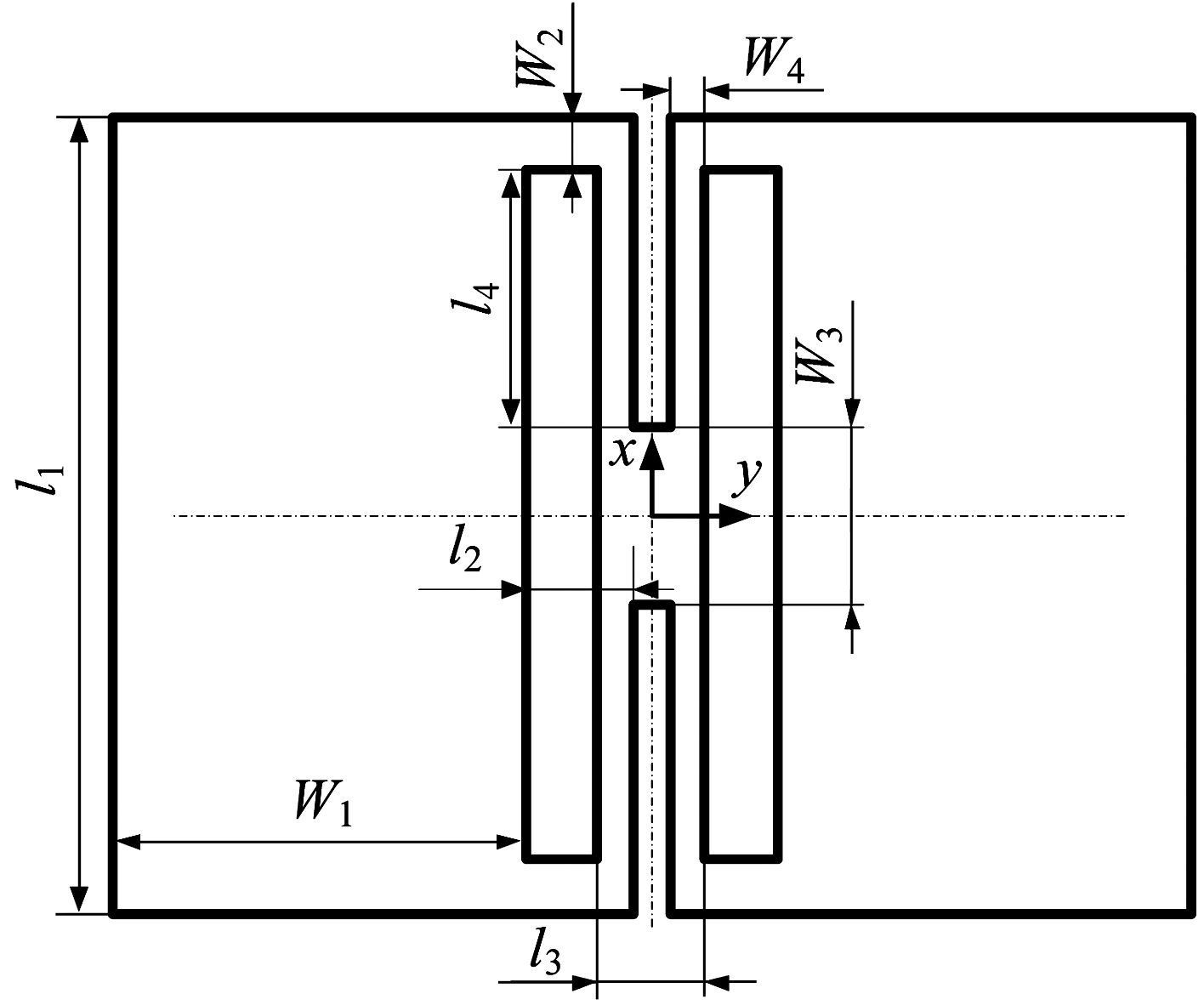
为了比较抗压内LET柔性铰链和内LET柔性铰链的性能, 将对外形尺寸同样为30.5 mm×22.2 mm的内LET铰链(如图 11所示)进行有限元仿真分析, 其具体尺寸值如表 4所示.
|
| 图 11 内LET柔性铰链各柔性片段尺寸示意图 Fig.11 Dimension parameter diagram of compliant segments of the inside LET flexure hinge |
| 尺寸 | 量值/mm |
| l1 | 22.2 |
| W1 | 11.7 |
| l2 | 3.0 |
| W2 | 1.5 |
| l3 | 3.1 |
| 尺寸 | 量值/mm |
| W3 | 5.0 |
| l4 | 7.1 |
| W4 | 1.0 |
| t | 0.5 |
在CAE有限元仿真软件中建立内LET柔性铰链的三维模型, 且同样采用弹性模量E=2 200 MPa, 泊松比v=0.34的ABS工程塑料作为铰链的材料.对其加载x轴方向的转矩, 所得的仿真数据如表 5所示.加载y轴方向的压力载荷, 所得的仿真数据如表 6所示.
| 转矩/N·mm | 转角仿真值/rad | 弯曲刚度/(N·mm/rad) |
| 0.3 | 0.150 7 | 1.990 7 |
| 0.6 | 0.301 4 | 1.990 7 |
| 0.9 | 0.452 0 | 1.991 2 |
| 1.2 | 0.602 7 | 1.991 0 |
| 1.5 | 0.753 4 | 1.991 0 |
| 1.8 | 0.904 1 | 1.991 0 |
| 2.1 | 1.055 0 | 1.991 0 |
| 2.4 | 1.205 0 | 1.991 7 |
| 2.7 | 1.356 0 | 1.991 2 |
| 3.0 | 1.507 0 | 1.990 7 |
| 压力/N | 位移仿真值/mm | 抗压刚度/(N/mm) |
| -0.2 | -0.114 2 | 1.751 3 |
| -0.4 | -0.232 4 | 1.721 2 |
| -0.6 | -0.354 5 | 1.692 5 |
| -0.8 | -0.480 6 | 1.664 6 |
| -1.0 | -0.610 5 | 1.638 0 |
| -1.2 | -0.744 1 | 1.612 7 |
| -1.4 | -0.881 3 | 1.588 6 |
| -1.6 | -1.022 0 | 1.565 6 |
| -1.8 | -1.165 0 | 1.545 1 |
| -2.0 | -1.310 0 | 1.526 7 |
由表 5可知, 内LET柔性铰链的弯曲刚度比较稳定,基本维持在1.991 0 N·mm/rad左右;由表 6可以发现, 内LET柔性铰链的抗压刚度随力的增加逐渐减小, 呈非线性变形.
将有限元分析所得的抗压内LET柔性铰链与内LET柔性铰链的弯曲刚度及抗压刚度汇总于表 7.
| 项目 | 抗压内LET柔性铰链 | 内LET柔性铰链 | 比值 |
| keq, bend/(N·mm/rad) | 2.379 6 | 1.991 0 | 1.195 |
| keq, comp/(N/mm) | 42.962 8 | 1.526 7~1.751 3 | 24.532~28.141 |
由表 7中的2组数据对比发现, 在外形尺寸一致的情况下, 抗压内LET柔性铰链的弯曲刚度仅是内LET柔性铰链的1.195倍, 而抗压刚度却是内LET柔性铰链的24.532~28.141倍, 这表明在弯曲刚度没有明显增加的情况下, 抗压内LET柔性铰链的抗压刚度显著增大, 其结构设计符合预期要求.
5 结论1) 基于倒置原则, 本文提出了一种抗压内LET柔性铰链, 分别推导了其弯曲等效刚度和抗压等效刚度的理论计算模型, 并通过有限元分析实例验证了理论模型的正确性.
2) 通过抗压内LET柔性铰链与内LET柔性铰链之间的性能比较, 证明了抗压内LET柔性铰链在弯曲刚度没有明显变化的前提下, 抗压刚度大幅提高, 体现了其优越性.
| [1] | HOWELL L L. Compliant mechanisms[M]. New York: John Wiley and Sons , 2001 : 1 -30. |
| [2] |
王雯静, 余跃庆, 王华伟.
柔顺机构国内外研究现状分析[J]. 机械设计 , 2007, 24 (6) : 1–4.
WANG Wen-jing, YU Yue-qing, WANG Hua-wei. Analysis on the research status of compliant mechanism at home and abroad[J]. Journal of Machine Design , 2007, 24 (6) : 1–4. |
| [3] |
于靖军, 郝广波, 陈贵敏, 等.
柔性机构及其应用研究进展[J]. 机械工程学报 , 2015, 51 (13) : 53–68.
YU Jing-jun, HAO Guang-bo, CHEN Gui-min, et al. State-of-art of compliant mechanisms and their applications[J]. Journal of Mechanical Engineering , 2015, 51 (13) : 53–68. DOI:10.3901/JME.2015.13.053 |
| [4] | ALBRECHTSEN N B, MAGLEBY S P, HOWELL L L. Identifying potential applications for lamina emergent mechanisms using technology push product development[C]//Proceeding of the ASME IDETC/CIE 2010. Montreal, Canada:ASME, 2010:513-521. |
| [5] | WILDING S E, HOWELL L L, MAGLEBY S P. Spherical lamina emergent mechanisms[J]. Mechanism and Machine Theory , 2012, 49 (3) : 187–197. |
| [6] | GOLLNICK P S, MAGLEBY S P, HOWELL L L. An introduction to multilayer lamina emergent mechanisms[J]. Journal of Mechanical Design , 2011, 133 (8) : 602–610. |
| [7] |
楚红岩. 多层LEMs机构设计与分析[D]. 北京:北京科技大学机械工程学院,2012:39-71.
CHU Hong-yan. Design and analysis of multi-layered lamina emergent mechanisms[D]. Beijing:University of Science and Technology Beijing, School of Mechanical Engineering, 2012:39-71. |
| [8] |
邱丽芳, 陈家兴, 张九俏, 等.
平面折展升降柔顺机构设计[J]. 农业机械学报 , 2015, 46 (10) : 370–375.
QIU Li-fang, CHEN Jia-xing, ZHANG Jiu-qiao, et al. Design of lamina emergent elevator mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery , 2015, 46 (10) : 370–375. |
| [9] | JACOBSEN J O, WINDER B G, HOWELL L L, et al. Lamina emergent mechanisms and their basic elements[J]. Journal of Mechanisms and Robotics , 2010, 2 (1) : 298–320. |
| [10] | JACOBSEN J O, CHEN G, HOWELL L L, et al. Lamina emergent torsional (LET) joint[J]. Mechanism and Machine Theory , 2009, 44 (11) : 2098–2109. DOI:10.1016/j.mechmachtheory.2009.05.015 |
| [11] |
韦志鸿. LET柔性铰链的参数化设计及分析[D]. 北京:北京科技大学机械工程学院,2012:39-52.
WEI Zhi-hong. Parameter design and analysis of LET flexure hinge[D]. Beijing:University of Science and Technology Beijing, School of Mechanical Engineering, 2012:39-52. |
| [12] | MAGLEBY S P, FERRELL D B, ISAAC Y F, et al. Development of criteria for lamina emergent mechanism flexures with specific application to metals[J]. Journal of Mechanical Design , 2011, 133 (3) : 586–599. |
| [13] | WILDING S E, HOWELL L L, MAGLEBY S P. Introduction of planar compliant joints designed for combined bending and axial loading conditions in lamina emergent mechanisms[J]. Mechanism and Machine Theory , 2012, 56 (1) : 1–15. |
| [14] |
邱丽芳, 孟天祥, 张九俏, 等.
平面折展机构S形柔性铰链设计与试验[J]. 农业机械学报 , 2014, 45 (9) : 323–328.
QIU Li-fang, MENG Tian-xiang, ZHANG Jiu-qiao, et al. Design and test of lamina emergent mechanisms S-shaped flexure hinge[J]. Transactions of the Chinese Society for Agricultural Machinery , 2014, 45 (9) : 323–328. |
| [15] |
邱丽芳, 孟天祥, 张九俏, 等.
梳齿形柔性铰链的设计与分析[J]. 东北大学学报(自然科学版) , 2014, 35 (9) : 1316–1320.
QIU Li-fang, MENG Tian-xiang, ZHANG Jiu-qiao, et al. Design and analysis of comb-shaped flexure joint[J]. Journal of Northeastern University (Nature Science) , 2014, 35 (9) : 1316–1320. |
| [16] |
邱丽芳, 庞大千, 陈家兴, 等.
S-LET复合型柔性铰链设计与性能研究[J]. 农业机械学报 , 2016, 47 (2) : 408–412.
QIU Li-fang, PANG Da-qian, CHEN Jia-xing, et al. Design and performance analysis of lamina emergent mechanisms S-LET-shaped flexure Hinge[J]. Transactions of the Chinese Society for Agricultural Machinery , 2016, 47 (2) : 408–412. |
| [17] | ALEXANDRE E G, MAGLEBY S P, HOWELL L L, et al. Compliant joint design principles for high compressive load situations[J]. Journal of Mechanical Design , 2005, 127 (4) : 774–781. DOI:10.1115/1.1862677 |
| [18] | CHEN G, HOWELL L L. Two general solutions of torsional compliance for variable rectangular cross-section hinges in compliant mechanisms[J]. Precision Engineering , 2009, 33 (3) : 268–274. DOI:10.1016/j.precisioneng.2008.08.001 |



