在齿轮啮合传动的过程中, 由于啮合面的压力较大, 相对滑动速度较高, 发热量大, 产生的瞬时高温使润滑油膜破裂, 导致齿面直接接触, 产生干摩擦或半干摩擦, 这种摩擦将进一步提升温度, 从而在齿面局部产生固有熔焊粘附, 继而沿滑动方向撕裂, 形成两齿面间表层材料的转移, 容易造成齿面胶合、齿面较大的热应力变形、润滑油的稀释变形, 严重影响齿轮的传动性能.
目前, 在防止齿轮高温失效方面, 黄永晶等[1]利用模糊神经网络技术定性地预测了齿轮各参数对齿轮温度的影响.孙首群等[2]研究了在不同转速、转矩和环境温度下啮合轮齿温度的变化情况.何国旗等[3]分析了齿轮压力角的变化对齿轮本体温度的影响.陈磊等[4]基于ANSYS研究了高速齿轮在啮入、啮出时啮合区的接触压力和相对速度对齿轮温度的影响.王胜伟等[5]利用APDL语言进行移动热源加载, 发现提高面齿轮齿面精度、减小齿轮转速、使用动力黏度较大的润滑油或者减小接触载荷, 可在一定程度上延长齿轮的使用寿命.经查阅资料可知影响渐开线齿轮本体温度的主要因素有齿轮转矩、齿轮转速、齿轮的齿宽和齿轮压力角[2-6].采用二次回归正交的方法, 可设计这4个因素在不同水平的参数组合下对齿轮本体最高温度的影响[7].通过ANSYS有限元软件可分析得到齿轮表面最高温度值, 再利用Design-Expert软件得出齿轮表面的最高温度与齿轮转矩、齿轮转速、齿轮的齿宽和齿轮压力角的关系方程式, 将方程通过MATLAB转化为三维图形, 可清晰地看出这4个因素相互之间的变化对齿轮本体最高温度的影响, 以便为齿轮的设计提供借鉴[8-11].
1 二次回归正交设计实例及分析高速平稳运转的齿轮在啮合过程中啮合面处摩擦产生的热量会传到齿轮本体内, 齿轮的齿体会通过齿轮端面的润滑油和其间空气实现传热冷却, 在此过程中伴随着摩擦热量的散失.在这个不断啮合生热、不断对流传热的过程中热量最终会达到平衡, 形成一个比较稳定的温度场.现以某高速平稳运行机床的标准渐开线圆柱齿轮为例进行分析.齿轮的结构参数、工况及材料参数如表 1所示.
1.1 确定因子及二次多项式回归方程通过查阅文献和利用ANSYS进行温度分析时添加的边界条件公式可知, 影响轮齿齿面本体温度的主要因素有齿轮转速z1、转矩z2、齿宽z3和压力角z4.因此选取它们为自变量建立四元二次回归方程为
| $y={{b}_{0}}+\sum\limits_{j=1}^{4}{{{b}_{j}}{{z}_{j}}}+\sum\limits_{j=1}^{4}{{{b}_{jj}}{{z}_{j}}^{2}}+\sum\limits_{i <j}{{{b}_{ij}}{{z}_{i}}{{z}_{j}}},$ |
式中:b0为常数项, bj为一次项回归系数, bjj为二次项回归系数, bij为交互项回归系数.
| 主要参数 | 主动轮 | 从动轮 |
| 齿数z | 47 | 73 |
| 模数/mm | 2 | 2 |
| 压力角/(°) | 20 | 20 |
| 齿宽/mm | 35 | 30 |
| 变位系数x | 0 | 0 |
| 传动比i | 1.55 | 1.55 |
| 重合度ε | 1.78 | 1.78 |
| 输入转矩T/(N·m) | 52 | — |
| 转速n/(r/min) | 5 000 | 3 219 |
| 润滑方式 | 喷油润滑 | 喷油润滑 |
| 润滑油 | Mobil Jet Ⅱ | Mobil Jet Ⅱ |
| 工况条件 | 高速、平稳 | 高速、平稳 |
| 齿轮材料 | 20Cr | 20Cr |
| 弹性模量/MPa | 2.06×1011 | 2.06×1011 |
| 泊松比 | 0.29 | 0.29 |
| 热传导率/(W/m·K) | 44 | 44 |
| 密度(kg/m3) | 7.82×103 | 7.82×103 |
| 比热容/(kJ/(kg·℃)) | 0.46 | 0.46 |
| 热处理方式 | 渗碳淬火 | 渗碳淬火 |
| 接触疲劳许用应力/MPa | 667.5 | 634.0 |
| 弯曲疲劳许用应力/MPa | 428 | 417.5 |
试验次数N为
| $N={{m}_{c}}+2p+{{m}_{0}}={{2}^{4}}+2\times 4+3=27,$ |
式中:mc为第1类点, 为二水平(1和-1) 全因素试验的试验点, 这类试验点共有2p个;2p为第2类点, 为分布在p个坐标上的星号点, 这类试验点共有2p个, 它们与中心点的距离为γ;m0为第3类点, 为中心点, 即各变量都取零水平的试验点次数, 当m0=3, p=4时, 由γ2表查出γ2=2.390, 即星号臂γ=1.546[12].
确定试验因素Zj的变化范围并进行因素编码, 相应的计算公式为
| ${{Z}_{0j}}=\frac{{{Z}_{1j}}+{{Z}_{2j}}}{2},$ |
式中:Z0j为第j个因子的零水平;Z1j为第j个因子的下界;Z2j为第j个因子的上界.
| ${{\Delta }_{j}}=\frac{{{Z}_{2j}}-{{Z}_{0j}}}{\gamma },$ |
式中Δj为第j个因子的变化区间.
根据以往试验研究的结果和实际情况, 按照二次回归正交设计的基本原理与主要方程式, 确定z1, z2, z3, z4四个因子的编码表, 如表 2所示.
| xj | 因子 | |||
| n/(r/min) | T/(N·m) | b/mm | α/(°) | |
| +γ | 6 000 | 80 | 50 | 25 |
| 1 | 5 646.83 | 70.11 | 44.70 | 23.23 |
| 0 | 5 000 | 52 | 35 | 20 |
| -1 | 4 353.17 | 33.89 | 25.30 | 16.77 |
| -γ | 4 000 | 24 | 20 | 15 |
| Δj | 646.83 | 24.58 | 2.59 | 3.23 |
| 编码公式 | ||||
x1, x2, x3, x4的编码值分别为齿轮的转速z1、转矩z2、齿宽z3和压力角z4正交后的各水平编码值, 将其安排在所选正交表的相关列上, 正交表的表头就是试验方案, 表内的试验号即为处理组合号.另外在正交表的最前面添加1个x0列, 编码值全为1, 来估算常数项b0的值.按照正交组合设计安排27次试验, 试验方案见表 3.表中各平方项按照
| 处理 | x0 | x1 | x2 | x3 | x4 | x1x2 | x1x3 | x1x4 | x2x3 | x2x4 | x3x4 | x′1 | x′2 | x′3 | x′4 | y |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 101.99 |
| 2 | 1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 104.8 |
| 3 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | 1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 96.444 |
| 4 | 1 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | -1 | -1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 82.4 |
| 5 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 80.532 |
| 6 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 81.34 |
| 7 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 74.984 |
| 8 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 82.792 |
| 9 | 1 | -1 | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 89.944 |
| 10 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | -1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 90.752 |
| 11 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 83.394 |
| 12 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 84.204 |
| 13 | 1 | -1 | -1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 73.484 |
| 14 | 1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 70.292 |
| 15 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | -1 | -1 | 0.23 | 0.23 | 0.23 | 0.23 | 60.936 |
| 16 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.23 | 0.23 | 0.23 | 0.23 | 66.744 |
| 17 | 1 | 1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.62 | -0.77 | -0.77 | -0.77 | 92.891 |
| 18 | 1 | -1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.62 | -0.77 | -0.77 | -0.77 | 78.634 |
| 19 | 1 | 0 | 1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | 1.62 | -0.77 | -0.77 | 102.9 |
| 20 | 1 | 0 | -1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | 1.62 | -0.77 | -0.77 | 69.723 |
| 21 | 1 | 0 | 0 | 1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | 1.62 | -0.77 | 90.065 |
| 22 | 1 | 0 | 0 | -1.546 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | 1.62 | -0.77 | 80.493 |
| 23 | 1 | 0 | 0 | 0 | 1.546 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | -0.77 | 1.62 | 79.279 |
| 24 | 1 | 0 | 0 | 0 | -1.546 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | -0.77 | 1.62 | 91.404 |
| 25 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | -0.77 | -0.77 | 85.779 |
| 26 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | -0.77 | -0.77 | 85.78 |
| 27 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -0.77 | -0.77 | -0.77 | -0.77 | 85.776 |
对齿轮进行有限元分析时需添加啮合过程中摩擦热流量的分布值和端面的对流传热系数分布值这2个边界条件, 分析如下.
2.1 齿轮摩擦生热分析与计算主、从动轮啮合齿轮齿面的热流密度q1, q2分别为:
| ${{q}_{1}}=\frac{b{{w}_{1}}{{Q}_{C1}}}{2\pi {{v}_{C1}}},\text{ }{{q}_{2}}=\frac{b{{w}_{2}}{{Q}_{C2}}}{2\pi {{v}_{C2}}},$ |
式中:QC1, QC2分别为主、从动轮齿轮啮合面上啮合点处的瞬时热流输入量;w1, w2分别为主、从动轮角速度;vC1, vC2为主、从动轮在啮合点处的线速度;b为主、从动轮的齿宽.
| $\begin{array}{*{35}{l}} {{Q}_{C1}}=\beta {{Q}_{C}}=\beta \eta {{v}_{gC}}{{p}_{nC}}\times {{10}^{6}}, \\ {{Q}_{C2}}=\left( 1-\beta \right){{Q}_{C}}=\left( 1-\beta \right)\eta {{\mu }_{C}}{{v}_{gC}}{{p}_{nC}}\times {{10}^{6}}. \\ \end{array}$ |
主、从动齿轮齿面摩擦热流量的分配系数β为
| $\beta =\frac{\sqrt{{{\lambda }_{1}}{{\rho }_{1}}{{c}_{1}}{{v}_{C1}}}}{\sqrt{{{\lambda }_{1}}{{\rho }_{1}}{{c}_{1}}{{v}_{C1}}}+\sqrt{{{\lambda }_{2}}{{\rho }_{2}}{{c}_{2}}{{v}_{C2}}}},$ |
式中:η为摩擦能转换热能系数, 通常在0.9~0.95之间取值;μC为齿面间摩擦系数, 平均值为0.023;vC1, vC2分别为主、从动轮轮齿任意啮合点C处沿切线方向上的速度;vgC为主、从动轮在啮合点C处相对滑动速度;pnC为啮合点C处法向压力,
| ${{p}_{nC}}=\frac{\pi }{4}\sqrt{\frac{{{F}_{nC}}}{\pi \left( \frac{1-{{\nu }_{1}}^{2}}{{{E}_{1}}}+\frac{1-{{\nu }_{2}}^{2}}{{{E}_{2}}} \right)L}\cdot \frac{{{\rho }_{1C}}+{{\rho }_{2C}}}{{{\rho }_{1C}}{{\rho }_{2C}}}},$ |
式中:FnC为啮合齿面法向载荷, N;ν1, ν2为主、从动轮的泊松比;E1, E2为主、从动轮的弹性模量, MPa;L为齿轮啮合接触线长度, mm;ρ1C, ρ2C为主、从动轮在啮合点C处的曲率半径, mm, ρ1C=r1sin α±gyC, ρ2C=r2sin α±gyC, 主、从动轮不同接触点处的曲率半径是不同的[6, 13].
| ${{g}_{yC}}=\mp {{r}_{1}}sin\text{ }\alpha \pm \sqrt{{{({{r}_{1}}sin\text{ }\alpha )}^{2}}-{{r}_{1}}^{2}+{{r}_{C}}^{2}},$ |
式中:rC为啮合点主动轮半径, mm;r1为主动轮分度圆半径, mm;α为主、从动轮分度圆压力角, (°).
2.2 齿轮对流传热分析与计算主、从动轮啮合面的对流散热系数[14]为
| ${{h}_{t}}=\frac{\sqrt{\omega }}{2\pi }\sqrt{\lambda {{p}_{f}}{{c}_{f}}}{{\left( \frac{{{v}_{f}}{{H}_{C}}}{\gamma {{r}_{C}}} \right)}^{\frac{1}{4}}}{{q}_{tot}},$ |
式中:ω为主动轮或从动轮角速度;λ, pf, cf, vf, γ分别为润滑油热传导率、密度、比热、运动黏度和热扩散系数;HC为齿轮啮合点C处距齿轮最低端平面的高度;rC为主动或从动轮在啮合点C处的曲率半径;qtot为标准化冷却总量.
根据上述计算将边界条件添加在有限元分析中即可得主动轮齿轮本体最高温度响应值, 根据因素水平编码表, 依次分析得出y值, 如表 3所示.图 1为4个参数均在零水平下, 利用ANSYS有限元分析得出的主动轮齿轮本体最高温度响应值为85.779℃.

|
| 图 1 主动轮齿轮本体温度分布 Fig.1 Bulk temperature distribution of driving gear |
利用Design-Expert软件[15], 按照二次回归组合设计的试验点进行试验并对数据进行处理, 可得二次回归方程方差分析表, 如表 4所示.
| 差异源1) | 平方和SS | 自由度df | 均方MS | 比值F | p |
| x1 | 556.82 | 1 | 556.82 | 26.30 | 0.000 3 |
| x2 | 1 813.69 | 1 | 1 813.69 | 85.65 | <0.000 1 |
| x3 | 278.17 | 1 | 278.17 | 13.14 | 0.003 5 |
| X4 | 20.02 | 1 | 20.02 | 0.95 | 0.350 1 |
| X1X2Δ | 7.36 | 1 | 7.36 | 0.35 | 0.566 5 |
| X1X3Δ | 0.51 | 1 | 0.51 | 0.024 | 0.879 5 |
| X1X4Δ | 2.94 | 1 | 2.94 | 0.14 | 0.716 1 |
| X2X3 | 27.18 | 1 | 27.18 | 1.28 | 0.279 4 |
| X2X4 | 27.17 | 1 | 27.17 | 1.28 | 0.279 4 |
| X3X4Δ | 0.045 | 1 | 0.045 | 0.002 | 0.963 9 |
| X′1Δ | 9.40 | 1 | 9.40 | 0.44 | 0.517 9 |
| X′2Δ | 5.24 | 1 | 5.24 | 0.25 | 0627 8 |
| X′3 | 14.05 | 1 | 14.05 | 0.66 | 0.431 2 |
| X′4 | 13.40 | 1 | 13.40 | 0.63 | 0.441 8 |
| 回归 | 2 750.545 | 8 | 212.39 | 242.74 | |
| 剩余 | 25.495 | 18 | 1.416 | ||
| 误差 | 1.866 | 2 | 0.933 | ||
| 失拟 | 23.635 | 16 | 1.477 | 1.583 | |
| 总和 | 2 775.99 | 26 | |||
| 注:1) Δ表示将小于或接近实验误差平方和的各项回归平方和并入剩余平方和中. | |||||
回归系数检验临界值F0.25(1, 18) =1.41, F0.05(1, 18) =4.41, F0.01(1, 18) =8.29;方程显著性检验临界值F0.05(8, 18) =2.51, F0.01(1, 18) =8.28;方程拟合度检验临界值F0.25(16, 2) =3.42, F0.05(16, 2) =19.4, F0.01(16, 2) =99.4[12].
p值中, 如果p≤0.05 的项对y影响显著, p≤0.01的项对y影响极显著, p>0.5的项对y影响不显著, 一般将该项剔除, 重新计算.
由表 4可以看出, 失拟检验
方程为
| $\begin{array}{*{35}{l}} y=86.890+5.173{{x}_{1}}+9.337{{x}_{2}}+3.657{{x}_{3}}- \\ 0.981{{x}_{4}}+1.303{{x}_{2}}{{x}_{3}}+1.303{{x}_{2}}{{x}_{4}}- \\ 1.105x{{\prime }_{3}}-1.079x{{\prime }_{4}}. \\ \end{array}$ |
将
| $\begin{array}{*{35}{l}} y=-203.206+0.008{{z}_{1}}-0.665{{z}_{2}}+ \\ 11.879{{z}_{3}}+2.981{{z}_{4}}+0.021{{z}_{2}}{{z}_{3}}+ \\ 0.016{{z}_{2}}{{z}_{4}}-0.165{{z}_{3}}^{2}-0.104{{z}_{4}}^{2}, \\ \end{array}$ |
式中:z1为齿轮转速, z2为齿轮转矩, z3为齿轮齿宽, z4为齿轮压力角, y为齿轮本体最高温度响应值.
4 各因素重要性分析由表 4可以看出x1, x2, x3, x4的均方分别为556.82, 1 813.69, 278.17, 20.02, 所以影响齿轮最高温度响应值的四因素主次顺序依次为转矩、转速、齿宽、压力角.
从图 2各因素对齿轮最高温影响的变化趋势来看, 齿轮本体最高温度会随着齿轮的转速、转矩和齿宽增大而增大, 随着压力角增大而减小.

|
| 图 2 单因素效应分析 Fig.2 Effect analysis of single factor |
从图 3可以看出, 当齿轮的转速和转矩同时增加时, 齿轮表面温度增加;同时降低时, 齿轮表面温度降低.表明:适当降低齿轮的转速或转矩, 可在一定程度上减小齿轮表面的最高温度;齿轮转矩的变化对齿轮表面最高温度的影响较齿轮转速的大.

|
| 图 3 齿轮的转速与转矩对齿轮温度的影响 Fig.3 The influence of gear rotational speed and torque on the gear temperature |
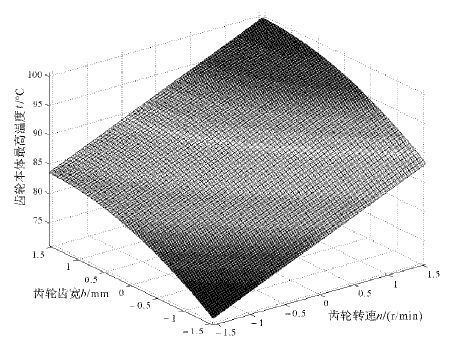
从图 4中可以看出, 增加齿轮转速或增加齿轮的齿宽时, 齿轮表面最高温度升高.表明:适当减小齿轮转速或减小齿轮的齿宽可在一定程度上减小齿轮表面的最高温度;齿轮转速的变化对齿轮表面最高温度的影响较齿轮齿宽的大.
|
| 图 4 齿轮的转速与齿宽对齿轮温度的影响 Fig.4 The influence of gear rotational speed and tooth width on the gear temperature |
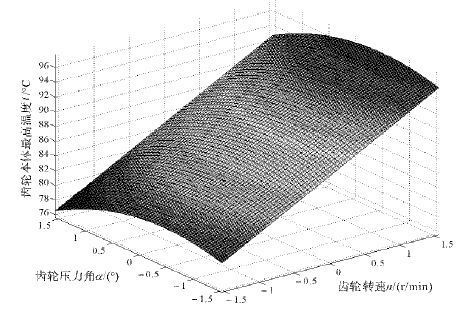
从图 5中可以看出, 增加齿轮转速或者减小齿轮压力角会使齿轮表面的温度增加.表明:适当增加齿轮的压力角可在一定程度上降低齿轮本体最高温度;轮齿转速的变化对齿轮表面最高温度的影响较齿轮压力角的大.
|
| 图 5 齿轮的转速与压力角对齿轮温度的影响 Fig.5 The influence of gear rotational speed and pressure angle on the gear temperature |
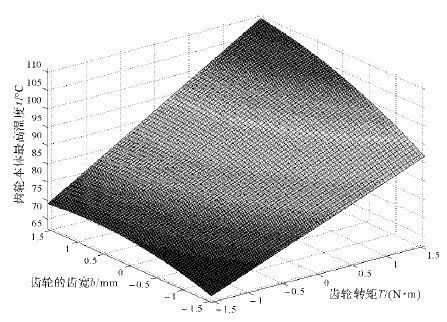
从图 6中可以看出, 增加齿轮转矩且增加齿轮齿宽时, 齿轮表面的最高温度升高.表明:减小齿轮转矩或者减小齿轮的齿宽可在一定程度降低齿轮表面的最高温度;齿轮转矩的变化对齿轮表面最高温度的影响较齿轮齿宽的大.
|
| 图 6 齿轮的转矩与齿宽对齿轮温度的影响 Fig.6 The influence of gear torque and tooth width on the gear temperature |
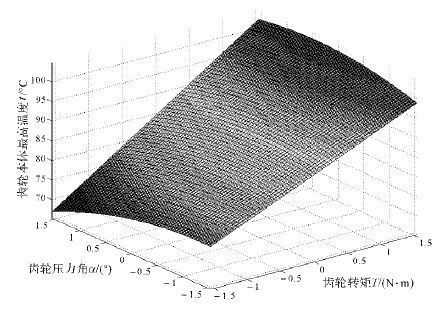
从图 7中可以看出, 增加齿轮转矩且减小齿轮压力角时, 齿轮表面的最高温度升高.表明:减小齿轮转矩或者增大齿轮的压力角可在一定程度降低齿轮表面的最高温度;齿轮转矩的变化对齿轮表面最高温度的影响较齿轮压力角的大.
|
| 图 7 齿轮的转矩与压力角对齿轮温度的影响 Fig.7 The influence of gear torque and pressure angle on the gear temperature |
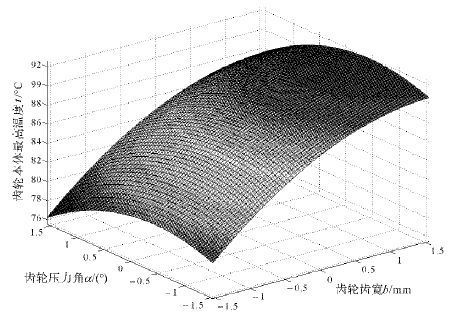
从图 8中可以看出:增加齿轮的齿宽且减小齿轮的压力角时, 齿轮本体的最高温度增加.表明:减小齿轮的齿宽或者增大齿轮的压力角可在一定程度上减小齿轮本体最高温度;齿轮齿宽的变化对齿轮本体最高温度的影响较齿轮压力角的大.
|
| 图 8 齿轮的齿宽与压力角对齿轮温度的影响 Fig.8 The influence of gear tooth width and pressure angle on the gear temperature |
1) x1, x2, x3, x4的均方分别为556.82, 1 813.69, 278.17, 20.02, 所以影响齿轮最高温度响应值的四因素主次顺序为齿轮的转矩、齿轮的转速、齿轮的齿宽和齿轮压力角.
2) 齿轮本体最高温度会随着齿轮的转矩、齿轮的转速和齿轮的齿宽增大而增大;齿轮本体最高温度随着齿轮压力角增大而减小.
3) 实际工程中为减小齿轮表面的最高温度, 在满足实际生产要求的前提下可适当减小齿轮的转速、齿轮的转矩、齿轮的齿宽或者增大齿轮压力角.
| [1] |
黄永晶, 阮文韬, 宫霞霞.
模糊神经网络技术在齿轮热分析中的应用[J]. 制造业自动化 , 2012, 34 (7) : 76–78.
HUANG Yong-jing, RUAN Wen-tao, GONG Xia-xia. The application of fuzzy neural network technology in gear thermal analysis[J]. Manufacturing Automation , 2012, 34 (7) : 76–78. |
| [2] |
孙首群, 朱卫光, 赵玉香.
渐开线轮齿温度场影响因素分析[J]. 机械设计 , 2009, 26 (2) : 59–62.
SUN Shou-qun, ZHU Wei-guang, ZHAO Yu-xiang. Involute gear temperature field influence factor analysis[J]. Journal of Mechine Design , 2009, 26 (2) : 59–62. |
| [3] |
何国旗, 严宏志, 胡威, 等.
面齿轮啮合过程中压力角对齿面摩擦生热的影响分析[J]. 中南大学学报(自然科学版) , 2012, 43 (9) : 3415–3419.
HE Guo-qi, YAN Hong-zhi, HU Wei, et al. Influence of pressure angle on friction heat during face-gear meshing process[J]. Journal of Central South University (Science and Technology) , 2012, 43 (9) : 3415–3419. |
| [4] |
陈磊, 马希直.
基于ANSYS的高速齿轮温度场研究[J]. 机械制造与研究 , 2009, 38 (2) : 110–112.
CHEN Lei, MA Xi-zhi. Temperature analysis of high speed gear based on ANSYS[J]. Journal of Machinery Manufacturing and Research , 2009, 38 (2) : 110–112. |
| [5] |
王胜伟, 何瑛, 何国旗, 等.
面齿轮啮合齿面瞬态温度场影响因素的仿真分析[J]. 湖南工业大学学报 , 2014, 5 (2) : 110–112.
WANG Sheng-wei, HE Ying, HE Guo-qi, et al. Surface gear mesh surface transient temperature field simulation analysis of influencing factors[J]. Journal of Hunan University of Technology , 2014, 5 (2) : 110–112. |
| [6] |
龙慧, 张光辉, 罗文军.
旋转齿轮瞬时接触应力和温度的分析模拟[J]. 机械工程学报 , 2004, 40 (8) : 24–29.
LONG Hui, ZHANG Guang-hui, LUO Wen-jun. Rotary gear instantaneous contact stress and temperature analysis of the simulation[J]. Journal of Mechanical Engineering , 2004, 40 (8) : 24–29. DOI:10.3901/JME.2004.08.024 |
| [7] |
刘彩霞, 孙振元, 刘军, 等.
利用二次回归正交设计优化香石竹叶片再生体系中6-BA和NAA的浓度组合[J]. 核农学报 , 2008, 22 (1) : 45–48.
LIU Cai-xia, SUN Zhen-yuan, LIU Jun, et al. Application of quadratic regressive orthogonal design to optimize regeneration system of dianthus caryophyllus L[J]. Journal of Nuclear Agricultural Sciences , 2008, 22 (1) : 45–48. |
| [8] |
工惠, 吴兆亮, 童应凯, 等.
应用二次回归正交旋转组合设计优化黄霉素发酵培养基[J]. 食品研究与开发 , 2006, 27 (6) : 19–24.
GONG Hui, WU Zhao-liang, TONG Ying-kai, et al. Optimization of the flavomycin fermentation medium by the design of rotation-regression-orthogonal combination[J]. Food Research and Development , 2006, 27 (6) : 19–24. |
| [9] |
朱彩平, 曹慧.
应用二次回归旋转正交组合设计提取平菇多糖的工艺研究[J]. 中药材 , 2010, 33 (9) : 1490–1494.
ZHU Cai-ping, CAO Hui. Application of quadratic regression orthogonal rotating combination design extraction mushroom polysaccharide technology was studied[J]. Journal of Chinese Medicinal Materials , 2010, 33 (9) : 1490–1494. |
| [10] |
马文杰, 郭玉蓉, 魏决.
应用二次回归旋转正交组合设计提取水溶性苹果多糖的工艺研究[J]. 食品科学 , 2009, 30 (20) : 105–108.
MA Wen-jie, GUO Yu-rong, WEI Jue. Optimization of water-soluble apple polysaccharides extraction using quadratic orthogonal rotation combination design[J]. Food Science , 2009, 30 (20) : 105–108. |
| [11] |
韩秀慧, 尹伟伦, 工华芳.
二次回归正交设计在微型月季组织培养中的应用[J]. 林业科学 , 2004, 40 (4) : 189–192.
HAN Xiu-hui, YI Wei-lun, GONG Hua-fang. Application of quadratic regressive factorial experiment to in vitro culture of miniature rose[J]. Scientia Silvae Sinicae , 2004, 40 (4) : 189–192. |
| [12] |
李志西, 杜双奎.
试验优化设计与统计分析[M]. 北京: 科学出版社 ,2010 : 226 -235.
LI Zhi-xi, DU Shuang-kui. Test optimization design and statistical analysis[M]. Beijing: Science Press , 2010 : 226 -235. |
| [13] | LONG H, LORD A A, GETHIN D T, et al. Operating temperatures of oil-lubricated edium-speed gears numerical models and experimental results[J]. Journal of Aerospace Engineering , 2003, 217 (2) : 87–106. |
| [14] |
龙慧.高速齿轮传动轮齿的温度模拟及过程参数的敏感性分析[D].重庆:重庆大学机械工程学院,2001:16-76.
LONG Hui.Modelling of surface temperature in high-speed gears and sensitivity analysis[D].Chongqing:Chongqing University, College of Mechanical Engineering, 2001:16-76. |
| [15] |
徐向宏, 何明珠.
试验设计与Design-Expert、SPSS应用[M]. 北京: 科学出版社 ,2010 : 146 -157.
XU Xiang-hong, HE Ming-zhu. The test design and the Design-Expert,SPSS application[M]. Beijing: Science Press , 2010 : 146 -157. |


