蠕变时效成形是一种将材料的人工时效和蠕变成形相结合的成形方法.这种方法是利用材料在一定温度下应力随时间减小而使部分弹性应变转化为塑性应变的特性,实现零件的成形并同时完成时效处理,大大改善了合金内部的微结构状态,提高了合金的强度[1].经过蠕变时效成形后的构件,往往具有残余应力小、产品精度高、材料机械性能好等特点.这种成形方法适用于可时效强化型合金的整体带筋和变厚度大曲率复杂外形和结构的整体壁板结构的成形制造,其被认为是下一代大型民用飞机建造过程中特别重要的金属成形工艺之一[2].但该方法在成形过程中弹性应变并不能完全转化为塑性应变,因此板料成形过后会出现回弹.为提高成形精度,需要对模具型面进行修正.目前,以有限元数值模拟技术为基础,蠕变时效成形的回弹预测和型面补偿研究已经广泛开展.
目前主要的回弹补偿方法有回弹向前法[3-4]、响应面法[5-7]和偏差调节法[8-9]等.Gan等[8]提出的偏差调节法(displacement adjustment method)将板料成形结束后的回弹量反向补偿到初始模具上,并以此构造出新模具型面,这种方法收敛速度快、适用范围广;甘忠等[10-11]通过线性函数、小波变换闭环控制等方法实现了蠕变时效成形的回弹补偿;刘大海等[12]应用有限元软件ABAQUS实现了筋板件的时效成形型面补偿;黄霖等[13]用偏差调节法实现了在时效成形中的模面修正.但板料上同一位置在回弹前后存在水平方向的位移[14],而偏差调节法仅将回弹量补偿到竖直方向.因此本文在其基础上,在蠕变时效成形的模面修正中考虑了水平方向的补偿,并用有限元模型进行验证.
1 考虑水平方向的补偿方案 1.1 偏差调节法偏差调节法由Wagoner提出,是一种基于有限元的迭代修正方法.其基本含义是在板料上取一定数量的节点,以节点为补偿对象,通过向回弹反方向移动节点的位置来构造新的模具型面,即:将成形回弹前后各节点的位移量加到回弹的反方向来确定新模具型面.在图 1中,以目标形状为模具,板料经过成形、卸载后出现回弹,与目标形状间有偏差,记为Δy.在构造新的模具时,将Δy加到节点的位置上,得到新的模具型面,然后板料用新模具进行成形.如果回弹后的形状仍然不能满足精度要求,则进行下一次迭代.
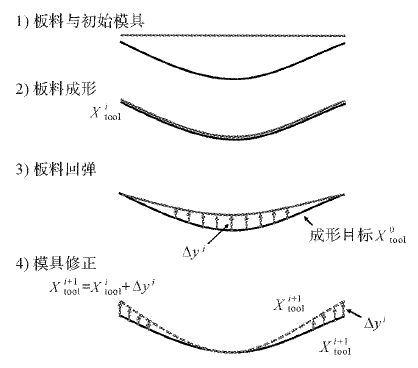
|
| 图 1 偏差调节法示意图 Fig.1 Diagram of displacement adjustment method |
图 1中,i表示迭代补偿次数,表示回弹后构件与成形目标型面Xtool0间的偏差,Xtooli表示第i次修正后得到的模具型面,得到Xtooli+1的过程可用下式表示:
| ${{X}_{tool}}^{i+1}={{X}_{tool}}^{i}+K\cdot \Delta {{y}^{i}},$ | (1) |
式中K为调整控制系数,其值一般取0.8~1.2,根据回弹率来确定.回弹量较大时,K取较大值,可提高回弹下降速度;回弹量较小时,K取较小值,可避免修正过度.
如图 2所示,设Y为目标型面的拱高,回弹大小的评价方法为
| ${S_P} = \frac{{\Delta y}}{Y} \times 100\% .$ | (2) |
式中SP为最大回弹量,当SP≤ε时,则视为构件满足精度要求.本文中ε=5%.
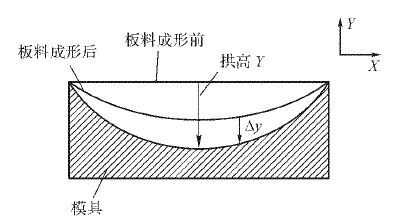
|
| 图 2 板料成形前后状态图 Fig.2 The state diagram of sheet before and after forming |
Wagnoer提出的偏差调节法将回弹量补偿到冲压成形的反方向,但未考虑回弹前后节点位置存在的水平方向偏移量.因此本文在Wagnoer的补偿法基础上,考虑在水平方向进行一定补偿,并检验其效果.
图 3中,根据等弧长原则,o,o′,o″分别为构件回弹前、回弹后及紧贴补偿后模具时同一节点的位置;oa是竖直方向,也是传统偏差调节法的补偿方向;ob是oo′的连线方向;oc是o点所在弧线的法线方向.本文选用连线方向补偿和法线方向补偿这2种考虑水平方向补偿的方案,分别对应图 3中ob和oc方向.连线补偿是将回弹量补偿到节点回弹前后位置的连线方向,即ob方向;法向补偿则是将回弹量补偿到回弹前该节点的法线方向上,即oc方向,每次补偿的大小为板料上同一节点回弹前后的距离.由于ob,oc与竖直方向夹角不同,所以2种补偿方案在水平方向的分量是不同的.
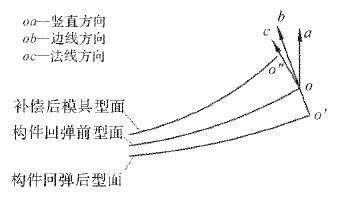
|
| 图 3 补偿方向示意图 Fig.3 Diagram of compensation direction |
选用2324铝合金板作为研究对象,其泊松比为0.33,弹性模量为68 GPa.
蠕变本构模型是反映金属蠕变行为的表达模型.目前描述金属蠕变行为的本构模型一般分为幂指数函数和双曲正弦函数两种基本形式.Kowalewski等[15]提出了幂指数函数形式的基于机理的单向受力条件下蠕变本构方程,其能够更好地描述金属蠕变行为的3个阶段:瞬时蠕变阶段、稳态蠕变阶段和加速蠕变阶段.其中第3阶段为金属蠕变速率快速升高直到材料发生断裂破坏.而蠕变时效成形过程中应力小、时间短,一般认为时效成形没有进入第3阶段.因此Huang等[16]在不考虑第3阶段的情况下,针对Kowalewski的蠕变损伤本构方程提出了更简化的本构模型.其本构形式如下:
| ${\begin{array}{*{20}{l}} {\dot \varepsilon = Asin{\rm{ }}h\left[ {B\left( {\sigma - {\sigma _0}} \right)\left( {1 - H} \right)} \right],}\\ {\dot H = h{\sigma ^m}\left( {1 - H{H^*}} \right).} \end{array}}$ | (3) |
通过标准蠕变试验获得2324铝合金在190 ℃下不同应力水平的蠕变应变数曲线.通过拟合,得到本构模型的参数如表 1[17].
| 参数 | 数值 |
| A | 1.42×10-6 |
| B | 0.04 |
| H* | 0.99 |
| h | 194.97 |
| m | -0.54 |
| σ0 | 17.98 |
在ABAQUS中建立板料和模具的有限元模型.板料采用可变形实体建模,尺寸为400 mm×80 mm×1.5 mm;模具的设计型面为半径为800 mm的圆柱面,并以此作为初始模具型面,设置为离散刚体,如图 4.

|
| 图 4 板料和模具的有限元模型 Fig.4 Finite element model of sheet and die |
分析过程为:
1) 加载.在板料上施加大小为1 MPa的均布载荷,使板料变形并贴紧模具表面,分析时间为1 s.
2) 保压.保持载荷不变,进行蠕变时效模拟.在此阶段,材料内部发生应力松弛,弹性应变转化为塑性应变,回弹量减小,分析时间为18 000 s (5 h).
3) 卸载.将施加在板料上的载荷作用解除,使板料自由回弹.
使用Newton-Cotes积分方法,采用Fortran语言将2324铝合金的蠕变本构方程编写成ABAQUS/Standard蠕变子程序(user subroutines,creep),在提交分析任务时调用,实现对蠕变时效过程的模拟.
3 不同方案的模面修正为对比不同补偿方案的效果,本文中取调整控制系数K=1.
3.1 第1次成形模拟以设计型面为初始模具进行第1次成形模拟.图 5为二分之一截面的分析结果,计算得出最大回弹量SP =41.8%,需要进行模具型面修正.

|
| 图 5 第1次成形前后板料状态 Fig.5 The states of sheet before and after the first forming |
使用偏差调节法进行模面修正,修正过程中仅将补偿量补偿到竖直方向.图 6为模面迭代修正的计算结果.可以看出经过5次修正,板料的最大回弹量为3.21%,满足精度要求.
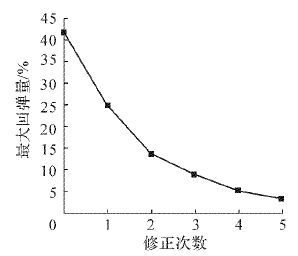
|
| 图 6 竖直方向补偿时的最大回弹量下降趋势 Fig.6 The downward trend of maximum SP by compensation in vertical direction |
使用考虑水平方向补偿的方案进行补偿.分别将第1次成形回弹前后各个节点在软件中的坐标输入计算程序中,得出修正后模具型面的节点坐标,构造出下一次成形的模具型面,然后进行成形模拟.表 2为使用第1次补偿后,3种补偿方向的最大回弹量,可以看出考虑了水平补偿的连线和法线方向补偿使回弹量下降更快.
| 补偿方向 | 最大回弹量 |
| 竖直方向 | 24.83% |
| 连线方向 | 19.81% |
| 法线方向 | 12.17% |
在第1次修正后继续进行修正,直到成形后构件最大回弹量在允许范围内.图 7为竖直方向、连线方向及法线方向补偿的最大回弹量下降趋势图.
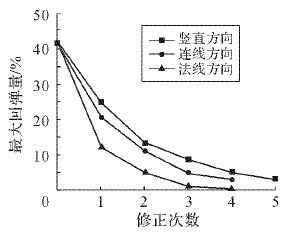
|
| 图 7 不同方向补偿的最大回弹量下降趋势 Fig.7 The downward trends of maximum SP by compensation in different directions |
图 7表明:连线方向补偿经过4次修正后构件就满足精度要求;而法线方向补偿只需要3次;第1次补偿时,法线方向补偿在水平方向的补偿分量最大,竖直方向补偿分量最小,经过第1次补偿后法线方向补偿的构件回弹量下降最为明显.
表 3表明,当构件经过最少次数的补偿均满足精度要求时,使用考虑水平方向补偿的方法得到的构件最大回弹更小,精度更高.
| 补偿方向 | 最大回弹量 |
| 竖直方向 | 3.21% |
| 连线方向 | 3.07% |
| 法线方向 | 0.58% |
本文将有限元方法、蠕变本构方程、数值模拟等方法运用到了蠕变时效成形的数值模拟及型面修正中.
1) 对偏差调节法进行了改进,考虑了水平方向补偿在模具型面修正中的作用.
2) 研究结果表明,考虑了水平方向补偿的方法比仅在竖直方向补偿具有更快的收敛速度;而且在构件满足精度要求时,利用法向补偿获得的构件的最大回弹量最小,精度较高.
3) 3种补偿方案的结果对比表明,水平方向补偿对回弹补偿效果有较大影响.
| [1] |
湛利华, 阳凌.
时效蠕变与时效应力松弛行为转换关系[J]. 塑性工程学报 , 2013, 20 (3) : 126–131.
ZHAN Li-hua, YANG Ling. Research on conversion relationship between aging reep and aging stress relaxation[J]. Journal of Plasticity Engineering , 2013, 20 (3) : 126–131. |
| [2] |
曾元松, 黄遐, 黄硕.
蠕变成形技术研究现状及发展趋势[J]. 塑性工程学报 , 2008, 15 (3) : 1–8.
ZENG Yuan-song, HUANG Xia, HUANG Shuo. The research situation and the developing tendency of creep age forming technology[J]. Journal of Plasticity Engin-eering , 2008, 15 (3) : 1–8. |
| [3] | KARAFILLIS A P, BOYCE M C. Tooling design in sheet metal forming using springback calculation[J]. International Journal of Mechanical Sciences , 1992, 34 (2) : 113–131. DOI:10.1016/0020-7403(92)90077-T |
| [4] | KARAFILLIS A P, BOYCE M C. Tooling design accommodating springback error[J]. Journal of Materials Processing Technology , 1992, 32 (1/2) : 499–508. |
| [5] | GUO Y Q, GATI W, NACEUR H, et al. An efficient DKT rotation free shell element for springback simulation in sheet metal forming[J]. Computer & Structur-es , 2002, 80 (27/30) : 2299–2312. |
| [6] | NACEUR H, GUO Y Q, BEN-ELECHI S. Response surface methodology for design of sheet forming parameters to control springback effects[J]. Computers and Structures , 2006, 84 (26/27) : 1651–1663. |
| [7] |
阮光明.
基于响应面法的DP800高强钢冲压回弹工艺参数优化[J]. 锻压技术 , 2015, 40 (4) : 40–44.
RUAN Guang-ming. Technological parameters optimization of springback for DP800 high strength steel based on response surface method[J]. Forming & Stamping Technology , 2015, 40 (4) : 40–44. |
| [8] | GAN W, WAGONER R H. Die design method for sheet springback[J]. International Journal of Mechanical Sciences , 2004, 46 (7) : 1097–1113. DOI:10.1016/j.ijmecsci.2004.06.006 |
| [9] | LINGBEEK R A, GAN W, WAGONER R H, et al. Theoretical verification of the displacement adjustment and springforward algorithms for springback compensation[J]. International Journal of Material Forming , 2008, 1 (3) : 159–168. DOI:10.1007/s12289-008-0369-5 |
| [10] |
甘忠, 庄振民, 黄官平.
基于传递函数的时效成形模具修正算法[J]. 塑性工程学报 , 2013, 20 (5) : 38–86.
GAN Zhong, ZHUANG Zhen-min, HUANG Guan-ping. Springback correction algorithm of age forming experiments based on transfer function[J]. Journal of Plasticity Engineering , 2013, 20 (5) : 38–86. |
| [11] |
甘忠, 冯爽, 钱志伟, 等.
基于小波变换闭环控制的时效成形回弹补偿[J]. 塑性工程学报 , 2015, 22 (1) : 111–118.
GAN Zhong, FENG Shuang, QIAN Zhi-wei, et al. Age forming springback compensation using wavelet transform based closed loop control[J]. Journal of Plasticity Engineering , 2015, 22 (1) : 111–118. |
| [12] |
刘大海, 黎俊初, 常春.
基于ABAQUS的筋板件时效成形型面回弹补偿算法[J]. 塑性工程学报 , 2012, 19 (6) : 74–78.
LIU Da-hai, LI Jun-chu, CHANG Chun. An ABAQUS-based springback compensation algorithm of die profile for creep age forming of ribweb parts[J]. Journal of Plasticity Engineering , 2012, 19 (6) : 74–78. |
| [13] |
黄霖, 万敏.
铝合金厚板时效成形回弹补偿算法[J]. 航空学报 , 2008, 29 (5) : 1406–1410.
HUANG Lin, WAN Min. Compensation algorithm for springback in age forming for aluminum alloy thick plate[J]. Acta Aeronautica et Astronautica Sinica , 2008, 29 (5) : 1406–1410. |
| [14] |
阳湘安,阮峰.模面几何修正的回弹补偿方向分析[J].塑性工程学报,2010,17(2)2:6-10.
YANG Xiang-an, RUAN Feng. Analysis on springback compensation direction for die-face adjustment[J]. Journal of Plasticity Engineering, 2010, 17(2):6-10. |
| [15] | KOWALEWSKI Z L, HAUHURST D R, DYSON B F. Mechansims-based creep constitutive equations for an aluminum alloy[J]. Journal of Strain Analysis , 1994, 29 (4) : 309–316. DOI:10.1243/03093247V294309 |
| [16] | HUANG L, WAN M, CHI C L, et al. FEM analysis of springback in age forming for aluminum alloy plate[J]. Chinese Journal of Aeronautics , 2007, 20 (6) : 564–569. DOI:10.1016/S1000-9361(07)60083-1 |
| [17] |
黄硕, 曾元松, 黄遐.
2324铝合金蠕变时效成形有限元分析[J]. 塑性工程学报 , 2009, 16 (4) : 129–133.
HUANG Shuo, ZENG Yuan-song, HUANG Xia. FE analysis of creep age forming for Aluminum alloy 2324[J]. Journal of Plasticity Engineering , 2009, 16 (4) : 129–133. |



